1 Introduction

As an unconventional natural gas resource, shale gas has attracted a considerable amount of attention because it is clean, efficient and abundant (Faraj et al. 2004; Jarvie et al. 2007; Owolabi et al. 2013; Liu et al. 2021b). The verified recoverable shale gas resources in the major basins of China total approximately 3.1 × 1013 m3, accounting for 14.3% of the technically recoverable shale gas reserves in the world (Zhang et al. 2008; Zou et al. 2010). Shale gas basins in China are typically composed of hard and brittle shale and characterized by large burial depths and complex geological conditions. The mechanical properties of shale masses are affected by both sedimentary bedding and natural fractures and are therefore more complex than those of other rock masses; additionally, these features contribute to the frequent occurrence of borehole wall collapse during drilling (Liu et al. 2019; Wang et al. 2012). Improvement in the accurate measurement of mechanical properties is therefore of great theoretical and practical significance for shale gas exploration and general development.

The bedded characteristics of shale resulting from a preferred orientation of the deposited clay minerals lead to the significant anisotropy of shale (Khan et al. 2012; Li et al. 2019). Many studies have focused on measuring the mechanical properties of shale with anisotropy relative to the bedding plane (Cho et al. 2012; Dewhurst and Siggins 2006; Hou et al. 2016; Kuila et al. 2011; Lora et al. 2016). In these studies, shale cores were prepared as standard cylindrical samples with different bedding angles. Uniaxial and triaxial compression experiments have also been conducted, from which scholars have analyzed the effect of the bedding plane direction on shale mechanics and established anisotropic constitutive equations for shale.

Natural fractures affect the recovery of fractured oil and gas reservoir; thus, their characteristics and geological genesis have always been closely considered during well planning (Lamarche et al. 2012; Larsen and Gudmundsson 2012). Scholars have carried out geological surveys and research on the characteristics of natural fractures in shale gas reservoirs, including outcrop investigations, core analyses, image log analyses, seismic detection (Lamarche et al. 2012; Cobbold et al. 2013; Engelder et al. 2009; Gale et al. 2014; Hennings et al. 2000) and geostatistical analyses, which were integrated to construct discrete fracture networks (DFNs) to estimate reservoirs and plan the development of shale gas (Akbarnejad-Nesheli et al. 2012; Emsley et al. 2014). New numerical calculation models have been subsequently developed to evaluate the fracturing effect of hydraulic cracks encountering natural fractures (Cohen et al. 2017; Taleghani et al. 2018; Weng et al. 2011). Consequently, determining the natural fracture characteristics during shale reservoir surveys is an essential task in shale gas resource exploration and development engineering.

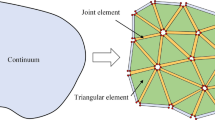
As mentioned above, a considerable amount of work has been perfomred to study the effects of bedding or natural fractures on shale reservoirs; however, few studies have investigated the combined effects of both bedding and natural fractures on the mechanical properties of shale masses. There are many methods to determine rock mass parameters (Wang and Zheng 2015); for example, a DFN based on Monte Carlo stochastic theory can generate joint sets using statistical parameters obtained from measured fractures, which are used to determine rock structural planes and rock block geometry parameters (Yu et al. 2007). Min and Jing (2003) used the discrete element method (DEM) to calculate the representative elementary volume (REV) of fractured rock masses and obtained the equivalent parameters of fractured rock masses. Baghbanan and Jing (2008) developed a DEM model to correlate the fracture length and aperture for determining the REV rock mass from the perspective of rock penetration and evaluated stress effects on permeability. Kulatilake et al. (1992) introduced "fictitious joints" and combined DFN simulation technology with the DEM to analyze the mechanical properties of rock masses containing nonpenetrating joints. Currently, DFN codes have been embedded in the main 3DEC program, which can be used to easily construct a DEM fracture model for further performing mechanical analysis (Itasca Consulting Group Inc. 2013). The DEM method provides a good foundation for studying the mechanical properties of rock masses with fractures. However, Wu (2012) proposed that the deformation parameters of fictitious joints impact the deformation characteristics of the DEM model; thus, analytical equations have been theoretically derived to determine the normal stiffness and shear stiffness of fictitious joints considering the effect of model size, stress boundary condition and geometry distribution of fictitious joints. The proposed fictitious joint parameters of the rock mass were based on the isotropic constitutive equation, which are only applicable to homogeneous matrices. To simulate bedded shale masses with natural fractures, calculating the parameters of fictitious joints based on the transversely isotropic constitutive equation is still needed.

The objective of this study is to establish a DEM for bedded shale masses containing natural fractures, which solves the key issue in 3-DEM numerical simulations of bedded shale masses. The proposed DEM can be used to evaluate the REV of a shale mass. During the course of this study, field measurements of natural fractures in the Shihuigou area of the Carboniferous system, Qaidam Basin (Zhang et al. 2016), are used to develop the DFN and DEM models. Various sample sizes and key mechanical properties are examined to evaluate their dependence on the sample sizes, thus identifying the optimal REV of the shale mass for reliable mechanical property measurements. This study will provide a necessary modeling basis for analyzing and discussing the mechanism of wellbore instability in shale gas reservoirs.

2 Natural fractures and bedding of the Carboniferous shale in the eastern Qaidam Basin

2.1 Characteristics of the natural fractures in the Carboniferous shale outcrop in the eastern Qaidam Basin

The Qaidam Basin, located in the northern Qinghai-Tibet Plateau and rich in oil and gas resources, is a large oil-and-gas-bearing basin in Western China. Oil sands have also been discovered in Carboniferous strata, indicating that the eastern Carboniferous strata in the basin have a certain hydrocarbon-generation potential (Li et al. 2014). The Carboniferous shale in this area is more developed, has a moderate maturity and is unmetamorphosed, demonstrating that this area is extremely favorable for shale gas exploration (Chen et al. 2021; Liu et al. 2021a, b).

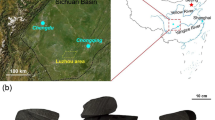
This study selected the measured fracture data (Zhang et al. 2016) from a typical Carboniferous shale outcrop in the Shihuigou area of the eastern Qaidam Basin as the basis for establishing a fracture network model and a discrete element numerical model. As shown in Fig. 1, the selected outcrop with geographical coordinates of longitude 37°23′54.57″N and latitude 96°06′05.06″E is of the Carboniferous Hurleg Formation shale. The shale outcrop is yellowish-brown with an underlying black coal seam, the thickness of which is approximately 50 cm. The outcrop profile is 3.2 m in length and 1.4 m in height, and the formation occurrence is 6°∠46°, with an average foliation spacing of approximately 10 mm. Sixty-seven fractures were measured in the outcrop. Some of these fractures are shown in Fig. 1: the fractures are horizontal, and some are filled with calcite. The measured fractures were statistically analyzed and grouped, and the corresponding pole diagram is shown in Fig. 2. After grouping, the Fisher distribution function was selected to fit the geometric distribution of fractures in each group, and the unknown parameters in the distribution function were determined. At the same time, geometric parameters such as the average tendency and inclination, trace length, and density of each group of fractures in the outcrop profile were calculated, as shown in Table 1. The results show that the occurrence of fractures can be roughly divided into two groups: one set of 46 fractures with low dips and NW–SE strikes, and another set of 21 fractures with low dips and nearly NW–SE strikes. The minimum crack length of the observed outcrop is 5 cm, and the maximum is 100 cm. Crack lengths of 10–20 cm account for 26%, whereas crack lengths of 20–30 cm account for 31%. The mean length of the fractures in the simulation is approximately 30 cm, and the fractures are mainly tectonic fractures. Observations of the fractures from a core obtained from the study area (Li and Yu 2017) revealed that some of the fractures were filled with calcite, whereas others remained open; thus, these fractures can affect the mechanical properties of the rock mass.

Fig. 1
figure 1

Shale outcrop of the Carboniferous Hurleg Formation in the eastern Qaidam Basin (Zhang et al. 2016)

Full size image
Fig. 2
figure 2

Pole diagram of the measured fractures

Full size image
Table 1 Statistical parameters of the fractures in the outcrop of the Carboniferous Hurleg Formation shale in the Shihuigou area
Full size table

The fractures observed on the outcrop were reconstructed as a 3-D fracture network model by using the DFN approach. Based on the statistical law of the geometric parameters of the fractures (Table 1), the number of joints was converted to joint density, and the occurrence of joints was simulated using the distribution function. The probability distribution of various structural plane information in the DFN model was consistent with the actual situation. Figure 3a shows the 3-D fracture network model using a DFN. The dimensions of the 3-D fracture network model were 5 m × 5 m × 5 m, which was larger than the measured outcrop scale. To verify the rationality of the established model, horizontal and vertical sections were cut out from the established model, as shown in Fig. 3b–e, and 3 random measurement lines were arranged in the sections. The linear density and the mean trace length of the simulated joints along each measurement line were calculated. The data from the three lines were averaged and compared with the linear density and average trace length of the measured fractures. The results are shown in Table 2. The density and trace length of a measured fracture were very close to those of the simulated fracture. The established 3-D fracture network model of shale can output geometric parameter information that closely replicates the actual fractures in a shale formation, laying the foundation for the establishment of other discrete element numerical models of fractures in shale reservoirs.

Fig. 3
figure 3

A 3-D fracture network model and profiles of the outcrop of the Carboniferous Hurleg Formation shale in the eastern Qaidam Basin

Full size image
Table 2 Comparison of the measured and simulated data of the fractures in the shale outcrop in the Shihuigou area
Full size table

2.2 Bedding characteristics of the Carboniferous shale in the eastern Qaidam Basin

The bedding of Carboniferous shale in the eastern Qaidam Basin is generally well developed, and the strata contain a large amount of mica and common plant fossils. Banded and granular pyrite is often found in shales (Li and Yu 2017). Figure 4a–d shows the bedding characteristics of the Carboniferous Hurleg Formation shale in the Qaidam Basin, which is dominated by massive bedding (Fig. 4a) and tidal bedding (Fig. 4b–d).

Fig. 4
figure 4

Structural characteristics of the Carboniferous Hurleg Formation shale (from the Chaiye 2 well) (Li and Yu 2017)

Full size image

The experimental and numerical simulation results show that the transversely isotropic constitutive model can be used to characterize the properties of shale formations (Kanfar et al. 2015; Zhou et al. 1992; Hou et al. 2015). The transversely isotropic constitutive stress–strain relationship satisfies formula (1), in which there are five independent elastic constants: Ex and μx are the elastic modulus and Poisson's ratio of the parallel transversely isotropic plane, respectively; Ez and μz are the elastic modulus and Poisson's ratio of the vertical isotropic plane, respectively; and Gz is the shear modulus in the vertical bedding direction.

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{zx} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{x} }}} & { - \frac{{\mu_{x} }}{{E_{x} }}} & { - \frac{{\mu_{z} }}{{E_{z} }}} & 0 & 0 & 0 \\ { - \frac{{\mu_{x} }}{{E_{x} }}} & {\frac{1}{{E_{x} }}} & { - \frac{{\mu_{z} }}{{E_{z} }}} & 0 & 0 & 0 \\ { - \frac{{\mu_{z} }}{{E_{z} }}} & { - \frac{{\mu_{z} }}{{E_{z} }}} & {\frac{1}{{E_{z} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{{E_{x} }}{{2\left( {1 + \mu_{x} } \right)}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{1}{{G_{z} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{1}{{G_{z} }}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ {\tau_{xy} } \\ {\tau_{yz} } \\ {\tau_{zx} } \\ \end{array} } \right\}$$
(1)

Batugin and Nirenburg obtained the solution of the shear modulus perpendicular to the isotropic plane by mathematical methods (Batugin and Nirenburg, 1972), as shown in Eq. (2).

$$G_{z} = \frac{{E_{x} E_{z} }}{{E_{x} + E_{z} + 2\mu_{z} E_{x} }}$$
(2)

3 3-D discrete element calculation model for shale masses

In the following section, a 3-D discrete element model considering the statistical analysis results of bedded shale containing natural fractures is constructed, and the size effect of rock mechanics parameters is evaluated.

3.1 Determination of the REV

To determine the REV of a shale mass under the combined action of natural fractures and bedding, it is necessary to cut the established 5 m block into smaller blocks. The dimensions of these smaller cubic blocks are 0.8, 1.2, 1.6, 2.0, 2.4, 2.8, 3.2, and 3.6 m, respectively. After the scope of the REV is basically determined, more accurate blocks can be cut out in the reduced scope to determine the size of the REV. The mechanical properties of the blocks are affected by the different geometrical distributions of the fractures in different positions, and the influence is especially obvious when the block size is smaller. To improve calculation precision and reduce error, we performed calculations at five different positions in each block model and then took the mean mechanical parameters as the final result. Figure 5 shows the five positions in the 0.8 m blocks.

Fig. 5
figure 5

Block selections at different locations (\(0.8\,{\text{m}} \times 0.8\,{\text{m}} \times 0.8\,{\text{m}}\))

Full size image

3.2 Parameters of the discrete element numerical model

  1. (1)

    Transversely isotropic constitutive parameters

The ratio of the elastic modulus in the parallel bedding direction to that in the vertical bedding direction was defined as the anisotropy ratio \(k\). In this study, \(k\) was set to 0.5, 1.0, 1.5 and 2.0; hence, \(E_{x} = 0.5\, E_{z},\, E_{x} = 1.0\, E_{z},\, E_{x} = 1.5\, E_{z} ,\;{\text{and}}\;E_{x} = 2\, E_{z}\). The influence of different \(k\) values on the compressive strength, elastic modulus, shear strength and volume modulus of shale with natural fractures were studied. The relevant parameters of the transversely isotropic shale were reasonably selected, as shown in Table 3.

  1. (2)

    Parameters of actual and fictitious joints

Table 3 Transversely isotropic constitutive parameters for shale
Full size table

Geological measurements indicate that nonpenetrating joints widely exist in shale masses. In the discrete element numerical simulation program, a DFN can include fictitious joints combined with nonpenetrating joints to generate polyhedral blocks, which can be recognized by DEM. The natural fracture network model of the shale mass in the study area was established with the DFN method in Sect. 1.1, the fractures of which can be assigned to the parameters according to the literature (Wu and Kulatilake 2012), as shown in Table 4. Parameters also need to be assigned to the fictitious joints. The main parameters of fictitious joints include normal stiffness and tangential stiffness. A new calculation method suitable for transversely anisotropic shale should be established because the current assignment method for fictitious joints is applicable to only certain rocks such as granite.

Table 4 Actual and fictitious joint parameters
Full size table

Biaxial compression mechanical models with fictitious joints were established first, as shown in Fig. 6. The horizontal ground stress was \(\sigma_{2}\), and vertical the ground stress was \(\sigma_{1}\). In the model, the angle between the transversely isotropic plane and the vertical direction was α, whereas the angle between the transversely isotropic plane and the horizontal direction was β. According to the theory of elastic mechanics, the relationship between the elastic modulus \(E_{\alpha }\) and Poisson's ratio \(v_{\alpha }\) of the stratified shale with a bedding dip angle of α and the vertical deformation \(\Delta L_{{\text{V}}}\) and horizontal deformation \(\Delta L_{{\text{H}}}\) of the model without fictitious joints can be expressed with Eqs. (3), (4) and (5).

$$E_{\alpha } = \frac{1}{{\frac{1}{{E_{1} }}\sin^{4} \alpha + \left( {\frac{1}{{G_{2} }} - \frac{{2v_{2} }}{{E_{2} }}} \right)\sin^{2} \alpha \cos^{2} \alpha + \frac{1}{{E_{2} }}\cos^{4} \alpha }}$$
(3)
$$v_{\alpha } = - \left[ {\left( {\frac{1}{{E_{1} }} + \frac{1}{{E_{2} }} + \frac{{2v_{2} }}{{E_{2} }} - \frac{1}{{G_{2} }}} \right)\sin^{2} \alpha \cos^{2} \alpha - \frac{{v_{2} }}{{E_{2} }}} \right]E_{\alpha }$$
(4)
$$\Delta L_{{\text{V}}} = \frac{{\sigma_{1} L_{1} }}{{E_{\alpha } }} - \frac{{\sigma_{2} L_{1} }}{{E_{\beta } }}\nu_{\beta } ;\;\Delta L_{{\text{H}}} = \frac{{\sigma_{2} L_{2} }}{{E_{\beta } }} - \frac{{\sigma_{1} L_{2} }}{{E_{\alpha } }}\nu_{\alpha }$$
(5)
Fig. 6
figure 6

Mechanical model with fictitious joints

Full size image

The vertical deformation \(S_{{\text{v}}}\) and horizontal deformation \(S_{{\text{h}}}\) generated with a single fictitious joint can be calculated by Eq. (6), where \(K_{{\text{n}}} \;{\text{and}}\;K_{{\text{s}}}\) are the normal stiffness and tangential stiffness of the fictitious joint, respectively.

$$S_{{\text{v}}} = \frac{{\sigma_{2} \cos^{2} \varphi + \sigma_{1} \sin \varphi \cos \varphi }}{{K_{{\text{n}}} }} + \frac{{\sigma_{2} \sin \varphi \cos \varphi + \sigma_{1} \sin^{2} \varphi }}{{K_{{\text{s}}} }};\; S_{{\text{h}}} = \frac{{\sigma_{1} \cos^{2} \varphi + \sigma_{2} \sin \varphi \cos \varphi }}{{K_{{\text{n}}} }} - \frac{{\sigma_{1} \sin \varphi \cos \varphi - \sigma_{2} \cos^{2} \varphi }}{{K_{{\text{s}}} }}$$
(6)

The rock mass deformation error \(\eta\) caused by the fictitious joints is defined as the ratio between \(S_{{\text{v}}}\) (\(S_{{\text{h}}}\)) and \(\Delta L_{{\text{V}}} (\Delta L_{{\text{H}}} )\), as shown in Eq. (7).

$$\eta = \frac{{S_{{\text{v}}} }}{{\Delta L_{{\text{V}}} }};\;\eta = \frac{{S_{{\text{h}}} }}{{\Delta L_{{\text{H}}} }}$$
(7)

Equations (3)–(7) can be combined to form Eq. (8), which is an expression of the normal stiffness and shear stiffness of a single fictitious joint; in this formula, a, b, c and d are parameters related to the boundary stress and joint inclination and are introduced for the convenience of calculation.

$$K_{{\text{n}}} = \frac{{a + \frac{b*c}{d}}}{{\eta \left( {\Delta L_{{\text{V}}} - \frac{b}{a}\Delta L_{{\text{H}}} } \right)}};\;K_{{\text{s}}} = \frac{d}{{\frac{c}{{K_{{\text{n}}} }} - \eta \Delta L_{{\text{H}}} }}$$
(8)
$$\begin{aligned} & a = \sigma_{2} \cos^{2} \varphi + \sigma_{1} \sin \varphi \cos \varphi \;b = \sigma_{1} \sin^{2} \varphi + \sigma_{2} \sin \varphi \cos \varphi \\ & c = \sigma_{1} \cos^{2} \varphi + \sigma_{2} \sin \varphi \cos \varphi \;d = \sigma_{1} \sin \varphi \cos \varphi - \sigma_{2} \cos^{2} \varphi \\ \end{aligned}$$
(9)

Suppose the model contains N fictitious joints with inclination angles of φ1, φ3,…, φN. In this case, the total error caused by the fictitious joint is equal to the sum of the error values caused by a single fictitious joint, as shown in Eq. (10), where \(\eta_{i}\) is the deformation error caused by the ith joint.

$$\eta_{{{\text{sum}}}} = \eta_{1} + \eta_{2} + \cdots + \eta_{i} + \cdots + \eta_{{N}}$$
(10)

To facilitate the calculation, the average error \(\eta_{{{\text{avr}}}}\) is introduced, wherein \(\eta_{{{\text{avr}}}} = \eta_{{{\text{sum}}}} /N\). Equation (11) expresses the normal stiffness and tangential stiffness when the deformation of the ith fictitious joint satisfies the error limit condition.

$$K_{\text{n}i} = \frac{{N\left( {a_{i} + \frac{{b_{i} *c_{i} }}{{d_{i} }}} \right)}}{{\eta_{{{\text{sum}}}} \left( {\Delta L_{{\text{V}}} - \frac{{b_{i} }}{{a_{i} }}\Delta L_{{\text{H}}} } \right)}};\;K_{\text{s}i} = \frac{{Nd_{i} }}{{\frac{Nc}{{K_{{\text{n}}} }} - \eta_{{{\text{sum}}}} \Delta L_{{\text{H}}} }}$$
(11)

If there are many nonpenetrating joints in the rock mass, it is unrealistic to assign fictitious joints individually. Therefore, Eq. (12) can be used to approximate the normal stiffness and tangential stiffness of the fictitious joints in bedded shale from the mean values of the deformation parameters of each fictitious joint.

$$K_{{\text{n}}} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} K_{{{\text{n}i}}} }}{N} = \mathop \sum \limits_{i = 1}^{N} \frac{{a_{i} + \frac{{b_{i} *c_{i} }}{{d_{i} }}}}{{\eta_{{{\text{sum}}}} \left( {\Delta L_{{\text{V}}} - \frac{{b_{i} }}{{a_{i} }}\Delta L_{{\text{H}}} } \right)}};\;K_{{\text{s}}} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} K_{{{\text{s}i}}} }}{N} = \mathop \sum \limits_{i = 1}^{N} \frac{{d_{{\text{i}}} }}{{\frac{{N\text{c}_{{i}} }}{{K_{{{\text{n}i}}} }} - \eta_{{{\text{sum}}}} \Delta L_{{\text{H}}} }}$$
(12)

From Eq. (12), the normal stiffness and shear stiffness of the fictitious joints under different anisotropy ratios and different bedding angles are calculated, and the results are shown in Table 5. Kn and Ks of the fictitious joints change with changes in the bedding angle, block size and anisotropy ratio, which lays the foundation for subsequent simulation work.

Table 5 Parameters of the fictitious joints at different bedding angles and anisotropy ratios
Full size table

3.3 Test schemes

Three different numerical loading paths were designed to calculate the compressive strength, deformation modulus, shear modulus and volume modulus of the shale mass, which were realized by using the built-in Fish language in 3DEC.

Figure 7 shows the loading schematic diagrams of the numerical simulation for the uniaxial compression, pure shear, and triaxial compressive tests, respectively. For each loading scheme, compressive stresses σx, σy, and σz that are far less than the compressive strength are first applied in the vertical direction of blocks X, Y and Z to keep the blocks in a stable state, and then the boundary stress is kept unchanged. Subsequently, the loading is applied in the Z direction at a displacement rate of 0.01 m/s until the model fails in the uniaxial compression test. The loading is applied to any adjacent block surface at a displacement rate of 0.01 m/s in the pure shear test. Additionally, the loading is applied in the three principal directions at a displacement rate of 0.01 m/s in the triaxial compressive test.

Fig. 7
figure 7

Schematic diagram of the numerical test (Wu and Kulatilake 2012)

Full size image

Monitoring points were arranged on the block surface to record the displacement and stress in the block during the loading process, and these recorded data were used to draw the stress–strain curve. During the loading process, the stress distribution at each point on the block surface was not uniform, which introduces substantial error into the calculation results. To reduce the error, different numbers of monitoring points were set up according to the block size to monitor the stress and strain in the block. Figure 8 shows the layout diagrams of the monitoring points when the block size was L = 0.5–1.0 m, L = 1.0–2.0 m, and L = 2.0–5.0 m, respectively.

Fig. 8
figure 8

Schematic diagram of the monitoring points in blocks of different sizes

Full size image

4 Results and analysis from the 3-D discrete element numerical simulations of a shale mass

Figure 9 shows the uniaxial compressive stress–strain curves, shear stress–strain curves, and volumetric stress–strain curves of the block (\(0.8\,{\text{m}} \times 0.8\,{\text{m}} \times 0.8\,{\text{m}}\)), respectively. On this basis, the compressive strength, deformation modulus, shear strength and volume modulus of shale blocks with different sizes, anisotropy ratios and bedding angles can be obtained.

Fig. 9
figure 9

Stress–strain curve from the discrete element numerical simulation (K = 1.0, θ = 45°)

Full size image

4.1 Influence of different anisotropy ratios on the REV of a shale mass

The variation in the mechanical parameters of the shale blocks with respect to different anisotropy ratios and block sizes under the same bedding angle is shown in Fig. 10. The results show that with increasing anisotropy ratio, the compressive strength, deformation modulus, bulk modulus and shear modulus of the block increase. At the same anisotropy ratio, these parameters gradually decrease as the block size increases until they stabilize. The size of the block that allows this stability is regarded as the REV. When the anisotropy ratio is 1 (i.e., \(E_{{\text{h}}} = E_{{\text{v}}}\)), the sizes of the REV determined by the four parameters are the smallest. In this case, the block can be approximately regarded as homogeneous, and the size of the REV is under the influence of only the action of natural fractures. When the anisotropy ratio is not 1 (i.e., \(E_{{\text{h}}} \ne E_{{\text{v}}}\)), the size of the REV increases.

Fig. 10
figure 10

Variations in mechanical parameters with respect to the anisotropy ratio and block size under the same bedding angle

Full size image

As the anisotropy ratio changes from 2.0 to 0.5 to 1.5 (i.e., \(E_{{\text{h}}} = 2.0E_{{\text{v}}}\), \(E_{{\text{h}}} = 0.5E_{{\text{v}}}\), and \(E_{{\text{h}}} = 1.5E_{{\text{v}}}\)), the size of the REV determined by the four parameters decreases successively. For \(E_{{\text{h}}} = 2.0E_{{\text{v}}}\) and \(E_{{\text{h}}} = 0.5E_{{\text{v}}}\), the anisotropy degrees of the block are similar and strong. In this case, the homogenization process of the block requires a greater number of fractures, so the corresponding REV size is larger. The anisotropy degree of \(E_{{\text{h}}} = 1.5E_{{\text{v}}}\) is smaller than that of the first two, leading to a slightly smaller REV.

4.2 Influence of the shale bedding angle on the mechanical parameters and REV of a shale mass

The variations in the mechanical parameters (compressive strength, deformability modulus, bulk modulus, and shear modulus) of a shale mass with respect to the bedding angle and block size under the same anisotropy ratio are shown in Fig. 11. The mechanical parameters of each block gradually decrease with increasing block size at different bedding angles until they become stable. For the same mechanical parameters of a rock mass, as long as the anisotropy ratio is constant, the REV size does not substantially change with changes in the bedding angle. We speculated that the block will contain more fractures as the block size increases, which makes the block exhibit a homogeneous state and weakens the influence of stratigraphic anisotropy on the size of the REV. Comparing the influence of different bedding angles on various parameters, it was found that regardless of the anisotropy ratio, various parameters corresponding to a 45° bedding angle under each block size are the smallest. This may be due to the average orientation of natural fractures in the simulated shale mass being approximately 40°, which is close to the bedding angle of 45°. The combined effects of bedding and natural fractures greatly weaken the properties of a rock mass.

Fig. 11
figure 11

Variation in the mechanical parameters with respect to the bedding angle and block size under the same anisotropy ratio

Full size image

By comparing each of the four panels in Fig. 11, in which the same mechanical parameter is assessed under different anisotropy ratios, we found that the greater the anisotropy ratio is, the more obvious the influence of the bedding angle on the mechanical properties of the block.

5 Discussion

In this research, the DEM was used to evaluate the mechanical properties of shale under the combined action of fracturing and bedding. Compared with the method that analyzes shale mechanical properties from a microscopic perspective, this method analyzes the overall shale mechanical parameters from a macroscopic perspective. The numerical experimental results in this paper show that the mechanical parameters of the block basically change in the range of 0.8–2.0 m, 0.8–2.6 m, 0.8–2.8 m and 0.8–3.0 m at different anisotropy ratios. When the block size is larger than the critical size, these parameters do not change significantly. It was determined that the REV size of the rock mass is approximately 2.0–3.0 m. When the numerical model size is larger than the REV, the fractured rock mass discontinuities can be transformed into equivalent continuities. The results of this study illustrate that the anisotropy ratio of shale has a great influence on the size of the REV, which must be considered when determining the size of the REV for bedding shale.

When using the equivalent continuity numerical simulation method, the mechanical parameters of the REV can be used to analyze the stability of a shale borehole wall. Figure 12 shows the distribution of the four REV parameters (compressive strength, deformability modulus, bulk modulus, and shear modulus). Figure 12 shows that for each bedding angle, the mechanical parameters of the equivalent rock mass are the smallest when the anisotropy ratio is 0.5. The mechanical parameters of the equivalent rock mass increase as the anisotropy ratio increases, and the mechanical parameters reach the largest values when the anisotropy ratio is 2.0. The results indicate that the mechanical properties of the shale bedding matrix have an important influence on the mechanical parameters of the entire rock mass.

Fig. 12
figure 12

Mechanical parameters under different anisotropy ratios and bedding angles

Full size image

Under the same anisotropy ratio, the mechanical parameters (compressive strength, deformability modulus, bulk modulus, shear modulus) of the REV at a bedding angle of 45° are the smallest. Similar to the previous analysis, because the 45° bedding angle was close to the natural fracture orientation, the mechanical parameters of the REV lowered more at this angle. When the anisotropy ratio is 0.5, which was close to the actual situation, the research results show that the mechanical properties of the shale mass are weakened the most among the results of all of the conditions tested. Compared with the properties of the original block, the compressive strength of the REV decreases up to 58.35%; the deformation modulus of the REV decreases up to 61.39%; the shear modulus of the REV decreases up to 67.6%; and the bulk modulus of the REV decreases up to 53.83%. This can explain why the parameters, such as the compressive strength, of the standard shale sample were very high while actual horizontal shale wells often collapse in large sections.

6 Conclusions

  1. (1)

    The DEM was explored to address the problem of simulating bedding and natural fractures within shale masses. In the numerical simulation, DFN simulation technology and the transversely isotropic constitutive model were used to characterize the natural fractures and bedding, respectively. In addition, fictitious joint deformation parameters suitable for bedding shale have been analytically derived.

  2. (2)

    A procedure was proposed to investigate the influence of the degree of anisotropy introduced by bedding on the REV and mechanical properties of shale mass. The results showed that when \(E_{{\text{h}}} \ne E_{{\text{v}}}\), the degree of anisotropy was higher, and more fractures were required for to reach the mechanical properties of a homogenous block, leading to a larger REV. With the same anisotropy ratio, a change in bedding angle did not affect the size of the REV. The bedding angle had a great influence on the mechanical parameters of the shale at various scales. Under different anisotropy ratios, the mechanical parameters corresponding to a 45° bedding angle were the smallest for each block size, indicating that the closer the bedding angles were to the orientation of the natural fractures, the greater the decrease in the rock properties.

  3. (3)

    The REV size required to represent the mechanical properties of the Carboniferous shale masses in the eastern Qaidam Basin is approximately 2.0–3.0 m. When the numerical model size is larger than the REV, the fractured rock mass discontinuities can be transformed into equivalent continuities. In this case, the mechanical parameters of the REV are much lower than those of the shale sample due to the influence of the anisotropy ratio and bedding angle, which must be considered when analyzing the stability of a borehole wall in shale.