Nonlinear continuum mechanics of thick hyperelastic sandwich beams using various shear deformable beam theories

Abstract

In this study, the time-dependent mechanics of multilayered thick hyperelastic beams are investigated for the first time using five different types of shear deformation models for modelling the beam (i.e. the Euler–Bernoulli, Timoshenko, third-order, trigonometric and exponential shear deformable models), together with the von Kármán geometrical nonlinearity and Mooney–Rivlin hyperelastic strain energy density. The laminated hyperelastic beam is assumed to be resting on a nonlinear foundation and undergoing a time-dependent external force. The coupled highly nonlinear hyperelastic equations of motion are obtained by considering the longitudinal, transverse and rotation motions and are solved using a dynamic equilibrium technique. Both the linear and nonlinear time-dependent mechanics of the structure are analysed for clamped–clamped and pinned–pinned boundaries, and the impact of considering the shear effect using different shear deformation theories is discussed in detail. The influence of layering, each layer’s thickness, hyperelastic material positioning and many other parameters on the nonlinear frequency response is analysed, and it is shown that the resonance position, maximum amplitude, coupled motion and natural frequencies vary significantly for various hyperelastic and layer properties. The results of this study should be useful when studying layered soft structures, such as multilayer plastic packaging and laminated tubes, as well as modelling layered soft tissues.

1 Introduction

Layering structures is an effective method for optimising their mechanical, physical and electrical properties for a specific purpose. For instance, in the automotive industry, reducing the weight of the structure and increasing the stiffness lead to significant environmental benefits (lowering the fuel consumption and increasing automobile’s performance [1, 2]) which is made feasible by fabricating multilayered parts.

In many engineering applications, structures are fabricated with three layers (e.g. in laminated packaging); the outer layers are called the skins (upper skin and lower skin) and the middle layer is the core. If the purpose of the design is to increase the strength against bending loads, the core is usually made of a softer material with a higher thickness and the outer skins are thinner and stiffer. If the structure is used in an uncertain environment, the outer skins are made of softer materials to propagate the force throughout the structure and avoid cracks in a brittle core. In some other engineering structures, researchers gradually change the material properties to fabricate functionally graded structures which have been studied in Refs. [3,4,5,6].

Over the past few years, researchers have analysed different layered elastic (versus hyperelastic in this paper) structures to understand their mechanical behaviour under diverse conditions. A brief review of previous studies in this field is given in this section; however, interested readers seeking a more detailed literature review are referred to Refs. [7,8,9,10].

For bending analysis of layered elastic beams [11, 12], researchers have used different beam theories and analysed layered beam structures. By neglecting the shear effects, Chai and Yap [13] examined the bending behaviour of layered composite structures using classic beam theory (CBT). By comparing the results with those of a finite element modelling (FEM), it was shown that the coupling terms between the layers play a significant role in predicting the mechanical behaviour accurately. Chen et al [14] added the shear influence to the model using the first-order shear deformable beam theory; it was shown that the bending deformation of the Timoshenko beam model is higher than the CBT and the difference is higher for any lower thickness-to-length ratio. Özütok and Madenci [15] used a higher-order shear deformation theory together with FEM for timed-independent analysis of layered composite beams and verified the results by comparing them with those available in the literature.

For linear vibration analysis of layered elastic beams [16,17,18], Emam and Nayfeh [19] investigated the free vibration of layered composites using the Euler–Bernoulli beam theory. The axial motion was considered in the formulation and was substituted in the transverse equation of motion. Natural frequencies were obtained for different axial loads and boundary conditions; it was reported that for the studied six-layer beam model, the layer positioning has a significant effect in varying the fundamental frequency for different axial loads. A first-order shear deformable beam theory was used by Banerjee and Sobey [20] to examine the free oscillation of laminated structures under axial loading. A closed-form analytical solution was presented showing accuracy in predicting the natural frequencies and mode shapes of layered beams. Damanpack and Khalili [21] used higher-order beam theory to model the longitudinal–transverse coupled motion of layered structures. Hamilton’s principle was used to reach the equations of motion showing that the natural frequencies obtained from this model agree with the experimental results presented in Ref. [22].

For nonlinear vibration analysis of elastic beams, Zhang et al. [23] studied the nonlinear forced oscillation of laminated beams in a humid thermal condition. Only the transverse motion was considered in the formulation, and a nonlinear energy sink was added to the model. The equations of motion were solved using a fourth-order Rung–Kutta (RK4) method and a two-term harmonic balance (HB) scheme. It was shown that the nonlinear studied model has a hardening behaviour and adding a nonlinear energy sink can reduce the maximum amplitude of the transverse vibration significantly. Shen et al. [24] examined the nonlinear free oscillation behaviour of layered graphene-strengthened beams; Halpin–Tsai model was employed to predict the physical properties of the combination of the matrix and fibres. A higher-order shear deformable theory, together with the von-Kármán geometrical nonlinearity, was used to model the beam. By employing a two-step perturbation technique, it was shown that the layering and positioning of fibres has a significant effect in varying the nonlinear frequency ratio and the natural frequencies. Three-layered and bi-layered shear deformable elastic beams have been studied by Ghayesh et al. [25]; it was shown that the resonance region change based on the layer sorting and both hardening and softening behaviour can be observed while considering geometrical imperfections. Other types of layered structures have also been examined by researchers, and interested authors are referred to Refs. [26, 27] for more information about layered-plate and layered-shell structures focused investigations.

The previously mentioned studies focus on elastic structures that undergo small strains while facing different types of loadings; even the nonlinear ones are based on geometric nonlinearities and small strains. Soft structures cannot be modelled as a linear elastic material and require more accurate hyperelastic assumptions and formulations; in other words, a material nonlinearity should be taken into account, as done in this paper.

Multilayered hyperelastic structures have been used widely in many products. For instance, multilayer plastic packaging is used for packaging different products, such as food packaging which has been a trending topic over the last few years in waste management, recycling and optimised packaging [28,29,30,31]. Furthermore, human body organs act as hyperelastic components and many parts are made of different layers, such as the artery, which is made of three hyperelastic layers (intima, media and adventitia) [32].

Previously, axially moving hyperelastic structures and porous-hyperelastic structures have been investigated by Khaniki et al. [33, 34]; however, until now, there have been no studies on the time-dependent mechanics of layered hyperelastic structures. In this study, a comprehensive analysis of the mechanics of multilayered thick hyperelastic structures is presented for the first time as having different boundary conditions via different shear theories. Large strain modelling, together with large-amplitude displacements, is modelled using the Mooney–Rivlin strain energy model (for material nonlinearity) and the von Kármán geometrical nonlinearity. Different types of shear deformable beam theories (Euler–Bernoulli, Timoshenko, third-order, trigonometric and exponential shear deformable models) are used to model the layered structures and the influence of layering, material positioning and the thickness of the core and skins is discussed in detail.

2 Layered hyperelastic shear deformable beam formulation

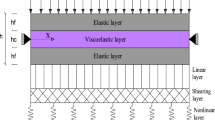
For a thick-layered shear deformable beam (Fig. 1), considering the plane motion, the axial and transverse deformations are written as [35]

$$\begin{aligned}&u\left( {x,z,t} \right) = \chi \left( z \right) {w_x}\left( {x,t} \right) - \chi \left( z \right) \phi \left( {x,t} \right) + u\left( {x,t} \right) - z{w_x}\left( {x,t} \right) , \end{aligned}$$

(1)

$$\begin{aligned}&w\left( {x,z,t} \right) = w\left( {x,t} \right) , \end{aligned}$$

(2)

where u and w are the axial and transverse displacements in the x and z directions (Fig. 1), respectively, subscript x indicates derivations with respect to x, $\phi$ is the rotation and $\chi (z)$ is the higher-order shear function, which the definition depends on the shear deformable theory used. In this study, five different definitions for $\chi (z)$ are used, which are defined as [36,37,38,39]

$$\begin{aligned}&{\mathrm{Case}}\,1\,\,\,({\mathrm{Euler{-}Bernoulli }}\,{\mathrm{beam}}\,{\mathrm{theory}}):\qquad \;\; \chi \left( z \right) = 0, \end{aligned}$$

(3)

$$\begin{aligned}&{\mathrm{Case}}\,2\,\,\,\,({\mathrm{Timoshenko }}\,{\mathrm{beam }}\,{\mathrm{theory}}):\qquad \qquad \chi \left( z \right) = z, \end{aligned}$$

(4)

$$\begin{aligned}&{\mathrm{Case}}\,3\,\,\,\,({\mathrm{Third{-}order }}\,{\mathrm{beam }}\,{\mathrm{theory}}):\qquad \quad \chi \left( z \right) = z\left( {1 - \frac{4}{3}\frac{{{z^2}}}{{{h^2}}}} \right) , \end{aligned}$$

(5)

$$\begin{aligned}&{\mathrm{Case}}\,4\,\,\,\,({\mathrm{Exponential }}\,{\mathrm{beam }}\,{\mathrm{theory}}):\qquad \qquad \chi \left( z \right) = z{e^{ - 2{{\left( z/h\right) }^2}}}, \end{aligned}$$

(6)

$$\begin{aligned}&{\mathrm{Case}}\,5\,\,\,({\mathrm{Trigonometric }}\,{\mathrm{beam }}\,{\mathrm{theory}}):\qquad \quad \chi \left( z \right) = \frac{h}{\pi }\sin \left( {\frac{{\pi z}}{h}} \right) , \end{aligned}$$

(7)

where Case 1 indicates that the shear deformation effect is neglected, following the Euler–Bernoulli beam assumption (classic beam theory) when the rotary inertia is also neglected; the advantage of using this model is that the model is simplified by neglecting the rotational degree of freedom by only considering axial and transverse motions. Case 2 defines a linearly varying shear deformation through the thickness of the beam, which represents the Timoshenko beam theory. In this model, the transverse normal plates do not necessarily remain perpendicular (to the mid-surface) after deformation leading to an extra degree of freedom for the rotary inertia. Case 3 shows the shear deformation using a higher-order model following the third-order shear deformable beam theory [36, 37]. In this model, the transverse shear stress in the Cases 4 and 5 defines the shear deformation of the beam using an exponential [38] and trigonometric [39] functions, which follow the beam theories of exponential shear deformable and trigonometric, respectively. For all the five cases, the strains are written as

$$\begin{aligned}&{\varepsilon _{xx}}\left( {x,y,t} \right) = {u_x}\left( {x,t} \right) - z{w_{xx}}\left( {x,t} \right) + \chi \left( z \right) {w_{xx}}\left( {x,t} \right) - \chi \left( z \right) {\phi _x}\left( {x,t} \right) + \frac{1}{2}{w_x}^2\left( {x,t} \right) , \end{aligned}$$

(8)

$$\begin{aligned}&{\gamma _{xz}}\left( {x,y,t} \right) = 2{\varepsilon _{xz}}\left( {x,y,t} \right) = {\chi _z}\left( z \right) {w_x}\left( {x,t} \right) - {\chi _z}\left( z \right) \phi \left( {x,t} \right) , \end{aligned}$$

(9)

$$\begin{aligned}&{\varepsilon _{zz}} \ne 0, \end{aligned}$$

(10)

where $\varepsilon _{xx}$ is the axial strain, $\gamma _{xz}$ is the shear strain and $\varepsilon _{zz}$ is the transverse strain that is not equal to zero and should satisfy the incompressibility condition of hyperelastic structures. The deformation gradient (F) is given in Refs. [33, 40] which can be used for defining the left Cauchy–Green strain tensor (C) for planar motion as

$$\begin{aligned} C = {F^T}F = \left[ {\begin{array}{ccc} {{{\left( {1 + {\varepsilon _{xx}}} \right) }^2} + {\varepsilon _{xz}}^2}&{}0&{}{{\varepsilon _{xz}}\left( {2 + {\varepsilon _{xx}} + {\varepsilon _{zz}}} \right) }\\ 0&{}1&{}0\\ {{\varepsilon _{xz}}\left( {2 + {\varepsilon _{xx}} + {\varepsilon _{zz}}} \right) }&{}0&{}{{{\left( {1 + {\varepsilon _{zz}}} \right) }^2} + {\varepsilon _{xz}}^2} \end{array}} \right] , \end{aligned}$$

(11)

where the higher-order strain terms are due to the soft behaviour of hyperelastic materials, which undergo large strains and cannot be ignored. The strain term $\varepsilon _{zz}$ can be obtained as a function of $\varepsilon _{zz}$ and $\varepsilon _{zz}$ by considering det($C) = 0$ (the incompressibility condition). For linear elastic models, by neglecting the higher-order strain terms, the Cauchy–Green strain tensor will be [27]

Fig. 1

Schematics of three-layered hyperelastic beam with (a) fixed and (b) simply supported boundary conditions and (c) layer characteristics

$$\begin{aligned} C = {F^T}F = \left[ {\begin{array}{ccc} {1 + 2{\varepsilon _x}}&{}0&{}{2{\varepsilon _{xz}}}\\ 0&{}1&{}0\\ {2{\varepsilon _{xz}}}&{}0&{}{1 + 2{\varepsilon _z}} \end{array}} \right] , \end{aligned}$$

(12)

which is equal to the elastic material strain tensor model. By using the Mooney–Rivlin hyperelastic strain energy density model [41, 42], the variation of the total potential energy of the system is written as

$$\begin{aligned} \delta U= & {} \int \limits _0^L \int \limits _A \left[ {{U_1}\left( {x,z} \right) \delta {u_x}\left( {x,t} \right) + {U_2}\left( {x,z} \right) \delta {w_x}\left( {x,t} \right) } \right. \nonumber \\&\left. +\, {U_3}\left( {x,z} \right) \delta {w_{xx}}\left( {x,t} \right) + {U_4}\left( {x,z} \right) \delta \phi \left( {x,t} \right) + {U_5}\left( {x,z} \right) \delta {\phi _x}\left( {x,t} \right) \right] \mathrm{{d}}A\mathrm{{d}}x, \end{aligned}$$

(13)

where

$$\begin{aligned} {U_1}\left( {x,z} \right)= & {} 8{C_T}{u_x}\left( {x,t} \right) + 8{C_T}\left[ {\chi \left( z \right) - z} \right] {w_{xx}}\left( {x,t} \right) + 4{C_T}{w_x}^2\left( {x,t} \right) - 8{C_T}\chi \left( z \right) {\phi _x}\left( {x,t} \right) \nonumber \\&-\, 12{C_T}{u_x}^2\left( {x,t} \right) - 24{C_T}\left[ {\chi \left( z \right) - z} \right] {u_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) + 24{C_T}\chi \left( z \right) {u_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&-\, 12{C_T}{u_x}\left( {x,t} \right) {w_x}^2\left( {x,t} \right) - 12{C_T}{\left[ {\chi \left( z \right) - z} \right] ^2}{w_{xx}}^2\left( {x,t} \right) + 12{C_T}\chi \left( z \right) {w_x}^2\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&+\, 24{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_{xx}}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) - 12{C_T}\left[ {\chi \left( z \right) - z} \right] {w_x}^2\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) \nonumber \\&-\, 3{C_T}{w_x}^4\left( {x,t} \right) - 12{C_T}\chi {\left( z \right) ^2}{\phi _x}^2\left( {x,t} \right) - {C_T}{\chi _z}^2\left( z \right) {w_x}^2\left( {x,t} \right) \nonumber \\&+ \, 2{C_T}{\chi _z}^2\left( z \right) {w_x}\left( {x,t} \right) \phi \left( {x,t} \right) - {C_T}{\chi _z}^2\left( z \right) {\phi ^2}\left( {x,t} \right) , \end{aligned}$$

(14)

$$\begin{aligned} {U_2}\left( {x,z} \right)= & {} 8{C_T}{u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) + 8{C_T}\left[ {\chi \left( z \right) - z} \right] {w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) + 4{C_T}{w_x}^3\left( {x,t} \right) \nonumber \\&-\, 8{C_T}\chi \left( z \right) {w_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) - 12{C_T}{u_x}^2\left( {x,t} \right) {w_x}\left( {x,t} \right) \nonumber \\&-\, 24{C_T}\left[ {\chi \left( z \right) - z} \right] {u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) + 24{C_T}\chi \left( z \right) {u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&- 12{C_T}{u_x}\left( {x,t} \right) {w_x}^3\left( {x,t} \right) - 12{C_T}{\left[ {\chi \left( z \right) - z} \right] ^2}{w_x}\left( {x,t} \right) {w_{xx}}^2\left( {x,t} \right) \nonumber \\&+\, 24{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) + 12{C_T}\chi \left( z \right) {w_x}^3\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&- \, 12{C_T}\left[ {\chi \left( z \right) - z} \right] {w_x}^3\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) - 3{C_T}{w_x}^5\left( {x,t} \right) - 12{C_T}\chi {\left( z \right) ^2}{w_x}\left( {x,t} \right) {\phi _x}^2\left( {x,t} \right) \nonumber \\&-\, {C_T}{\chi _z}^2\left( z \right) {w_x}^3\left( {x,t} \right) + 2{C_T}{\chi _z}^2\left( z \right) {w_x}^2\left( {x,t} \right) \phi \left( {x,t} \right) - {C_T}{\chi _z}^2\left( z \right) {w_x}\left( {x,t} \right) {\phi ^2}\left( {x,t} \right) \nonumber \\&+\, 2{C_T}{\chi _z}^2\left( z \right) {w_x}\left( {x,t} \right) - 2{C_T}{\chi _z}^2\left( z \right) \phi \left( {x,t} \right) - 2{C_T}{\chi _z}^2\left( z \right) {u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) \nonumber \\&+\, 2{C_T}{\chi _z}^2\left( z \right) {u_x}\left( {x,t} \right) \phi \left( {x,t} \right) - 2{C_T}{\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) \nonumber \\&-\, {C_T}{\chi _z}^2\left( z \right) {w_x}^3\left( {x,t} \right) + 2{C_T}{\chi _z}^2\left( z \right) \chi \left( z \right) {w_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&+\, 2{C_T}{\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_{xx}}\left( {x,t} \right) \phi \left( {x,t} \right) + {C_T}{\chi _z}^2\left( z \right) {w_x}^2\left( {x,t} \right) \phi \left( {x,t} \right) \nonumber \\&-\, 2{C_T}{\chi _z}^2\left( z \right) \chi \left( z \right) \phi \left( {x,t} \right) {\phi _x}\left( {x,t} \right) , \end{aligned}$$

(15)

$$\begin{aligned} {U_3}\left( {x,z} \right)= & {} 8{C_T}\left[ {\chi \left( z \right) - z} \right] {u_x}\left( {x,t} \right) + 8{C_T}{\left[ {\chi \left( z \right) - z} \right] ^2}{w_{xx}}\left( {x,t} \right) + 4{C_T}\left[ {\chi \left( z \right) - z} \right] {w_x}^2\left( {x,t} \right) \nonumber \\&-\, 8{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] {\phi _x}\left( {x,t} \right) - 12{C_T}\left[ {\chi \left( z \right) - z} \right] {u_x}^2\left( {x,t} \right) \nonumber \\&-\, 24{C_T}{\left[ {\chi \left( z \right) - z} \right] ^2}{u_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) + 24{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] {u_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&- \,12{C_T}\left[ {\chi \left( z \right) - z} \right] {u_x}\left( {x,t} \right) {w_x}^2\left( {x,t} \right) - 12{C_T}{\left[ {\chi \left( z \right) - z} \right] ^3}{w_{xx}}^2\left( {x,t} \right) \nonumber \\&+\, 24{C_T}\chi \left( z \right) {\left[ {\chi \left( z \right) - z} \right] ^2}{w_{xx}}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) + 12{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_x}^2\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&- \,12{C_T}{\left[ {\chi \left( z \right) - z} \right] ^2}{w_x}^2\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) - 3{C_T}\left[ {\chi \left( z \right) - z} \right] {w_x}^4\left( {x,t} \right) \nonumber \\&-\, 12{C_T}\chi {\left( z \right) ^2}\left[ {\chi \left( z \right) - z} \right] {\phi _x}^2\left( {x,t} \right) - {C_T}{\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_x}^2\left( {x,t} \right) \nonumber \\&+\, 2{C_T}{\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_x}\left( {x,t} \right) \phi \left( {x,t} \right) - {C_T}{\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] {\phi ^2}\left( {x,t} \right) , \end{aligned}$$

(16)

$$\begin{aligned} {U_4}\left( {x,z} \right)= & {} - 2{C_T}{\chi _z}^2\left( z \right) {w_x}\left( {x,t} \right) + 2{C_T}{\chi _z}^2\left( z \right) \phi \left( {x,t} \right) \nonumber \\&+\, 2{C_T}{\chi _z}^2\left( z \right) {u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) - 2{C_T}{\chi _z}^2\left( z \right) {u_x}\left( {x,t} \right) \phi \left( {x,t} \right) \nonumber \\&+\, 2{C_T}{\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) + {C_T}{\chi _z}^2\left( z \right) {w_x}^3\left( {x,t} \right) \nonumber \\&- \, 2{C_T}\chi \left( z \right) {\chi _z}^2\left( z \right) {w_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) - {C_T}{\chi _z}^2\left( z \right) {w_x}^2\left( {x,t} \right) \phi \left( {x,t} \right) \nonumber \\&-\, 2{C_T}{\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_{xx}}\left( {x,t} \right) \phi \left( {x,t} \right) \nonumber \\&+\, 2{C_T}\chi \left( z \right) {\chi _z}^2\left( z \right) \phi \left( {x,t} \right) {\phi _x}\left( {x,t} \right) , \end{aligned}$$

(17)

$$\begin{aligned} {U_5}\left( {x,z} \right)= & {} - 8{C_T}\chi \left( z \right) {u_x}\left( {x,t} \right) - 8{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_{xx}}\left( {x,t} \right) \nonumber \\&- \, 4{C_T}\chi \left( z \right) {w_x}^2\left( {x,t} \right) + 8{C_T}{\chi ^2}\left( z \right) {\phi _x}\left( {x,t} \right) + 12{C_T}\chi \left( z \right) {u_x}^2\left( {x,t} \right) \nonumber \\&+\, 24{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] {u_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) - 24{C_T}{\chi ^2}\left( z \right) {u_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&+\, 12{C_T}\chi \left( z \right) {u_x}\left( {x,t} \right) {w_x}^2\left( {x,t} \right) + 12{C_T}\chi \left( z \right) {\left[ {\chi \left( z \right) - z} \right] ^2}{w_{xx}}^2\left( {x,t} \right) \nonumber \\&-\, 24{C_T}{\chi ^2}\left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_{xx}}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) - 12{C_T}{\chi ^2}\left( z \right) {w_x}^2\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&+\, 12{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] {w_x}^2\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) + 3{C_T}\chi \left( z \right) {w_x}^4\left( {x,t} \right) \nonumber \\&+\, 12{C_T}{\chi ^3}\left( z \right) {\phi _x}^2\left( {x,t} \right) + {C_T}\chi \left( z \right) {\chi _z}^2\left( z \right) {w_x}^2\left( {x,t} \right) \nonumber \\&-\, 2{C_T}\chi \left( z \right) {\chi _z}^2\left( z \right) {w_x}\left( {x,t} \right) \phi \left( {x,t} \right) + {C_T}\chi \left( z \right) {\chi _z}^2\left( z \right) {\phi ^2}\left( {x,t} \right) , \end{aligned}$$

(18)

for which, by assuming the hyperelastic beam has three layers (Fig. 1) with layers attached perfectly (with no delamination), the stiffness parameters ($A_{ii}$, $B_{ii}$, $D_{ii}$ and $E_{ii})$ are defined as

$$\begin{aligned} {A_{11}}= & {} \int \limits _A {{C_T}} \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} \mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}} \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}} \mathrm{{d}}{A_3}, \end{aligned}$$

(19)

$$\begin{aligned} {B_{11}}= & {} \int \limits _A {{C_T}} \chi \left( z \right) \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} \chi \left( z \right) \mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}} \chi \left( z \right) \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}} \chi \left( z \right) \mathrm{{d}}{A_3}, \end{aligned}$$

(20)

$$\begin{aligned} {B_{22}}= & {} \int \limits _A {{C_T}} \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}} \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}} \nonumber \\&\left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_3}, \end{aligned}$$

(21)

$$\begin{aligned} {D_{11}}= & {} \int \limits _A {{C_T}{\chi ^2}\left( z \right) } \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}{\chi ^2}\left( z \right) } \mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}{\chi ^2}\left( z \right) } \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}{\chi ^2}\left( z \right) } \mathrm{{d}}{A_3}, \end{aligned}$$

(22)

$$\begin{aligned} {D_{22}}= & {} \int \limits _A {{C_T}} {\left[ {\chi \left( z \right) - z} \right] ^2}\mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} {\left[ {\chi \left( z \right) - z} \right] ^2}\mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}} {\left[ {\chi \left( z \right) - z} \right] ^2}\mathrm{{d}}{A_2}\nonumber \\&+ \int \limits _{{A_3}} {{C_{T3}}} {\left[ {\chi \left( z \right) - z} \right] ^2}\mathrm{{d}}{A_3}, \end{aligned}$$

(23)

$$\begin{aligned} {D_{33}}= & {} \int \limits _A {{C_T}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] } \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] } \mathrm{{d}}{A_1}\nonumber \\&+ \int \limits _{{A_2}} {{C_{T2}}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] } \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] } \mathrm{{d}}{A_3}, \end{aligned}$$

(24)

$$\begin{aligned} {D_{44}}= & {} \int \limits _A {{C_T}{\chi _z}^2\left( z \right) } \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}{\chi _z}^2\left( z \right) } \mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}{\chi _z}^2\left( z \right) } \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}{\chi _z}^2\left( z \right) } \mathrm{{d}}{A_3}, \end{aligned}$$

(25)

$$\begin{aligned} {E_{11}}= & {} \int \limits _A {{C_T}} {\chi ^3}\left( z \right) \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} {\chi ^3}\left( z \right) \mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}} {\chi ^3}\left( z \right) \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}} {\chi ^3}\left( z \right) \mathrm{{d}}{A_3}, \end{aligned}$$

(26)

$$\begin{aligned} {E_{22}}= & {} \int \limits _A {{C_T}} {\chi ^2}\left( z \right) \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} {\chi ^2}\left( z \right) \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_1}\nonumber \\&+ \int \limits _{{A_2}} {{C_{T2}}} {\chi ^2}\left( z \right) \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}} {\chi ^2}\left( z \right) \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_3}, \end{aligned}$$

(27)

$$\begin{aligned} {E_{33}}= & {} \int \limits _A {{C_T}\chi \left( z \right) {{\left[ {\chi \left( z \right) - z} \right] }^2}} \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}\chi \left( z \right) {{\left[ {\chi \left( z \right) - z} \right] }^2}} \mathrm{{d}}{A_1}\nonumber \\&+ \int \limits _{{A_2}} {{C_{T2}}\chi \left( z \right) {{\left[ {\chi \left( z \right) - z} \right] }^2}} \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}\chi \left( z \right) {{\left[ {\chi \left( z \right) - z} \right] }^2}} \mathrm{{d}}{A_3}, \end{aligned}$$

(28)

$$\begin{aligned} {E_{44}}= & {} \int \limits _A {{C_T}} {\left[ {\chi \left( z \right) - z} \right] ^3}\mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} {\left[ {\chi \left( z \right) - z} \right] ^3}\mathrm{{d}}{A_1}\nonumber \\&+ \int \limits _{{A_2}} {{C_{T2}}} {\left[ {\chi \left( z \right) - z} \right] ^3}\mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}} {\left[ {\chi \left( z \right) - z} \right] ^3}\mathrm{{d}}{A_3}, \end{aligned}$$

(29)

Fig. 2

Mode shapes of the first (a) transverse, (b) longitudinal and (c) rotation vibration modes with clamped–clamped and pinned–pinned boundary conditions

$$\begin{aligned} {E_{55}}= & {} \int \limits _A {{C_T}} {\chi _z}^3\left( z \right) \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} {\chi _z}^3\left( z \right) \mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}} {\chi _z}^3\left( z \right) \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}} {\chi _z}^3\left( z \right) \mathrm{{d}}{A_3}, \end{aligned}$$

(30)

$$\begin{aligned} {E_{66}}= & {} \int \limits _A {{C_T}} {\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}} {\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_1}\nonumber \\&+ \int \limits _{{A_2}} {{C_{T2}}} {\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_2} + \int \limits _{{A_3}} {{C_{T3}}} {\chi _z}^2\left( z \right) \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_3}, \end{aligned}$$

(31)

$$\begin{aligned} {E_{77}}= & {} \int \limits _A {{C_T}} \chi \left( z \right) {\chi _z}^2\left( z \right) \mathrm{{d}}A = \int \limits _{{A_1}} {{C_{T1}}\chi \left( z \right) } {\chi _z}^2\left( z \right) \mathrm{{d}}{A_1} + \int \limits _{{A_2}} {{C_{T2}}\chi \left( z \right) } {\chi _z}^2\left( z \right) \mathrm{{d}}{A_2}\nonumber \\&+ \int \limits _{{A_3}} {{C_{T3}}} \chi \left( z \right) {\chi _z}^2\left( z \right) \mathrm{{d}}{A_3}, \end{aligned}$$

(32)

which, for the case considering the Timoshenko beam model ($\chi (z) = z)$, uses a shear correction factor of $\kappa = 5/6$ [43]. Accordingly, by using Eqs. (19–32), the potential energy of a three-layered hyperelastic beam can be rewritten, which is not presented here for the sake of brevity. It should be mentioned that for having more layers in the laminated hyperelastic beam model, Eqs. (19–32) should be rewritten on the right side, based on the number of layers. The kinetic energy of the structure is written as

$$\begin{aligned} \delta KE= & {} \int \limits _0^L {\int \limits _A {\rho \left( z \right) } } \left[ {{u_t}\left( {x,t} \right) + \left( {\chi \left( z \right) - z} \right) {w_{xt}}\left( {x,t} \right) - \chi \left( z \right) {\phi _t}\left( {x,t} \right) } \right] \delta {u_t}\left( {x,t} \right) \mathrm{{d}}A\mathrm{{d}}x\nonumber \\&+ \int \limits _0^L {\int \limits _A {\rho \left( z \right) } } \left( {\chi \left( z \right) - z} \right) \left[ {{u_t}\left( {x,t} \right) + \left( {\chi \left( z \right) - z} \right) {w_{xt}}\left( {x,t} \right) - \chi \left( z \right) {\phi _t}\left( {x,t} \right) } \right] \delta {w_{xt}}\left( {x,t} \right) \mathrm{{d}}A\mathrm{{d}}x\nonumber \\&- \int \limits _0^L {\int \limits _A {\rho \left( z \right) } } \chi \left( z \right) \left[ {{u_t}\left( {x,t} \right) + \left( {\chi \left( z \right) - z} \right) {w_{xt}}\left( {x,t} \right) - \chi \left( z \right) {\phi _t}\left( {x,t} \right) } \right] \delta {\phi _t}\left( {x,t} \right) \mathrm{{d}}A\mathrm{{d}}x\nonumber \\&+ \int \limits _0^L {\int \limits _A {\rho \left( z \right) } } {w_t}\left( {x,t} \right) \delta {w_t}\left( {x,t} \right) \mathrm{{d}}A\mathrm{{d}}x, \end{aligned}$$

(33)

which, by defining the moment of inertia in terms of area ($I_{i})$ for a three-layered hyperelastic thick beam, is written as

$$\begin{aligned} {I_0}= & {} \int \limits _A {\rho \left( z \right) } \mathrm{{d}}A = \int \limits _{A_{1}} {\rho _{1}} \mathrm{{d}}{A_1} + \int \limits _{A_{2}} {\rho _{2}} \mathrm{{d}}{A_2} + \int \limits _{A_{3}} {\rho _{3}} \mathrm{{d}}{A_3}, \end{aligned}$$

(34)

$$\begin{aligned} {I_1}= & {} \int \limits _A {\rho \left( z \right) } \chi \left( z \right) \mathrm{{d}}A = \int \limits _{A_{1}} {\rho _{1}} \chi \left( z \right) \mathrm{{d}}{A_1} + \int \limits _{A_{2}} {\rho _{2}} \chi \left( z \right) \mathrm{{d}}{A_2} + \int \limits _{A_{3}} {\rho _{3}} \chi \left( z \right) \mathrm{{d}}{A_3}, \end{aligned}$$

(35)

$$\begin{aligned} {I_2}= & {} \int \limits _A {\rho \left( z \right) } \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}A = \int \limits _{A_{1}} {\rho _{1}} \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_1} + \int \limits _{A_{2}} {\rho _{2}} \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_2} + \int \limits _{A_{3}} {\rho _{3}} \left[ {\chi \left( z \right) - z} \right] \mathrm{{d}}{A_3}, \nonumber \\\end{aligned}$$

(36)

$$\begin{aligned} {I_3}= & {} \int \limits _A {\rho \left( z \right) {\chi ^2}\left( z \right) } \mathrm{{d}}A = \int \limits _{A_{1}} {{\rho _1}{\chi ^2}\left( z \right) } \mathrm{{d}}{A_1} + \int \limits _{A_{2}} {{\rho _2}{\chi ^2}\left( z \right) } \mathrm{{d}}{A_2} + \int \limits _{A_{3}} {{\rho _3}{\chi ^2}\left( z \right) } \mathrm{{d}}{A_3}, \end{aligned}$$

(37)

$$\begin{aligned} {I_4}= & {} \int \limits _A {\rho \left( z \right) } {\left[ {\chi \left( z \right) - z} \right] ^2}\mathrm{{d}}A = \int \limits _{A_{1}} {\rho _{1}} {\left[ {\chi \left( z \right) - z} \right] ^2}\mathrm{{d}}{A_1}\nonumber \\&+ \int \limits _{A_{2}} {\rho _{2}} {\left[ {\chi \left( z \right) - z} \right] ^2}\mathrm{{d}}{A_2} + \int \limits _{A_{3}} {\rho _{3}} {\left[ {\chi \left( z \right) - z} \right] ^2}\mathrm{{d}}{A_3}, \end{aligned}$$

(38)

$$\begin{aligned} {I_5}= & {} \int \limits _A {\rho \chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] } \mathrm{{d}}A = \int \limits _{A_{1}} {{\rho _1}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] } \mathrm{{d}}{A_1}\nonumber \\&+ \int \limits _{A_{2}} {{\rho _2}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] } \mathrm{{d}}{A_2} + \int \limits _{A_{3}} {{\rho _3}\chi \left( z \right) \left[ {\chi \left( z \right) - z} \right] } \mathrm{{d}}{A_3}, \end{aligned}$$

(39)

and by substituting Eqs. (34–39) into Eq. (33), one can reach the kinetic energy of layered thick hyperelastic beams, as

$$\begin{aligned} \delta KE= & {} \int \limits _0^L { - \left[ {{I_0}{u_{tt}}\left( {x,t} \right) + {I_2}{w_{xtt}}\left( {x,t} \right) - {I_1}{\phi _{tt}}\left( {x,t} \right) } \right] \delta u\left( {x,t} \right) } \nonumber \\&+ \left[ {{I_2}{u_{xtt}}\left( {x,t} \right) + {I_4}{w_{xxtt}}\left( {x,t} \right) - {I_5}{\phi _{xtt}}\left( {x,t} \right) } \right] \delta w\left( {x,t} \right) \nonumber \\&- {I_0}{w_{tt}}\left( {x,t} \right) \delta w\left( {x,t} \right) + \left[ {{I_1}{u_{tt}}\left( {x,t} \right) + {I_5}{w_{xtt}}\left( {x,t} \right) - {I_3}{\phi _{tt}}\left( {x,t} \right) } \right] \delta \phi \left( {x,t} \right) \mathrm{{d}}x. \end{aligned}$$

(40)

Moreover, the beam is assumed to be lying on a nonlinear elastic foundation (Fig. 1) and externally actuated by a periodic load, which gives the external work on the beam as

$$\begin{aligned} \delta {U_F}= & {} \int \limits _0^L {\left( {{F_{linear}}\left( {x,t} \right) + {F_{nonlinear}}\left( {x,t} \right) + {F_{shear}}\left( {x,t} \right) } \right) \delta w} \mathrm{d}x + \mathop {\smallint } \limits _0^L F\cos \left( {\omega t} \right) \delta w\mathrm{{d}}x\nonumber \\= & {} \int \limits _0^L {\left[ { - {K_L}w\left( {x,t} \right) - {K_{NL}}{w^3}\left( {x,t} \right) + {K_S}{w_{xx}}\left( {x,t} \right) + F\cos \left( {\omega t} \right) } \right] \delta w}, \end{aligned}$$

(41)

where $K_{L}$, $K_{NL}$ and $K_{S}$ are the linear, nonlinear and shear coefficients of the foundation, respectively, and F is the external force acting periodically with a frequency of $\omega$. Using Hamilton’s principle, the coupled longitudinal, transverse and rotation equations of motion are obtained as

$$\begin{aligned}&{I_0}{u_{tt}}\left( {x,t} \right) + {I_2}{w_{xtt}}\left( {x,t} \right) - {I_1}{\phi _{tt}}\left( {x,t} \right) - 8{A_{11}}{u_{xx}}\left( {x,t} \right) - 8{B_{22}}{w_{xxx}}\left( {x,t} \right) + 8{B_{11}}{\phi _{xx}}\left( {x,t} \right) \nonumber \\&\quad +\, 12{A_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}^2\left( {x,t} \right) } \right] + 24{B_{22}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] - 24{B_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] \nonumber \\&\quad -\, \left( {4{A_{11}} - {D_{44}}} \right) \frac{\partial }{{\partial x}}\left[ {{w_x}^2\left( {x,t} \right) } \right] + 12{D_{22}}\frac{\partial }{{\partial x}}\left[ {{w_{xx}}^2\left( {x,t} \right) } \right] - 2{D_{44}}\frac{\partial }{{\partial x}}\left[ {{w_x}\left( {x,t} \right) \phi \left( {x,t} \right) } \right] \nonumber \\&\quad - \,24{D_{33}}\frac{\partial }{{\partial x}}\left[ {{w_{xx}}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] + {D_{44}}\frac{\partial }{{\partial x}}\left[ {{\phi ^2}\left( {x,t} \right) } \right] + 12{D_{11}}\frac{\partial }{{\partial x}}\left[ {{\phi _x}^2\left( {x,t} \right) } \right] \nonumber \\&\quad +\, 12{A_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {w_x}^2\left( {x,t} \right) } \right] + 12{B_{22}}\frac{\partial }{{\partial x}}\left[ {{w_x}^2\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] \nonumber \\&\quad -\, 12{B_{11}}\frac{\partial }{{\partial x}}\left[ {{w_x}^2\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] + 3{A_{11}}\frac{\partial }{{\partial x}}\left[ {{w_x}^4\left( {x,t} \right) } \right] = 0, \end{aligned}$$

(42)

$$\begin{aligned}&- {I_2}{u_{xtt}}\left( {x,t} \right) + {I_0}{w_{tt}}\left( {x,t} \right) -\, {I_4}{w_{xxtt}}\left( {x,t} \right) + {I_5}{\phi _{xtt}}\left( {x,t} \right) - 8{B_{22}}{u_{xxx}}\left( {x,t} \right) - 2{D_{44}}{w_{xx}}\left( {x,t} \right) \nonumber \\&\quad -\, 8{D_{22}}{w_{xxxx}}\left( {x,t} \right) + {K_L}w\left( {x,t} \right) - {K_S}{w_{xx}}\left( {x,t} \right) + 2{D_{44}}{\phi _x}\left( {x,t} \right) + 8{D_{33}}{\phi _{xxx}}\left( {x,t} \right) \nonumber \\&\quad +\, 12{B_{22}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{u_x}^2\left( {x,t} \right) } \right] + 24{D_{22}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{u_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] \nonumber \\&\quad -\, \left( {8{A_{11}} - 2{D_{44}}} \right) \frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) } \right] - 24{D_{33}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{u_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] \nonumber \\&\quad -\, 2{D_{44}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) \phi \left( {x,t} \right) } \right] - \left( {4{B_{22}} - {E_{66}}} \right) \frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{w_x}^2\left( {x,t} \right) } \right] \nonumber \\&\quad -\, \left( {8{B_{22}} - 2{E_{66}}} \right) \frac{\partial }{{\partial x}}\left[ {{w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] + 12{E_{44}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{w_{xx}}^2\left( {x,t} \right) } \right] \nonumber \\&\quad -\, 2{E_{66}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{w_x}\left( {x,t} \right) \phi \left( {x,t} \right) } \right] + \left( {8{B_{11}} - 2{E_{77}}} \right) \frac{\partial }{{\partial x}}\left[ {{w_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] \nonumber \\&\quad -\, 2{E_{66}}\frac{\partial }{{\partial x}}\left[ {{w_{xx}}\left( {x,t} \right) \phi \left( {x,t} \right) } \right] - 24{E_{33}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{w_{xx}}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] \nonumber \\&\quad +\, {E_{66}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{\phi ^2}\left( {x,t} \right) } \right] + 2{E_{77}}\frac{\partial }{{\partial x}}\left[ {\phi \left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] + 12{E_{22}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{\phi _x}^2\left( {x,t} \right) } \right] \nonumber \\&\quad + \,12{A_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}^2\left( {x,t} \right) {w_x}\left( {x,t} \right) } \right] + 12{B_{22}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{u_x}\left( {x,t} \right) {w_x}^2\left( {x,t} \right) } \right] \nonumber \\&\quad +\, 24{B_{22}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] - 24{B_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] \nonumber \\&\quad -\, \left( {4{A_{11}} - 2{D_{44}}} \right) \frac{\partial }{{\partial x}}\left[ {{w_x}^3\left( {x,t} \right) } \right] + {K_{NL}}{w^3}\left( {x,t} \right) + 12{D_{22}}\frac{\partial }{{\partial x}}\left[ {{w_x}\left( {x,t} \right) {w_{xx}}^2\left( {x,t} \right) } \right] \nonumber \\&\quad +\, 12{D_{22}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{w_x}^2\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] - 12{D_{33}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{w_x}^2\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] \nonumber \\&\quad -\, 3{D_{44}}\frac{\partial }{{\partial x}}\left[ {{w_x}^2\left( {x,t} \right) \phi \left( {x,t} \right) } \right] - 24{D_{33}}\frac{\partial }{{\partial x}}\left[ {{w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] \nonumber \\&\quad +\, {D_{44}}\frac{\partial }{{\partial x}}\left[ {{w_x}\left( {x,t} \right) {\phi ^2}\left( {x,t} \right) } \right] + 12{D_{11}}\frac{\partial }{{\partial x}}\left[ {{w_x}\left( {x,t} \right) {\phi _x}^2\left( {x,t} \right) } \right] \nonumber \\&\quad +\, 12{A_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {w_x}^3\left( {x,t} \right) } \right] + 3{B_{22}}\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {{w_x}^4\left( {x,t} \right) } \right] + 12{B_{22}}\frac{\partial }{{\partial x}}\left[ {{w_x}^3\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] \nonumber \\&\quad -\, 12{B_{11}}\frac{\partial }{{\partial x}}\left[ {{w_x}^3\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] + 3{A_{11}}\frac{\partial }{{\partial x}}\left[ {{w_x}^5\left( {x,t} \right) } \right] = F\cos \left( {\omega t} \right) , \end{aligned}$$

(43)

$$\begin{aligned}&- {I_1}{u_{tt}}\left( {x,t} \right) - {I_5}{w_{xtt}}\left( {x,t} \right) + {I_3}{\phi _{tt}}\left( {x,t} \right) + 8{B_{11}}{u_{xx}}\left( {x,t} \right) - 2{D_{44}}{w_x}\left( {x,t} \right) + 8{D_{33}}{w_{xxx}}\left( {x,t} \right) \nonumber \\&\quad -\, 8{D_{11}}{\phi _{xx}}\left( {x,t} \right) + 2{D_{44}}\phi \left( {x,t} \right) - 12{B_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}^2\left( {x,t} \right) } \right] - 24{D_{33}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] \nonumber \\&\quad +\, 2{D_{44}}{u_x}\left( {x,t} \right) {w_x}\left( {x,t} \right) + 24{D_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] - 2{D_{44}}{u_x}\left( {x,t} \right) \phi \left( {x,t} \right) \nonumber \\&\quad +\, \left( {4{B_{11}} - {E_{77}}} \right) \frac{\partial }{{\partial x}}\left[ {{w_x}^2\left( {x,t} \right) } \right] - 12{E_{33}}\frac{\partial }{{\partial x}}\left[ {{w_{xx}}^2\left( {x,t} \right) } \right] + 2{E_{66}}{w_x}\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) \nonumber \\&\quad +\, 2{E_{77}}\frac{\partial }{{\partial x}}\left[ {{w_x}\left( {x,t} \right) \phi \left( {x,t} \right) } \right] + 24{E_{22}}\frac{\partial }{{\partial x}}\left[ {{w_{xx}}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] - 2{E_{77}}{w_x}\left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&\quad -\, 2{E_{66}}{w_{xx}}\left( {x,t} \right) \phi \left( {x,t} \right) - 12{E_{11}}\frac{\partial }{{\partial x}}\left[ {{\phi _x}^2\left( {x,t} \right) } \right] - {E_{77}}\frac{\partial }{{\partial x}}\left[ {{\phi ^2}\left( {x,t} \right) } \right] + 2{E_{77}}\phi \left( {x,t} \right) {\phi _x}\left( {x,t} \right) \nonumber \\&\quad -\, 12{B_{11}}\frac{\partial }{{\partial x}}\left[ {{u_x}\left( {x,t} \right) {w_x}^2\left( {x,t} \right) } \right] - 12{D_{33}}\frac{\partial }{{\partial x}}\left[ {{w_x}^2\left( {x,t} \right) {w_{xx}}\left( {x,t} \right) } \right] + {D_{44}}{w_x}^3\left( {x,t} \right) \nonumber \\&\quad +\, 12{D_{11}}\frac{\partial }{{\partial x}}\left[ {{w_x}^2\left( {x,t} \right) {\phi _x}\left( {x,t} \right) } \right] - {D_{44}}{w_x}^2\left( {x,t} \right) \phi \left( {x,t} \right) - 3{B_{11}}\frac{\partial }{{\partial x}}\left[ {{w_x}^4\left( {x,t} \right) } \right] = 0. \end{aligned}$$

(44)

It can therefore be seen that the equations of motion are highly nonlinear and coupled, which emphasises the importance of having the axial motion while analysing the mechanical behaviour of the structure. The linear coupling sources between the axial and transverse motions are the stiffness terms $B_{11}$ and $B_{22}$ and inertia terms $I_{1}$ and $I_{2}$, for which, for a single-layer hyperelastic beam, due to the homogeneity in the thickness direction, these terms will be equal to zero and the linear coupling terms vanish. In the next section, the equations of motion are nondimensionalised, discretised and solved.

3 Solution procedure

For the first step of solving the equations of motion, the new nondimensional parameters are defined as

$$\begin{aligned} \gamma ^{*}= & {} \frac{x}{L},\beta ^{*} = \frac{w}{h},\alpha ^{*} = \frac{u}{h},\phi ^{*} = \phi ,{A_{11}}^{*} = \frac{{{A_{11}}}}{{{A_{110}}}},{B_{11}}^{*} = \frac{{{B_{11}}}}{{{A_{110}}h}},{B_{22}}^{*} = \frac{{{B_{22}}}}{{{A_{110}}h}},{D_{44}}^{*} = \frac{{{D_{11}}}}{{{A_{110}}}},\nonumber \\ {D_{11}}^{*}= & {} \frac{{{D_{11}}}}{{{A_{110}}{h^2}}},{D_{22}}^{*} = \frac{{{D_{11}}}}{{{A_{110}}{h^2}}},{D_{33}}^{*} = \frac{{{D_{11}}}}{{{A_{110}}{h^2}}},{E_{11}}^{*} = \frac{{{E_{11}}}}{{{A_{110}}{h^3}}},{E_{22}}^{*} = \frac{{{E_{22}}}}{{{A_{110}}{h^3}}},\nonumber \\ {E_{33}}^{*}= & {} \frac{{{E_{33}}}}{{{A_{110}}{h^3}}},{E_{44}}^{*} = \frac{{{E_{44}}}}{{{A_{110}}{h^3}}},{E_{55}}^{*} = \frac{{{E_{55}}}}{{{A_{110}}}},{E_{66}}^{*} = \frac{{{E_{66}}}}{{{A_{110}}h}},{E_{77}}^{*} = \frac{{{E_{77}}}}{{{A_{110}}h}},\nonumber \\ {I_0}^{*}= & {} \frac{{{I_0}}}{{{I_{00}}}},{I_1}^{*} = \frac{{{I_1}}}{{{I_{00}}h}},{I_2}^{*} = \frac{{{I_2}}}{{{I_{00}}h}},{I_3}^{*} = \frac{{{I_3}}}{{{I_{00}}{h^2}}},{I_4}^{*} = \frac{{{I_4}}}{{{I_{00}}{h^2}}},{I_5}^{*} = \frac{{{I_5}}}{{{I_{00}}{h^2}}},\nonumber \\ \eta= & {} \frac{h}{L},\Omega = \omega \sqrt{\frac{{{I_{00}}{L^3}}}{{{A_{110}}h}}} ,t^{*} = t \sqrt{\frac{{{A_{110}}h}}{{{I_{00}}{L^3}}}} ,\nonumber \\ F^{*}= & {} F\frac{{{L^2}}}{{{A_{11}}h}},{K_L}^{*} = {K_L}\frac{{{L^2}}}{{{A_{11}}}},{K_{NL}}^{*} = {K_{NL}}\frac{{{h^2}{L^2}}}{{{A_{11}}}},{K_S}^{*} = {K_S}\frac{1}{{{A_{11}}}}, \end{aligned}$$

(45)

and by using these terms, the equations of motion are nondimensionalised as

$$\begin{aligned}&{I_0}\eta {\alpha _{tt}}\left( {\gamma ,t} \right) + {I_2}{\eta ^2}{\beta _{\gamma tt}}\left( {\gamma ,t} \right) - {I_1}\eta {\phi _{tt}}\left( {\gamma ,t} \right) - 8{A_{11}}{\alpha _{\gamma \gamma }}\left( {\gamma ,t} \right) - 8{B_{22}}\eta {\beta _{\gamma \gamma \gamma }}\left( {\gamma ,t} \right) + 8{B_{11}}{\phi _{\gamma \gamma }}\left( {\gamma ,t} \right) \nonumber \\&\quad +\, 12{A_{11}}\eta \frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }^2\left( {\gamma ,t} \right) } \right] + 24{B_{22}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] - 24{B_{11}}\eta \frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, \eta \left( {4{A_{11}} - {D_{44}}} \right) \frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) } \right] + 12{D_{22}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _{\gamma \gamma }}^2\left( {\gamma ,t} \right) } \right] - 2{D_{44}}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) \phi \left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, 24{D_{33}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] + {D_{44}}\frac{1}{\eta }\frac{\partial }{{\partial \gamma }}\left[ {{\phi ^2}\left( {\gamma ,t} \right) } \right] + 12{D_{11}}\eta \frac{\partial }{{\partial \gamma }}\left[ {{\phi _\gamma }^2\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad +\, 12{A_{11}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _\gamma }^2\left( {\gamma ,t} \right) } \right] + 12{B_{22}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, 12{B_{11}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] + 3{A_{11}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^4\left( {\gamma ,t} \right) } \right] = 0, \end{aligned}$$

(46)

$$\begin{aligned}&- {I_2}{\eta ^2}{\alpha _{\gamma tt}}\left( {\gamma ,t} \right) + {I_0}\eta {\beta _{tt}}\left( {\gamma ,t} \right) - {I_4}{\eta ^3}{\beta _{\gamma \gamma tt}}\left( {\gamma ,t} \right) + {I_5}{\eta ^2}{\phi _{\gamma tt}}\left( {\gamma ,t} \right) - 8{B_{22}}\eta {\alpha _{\gamma \gamma \gamma }}\left( {\gamma ,t} \right) \nonumber \\&\quad - \, 2{D_{44}}{\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) - 8{D_{22}}{\eta ^2}{\beta _{\gamma \gamma \gamma \gamma }}\left( {\gamma ,t} \right) + {K_L}\beta \left( {\gamma ,t} \right) - {K_S}{\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) + 2{D_{44}}\frac{1}{\eta }{\phi _\gamma }\left( {\gamma ,t} \right) \nonumber \\&\quad +\, 8{D_{33}}\eta {\phi _{\gamma \gamma \gamma }}\left( {\gamma ,t} \right) + 12{B_{22}}{\eta ^2}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\alpha _\gamma }^2\left( {\gamma ,t} \right) } \right] + 24{D_{22}}{\eta ^3}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, \eta \left( {8{A_{11}} - 2{D_{44}}} \right) \frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _\gamma }\left( {\gamma ,t} \right) } \right] - 24{D_{33}}{\eta ^2}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, 2{D_{44}}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) \phi \left( {\gamma ,t} \right) } \right] - {\eta ^2}\left( {4{B_{22}} - {E_{66}}} \right) \frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, {\eta ^2}\left( {8{B_{22}} - 2{E_{66}}} \right) \frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] + 12{E_{44}}{\eta ^4}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\beta _{\gamma \gamma }}^2\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, 2{E_{66}}\eta \frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) \phi \left( {\gamma ,t} \right) } \right] + \eta \left( {8{B_{11}} - 2{E_{77}}} \right) \frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, 2{E_{66}}\eta \frac{\partial }{{\partial \gamma }}\left[ {{\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) \phi \left( {\gamma ,t} \right) } \right] - 24{E_{33}}{\eta ^3}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] \nonumber \end{aligned}$$

$$\begin{aligned}&\quad +\, {E_{66}}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\phi ^2}\left( {\gamma ,t} \right) } \right] + 2{E_{77}}\frac{\partial }{{\partial \gamma }}\left[ {\phi \left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] + 12{E_{22}}{\eta ^2}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\phi _\gamma }^2\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad +\, 12{A_{11}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }^2\left( {\gamma ,t} \right) {\beta _\gamma }\left( {\gamma ,t} \right) } \right] + 12{B_{22}}{\eta ^3}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _\gamma }^2\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad +\, 24{B_{22}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _\gamma }\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] - 24{B_{11}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _\gamma }\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, {\eta ^2}\left( {4{A_{11}} - 2{D_{44}}} \right) \frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^3\left( {\gamma ,t} \right) } \right] + {K_{NL}}{\beta ^3}\left( {\gamma ,t} \right) + 12{D_{22}}{\eta ^4}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}^2\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad +\, 12{D_{22}}{\eta ^4}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] - 12{D_{33}}{\eta ^3}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad -\, 3{D_{44}}\eta \frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) \phi \left( {\gamma ,t} \right) } \right] - 24{D_{33}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad +\, {D_{44}}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) {\phi ^2}\left( {\gamma ,t} \right) } \right] + 12{D_{11}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) {\phi _\gamma }^2\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad +\, 12{A_{11}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _\gamma }^3\left( {\gamma ,t} \right) } \right] + 3{B_{22}}{\eta ^4}\frac{{{\partial ^2}}}{{\partial {\gamma ^2}}}\left[ {{\beta _\gamma }^4\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad +\, 12{B_{22}}{\eta ^4}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^3\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] - 12{B_{11}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^3\left( {\gamma ,t} \right) {\beta _\gamma }\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad + \,3{A_{11}}{\eta ^4}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^5\left( {\gamma ,t} \right) } \right] = F\cos \left( {\Omega t} \right) , \end{aligned}$$

(47)

$$\begin{aligned}&- {I_1}\eta {\alpha _{tt}}\left( {\gamma ,t} \right) - {I_5}{\eta ^2}{\beta _{\gamma tt}}\left( {\gamma ,t} \right) + {I_3}\eta {\phi _{tt}}\left( {\gamma ,t} \right) + 8{B_{11}}{\alpha _{\gamma \gamma }}\left( {\gamma ,t} \right) - 2{D_{44}}\frac{1}{\eta }{\beta _\gamma }\left( {\gamma ,t} \right) + 8{D_{33}}\eta {\beta _{\gamma \gamma \gamma }}\left( {\gamma ,t} \right) \nonumber \\&\quad -\, 8{D_{11}}{\phi _{\gamma \gamma }}\left( {\gamma ,t} \right) + 2{D_{44}}\frac{1}{{{\eta ^2}}}\phi \left( {\gamma ,t} \right) - 12{B_{11}}\eta \frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }^2\left( {\gamma ,t} \right) } \right] - 24{D_{33}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] \nonumber \\&\quad +\, 2{D_{44}}{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _\gamma }\left( {\gamma ,t} \right) + 24{D_{11}}\eta \frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] - 2{D_{44}}\frac{1}{\eta }{\alpha _\gamma }\phi \left( {x,t} \right) \nonumber \\&\quad +\, \left( {4{B_{11}} - {E_{77}}} \right) \eta \frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) } \right] - 12{E_{33}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _{\gamma \gamma }}^2\left( {\gamma ,t} \right) } \right] + 2{E_{66}}\eta {\beta _\gamma }\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) \nonumber \\&\quad +\, 2{E_{77}}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }\left( {\gamma ,t} \right) \phi \left( {\gamma ,t} \right) } \right] + 24{E_{22}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] - 2{E_{77}}{\beta _\gamma }\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) \nonumber \\&\quad -\, 2{E_{66}}{\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) \phi \left( {\gamma ,t} \right) - 12{E_{11}}\eta \frac{\partial }{{\partial \gamma }}\left[ {{\phi _\gamma }^2\left( {\gamma ,t} \right) } \right] - {E_{77}}\frac{1}{\eta }\frac{\partial }{{\partial \gamma }}\left[ {{\phi ^2}\left( {\gamma ,t} \right) } \right] + 2{E_{77}}\frac{1}{\eta }\phi \left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) \nonumber \\&\quad -\, 12{B_{11}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\alpha _\gamma }\left( {\gamma ,t} \right) {\beta _\gamma }^2\left( {\gamma ,t} \right) } \right] - 12{D_{33}}{\eta ^3}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) {\beta _{\gamma \gamma }}\left( {\gamma ,t} \right) } \right] + {D_{44}}\eta {\beta _\gamma }^3\left( {\gamma ,t} \right) \nonumber \\&\quad +\, 12{D_{11}}{\eta ^2}\frac{\partial }{{\partial \gamma }}\left[ {{\beta _\gamma }^2\left( {\gamma ,t} \right) {\phi _\gamma }\left( {\gamma ,t} \right) } \right] - {D_{44}}{\beta _\gamma }^2\left( {\gamma ,t} \right) \phi \left( {\gamma ,t} \right) - 3{B_{11}}{\eta ^3}\frac{\partial }{{\partial x}}\left[ {{\beta _\gamma }^4\left( {\gamma ,t} \right) } \right] = 0. \end{aligned}$$

(48)

For the sake of brevity and ease notation, the superscript * is neglected in the formulation. Using the Galerkin scheme, each motion component can be written in a series expansion of orthogonal spatial functions as

$$\begin{aligned} \left\{ \begin{array}{l} \alpha \\ \phi \\ \beta \end{array} \right\} = \sum \limits _{n = 1}^N {\left\{ \begin{array}{l} {U_n}\left( \gamma \right) {r_n}\left( t \right) \\ {\Phi _n}\left( \gamma \right) {p_n}\left( t \right) \\ {W_n}\left( \gamma \right) {q_n}\left( t \right) \end{array} \right\} }, \end{aligned}$$

(49)

where $U_{n}, \Phi _{n}, W_{n}$ are the set of trial functions that should satisfy the boundary conditions of longitudinal, rotation and transverse motions at the middle of the thickness. (Studies on layered structures based on various thickness assumptions can be found in Refs. [44,45,46,47,48,49,50].) For pinned–pinned and fixed–fixed boundary conditions, these trial functions are written as

$$\begin{aligned}&{U_p}\left( \gamma \right) = \sin \left( {{\mu _p}\gamma } \right) , \end{aligned}$$

(50)

$$\begin{aligned}&\left\{ \begin{array}{l} Fixed \!-\! Fixed \rightarrow {W_p}\left( \gamma \right) \!=\! -\! \cos \left( {{\mu _p}\gamma } \right) \!+\! \cosh \left( {{\mu _p}\gamma } \right) \! -\! \psi \left( {{\mu _p}} \right) \left[ { \!-\! \sin \left( {{\mu _p}\gamma } \right) \! +\! \sinh \left( {{\mu _p}\gamma } \right) } \right] ,\\ Pinned - Pinned \rightarrow {W_p}\left( \gamma \right) = \sin \left( {{\mu _p}\gamma } \right) , \end{array} \right. \end{aligned}$$

(51)

$$\begin{aligned}&{\Phi _p}\left( \gamma \right) = \left( {\frac{1}{{{\mu _p}}}} \right) \left( {\frac{{\partial {W_p}\left( \gamma \right) }}{{\partial x}}} \right) , \end{aligned}$$

(52)

where

$$\begin{aligned} \psi \left( {\mu _{p} } \right) =\frac{-\cos \left( {\mu _{p} } \right) +\cosh \left( {\mu _{p} } \right) }{-\sin \left( {\mu _{p} } \right) +\sinh \left( {\mu _{p} } \right) }, \end{aligned}$$

(53)

and the equations of motion are rewritten as

$$\begin{aligned}&\left[ {\begin{array}{ccc} {{{\varvec{M}}_{11}}}&{}{{{\varvec{M}}_{12}}}&{}{{{\varvec{M}}_{13}}}\\ {{{\varvec{M}}_{21}}}&{}{{{\varvec{M}}_{22}}}&{}{{{\varvec{M}}_{23}}}\\ {{{\varvec{M}}_{31}}}&{}{{{\varvec{M}}_{32}}}&{}{{{\varvec{M}}_{33}}} \end{array}} \right] \left\{ \begin{array}{l} {{\ddot{r}}_n}\\ {{\ddot{p}}_n}\\ {{\ddot{q}}_n} \end{array} \right\} + \left[ {\begin{array}{ccc} \xi &{}0&{}0\\ 0&{}\xi &{}0\\ 0&{}0&{}\xi \end{array}} \right] \left\{ \begin{array}{l} {{\dot{r}}_n}\\ {{\dot{p}}_n}\\ {{\dot{q}}_n} \end{array} \right\} \nonumber \\&\quad + \left[ {\begin{array}{ccc} {{\varvec{KL}}_{11}}&{}{{\varvec{KL}}_{12}}&{}{{\varvec{KL}}_{13}}\\ {{\varvec{KL}}_{21}}&{}{{\varvec{KL}}_{22}}&{}{{\varvec{KL}}_{23}}\\ {{\varvec{KL}}_{31}}&{}{{\varvec{KL}}_{32}}&{}{{\varvec{KL}}_{33}} \end{array}} \right] \left\{ \begin{array}{l} {r_n}\\ {p_n}\\ {q_n} \end{array} \right\} = \left\{ \begin{array}{l} 0\\ 0\\ F_{n}^{external} \end{array} \right\} + \left\{ \begin{array}{l} {\varvec{KN1}}_n^{system}\\ {\varvec{KN2}}_n^{system}\\ {\varvec{KN3}}_n^{system} \end{array} \right\} , \end{aligned}$$

(54)

where ${{\varvec{M}}}_{ij}$ are the mass tensors of the discretised equations and the components are defined as

$$\begin{aligned}&M_{11} \left( {l,i} \right) :\eta I_{0} \int \limits _0^1 {U_{l} \left( \gamma \right) } U_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(55)

$$\begin{aligned}&M_{12} \left( {l,i} \right) :\eta ^{2}I_{2} \int \limits _0^1 {U_{l} \left( \gamma \right) } {W}'_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(56)

$$\begin{aligned}&M_{13} \left( {l,i} \right) :-\eta I_{1} \int \limits _0^1 {U_{l} \left( \gamma \right) } \Phi _{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(57)

$$\begin{aligned}&M_{21} :-\eta ^{2}I_{2} \int \limits _0^1 {W_{l} \left( \gamma \right) } {U}'_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(58)

$$\begin{aligned}&M_{22} \left( {l,i} \right) :\eta I_{0} \int \limits _0^1 {W_{l} \left( \gamma \right) } W_{i} \left( \gamma \right) \mathrm{{d}}\gamma -\eta ^{3}I_{4} \int \limits _0^1 {W_{l} \left( \gamma \right) } {W}''_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(59)

$$\begin{aligned}&M_{23} \left( {l,i} \right) :\eta ^{2}I_{5} \int \limits _0^1 {W_{l} \left( \gamma \right) } {\Phi }'_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(60)

$$\begin{aligned}&M_{31} :-\eta I_{1} \int \limits _0^1 {\Phi _{l} \left( \gamma \right) } U_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(61)

$$\begin{aligned}&M_{32} \left( {l,i} \right) :-\eta ^{2}I_{5} \int \limits _0^1 {\Phi _{l} \left( \gamma \right) } {W}'_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(62)

$$\begin{aligned}&M_{33} \left( {l,i} \right) :\eta I_{3} \int \limits _0^1 {\Phi _{l} \left( \gamma \right) } \Phi _{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(63)

and ${{\varvec{KL}}}_{ij}$ are the linear stiffness tensors, defined as

$$\begin{aligned}&KL_{11} \left( {l,i} \right) :-8A_{11} \int \limits _0^1 {U_{l} \left( \gamma \right) } {U}''_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(64)

$$\begin{aligned}&KL_{12} \left( {l,i} \right) :-8\eta B_{22} \int \limits _0^1 {U_{l} \left( \gamma \right) } W_{i}^{\prime \prime \prime }\left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(65)

$$\begin{aligned}&KL_{13} \left( {l,i} \right) :8B_{11} \int \limits _0^1 {U_{l} \left( \gamma \right) } {\Phi }''_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(66)

$$\begin{aligned}&KL_{21} \left( {l,i} \right) :-8\eta B_{22} \int \limits _0^1 {W_{l} \left( \gamma \right) } {U}'''_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(67)

$$\begin{aligned}&K{L_{22}}\left( {l,i} \right) : - \int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {2{D_{44}}{{W'}_i}\left( \gamma \right) } \right] \mathrm{{d}}\gamma - 8{\eta ^2}{D_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } {W_i}^{(4)}\left( \gamma \right) \mathrm{{d}}\gamma \nonumber \\&\quad + {K_L}\int \limits _0^1 {{W_l}\left( \gamma \right) } {W_i}\left( \gamma \right) \mathrm{{d}}\gamma - {K_S}\int \limits _0^1 {{W_l}\left( \gamma \right) } {{W''}_i}\left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(68)

$$\begin{aligned}&KL_{23} \left( {l,i} \right) :2\frac{1}{\eta }D_{44} \int \limits _0^1 {W_{l} \left( \gamma \right) } {\Phi }'_{i} \left( \gamma \right) \mathrm{{d}}\gamma +8\eta D_{33} \int \limits _0^1 {W_{l} \left( \gamma \right) } {\Phi }'''_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(69)

$$\begin{aligned}&KL_{31} \left( {l,i} \right) :8B_{11} \int \limits _0^1 {\Phi _{l} \left( \gamma \right) } {U}''_{i} \left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(70)

$$\begin{aligned}&KL_{32} \left( {l,i} \right) :-2\frac{1}{\eta }D_{44} \int \limits _0^1 {\Phi _{l} \left( \gamma \right) } {W}'_{i} \left( \gamma \right) \mathrm{{d}}\gamma +8\eta D_{33} \int \limits _0^1 {\Phi _{l} \left( \gamma \right) } W_{i}^{\prime \prime \prime }\left( \gamma \right) \mathrm{{d}}\gamma , \end{aligned}$$

(71)

$$\begin{aligned}&KL_{33} \left( {l,i} \right) :-8D_{11} \int \limits _0^1 {\Phi _{l} \left( \gamma \right) } {\Phi }''_{i} \left( \gamma \right) \mathrm{{d}}\gamma +2\frac{1}{\eta ^{2}}D_{44} \int \limits _0^1 {\Phi _{l} \left( \gamma \right) } \Phi _{i} \left( \gamma \right) \mathrm{{d}}\gamma . \end{aligned}$$

(72)

KN1, KN2 and KN3 are the nonlinear stiffness terms in the coupled equation where

$$\begin{aligned}&{\varvec{KN}}1_n^{system} = {{\varvec{KN}}_{11}}{r^2}\left( t \right) + {{\varvec{KN}}_{12}}r\left( t \right) p\left( t \right) + {{\varvec{KN}}_{13}}r\left( t \right) q\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{14}}{p^2}\left( t \right) + {{\varvec{KN}}_{15}}p\left( t \right) q\left( t \right) + {{\varvec{KN}}_{16}}{q^2}\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{17}}r\left( t \right) {p^2}\left( t \right) + {{\varvec{KN}}_{18}}{p^3}\left( t \right) + {{\varvec{KN}}_{19}}{p^2}\left( t \right) q\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{110}}{p^4}\left( t \right) , \end{aligned}$$

(73)

$$\begin{aligned}&{\varvec{KN}}2_n^{system} = {{\varvec{KN}}_{21}}{r^2}\left( t \right) + {{\varvec{KN}}_{22}}r\left( t \right) p\left( t \right) + {{\varvec{KN}}_{23}}r\left( t \right) q\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{24}}{p^2}\left( t \right) + {{\varvec{KN}}_{25}}p\left( t \right) q\left( t \right) + {{\varvec{KN}}_{26}}{q^2}\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{27}}{r^2}\left( t \right) p\left( t \right) + {{\varvec{KN}}_{28}}r\left( t \right) {p^2}\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{29}}r\left( t \right) p\left( t \right) q\left( t \right) + {{\varvec{KN}}_{210}}{p^3}\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{211}}{p^2}\left( t \right) q\left( t \right) + {{\varvec{KN}}_{212}}p\left( t \right) {q^2}\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{213}}r\left( t \right) {p^3}\left( t \right) + {{\varvec{KN}}_{214}}{p^4}\left( t \right) + {{\varvec{KN}}_{215}}{p^3}\left( t \right) q\left( t \right) + {{\varvec{KN}}_{216}}{p^5}\left( t \right) , \end{aligned}$$

(74)

$$\begin{aligned}&{\varvec{KN}}3_n^{system} = {{\varvec{KN}}_{31}}{r^2}\left( t \right) + {{\varvec{KN}}_{32}}r\left( t \right) p\left( t \right) + {{\varvec{KN}}_{33}}r\left( t \right) q\left( t \right) + {{\varvec{KN}}_{34}}{p^2}\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{35}}p\left( t \right) q\left( t \right) + {{\varvec{KN}}_{36}}{q^2}\left( t \right) + {{\varvec{KN}}_{37}}r\left( t \right) {p^2}\left( t \right) + {{\varvec{KN}}_{38}}{p^3}\left( t \right) \nonumber \\&\quad +\, {{\varvec{KN}}_{39}}{p^2}\left( t \right) q\left( t \right) + {{\varvec{KN}}_{310}}{p^4}\left( t \right) , \end{aligned}$$

(75)

and the coefficients of the nonlinear stiffnesses $(\textit{KN}_{ij})$ are defined in “Appendix A” for the sake of brevity. By employing a dynamic equilibrium technique, the time-dependent terms of the degrees of freedom are written in a series expansion of exponential functions as

$$\begin{aligned} r_{m}= & {} \sum \limits _{n=-N}^N {A_{mn} e^{in\varOmega t}} , \end{aligned}$$

(76)

$$\begin{aligned} p_{m}= & {} \sum \limits _{n=-N}^N {B_{mn} e^{in\varOmega t}} , \end{aligned}$$

(77)

$$\begin{aligned} q_{m}= & {} \sum \limits _{n=-N}^N {C_{mn} e^{in\varOmega t}} , \end{aligned}$$

(78)

and the general dynamic complex equilibrium equations are written as

$$\begin{aligned}&\left\{ { - {n^2}{\varOmega ^2}{{{\varvec{M}}}_{3n \times 3n}} + in\varOmega {{{\varvec{C}}}_{3n \times 3n}} + {{{\varvec{K}}}_{3n \times 3n}}} \right\} {\left\{ \begin{array}{l} {r_n}\\ {p_n}\\ {q_n} \end{array} \right\} _{3n \times 1}}\nonumber \\&\quad = {\left\{ \begin{array}{l} 0\\ 0\\ {{\varvec{F}}}_{n}^{external}\left( \varOmega \right) \end{array} \right\} _{3n \times 1}} + {\left\{ \begin{array}{l} {\varvec{KN}}1_n^{system}\left( {{A_{mn}},{B_{mn}},{C_{mn}},\varOmega } \right) \\ {\varvec{KN}}2_n^{system}\left( {{A_{mn}},{B_{mn}},{C_{mn}},\varOmega } \right) \\ {\varvec{KN}}3_n^{system}\left( {{A_{mn}},{B_{mn}},{C_{mn}},\varOmega } \right) \end{array} \right\} _{3n \times 1}}. \end{aligned}$$

(79)

By solving the discretised coupled 3N equations of motion presented in Eq. (79) using a continuation technique [51,52,53], the nonlinear forced time-dependent mechanical response of the layered hyperelastic structure is obtained.

4 Results and discussion for linear and nonlinear analyses

The coupled motion of shear deformable layered hyperelastic structures is formulated, discretised and solved in the previous sections. In this section, the linear and nonlinear mechanics of the system are analysed and discussed in two main subsections.

4.1 Linear analysis for different shear models

In this subsection, the natural frequencies of the layered hyperelastic structures are analysed and the influence of layering, shear deformation theory and the foundation is discussed in detail.

4.1.1 Model verification

In the first step, in order to verify the current model for analysing layered beam models, the natural frequencies of a three-layered elastic beam structure are obtained for clamped–clamped and pinned–pinned boundaries. Layering is achieved by having steel as the top layer, aluminium in the middle and silicon carbide at the bottom (the elastic material properties of the layers can be found in Ref. [54]), with geometry properties at a length of $L = 2.4 \hbox { m}$, total thickness of $h = 0.03 \hbox { m}$ (0.01 m for each layer) and width of $b = 0.12 \hbox { m}$. The first four transverse natural frequencies and the first axial and rotational natural frequencies are obtained using the third-order shear deformable beam theory and compared with those obtained by ANSYS Workbench [55] in Table 1, and the mode shapes are shown in Fig. 2; it can be seen that the current modelling shows great accuracy in computing the natural frequency terms.

Table 1 Linear natural frequencies of a three-layered elastic beam with pinned–pinned and fixed–fixed boundary conditions in hertz

4.1.2 Layer sorting, slenderness ratio and shear model effect

Properly layering the structure can have a significant effect in changing the natural frequencies of a hyperelastic beam. To make this possible, three different soft materials are assumed with known Mooney–Rivlin hyperelastic coefficients, as shown in Table 2. For the first step, by assuming a single-layer homogeneous hyperelastic beam with the length of 0.2 mm and nondimensional foundation of $K_{L} = 1$ and $K_{S} = 1$, the slenderness ratio ($r = L/h)$ is varied and the fundamental natural frequency is obtained for different shear deformation theories in Table 3. It can be seen that for the single-layer model, the fundamental natural frequency of all the five shear models is in good agreement, especially for the vulcanised rubber beam.

Table 2 Hyperelastic physical properties of soft materials from the literature [56, 57]

Table 3 Fundamental natural frequencies of single-layer hyperelastic beams with different slenderness ratios and shear deformation theories

By increasing the number of layers to two and three, the fundamental natural frequencies are given in Tables 4 and 5, respectively. It can be seen that by having more than a single layer, the homogeneity in the thickness direction is lost, the coupling terms are considerable and, therefore, the difference between different shear models is slightly more than for the homogeneous single-layer model. Furthermore, it can be seen that for all the layered models and boundary conditions, by increasing the slenderness ratio (L/h), the shear effect loses its importance and the results for different shear models become unique.

4.1.3 Foundation effect

To show the influence of a foundation support on the natural frequencies of layered hyperelastic beams, the structure is assumed to be three-layered with equal thicknesses, ($L/h = 20$) and the foundation terms are varied as $K_{L} = [0.0, 1.0, 1.0, 3.0, 4.0, 5.0]$ and $K_{S} = [0.1, 0.2, 0.4, 0.6, 0.8, 1.0]$. The fundamental natural frequencies are shown for both pinned–pinned and clamped–clamped boundary conditions in Tables 6, 7 and 8 for layering as [thermoplastic–silicone–vulcanised rubber], [thermoplastic– vulcanised rubber–silicone] and [silicone–thermoplastic–vulcanised rubber], respectively, using the third-order shear deformable beam model. It can be seen that the layered hyperelastic beam models are more sensitive to variations of the shear term ($K_{s})$ compared with the linear term ($K_{L})$, and adding the foundation increases the fundamental frequency parameter significantly.

Table 4 Fundamental natural frequencies of two-layered hyperelastic beams with different slenderness ratios and shear deformation theories

Table 5 Fundamental natural frequencies of three-layered hyperelastic beams with different slenderness ratios and shear deformation theories

Table 6 Fundamental natural frequencies of three-layered hyperelastic beams [thermoplastic–silicone–vulcanised rubber] with different slenderness ratios and shear deformation theories

Table 7 Fundamental natural frequencies of three-layered hyperelastic beams [thermoplastic–vulcanised rubber–silicone] with different slenderness ratios and shear deformation theories

Table 8 Fundamental natural frequencies of three-layered hyperelastic beams [silicone–thermoplastic–vulcanised rubber] with different slenderness ratios and shear deformation theories

4.2 Nonlinear analysis

The nonlinear dynamics of layered hyperelastic thick beam structures is investigated in this section for various layer, shear and material position models.

4.2.1 Comparison of different shear models

Five different shear deformable beam theories were used in previous sections for modelling and formulation of the layered hyperelastic beam structure. In this section, the amplitude response of the sandwich structure for different shear models is examined. Three layers are assumed, and the thickness of the layers is assumed as $h = [h/4, h/2, h/4]$ with $L/h = 10$, $K_{L} = K_{NL} = 1$, $K_{s} = 0.1$, with the material sorting as [silicone–vulcanised rubber–thermoplastic]. In the first step, the influence of considering the shear effect as negligible (CBT), linear (Timoshenko) or higher order (third order) is examined, and the axial, transverse and rotation amplitudes are obtained, as shown in Figs. 3, 4 and 5 for clamped–clamped and Figs. 6, 7 and 8 for pinned–pinned boundary conditions. It can be seen that for both boundary conditions, the Timoshenko beam model gives the highest maximum amplitude for the dominant axial, transverse and rotation deformation. Furthermore, increasing the shear effect from the linear model to higher-order moves the resonance peak to lower frequencies.

Fig. 3

Influence of considering shear effect on the axial amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{A}_{{21}}$, b $\textit{A}_{{22}}$ and c $\textit{A}_{{23}}$

Fig. 4

Influence of considering shear effect on the transverse amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{C}_{{11}}$, b $\textit{C}_{{31}}$, c $\textit{C}_{{12}}$, d $\textit{C}_{{32}}$, e $\textit{C}_{{13}}$, and f $\textit{C}_{{33}}$

Fig. 5

Influence of considering shear effect on the rotation amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{B}_{{11}}$, b $\textit{B}_{{31}}$, c $\textit{B}_{{12}}$, d $\textit{B}_{{32}}$, e $\textit{B}_{{13}}$, and f $\textit{B}_{{33}}$

Fig. 6

Influence of considering shear effect on the axial amplitude response of the sandwich hyperelastic pinned–pinned beam a $\textit{A}_{{21}}$, b $\textit{A}_{{22}}$ and c $\textit{A}_{{23}}$

Fig. 7

Influence of considering shear effect on the transverse amplitude response of the sandwich hyperelastic pinned–pinned beam a $\textit{C}_{{11}}$, b $\textit{C}_{{31}}$, c $\textit{C}_{{12}}$, d $\textit{C}_{{32}}$, e $\textit{C}_{{13}}$ and f $\textit{C}_{{33}}$

Fig. 8

Influence of considering shear effect on the rotation amplitude response of the sandwich hyperelastic pinned–pinned beam a $\textit{B}_{{11}}$, b $\textit{B}_{{31}}$, c $\textit{B}_{{12}}$, d $\textit{B}_{{32}}$, e $\textit{B}_{{13}}$ and f $\textit{B}_{{33}}$

The influence of using different types of higher-order shear deformable theories on the amplitude response is investigated for the similar three-layered hyperelastic beams with the given properties. Figures 9, 10, 11, 12, 13 and 14 show the axial, transverse and rotation amplitudes of clamped–clamped and pinned–pinned thick beam models, respectively. The results for the different higher-order shear models are fairly in good agreement, especially for the pinned–pinned boundary condition. Comparing the amplitude response of the dominant terms of axial, transverse and rotation motions, it can be seen that the highest amplitude is for the third-order beam model and the lowest belongs to the exponential beam model.

Fig. 9

Influence of different higher-order shear effect models on the axial amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{A}_{{21}}$, b $\textit{A}_{{22}}$, and c $\textit{A}_{{23}}$

Fig. 10

Influence of different higher-order shear effect models on the transverse amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{C}_{{11}}$, b $\textit{C}_{{31}}$, c $\textit{C}_{{12}}$, d $\textit{C}_{{32}}$, e $\textit{C}_{{13}}$, and f $\textit{C}_{{33}}$

Fig. 11

Influence of different higher-order shear effect models on the rotation amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{B}_{{11}}$, b $\textit{B}_{{31}}$, c $\textit{B}_{{12}}$, d $\textit{B}_{{32}}$, e $\textit{B}_{{13}}$ and f $\textit{B}_{{33}}$

Fig. 12

Influence of different higher-order shear effect models on the axial amplitude response of the sandwich hyperelastic pinned–pinned beam a $\textit{A}_{{21}}$, b $\textit{A}_{{22}}$ and c $\textit{A}_{{23}}$

Fig. 13

Influence of different higher-order shear effect models on the transverse amplitude response of the sandwich hyperelastic pinned–pinned beam a $\textit{C}_{{11}}$, b)$\textit{C}_{{31}}$, c $\textit{C}_{{12}}$, d $\textit{C}_{{32}}$, e $\textit{C}_{{13}}$ and f $\textit{C}_{{33}}$

Fig. 14

Influence of different higher-order shear effect models on the rotation amplitude response of the sandwich hyperelastic pinned–pinned beam a $\textit{B}_{{11}}$, b $\textit{B}_{{31}}$, c $\textit{B}_{{12}}$, d $\textit{B}_{{32}}$, e $\textit{B}_{{13}}$ and f $\textit{B}_{{33}}$

4.2.2 Influence of layering

Layering a hyperelastic structure for different purposes can change the dynamic behaviour of the structure significantly. In Sect. 4.1.1., this influence on the linear vibration response is analysed, and in this section, the nonlinear vibration response of the structure based on the number of layers is examined. To this end, for a homogeneous single-layer structure, the dominant amplitude responses are shown in Fig. 15, for thermoplastic, vulcanised rubber and silicone hyperelastic thick beams using the third-order shear deformable beam theory model. It can be seen that thermoplastic and silicone show a stiffness hardening effect, while the vulcanised rubber beam model shows a drop in the amplitude response of the axial motion while increasing the frequency and continues to go up afterwards.

Fig. 15

The amplitude response of the single-layer hyperelastic clamped–clamped beam a $\textit{A}_{{22}}$, b $\textit{C}_{{11}}$, c $\textit{B}_{{11}}$

By increasing the layers to two by having $h_{1} = h_{2} = h/2$, the dominant longitudinal, transverse and rotation amplitude responses of the structure are shown for different hyperelastic materials in Fig. 16 for a combination of different hyperelastic materials which the combination is given as Mat = ([mat1- mat2], [mat1- mat3], [mat2- mat3]) with mat1 = thermoplastic, mat2 = silicone, mat3 = vulcanised rubber. It can be seen that the highest transverse amplitude belongs to the material combination of [mat2- mat3], while the other two models have almost the same behaviour.

Fig. 16

The amplitude response of the two-layered hyperelastic clamped–clamped beam a $\textit{A}_{{21}}$, b $\textit{C}_{{11}}$, c $\textit{B}_{{11}}$

Finally, by having three layers $(h_{1} = h_{2} = h_{3} = h/3)$ and varying the layers as Mat = ([mat1-mat2-mat3], [mat2-mat1-mat3], [mat1-mat3-mat2]), the dominant amplitude responses of the longitudinal, transverse and rotation motions are shown in Fig. 17. It can be seen that the material distribution [mat2- mat1- mat3] has the lowest maximum axial amplitude and the highest transverse and rotation amplitudes; this shows that for the other two material models, the coupling between the axial and transverse motion is noticeably higher and should be considered.

Fig. 17

The amplitude response of the three-layered hyperelastic clamped–clamped beam a $\textit{A}_{{21}}$, b $\textit{C}_{{11}}$, c $\textit{B}_{{11}}$

4.2.3 Influence of layer thickness

Changing the thickness of the layers can change the nonlinear vibration response of the structure significantly. To show this influence, the material distribution is Mat = [mat1-mat2-mat3] and the thickness of layers are $h = ([h/4, h/4, h/2], [h/2\, h/4, h/4]$, [h/4, h/2, h/4]). The frequency–amplitude response of the structure is plotted in Figs. 18, 19 and 20 for axial, transverse and rotation deformations, respectively. It can be seen that changing the thickness of the layers has a significant effect in varying the nonlinear behaviour of the system. Besides, the maximum amplitude of all the deformation coordinates moves to higher frequencies for $h = [h/2, h/4, h/4]$ and the other two models show similar behaviour in dominant amplitude coordinates.

Fig. 18

Influence of the thickness of each layer on the axial amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{A}_{{21}}$, b $\textit{A}_{{22}}$ and c $\textit{A}_{{23}}$

Fig. 19

Influence of the thickness of each layer on the transverse amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{C}_{{11}}$, b $\textit{C}_{{31}}$, c $\textit{C}_{{12}}$, d $\textit{C}_{{32}}$, e $\textit{C}_{{13}}$ and f $\textit{C}_{{33}}$

Fig. 20

Influence of the thickness of each layer on the rotation amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{B}_{{11}}$, b $\textit{B}_{{31}}$, c $\textit{B}_{{12}}$, d $\textit{B}_{{32}}$, e $\textit{B}_{{13}}$, and f $\textit{B}_{{33}}$

4.2.4 Influence of material positioning

To show the importance of the position of the hyperelastic material in a layered structure, a three-layered beam is assumed with the thickness of $h= [h/4, h/2, h/4]$ which shows that the middle layer (the core) is thicker than the outer layers. In this section, by varying the materials in the layers, the nonlinear forced vibration response of the system is studied. To do this, the position of the material is varied and the dominant amplitude–frequency responses in axial, transverse and rotation motions of the structure are shown in Figs. 21 and 22 for pinned–pinned and clamped–clamped conditions, respectively. It can be seen that for both boundary conditions, the maximum amplitudes sweep to lower frequencies when the material positioning is [mat1-mat2-mat3]; the clamped–clamped and pinned-pinned beam models show that the dominant rotation coordinate reaches its highest when the material positioning is [mat1-mat2-mat3].

Fig. 21

Influence of the material positioning on the amplitude response of the sandwich hyperelastic pinned–pinned beam a $\textit{A}_{{21}}$, b $\textit{B}_{{11}}$, c $\textit{C}_{{11}}$

Fig. 22

Influence of the material positioning on the amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{A}_{{21}}$, b $\textit{C}_{{11}}$, c $\textit{B}_{{11}}$

4.2.5 Influence of layer positioning

Another important goal of this study is to show the influence of layering and positioning the layers in manufacturing sandwich hyperelastic structures. To demonstrate this effect, the position of the layers is varied with the thickness of $h = [h/4, h/2, h/4]$ and the amplitude–frequency responses of the structures are shown in Figs. 23, 24 and 25 for clamped–clamped third-order shear deformable hyperelastic thick beams. It can be seen that the layer positioning has a notable effect in changing the coupling motion of the structure, based on the requirements of the design.

Fig. 23

Influence of the layer positioning on the axial amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{A}_{{21}}$, b $\textit{A}_{{22}}$ and c $\textit{A}_{{23}}$

Fig. 24

Influence of the layer positioning on the transverse amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{C}_{{11}}$, b $\textit{C}_{{31}}$, c $\textit{C}_{{12}}$, d $\textit{C}_{{32}}$, e $\textit{C}_{{13}}$ and f $\textit{C}_{{33}}$

Fig. 25

Influence of the layer positioning on the rotation amplitude response of the sandwich hyperelastic clamped–clamped beam a $\textit{B}_{{11}}$, b $\textit{B}_{{31}}$, c $\textit{B}_{{12}}$, d $\textit{B}_{{32}}$, e $\textit{B}_{{13}}$ and f $\textit{B}_{{33}}$

5 Summary and conclusions

In this study, a detailed layerwise analysis of the time-dependent mechanics of hyperelastic beams structures is given using five different shear deformation theories. The hyperelasticity was modelled following the Mooney–Rivlin hyperelastic strain energy density model, and the beam was assumed to lie on a foundation including linear, nonlinear and shear layers. Equations of motion were derived using Hamilton’s principle together with different shear deformable beam theories. Solving the equations of motion using a dynamic equilibrium technique, it was shown that:

• The classic beam theory predicts the fundamental frequency term of hyperelastic-layered beam models higher than the studied shear deformable beam models.

• By increasing the length-to-thickness ratio, the influence of the type of boundary conditions decreases.

• Similar to elastic beams, the hyperelastic-layered beam model shows higher sensitivity to shear effects when the length-to-thickness ratio is lower.

• The higher-order shear deformable beam models (namely third-order, exponential and trigonometric) give very close results for natural frequency terms, while the nonlinear behaviours are slightly different.

• For linear natural frequencies, it was shown that having a foundation can increase the fundamental natural frequency of hyperelastic-layered beams significantly and this effect is higher for the shear layer compared with the linear layer.

• For nonlinear forced time-dependent analysis of layered hyperelastic beams, the Timoshenko beam model gives the highest maximum amplitude for the dominant longitudinal, transverse and rotation deformations, compared with the other shear deformable models. Similarly, for higher-order shear models, the highest amplitudes are for the third-order beam model and the lowest one belongs to the exponential beam model.

• For the two-layered hyperelastic beam model examined in this study, it is shown that the highest transverse amplitude belongs to the material combination of silicone and vulcanised rubber. Similarly, for the three-layered model, the material distribution silicone–thermoplastic–vulcanised rubber has the lowest maximum axial amplitude and the highest transverse and rotation amplitudes.

• The influence of each layer’s thickness is examined showing that changing the thickness of the layers can change the nonlinear vibration response of the structure significantly.

• Hyperelastic material sorting has been shown to be a promising designing parameter in changing the dynamic behaviour of the structure for both linear and nonlinear analysis. For the studied model, both boundary conditions, the maximum amplitudes sweep to lower frequencies when the material positioning is [mat1- mat2- mat3].

Overall, since layered hyperelastic structures are replacing single-layer hyperelastic structures in many designs and applications such as food packaging, bottles, tubes and pipes, it is important to comprehend and predict the changes in their mechanical behaviour before employing them, especially their coupling motion behaviour. The results of this study are a step forward in realising the changes in the mechanical response of laminated hyperelastic beams when different materials and layers are used.

Appendix A

The nonlinear coefficients are defined as

$$\begin{aligned}&KN_{11} \left( {l,i,j} \right) :12\eta A_{11} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{U}'_{i} \left( \gamma \right) {U}'_{j} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A1)

$$\begin{aligned}&KN_{12} \left( {l,i,j} \right) :24\eta ^{2}B_{22} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{U}'_{i} \left( \gamma \right) {W}''_{j} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A2)

$$\begin{aligned}&KN_{13} \left( {l,i,j} \right) :-24\eta B_{11} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{U}'_{i} \left( \gamma \right) {\Phi }'_{j} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A3)

$$\begin{aligned}&K{N_{14}}\left( {l,i,j} \right) : - \eta \left( {4{A_{11}} - {D_{44}}} \right) \int \limits _0^1 {{U_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W'}_i}\left( \gamma \right) {{W'}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad + 12{\eta ^3}{D_{22}}\int \limits _0^1 {{U_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W''}_i}\left( \gamma \right) {{W''}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A4)

$$\begin{aligned}&K{N_{15}}\left( {l,i,j} \right) : - 2{D_{44}}\int \limits _0^1 {{U_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W'}_i}\left( \gamma \right) {\Phi _j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma - 24{\eta ^2}{D_{33}}\int \limits _0^1 {{U_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W''}_i}\left( \gamma \right) {{\Phi '}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\ \end{aligned}$$

(A5)

$$\begin{aligned}&KN_{16} \left( {l,i,j} \right) :\frac{1}{\eta }D_{44} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {\Phi _{i} \left( \gamma \right) \Phi _{j} \left( \gamma \right) } \right] \mathrm{{d}}\gamma +12\eta D_{11} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{\Phi }'_{i} \left( \gamma \right) {\Phi }'_{j} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A6)

$$\begin{aligned}&KN_{17} \left( {l,i,j,k} \right) :12\eta ^{2}A_{11} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{U}'_{i} \left( \gamma \right) {W}'_{j} \left( \gamma \right) {W}'_{k} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A7)

$$\begin{aligned}&KN_{18} \left( {l,i,j,k} \right) :12\eta ^{3}B_{22} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{W}'_{i} \left( \gamma \right) {W}'_{j} \left( \gamma \right) {W}''_{k} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A8)

$$\begin{aligned}&KN_{19} \left( {l,i,j,k} \right) :-12\eta ^{2}B_{11} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{W}'_{i} \left( \gamma \right) {W}'_{j} \left( \gamma \right) {\Phi }'_{k} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A9)

$$\begin{aligned}&KN_{110} \left( {l,i,j,k,m} \right) :3\eta ^{3}A_{11} \int \limits _0^1 {U_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{W}'_{i} \left( \gamma \right) {W}'_{j} \left( \gamma \right) {W}'_{k} \left( \gamma \right) {W}'_{m} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A10)

$$\begin{aligned}&KN_{21} \left( {l,i,j} \right) :12\eta ^{2}B_{22} \int \limits _0^1 {W_{l} \left( \gamma \right) } \frac{\mathrm{{d}}^{2}}{\mathrm{{d}}\gamma ^{2}}\left[ {{U}'_{i} \left( \gamma \right) {U}'_{j} \left( x \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A11)

$$\begin{aligned}&K{N_{22}}\left( {l,i,j} \right) :24{\eta ^3}{D_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{{U'}_i}\left( \gamma \right) {{W''}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad - \left( {8{A_{11}} - 2{D_{44}}} \right) \eta \int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{U'}_i}\left( \gamma \right) {{W'}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A12)

$$\begin{aligned}&KN_{23} \left( {l,i,j} \right) :-24\eta ^{2}D_{33} \int \limits _0^1 {W_{l} \left( \gamma \right) } \frac{\mathrm{{d}}^{2}}{\mathrm{{d}}\gamma ^{2}}\left[ {{U}'_{i} \left( \gamma \right) {\Phi }'_{j} \left( \gamma \right) } \right] \mathrm{{d}}\gamma -2D_{44} \int \limits _0^1 {W_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{U}'_{i} \left( \gamma \right) \Phi _{j} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A13)

$$\begin{aligned}&{KN_{24}}\left( {l,i,j} \right) : - \left( {4{B_{22}} - {E_{66}}} \right) {\eta ^2}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{x^2}}}\left[ {{{W'}_i}\left( \gamma \right) {{W'}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad - \left( {8{B_{22}} - 2{E_{66}}} \right) {\eta ^2}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W'}_i}\left( \gamma \right) {{W''}_j}\left( \gamma \right) } \right] \mathrm{{d}}x\nonumber \\&\quad + 12{\eta ^4}{E_{44}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{{W''}_i}\left( \gamma \right) {{W''}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A14)

$$\begin{aligned}&{KN_{25}}\left( {l,i,j} \right) : - 2\eta {E_{66}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{{W'}_i}\left( \gamma \right) {\Phi _j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma - 24{\eta ^3}{E_{33}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{{W''}_i}\left( \gamma \right) {{\Phi '}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad + \left( {8{B_{11}} - 2{E_{77}}} \right) \eta \int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W'}_i}\left( \gamma \right) {{\Phi '}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma - 2\eta {E_{66}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W''}_i}\left( \gamma \right) {\Phi _j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A15)

$$\begin{aligned}&{KN_{26}}\left( {l,i,j} \right) :{E_{66}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{\Phi _i}\left( \gamma \right) {\Phi _j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma + 2{E_{77}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{\Phi _i}\left( \gamma \right) {{\Phi '}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad + 12{\eta ^2}{E_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{\Phi _i}^\prime \left( \gamma \right) {{\Phi '}_j}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A16)

$$\begin{aligned}&{KN_{27}}\left( {l,i,j,k} \right) :12{\eta ^2}{A_{11}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{U_i}^\prime \left( \gamma \right) {{U'}_j}\left( \gamma \right) {{W'}_k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A17)

$$\begin{aligned}&K{N_{28}}\left( {l,i,j,k} \right) :12{\eta ^3}{B_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{{U'}_i}\left( \gamma \right) {{W'}_j}\left( \gamma \right) {{W'}_k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad + 24{\eta ^3}{B_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{U'}_i}\left( \gamma \right) {{W'}_j}\left( \gamma \right) {{W''}_k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A18)

$$\begin{aligned}&{KN_{29}}\left( {l,i,j,k} \right) : - 24{\eta ^2}{B_{11}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{U'}_i}\left( \gamma \right) {{W'}_j}\left( \gamma \right) {{\Phi '}_k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A19)

$$\begin{aligned}&{KN_{210}}\left( {l,i,j,k} \right) : - \left( {4{A_{11}} - 2{D_{44}}} \right) {\eta ^2}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W'}_i}\left( \gamma \right) {W_j}^\prime \left( \gamma \right) {W_k}^\prime \left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad - {K_{NL}}\int \limits _0^1 {{W_l}\left( \gamma \right) } {W_i}\left( \gamma \right) {W_j}\left( \gamma \right) {W_k}\left( \gamma \right) \mathrm{{d}}\gamma \nonumber \\&\quad + 12{\eta ^4}{D_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{W_i}^\prime \left( \gamma \right) {W_j}^{\prime \prime }\left( \gamma \right) {W_k}^{\prime \prime }\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad + 12{\eta ^4}{D_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{W_i}^\prime \left( \gamma \right) {W_j}^\prime \left( \gamma \right) {W_k}^{\prime \prime }\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A20)

$$\begin{aligned}&{KN_{211}}\left( {l,i,j,k} \right) : - 12{\eta ^3}{D_{33}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{{W'}_i}\left( \gamma \right) {W_j}^\prime \left( \gamma \right) {{\Phi '}_k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad - 3\eta {D_{44}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W'}_i}\left( \gamma \right) {W_j}^\prime \left( \gamma \right) {\Phi _k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad - 24{\eta ^3}{D_{33}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W'}_i}\left( \gamma \right) {W_j}^{\prime \prime }\left( \gamma \right) {{\Phi '}_k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A21)

$$\begin{aligned}&{KN_{212}}\left( {l,i,j,k} \right) :{D_{44}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{W_i}^\prime \left( \gamma \right) {\Phi _j}\left( \gamma \right) {\Phi _k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad + 12{\eta ^2}{D_{11}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{W_i}^\prime \left( \gamma \right) {{\Phi '}_j}\left( \gamma \right) {{\Phi '}_k}\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A22)

$$\begin{aligned}&KN_{213} \left( {l,i,j,k,m} \right) :12\eta ^{3}A_{11} \int \limits _0^1 {W_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{U}'_{i} \left( \gamma \right) {W}'_{j} \left( \gamma \right) W_{k}^{\prime }\left( \gamma \right) W_{m}^{\prime }\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A23)

$$\begin{aligned}&{KN_{214}}\left( {l,i,j,k,m} \right) :3{\eta ^4}{B_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{{{\mathrm{{d}}^2}}}{{\mathrm{{d}}{\gamma ^2}}}\left[ {{{W'}_i}\left( \gamma \right) {{W'}_j}\left( \gamma \right) {W_k}^\prime \left( \gamma \right) {W_m}^\prime \left( \gamma \right) } \right] \mathrm{{d}}\gamma \nonumber \\&\quad + 12{\eta ^4}{B_{22}}\int \limits _0^1 {{W_l}\left( \gamma \right) } \frac{\mathrm{{d}}}{{\mathrm{{d}}\gamma }}\left[ {{{W'}_i}\left( \gamma \right) {{W'}_j}\left( \gamma \right) {W_k}^\prime \left( \gamma \right) {W_m}^{\prime \prime }\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A24)

$$\begin{aligned}&KN_{215} \left( {l,i,j,k,m} \right) :-12\eta ^{3}B_{11} \int \limits _0^1 {W_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{W}'_{i} \left( \gamma \right) {W}'_{j} \left( \gamma \right) W_{k}^{\prime }\left( \gamma \right) {\Phi }'_{m} \left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A25)

$$\begin{aligned}&KN_{216} \left( {l,i,j,k,m,n} \right) :3\eta ^{4}A_{11} \int \limits _0^1 {W_{l} \left( \gamma \right) } \frac{\mathrm{{d}}}{\mathrm{{d}}\gamma }\left[ {{W}'_{i} \left( \gamma \right) {W}'_{j} \left( \gamma \right) W_{k}^{\prime }\left( \gamma \right) W_{m} ^{\prime }\left( \gamma \right) W_{n}^{\prime }\left( \gamma \right) } \right] \mathrm{{d}}\gamma , \end{aligned}$$

(A26)