Residual Terrain Modelling: The Harmonic Correction for Geoid Heights

Abstract

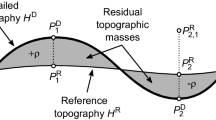
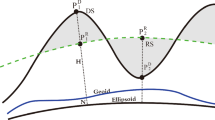
The harmonic correction (HC) is one of the key quantities when using residual terrain modelling (RTM) for high-frequency gravity field modelling. In the RTM technique, high-frequency topographic gravitational signals are obtained through removing gravitational effects of a long-wavelength reference surface, e.g., MERIT2160. There might be points located below the reference surface. In such cases, the RTM gravity field is calculated in the non-harmonic condition, HC is therefore required. Over past decades, though various methods have been proposed to handle the HC issue for the RTM technique, most of them were focused on the HC for RTM gravity anomaly rather than for other gravity functionals, such as RTM geoid height. In practice, the HC for RTM geoid height was generally assumed to be negligible, but a detailed quantification was missing for present-day RTM computations. This might cause large errors in the regional geoid determination over rugged areas. In this study, we derive HC expressions for the RTM geoid height in the framework of the classical condensation method. The HC terms are derived under four different assumptions separately: residual masses approximated by an unlimited Bouguer plate, residual masses approximated by a limited Bouguer plate which overcomes the mass inconsistency effect, residual masses approximated by a Bouguer shell which overcomes the effect of planar approximation, and residual masses approximated by a limited Bouguer shell which overcomes the errors induced by both planar approximation and mass-inconsistency. The errors due to various approximations in HC terms are investigated through comparison among various terms. Besides, HC terms are computed using an expansion up to degree and order 2159. Our results show that HC for RTM geoid height is less 1 mm and could be ignored over $\sim 99$% of continental areas, but be of great significance for regional geoid determination over mountain areas, e.g., more than 10 cm effect over very rugged areas. The validation through comparison with terrestrial measurements and a baseline solution of the RTM technique proves that the HC terms provided in this study can improve the accuracy of RTM geoid heights and are expected to be useful for applications of the RTM technique in regional and global gravity field modelling.

Appendices

Appendix A: Derivation of Harmonic Correction for the Geoid Height under Unlimited Bouguer Plate Approximation

As is introduced in Sect. 2.1, the HC-UBP with unlimited Bouguer plate approximation is value of HC-LBP with limited Bouguer plate approximation when $R\rightarrow \infty$,

$$\begin{aligned} N^{\text {HC-UBP}}(P_+)= & {} \frac{1}{\gamma }\lim _{R\rightarrow \infty }V^{\text {HC-LBP}}(P_+) \nonumber \\= & {} \frac{1}{\gamma }\lim _{R\rightarrow \infty }[2\pi G\rho hR-\pi G\rho (R^2\mathrm {\ln }\frac{R}{\sqrt{R^2+h^2}-h}-h^2+h\sqrt{R^2+h^2})]\nonumber \\= & {} \frac{\pi G\rho }{\gamma }\lim _{R\rightarrow \infty }[2hR-R^2\mathrm {\ln }\frac{R}{\sqrt{R^2+h^2}-h}+h^2-h\sqrt{R^2+h^2}]\nonumber \\= & {} \frac{\pi G\rho }{\gamma }\lim _{R\rightarrow \infty }[2hR-R^2\mathrm {\ln }\frac{R}{\sqrt{R^2+h^2}-h}-h\sqrt{R^2+h^2}]+\frac{\pi G\rho h^2 }{\gamma } \end{aligned}$$

(21)

Let $\kappa =\frac{1}{R}$, then

$$\begin{aligned}&\lim _{R \rightarrow \infty }[2hR-R^2\ln \frac{R}{\sqrt{R^2+h^2}-h}-h\sqrt{R^2+h^2}]\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}[\frac{2h}{\kappa }+\frac{1}{\kappa ^2}\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-\frac{h}{\kappa }\sqrt{1+\kappa ^2h^2}]\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}\frac{2h+\frac{1}{\kappa }\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-h\sqrt{1+\kappa ^2h^2}}{\kappa } \end{aligned}$$

(22)

It follows from L’Hospital’s rule (Taylor 1952) that

$$\begin{aligned}&\lim _{\kappa \rightarrow 0}\frac{2h+\frac{1}{\kappa }\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-h\sqrt{1+\kappa ^2h^2}}{\kappa }\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}\frac{d}{d\kappa }[2h+\frac{1}{\kappa }\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-h\sqrt{1+\kappa ^2h^2}]\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}[\frac{h^2-\kappa h^3(\sqrt{1+\kappa ^2h^2}-\kappa h)}{\sqrt{1+\kappa ^2h^2}(\sqrt{1+\kappa ^2h^2}-\kappa h)}-\frac{\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}+\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)}{\kappa ^2}] \end{aligned}$$

(23)

When $\kappa \rightarrow 0$, the first term above tends to $h^2$. The limit of the second term is concluded by applying L’Hospital’s rule again, that is

$$\begin{aligned}&\lim _{\kappa \rightarrow 0}\frac{\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}+\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)}{\kappa ^2} \nonumber \\&\quad =\lim _{\kappa \rightarrow 0}\frac{\frac{d}{d\kappa }[\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}+\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)]}{2\kappa } \end{aligned}$$

(24)

By direct computation of derivatives, we yield

$$\begin{aligned}&\frac{d}{d\kappa }[\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}]=\frac{h}{\sqrt{1+\kappa ^2h^2}-\kappa h}-\frac{\kappa ^2h^3}{(\sqrt{1+\kappa ^2h^2}-\kappa h)^2\sqrt{1+\kappa ^2h^2}}+\frac{\kappa h^2}{(\sqrt{1+\kappa ^2h^2}-\kappa h)^2}\end{aligned}$$

(25)

$$\begin{aligned}&\frac{d}{d\kappa }[\ln (\sqrt{1+\kappa ^2h^2}-\kappa h]=\frac{\kappa h^2}{(\sqrt{1+\kappa ^2h^2}-\kappa h)\sqrt{1+\kappa ^2h^2}}-\frac{h}{\sqrt{1+\kappa ^2h^2}-\kappa h} \end{aligned}$$

(26)

Therefore,

$$\begin{aligned}&\lim _{\kappa \rightarrow 0}\frac{\frac{d}{d\kappa }[\frac{\kappa h}{\sqrt{1+\kappa ^2h^2}-\kappa h}+\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)]}{2\kappa }\nonumber \\&\quad =\lim _{\kappa \rightarrow 0}\frac{1}{2}[\frac{h^2(2\sqrt{1+\kappa ^2h^2}-\kappa h)}{(\sqrt{1+\kappa ^2h^2}-\kappa h)^2\sqrt{1+\kappa ^2h^2}}-\frac{\kappa h^3}{(\sqrt{1+\kappa ^2h^2}-\kappa h)^2\sqrt{1+\kappa ^2h^2}}]\nonumber \\&\quad =h^2 \end{aligned}$$

(27)

Combing Eqs. (23), (24) and (27), we obtain

$$\begin{aligned} \lim _{\kappa \rightarrow 0}\frac{2h+\frac{1}{\kappa }\ln (\sqrt{1+\kappa ^2h^2}-\kappa h)-h\sqrt{1+\kappa ^2h^2}}{\kappa }=0 \end{aligned}$$

(28)

Therefore,

$$\begin{aligned} N^{\text {HC-UBP}}(P_+)=\frac{\pi G\rho h^2}{\gamma } \end{aligned}$$

(29)

Appendix B: Derivation of Harmonic Correction for Geoid Height under Limited Bouguer Shell Approximation

Fig. 14

Geometry of limited Bouguer shell (spherical cap) and respective compressed mass layer. The left panel displays a limited Bouguer shell where the inner radius is denoted as $r_1$, the outer radius $r_2$, the thickness h, and the density $\rho$. The computation point $P_+$ locates above the inner boundary and its respective point on the outer boundary is $P^\mathrm {R}$. The right panel displays the respective compressed mass layer of the limited Bouguer shell. It shares the same masses with the spherical cap. $\psi _0$ is the half-angle subtended at the Earth’s centre

The geometry of the limited Bouguer shell is represented by a spherical cap at the left panel of Fig. 14. The inner radius of spherical cap is $r_1$, outer radius $r_2$, and density $\rho$. $\psi _0$ is the half-angle subtended at the Earth’s centre. $P_+ (0,0,r)$ denotes the computation point when it is located below the reference surface and the subscript $'+'$ indicates that the point adheres to or just above the Earth’s surface. The magnitude of height difference between $P_+$ and its respective point $P^{\mathrm {R}}$ on the reference surface is h. Its generated gravitational potential is (Tenzer et al. 2007; Kadlec 2011)

$$\begin{aligned} V=G\rho \int _{0}^{2\pi }\int _{0}^{\psi }\int _{r_1}^{r_2}\frac{1}{l}r'^2\sin \psi 'dr'd\psi 'd\alpha ' \end{aligned}$$

(30)

with $(\psi ',\alpha ',r')$ indicating the coordinates of integration point and

$$\begin{aligned} l=\sqrt{r^2+r'^2-2rr'\cos \psi '} \end{aligned}$$

(31)

Its analytical solution was widely discussed by LaFehr (1991), Hensel (1992), Heck and Seitz (2007), Tenzer et al. (2007), and Kadlec (2011). Here, the general solution in Kadlec (2011) was adopted. It adapts for various cases when computation points are located out or in the spherical cap.

$$\begin{aligned} V^{\mathrm {SC}}= & {} 2\pi G\rho \left[ \frac{(r_1-r)\vert r-r_1\vert (r+2r_1)+(r-r_2)\vert r-r_2\vert (r+2r_2)}{6r}\right. \nonumber \\&\quad +\,\frac{1}{2}r^2\sin ^2\psi \cos \psi \ln (\frac{r_2+l_2-r\cos \psi }{r_1+l_1-r\cos \psi })+\frac{l_2^3-l_1^3}{3r}\nonumber \\&\quad +\,\frac{1}{2}\cos \psi (l_2(r_2-r\cos \psi )-l_1(r_1-r\cos \psi )))\left. \right] \end{aligned}$$

(32)

where

$$\begin{aligned} l_1= & {} \sqrt{r^2+r_1^2-2rr_1\cos \psi }\nonumber \\ l_2= & {} \sqrt{r^2+r_2^2-2rr_2\cos \psi } \end{aligned}$$

(33)

In the framework of the condensation method under limited Bouguer shell approximation, the spherical cap is compressed into a mass layer with a constant radius $r_1$, infinitesimal thickness, and shares the same mass with the spherical cap. The spherical cap layer is moved down to just below the computation point $P_+$ (right panel at Fig. 14). Its generated gravitational potential could be derived following (Tenzer et al. 2007; Kadlec 2011)

$$\begin{aligned} V^{\mathrm {SCL}}=G\rho _c\int _{0}^{2\pi }\int _{0}^{\psi }\frac{1}{l}r_1^2\sin \psi 'd\psi ' \end{aligned}$$

(34)

with $\rho _c$ indicating the density of compressed masses, $(\psi ',\alpha ',r_1)$ the coordinates of integration point and

$$\begin{aligned} l=\sqrt{2r_1^2-2r_1^2\cos \psi '} \end{aligned}$$

(35)

After integration over $\alpha '$, we get

$$\begin{aligned} V^{\mathrm {SCL}}=2\pi G\rho _c\int _{0}^{\psi }\frac{1}{l}r_1^2\sin \psi 'd\psi 'd\alpha ' \end{aligned}$$

(36)

After integration over $\psi '$, we get

$$\begin{aligned} V^{\mathrm {SCL}}=\frac{2\pi G\rho _c r_1}{r}({\sqrt{r^2+r_1^2-2rr_1\cos \psi }-\sqrt{r^2+r_1^2-2rr_1}}) \end{aligned}$$

(37)

For computation point $P_+$, the HC for geoid height is

$$\begin{aligned} N^{\text {HC-LBS}}_{\mathrm {Spherical\, Cap}}(P_+)=\frac{V^{\mathrm {SCL}}(P_+)-V^{\mathrm {SC}}(P_+)}{\gamma (P_+)} \end{aligned}$$

(38)

Fig. 15

Differences of HC for geoid height based on various LBS, one using tesseroid for calculation, another uses spherical cap. $N^{\text {HC-LBS}}$ indicates HC for geoid height under LBS using tesseroid for calculation, $N^{\text {HC-LBS}}_{\text {Spherical Cap}}$ HC for geoid height under LBS using spherical cap for calculation

The comparison between two kinds of HC under LBS is implemented with an integration radius varying from 0 to 550 km. In this experiment, $N^{\text {HC-LBS}}$ is calculated following the method introduced in Sect. 2.3. The tesseroid is bounded by surfaces defined by $\lambda =-\psi$ and $\lambda =\psi$, $\varphi =-\psi$ and $\varphi =\psi$, and $r=r_1$ and $r=r_2$. The HC has calculated through diving the integration masses into a series of the prism at a resolution of $15^{\prime \prime }$. $N^{\text {HC-LBS}}_{\text {Spherical Cap}}$ is calculated with Eq.(38). The differences are shown in Fig. 15. It is obvious that the differences between $N^{\text {HC-LBS}}$ and $N^{\text {HC-LBS}}_{\text {Spherical Cap}}$ reduce with increasing integration radius. When the integration radius is larger than $\sim 20$ km, the differences would be less than 0.05 cm, which is able to be ignored in the most practical applications.