1 Introduction

Although stochastic differential equations (SDEs) have been ubiquitously applied in areas such as finance (see e.g. Kalogeropoulos et al. 2010; Stramer et al. 2017,), climate modelling (see e.g. Majda et al. 2009; Chen et al. 2014,) and life sciences (see e.g. Golightly and Wilkinson 2011; Fuchs 2013; Wilkinson 2018; Picchini and Forman 2019,), their widespread uptake is hindered by the significant challenge of fitting such models to partial data at discrete times. General nonlinear, multivariate SDEs rarely admit analytic solutions, necessitating the use of a numerical solution (such as that obtained from the Euler–Maruyama scheme). The resulting discretisation error can be controlled through the use of intermediate time steps between observation instants. However, integrating over the uncertainty at these intermediate times can be computationally expensive.

Upon resorting to discretisation, two approaches to Bayesian inference are apparent. If learning of both the static parameters and latent process is required, a Gibbs sampler provides a natural way of exploring the joint posterior. The well-studied dependence between the parameters and latent process can be problematic; see Roberts and Stramer (2001) for a discussion of the problem. Gibbs strategies that overcome this dependence have been proposed by Roberts and Stramer (2001) for reducible SDEs and by Golightly and Wilkinson (2008), Fuchs (2013), Papaspiliopoulos et al. (2013) and van der Meulen and Schauer (2017) (among others) for irreducible SDEs. If primary interest lies in learning the parameters, pseudo-marginal Metropolis–Hastings (PMMH) schemes (Andrieu et al. 2010; Andrieu and Roberts 2009; Stramer and Bognar 2011; Golightly and Wilkinson 2011) can be constructed to directly target the marginal parameter posterior, or, with simple modification, the joint posterior over both parameters and the latent process. PMMH requires running a particle filter (conditional on a proposed parameter value) at each iteration of the sampler to obtain an estimate of the marginal likelihood (henceforth referred to simply as the likelihood). This can be computationally costly, especially in applications involving long time series, since the number of particles should be scaled in proportion to the number of data points n to maintain a desired likelihood estimator variance (Bérard et al. 2014). To reduce the variance of the acceptance ratio (for a given number of particles), successive likelihood estimates can be positively correlated (Dahlin et al. 2015; Deligiannidis et al. 2018). The resulting correlated PMMH (CPMMH) scheme has been applied in the discretised SDE setting by Golightly et al. (2019); see also Choppala et al. (2016) and Tran et al. (2016).

As a starting point for this work, we consider a CPMMH scheme. A well-known problem with this approach is the use of resampling steps in the particle filter, which can destroy correlation between successive likelihood estimates. This problem can be alleviated by sorting each particle before propagation using e.g. a Hilbert sorting procedure (Deligiannidis et al. 2018) or simple Euclidean sorting (Choppala et al. 2016). However, Golightly et al. (2019) find that as the level of the noise in the observation process increases, correlation deteriorates. Moreover, the empirical findings of Deligiannidis et al. (2018) suggest that the number of particles should scale as \(n^{d/(d+1)}\) (where d is the dimension of the state space of the SDE), so that the advantage of CPMMH over PMMH degrades as the state dimension increases. Our aim is to avoid resampling altogether. A joint update of the entire latent process would avoid the need for resampling (as implemented by Stramer and Bognar (2011) in the PMMH setting) but to be computationally efficient this usually requires an extremely accurate method for sampling the latent process.

Our novel approach is to augment the parameter vector to include the latent process at the observation times, but not at the intermediate times between observation time instants. Given observations y, latent values \(x^o\) at observation instants and parameters \(\theta \), a Gibbs sampler is used to update \(\theta \) conditional on \((x^o,y)\), and \(x^o\) conditional on \((\theta ,y)\). Both steps require estimating likelihoods of the form \(p(x^o_{t+1}|x^o_t,\theta )\) for which we obtain unbiased estimators via importance sampling. Consequently, our approach can be cast within the pseudo-marginal framework and we further use correlation to improve computational efficiency. Crucially, we avoid the need for resampling, thus preserving induced positive correlation between likelihood estimates. Furthermore, each iteration of our proposed scheme admits steps that are embarrassingly parallel. We refer to the resulting sampler as augmented CPMMH (aCPMMH). It should be noted that aCPMMH requires careful initialisation of \(x^o\) and subsequently, a suitable proposal mechanism. We provide practical advice for initialisation and tuning of proposals for a wide class of SDEs. Special cases of aCPMMH are also considered, and a byproduct of our approach is an inferential framework that encompasses both the pseudo-marginal strategy and Gibbs samplers described in the second paragraph of this section. In particular, we make clear the connection between aCPMMH and the Gibbs sampler (with reparameterisation) described in Golightly and Wilkinson (2008). We apply aCPMMH in three examples of increasing complexity and compare against state-of-the-art CPMMH and PMMH schemes. We find that the proposed approach offers an increase in overall efficiency of over an order of magnitude in several settings.

The remainder of this paper is organised as follows. Background information on the inference problem, PMMH and CPMMH approaches is provided in Sect. 2. Our novel contribution is described in Sect. 3 and we explore connections between our proposed approach and existing samplers that use data augmentation in Sect. 3.3. Applications are given in Sect. 4, and conclusions are provided in Sect. 5, alongside directions for future research.

2 Bayesian inference via time discretisation

Consider a continuous-time d-dimensional Itô process \(\{X_t, t\ge 0\}\) satisfying an SDE of the form

$$\begin{aligned} dX_t=\alpha (X_t,\theta )\,dt+\sqrt{\beta (X_t,\theta )}\,dW_t, \quad X_{0}\sim p(x_{0}). \end{aligned}$$
(1)

Here, \(\alpha \) is a d-vector of drift functions, the diffusion coefficient \(\beta \) is a \(d \times d\) positive definite matrix with a square-root representation \(\sqrt{\beta }\) such that \(\sqrt{\beta }\sqrt{\beta }^T=\beta \) and \(W_t\) is a d-vector of (uncorrelated) standard Brownian motion processes. We assume that both \(\alpha \) and \(\beta \) depend on \(X_t=(X_{1,t},\ldots ,X_{d,t})^T\) and denote the parameter vector with \(\theta =(\theta _{1},\ldots ,\theta _{p})^T\)

Suppose that \(\{X_t,t\ge 0\}\) cannot be observed exactly, but observations \(y=(y_{1},\ldots ,y_{n})^T\) are available on a regular time grid and these are conditionally independent (given the latent process). We link the observations to the latent process via an observation model of the form

$$\begin{aligned} Y_t = F^T X_t + \epsilon _t, \qquad \epsilon _t|\Sigma \overset{indep}{\sim }N(0,\Sigma ), \end{aligned}$$
(2)

where \(Y_t\) is a \(d_o\)-vector, F is a constant \(d\times d_o\) matrix and \(\epsilon _t\) is a random \(d_o\)-vector. Note that this setup allows for only observing a subset of components (\(d_o<d\)). In settings where learning \(\Sigma \) is also of interest, the parameter vector \(\theta \) can be augmented to include the components of \(\Sigma \).

For most problems of interest the form of the SDE in (1) will not permit an analytic solution. We therefore work with the Euler–Maruyama approximation

$$\begin{aligned} \Delta X_t\equiv X_{t+\Delta t}-X_t=\alpha (X_t,\theta )\,\Delta t+\sqrt{\beta (X_t,\theta )}\,\Delta W_t \end{aligned}$$

where \(\Delta W_t\sim N(0,I_d\Delta t)\). To allow arbitrary accuracy of this approximation, we adopt a partition of [\(t,t+1\)] as

$$\begin{aligned} t=\tau _{t,0}<\tau _{t,1}<\tau _{t,2}<\ldots<\tau _{t,m-1}<\tau _{t,m}=t+1 \end{aligned}$$

thus introducing \(m-1\) intermediate time points with interval widths of length

$$\begin{aligned} \Delta \tau \equiv \tau _{t,k+1}-\tau _{t,k}=\frac{1}{m}. \end{aligned}$$
(3)

The Euler–Maruyama approximation is then applied over each interval of width \(\Delta \tau \), with m chosen by the practitioner, to balance accuracy and computational efficiency. The transition density under the Euler–Maruyama approximation of \(X_{\tau _{t,k+1}}|X_{\tau _{t,k}}=x_{\tau _{t,k}}\) is denoted by

$$\begin{aligned}&p_{e}(x_{\tau _{t,k+1}}|x_{\tau _{t,k}},\theta ) \\&=N\left( x_{\tau _{t,k+1}};x_{\tau _{t,k}}+\alpha (x_{\tau _{t,k}},\theta )\Delta \tau \,,\,\beta (x_{\tau _{t,k}},\theta )\Delta \tau \right) \end{aligned}$$

where \(N(\cdot ; \mu ,V)\) denotes the Gaussian density with mean vector \(\mu \) and variance matrix V.

In what follows, we adopt the shorthand notation

$$\begin{aligned} x_{[t,t+1]} = (x_{\tau _{t,0}},\ldots ,x_{\tau _{t,m}})^T \end{aligned}$$

for the latent process over the time interval \([t,t+1]\) with an analogous notation for intervals of the form \((t,t+1]\) and \((t,t+1)\) which ignore \(x_{\tau _{t,0}}\) and \((x_{\tau _{t,0}},x_{\tau _{t,m}})\), respectively. Hence, the complete latent trajectory is given by

$$\begin{aligned} x=(x_{[0,1]}^T,x_{(1,2]}^T,\ldots ,x_{(n-1,n]}^T)^T. \end{aligned}$$

The joint density of the latent process over an interval of interest is then given by a product of Gaussian densities; for example

$$\begin{aligned} p_e^{(m)}(x_{(t,t+1]}|x_t,\theta )=\prod _{k=0}^{m-1}p_e(x_{\tau _{t,k+1}}|x_{\tau _{t,k}},\theta ) \end{aligned}$$
(4)

with explicit dependence on the number of intermediate sub-intervals made clear via the superscript (m).

2.1 Pseudo-marginal Metropolis–Hastings (PMMH)

Suppose that interest lies in the marginal parameter posterior

$$\begin{aligned} \pi ^{(m)}(\theta |y)&\propto \pi (\theta )p^{(m)}(y|\theta ) \end{aligned}$$
(5)

where \(\pi (\theta )\) is the prior density ascribed to \(\theta \) and \(p^{(m)}(y|\theta )\) is the (marginal) likelihood under the augmented Euler–Maruyama approach. That is,

$$\begin{aligned} p^{(m)}(y|\theta )&=\int p^{(m)}(x|\theta )p(y|x,\theta )dx \end{aligned}$$

where

$$\begin{aligned} p^{(m)}(x|\theta )&=p(x_{0})\prod _{t=0}^{n-1}p_{e}^{(m)}(x_{(t,t+1]}|x_t,\theta ) \end{aligned}$$

and

$$\begin{aligned} p(y|x,\theta )=\prod _{t=1}^{n}p(y_{t}|x_{t},\theta ). \end{aligned}$$
(6)

Although \(\pi ^{(m)}(\theta |y)\) is typically complicated by the intractable likelihood term, \(p^{(m)}(y|\theta )\), the latter can be unbiasedly estimated using a particle filter (Del Moral 2004; Pitt et al. 2012). We write the estimator as \({\hat{p}}_U^{(m)}(y|\theta )\) with explicit dependence on \(U\sim p(u)\), that is, the collection of all random variables of which a realisation u gives the estimate \({\hat{p}}_u^{(m)}(y|\theta )\). Algorithm 1 gives the necessary steps for the generation of \({\hat{p}}_u^{(m)}(y|\theta )\), with the explicit role of u suppressed for simplicity. A key requirement of the particle filter is the ability to simulate latent trajectories \(x_{(t,t+1]}\) at each time t. To yield a reasonable particle weight, such trajectories must be consistent with \(x_t\) and \(y_{t+1}\) and are typically termed bridges. In this article we generate bridges by drawing from a density of the form

$$\begin{aligned} g\left( x_{(t,t+1]}|x_{t},y_{t+1},\theta \right) =\prod _{k=0}^{m-1}g(x_{\tau _{t,k+1}}|x_{\tau _{t,k}},y_{t+1},\theta ) \end{aligned}$$

where the constituent terms take the form

$$\begin{aligned}&g(x_{\tau _{t,k+1}}|x_{\tau _{t,k}},y_{t+1},\theta ) \nonumber \\&=N\left( x_{\tau _{t,k+1}};x_{\tau _{t,k}}+\mu (x_{\tau _{t,k}},y_{t+1},\theta )\Delta \tau \,,\, \Psi (x_{\tau _{t,k}},\theta )\Delta \tau \right) \end{aligned}$$
(7)

for suitable choices of \(\mu (x_{\tau _{t,k}},y_{t+1},\theta )\) and \(\Psi (x_{\tau _{t,k}},\theta )\). The form of (7) permits a wide choice of bridge construct and we refer the reader to Whitaker et al. (2017) and Schauer et al. (2017) for several options. Throughout this paper, we take

$$\begin{aligned} \mu (x_{\tau _{t,k}},y_{t+1},\theta )&=\alpha _{k}+\beta _{k} F\left( F^T\beta _{k}F\Delta _k + \Sigma \right) ^{-1} \nonumber \\&\qquad \times \left\{ y_{t+1}-F^T(x_{\tau _{t,k}}+\alpha _{k}\Delta _k)\right\} \end{aligned}$$
(8)

and

$$\begin{aligned} \Psi (x_{\tau _{t,k}},\theta )=\beta _{k}-\beta _{k} F\left( F^T\beta _{k} F\Delta _k + \Sigma \right) ^{-1}F^T\beta _{k}\Delta \tau \nonumber \\ \end{aligned}$$
(9)

where \(\Delta _{k}=t+1-\tau _{t,k}\) and we adopt the shorthand notation that \(\alpha _{k}{:}{=}\alpha (x_{\tau _{t,k}},\theta )\) and \(\beta _k{:}{=}\beta (x_{\tau _{t,k}},\theta )\). We note that (8) and (9) correspond to the (extension to partial and noisy observations of the) modified diffusion bridge construct of Durham and Gallant (2002). We may write the construct generatively as

$$\begin{aligned} x_{\tau _{t,k+1}}= & {} x_{\tau _{t,k}}+\mu (x_{\tau _{t,k}},y_{t+1},\theta )\Delta \tau \nonumber \\&+ \sqrt{\Psi (x_{\tau _{t,k}},\theta )\Delta \tau }\,u_{\tau _{t,k}} \end{aligned}$$
(10)

where \(u_{\tau _{t,k}}\sim N(0,I_d)\). It should then be clear that an estimate of the likelihood, \({\hat{p}}_u^{(m)}(y|\theta )\), is a deterministic function of the Gaussian innovations driving the bridge construct, and additionally, any random variates required in the resampling step of Algorithm 1. We use systematic resampling, which requires a single uniform innovation per resampling step.

figure a

The pseudo-marginal Metropolis–Hastings (PMMH) scheme (Andrieu and Roberts 2009; Andrieu et al. 2009) is a Metropolis–Hastings (MH) scheme targeting the joint density

$$\begin{aligned} \pi ^{(m)}(\theta ,u|y)\propto \pi (\theta ){\hat{p}}_{u}^{(m)}(y|\theta )p(u) \end{aligned}$$

for which it is easily checked (using \(\int {\hat{p}}_{u}^{(m)}(y|\theta )p(u)du=p^{(m)}(y|\theta )\)) that \(\pi ^{(m)}(\theta |y)\) is a marginal density. Hence, for a proposal density that factorises as \(q(\theta '|\theta )q(u')\), the MH acceptance probability is

$$\begin{aligned}&\alpha (\theta ',u'|\theta ,u) \nonumber \\&\quad =\min \left\{ 1\,,\,\frac{\pi (\theta ')}{\pi (\theta )}\times \frac{{\hat{p}}_{u'}^{(m)}(y|\theta ')}{{\hat{p}}_{u}^{(m)}(y|\theta )}\times \frac{q(\theta |\theta ')}{q(\theta '|\theta )}\right\} . \end{aligned}$$
(11)

The variance of \({\hat{p}}_{U}^{(m)}(y|\theta )\) is controlled by the number of particles N, which should be chosen to balance both mixing and computational efficiency. For example, as the variance of the likelihood estimator increases, the acceptance probability of the pseudo-marginal MH scheme decreases to 0 (Pitt et al. 2012). Increasing N results in more acceptances at increased computational cost. Practical advice for choosing N is given by Sherlock et al. (2015) and Doucet et al. (2015) under two different sets of simplifying assumptions. Given a parameter value with good support under the posterior (e.g. the marginal posterior mean, estimated from a pilot run), we select N so that the estimated log-likelihood at this parameter value has a standard deviation of roughly 1.5. Unfortunately, the value of N required to meet this condition is often found to be impractically large. Therefore, we consider a variance reduction technique which is key to our proposed approach.

2.2 Correlated pseudo-marginal Metropolis–Hastings (CPMMH)

The correlated pseudo-marginal scheme (Deligiannidis et al. 2018; Dahlin et al. 2015) aims to reduce the variance of the acceptance ratio in (11) by inducing strong and positive correlation between successive estimates of the observed data likelihood in the MH scheme. This can be achieved by taking a proposal \(q(\theta '|\theta )K(u'|u)\) where \(K(u'|u)\) satisfies the detailed balance equation

$$\begin{aligned} K(u'|u)p(u)=K(u|u')p(u'). \end{aligned}$$

Recall that u consists of the collection of Gaussian random variates used to propagate the state particles (2(b) in Algorithm 1) and any variates required in the resampling step (2(a) in Algorithm 1). The Uniform random variate required for systematic resampling can be obtained by applying the inverse Gaussian cdf to a Gaussian draw. Hence, u consists entirely of standard Gaussian variates and it is then natural to set

$$\begin{aligned} K(u'|u)=\text {N}\left( u';\,\rho u\,,\,\left( 1-\rho ^2\right) I_{d^*}\right) \end{aligned}$$
(12)

where \(d^*\) is the total number of required innovations. We note that the density in (12) corresponds to a Crank–Nicolson proposal density for which it is easily checked that \(p(u)=N(u;0,I_{d^*})\) is invariant. The parameter \(\rho \) is chosen by the practitioner, with \(\rho \approx 1\) inducing strong and positive correlation between \({\hat{p}}_{u'}^{(m)}(y|\theta ')\) and \({\hat{p}}_{u}^{(m)}(y|\theta )\). The correlated pseudo-marginal Metropolis–Hastings scheme is given by Algorithm 2, which should be used in conjunction with a modified version of Algorithm 1 to induce the desired correlation. However, the resampling step has the effect of breaking down correlation between successive likelihood estimates. To alleviate this problem, the particles can be sorted immediately after propagation e.g. using a Hilbert sorting procedure (Deligiannidis et al. 2018) or simple Euclidean sorting (Choppala et al. 2016). Given a distance metric between particles, the particles are sorted as follows: the first particle in the sorted list is the one which has the smallest first component; for \(j=2,\dots ,N\), the jth particle in the sorted list is chosen to be the one among the unsorted \(N-j+1\) particles that is closest to the \(j-1\)th sorted particle.

Upon choosing a value of \(\rho \) (e.g. \(\rho =0.99\)), the number of particles N can be chosen to minimise the distance between successive log estimates of marginal likelihood (Deligiannidis et al. 2018). In practice, we choose N so that the variance of the logarithm of the ratio \({\hat{p}}_{U'}^{(m)}(y|\theta ) / {\hat{p}}_{U}^{(m)}(y|\theta )\) is around 1, for \(\theta \) set at some central posterior value.

figure b

There are a number of limitations regarding the implementation of CPMMH as described here, which motivate the approach of Sect. 3. Although sorting particle trajectories after propagation can in theory alleviate the effect of resampling on maintaining correlation between successive likelihood estimates, the sorting procedure can be unsatisfactory in practice. For example, the Euclidean sorting procedure described above (and implemented within the SDE context in Golightly et al. (2019)) sorts trajectories \(x_{(t,t+)]}^{1:N}\) between observation times by applying the procedure to the particle states \(x_{t+1}^{1:N}\) at the observation times. Consequently, trajectories with similar values at time \(t+1\) may exhibit qualitatively different behaviour between observation times, leading to potentially significant differences in likelihood contributions (via the particle weights). In turn, this may break down correlation between likelihood values at successive iterations. The procedure is therefore likely to be particularly ineffectual when the measurement error variance is large relative to stochasticity inherent in the latent diffusion process, or, as the dimension of the SDE increases. Resampling may be executed less often, although choosing a resampling schedule a priori may necessarily be ad hoc. Moreover, reducing the number of resampling steps, or indeed omitting the resampling step altogether (so that an importance sampler is obtained) would necessitate a bridge construct that samples over the entire inter-observation interval from an approximation that is very close to the true (but intractable) conditioned diffusion process, otherwise the resulting importance sampler weights are likely to have high variance. In what follows, we derive a novel approach which avoids resampling altogether, without recourse to importance sampling of the entire latent process.

3 Augmented CPMMH (aCPMMH)

It will be helpful throughout this section to denote \(x^o\) as the values of x at the observation times \(1,2,\ldots ,n\), and \(x^L\) as the values of x at the remaining intermediate times. That is

$$\begin{aligned} x^L=(x_{[0,1)}^T,x_{(1,2)}^T,\ldots ,x_{(n-1,n)}^T)^T. \end{aligned}$$

It is also possible to treat \(x_n\) as a latent variable. In what follows, we include \(x_n\) in \(x^o\) for ease of exposition.

Rather than target the posterior in (5), we target the joint posterior

$$\begin{aligned} \pi ^{(m)}(\theta ,x^o|y)\propto \pi (\theta )p^{(m)}(x^o|\theta ) p(y|x^o,\theta ) \end{aligned}$$
(13)

where

$$\begin{aligned} p^{(m)}(x^o|\theta )=\int p^{(m)}(x|\theta ) dx^L \end{aligned}$$
(14)

and \(p(y|x^o,\theta )=p(y|x,\theta )\) as in (6). Although the integral in (14) will be intractable, we may estimate it unbiasedly as follows.

3.1 Sequential importance sampling

We adopt the factorisation

$$\begin{aligned} p^{(m)}(x^o|\theta )=p^{(m)}(x_1|\theta )\prod _{t=1}^{n-1}p^{(m)}(x_{t+1}|x_{t},\theta ) \end{aligned}$$

and note that the constituent terms can be written as

$$\begin{aligned}&p^{(m)}(x_1|\theta )=\int p(x_0) p_{e}^{(m)}(x_{(0,1]}|x_0,\theta )dx_{[0,1)}, \nonumber \\&p^{(m)}(x_{t+1}|x_{t},\theta )=\int p_{e}^{(m)}(x_{(t,t+1]}|x_t,\theta )dx_{(t,t+1)}; \end{aligned}$$
(15)

recall that \(p_{e}^{(m)}(x_{(t,t+1]}|x_t,\theta )\) is given by (4). Now, given some suitable importance density \(g(x_{(t,t+1)}|x_t,x_{t+1},\theta )\), we may write

$$\begin{aligned}&p^{(m)}(x_{t+1}|x_{t},\theta ) \\&=\int \frac{p_{e}^{(m)}(x_{(t,t+1]}|x_t,\theta )}{g(x_{(t,t+1)}|x_t,x_{t+1},\theta )}g(x_{(t,t+1)}|x_t,x_{t+1},\theta )dx_{(t,t+1)}\\&=E_{x_{(t,t+1)}\sim g}\left\{ \frac{p_{e}^{(m)}(x_{(t,t+1]}|x_t,\theta )}{g(x_{(t,t+1)}|x_t,x_{t+1},\theta )}\right\} , \end{aligned}$$

and a similar expression can be obtained for \(p^{(m)}(x_1|\theta )\). Hence, given N draws \(x_{(t,t+1)}^i\), \(i=1,\ldots ,N\) from the density \(g(\cdot |x_t,x_{t+1},\theta )\), a realisation of an unbiased estimator of \(p^{(m)}(x_{t+1}|x_{t},\theta )\) is

$$\begin{aligned} {\hat{p}}^{(m)}_{u_t}(x_{t+1}|x_{t},\theta )=\frac{1}{N}\sum _{i=1}^{N}\frac{p_{e}^{(m)}(x_{(t,t+1]}^i|x_t,\theta )}{g(x_{(t,t+1)}^i|x_t,x_{t+1},\theta )} \end{aligned}$$
(16)

with the convention that \(x_{t+1}^i=x_{t+1}\) for all i. We recognise (16) as an importance sampling estimator of (15). An unbiased importance sampling estimator of \(p^{(m)}(x_1|\theta )\) can be obtained in a similar manner, by using an importance density \(p(x_0)g(x_{(0,1)}|x_0,x_{1},\theta )\).

We take \(g(x_{(t,t+1)}|x_t,x_{t+1},\theta )\) as a simplification of the bridge construct used in Sect. 2.1 so that

$$\begin{aligned} g\left( x_{(t,t+1)}|x_{t},x_{t+1},\theta \right) =\prod _{k=0}^{m-2}g(x_{\tau _{t,k+1}}|x_{\tau _{t,k}},x_{t+1},\theta ) \end{aligned}$$

where \(g\left( x_{(t,t+1)}|x_{t},x_{t+1},\theta \right) \) has form (7) but with the exact \(x_{t+1}\) taking the place of the noisy \(y_{t+1}\). Since \(\Sigma =0\), (8) and (9) simplify to

$$\begin{aligned}&\mu (x_{\tau _{t,k}},x_{t+1})=\frac{x_{t+1}-x_{\tau _{t,k}}}{t+1-\tau _{t,k}},\nonumber \\&\Psi (x_{\tau _{t,k}},\theta )=\frac{t+1-\tau _{t,k+1}}{t+1-\tau _{t,k}}\beta (x_{\tau _{t,k}},\theta ). \end{aligned}$$
(17)

We make clear the role of the of the innovation vector \(u_t=(u_{t,0},\ldots ,u_{t,m-2})^T\) in (16) by writing the bridge construct generatively as in (10) but with \(\mu \) and \(\Psi \) given by (17).

Now, since the \(x_{(t,t+1)}\), \(t=0,\ldots ,n-1\) are conditionally independent given \(x^o\), we may unbiasedly estimate \(p^{(m)}(x^o|\theta )\) with

$$\begin{aligned} {\hat{p}}_U^{(m)}(x^o|\theta )=p^{(m)}_{U_0}(x_1|\theta )\prod _{t=1}^{n-1}{\hat{p}}_{U_t}^{(m)}(x_{t+1}|x_{t},\theta ), \end{aligned}$$
(18)

realisations of which may be computed by running the importance sampler in Algorithm 3 for each \(t=0,\ldots ,n-1\). Note that each t-iteration of Algorithm 3 can be performed in parallel if desired.

figure c

3.2 Algorithm

We adopt a pseudo-marginal approach by targeting the joint density

$$\begin{aligned} \pi ^{(m)}(\theta ,x^o,u|y)\propto \pi (\theta ){\hat{p}}_{u}^{(m)}(x^o|\theta )p(y|x^o,\theta )p(u) \end{aligned}$$
(19)

for which it is easily checked that the posterior of interest, \(\pi ^{(m)}(\theta ,x^o|y)\) given by (13), is a marginal density. The form of (19) immediately suggests a Gibbs sampler which alternates between draws from the full conditional densities (FCDs)

  1. 1.

    \(\pi ^{(m)}(\theta |u,x^o,y)\propto \pi (\theta ){\hat{p}}_{u}^{(m)}(x^o|\theta )p(y|x^o,\theta )\)

  2. 2.

    \(\pi ^{(m)}(x^o,u|\theta ,y)\propto {\hat{p}}_{u}^{(m)}(x^o|\theta )p(y|x^o,\theta )p(u)\).

Hence, unlike the (C)PMMH scheme, the latent process at the observation times is no longer integrated out. Nevertheless, the sampler targets a posterior for which the latent process between observation instants is marginalised over, and this is crucial for side-stepping the well-known dependence problem between the parameters and latent process. Note that as the number of importance samples \(N\rightarrow \infty \), the scheme can be seen as an idealised Gibbs sampler that alternates between draws of \(\pi ^{(m)}(\theta |x^o,y)\) and \(\pi ^{(m)}(x^o|\theta ,y)\). For \(N=1\), the scheme is an extension of the modified innovation scheme of Golightly and Wilkinson (2008), as discussed further in Sect. 3.3.

Metropolis-within-Gibbs steps are necessary for generating draws from the FCDs above. To sample the FCD \(\pi ^{(m)}(\theta |u,x^o,y)\) we use a proposal density \(q(\theta '|\theta )\) so that the acceptance probability is given by

$$\begin{aligned}&\alpha (\theta '|\theta ,u,x^o) \nonumber \\&\quad =\min \left\{ 1\,,\,\frac{\pi (\theta ')}{\pi (\theta )}\times \frac{{\hat{p}}_{u}^{(m)}(x^o|\theta ')}{{\hat{p}}_{u}^{(m)}(x^o|\theta )}\times \frac{p(y|x^o,\theta ')}{p(y|x^o,\theta )} \times \frac{q(\theta |\theta ')}{q(\theta '|\theta )}\right\} . \end{aligned}$$
(20)

Given that \(\pi ^{(m)}(x^o,u|\theta ,y)\) may be high dimensional, we propose to update \((x^o,u)\) in separate blocks corresponding to each time component of \(x^o\). For \(t=1,\ldots ,n-1\) we have that

$$\begin{aligned}&\pi ^{(m)}(x_t,u_{t-1},u_t|x_{t-1},x_{t+1},y_t,\theta ) \propto {\hat{p}}_{u_{t-1}}^{(m)} (x_t|x_{t-1},\theta ){\hat{p}}_{u_t}^{(m)}\\&\quad \times (x_{t+1}|x_{t},\theta )p(y_t|x_t,\theta )p(u_{t-1})p(u_t) \end{aligned}$$

where, for example \(p(u_t)=N(u_t;0,I_{N(m-1)d})\) (assuming N importance samples, \((m-1)\) intermediate time points between observation instants and a d-dimensional latent process). For \(t=1\), \({\hat{p}}_{u_{t-1}}^{(m)}(x_t|x_{t-1},\theta )\) is replaced by \({\hat{p}}_{u_{0}}^{(m)}(x_1|\theta )\). The full conditional for the remaining end-point is given by

$$\begin{aligned}&\pi ^{(m)}(x_n,u_{n-1}|x_{n-1},y_n,\theta ) \\&\propto {\hat{p}}_{u_{n-1}}^{(m)}(x_n|x_{n-1},\theta )p(y_n|x_n,\theta )p(u_{n-1}). \end{aligned}$$

We sample from each FCD using a Metropolis-within-Gibbs step. For each \(t=1,\ldots ,n-1\) we use a proposal density of the form

$$\begin{aligned} q(x_t',u_{(t-1,t)}'|x_t,u_{(t-1,t)})=q(x_t'|x_t)K_2(u_{(t-1,t)}'|u_{(t-1,t)}) \end{aligned}$$

where \(K_2(u'_{(t-1,t)}|u_{(t-1,t)})=K(u'_{t-1}|u_{t-1})K(u'_t|u_t)\) and we use the shorthand notation \(u_{(t-1,t)}=(u_{t-1},u_t)\). Hence, the innovations are updated using a Crank-Nicolson kernel. The end-point proposal is defined similarly, with \(q(x_n',u_{n-1}'|x_n,u_{n-1})=q(x_n'|x_n)K(u_{n-1}'|u_{n-1})\). We recall that the Crank-Nicolson kernel satisfies detailed balance with respect to the innovation density to arrive at the acceptance probabilities

$$\begin{aligned}&\alpha (x_t',u_{(t-1,t)}'|x_t,u_{(t-1,t)},x_{t-1},x_{t+1},\theta ) \nonumber \\&=\min \left\{ 1\,,\,\frac{{\hat{p}}_{u_{t-1}'}^{(m)}(x_t'|x_{t-1},\theta )}{{\hat{p}}_{u_{t-1}}^{(m)}(x_t|x_{t-1},\theta )}\times \frac{{\hat{p}}_{u_t'}^{(m)}(x_{t+1}|x_{t}',\theta )}{{\hat{p}}_{u_t}^{(m)}(x_{t+1}|x_{t},\theta )} \right. \nonumber \\&\left. \quad \times \frac{p(y_t|x_t',\theta )}{p(y_t|x_t,\theta )} \times \frac{q(x_t | x_t')}{q(x_t' | x_t)}\right\} \end{aligned}$$
(21)

for \(t=1,\ldots ,n-1\). For the end-point update, the acceptance probability is

$$\begin{aligned}&\alpha (x_n',u_{n-1}'|x_n,u_{n-1}',x_{n-1},\theta )= \nonumber \\&\min \left\{ 1\,,\,\frac{{\hat{p}}_{u_{n-1}'}^{(m)}(x_n'|x_{n-1},\theta )}{{\hat{p}}_{u_{n-1}}^{(m)}(x_n|x_{n-1},\theta )}\times \frac{p(y_n|x_n',\theta )}{p(y_n|x_n,\theta )} \times \frac{q(x_n | x_n')}{q(x_n' | x_n)}\right\} . \end{aligned}$$
(22)

It is evident that the innovations \((u_1,\ldots ,u_{n-1})\) are updated twice per Gibbs iteration. We note that a scheme that only updates these innovations once per Gibbs iteration is also possible, but eschew this approach in favour of the above, which promotes better exploration of the innovation variable space. Further tuning considerations are discussed in Sect. 3.4.

We refer to the resulting inference scheme as augmented CPMMH (aCPMMH). The scheme is summarised by Algorithm 4. Note that the components of the latent process \(X^o\) at the observation times and auxiliary variables u are updated in steps 3-5; step 3 updates \((x_t,u_{(t-1,t)})\) for \(t=1,3,\ldots ,n-1\) and step 4 for \(t=2,4,\ldots ,n-2\) (assuming, WLOG, that n is even). Step 5 updates the final value \((x_n,u_{n-1})\). Updating in this way allows for embarrassingly parallel operations over t (at steps 2, 3 and 4). Note that, as presented, uncertainty for the initial value \(x_0\) is integrated over as part of the importance sampler (Algorithm 3). If required, aCPMMH can be modified either to treat \(x_0\) as part of the parameter vector \(\theta \) or with an extra step that updates \(x_0\) (and therefore \(u_0\)) conditional on \(x_1\) and \(\theta \).

figure d

As presented, Algorithm 4 is appropriate for the general case of noisy and partial observation of \(X_t\). In the special case of data consisting of noise free observation of all SDE components (so that \(\Sigma =0\) and \(F=I_d\) in (2)), steps 3-5 are not required. Additionally, step 2 should propose the full auxiliary vector \(u'\) from \(K(u'|u)\) in (12) . Hence, this special case corresponds to the CPMMH algorithm with \({\hat{p}}_{u'}^{(m)}({y}|\theta ')\) obtained by importance sampling and the acceptance probability is as in (11). In the case of noise free observation of a subset of components of \(X_t\), the scheme proceeds as in Algorithm 4, with the unobserved components of \(X_t\) updated in steps 3-5.

3.3 Connection with existing samplers for SDEs

Consider aCPMMH with \(N=1\) particle and \(\rho =0\). In this case aCPMMH exactly coincides with the modified innovation scheme introduced by Golightly and Wilkinson (2008) (see also Golightly and Wilkinson 2010; Papaspiliopoulos et al. 2013; Fuchs 2013; van der Meulen and Schauer 2017,). We note that for this choice of N there is a one-to-one correspondence between the innovations u and the latent path x. Hence, step 2 of the Gibbs sampler in Section 3.2 is equivalent to directly updating the latent path x in blocks of size \(2m-1\). To make this clear, consider updating \(x_{(t-1,t+1)}\). Upon substituting (16) into the acceptance probability in (21) we obtain

$$\begin{aligned}&\min \left\{ 1\,,\, \frac{p_{e}^{(m)}(x_{(t-1,t]}'|x_{t-1},\theta )}{p_{e}^{(m)}(x_{(t-1,t]}|x_{t-1},\theta )}\times \frac{p_{e}^{(m)}(x_{(t,t+1]}'|x_t',\theta )}{p_{e}^{(m)}(x_{(t,t+1]}|x_t,\theta )}\right. \\&\quad \times \frac{g(x_{(t-1,t)}|x_{t-1},x_{t},\theta )}{g(x_{(t-1,t)}'|x_{t-1},x_{t}',\theta )}\times \frac{g(x_{(t,t+1)}|x_t,x_{t+1},\theta )}{g(x_{(t,t+1)}'|x_t',x_{t+1},\theta )}\\&\left. \quad \times \frac{p(y_t|x_t',\theta )}{p(y_t|x_t,\theta )} \times \frac{q(x_t | x_t')}{q(x_t' | x_t)}\right\} \end{aligned}$$

corresponding to a MH step that uses a RWM proposal to obtain \(x_t'\) and then conditional on this value, uses the bridge construct to propose \(x_{(t-1,t)}'\) and \(x_{(t,t+1)}'\). Step 1 of the Gibbs sampler is equivalent to the reparameterisation used by the modified innovation scheme. Rather than update \(\theta \) conditional on x (and y), the innovations u are the effective components being conditioned on. The motivation for this reparameterisation is to break down the well-known problematic dependence between \(\theta \) and x (Roberts and Stramer 2001). To make the connection clear, note that upon combining (18) with (16) and substituting the result into the acceptance probability in (20), we obtain

$$\begin{aligned}&\min \left\{ 1\,,\,\frac{\pi (\theta ')}{\pi (\theta )}\times \prod _{t=0}^{n-1} \frac{p_{e}^{(m)}(x_{(t,t+1]}|x_t,\theta ')}{p_{e}^{(m)}(x_{(t,t+1]}|x_t,\theta )}\right. \\&\quad \left. \times \prod _{t=0}^{n-1} \frac{g(x_{(t,t+1)}|x_t,x_{t+1},\theta )}{g(x_{(t,t+1)}|x_t,x_{t+1},\theta ')}\times \frac{p(y|x^o,\theta ')}{p(y|x^o,\theta )}\times \frac{q(\theta |\theta ')}{q(\theta '|\theta )}\right\} . \end{aligned}$$

It is straightforward to show that the Jacobian associated with the change of variables (from x to u) is given by \(\prod _{t=0}^{n-1}g(x_{(t,t+1)}|x_t,x_{t+1},\theta )^{-1}\) and therefore the above acceptance probability coincides with that obtained for the parameter update in the modified innovation scheme (see e.g. page 14 of Golightly and Wilkinson 2010, ).

For \(N=1\) and \(0<\rho <1\), aCPMMH can be seen as an extension of the modified innovation scheme that uses a Crank-Nicolson proposal for the innovations. A recent application can be found in Arnaudon et al. (2020). We assess the performance of aCPMMH for different values of \(\rho \) and N in Sect. 4.

3.4 Initialisation and tuning choices

Recall that both CPMMH and PMMH require setting the number of particles N and, if using a random walk Metropolis (RWM) proposal, a suitable innovation variance. Practical advice on choosing N for (C)PMMH is discussed at the end of Sects. 2.1 and 2.2. For a RWM proposal of the form \(q(\theta '|\theta )=N(\theta ^*;\theta ,\Omega )\), a rule of thumb for the innovation variance \(\Omega \) is to take \(\Omega =\frac{2.56^2}{p}\widehat{\text {var}}(\theta |y)\) (Sherlock et al. 2015), which could be obtained from an initial pilot run (such as that required to find a plausible \(\theta \) value for subsequently choosing N).

Fig. 1
figure 1

Birth–Death model. Data sets (circles) and summaries (mean and \(95\%\) credible intervals obtained from the output of aCPMMH) of the within-sample predictive \(\pi (y|{\mathcal {D}}_1)\) (left) and \(\pi (y|{\mathcal {D}}_2)\) (right)

Full size image

For (C)PMMH, both the pilot and main monitoring runs require careful initialisation of \(\theta \) (Owen et al. 2015). The aCPMMH scheme additionally requires initialisation of \(x^o\), with poor choices likely to slow initial convergence of the Gibbs sampler. One possibility is to seek an approximation to \(\pi ^{(m)}(\theta ,x^o|y)\), denoted \(\pi ^{(a)}(\theta ,x^o|y)\), for which samples can be obtained (e.g. via MCMC) at relatively low computational cost. These samples can then be used to compute estimates \(\hat{\text {E}}(\theta |y)\) and \(\hat{\text {E}}(x_t|y)\), which can be used to initialise aCPMMH. Further, the proposal variances for \(\theta \) and \(x_t\) can be made proportional to the estimates \(\widehat{\text {var}}(\theta |y)\) and \(\widehat{\text {var}}(x_t|y)\), respectively, which can also be computed from the samples. For SDE models of form (1), the linear noise approximation (LNA) (Stathopoulos and Girolami 2013; Fearnhead et al. 2014) provides a tractable Gaussian approximation. We describe the LNA, its solution and sampling of \(\pi ^{(a)}(\theta ,x^o|y)\) in Appendix A. In scenarios where using the LNA is not practical, we suggest initialising a pilot run of aCPMMH with \(x^o=y\) (if \(d_o=d\) so that all components are observed) or sampling \(x^o\) via recursive application of the bridge construct in (7). The pilot run can be used to obtain further quantities required for tuning the proposal densities \(q(\theta '|\theta )\) and \(q(x_t'|x_t)\). Hence, our initialisation and tuning advice can be summarised by the following two options:

  1. 1.

    Perform a short pilot run of an MCMC scheme targeting \(\pi ^{(a)}(\theta ,x^o|y)\) (as described in Appendix A for the LNA) to obtain the estimates \(\hat{\text {E}}(\theta |y)\), \(\hat{\text {E}}(x_t|y)\), \(\widehat{\text {var}}(\theta |y)\) and \(\widehat{\text {var}}(x_t|y)\). These quantities are used to initialise the main monitoring run of aCPMMH and in the RWM proposals for \(\theta \) and the components of \(x^o\).

  2. 2.

    Perform a short pilot run of aCPMMH with \(x^o\) initialised at the data y (if all SDE components are observed) or, in the case of incomplete observation of all SDE components, recursively draw from (7), retaining only those values at the observation times. Compute estimates as in option 1, for use in the main monitoring run.

The length of the pilot run can be set by choosing a fraction of the main monitoring run to fix the overall computational budget. For simplicity, we use RWM proposals in the pilot runs with diagonal innovation variances chosen to obtain (approximately) a desired acceptance rate. We note that Option 2 additionally requires specifying an initial number of particles N for the pilot run. In our experiments, we find that \(N=1\) is often sufficient. For either option, the number of particles can be further tuned if desired, before the main monitoring run.

Table 1 Birth–Death model. Number of particles N, correlation parameter \(\rho \), CPU time (in seconds s), minimum ESS (over \(\theta \) and \(x^o\) chains), minimum ESS per second and relative (to PMMH) minimum ESS per second. All results are based on \(5\times 10^4\) iterations of each scheme
Full size table

4 Applications

We consider three applications of increasing complexity. All algorithms are coded in R and were run on a desktop computer with an Intel quad-core CPU. For all experiments, we compare the performance of competing algorithms using minimum (over each parameter chain and for aCPMMH, \(x^o\) chain) effective sample size per second (mESS/s). Effective sample size (ESS) is the number of independent and identically distributed samples from the target that would produce an estimator with the same variance as the auto-correlated MCMC output. We computed ESS using the R coda package, details of which can be found in Plummer et al. (2006). When running CPMMH and aCPMMH with \(\rho >0\) we set \(\rho =0.99\). This pragmatic choice promotes good mixing in the \(\theta \) chain (for CPMMH and aCPMMH) and \(x^o\) chain (for aCPMMH) while allowing the auxiliary variables to mix on a scale comparable to \(\theta \) and \(x^o\). We report CPU time based on the main monitoring runs and note that CPU cost of tuning was small relative to the cost of the main run (and typically less than \(10\%\) of the reported CPU time). For all experiments (unless stated otherwise) we used a discretisation of \(\Delta \tau =0.2\) which we found gave a good balance between accuracy (in the sense of limiting discretisation bias) and computational performance.

Fig. 2
figure 2

Birth–Death model. Marginal posterior distributions using data set \({\mathcal {D}}_2\) and based on the output of aCPMMH (solid lines) and the LNA (dashed lines). The true values of \(\theta _1\), \(\theta _2\) and \(\theta _1 - \theta _2\) are indicated

Full size image

4.1 Square-root diffusion process

Consider a univariate diffusion process satisfying an Itô SDE of the form

$$\begin{aligned} dX_{t}=\left( \theta _{1}-\theta _{2}\right) X_{t}\,dt + \sqrt{\left( \theta _{1}+\theta _{2}\right) X_{t}}\,dW_{t}, \end{aligned}$$
(23)

which can be seen as a degenerate case of a Feller square-root diffusion (Feller 1952). We generated two synthetic data sets consisting of 101 observations at integer times using \(\theta =(0.05,0.06)^T\) and a known initial condition of \(x_{0}=25\). The observation model is \(Y_t\sim N(X_t,\sigma ^2)\) where \(\sigma \in \{1,5\}\) giving data sets designated as \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\), respectively (and shown in Fig. 1). We took independent \(N(0,10^2)\) priors for each \(\log \theta _i\), \(i=1,2\), and work on the logarithmic scale when using the random walk proposal mechanism.

We ran aCPMMH for 50K iterations with \(\rho \) fixed at 0.99. We report results for \(N=1\) particle, since \(N>1\) gave no increase in overall performance. Both tuning and initialisation methods (options 1 and 2 of Sect. 3.4) were implemented and denoted “aCPMMH (1)” and “aCPMMH (2)”. We additionally include results based on the output of PMMH and CPMMH, which were tuned in line with the guidance given at the end of Sects. 2.1 and 2.2.

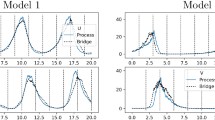
Table 1 and Fig. 2 summarise our results. The latter shows marginal posteriors obtained from the output of aCPMMH, and for comparison, from the LNA as an inferential model. We note substantial differences in posteriors obtained when using the discretised SDE in (23) as the inferential model compared to inferences made under the LNA. This is not surprising since for this example, the ground truth \(\theta _1\) and \(\theta _2\) values are similar, for which the assumption that fluctuations about the mean of \(X_t\) are small (as is necessary for an accurate LNA), is unreasonable. Nevertheless, we were still able to use the LNA to adequately initialise and tune aCPMMH. We also note that both initialisation and tuning options give comparable results.

It is evident from Table 1 that aCPMMH offers substantial improvements in overall efficiency compared to PMMH and, to a lesser extent, CPMMH. Minimum effective sample size per second for PMMH : CPMMH : aCPMMH scales as 1 : 2.7 : 6 for data set \({\mathcal {D}}_{1}\) and 1 : 2.5 : 2.5 for data set \({\mathcal {D}}_{2}\). We found that as the measurement error variance (\(\sigma ^2\)) is increased, the optimal number of particles N for both PMMH and CPMMH also increased. Although aCPMMH required \(N=1\) (that is, we observed no additional improvement in overall efficiency for \(N>1\)), the mixing deteriorates, due to having to integrate over the additional uncertainty in the latent process at the observation times. Finally, although the Euclidean sorting algorithm used in CPMMH is likely to be effective for this simple univariate example, we anticipate its deterioration in subsequent examples with increasing state dimension.

Fig. 3
figure 3

Lotka–Volterra model. Data set \({\mathcal {D}}_3\) (circles) and summaries (mean and \(95\%\) credible intervals obtained from the output of aCPMMH) of the within-sample predictive \(\pi (y|{\mathcal {D}}_3)\) (left: prey component, right: predator component)

Full size image
Fig. 4
figure 4

Lotka–Volterra model. Marginal posterior distributions using data set \({\mathcal {D}}_3\) and based on the output of aCPMMH (solid lines) and the LNA (dashed lines). The true values of \(\theta _1\), \(\theta _2\) and \(\theta _3\) are indicated

Full size image

4.2 Lotka–Volterra

The Lotka–Volterra system describes the time-course behaviour of two interacting species: prey \(X_{1,t}\) and predators \(X_{2,t}\). The stochastic differential equation describing the dynamics of \(X_t=(X_{1,t},X_{2,t})^T\) is given by

$$\begin{aligned} d\begin{pmatrix}X_{1}\\ X_{2}\end{pmatrix}&= \begin{pmatrix} \theta _{1}X_{1}-\theta _{2}X_{1}X_{2} \\ \theta _{2}X_{1}X_{2}-\theta _{3}X_{2} \end{pmatrix}\,dt \nonumber \\&\quad + \begin{pmatrix}\theta _{1}X_{1}+\theta _{2}X_{1}X_{2} &{} -\theta _{2}X_{1}X_{2} \\ -\theta _{2}X_{1}X_{2} &{} \theta _{2}X_{1}X_{2}+\theta _{3}X_{2} \end{pmatrix}^{\frac{1}{2}}\,d \begin{pmatrix}W_{1}\\ W_{2}\end{pmatrix} \end{aligned}$$
(24)

after suppressing dependence on t.

We repeated the experiments of Golightly et al. (2019) which, for this example, involved three synthetic data sets generated with \(\theta =(0.5,0.0025,0.3)^T\) and a known initial condition of \(x_{0}=(100,100)^T\). The observation model is

$$\begin{aligned} Y_{t}\sim \text {N}\left( X_t,\sigma ^{2}I_{2}\right) \end{aligned}$$

where \(I_{2}\) is the \(2\times 2\) identity matrix and \(\sigma \in \{1,5,10\}\) giving data sets designated as \({\mathcal {D}}_1\), \({\mathcal {D}}_2\) and \({\mathcal {D}}_3\), respectively. Data set \({\mathcal {D}}_3\) is shown in Figure 3, and gives dynamics typical of the parameter choice taken. The parameters correspond to the rates of prey reproduction, prey death and predator reproduction, and predator death. As the parameters must be strictly positive, we work on the logarithmic scale with independent \(N(0,10^2)\) priors assumed for each \(\log \theta _i\), \(i=1,2,3\). The main monitoring runs consisted of \(10^5\) iterations of aCPMMH, CPMMH (with \(\rho =0.99\)) and PMMH. Note that aCPMMH used random walk proposals in the \(\log \theta \) and \(x^o\) updates, with variances obtained from the output of an MCMC pilot run based on the LNA, which was also used to initialise \(\theta \) and \(x^o\).

Table 2 Lotka–Volterra model. Number of particles N, correlation parameter \(\rho \), CPU time (in seconds s), minimum ESS (over \(\theta \) and \(x^o\) chains), minimum ESS per second and relative (to PMMH) minimum ESS per second. All results are based on \(10^5\) iterations of each scheme
Full size table
Fig. 5
figure 5

Lotka–Volterra model. Difference (2 cores vs 1 core) in \(\log _2\) CPU times (\(\Delta \log _{2}\text {CPU}\)) against \(\log _{10} \Delta \tau \) using aCPMMH with \(N=1\) (solid lines) and CPMMH (dashed lines) with \(N=3\) (data set \({\mathcal {D}}_1\), left), \(N=8\) (data set \({\mathcal {D}}_2\), centre) and \(N=18\) (data set \({\mathcal {D}}_3\), right)

Full size image

From Figure 4 we see that aCPMMH gives parameter posterior output that is consistent with the ground truth (and also with the output of PMMH and CPMMH – not shown). In this case, the LNA gives accurate output when used as an inferential model. We compare efficiency of PMMH, CPMMH and aCPMMH in Table 2. We found that \(N=1\) was sufficient for aCPMMH but also include results for \(N=2\), which gave a small increase in minimum ESS but a decrease in overall efficiency, due to the increase (doubling) in CPU time. It is clear that as \(\sigma \) increases, PMMH and CPMMH require an increase in N to maintain a reasonable minimum ESS. Consequently, their performance degrades. Although the statistical efficiency (mESS) of aCPMMH reduces as \(\sigma \) increases, the reduction is gradual (compared to that of CPMMH) and we see an increase in overall efficiency of aCPMMH (with \(\rho =0.99\)) of an order of magnitude over PMMH in all experiments, and over CPMMH for data sets \({\mathcal {D}}_2\) and \({\mathcal {D}}_3\). We also include the output of aCPMMH with \(N=1\) and \(\rho =0.0\), corresponding to the modified innovation scheme of Golightly and Wilkinson (2008) (and as discussed in Sect. 3.3). Although this approach works well compared to CPMMH and PMMH, and gives well-mixing parameter chains, we see a decrease in mESS (relative to aCPMMH with \(\rho =0.99\)) calculated from the \(x^o\) chains, and this relative difference increases as \(\sigma \) increases.

Fig. 6
figure 6

Autoregulatory model. Data set (circles) and summaries (mean and \(95\%\) credible intervals obtained from the output of aCPMMH) of the within-sample predictive \(\pi (y|{\mathcal {D}})\)

Full size image

Finally, we compare the performance of CPMMH and aCPMMH when parallelised over two cores. For aCPMMH (and as discussed at the end of Sect. 3.2), operations over t in steps 2,3 and 4 of Algorithm 4 can be performed in parallel. For CPMMH, we perform the propagate step of the particle filter (step 2(b) of Algorithm 1) in parallel. Figure 5 shows the difference (2 cores vs 1 core) in \(\log _2\) CPU times (denoted \(\Delta \log _{2}\text {CPU}\)) against \(\log _{10} \Delta \tau \), where the discretisation level is \(\Delta \tau \in \{10^{-4},10^{-3},10^{-2},10^{-1}\}\); for a perfect speed up from the use of two cores, this would be \(-1\). Results based on aCPMMH used \(N=1\) in all cases, whereas CPMMH used \(N=3\), \(N=8\) and \(N=18\). These values correspond to the numbers of particles required for each synthetic data set. For aCPMMH, we see that using 2 cores is beneficial for \(\Delta \tau \le 10^{-2}\). For CPMMH and \(N=1\), there is almost no benefit in a multi-core approach (and CPU time using 2 cores is typically higher than a single core approach). This is unsurprising given the resampling steps (performed in serial) between the propagate steps. As N increases, the benefit of using 2 cores can be seen.

4.3 Autoregulatory gene network

A commonly used mechanism for auto-regulation in prokaryotes which has been well-studied and modelled is a negative feedback mechanism whereby dimers of a protein repress its own transcription (e.g. Arkin et al. 1998, ). A simplified model for such a prokaryotic auto-regulation, based on this mechanism can be found in Golightly and Wilkinson (2005) (see also Golightly and Wilkinson 2011). We consider the SDE representation of the dynamics of the key species involved in this mechanism. These are \(\textsf {RNA}\), \(\textsf {P}\), \(\textsf {P}_2\) and \(\textsf {DNA}\), denoted as \(X_1\), \(X_2\), \(X_3\) and \(X_4\), respectively. The SDE takes form (1) where

$$\begin{aligned} \alpha (X_t,\theta )=S\,h(X_t,\theta ),\qquad \beta (X_t,\theta )= S\,h(X_t,\theta )\, S^T, \end{aligned}$$

the stoichiometry matrix S is

$$\begin{aligned} S = \left( \begin{array}{rrrrrrrr} 0&{}0&{}1&{}0&{}0&{}0&{}-1&{}0\\ 0&{}0&{}0&{}1&{}-2&{}2&{}0&{}-1\\ -1&{}1&{}0&{}0&{}1&{}-1&{}0&{}0\\ -1&{}1&{}0&{}0&{}0&{}0&{}0&{}0\\ \end{array}\right) , \end{aligned}$$

and the hazard function \(h(X_t,\theta )\) is

$$\begin{aligned}&h(X,\theta ) = (0.1 X_{4}X_{3}, \theta _1(10-X_{4}), \theta _2 X_{4}, 0.2 X_{1}, \\&\qquad \qquad \qquad \qquad 0.1 X_{2}(X_{2}-1)/2, \theta _3 X_{3}, \theta _4 X_{1}, \theta _8 X_{2} )^T \end{aligned}$$

after dropping t to ease the notation. Further details regarding the derivation of the SDE can be found in Golightly and Wilkinson (2005).

Table 3 Autoregulatory model. Number of particles N, correlation parameter \(\rho \), CPU time (in seconds s), minimum ESS (over \(\theta \) and \(x^o\) chains), minimum ESS per second and relative (to PMMH) minimum ESS per second. All results are based on \(10^5\) iterations of each scheme
Full size table

The parameters \(\theta =(\theta _{1},\theta _{2},\theta _{3},\theta _{4})^T\) correspond to the rate of protein unbinding at an operator site, the rate of transcription of a gene into mRNA, the rate at which protein dimers disassociate and the rate at which protein molecules degrade. We generated a single synthetic data set with \(\theta =(0.7,0.35,0.9,0.3)^T\) and an initial condition of \(x_{0}=(8,8,8,5)^T\). The observation model is

$$\begin{aligned} Y_{t}\sim \text {N}\left( X_t,\Sigma \right) \end{aligned}$$

where \(\Sigma \) is a diagonal matrix with elements 1, 1, 1, 0.25. The data are shown in Fig. 6. Independent \(U(-5,5)\) priors were assumed for each \(\log \theta _i\), \(i=1,2,3,4\). A short MH run was performed using the LNA, to obtain estimates of \(\text {var}(\log \theta |y)\) and \(\text {var}(x_t|y)\) (to be used the innovation variances of the random walk proposal mechanisms in (a)CPMMH) and plausible values of \(\theta \) and \(x^o\) (to be used to initialise the main monitoring runs of (a)CPMMH). Pilot runs of aCPMMH and CPMMH suggested taking \(N=1\) and \(N=20\) for each respective scheme. We then ran aCPMMH and CPMMH for \(10^5\) iterations with these tuning choices. Table 3 and Fig. 6 summarise our findings.

It is clear that aCPMMH with \(\rho =0.99\) results in a considerable improvement in statistical efficiency over aCPMMH with \(\rho =0.0\) (which is the modified innovation scheme). In particular, minimum ESS (calculated over the \(x^o\) chains) is almost an order of magnitude higher for \(\rho =0.99\) (866 vs 5524). An improvement in overall efficiency of aCPMMH over CPMMH is evident, irrespective of the choice of \(\rho \). Increasing N to 2 gives results in better mixing of the \(x^o\) chains, but no appreciable increase in minimum ESS over all chains.

5 Discussion

Fig. 7
figure 7

Autoregulatory model. Marginal posterior distributions based on the output of aCPMMH (solid lines) and the LNA (dashed lines). The true parameter values are indicated

Full size image

Given observations at discrete times, performing fully Bayesian inference for the parameters governing nonlinear, multivariate stochastic differential equations is a challenging problem. A discretisation approach allows inference for a wide class of SDE models, at the cost of introducing an additional bias (the so-called discretisation bias). The simplest such approach uses the Euler–Maruyama approximation in combination with intermediate time points between observations, to allow a time step chosen by the practitioner, that should trade off computational cost and accuracy. It is worth emphasising that although a Gaussian transition density is assumed, the mean and variance are typically nonlinear functions of the diffusion process, and consequently, the data likelihood (after integrating out at intermediate times) remains intractable, even under the assumption of additive Gaussian noise.

These remarks motivate the use of pseudo-marginal Metropolis–Hastings (PMMH) schemes, which replace an evaluation of the intractable likelihood with a realisation of an unbiased estimator, obtained from a single run of a particle filter over dynamic states (Andrieu et al. 2010). It is crucial that the number of particles is carefully chosen to balance computational efficiency whilst allowing for reasonably accurate likelihood estimates. Inducing strong and positive correlation between successive likelihood estimates can reduce the variance of the acceptance ratio, permitting fewer particles (Dahlin et al. 2015; Deligiannidis et al. 2018). Essentially, the (assumed Gaussian) innovations that are used to construct the likelihood estimates are updated with a Crank-Nicolson (CN) proposal. The resampling steps in the particle filter are also modified in order to preserve correlation; the random numbers used during this step are included in the CN update, and the particle trajectories are sorted before resampling takes place at the next time point. We follow Choppala et al. (2016) and Golightly et al. (2019) by using a simple Euclidean sorting procedure based on the state of the particle trajectory at the current observation time. We find that the effectiveness of this correlated PMMH (CPMMH) approach degrades as the observation variance and state dimension increases.

Our novel approach avoids the use of resampling steps, by updating parameters conditional on the values of the latent diffusion process at the observation times (and the observations themselves), whilst integrating over the state uncertainty at the intermediate times. An additional step is then used to update the latent process at the observation times, conditional on the parameters and data. The resulting algorithm can be seen as a pseudo-marginal scheme, with unbiased estimators of the likelihood terms obtained via importance sampling. We further block together the updating of the latent states and the innovations used to construct the likelihood estimates, and adopt a CN proposal mechanism for the latter. We denote the resulting sampler as augmented, correlated PMMH (aCPMMH). A related approach is given by Fearnhead and Meligkotsidou (2016), who use particle MCMC with additional latent variables, carefully chosen to trade-off the error in the particle filter against the mixing of the MCMC steps. We emphasise that unlike this approach, the motivation behind aCPMMH is to avoid use of a particle filter altogether, the benefits of which are two-fold: positive correlation between successive likelihood estimates is preserved and the method for obtaining these likelihood estimates can be easily parallelised over observation intervals. Section 4.2 shows that once the updating over an inter-observation interval is sufficiently costly substantial gains can be obtained by parallelising this task over the different inter-observation intervals: this could be useful for stiff SDEs, high-dimensional SDEs, or if multiple inter-observation intervals are tackled by a single importance sampler.

In addition to the tuning choices required by CPMMH (that is, the number of particles N, correlation parameter \(\rho \) in the CN proposal and parameter proposal mechanism), aCPMMH requires initialisation of the latent process at the observation times and a suitable proposal mechanism. If a computationally cheap approximation of the joint posterior can be found, this may be used to initialise and tune aCPMMH. To this end, we found that use of a linear noise approximation (LNA) can work well, even in settings when inferences made under the LNA are noticeably discrepant, compared to those obtained under the SDE. In scenarios where use of the LNA is not practical, a pilot run of aCPMMH can be used instead.

We compared the performance of aCPMMH with both PMMH and CPMMH using three examples of increasing complexity. In terms of overall efficiency (as measured by minimum effective sample size per second), aCPMMH offered an increase of up to a factor of 28 over PMMH. We obtained comparable performance with CPMMH for a univariate SDE application, and an increase of up to factors of 10 and 14 in two applications involving SDEs of dimension 2 and 4, respectively. Our experiments suggest that although the mixing efficiency of aCPMMH increases with N, the additional computational cost results in little benefit (in terms of overall efficiency) over using \(N=1\). A special case of aCPMMH (when \(\rho =0\) and \(N=1\)) is the modified innovation scheme of Golightly and Wilkinson (2008), which is typically outperformed (in terms of overall efficiency) with \(\rho >0\).

5.1 Limitations and future directions

There are some limitations of aCPMMH which form the basis of future research. For example, in each of our applications the associated latent process exhibits unimodal marginal distributions and linear dynamics between observation instants that are well approximated by the modified diffusion bridge construct. Extension to the multimodal case would require an important proposal that captures the multimodality of the marginal distributions of the true bridge between observation instants. We refer the reader to the guided proposals of van der Meulen and Schauer (2017) and Schauer et al. (2017) for possible candidate proposal processes.

Additional directions for future research include the use of methods based on adaptive proposals which may be of benefit in both the parameter and latent state update steps. Proposal mechanisms that exploit gradient information such as the Hamiltonian Monte Carlo (HMC) method (Duane et al. 1987) may also be of interest. We note that in the case of \(N=1\), it is possible to directly calculate the required log-likelihood gradient. For \(N>1\), importance samples generated from \(\pi (x^L |x^o, \theta )\) could be used to estimate

$$\begin{aligned} \nabla _{\theta }\log \pi (x^o|\theta ) = \int \nabla _{\theta } \log \pi (x|\theta ) \pi (x^L |x^o, \theta )dx^L . \end{aligned}$$

For a general discussion on the use of particle filters for estimating log-likelihood gradients we refer the reader to Poyiadjis et al. (2011); see also Nemeth et al. (2016). A comparison of aCPMMH with approaches that target the joint posterior of the parameters and latent process also warrants further attention; see e.g. Botha (2020) for an implementation of the latter.

Although we have focussed on updating the latent states in separate blocks (single site updating), other blocking schemes may offer improved mixing efficiency. Alternatively, it might be possible to reduce the number of latent variables, for example, by only explicitly including latent states in the joint posterior at every (say) kth observation instant. The success of such a scheme is likely to depend on the accuracy of an importance sampler that covers k observations, and whether or not the resulting likelihood estimates can be made sufficiently correlated. This is the subject of ongoing work.