Abstract
Graph matching is a fruitful area in terms of both algorithms and theories. Given two graphs \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\), where \(V_1\) and \(V_2\) are the same or largely overlapped upon an unknown permutation \(\pi ^*\), graph matching is to seek the correct mapping \(\pi ^*\). In this paper, we exploit the degree information, which was previously used only in noiseless graphs and perfectly-overlapping Erdős–Rényi random graphs matching. We are concerned with graph matching of partially-overlapping graphs and stochastic block models, which are more useful in tackling real-life problems. We propose the edge exploited degree profile graph matching method and two refined variations. We conduct a thorough analysis of our proposed methods’ performances in a range of challenging scenarios, including coauthorship data set and a zebrafish neuron activity data set. Our methods are proved to be numerically superior than the state-of-the-art methods. The algorithms are implemented in the R (A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, 2020) package GMPro (GMPro: graph matching with degree profiles, 2020).
Similar content being viewed by others
1 Introduction
Graph matching has been an active area of research for decades. The research on graph matching can be traced back to at least 1970s (e.g. Ullmann 1976), and interpreted as “graph matching”, “network alignment” and “graph isomorphism”. In this paper, we do not distinguish these terms, nor the terms “graph” and “networks”, or “nodes” and “vertices”. Mathematically, the graph matching problem can be loosely stated as follows. Given two graphs \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\), it is assumed that \(V_1\) and \(V_2\) are the same or largely overlapped upon an unknown permutation \(\pi ^*\). Graph matching seeks the mapping \(\pi ^*\) between the vertex sets \(V_1\) and \(V_2\). A correct matching would help to augment the connectivity information between the vertices, and hence improve the graph analysis. In recent years, due to the advancements in collecting, storing and processing large volume of data, graph matching is going through a renaissance, with a surge of work on graph matching in different application areas. For instance, Narayanan and Shmatikov (2009) targeted at acquiring information from an anonymous graph of Twitter with the graph of Flickr as the auxiliary information; Kazemi et al. (2016) seek the alignment of protein-protein interaction networks in order to uncover the relationships between different species; Haghighi et al. (2005) constructed graphs based on texts relationship and developed a system for deciding whether a given sentence can be inferred from text by matching graphs.
Graph matching is an extremely fruitful research area. In the following, we review the existing literature from three different aspects, based on which, we characterize our main interest of this paper.
In terms of methodology, broadly speaking, the graph matching algorithms can be categorized into two schools: exact matching and inexact matching. The exact graph matching, requiring a strict correspondence between two graphs and with graph isomorphism as a special case, focuses on deterministic graphs. It seeks a perfect matching, which is NP-hard in most cases, with exceptions in some special graph structures, for instance planar graphs (see e.g. Eppstein 2002). When we move from deterministic graphs to random graphs, it is challenging and not natural to seek a perfect matching. The inexact matching approaches, which allow for the two graphs to be different, are considered in this case. Existing methods designed for inexact matching include tree search types of methods (see e.g. Sanfeliu and Fu 1983), continuous optimization types of methods (see e.g. Liu et al. 2012) and spectral-based convex relaxation types of methods. Due to the demand of computational feasibility when dealing with large-scale datasets, the spectral-based methods have been, arguably, the most popular type of methods. To be more specific, spectral-based methods include spectral matching (see e.g. Leordeanu and Hebert 2005), semidefinite-programming approaches (see e.g. Schellewald and Schnörr 2005) and doubly-stochastic relaxation methods (see e.g. Gold and Rangarajan 1996). For comprehensive reviews, we refer to Conte et al. (2004), Foggia et al. (2014) and Yan et al. (2016).
In terms of the underlying models, despite the large amount of algorithms proposed over the years, the majority of the efforts are on the Erdős–Rényi random graphs (Erdös and Rényi 1959), which are fundamental but unrealistic. Beyond the Erdős–Rényi random graphs, Patsolic et al. (2017) studied the graph matching in a random dot product graph (see e.g. Young and Scheinerman 2007) framework. Li and Campbell (2016) is concerned with the community matching in a multi-layer graph, the matching resolution thereof is at the community level, but not at the individual level. The study in this area usually is complicated by the misclustered vertices.
In terms of the proportion of overlapping vertices in two graphs. Some of the existing works consider the situations where the two graphs have identical vertex sets, while some consider the situations where the difference between two vertex sets is nonempty. In the sequel, we will refer to these two situations as perfectly-overlapping and partially-overlapping. Work on the latter includes the following: Pedarsani and Grossglauser (2011) studied the privacy of anonyized networks; Kazemi et al. (2015) defined a cost function for structural mismatch under a particular alignment and established a threshold for perfect matchability; and Patsolic et al. (2017) provided a vector of probabilities of possible matchings.
We now specify the problem we are concerned about in this paper. (1) We intend to exploit the degree information and extend the degree profile method, which shares connection with the doubly stochastic relaxation methods and which has been previously studied in Czajka and Pandurangan (2008) and Mossel and Ross (2017) for deterministic graphs and in Ding et al. (2018) for perfectly-overlapping Erdős–Rényi random graphs. (2) We consider network models with community structures, including stochastic block models, which are arguably the most popular network models for both theoretical and practical studies. (3) We tackle partially-overlapping graphs, e.g. the two graphs to be matched do not have identical vertex sets.
1.1 Coauthorship data set: a teaser
Before we formally state the problem framework and our proposed methods, we present some real data analysis based on the coauthorship data set generated from the coauthor relationship between authors who published papers in the Annals of Statistics (AoS), Biometrika, the Journal of American Statistician Association (JASA) and the Journal of Royal Statistical Society, Series B (JRSSB). It is originally studied in Ji and Jin (2016). The details of the methods will be explained in Sect. 2. More details of data processing and more analysis based on this data set are deferred to Sect. 4.1.
We create two coauthorship networks. The first one combines the authors and their coauthorship within AoS and Biometrika, and the second one is based on JRSSB and Biometrika. These two resulting networks are obviously overlapped, due to the common inclusion of Biometrika, but also differ, due to the inclusions of the AoS and JRSSB, respectively. We choose this triplet since among these four journals, AoS and JRSSB tend to have longer papers, while Biometrika has a specific taste of the writing style.
After some data pre-processing, these two networks are of sizes 474 and 518, where 401 nodes appear in both networks. There are 763 and 834 edges in these two networks, respectively. Note that, the resulting two networks are partially-overlapping, in the sense that
-
the sets of nodes are largely overlapping but not identical, and
-
even if two nodes are present in both networks, they may be connected in one network but not the other.
We apply one of our proposed methods, namely EE-post, compared with the state-of-the-art method, namely degree profile graph matching (DP) (Ding et al. 2018). DP matches 359 nodes and 96 among them are correctly matched. Our newly proposed EE-post method matches 467 nodes and 186 among them are correctly matched. The number of correct matchings double. We further calculate the recovery rates for the two methods:
Our proposed EE-post almost doubles the recovery rate of DP – the recovery rates of EE-post and DP are 46.4% and 23.9%, respectively.
1.2 List of contributions
Our contribution is listed below.
-
We formally describe a partially-overlapping correlated Bernoulli networks model in Definition 1. Further, we explore the degree profile graph matching method for the newly defined partially-overlapping Erdős–Rényi random graphs and also the stochastic block random graphs. To the best of our knowledge, this is the first work to exploit the degree profile-type method in stochastic block model graph matching problems.
-
We propose the edge exploited (EE) degree profile graph matching method. In addition, we propose refined EE algorithms, including pre-processing and post-processing steps. These proposed methods are demonstrated to outperform the state-of-the-art methods when the graphs are partially overlapping.
-
The degree profile core of our methods enable us to conduct graph matching for graphs with sparse connections, where the spectral-based methods usually fail.
The rest of this paper is organized as follows. In Sect. 2, we present our proposed methods. We kick off by reviewing a state-of-the-art degree profile method, extend it to handle the partially-overlapping scenarios, and finally tackle stochastic block model graph matching. Our proposed methods are supported by extensive numerical evidence on both simulated and real datasets in Sects. 3–4. The paper is concluded by discussions in Sect. 5.
2 Methodology
In this section, we first introduce the motivating model in Sect. 2.1, and review the degree profile graph matching method in Sect. 2.2. The main algorithm is proposed in Sect. 2.3, with its refinements in Sect. 2.4. We then move on to the stochastic block models graph matching in Sect. 2.5 and conclude the section with a summary in Sect. 2.6.
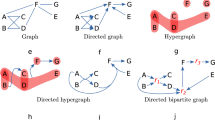
Eight algorithms are presented in this section. As a reading guide, we show their relationship in Fig. 1. Algorithms 1, 2 and 6 are existing methods in the literature. Our main proposals are Algorithm 3, which has two refinements in Algorithms 4 and 5. As for the stochastic block models, we propose two methods Algorithm 7 and . The arrows in the figures mean the head is used in the tail.
A summary of algorithms in Sect. 2. The arrows in the figures mean the head is used in the tail



2.1 Motivating models: correlated Bernoulli networks
Generally, it is assumed the two graphs to match are generated from the same underlying parent graph, and the difference between two graphs are due to a permutation and possible information loss, such as missing edges or vertices. In this paper, we only consider simple graphs, i.e. undirected graphs without self-loops or multiple edges. We use adjacency matrices to characterize graphs, i.e. \(A_{ij} = 1\) if and only if the nodes i and j in graph A are connected by an edge, zero otherwise. In this section, we set up a motivating model for the parent graph and specify the parameters for the missing part.
Definition 1
(Partially-overlapping correlated Bernoulli networks) Let G be the adjacency matrix of a given graph and \(s, \rho \in [0, 1]\) be the overlapping and correlation parameters, respectively. Construct a matrix \(A'\) by independently keeping or removing each row (and the corresponding column) in G with probability s and \(1 - s\). Further, construct A by \(A_{ji} = A_{ij} = A'_{ij} X_{ij}\) where \(X_{ij} {\mathop {\sim }\limits ^{i.i.d.}} Bernoulli(\rho )\), \(i < j\). The graph with adjacency matrix A is called a child graph of G. Relabel the vertices of G according to a latent permutation \(\pi ^*\) and then repeat the sampling process independently to obtain another child graph B. A and B are partially-overlapping correlated Bernoulli networks.
We list a few cases to better understand Definition 1. When \(s = \rho = 1\), A and B are exactly the same up to a permutation \(\pi ^*\) (isomorphic graphs, e.g. Scheinerman and Ullman 2011). If we fix \(s = 1\) only, then both A and B have all n vertices.
Compared to the perfectly-overlapping correlated Erdős–Rényi random graphs, Definition 1 characterizes a general model, but inherits the key features that (i) A and B have identical marginal distributions, and (ii) the corresponding entries of A and B are correlated with correlation \(\rho \). In practice, the underlying G is usually unknown, but A and B can be obtained from different studies. For instance, one may obtain a fully-known Amazon users network and an anonymized eBay users network, while the underlying true network is unknown. Due to the anonymity, it is only reasonable to assume the users are largely overlapping in these two networks, but not perfectly.
The goal of this paper is to match the vertices between A and B. Since exact matching between A and B may not exist, we seek best matching between largest overlapped subgraphs of A and B. Mathematically, for networks A and B with \(n_A\) and \(n_B\) vertices, respectively, we seek a permutation \({\widehat{\pi }}\) defined as
where \(\varPi _m\) ranges over all \(m \times m\) permutation matrices and \(\langle \cdot , \cdot \rangle \) denotes the matrix inner product.
2.2 A review on degree profile graph matching
The degree profile method was pioneered in Czajka and Pandurangan (2008) and Mossel and Ross (2017) on graph matching of two identical graphs generated from Erdős–Rényi random graph models. This method is further studied in Ding et al. (2018) and is extended to correlated Erdős–Rényi random graphs. The key of the degree profile graph matching is to assign each vertex an empirical distribution of its neighbours’ degrees, and match vertices by measuring the distance between each pair of the empirical distributions. In this section, we first detail the definition of degree profile and then explain the simplest form of the degree profile method in Algorithm 2.
Definition 2
(Degree profile) Let \(A \in {\mathbb {R}}^{n \times n}\) be an adjacency matrix. For any \(i \in \{1, \ldots , n\}\), let \(a_i = \sum _{j = 1}^n A_{ij}\) and \(N_A(i) = \{j: \, A_{ij} = 1\}\) be the degree and the neighbourhood of i, respectively. Further denote \(a_k^{(i)}\) as the degree of i’s neighbour k, that is \(a_k^{(i)} = \sum _{l = 1}^n A_{lk}\). Let \(\mu _i(x) = a_i^{-1} \sum _{k \in N_A(i)} \mathbb {1}\{a_k^{(i)} \le x\}\), \(x \in {\mathbb {R}}\), be the empirical cumulative distribution functions of the set \(\{a_k^{(i)}, \, k \in N_A(i)\}\). The degree profile of vertex i in A is defined to be \(\mu _i(\cdot )\) and denoted as \(\mathrm {DP}(A, i)\).
The degree profile defined in Definition 2 is the second term of the iterated degree sequence. A necessary and sufficient condition for fractional isomorphism is that two graphs have identical iterated degree sequences. See Scheinerman and Ullman (2011) for more details.
In Ding et al. (2018), a similar definition is studied for the perfectly-overlapping Erdős–Rényi random graphs. In detail, the degree profile in Ding et al. (2018) is a normalized empirical distribution of neighbours’ degrees, excluding edges between neighbours when counting degrees and standardizing the degrees such that they are mean zero and variance one random variables. This normalization is for theoretical simplicity when dealing with the behaviours of the empirical distributions.
With the degree profiles for all vertices in A and B, our next step is to introduce a distance (or similarity) metric between each pair (i, j), \(i \in A\) and \(j \in B\) and construct an \(n_A \times n_B\) distance matrix W (or similarity matrix), where \(W_{ij}\) denotes the distance (or similarity) between the degree profiles of i and j. Intuitively, if \(i \in A\) and \(j \in B\) is a true pair, that is to say \(\pi ^*(i) = j\), then the distance \(W_{ij}\) is small (or the similarity \(W_{ij}\) is large), otherwise large (small). For each \(i \in A\), hence, we seek the mapping \({\widehat{\pi }}(i) = argmin_{j \in B} W_{ij}\) (or \({\widehat{\pi }}(i) = argmax_{j \in B} W_{ij}\)). We remark that, as for the model described in Definition 1, the computational complexity of Algorithm 1 is of order \(O(n^3\rho + n^2)\) (see Remark 3 in Ding et al. 2018).
The mapping \({\hat{\pi }}\) may not be a permutation, since multiple vertices in A might be mapped to the same vertex j in B. Hence, the final graph matching is output by applying a maximal bipartite matching algorithm to this mapping \({\hat{\pi }}\). Every vertex in B is matched to at most one vertex in A and there is no guarantee that all the vertices in A are matched to vertices in B. It is ensured that there exists no other bipartite matching which can match more vertices. In this paper, this is done by R (R Core Team 2020) package igraph (Csardi and Nepusz 2006), which uses the push-relabel algorithm introduced in Cherkassky et al. (1998).
With the analysis, we detail the, arguably, simplest degree profile algorithm, which involves a subroutine of calculating the distance matrix in Algorithm 1 and implements the degree profile graph matching in Algorithm 2.
In Algorithm 1, the distance used thereof is \(W_1\), the 1-Wasserstein distance (e.g. Villani 2009). In fact, any distance or similarity measure can be used here. We choose \(W_1\) to demonstrate numerical results and it will be used throughout this paper. In Sect. 2.4, in the refined algorithms that Algorithms 4 and 5, the similarity measure is introduced in the pre-processing or post-processing step, which delivers satisfactory results.
Algorithm 2 is similar to Algorithm 1 proposed in Ding et al. (2018). A difference is that Algorithm 2 seeks the pair with minimal distance for each vertex, but Ding et al. (2018) consider n pairs with smallest distances among all \(n_A \times n_B\) pairs. The two approaches deliver the same result if two networks are perfectly overlapping, yet Algorithm 2 can also provide possible matchings for vertices without counterparts. More discussions on this are available later.
The theoretical properties of degree profile graph matching have been extensively studied in Ding et al. (2018). The main advantage of degree profile graph matching over competitors is the ability to conduct polynomial-time graph matching in a sparse regime, where the spectral-type methods would fail. The main challenges in deriving the theoretical properties of the output of Algorithm 2 is to carefully control the fact that the degree profiles are linear combinations of correlated random variables, and this is out of the scope of this paper.
2.3 Main proposal: edge exploited methods for partially-overlapping graphs
The state-of-the-art methodology on the degree profile graph matching method was restricted to the cases where a bijection exists between the vertex sets of two graphs. This, however, is by no means realistic in more real-life problem. It is, therefore, of great interest to extend Algorithm 2 to handle the partially-overlapping networks. In Sect. 2.2, we added the maximum bipartite matching step to allow the bijection exists on only two subsets of the vertex sets. In this section, we explore further to allow information even when the bijection does not exist.
There are two differences between Algorithms 2 and 3. First, in Algorithm 3, we introduce an additional parameter d, which is in fact taken to be 1 in Algorithm 2. In Algorithm 3, the matrix Z is an adjacency matrix of a bipartite graph, where each vertex in A is connected to one and only one vertex in B. In the edge exploited version Algorithm 3, we allow for d edges for each vertex in A. A demonstration is depicted in Algorithm 3 with \(d = 3\). Instead of matching each vertex in A to an individual vertex in B, we match A to a hypergraph built upon B with hyper-edges of size at most \(d = 3\). Second, the final output of Algorithm 2 is from a maximum bipartite graph matching algorithm, and it does not allow for matching one vertex to a collection of vertices. To overcome this, we omit the maximum bipartite graph matching step in Algorithm 3 and output the matching matrix Z directly (Fig. 2).
To see why it is necessary to consider matching a node with more than one nodes, we match two partially-overlapping graphs A and B from Definition 1, with \(\varTheta _{ij} = 0.1\), \(1 \le i \ne j \le n\), \(n = 300\) and \((s, \rho ) = (0.9, 1)\). Ideally, for each vertex i in A, its true match \(\pi ^*(i)\) in B should be closest to i, in terms of the \(W_1\) distance. In practice, this is not always true, even though the correlation parameter \(\rho = 1\). In Fig. 3, we plot the ranks of \(\pi ^*(i)\), for all i, among all their competitors. The left panel includes all the vertices, and the right panel is a zoomed-in version of the top 50 of the left panel. As we can see, the true ones do not always possess the smallest distance to their matches, but are among the smallest ones most of the cases.
With the introduction of the parameter d, in terms of correctly matched pairs, Algorithm 3 of course improves substantially over Algorithm 2, which we will elaborate in Sect. 3. The rationale behind this is that in reality, adopting Algorithm 3 will nail down the matching to a small size of candidates. If the requirements on accuracy are not to the individual level, then instead of matching each vertex to at most one vertex, one would pay the price of increasing the matching size in order to find the correct matching. This is common in advertizing, for instance. This also shares similarity with Fishkind et al. (2012), where the output is a probability distribution attached to each vertex representing the probability of potential matches. The output of Algorithm 3 can be regarded as a uniform distribution over d potential matches. In fact, within the top d matches, the entries in the matrix W can also be used as a ranking among these matches.
2.4 Refinement
The key component of the degree profile graph matching algorithms in Bernoulli networks is discussed in Algorithms 2 and 3. In practice, Algorithm 2 suffers from the small matching size and unsatisfactory recovery rate, and the Algorithm 3 can only provide a matching set for each vertex. It is of question whether any additional steps can help to refine the matching result. In this subsection, we discuss two refinement algorithms, focusing on preprocessing and post processing, respectively.
2.4.1 Preprocessing
In practice, the high degree vertices have many neighbours and enjoy ample information for a successful matching. A natural idea is to first find such high degree vertices and their counterparts in the other graph, and then extend the matchings of high degree vertices only to matchings of all. This can be done by finding vertices with degrees larger than a pre-specified threshold.
Based on this idea, we propose the seeded edge exploited graph matching algorithm in Algorithm 4. We first establish a collection of matches \(\pi _0\) for the high degree vertices (degrees are at least \(\tau _1\)), the distances of which are the smallest among the pairs in consideration (distances are at most \(\tau _2\)). The set of these vertices is called the seeds set, \({\mathcal {S}}\). Next, we calculate the similarity between \(i \in A\) and \(j \in B\) using \(W_{ij} = \sum _{k \in {\mathcal {S}}} A_{ik} B_{j \pi _0(k)}\), the number of common neighbours between i and j based on \(\pi _0\). We then turn the similarity matrix W to a bipartite adjacency matrix using the threshold \(\tau _3\). With the maximum bipartite matching, we find a one-to-one correspondence between A and B as \(\pi _1\), so that the number of common neighbours is maximized. Finally, we calculate the similarity again based on \(\pi _1\), and find the matching set for each vertex as the vertex set with largest similarity. Details can be found in Algorithm 4.

In Algorithm 4, there are three thresholds to find a proper original matching. In practice, we conduct grid search to determine \(\{\tau _1, \tau _2, \tau _3\}\). For the two graphs, we calculate the degrees of all vertices and select 7 candidates for \(\tau _1\), which correspond to the i-th quantile of vertices’ degrees, \(i \in \{0.5, 0.55, 0.6, 0.65\), \(0.7, 0.75, 0.8\}\). Possible \(\tau _2\) is chosen from the j-th, \(j\in \{0.2, 0.25, 0.3, 0.35, 0.4\), \(0.45, 0.5\}\), quantile of the minimum distance between vertices in two graphs. The best combination of \(\tau _1\) and \(\tau _2\) is supposed to give the largest collection of seeds. Having obtained seeds, the number of common neighbours are calculated between all pairs of vertices and denoted as \(U_{ik}\). The parameter \(\tau _3\) is defined as the \(\frac{n-1}{n}\)-th quantile of \(U_{ik}\), which guarantees that the number of nonzero elements in U is approximately n. If all possible combinations provided empty seed sets, Algorithm 3 is summoned instead.
The concept of seeded graph matching is used in other ways in the literature. For instance, in Lyzinski et al. (2014) and Lyzinski et al. (2015), the seeds mean the information of some known vertices correspondence and seeded graph matching utilizes these known partial matching and includes them as constraints in the optimization. In Ding et al. (2018), the seeded degree profile graph matching starts with no known partial matchings and aims to refine Algorithm 1 in relatively dense graphs. We would like to emphasize that this relatively dense regime studied there is even too sparse for spectral-based graph matching methods to perform well.
Algorithm 4 can be regarded as an edge exploited version of Algorithms 2 and 3 in Ding et al. (2018). As we have mentioned, the main task of this paper is to move beyond the perfectly-overlapping Erdős–Rényi random graphs, therefore, in Algorithm 4, we adopt an edge exploited version. To motivate the preprocessing step, we alter the settings in Fig. 3 slightly, by increasing the overlapping parameter s from 0.9 to 0.99, which results in an easier problem. In Fig. 4, we again exhibit the true ranks. Different from Fig. 3, we can see that in this easier setting, almost all the true matchings are the ones with smallest distances. A preprocessing step will return a set of true matching.
2.4.2 Post processing
The way to produce a seeds set in Algorithm 4 sheds light on the post-processing step. With any preliminary graph matching result \(\pi _t\) (this can be from either Algorithm 2 or Algorithm 3), we can define the similarity between \(i \in A\) and \(j \in B\) as
which is the number of common neighbours between i and j according to the matching \(\pi _0\). Based on the similarity matrix, we use maximum bipartite matching to maximize the number of common neighbours for the matched vertices and provide a bijection as the final result.
Now we rewrite the matching \(\pi _t\) as \(\varPi _t\), where \(\varPi _t\) is an \(n_A \times n_B\) permutation matrix with \((\varPi _t)_{ij} = 1\) if \(j \in \pi _t(i)\) and 0 otherwise. Given \(\varPi _t\), The post processing step is to seek a refinement \(\varPi _{t+1}\) satisfying
The intuition is to refine the result iteratively by optimizing this linear assignment problem. Details are collected in Algorithm 5.


In addition to the graph matching output \(\varPi _0\), we also output a convergence indicator vector FLAG. In practice, we have observed that the true matches usually reach the convergence and stay the same after a few iterations, while the false matches may keep changing in the iterations. Instead of giving a guidance on the choice of \(n_{\mathrm {rep}}\), we report the convergence indicators for each matching as a reference for the certainty about the matching. Default value for \(\tau \) is \(n_{\mathrm {rep}}/10\), which means for the final \(10\%\) iterations, the matchings staying the same are regarded as “converged”.
A special case is when \(\rho = 0\), i.e. the two graphs are uncorrelated. In this case, by definition, no node actually has a counterpart in the other graph and we should not expect a graph matching. It is shown through numerical experiment that in this case, FLAG returns an all-zero vector as expected.
Starting with Algorithm 3 where a set of possible matchings are provided for one vertex, Algorithm 5 gives a one-to-one mapping as the final result with the post-processing step. It is shown to be numerically superior in more challenging setting and provides more information to improve the matching accuracy.
We remark that the matrix W defined in (1) and the iterative optimization procedure in (2) share similarities with the seeded graph matching algorithm in Lyzinski et al. (2014), in the sense that the preliminary matching result \(\pi _t\) can be seen as the seeds used in Lyzinski et al. (2014) and the optimization procedure (2) has the same formulation as the procedure discussed in Sect. 2.3 in Lyzinski et al. (2014). In Lyzinski et al. (2014), given a set of known matches, an extension of the Frank–Wolfe methodology (e.g. Jaggi 2013) was adopted to facilitate the algorithm and the seeded graph matching algorithm is shown to perform well given a set of known matches.
2.5 Graph matching in community-structured networks
Since most of the theoretically-justified graph matching algorithms are designed for perfectly-overlapping Erdős–Rényi random graphs, including the degree profile graph matching, a natural question when we move beyond is whether to conduct graph matching directly on, say stochastic block models, or to conduct community detection first then match the graphs.
Before we investigate this problem, we first state the community detection algorithm we adopt in this paper. The spectral clustering on ratios-of-eigenvectors was proposed in Jin (2015) and detailed below for completeness.
In Sect. 3.2, we conduct a systematic investigation on the following two approaches:
-
(1)
first applying Algorithm 6, then applying a graph matching algorithm within communities;
-
(2)
directly applying a graph matching algorithm.
There are various different community detection methods, even within the category of spectral-based methods. As for the methods we have applied, there is no obvious differences between those based on Algorithm 6 and those based on other spectral clustering methods.


As for the first approach, we further detail two algorithms listed in Algorithms 7 and 8. In Algorithm 7, we first apply Algorithm 6 and then use a certain graph matching method to match different communities. Note that \({\mathcal {S}}_K\) is the collection of all possible permutations on \(\{1, \ldots , K\}\). We write Algorithm 7 in a generic and, in fact, incomplete way. The output of Algorithm 7 has K! many matching results. Algorithm 8 can be regarded a post processing version of Algorithm 7 using the post processing method we introduced in Algorithm 5. The quantity Eval in Algorithm 8 is short for evaluation, which is algorithm-specific. For instance, if the graph matching algorithm used thereof is chosen to be Algorithm 2 or Algorithm 5, then Eval can be taken as the number of matched vertices or the number of converged vertices, respectively.
We now come back to investigate the choice between approaches (1) and (2). In terms of the violations of the theoretical guarantees provided in Ding et al. (2018), we first state the rationale behind the approach (1). Since Algorithm 2 is only theoretically justified on correlated Erdős–Rényi random graphs, it might be helpful to conduct community detection first to reduce a stochastic block model graph matching problem to a patially-overlapping Erdős–Rényi one. In fact, we cannot guarantee that with probability tending to 1, there is no misclustered vertex. This means even if we are in a regime where the community detection is strongly consistent, the resulting community may still contain misclustered vertices. The matching conducted in the approach (1) is a graph matching over partially-overlapping graphs.
2.6 Conclusion
Algorithm 1 calculates a core matrix which is used in repeatedly. As explained in Remark 3 in Ding et al. (2018), the time complexity of calculating W is of order \(O(n^3\rho + n^2)\), where n and \(\rho \) represent the magnitude of the network sizes and the upper bound on the connectivity probabilities in both networks, respectively. The matrix \(W \in {\mathbb {R}}^{n_A \times n_B}\) is stored once constructed, and the consequential storage cost is of order \(n^2\). Algorithm 3 is the main algorithm proposed in this paper. If we do not care about the order of the top d matches, then the time complexity of Algorithm 3 is of order \(O(n^2)\), otherwise, \(O(n^2 + nd\log (d))\), using Introselect algorithms. Algorithms 4 and 5 are two refinement algorithms based on Algorithm 3, both of which have the most time-consuming step being the calculation of the matrix W. Therefore the time complexity of these two algorithms are of order \(O(n^3\rho + n^2)\).
3 Simulation analysis
In this section, we conduct a thorough simulation analysis on the numerical performances of the algorithms proposed in Sect. 2. For notational simplicity, we refer to Algorithms 2, 3, 4 and 5 as DP (degree profile), EE (edge exploited version), EE-pre (edge exploited version with preprocessing, EE-) and EE-post (edge exploited version with post processing, EE+), respectively. We will see that our proposed methods can perform well in challenging situations for partially-overlapping graphs and for stochastic block models. We have implemented all the methods in the R (R Core Team 2020) package GMPro (Hu et al. 2020).
3.1 Partially-overlapping correlated Erdős–Rényi random graphs
In this subsection, we consider graph matching in patially-overlapping correlated Erdős–Rényi random graphs.
The simulation settings involve the following parameters: (i) the network size \(n = 300\), (ii) the connection probability \(q \in \{0.10, 0.05\}\), and (iii) \((\rho , s) \in \{(1, 1), (0.95, 0.98), (0.9, 0.95)\}\), where \(\rho \) and s are the correlation and overlapping parameters, respectively. Each setting is repeated 50 times.
As for the tuning parameters used in the algorithms, we let \(d \in \{10, 30\}\), where d is the tuning parameter for the edge exploited step in Algorithms 3, 4 and 5. The tuning parameters required in Algorithm 4 are generated automatically based on the grid search method we introduced in Sect. 2.4.1.
The methods we adopt are DP, EE, EE-pre and EE-post. The performances are evaluated by the recovery rate over all nodes that have counterparts in the other graph. Note that we allow for partially-overlapping graphs, hence not every single node has a counterpart in the other graph, and the number of these overlapping nodes is usually smaller than the number of nodes in a single graph.
Simulation results in Sect. 3.1. All are the means and standard errors. The parameter settings are: Set 1, \((\rho , s) = (0.9, 0.95)\); Set 2, \((\rho , s) = (0.95, 0.98)\); Set 3, \((\rho , s) = (1, 1)\). The methods are: DP, Algorithm 2; EE10, Algorithm 3 with \(d = 10\); EE30, Algorithm 3 with \(d = 30\); EE-10, Algorithm 4 with \(d = 10\); EE-30, Algorithm 4 with \(d = 30\); EE+10, Algorithm 5 with \(d = 10\); EE+30, Algorithm 5 with \(d = 30\)
The results are collected in Fig. 5. Since our methods are asymmetry for the two graphs, we present the recovery rates for each graph separately. Despite the asymmetry, the difference between graphs are negligible.
The three parameter settings are in difficulty decreasing order. In Setting 1, \((\rho , s) = (0.9, 0.95)\), in terms of the recovery rate, EE algorithms are the best. This is not a surprise, since they are the only ones allowing for matching one node to multiple nodes. Even so, the recovery rate is still below half. In Setting 3, \((\rho , s) = (1, 1)\), the two graphs are identical. All algorithms behave well. In Setting 2, \((\rho , s) = (0.95, 0.98)\), we can see that EE-post dominantly outperformed all the other methods, even though EE algorithms allow for multiple matching while EE-post only for single matching.
Among all settings, EE-post with \(d = 30\) is similar or worse than the case \(d = 10\). It suggests a small tuning parameter d for successful results. Besides the recovery rate, there is also a convergence parameter FLAG for EE-post algorithm. Interestingly, if we roughly regard the iterations with \(\sum \hbox {FLAG}_i > n/2\) as iterations that EE-post succeeds, then EE-post has recovery rate around 0.9 for all the successful iterations, and approximately 0 for others. The convergence indicator provides supporting information to decide whether the matching is reliable or not.
The time cost is compared in Table 1. We only record EE and EE-pre with the choice \(d = 10\), since the time doesn’t change when \(d = 30\). Generally, the time cost for DP and EE are very similar since the main cost is to calculate W. EE-pre and EE-post is based on EE, so the time cost is larger. EE-pre usually costs longer time than EE-post, since searching for proper seeds is time-consuming. When the network becomes denser, all the algorithms tend to spend longer time.
Simulation results in Sect. 3.2. All are the means and standard errors. The parameter settings are: Set 1, \(\rho = 0.9\); Set 2, \(\rho = 0.93\); Set 3, \(\rho = 0.95\). The methods are: (i), Algorithm 2; (ii)-10, Algorithm 5 with \(d = 10\); (ii)-50, Algorithm 5 with \(d = 50\); (iii), Algorithm 7 with Algorithm 2; (iv)-10 Algorithm 7 with Algorithm 5, \(d = 10\); (iv)-50 Algorithm 7 with Algorithm 5, \(d = 50\); (v), Algorithm 8 with Algorithm 2; (vi)-10, Algorithm 8 with Algorithm 5, \(d = 10\); (vi)-50, Algorithm 8 with Algorithm 5, \(d = 50\)
3.2 Correlated stochastic block models
In this subsection, we consider graph matching in correlated stochastic block models. Different from Sect. 3.1, we only consider perfectly-overlapping graphs. In Sect. 2.5, we have discussed that different theoretical limits for community detection and graph matching may induce misclustered nodes and hence partially-overlapping graphs to match.
The simulation settings involve the following parameters: (i) the network size \(n = 1000\), (ii) the number of communities \(K = 2\), (iii) the within communities probability \(q \in \{0.10, 0.05\}\) and the between communities probability q/2, and (iv) the probability of keeping an edge from the parent graph \(\rho \in \{0.95, 0.93, 0.9\}\). Each setting is repeated 10 times.
As for the tuning parameters used in the algorithms, we let \(d \in \{10, 50\}\), where d is the tuning parameter for the edge exploited step in Algorithms 3, 4 and 5. The tuning parameters required in Algorithm 4 are generated automatically based on the grid search method we introduced in Sect. 2.4.1.
In this scenario, we compare results from six different methods. (i) Algorithm 2, (ii) Algorithm 5, (iii) Algorithm 7 with Algorithm 2, (iv) Algorithm 7 with Algorithm 5, (v) Algorithm 8 with Algorithm 2 and (vi) Algorithm 8 with Algorithm 5. In Sect. 2.5 we have mentioned that the output of Algorithms 7 and 8 are not necessarily unique. In (iii) and (v), we choose the permutations of the communities which return more matchings. In (iv) and (vi), we report the ones with larger converging matchings. The measurements we adopt here are similar to those in Sect. 3.1, except that in this section, we do not report the results for graphs A and B separately. Since we let \(s = 1\) and the algorithms we evaluate only report at most one matching, the recovery results for graphs A and B are identical (Fig. 6).
Setting 1 is the most difficult one. For this setting, EE-post methods (Approaches (ii), (iv) and (vi)) can actually achieve almost perfect recovery for relatively sparse graphs (\(q = 0.05\), right column panels). Another interesting thing to notice in Setting 1 is that, EE-post with \(d = 10\) can perform better in the sparse graphs while EE-post with \(d = 50\) performs better in the dense graphs. It may indicate a choice of small d for sparse graphs in practice. In Setting 3, all algorithms perform well except (i) and (iii), both of which are based on Algorithm 2.
In order to answer the question that if one should do community detection before matching two stochastic block models, we recall that algorithm (ii) is to directly match stochastic block models, (iv) is to conduct EE-post on estimated communities and (vi) is to conduct EE-post on the estimated communities first and then the whole graph. The comparable settings for this matter are Settings 1 and 2. We can see that in the denser graphs (left column panel), conducting EE-post on both the estimated communities and the whole graph perform best. In the sparser graphs (right column panel), directly matching graphs perform best. This is to some extent expected, since the success of community detection relies on more stringent density requirements than the degree profile algorithms.
4 Real data
In this section, we conduct analysis on two real datasets and focus on the performance of Algorithms 2, 3 and 5.
4.1 Coauthor dataset
In this section, we provide the details of the analysis we conducted in Sect. 1.1, along with more comprehensive analysis.
The coauthorship dataset in Ji and Jin (2016) includes the co-authorship patterns between statisticians according to the publications in the Annals of Statistics (AoS), Biometrika, Journal of American Statistician Association (JASA) and Journal of Royal Statistical Society, Series B (JRSSB), during the period Years 2003-2012.
Consider the same set of statisticians who published papers in the above mentioned four journals. Choose any three distinct journals A, B and C, and consider two networks G(A, B) formed by \(A \cup B\) and G(A, C) formed by \(A \cup C\). In G(A, B) (or G(A, C)), each node is an author who published papers in the journals A and/or B (or A and/or C), and an edge between nodes i and j indicate i and j coauthored one paper in A and/or B (or A and/or C). We only consider the authors that appear in both G(A, B) and G(A, C). Since one author tends to collaborate with the same set of colleagues but may publish papers in different journals, the edges in G(A, B) and G(A, C) are similar but not identical.
Recall the notation we use in Sect. 1.1. For any choices of the journals A, B and C, the two networks G(A, B) and G(A, C) contain isolated nodes and pairs, which provide little information for graph matching. Hence, we extract the giant components of these two networks respectively, denoted as \({\tilde{G}}(A, B)\) and \({\tilde{G}}(A, C)\). They are the final networks we work on. The extraction causes different sizes for \({\tilde{G}}(A, B)\) and \({\tilde{G}}(A, C)\), and provides partially-overlapping networks where methods in Ding et al. (2018) can not work.
As for EE and EE-post, we let \(d = 5\) and \(n_{\mathrm {rep}} = 50\). In EE-post, we let \(\tau = 5\). It means we consider a matching as “converged matching” when the matching stays the same for at least last 5 iterations. We introduce this new notion in the real data analysis, since our methods perform well without this additional criteria in the simulated data.
The detailed network sizes exhibited in Table 2. Note that, no matter which combination of journals is considered, the corresponding pairs of networks are partially overlapping. In fact, the sizes of overlapped nodes are much smaller than that of networks.
In Fig. 7, we depict the recovery rates over five different metrics. DP(all) is the recovery rate of Algorithm 2 over all nodes, and it is smaller than DP(mat), which is the recovery rate of Algorithm 2 over all matched nodes. Apparently, DP(mat) is alway larger than DP(all), so in Fig. 7, we stack the differences between these two on top of DP(all). The larger the differences are, the smaller the matched nodes ratios are. As for Algorithm 5, we also consider two metrics, EE+(all) – the recovery rate in terms of all nodes, and EE+(conv) – the recovery rate in terms of converged nodes. In Fig. 7, we also stack the difference between EE+(conv) and EE+(all) on top of EE+(all).
Results in Sect. 4.1. Each panel corresponds a different Journal A, as indicated at the top-left corner of the panel. Every three consecutive bars in a panel correspond to a different choice of Journals B and C, as indicated at the top of the bars. The metrics are: DP(mat), the recovery rate of Algorithm 2 over all matched pairs; DP(all), the recovery rate of Algorithm 2 over all nodes; EE, the recovery rate of Algorithm 3 in terms of all nodes; EE+(all), the recovery rate of Algorithm 5 over all nodes; EE+(conv), the recovery rate of Algorithm 5 over all converged pairs
A fair comparison is to compare EE+(conv) with DP(mat), and to compare EE+(all) with DP(all). As we can see, EE-post consistently and substantially outperform DP in all aspects. In particular, EE+(conv) shows an even more prominent improvement, which suggests that, for real data where the underlying truth is unknown and the matching accuracy is of concern, we can use the converged matchings of EE-post as a reliable matching.
To provide more insights of EE-post methods, we examine three specific authors in the coauthor dataset. We use the dataset AoS \(\cup \) Biometrika and AoS \(\cup \) JASA for illustration.
-
Converged and correctly matched. An example of this category is Author 60. It has in total three coauthors in the dataset concerned, and all these three coauthors occur in the AoS. This suggests that Author 60 has the same size of neighbourhood in AoS \(\cup \) Biometrika and AoS \(\cup \) JASA. In addition, at least one of these three neighbours is correctly matched. These two facts provide ample information for graph matching, and result in Author 60 being a converged node in EE-post algorithm and is correctly matched.
-
Converged but wrongly matched. An example of this category is Author 222. It has zero coauthor in AoS, four in JASA and four in Biometrika. The intersection of it’s JASA and Biometrika collaborators sets is of size three. In terms of graph matching Author 222, the interference signal comes from Author 655, who share two coauthors with Author 222 and who is wrongly matched to Author 222. A relatively large number of coauthors leads to the convergence, while the interference signal results in a wrong match.
-
Correctly matched but not converged. An example of this category is Author 115. Note that Author 115 has five coauthors in the dataset concerned, but only one of these five neighbours is correctly matched. This causes that in the iterations, the matching of Author 115 is not stable, but one possible matching is correct due to the relatively large number of neighbours. This example also sheds light on the rationale of adopting EE with \(d > 1\), when one can afford a multiple matching storage.
Results in Sect. 4.2, different thresholds scenarios. Each bar indicates the mean and standard error of a certain metric. The size m and the correlation parameter \(\rho \) are indicated in each panel. In each panel, every three consecutive bars represent metric values for a threshold value, indicated at the top. The metrics are: DP(mat), the recovery rate of Algorithm 2 over all matched pairs; DP(all), the recovery rate of Algorithm 2 over all nodes; EE, the recovery rate of Algorithm 3 in terms of all nodes; EE+(all), the recovery rate of Algorithm 5 over all nodes; EE+(conv), the recovery rate of Algorithm 5 over all converged pairs
Results in Sect. 4.2, same thresholds scenarios. Each bar indicates the mean and standard error of a certain metric. The size m and the correlation parameter \(\rho \) are indicated in each panel. In each panel, every three consecutive bars represent metric values for a threshold value, indicated at the top. The metrics are: DP(mat), the recovery rate of Algorithm 2 over all matched pairs; DP(all), the recovery rate of Algorithm 2 over all nodes; EE, the recovery rate of Algorithm 3 in terms of all nodes; EE+(all), the recovery rate of Algorithm 5 over all nodes; EE+(conv), the recovery rate of Algorithm 5 over all converged pairs
4.2 Zebrafish dataset
In this section, we analyse a zebrafish neuronal activity dataset. This dataset is originally acquired and processed in Prevedel et al. (2014) and is a time series of whole-brain zebrafish neuronal activity. We follow the preprocessing routine conducted in Lyzinski et al. (2017) and subtract a slice of neuronal activity network which is in fact the sample correlation matrix in a small window of time. This can be regarded as the adjacency matrix of a weighted undirected network, with 5105 nodes. The further analysis conducted in this section is based on thresholding the entries of this correlation matrix R to provide adjacency matrices in \(\{0, 1\}^{5105\times 5105}\).
We conduct two sets of simulation based on this dataset. One is to match graphs generated from two different thresholds and the other is based on the same thresholds. To be specific, in the different thresholds setting, we first use threshold \(t_1 \in \{0.5, 0.6, 0.7\}\) to produce a matrix \(A_1 \in \{0, 1\}^{5105 \times 5105}\), by letting \((A_1)_{ij} = \mathbb {1}\{R_{ij} \ge t_1\}\), and use \(t_2 = t_1 + 0.1\) to produce \(B_1 \in \{0, 1\}^{5105 \times 5105}\). For each of \(A_1\) and \(B_1\), we then subtract the leading principal sub-matrix \(A_2, B_2 \in \{0, 1\}^{m \times m}\), \(m \in \{100, 300, 1000\}\). Finally, for each node in \(A_2\)(\(B_2\)), we independently keep it with probability \(s \in \{0.95, 0.97\}\) to produce \(A_3\)(\(B_3\)), and output A(B) by deleting isolated nodes. When matching A and B, we also randomly permute the nodes in B to increase difficulty. In the same threshold setting, we let \(A_1 = B_1\) using the same threshold \(t \in \{0.5, 0.6, 0.7\}\), and follow the rest of the procedures as those in the different threshold scenarios. It is worth mentioning that, in the different threshold scenario, the higher threshold graph is a sub-graph of the lower threshold graph; in the same threshold scenario, we have that \(\rho = 1\).
Each combination of the parameters mentioned above is repeated 10 times. In particular, in the same threshold setting, the repetitions are conducted by permuting the nodes 10 times.
The numerical results are depicted in Figures 8 and 9, for the different and same thresholds settings, respectively. As for Algorithm 2, we calculate the recovery rates over all nodes, DP(all) and matched nodes, DP(mat), separately. Since DP(mat) is always larger than DP(all), we stack the difference between these two rates on top of the DP(all) in the figures. As for Algorithm 5, we calculate the recovery rates over all nodes, EE+(all) and converged nodes, EE+(conv), separately. For the same reasons as stated for Algorithm 2, we stack the two bars in one in each panel in the figures.
Generally speaking, as the thresholds increase, all the performances deteriorate, since the networks become sparser and the matching problems become harder. The two scenarios, different and same thresholds, show very similar information, and in most of cases, all methods perform slightly better in the same threshold scenario. It is interesting to see that EE has almost full recovery in most settings, even though this is based on real datasets. Since the convergence rates of EE-post are high across all settings, the recovery rates of EE-post in two different metrics are comparable. Overall, EE and EE-post outperform DP. We would like to point out, as the network size increases, EE and EE-post improve their performances, while DP deteriorates. This further suggests that in reality, EE-type methods are preferable over the original DP algorithm.
5 Discussions
In this paper, we investigated the extensions of the degree profile graph matching in perfectly-overlapping Erdős–Rényi random graphs. The extensions include partially-overlapping graphs matching and stochastic block model graph matching. We proposed the edge exploited graph matching algorithm and its variants, and conducted thorough numerical experiments to evaluate their performances.
It would be interesting to investigate the precision-recall tradeoff phenomenon in graph matching problems. However, in this paper, since we allow for partially-overlapping graphs, i.e. not all nodes have counterparts in the other graph, and since we include methods such as Algorithm 3 allowing for 1-to-d matching, it is rather complicated to define precision and recall reasonably, while showing some interesting precision-recall tradeoff patterns.
In this paper we focused on simple graphs, i.e. there are no multiple edges between any give pair of nodes. The extension to multiple edge networks is straightforward, since all our current methods are based on counting the edges. Other possible extensions include graph matching on directed graphs and the theoretical guarantees associated. We will leave these for future work.
References
Cherkassky, B.V., Goldberg, A.V., Martin, P., Setubal, J.C., Stolfi, J.: Augment or push: a computational study of bipartite matching and unit-capacity flow algorithms. J. Exp. Algo. (JEA) 3, 8–es (1998)
Conte, D., Foggia, P., Sansone, C., Vento, M.: Thirty years of graph matching in pattern recognition. Int. J. Pattern Recogn. Artif. Intell. 18(03), 265–298 (2004)
Csardi, G., Nepusz, T.: The igraph software package for complex network research. Int. J. Compl. Syst. 1695 (2006). http://igraph.org
Czajka, T., Pandurangan, G.: Improved random graph isomorphism. J. Disc. Algo. 6(1), 85–92 (2008)
Ding, J., Ma, Z., Wu, Y., Xu, J.: Efficient random graph matching via degree profiles. arXiv preprint arXiv:1811.07821 (2018)
Eppstein, D.: Subgraph isomorphism in planar graphs and related problems. In: Graph Algorithms and Applications I, pp. 283–309. World Scientific (2002)
Erdös, P., Rényi, A.: On random graphs. Publ. Math. 6(26), 290–297 (1959)
Fishkind, D.E., Adali, S., Patsolic, H.G., Meng, L., Singh, D., Lyzinski, V., Priebe, C.E.: Seeded graph matching. arXiv preprint arXiv:1209.0367 (2012)
Foggia, P., Percannella, G., Vento, M.: Graph matching and learning in pattern recognition in the last 10 years. Int. J. Pattern Recogn. Artif. Intell. 28(01), 1450001 (2014)
Gold, S., Rangarajan, A.: A graduated assignment algorithm for graph matching. IEEE Trans. Pattern Anal. Mach. Intell. 18(4), 377–388 (1996)
Haghighi, A.D., Ng, A.Y., Manning, C.D.: Robust textual inference via graph matching. In: Proceedings of the Conference on Human Language Technology and Empirical Methods in Natural Language Processing, pp. 387–394. Association for Computational Linguistics (2005)
Hu, Y., Wang, W., Yu, Y.: GMPro: Graph Matching with Degree Profiles (2020). https://CRAN.R-project.org/package=GMPro. R package version 0.1.0
Jaggi, M.: Revisiting frank-wolfe: projection-free sparse convex optimization. In: Proceedings of the 30th International Conference on Machine Learning, CONF, pp. 427–435 (2013)
Ji, P., Jin, J.: Coauthorship and citation networks for statisticians. Ann. Appl. Stat. 10(4), 1779–1812 (2016)
Jin, J.: Fast community detection by score. Ann. Stat. 43(1), 57–89 (2015)
Kazemi, E., Hassani, H., Grossglauser, M., Modarres, H.P.: Proper: global protein interaction network alignment through percolation matching. BMC Bioinform. 17(1), 527 (2016)
Kazemi, E., Yartseva, L., Grossglauser, M.: When can two unlabeled networks be aligned under partial overlap? In: 2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Allerton), pp. 33–42. IEEE (2015)
Leordeanu, M., Hebert, M.: A spectral technique for correspondence problems using pairwise constraints. In: Tenth IEEE International Conference on Computer Vision (ICCV’05), vols. 1, 2, pp. 1482–1489. IEEE (2005)
Li, L., Campbell, W.M.: Matching community structure across online social networks. arXiv preprint arXiv:1608.01373 (2016)
Liu, Z.Y., Qiao, H., Xu, L.: An extended path following algorithm for graph-matching problem. IEEE Trans. Pattern Anal. Mach. Intell. 34(7), 1451–1456 (2012)
Lyzinski, V., Fishkind, D.E., Fiori, M., Vogelstein, J.T., Priebe, C.E., Sapiro, G.: Graph matching: relax at your own risk. IEEE Trans. Pattern Anal. Mach. Intell. 38(1), 60–73 (2015)
Lyzinski, V., Fishkind, D.E., Priebe, C.E.: Seeded graph matching for correlated erdös-rényi graphs. J. Mach. Learn. Res. 15(1), 3513–3540 (2014)
Lyzinski, V., Park, Y., Priebe, C.E., Trosset, M.: Fast embedding for jofc using the raw stress criterion. J. Comput. Graph. Stat. 26(4), 786–802 (2017)
Mossel, E., Ross, N.: Shotgun assembly of labeled graphs. IEEE Trans. Netw. Sci. Eng. (2017)
Narayanan, A., Shmatikov, V.: De-anonymizing social networks. In: 2009 30th IEEE Symposium on Security and Privacy, pp. 173–187. IEEE (2009)
Patsolic, H.G., Park, Y., Lyzinski, V., Priebe, C.E.: Vertex nomination via seeded graph matching. arXiv preprint arXiv:1705.00674 (2017)
Pedarsani, P., Grossglauser, M.: On the privacy of anonymized networks. In: Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1235–1243 (2011)
Prevedel, R., Yoon, Y.G., Hoffmann, M., Pak, N., Wetzstein, G., Kato, S., Schrödel, T., Raskar, R., Zimmer, M., Boyden, E.S.: Simultaneous whole-animal 3d imaging of neuronal activity using light-field microscopy. Nat. Methods 11(7), 727–730 (2014)
R Core Team: R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria (2020). https://www.R-project.org/
Sanfeliu, A., Fu, K.S.: A distance measure between attributed relational graphs for pattern recognition. IEEE Trans. Syst. Man Cybern. 3, 353–362 (1983)
Scheinerman, E.R., Ullman, D.H.: Fractional Graph Theory: A Rational Approach to the Theory of Graphs. Courier Corp. (2011)
Schellewald, C., Schnörr, C.: Probabilistic subgraph matching based on convex relaxation. In: International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition, pp. 171–186. Springer (2005)
Ullmann, J.R.: An algorithm for subgraph isomorphism. J. ACM (JACM) 23(1), 31–42 (1976)
Villani, C.: The wasserstein distances. In: Optimal Transport, pp. 93–111. Springer (2009)
Yan, J., Yin, X.C., Lin, W., Deng, C., Zha, H., Yang, X.: A short survey of recent advances in graph matching. In: Proceedings of the 2016 ACM on International Conference on Multimedia Retrieval, pp. 167–174 (2016)
Young, S.J., Scheinerman, E.R.: Random dot product graph models for social networks. In: International Workshop on Algorithms and Models for the Web-Graph, pp. 138–149. Springer (2007)
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Wanjie Wang and Yaofang Hu are supported by Singapore Ministry of Education Academic Research Fund Tier 1 R-155-000-214-114.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, Y., Wang, W. & Yu, Y. Graph matching beyond perfectly-overlapping Erdős–Rényi random graphs. Stat Comput 32, 19 (2022). https://doi.org/10.1007/s11222-022-10079-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11222-022-10079-1