Abstract
The recent papers Gajek and Kucinsky (Insur Math Econ 73:1–19, 2017) and Avram et al. (Mathematics 9(9):931, 2021) cost induced dichotomy for optimal dividends in the cramr-lundberg model. Avram et al. (Mathematics 9(9):931, 2021) investigated the control problem of optimizing dividends when limiting capital injections stopped upon bankruptcy. The first paper works under the spectrally negative Lévy model; the second works under the Cramér-Lundberg model with exponential jumps, where the results are considerably more explicit. The current paper has three purposes. First, it illustrates the fact that quite reasonable approximations of the general problem may be obtained using the particular exponential case studied in Avram et al. cost induced dichotomy for optimal dividends in the Cramér-Lundberg model (Avram et al. in Mathematics 9(9):931, 2021). Secondly, it extends the results to the case when a final penalty P is taken into consideration as well besides a proportional cost \(k>1\) for capital injections. This requires amending the “scale and Gerber-Shiu functions” already introduced in Gajek and Kucinsky (Insur Math Econ 73:1–19, 2017). Thirdly, in the exponential case, the results will be made even more explicit by employing the Lambert-W function. This tool has particular importance in computational aspects and can be employed in theoretical aspects such as asymptotics.











Similar content being viewed by others
Data Availability
The datasets generated during the current study are available from the corresponding author upon request.
Notes
In Gajek and Kuciński (2017), these proceses are left-continuous. We have proceeded differently, since from an intuitive point of view, it all comes down to what happens at 0: left-continuous implies that no matter what the reserve, no dividends are to be paid (\(D_{0-}=0\), in principle). We argue differently, especially since these barrier policies say “pay the exceeding” as a lump sum... This is also valid for injections: bankruptcy is not declared when an important claim comes. Instead, injection may save the company. Finally, from a technical point of view, it all comes down to what precise Itô formula one employs when writing down the dynamic programming principle and how one constructs the admissible policies. The choice is rather important for the verification results, and we note that cg is also the standardized form in the Azcue-Muller papers.
essentially, this is the “dividend function with fixed barrier”, which had been also extensively studied in previous literature before the introduction of \(W_q(x)\)
This is called DeVylder B) method in Gerber et al. (2008) [(5.6-5.7)], since it is the result of fitting the first two cumulants of the risk process.
This equation is important in establishing the nonnegativity of the optimal dividends barrier.
This is called DeVylder B) method in Gerber et al. (2008) [(5.6-5.7)], since it is the result of fitting the first two cumulants of the risk process.
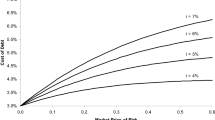
Laplace inversion done via Mathematica; coefficients and exponents are decimal approximations of the real values.
References
Albrecher H, Asmussen S (2010) Ruin probabilities, vol 14. World Scientific
Albrecher H, Azcue P, Muler N (2020) Optimal ratcheting of dividends in insurance. SIAM J Control Optim 58(4):1822–1845
Avram F, Pistorius M (2014) On matrix exponential approximations of ruin probabilities for the classic and brownian perturbed cramér-lundberg processes. Insurance: Mathematics and Economics 59:57–64
Avram F, Kyprianou A, Pistorius M (2004) Exit problems for spectrally negative Lévy processes and applications to (Canadized) Russian options. Ann Appl Probab 14(1):215–238
Avram F, Palmowski Z, Pistorius MR (2007) On the optimal dividend problem for a spectrally negative Lévy process. The Annals of Applied Probability pp. 156–180
Avram F, Chedom-Fotso D, Horváth A (2011) On moments based Padé approximations of ruin probabilities. J Comput Appl Math 235(10):3215–3228
Avram F, Banik AD, Horváth A (2018a) Ruin probabilities by Pad’s method: simple moments based mixed exponential approximations (Renyi, De Vylder, Cramér–Lundberg), and high precision approximations with both light and heavy tails. European Actuarial Journal pp. 1–27
Avram F, Pérez JL, Yamazaki K (2018b) Spectrally negative Lévy processes with Parisian reflection below and classical reflection above. Stochastic processes and Applications 128:255–290
Avram F, Grahovac D, Vardar-Acar C (2019a) The \(W,Z\) scale functions kit for first passage problems of spectrally negative Lévy processes, and applications to the optimization of dividends. arXiv preprint
Avram F, Horváth A, Provost S, Solon U (2019b) On the padé and laguerre–tricomi–weeks moments based approximations of the scale function w and of the optimal dividends barrier for spectrally negative lévy risk processes. Risks 7(4):121
Avram F, Goreac D, Li J, Wu X (2021) Equity cost induced dichotomy for optimal dividends with capital injections in the Cramér-Lundberg model. Mathematics 9(9):931. https://doi.org/10.3390/math9090931
Bertoin J (1998) Lévy processes, vol 121. Cambridge University Press
Beveridge CJ, Dickson DC, Wu X (2007) Optimal dividends under reinsurance. Centre for Actuarial Studies, Department of Economics, University of Melbourne
Bobbio A, Horváth A, Telek M (2005) Matching three moments with minimal acyclic phase type distributions. Stoch Model 21(2–3):303–326
Boyd J (1998) Global approximations to the principal real-valued branch of the lambert w-function. Appl Math Lett 11(6):27–31
Brito P, Fabiao F, Staubyn A (2008) Euler, lambert, and the lambert w-function today. Mathematical Scientist 33(2)
Corless RM, Gonnet GH, Hare DE, Jeffrey DJ, Knuth DE (1996) On the lambertw function. Adv Comput Math 5(1):329–359
De Finetti B (1957) Su un’impostazione alternativa della teoria collettiva del rischio. Transactions of the XVth international congress of Actuaries 2:433–443
De Vylder F (1978) A practical solution to the problem of ultimate ruin probability. Scand Actuar J 1978(2):114–119
Dickson D, Drekic S (2005) Optimal Dividends under a Ruin ProbabilityConstraint
Dumitrescu B, Şicleru BC, Avram F (2016) Modeling probability densities with sums of exponentials via polynomial approximation. J Comput Appl Math 292:513–525
Eisenberg J (2011) Schmidli H (2011) Minimising expected discounted capital injections by reinsurance in a classical risk model. Scand Actuar J 3:155–176
Gajek L, Kuciński L (2017) Complete discounted cash flow valuation. Insur Math Econ 73:1–19
Gerber HU (1969) Entscheidungskriterien für den zusammengesetzten poisson-prozess. PhD thesis, ETH Zurich
Gerber HU, Shiu ES, Smith N (2008) Methods for estimating the optimal dividend barrier and the probability of ruin. Insurance: Mathematics and Economics 42(1):243–254
Højgaard B (2002) Optimal dynamic premium control in non-life insurance. maximizing dividend pay-outs. Scandinavian Actuarial Journal 2002(4):225–245
Kulenko N, Schmidli H (2008) Optimal dividend strategies in a cramér–lundberg model with capital injections. Insurance: Mathematics and Economics 43(2):270–278
Kyprianou A (2014) Fluctuations of Lévy Processes with Applications: Introductory Lectures. Springer Science & Business Media
Lindensjö K, Lindskog F (2019) Optimal dividends and capital injection under dividend restrictions. arXiv preprint arXiv:190206294
Løkka A, Zervos M (2008) Optimal dividend and issuance of equity policies in the presence of proportional costs. Insurance: Mathematics and Economics 42(3):954–961
Noba K, Pérez JL, Yu X (2020) On the bailout dividend problem for spectrally negative markov additive models. SIAM J Control Optim 58(2):1049–1076
Pakes AG (2015) Lambert’s w meets kermack-mckendrick epidemics. IMA J Appl Math 80(5):1368–1386
Pérez JL, Yamazaki K, Bensoussan A (2018) Optimal periodic replenishment policies for spectrally positive Lévy demand processes. arXiv preprint arXiv:180609216
Ramsay CM (1992) A practical algorithm for approximating the probability of ruin. Transactions of the Society of Actuaries 44:443–461
Shreve SE, Lehoczky JP, Gaver DP (1984) Optimal consumption for general diffusions with absorbing and reflecting barriers. SIAM J Control Optim 22(1):55–75
Vatamidou E, Adan IJBF, Vlasiou M (2014) Zwart B (2014) On the accuracy of phase-type approximations of heavy-tailed risk models. Scand Actuar J 6:510–534
Vazquez-Leal H, Sandoval-Hernandez M, Garcia-Gervacio J, Herrera-May A, Filobello-Nino U (2019) Psem approximations for both branches of lambert function with applications. Discrete Dynamics in Nature and Society
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Apendix: The Proof of Theorem 1 when \(\sigma \equiv 0\)
Apendix: The Proof of Theorem 1 when \(\sigma \equiv 0\)
To simplify our readers’ journey, we sketch here the main elements of proof, in the case \(\sigma \equiv 0\), generalizing Avram et al. (2021). Please note that the main modification when diffusion is present applies to the computation of the term \(I_y\) below, in which \(\sigma ^2\) will appear accompanying a Dirac mass in the Gerber-Shiu measure.
We begin by applying the strong Markov property at the stopping time \(\tau ^x:=\tau _{0-}^x\wedge \tau _{b+}^x=\inf \left\{ t\ge 0: \ X_t^\pi <0\right\} \wedge \inf \left\{ t\ge 0:\ X_t^\pi >b\right\}\). It follows that, for \(0\le x\le b\),
where
The term \(I_y\) can be explicitly computed (using the Gerber-Shiu measure).
Since the term accompanying \(W_q(y)\) is a constant, by replacing this in Eq. (53), it follows that
With the particular choice of \(x=0\), by recalling that \(C_a(0)=G_a(0)=C(0)=0\), the last equation yields
which, combined with \(W_q(0)=\frac{1}{c}\) and \(C(x)=cW_q(x)-Z_q(x)\), leads to
Theorem 1 is now proven, in the case \(\sigma \equiv 0\).
Rights and permissions
About this article
Cite this article
Avram, F., Goreac, D., Adenane, R. et al. Optimizing Dividends and Capital Injections Limited by Bankruptcy, and Practical Approximations for the Cramér-Lundberg Process. Methodol Comput Appl Probab 24, 2339–2371 (2022). https://doi.org/10.1007/s11009-021-09916-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11009-021-09916-z