An efficient numerical method to solve the problems of 2D incompressible nonlinear elasticity

Abstract

Presented herein is a numerical variational approach to the two-dimensional (2D) incompressible nonlinear elasticity. The governing equations are derived based upon the minimum total energy principle by considering the displacement and a pressure-like field as the two independent unknowns. The tensor equations are replaced by equations in a novel matrix-vector form. The proposed solution method is based upon the variational differential quadrature (VDQ) method and a transformation procedure. Using the introduced VDQ-based approach, the energy functional is precisely discretized in a direct way. Being locking-free, simple implementation and computational efficiency are the main features of this method. Also, it is free from numerical artifacts and instabilities. Some important problems of 2D incompressible elasticity are addressed to test the method. It is revealed that it can be efficiently utilized to capture the large strains of incompressible solids.

Appendix: Details of the VDQ-based approach

1.1 Discretization operator

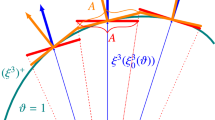
$\llbracket \blacksquare _{1} \rrbracket _{\blacksquare _{2}}$ is applied for indicating the discretized form of $\blacksquare _{1}$ on the domain $\blacksquare _{2}$. According to Fig. 15, 2D discretization of arbitrary scalar f on the area A in $s_{1}-s_{2}$ direction can be written as

$$\begin{aligned} \mathbbm {f}= & {} {\mathbf{f }} = \llbracket f \rrbracket _{A} \nonumber \\&\quad = \left[ {\mathfrak {f}}_{1}\, {\mathfrak {f}}_{2}\, \cdots \, {\mathfrak {f}}_{n_{1}}\, {\mathfrak {f}}_{n_{1}+1}\, {\mathfrak {f}}_{n_{1}+2}\, \cdots \, {\mathfrak {f}}_{2n_{1}}\, \cdots \, {\mathfrak {f}}_{\left( n_{2}-1 \right) n_{1}+1}\, {\mathfrak {f}}_{\left( n_{2}-1 \right) n_{1}+2}\, \cdots \, {\mathfrak {f}}_{n_{1}n_{2}} \right] ^{\mathrm {T}} \end{aligned}$$

(A.1a)

As well, the 2D discretization of matrix ${\mathbf{f }}$ on the area A in $s_{1}-s_{2}$ direction is expressed as follows

(A.1b)

where ${\mathbf{f }}_{{\varvec{IJ}}}$ denotes the discretized form of element $f_{ij}$ which is discretized according to Eq. (A.1a).

Fig. 15

Schematic of discretization process of $\mathrm {f}$ on a specified domain

1.2 Derivative and integral operators

The derivative operator is defined as

$$\begin{aligned} \llbracket f_{,\blacksquare _{1}} \rrbracket _{\blacksquare _{2}} = {\mathop {{\mathcal {D}}}\limits ^{\blacksquare _{3}}}_{\blacksquare _{1};\blacksquare _{2}}\llbracket f \rrbracket _{\blacksquare _{2}}= {\mathop {{\mathcal {D}}}\limits ^{\blacksquare _{3}}}_{\blacksquare _{1};\blacksquare _{2}}\mathbbm {f}, \end{aligned}$$

(A.2)

where

$\blacksquare _{1}:$ Variable with respect to which derivative is taken

$\blacksquare _{2}:$ Domain on which differentiation is performed

$\blacksquare _{3}:$ Dimension of problem (1d, 2d, 3d).

The integral operator is also introduced as

$$\begin{aligned} \int _{\blacksquare _{2}} {fd\blacksquare _{1}} = {\mathop {{\mathcal {S}}}\limits ^{\blacksquare _{3}}}_{\blacksquare _{1};\blacksquare _{2}}\llbracket f \rrbracket _{\blacksquare _{2}} = {\mathop {{\mathcal {S}}}\limits ^{\blacksquare _{3}}}_{\blacksquare _{1};\blacksquare _{2}}\mathbbm {f}, \end{aligned}$$

(A.3)

where

$\blacksquare _{1}:$ Variable with respect to which integral is taken

$\blacksquare _{2}:$ Domain on which integration is performed

$\blacksquare _{3}:$ Dimension of problem (1d, 2d, 3d).

The discretization is done using computational points (Chebyshev distribution) in the natural space:

$$\begin{aligned} {\varvec{\upzeta }}^{cheb} = \text {Chebyshev-distribution\,(domain, node number)} \end{aligned}$$

(A.4)

For the 1D case, one can write

$$\begin{aligned} \overline{{{\overline{\xi }}} } = \left[ {\begin{array}{cccc} {\varvec{\upxi }}_{;1} &{} {\varvec{\upxi }}_{;2} &{} \cdots &{} {\varvec{\upxi }}_{;n}\\ \end{array} } \right] = \llbracket \xi \rrbracket _{A} = {\varvec{\upzeta }}^{cheb} = \text { Chebyshev-distribution }(\left[ -1,1 \right] n) \end{aligned}$$

(A.5)

Also, in the 2D case one has

$$\begin{aligned} {\varvec{\upxi }}_{{\mathbf{1 }}}= & {} \left[ {\begin{array}{cccc} {\varvec{\upxi }}_\mathbf{1 ;1} &{} {\varvec{\upxi }}_\mathbf{1 ;2} &{} \cdots &{} {\varvec{\upxi }}_\mathbf{1 ;n}\\ \end{array} } \right] = \llbracket \xi _{1} \rrbracket _{A} = \left( {\mathbf{1 }}_{n_{2}*1} \circledast {\varvec{\upzeta }}_{1}^{cheb} \right) , \end{aligned}$$

(A.6a)

(A.6b)

where

$$\begin{aligned} {\varvec{\upzeta }}_{1}^{\mathrm{cheb}}= & {} \text { Chebyshev-distribution }(\left[ -1,1 \right] , n_{1})\\ {\varvec{\upzeta }}_{2}^{\mathrm{cheb}}= & {} \text { Chebyshev-distribution }(\left[ -1,1 \right] , n_{2}). \end{aligned}$$

Consequently, the 1D derivative operator in the natural space is defined as

$$\begin{aligned} \mathbbm {f}_{,\overline{{{\overline{\xi }}} }}^{(r)}= & {} \llbracket f_{,\xi }^{(r)} \rrbracket _{{\check{\varGamma }}}= {\mathop {\mathcal {D}}\limits ^{1d}}_{\xi }^{(r)}\llbracket f \rrbracket _{{\check{\varGamma }}}= {\mathop {{\mathcal {D}}}\limits ^{1d}}_{{\xi }}^{(r)}\mathbbm {f}, \end{aligned}$$

(A.7a)

$$\begin{aligned} D_{\xi \, ij}^{\left( r \right) }= & {} \left\{ {\begin{array}{ll} \delta _{ij} &{} r=0\\ \frac{P_{i}}{\left( {\varvec{\upxi }}_{;i}-{\varvec{\upxi }}_{;j} \right) P_{j}}&{} i\ne j,r=1\\ r\left( D_{\xi ij}^{\left( 1 \right) }D_{\xi ii}^{\left( r-1 \right) }-\frac{D_{\xi ij}^{\left( r-1 \right) }}{\left( {\varvec{\upxi }}_{;i}-{\varvec{\upxi }}_{;j} \right) } \right) &{} i\ne j,r=2,3,\ldots ,n-1\\ -{\mathop {\mathop {\sum }\limits _{j=1}}\limits _{j\ne 1}^n} D_{\xi ij}^{\left( r \right) }&{} i=j,r=1,2,3,\ldots ,n-1\\ \end{array}} \right. \end{aligned}$$

(A.7b)

in which

$$\begin{aligned} P_{j}= {\mathop {\mathop {\prod }\limits _{i=1}}\limits _{i\ne j}^n}\left( {\varvec{\upxi }}_{;j}-{\varvec{\upxi }}_{;i} \right) , \end{aligned}$$

(A.7c)

Furthermore, ${\varvec{\upxi }}_{;i}$ is $i-$th element of $\overline{{{\overline{\xi }}} }$ from Eq. (A.5). Finally,

$$\begin{aligned} {\mathop {{\mathcal {D}}}\limits ^{1d}}_{\xi }^{(r)}={\mathop {{\mathcal {D}}}\limits ^{1d}}_{,{\mathop {\underbrace{\xi \ldots \xi }}\limits _{r}}}=\left[ D_{\xi \, ij}^{\left( r \right) } \right] \end{aligned}$$

(A.8)

Accordingly, the 2D derivative operator is constructed as

$$\begin{aligned} \mathbbm {f}_{,{\varvec{\upxi }}_{{\mathbf {1}}}}^{(r)}= & {} \llbracket \mathbbm {f}_{,\xi _{1}}^{(r)} \rrbracket _{{\check{A}}} = {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{1}}^{(r)}\llbracket f \rrbracket _{{\check{A}}} = {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{1}}^{(r)}\mathbbm {f}, \quad \quad {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{1}}^{(r)} = \left( {\mathbf{I }}_{n_{2}} \circledast {\mathop {{\mathcal {D}}}\limits ^{1d}}_{\xi _{1}}^{\left( r \right) } \right) , \end{aligned}$$

(A.9a)

$$\begin{aligned} \mathbbm {f}_{,{\varvec{\upxi }}_{{\mathbf {2}}}}^{(r)}= & {} \llbracket f_{,\xi _{2}}^{(r)} \rrbracket _{{\check{A}}} = {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{2}}^{(r)}\llbracket f \rrbracket _{{\check{A}}} = {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{2}}^{\left( r \right) }\mathbbm {f} \quad \quad {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{2}}^{\left( r \right) } = \left( {\mathop {{\mathcal {D}}}\limits ^{1d}}_{\xi _{2}}^{\left( r \right) } \circledast {\mathbf{I }}_{n_{1}} \right) ,\nonumber \\ \mathbbm {f}_{,\overline{{{\overline{\xi }}} }}^{(r)}= & {} \llbracket f_{,{\varvec{\upxi }}}^{(r)} \rrbracket _{{\check{A}}}= {\mathop {{\mathcal {D}}}\limits ^{2d}}_{{\varvec{\upxi }}}^{(r)}\llbracket f \rrbracket _{{\check{A}}}= {\mathop {{\mathcal {D}}}\limits ^{2d}}_{{\varvec{\upxi }}}^{(r)}\mathbbm {f} \quad \quad {\mathop {{\mathcal {D}}}\limits ^{2d}}_{{\varvec{\upxi }}}^{(r)}=\left[ {\begin{array}{l} {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{1}}^{(r)} \\ {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{2}}^{\left( r \right) } \\ \end{array}} \right] . \end{aligned}$$

(A.9b)

The 1D integral operator in natural space is introduced as

$$\begin{aligned} I= & {} \int _{{\check{\varGamma }}} {f\left( \xi \right) \mathrm{d}\xi } = {\mathop {{\mathcal {S}}}\limits ^{1d}}_{\xi }\llbracket f \rrbracket _{{\check{\varGamma }}} = {\mathop {{\mathcal {S}}}\limits ^{1d}}_{\xi }\mathbbm {f}, \end{aligned}$$

(A.10a)

$$\begin{aligned} {\mathop {{\mathcal {S}}}\limits ^{1d}}_{\xi }= & {} \sum \limits _{r=0}^\infty {\mathbf{K }}_\mathrm{tay}^{\left( r \right) }{\mathop {{\mathcal {D}}}\limits ^{1d}}_{\xi }^{\left( r \right) }, \end{aligned}$$

(A.10b)

$$\begin{aligned} {\mathbf{K }}_\mathrm{tay}^{\left( r \right) }= & {} \left[ \frac{\left( {\varvec{\upxi }}_{;2}-{\varvec{\upxi }}_{;1} \right) ^{r+1}}{2^{r+1}\left( r+1 \right) !}\, \, \cdots \, \, \, \frac{\left( {\varvec{\upxi }}_{;i+1}-{\varvec{\upxi }}_{;i} \right) ^{r+1}-\left( {\varvec{\upxi }}_{;i-1}-{\varvec{\upxi }}_{;i} \right) ^{r+1}}{2^{r+1}\left( r+1 \right) !}\, \, \cdots \, \, \, \frac{\left( {\varvec{\upxi }}_{;n-1}-{\varvec{\upxi }}_{;n} \right) ^{r+1}}{2^{r+1}\left( r+1 \right) !} \right] .\qquad \quad \end{aligned}$$

(A.10c)

where ${\varvec{\upxi }}_{;i}$ denotes i-th element of $\overline{{{\overline{\xi }}} }$ from Eq. (A.5).

For the 2D operator, one has

$$\begin{aligned} \mathrm {I}= & {} \int _{{\check{A}}} {f\left( \xi _{1},\xi _{2} \right) \mathrm{d}\xi _{1}\mathrm{d}\xi _{2}} = {\mathop {{\mathcal {S}}}\limits ^{2d}}_{\xi _{1}\xi _{2}}\llbracket f \rrbracket _{{\check{A}}} = {\mathop {{\mathcal {S}}}\limits ^{2d}}_{\xi _{1}\xi _{2}}\mathbbm {f}, \end{aligned}$$

(A.11a)

$$\begin{aligned} {\mathop {{\mathcal {S}}}\limits ^{2d}}_{\xi _{1}\xi _{2}}= & {} \left( {\mathop {{\mathcal {S}}}\limits ^{1d}}_{\xi _{2}} \circledast {\mathop {{\mathcal {S}}}\limits ^{1d}}_{\xi _{1}} \right) , \end{aligned}$$

(A.11b)

in which ${\mathop {{\mathcal {S}}}\limits ^{1d}}_{\xi _{1}}$ and ${\mathop {{\mathcal {S}}}\limits ^{1d}}_{\xi _{2}}$ are evaluated based on Eq. (A.10b).

1.3 Transformation

The following figure can be used to indicate the mapping procedure of physical arbitrary shape domain into regular computational one:

Fig. 16

Mapping procedure of physical arbitrary shape domain into regular computational one

The shape functions are introduced as:

• 1D (3-node element):

  $$\begin{aligned} \overline{{{\overline{\xi }}} }^{tp}= & {} \left[ {\begin{array}{ccc} -1 &{} 1 &{} 0\\ \end{array} } \right] ^{\mathrm {T}}, \end{aligned}$$

  (A.12a)
  $$\begin{aligned} L_{1}\left( \xi \right)= & {} 1 / 2\xi \left( \xi -1 \right) ,\, \, \, \, \, \, \, L_{2}\left( \xi \right) = 1 / 2\xi \left( \xi +1 \right) ,\, \, L_{3}\left( \xi \right) =\left( 1-\xi \right) \left( 1+\xi \right) , \end{aligned}$$

  (A.12b)
  $$\begin{aligned} {\mathbf{L }}= & {} \left[ {\begin{array}{ccc} L_{1} &{} L_{2} &{} L_{3}\\ \end{array} } \right] ^{\mathrm {T}}. \end{aligned}$$

  (A.12c)

• 2D (8-node element):

  $$\begin{aligned}&{\varvec{\upxi }}_{{\mathbf {1}}}^{tp} = \left[ {\begin{array}{llllllll} -1 &{} 1 &{} 1 &{} -1 &{} 0 &{} 1 &{} 0 &{} -1\\ \end{array} } \right] ^{\mathrm {T}},\nonumber \\&{\varvec{\upxi }}_{{\mathbf {2}}}^{tp} = \left[ {\begin{array}{llllllll} -1 &{} -1 &{} 1 &{} 1 &{} -1 &{} 0 &{} 1 &{} 0\\ \end{array} } \right] ^{\mathrm {T}},\nonumber \\&\overline{{{\overline{\xi }}} }^{tp} = \left[ {\begin{array}{l} {\varvec{\upxi }}_{{\mathbf {1}}}^{tp} \\ {\varvec{\upxi }}_{{\mathbf {2}}}^{tp} \\ \end{array}} \right] , \end{aligned}$$

  (A.13a)
  $$\begin{aligned}&N_{m}\left( \xi _{1},\xi _{2} \right) = \frac{1}{4}\left( 1+\xi _{1}{\varvec{\upxi }}_{{\mathbf {1}};m}^{tp} \right) \left( 1+\xi _{2}{\varvec{\upxi }}_{{\mathbf {2}};m}^{tp} \right) \left( \xi _{1}{\varvec{\upxi }}_{{\mathbf {1}};m}^{tp}+\xi _{2}{\varvec{\upxi }}_{{\mathbf {2}};m}^{tp}-1 \right) ,\, \, \, \, \, \, \, \, m=1,2,3,4, \qquad \quad \end{aligned}$$

  (A.13b)
  $$\begin{aligned}&N_{m}\left( \xi _{1},\xi _{2} \right) = \frac{1}{2}\left( 1-\xi _{1}^{2} \right) \left( 1+\xi _{2}{\varvec{\upxi }}_{{\mathbf {2}};m}^{tp} \right) ,\, \, \, \, \, \, \, \, m=5,7 \end{aligned}$$

  (A.13c)
  $$\begin{aligned}&N_{m}\left( \xi _{1},\xi _{2} \right) = \frac{1}{2}\left( 1-\xi _{2}^{2} \right) \left( 1+\xi _{1}{\varvec{\upxi }}_{{\mathbf {1}};m}^{tp} \right) ,\, \, \, \, \, \, \, \, m=6,8 \end{aligned}$$

  (A.13d)
  $$\begin{aligned}&\hbox {where} \,{\varvec{\upxi }}_{{\mathbf {I}};j}^{tp}\text { is the }j\text {-th element of }{\varvec{\upxi }}_{{\mathbf {I}}}^{tp}\text { from Eq. (A.13a)}. \end{aligned}$$

  (A.13e)
  $$\begin{aligned}&{\mathbf{N }} = \left[ {\begin{array}{*{20}c} N_{1} &{} N_{2} &{} {\cdots } &{} N_{8}\\ \end{array} } \right] ^{\mathrm {T}}, \end{aligned}$$

  (A.13f)

The discretized forms are given as follows:

• 1D:

  $$\begin{aligned} {\mathbf{L }}_{{\mathbf {1}}}= & {} \llbracket L_{1} \rrbracket _{A}=1 / 2\overline{{{\overline{\xi }}} }\circ \left( \overline{{{\overline{\xi }}} }-1 \right) ,\, \, \end{aligned}$$

  (A.14a)
  $$\begin{aligned} {\mathbf{L }}_{{\mathbf {2}}}= & {} \llbracket L_{2} \rrbracket _{A}=1 / 2\overline{{{\overline{\xi }}} }\circ \left( \overline{{{\overline{\xi }}} }+1 \right) , \end{aligned}$$

  (A.14b)
  $$\begin{aligned} {\mathbf{L }}_{{\mathbf {3}}}= & {} \llbracket L_{3} \rrbracket _{A}=\left( 1-\overline{{{\overline{\xi }}} } \right) \circ \left( 1+\overline{{{\overline{\xi }}} } \right) ,\, \, \end{aligned}$$

  (A.14c)
  $$\begin{aligned} {{\mathbb {L}}}= & {} \llbracket L \rrbracket _{A}=\left[ {\begin{array}{ccc} {\mathbf{L }}_{{\mathbf{1 }}}^{\mathrm {T}} &{} {\mathbf{L }}_{{\mathbf{2 }}}^{\mathrm {T}} &{} {\mathbf{L }}_{{\mathbf {3}}}^{\mathrm {T}}\\ \end{array} } \right] ^{\mathrm {T}}, \end{aligned}$$

  (A.14d)

  where $\overline{{{\overline{\xi }}} }$ is evaluated using Eq. (A.5).

• 2D:

  $$\begin{aligned} {\mathbb {N}}_{{{\varvec{M}}}}= & {} \llbracket N_{m} \rrbracket _{A}=\frac{1}{4}\left( 1+{\varvec{\upxi }}_{{\mathbf{1 }}}{\varvec{\upxi }}_{{\mathbf {1}};m}^{tp} \right) \circ \left( 1+{\varvec{\upxi }}_{{\mathbf{2 }}}{\varvec{\upxi }}_{{\mathbf {2}};m}^{tp} \right) \circ \left( {\varvec{\upxi }}_{{\mathbf{1 }}}{\varvec{\upxi }}_{{\mathbf {1}};m}^{tp}+{\varvec{\upxi }}_{{\mathbf{2 }}}{\varvec{\upxi }}_{{\mathbf {2}};m}^{tp}-1 \right) , \quad m=1,2,3,4 \qquad \quad \nonumber \\\end{aligned}$$

  (A.15a)
  $$\begin{aligned} {\mathbb {N}}_{{{\varvec{M}}}}= & {} \llbracket N_{m} \rrbracket _{A}=\frac{1}{2}\left( 1-{\varvec{\upxi }}_{{\mathbf {1}}}^{\circ 2} \right) \circ \left( 1+{\varvec{\upxi }}_{{\mathbf{2 }}}{\varvec{\upxi }}_{{\mathbf {2}};m}^{tp} \right) , \quad m=5,7 \end{aligned}$$

  (A.15b)
  $$\begin{aligned} {\mathbb {N}}_{{{\varvec{M}}}}= & {} \llbracket N_{m} \rrbracket _{A}=\frac{1}{2}\left( 1-{\varvec{\upxi }}_{{\mathbf {2}}}^{\circ 2} \right) \left( 1+{\varvec{\upxi }}_{{\mathbf{1 }}}{\varvec{\upxi }}_{{\mathbf {1}};m}^{tp} \right) , \quad m=6,8 \end{aligned}$$

  (A.15c)
  $$\begin{aligned} {{\mathbb {N}}}= & {} \left[ {\begin{array}{cccc} {\mathbf{N }}_{{\mathbf{1 }}}^{\mathrm {T}} &{} {\mathbf{N }}_{{\mathbf{2 }}}^{\mathrm {T}} &{} {{\cdots }} &{} {\mathbf{N }}_{{\mathbf {8}}}^{\mathrm {T}}\\ \end{array} } \right] ^{\mathrm {T}}, \end{aligned}$$

  (A.15d)

where ${\varvec{\upxi }}_{{\mathbf{1 }}}$ and ${\varvec{\upxi }}_{{\mathbf{2 }}}$ evaluated from Eq. (A.6a).

1.3.1 Position field

The vector-matrix forms are given as follows:

• 1D:

  $$\begin{aligned} \mathrm {X}\left( \xi \right)= & {} \sum \limits _{m=1}^3 {L_{m}{\mathbf{X }}_{:;m}^{tp}} =\left[ {\begin{array}{ccc} L_{1} &{} L_{2} &{} L_{3}\\ \end{array} } \right] \left[ {\begin{array}{l} {\mathbf{X }}_{;1}^{tp} \\ {\mathbf{X }}_{;2}^{tp} \\ {\mathbf{X }}_{;3}^{tp} \\ \end{array}} \right] ={\mathbf{L }}_{X}^{\mathrm {T}}{{\mathbb {X}}}^{tp}, \end{aligned}$$

  (A.16a)
  $$\begin{aligned} {{\mathbb {X}}}^{tp}= & {} \left[ {\mathbf{X }}_{;1}^{tp}\, \, {\mathbf{X }}_{;2}^{tp}\, \, {\mathbf{X }}_{;3}^{tp} \right] ^{\mathrm {T}}, \end{aligned}$$

  (A.16b)

  where ${\mathbf{X }}_{;i}^{tp}$ is the Cartesian coordinate of $i-$th transformation node.

• 2D:

  $$\begin{aligned}&\left\{ {\begin{array}{l} X_{1}\left( \xi _{1},\xi _{2} \right) =\sum \limits _{m=1}^8 {N_{m}{\mathbf{X }}_{{\mathbf {1}};m}^{tp}} =\left[ {\begin{array}{ccc} N_{1} &{} \cdots &{} N_{8}\\ \end{array} } \right] \left[ {\begin{array}{l} {\mathbf{X }}_{{\mathbf {1}};1}^{tp} \\ \vdots \\ {\mathbf{X }}_{{\mathbf {1}};8}^{tp} \\ \end{array}} \right] ={\mathbf{N }}_{X}^{\mathrm {T}}{\mathbf{X }}_{{\mathbf {1}}}^{tp}\\ X_{2}\left( \xi _{1},\xi _{2} \right) =\sum \limits _{m=1}^8 {N_{m}{\mathbf{X }}_{{\mathbf {2}};m}^{tp}} =\left[ {\begin{array}{ccc} N_{1} &{} \cdots &{} N_{8}\\ \end{array} } \right] \left[ {\begin{array}{l} {\mathbf{X }}_{{\mathbf {2}};1}^{tp} \\ \vdots \\ {\mathbf{X }}_{{\mathbf {2}};8}^{tp} \\ \end{array}} \right] ={\mathbf{N }}_{X}^{\mathrm {T}}{\mathbf{X }}_{{\mathbf {2}}}^{tp} \\ \end{array}} \right. , \end{aligned}$$

  (A.17a)
  $$\begin{aligned}&{\mathbf{X }}\left( {\varvec{\upxi }} \right) = \left[ {\begin{array}{l} X_{1} \\ X_{2} \\ \end{array}} \right] = \left[ {\begin{array}{l} {\mathbf{N }}_{X}^{\mathrm {T}}{\mathbf{X }}_{1}^{tp} \\ {\mathbf{N }}_{X}^{\mathrm {T}}{\mathbf{X }}_{2}^{tp} \\ \end{array}} \right] = \left[ {\begin{array}{ll} {\mathbf{N }}_{X}^{\mathrm {T}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf{N }}_{X}^{\mathrm {T}}\\ \end{array} } \right] \left[ {\begin{array}{l} {\mathbf{X }}_{{\mathbf {1}}}^{tp} \\ {\mathbf{X }}_{{\mathbf {2}}}^{tp} \\ \end{array}} \right] = \left( {\mathbf{I }}_{2} \circledast {\mathbf{N }}_{X}^{\mathrm {T}} \right) \left[ {\begin{array}{l} {\mathbf{X }}_{{\mathbf {1}}}^{tp} \\ {\mathbf{X }}_{{\mathbf {2}}}^{tp} \\ \end{array}} \right] = {\mathbf{N }}_{X}^{{\varvec{*}}}{{\mathbb {X}}}^{tp}, \end{aligned}$$

  (A.17b)

  where $\left[ {\begin{array}{l} {\mathbf{X }}_{{\mathbf {1}};i}^{tp} \\ {\mathbf{X }}_{{\mathbf {2}};i}^{tp} \\ \end{array}} \right]$ is the Cartesian coordinate of $i-$th transformation node. Also,

  $$\begin{aligned} {{\mathbb {X}}}^{tp}= & {} \left[ {\begin{array}{l} {\mathbf{X }}_{{\mathbf {1}}}^{tp} \\ {\mathbf{X }}_{{\mathbf {2}}}^{tp} \\ \end{array}} \right] = \left[ {\mathbf{X }}_{{\mathbf {1}};1}^{tp}\, \, \cdots \, \, {\mathbf{X }}_{{\mathbf {1}};8}^{tp}\, \, {\mathbf{X }}_{{\mathbf {2}};1}^{tp}\, \, \cdots \, \, {\mathbf{X }}_{{\mathbf {2}};8}^{tp} \right] ^{\mathrm {T}}, \end{aligned}$$

  (A.17c)
  $$\begin{aligned} {\mathbf{N }}_{X}^{{\varvec{*}}}= & {} \left( {\mathbf{I }}_{2} \circledast {\mathbf{N }}_{X}^{\mathrm {T}} \right) . \end{aligned}$$

  (A.17d)

Discretized forms are also expressed as:

• 1D:

  $$\begin{aligned} {{\mathbb {X}}}=\llbracket X \rrbracket _{\varGamma } = \left[ {\begin{array}{lll} {\mathbf{L }}_{{\mathbf{1 }}} &{} {\mathbf{L }}_{{\mathbf{2 }}} &{} {\mathbf{L }}_{{\mathbf{3 }}}\\ \end{array} } \right] {{\mathbb {X}}}^{tp} \end{aligned}$$

  (A.18)

• 2D:

  $$\begin{aligned} {{\mathbb {X}}}= & {} \llbracket {\mathbf{X }} \rrbracket _{A}=\left[ {\begin{array}{l} {\mathbf{X }}_{{\mathbf {1}}} \\ {\mathbf{X }}_{{\mathbf {2}}} \\ \end{array}} \right] ={{\mathbb {N}}}_{X}^{{\varvec{*}}}{{\mathbb {X}}}^{tp}, \end{aligned}$$

  (A.19a)
  $$\begin{aligned} {{\mathbb {N}}}_{X}^{{\varvec{*}}}= & {} \llbracket {\mathbf{N }}_{X}^{{\varvec{*}}} \rrbracket _{A} = \left( {\mathbf{I }}_{2} \circledast \left[ {\begin{array}{llll} {\mathbf{N }}_{{\mathbf{1 }}} &{} {\mathbf{N }}_{{\mathbf{2 }}} &{} {{\cdots }} &{} {\mathbf{N }}_{{\mathbf {8}}}\\ \end{array} } \right] \right) . \end{aligned}$$

  (A.19b)

1.3.2 Derivative transformation (Cartesian derivative):

Vector-matrix form:

• 1D transformation:

  $$\begin{aligned} f_{,\xi }= & {} j_{tr}^{1d}f_{,X}\, \, \, \, \, \, \, \, \Rightarrow \, \, \, \, \, \, \, f_{,X}=j_{tr}^{1d\, -1}f_{{,}\xi }, \end{aligned}$$

  (A.20a)
  $$\begin{aligned} j_{tr}^{1d}= & {} X_{,\xi },\, \, \, \, \, \, \, \, \, j_{tr}^{1d\, -1}=\, 1/\, X_{,\xi }. \end{aligned}$$

  (A.20b)

• 2D transformation:

  $$\begin{aligned} f_{,{\varvec{\upxi }}}= & {} {\mathbf{J }}_{tr}^{2d}f_{,{\mathbf{X }}}\, \, \, \, \, \, \, \, \, \Rightarrow \, \, \, \, \, \, \, \, \, \, f_{,{\mathbf{X }}}={\mathbf{J }}_{tr}^{\mathrm {2d\, -1}}f_{,{\varvec{\upxi }}}, \end{aligned}$$

  (A.21a)
  $$\begin{aligned} {\mathbf{J }}_{tr}^{2d}= & {} \left[ {\begin{array}{ll} \frac{\partial X_{1}}{\partial \xi _{1}} &{} \frac{\partial X_{2}}{\partial \xi _{1}}\\ \frac{\partial X_{1}}{\partial \xi _{2}} &{} \frac{\partial X_{2}}{\partial \xi _{2}}\\ \end{array} } \right] {,\, \, \, \, \, \, \, \, \, \, \, \, \, \, }{\mathbf{J }}_{tr}^{\mathrm {2d\, -1}}=\frac{1}{j_{tr}^{2d}}\left[ {\begin{array}{ll} \frac{\partial X_{2}}{\partial \xi _{2}} &{} -\frac{\partial X_{2}}{\partial \xi _{1}}\\ -\frac{\partial X_{1}}{\partial \xi _{2}} &{} \frac{\partial X_{1}}{\partial \xi _{1}}\\ \end{array} } \right] , \end{aligned}$$

  (A.21b)

  Discretized form:

• 1D transformation:

  $$\begin{aligned} \mathbbm {f}_{,{\mathbf{X }}}= & {} \llbracket f_{,X} \rrbracket _{\varGamma } = {\mathop {{\mathcal {D}}}\limits ^{1d}}_{X}\mathbbm {f}, \end{aligned}$$

  (A.22a)
  $$\begin{aligned} {\mathop {{\mathcal {D}}}\limits ^{1d}}_{X}= & {} \left( {\mathbf{I }}_{2} \circledast \langle \left( \mathop {\mathbbm {j}}\nolimits ^{1d}_{tr}\right) ^{\circ -1}\rangle \right) {\mathop {{\mathcal {D}}}\limits ^{1d}}_{\xi }, \end{aligned}$$

  (A.22b)
  $$\begin{aligned} \mathbbm {j}_{tr}^{1d}= & {} \llbracket j_{tr}^{\mathrm {1}d} \rrbracket _{\varGamma }= {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi }{\mathbb {X}}, \end{aligned}$$

  (A.22c)

  where ${\mathbb {X}}$ is evaluated from Eq. (A.18).

• 2D transformation:

  $$\begin{aligned} \mathbbm {f}_{,{{\mathbb {X}}}}= & {} \llbracket f_{,{\mathbf{X }}} \rrbracket _{A} = {\mathop {{\mathcal {D}}}\limits ^{2d}}_{{\mathbf{X }}}\mathbbm {f}, \nonumber \\&\quad \left\{ {\begin{array}{l} \mathbbm {f}_{,{\mathbf{X }}_{{\mathbf{1 }}}}=\llbracket f_{,X_{1}} \rrbracket _{A}= {\mathop {{\mathcal {D}}}\limits ^{2d}}_{X_{1}}\mathbbm {f} \\ \mathbbm {f}_{,{\mathbf{X }}_{{\mathbf{2 }}}}=\llbracket f_{,X_{2}} \rrbracket _{A}= {\mathop {{\mathcal {D}}}\limits ^{2d}}_{X_{2}}\mathbbm {f} \\ \end{array}} \right. , \end{aligned}$$

  (A.23a)
  $$\begin{aligned} {\mathop {{\mathcal {D}}}\limits ^{2d}}_{{\mathbf{X }}}= & {} \left( {\mathbf{I }}_{2} \circledast \langle \left( \mathop {\mathbbm {j}}\nolimits ^{1d}_{tr}\right) ^{\circ -1}\rangle \right) \, \left[ {\begin{array}{cc} \langle {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{2}} \mathbf{X }_{\mathbf{2 }} \rangle &{} -\langle {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{1}} \mathbf{X }_{\mathbf{2 }} \rangle \\ -\langle {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{2}} \mathbf{X }_{\mathbf{1 }} \rangle &{} \langle {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{1}} \mathbf{X }_{\mathbf{1 }} \rangle \\ \end{array} } \right] {\mathop {{\mathcal {D}}}\limits ^{2d}}_{{\varvec{\upxi }}}, \end{aligned}$$

  (A.23b)
  $$\begin{aligned} \mathbbm {j}_{tr}^{2d}= & {} \llbracket \left| {\mathbf{J }}_{tr}^{2d} \right| \rrbracket _{A}=\left( {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{1}}{\mathbf{X }}_{{\mathbf {1}}} \right) \circ \left( {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{2}}{\mathbf{X }}_{{\mathbf {2}}} \right) -\left( {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{1}}{\mathbf{X }}_{{\mathbf {2}}} \right) \circ \left( {\mathop {{\mathcal {D}}}\limits ^{2d}}_{\xi _{2}}{\mathbf{X }}_{{\mathbf {1}}} \right) , \end{aligned}$$

  (A.23c)

where ${\mathbf{X }}_{{\mathbf {1}}}$ and ${\mathbf{X }}_{{\mathbf {2}}}$ are evaluated from Eq. (A.19a).

1.3.3 Integral transformation (Cartesian integral):

• 1D integration:

  $$\begin{aligned} I = \int _\varGamma {f\left( s \right) ds} = {\mathop {{\mathcal {S}}}\limits ^{1d}}_{s}\llbracket f \rrbracket _{\varGamma }= {\mathop {{\mathcal {S}}}\limits ^{1d}}_{s}\mathbbm {f}, \quad \quad {\mathop {{\mathcal {S}}}\limits ^{1d}}_{s}= {\mathop {{\mathcal {S}}}\limits ^{1d}}_{\xi } \langle \mathop {\mathbbm {j}}\nolimits ^{1d}_{tr}\rangle . \end{aligned}$$

  (A.24)

• 2D operator:

  $$\begin{aligned} I = \int _A {f\left( X_{1},X_{2} \right) dX_{1}dX_{2}} = {\mathop {{\mathcal {S}}}\limits ^{2d}}_{X_{1}X_{2}}\llbracket f \rrbracket _{A}= {\mathop {{\mathcal {S}}}\limits ^{2d}}_{X_{1}X_{2}}\mathbbm {f},\qquad {\mathop {{\mathcal {S}}}\limits ^{2d}}_{X_{1}X_{2}} = {\mathop {{\mathcal {S}}}\limits ^{2d}}_{\xi _{1}\xi _{2}} \langle \mathop {\mathbbm {j}}\nolimits ^{2d}_{tr}\rangle . \end{aligned}$$

  (A.25)