Abstract
The anatomy of the distorted and topologically disrupted images of an extended object after reflection by curved mirrors, and of their refraction analogues, e.g. in gravitational lensing, is determined by the caustic surfaces enveloping the ray family issuing from each point of the object. Simulations are presented of reflections of the same object when organised by each of the five caustics (elementary catastrophes) that are stable in three-dimensional space: the fold, cusp, swallowtail, elliptic and hyperbolic umbilic catastrophes. The object is a picture of a face, whose familiar features make the image distortions and disruptions easier to understand. An important distinction is between mirrors curved in one direction and those curved in two.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Most people have seen distorted reflections in curved surfaces such as the polished metal of cars, cosmetic mirrors in bathrooms, shiny spheres decorating Christmas trees, and deliberately deformed fairground 'funhouse' mirrors. Understanding these reflections requires geometrical optics. Each point of the object is the source of a family of light rays, issuing from it in different directions. The source can be seen multiply imaged, with the number of images changing as a caustic surface of its ray family crosses the observing eye. The multiple images are familiar, and their bifurcations well understood [1], for example in reflections of the sun from wavy water; they have been studied in detail in astronomical gravitational lensing [2–4], which is a refraction analogue. The images of small objects are distorted into magnified ellipses, the magnification being extreme at moments of bifurcation.
One way to understand the reflections of objects that are more extended is to regard them as assemblies of curves (for example, contours of their intensity), corresponding to a family of families of rays: a family of points on the curve, and a family of rays for each source point on the curve. The multiple images of each point on a curve C are associated not only with distortions of its reflection but also with topological disruption. Topological change occurs in accordance with the caustic-touching theorem [5]: if the eye is regarded as a source of false rays, the image of C is disrupted when the caustic of these false rays touches C.
Here we will explore the more interesting reflection of a two-dimensional extended object. This can be regarded as the aggregate of the image curves of all its constituent curves C: a family (the collection of Cs) of families (of source points on each C) of families of rays (from each source point on each C). As the eye moves, the reflection of each of the different curves C changes topology at a different time, as the caustic from one (or more) of its points crosses the eye, giving rise to additional richness in these images.
My purpose is to understand the anatomy of these more general reflections in detail, emphasising the effects of the different types of caustics that can be generated by curved mirrors. The caustics constitute a hierarchy, classified by the mathematics of catastrophe theory [6–10]. Therefore the explanation of the distortions and disruptions is an application of this mathematics, effectively an extension of catastrophe optics [8]. The mathematics lists the caustics that are stable under perturbation (the morphological antitheses of the ideal point focus of elementary optics). The mathematics concerns how critical points of a function (values of variables where its gradient vanishes) can meet and interact as parameters vary. In optics, the function is optical distance, whose variables are positions on an initial wavefront (e.g. just above the surface of a mirror); vanishing gradient represents the Fermat–Hamilton principle determining rays, whose envelopes are the caustics, on which critical points coincide, at positions in space whose coordinates are the parameters. The stable caustics form surfaces in 3D, connected in different numbers of ways. In mathematical language, these caustics correspond to catastrophes of codimension 1, 2 and 3. There are five of them: folds (codimension 1), cusps (codimension 2), and swallowtails and elliptic and hyperbolic umbilics (all codimension 3). (The butterfly and parabolic umbilic, included in the conventional list of seven elementary catasrophes, will not be considered because they are codimension 4 singularities and so do not stably occur as caustics in three-dimensional space.).
I recently wrote a pedagogical account [11] of the simplest case: details of reflections associated with a fold caustic, with simulations and observations with a mirror curved in one direction, with a line of inflection. This involved coalescence and separation of two images of an object. Here I will present simulations of the images of one picture (the object) close to all five caustics, involving coalescences and separation of up to four images. For the picture, I choose a face, because this contains familiar and identifiable features that can be recognised after distortion and multiplication (my face, because I would not wish to impose the deformations and fragmentations on anyone else's).
Section 2 is a reprise of the general theory of reflections of an object (e.g. a picture) seen in a curved surface. An important distinction is between mirrors curved in one direction, where the wavefront is essentially one-dimensional, and mirrors curved in both directions. Section 3 concerns the first case; mathematically, this deals with catastrophes of corank one, whose caustics of codimension 1, 2 and 3 are the cuspoids: folds, cusps and swallowtails. Section 4 concerns the more interesting and unfamiliar case: catastrophes of corank two, where the relevant caustics are the elliptic and hyperbolic umbilics, both with codimension 3. Section 4 contains some concluding remarks and suggests a further application.
Although the language throughout will be that of reflection from curved mirrors, exactly the same theory and images applies to refraction, as in mirages [12], images of a candle refracted by a cylinder of water [13], and above all in gravitational lensing, where the multiplications and distortions are largely understood [2, 4], though usually without the present emphasis on the hierarchy of catastrophes.
The treatment is restricted to geometrical optics. I will not consider the well-understood patterns of wave interferences decorating each caustic ('diffraction catastrophes') [8, 10, 14, 15], because wave optics is usually unnecessary for the description of the distorted reflections usually observed.
2. General theory of images
The mirror is described by its deviation h( r ') from the plane r '= {x',y'} (figure 1). The object is a picture, described by its intensity in the plane r 0 = {x0,y0} distant z0 from the mirror plane, and the position of the observing eye is r = {x,y} in the plane distant z from the mirror. Rays are determined by the vanishing gradient of the optical distance D( r '; r 0, r ). For present purposes it suffices to use the paraxial approximation, in which propagation directions are close to the z axis, and the mirror is close to the r ' plane:
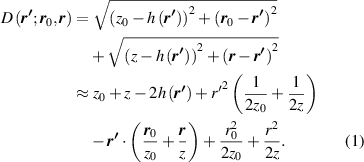
Figure 1. Geometry of mirror, object and observation planes.
Download figure:
Standard image High-resolution imageFor the analysis in terms of catastrophes, it is convenient to envisage caustics and image distortions from an initially ideally perfectly focusing mirror with curvature 1/R, and aberrations determined by its deviations f( r '), defined by:
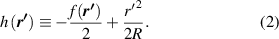
This, and the rest of this section, and section 4, refer to a mirror curved in both directions. For a mirror curved only in the x direction, and flat in y, i.e. h( r ') = h(x'), as we discuss in section 3, r'2/2R must be replaced by x'2/2R.
We define a parameter ζ representing distance from the ideal focal plane, and dimensionless object and observation positions ρ 0 = {ξ0,η0} and ρ = {ξ,η}, by:
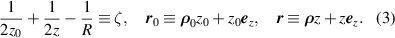
Thus the optical distance becomes, after removing irrelevant terms independent of r ',

In catastrophe theory terminology, f( r ') represents (with a minor exception) the germ of the singularity, and the quadratic and linear terms represent the unfolding of the singularity as the parameters ζ, ρ 0 and ρ vary.
The ray from an object point ρ 0 that strikes the mirror at r ' reaches ρ after reflection, determined by Fermat's principle:
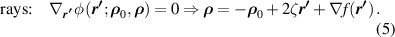
The observing eye at ρ sees this ray by looking in the direction towards r ', which can therefore be regarded as the image point of ρ 0. We are interested in how the reflection appears for different eye positions. If the original object picture has intensity I0( ρ 0), its reflection I( r ), determined by the ray mapping, is:
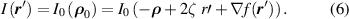
This simple explicit formula, not requiring the solution of an implicit equation, is the basis for all the simulations to follow. It describes the reflection of a fixed object from different eye positions ρ . When looking at one's own reflection, the object moves with the eye, and a moment's thought indicates that equation (6) still applies, but with ρ replaced by 2 ρ .
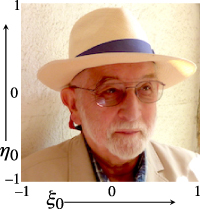
Figure 2 shows the object picture whose distorted reflections will be simulated. My right eye is at the centre; this will help in understanding the images to follow, as is the fact that the picture is not left–right symmetric. The picture is digital, so equation (6) could be applied pixel by pixel; but it was simpler to interpolate the digital array to give a smooth function on −1 ⩽ {ξ0,η0} ⩽ +1 (I used Mathematica's command ImageValue), and then apply equation (6) directly. The picture is coloured, so the simulations of its distortions requires the application of equation (6) to its R, G, and B channels.
Figure 2. Undistorted object picture before reflection.
Download figure:
Standard image High-resolution imageCaustics from object points ρ 0 are surfaces, determined by the focusing condition:

Focusing means that a ray interval ∂ r ' that is first-order small gets concentrated into an interval ∂ ρ in the observation plane that is second-order small. Considered in the opposite way, this explains the infinite magnification seen in the image r ' when viewed with the eye at a point ρ . When applied to the ray equation (5), the caustic condition gives the focal distances ζ along each ray where its image appears to lie:
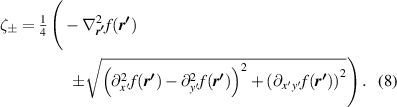
For given dimensionless observation plane ζ, the solution(s) of this implicit equation for r ', together with equation (5), determine the position(s) ρ where the caustics intersect it.
In the general case of a doubly curved mirror, the caustic of the family of rays from each object point ρ 0 consists of two sheets, represented by the two signs in equation (8). Each ray in the family touches each sheet once, at distances ζ± these foci lie at the two centres of principal curvature of the wavefront at the mirror from the family of rays from the object point ρ 0. I will not consider here the deep and apparently unsolved problem of why we perceive only one of these foci when looking along the ray towards r ', and what determines which one; it has been considered in detail by M Feigenbaum (unpublished) for the special case of anamorphic images seen in a reflecting cylinder.
3. Mirrors curved in one direction: cuspoids
In this special case, familiar in most fairground mirrors, the profile h depends only on x, as discussed following equation (2): the y' direction is inert. The ray and caustic equations (5) and (6) depend only on x', ξ0 and ξ, and with the observing eye always at η= 0 the image positions y0 map according to:
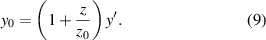
In the nontrivial x direction, catastrophe theory gives the mirror deviation function f(x') and the caustic for the fold catastrophe (codimension 1), for a source at ξ0, as:
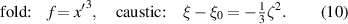
In this case, where the caustic is a smooth curve (figure 3(a)), the ζ dependence represents unimportant shifts in the image x' (by ζ/3) and eye position ξ (by ζ2/3), so in the simulations we can set ζ = 0 (i.e.  ). We will consider the distortions as the eye moves and two images of each object point collide and merge.
). We will consider the distortions as the eye moves and two images of each object point collide and merge.
Figure 3. Cuspoid catastrophe caustics from source at ξ0 = 0: (a) fold, codimension 1; (b) cusp, codimension 2; (c)–(e) swallowtail, codimension 3, for (c) a = −1, (d) a = 0, (e) a = 1; the numbers of rays in each region are indicated by bold numbers.
Download figure:
Standard image High-resolution imageFigure 4 shows the distorted reflections associated with the fold. Figure 4(a) corresponds to the observing eye located at ξ= 0, i.e. on the caustic of the ray from the centre of the picture (my right eye); therefore this point on the picture is most distorted (stretched by infinite magnification): the overlap of the two images is maximal. As ξ decreases (top sequence of figure 4(b)), the observing eye crosses the caustics from more object points, which progressively disappear from the reflection. In the opposite direction, in which ξ increases (bottom sequence of figure 4(b)), successive object points split into two, leading eventually to two recognisable images of the picture (ξ = 1), facing in opposite directions. These fold images were considered earlier [11, 13].
Figure 4. (a) Fold caustic reflections in ξ', η' plane, with eye at ξ = 0, i.e. on the caustic from the central point of the object in figure 2; (b) unfoldings, showing the two images merging and separating as the eye moves to different points ξ.
Download figure:
Standard image High-resolution imageFor the cusp catastrophe (codimension 2), the mirror deviation, and the caustic (figure 3(b)) for a source at ξ0, are,
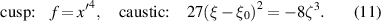
Two fold curves connect at the cusp point. For each object point, there are three images for eye positions within the region bounded by the two folds, and one image outside. The distortions depend on both ξ and ζ.
Figure 5 shows distorted reflections associated with the cusp. In figure 5(a), the observing eye is located on the cusp point of the caustic from the centre of the picture, and all three images overlap. Figure 5(b) shows how the reflected images separate as ξ varies (horizontal sequence: one image, emerging as |ξ| increases) and as ζ varies (vertical sequence: three images emerging as ζ decreases from zero, and one emerging as ζ increases from zero). These simulations are for 'longitudinal' cusps, where the variables are ξ, ζ, but the structural stability of cusps guarantees that the distortions would be the same, apart from possible shearing, for transverse cusps, i.e. with variables ξ, η (for examples in irregular water-droplet 'lenses', see for example [10]).
Figure 5. (a) Cusp caustic reflections in ξ', η' plane, with eye at ξ = ζ = 0, i.e. on the most singular point of the caustic from the central point of the object in figure 2; (b) unfoldings, showing the three images merging and separating as the eye moves to different points {ξ,ζ}.
Download figure:
Standard image High-resolution imageFor the swallowtail catastrophe (codimension 3), the mirror deviation, and the caustic for a source at ξ0 figures 3(c)–(e), are:
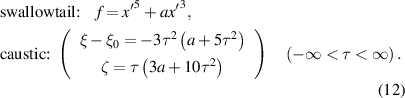
We will consider reflections I(ξ',η') depending on eye position ξ, ζ, regarding a as a third unfolding parameter, i.e. with the mirror curved in one direction, with y undistorted; in catastrophe theory, the germ of the swallowtail is simply x'5. (It is known [9, 16] that within paraxial optics it is not possible to create a swallowtail caustic from a doubly curved mirror in which figure 3(c) would represent a transverse section, i.e. with the parameters ξ,ζ a in equation (12) replaced by ξ, η, ζ, though some oblique partial realisations can occur, and can be seen in refraction from irregular water droplet 'lenses' [10].). Now there are four, two or no images, depending on the caustics from different object points in relation to the fold curves in figures 3(c)–(e).
Figure 6 shows distorted reflections associated with the swallowtail. In figure 6(a), the observing eye is located on the swallowtail point of the caustic from the centre of the picture, and all four images overlap. Figure 6(b) shows unfolding sequences for a= 0 (top, corresponding to figure 3(d)) and a = −1.5 (bottom, corresponding to figure 3(c)). In the unfolded sequence with a = −1.5, the image for ξ = −81/80 marks the crossing of the self-intersection in figure 3(c), as two pairs of images appear and become four, visible at ξ = −81/160, then coalescing into two across the fold at ξ = −0.
Figure 6. (a) Swallowtail caustic reflections in ξ', η' plane, with eye at ξ = ζ = a = 0, i.e. on the most singular point of the caustic from the central point of the object in figure 2; (b) unfoldings, showing the four images merging and separating as the eye moves to different points {ξ,ζ}, for parameters a = 0 (top) and a = 1.5 (bottom).
Download figure:
Standard image High-resolution image4. Mirrors curved in two directions: umbilics
There are two corank singularities with codimension 3, distinguished by the way the caustic sheets meet along the ray from the umbilic point r ' on the mirror, where the two curvatures of the reflected wavefront are equal and ζ+ = ζ− in equation (8). First is the elliptic umbilic catastrophe, for which the mirror deviation and caustic (figure 7(a)) are:
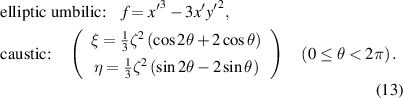
Figure 7. (a) Elliptic umbilic caustic, for ζ = 0 (central dot) and ζ = 1 (red curve); (b) hyperbolic umbilic caustic, for ζ = 0 (dashed red lines) and ζ = 1 (red curve); the numbers of images in each region for ζ ≠ 0 are indicated by bold numbers.
Download figure:
Standard image High-resolution imageIn each section labelled by ζ, the caustic is a 3-cusped astroid, shrinking to a point at ζ = 0 where the two sheets are connected. Inside the astroid, there are four rays, collapsing to two outside as the caustic surface is crossed.
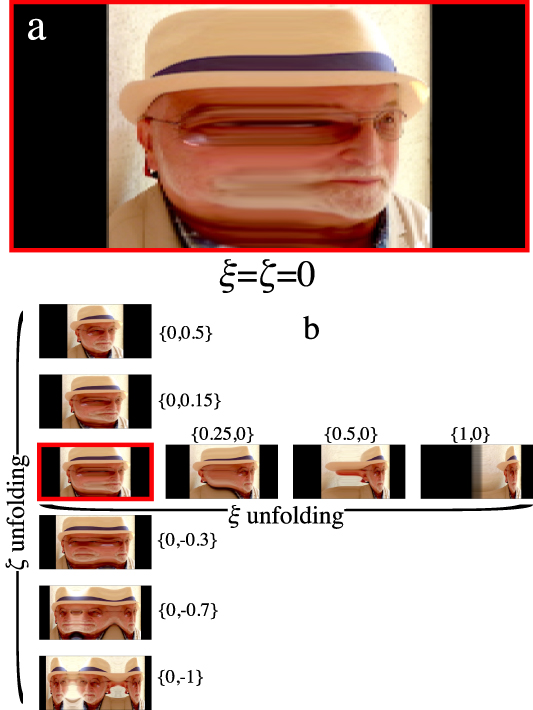
Figure 8 shows the distorted reflections as the observing eye moves in 3D relative to the caustic from the central point of the object picture. Figure 8(a) shows the most singular reflection, corresponding to the origin ξ = η = ζ = 0, where all four images overlap. The selection of unfoldings in figure 8(b) shows the four images (e.g. in the {0,0,1.8} picture) merging pairwise in different ways as the caustic surface is crossed in different directions.
Figure 8. (a) Elliptic umbilic caustic image in ξ', η' plane, with eye at ξ = η = ζ = 0, i.e. on the most singular point of the caustic from the central point of the object in figure 2; (b) unfoldings, showing the four images merging and separating as the eye moves to different points {ξ,η,ζ}.
Download figure:
Standard image High-resolution imageThe second corank singularity is the hyperbolic umbilic catastrophe, for which the mirror deviation and caustic are (figure 7(b)):

In each section |ζ| > 0, the caustic consists of a smooth curve and a cusped curve; the two sheets intersect at ζ= 0, where the caustic consists of two lines meeting at a finite-angled corner. Outside the smooth caustic sheet there are no rays; between the two sheets there are two, increasing to four inside the cusped sheet.
Figure 9 shows the distorted reflections as the observing eye moves in 3D relative to the caustic from the central point of the object picture. Figure 9(a) shows the most singular reflection, corresponding to the corner ξ = η = ζ = 0 (figure 7(b)), where all four images overlap. This is very different from the corresponding overlap for the elliptic umbilic (figure 8(a)). As the unfoldings in figure 9(b) illustrate, the ways in which the four images (e.g. in the {1,0,0} picture) merge across the caustics sheets are also very different from those for the elliptic umbilic.
Figure 9. (a) Hyperbolic umbilic caustic image in ξ', η' plane, with eye at ξ = η= ζ = 0, i.e. on the most singular point of the caustic from the central point of the object in figure 2; (b) unfoldings, showing the four images merging and separating as the eye moves to different points{ξ,η,ζ}.
Download figure:
Standard image High-resolution image5. Concluding remarks
We have extended catastrophe optics to explain the deformations of an extended object, in the form of a picture, when viewed in mirrors curved in one or two directions. The simulations were calculated by the mapping equation (6). Central to understanding the reflections has been the caustics of the families of rays issuing from each point of the object. As the observing eye moves across one of these caustics, the number of reflections of the object points changes. The intricacies of the sometimes amusing and at first sight puzzling reflections are associated with the fact that the eye crosses caustics from different object points at different times, successively splitting the reflected images of those points.
Since the reflections are organised by caustics, and since caustics in three-dimensional space are organised by the five elementary catastrophes, we have simulated reflections associated with each of the catastrophes separately. The most singular reflections (in figures 4(a), 5(a), 6(a), 8(a) and 9(a)), where the maximum numbers of images overlap, arise when the eye encounters the most singular point of the caustic from a central point of the object. Moving away from this encounter, the reflected images separate in ways determined by the unfolding of the corresponding catastrophe.
Studies of more complicated reflections can easily be envisaged. The five catastrophes are termed elementary because they are the structural elements ('atoms of form') that can organise more intricate focusing patterns in space with three or fewer dimensions, for example the caustic networks generated by reflection or refraction from rippling water [8, 17]. Extended objects whose different points generate different networks will produce distorted reflections that are combinations of those studied here. Familiar examples are the 'skypools and landpools' in reflections of the sky and coasts from wavy water on the ocean, and pebbles and plants on the sea bed seen viewed by refraction from above ([18–21], and many pictures on the internet). It would be interesting to explore the anatomy of such reflections and refractions in terms of caustic networks organised by elementary catastrophes.
Acknowledgments
I thank Professor James Lock for careful reading of the manuscript and helpful suggestions, and a referee for several corrections. My research is supported by the Leverhulme Trust.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).