Abstract
Rate distortion theory is concerned with optimally encoding signals from a given signal class \(\mathcal {S}\) using a budget of R bits, as \(R \rightarrow \infty \). We say that \(\mathcal {S}\) can be compressed at rate s if we can achieve an error of at most \(\mathcal {O}(R^{-s})\) for encoding the given signal class; the supremal compression rate is denoted by \(s^*(\mathcal {S})\). Given a fixed coding scheme, there usually are some elements of \(\mathcal {S}\) that are compressed at a higher rate than \(s^*(\mathcal {S})\) by the given coding scheme; in this paper, we study the size of this set of signals. We show that for certain “nice” signal classes \(\mathcal {S}\), a phase transition occurs: We construct a probability measure \(\mathbb {P}\) on \(\mathcal {S}\) such that for every coding scheme \(\mathcal {C}\) and any \(s > s^*(\mathcal {S})\), the set of signals encoded with error \(\mathcal {O}(R^{-s})\) by \(\mathcal {C}\) forms a \(\mathbb {P}\)-null-set. In particular, our results apply to all unit balls in Besov and Sobolev spaces that embed compactly into \(L^2 (\varOmega )\) for a bounded Lipschitz domain \(\varOmega \). As an application, we show that several existing sharpness results concerning function approximation using deep neural networks are in fact generically sharp. In addition, we provide quantitative and non-asymptotic bounds on the probability that a random \(f\in \mathcal {S}\) can be encoded to within accuracy \(\varepsilon \) using R bits. This result is subsequently applied to the problem of approximately representing \(f\in \mathcal {S}\) to within accuracy \(\varepsilon \) by a (quantized) neural network with at most W nonzero weights. We show that for any \(s > s^*(\mathcal {S})\) there are constants c, C such that, no matter what kind of “learning” procedure is used to produce such a network, the probability of success is bounded from above by \(\min \big \{1, 2^{C\cdot W \lceil \log _2 (1+W) \rceil ^2 - c\cdot \varepsilon ^{-1/s}} \big \}\).
Similar content being viewed by others
1 Introduction
Let \(\mathcal {S}\) be a signal class, that is, a relatively compact subset of a Banach space \((\mathbf {X}, \Vert \cdot \Vert _{\mathbf {X}})\). Rate distortion theory is concerned with the question of how well the elements of \(\mathcal {S}\) can be encoded using a prescribed number R of bits. In many cases of interest, the best achievable coding error scales like \(R^{-s^*}\), where \(s^*\) is the optimal compression rate of the signal class \(\mathcal {S}\). We show that a phase transition occurs: the set of elements \(\mathbf {x}\in \mathcal {S}\) that can be encoded using a strictly larger exponent than \(s^*\) is thin; precisely, it is a null-set with respect to a suitable probability measure \(\mathbb {P}\). Crucially, the measure \(\mathbb {P}\) is independent of the chosen coding scheme.
In order to rigorously formulate these results, we first review the needed notions of rate-distortion theory, see also [3, 4, 13, 15]. For later use, we state the definitions here in the setting of general Banach spaces, although our main results only focus on the Hilbert space \(L^2(\varOmega )\).
1.1 A Crash Course in Rate Distortion Theory
To formalize the notion of encoding a signal class \(\mathcal {S}\subset \mathbf {X}\), we define the set  of encoding/decoding pairs (E, D) of code-length \(R \in \mathbb {N}\) as
of encoding/decoding pairs (E, D) of code-length \(R \in \mathbb {N}\) as

We are interested in choosing  such as to minimize the (maximal) distortion .
such as to minimize the (maximal) distortion .
The intuition behind these definitions is that the encoder E converts any signal \(\mathbf {x}\in \mathcal {S}\) into a bitstream of code-length R (i.e., consisting of R bits), while the decoder D produces from a given bitstream \({b \in \{ 0, 1 \}^R}\) a signal \(D(b) \in \mathbf {X}\). The goal of rate distortion theory is to determine the minimal distortion that can be achieved by any encoder/decoder pair of code-length \(R \in \mathbb {N}\). Typical results concerning the relation between code-length and distortion are formulated in an asymptotic sense: One assumes that for every code-length \(R \in \mathbb {N}\), one is given an encoding/decoding pair  and then, studies the asymptotic behavior of the corresponding distortion
and then, studies the asymptotic behavior of the corresponding distortion  as \(R \rightarrow \infty \).
as \(R \rightarrow \infty \).
We refer to a sequence \(\big ( (E_R, D_R) \big )_{R \in \mathbb {N}}\) of encoding/decoding pairs as a codec, so that the set of all codecs is

For a given signal class \(\mathcal {S}\) in a Banach space \(\mathbf {X}\), it is of great interest to find an asymptotically optimal codec; that is, a sequence  such that the asymptotic decay of
such that the asymptotic decay of  is, in a sense, maximal. To formalize this, for each \(s \in [0,\infty )\) define the class of subsets of \(\mathbf {X}\) that admit compression rate s as
is, in a sense, maximal. To formalize this, for each \(s \in [0,\infty )\) define the class of subsets of \(\mathbf {X}\) that admit compression rate s as

For a given (bounded) signal class \(\mathcal {S}\subset \mathbf {X}\), we aim to determine the optimal compression rate for \(\mathcal {S}\) in \(\mathbf {X}\), that is

Although the calculation of the quantity  may appear daunting for a given signal class \(\mathcal {S}\), there exists in fact a large body of literature addressing this topic. A landmark result in this area states that the JPEG2000 compression standard represents an optimal codec for the compression of piecewise smooth signals [26]. This optimality is typically stated more generally for the signal class \(\mathcal {S}= {{\,\mathrm{Ball}\,}}\big ( 0, 1; B_{p,q}^\alpha (\varOmega ) \big )\), the unit ball in the Besov space \(B_{p,q}^\alpha (\varOmega )\), considered as a subset of \(\mathbf {X}= \mathcal {H}= L^2(\varOmega )\), for “sufficiently nice” bounded domains \(\varOmega \subset \mathbb {R}^d\); see [10].
may appear daunting for a given signal class \(\mathcal {S}\), there exists in fact a large body of literature addressing this topic. A landmark result in this area states that the JPEG2000 compression standard represents an optimal codec for the compression of piecewise smooth signals [26]. This optimality is typically stated more generally for the signal class \(\mathcal {S}= {{\,\mathrm{Ball}\,}}\big ( 0, 1; B_{p,q}^\alpha (\varOmega ) \big )\), the unit ball in the Besov space \(B_{p,q}^\alpha (\varOmega )\), considered as a subset of \(\mathbf {X}= \mathcal {H}= L^2(\varOmega )\), for “sufficiently nice” bounded domains \(\varOmega \subset \mathbb {R}^d\); see [10].
For a codec  , instead of considering the maximal distortion of \(\mathcal {C}\) over the entire signal class \(\mathcal {S}\), one can also measure the approximation rate that the codec \(\mathcal {C}\) achieves for each individual \(\mathbf {x}\in \mathcal {S}\). Precisely, the class of elements with compression rate s under \(\mathcal {C}\) is
, instead of considering the maximal distortion of \(\mathcal {C}\) over the entire signal class \(\mathcal {S}\), one can also measure the approximation rate that the codec \(\mathcal {C}\) achieves for each individual \(\mathbf {x}\in \mathcal {S}\). Precisely, the class of elements with compression rate s under \(\mathcal {C}\) is

If the signal class \(\mathcal {S}\) is “sufficiently regular”—for instance if \(\mathcal {S}\) is compact and convex—then one can prove (see Proposition 3) that the following dichotomy is valid:

Thus, all signals in \(\mathcal {S}\) can be approximated at any compression rate lower than the optimal rate for \(\mathcal {S}\) using a common codec. Furthermore, for any approximation rate s larger than the optimal rate for \(\mathcal {S}\), and for any codec \(\mathcal {C}\), there exists some \({\mathbf {x}^*= \mathbf {x}^*(s, \mathcal {C}) \in \mathcal {S}}\) that is not compressed at rate s by \(\mathcal {C}\).
Remark 1
(Encoding/decoding schemes vs. discretization maps) As the above considerations suggest, the crucial objects for our investigations are not the encoding/decoding pairs  , but the distortion they cause for each \(\mathbf {x}\in \mathcal {S}\). Therefore, we could equally well restrict our attention to the discretization map \(D \circ E : \mathcal {S}\rightarrow \mathbf {X}\), which has the crucial property \({|\mathrm {range} (D \circ E)| \le 2^R}\). Conversely, given any (discretization) map \(\varDelta : \mathcal {S}\rightarrow \mathbf {X}\) with \(|\mathrm {range}(\varDelta )| \le 2^R\), one can construct an encoding/decoding pair
, but the distortion they cause for each \(\mathbf {x}\in \mathcal {S}\). Therefore, we could equally well restrict our attention to the discretization map \(D \circ E : \mathcal {S}\rightarrow \mathbf {X}\), which has the crucial property \({|\mathrm {range} (D \circ E)| \le 2^R}\). Conversely, given any (discretization) map \(\varDelta : \mathcal {S}\rightarrow \mathbf {X}\) with \(|\mathrm {range}(\varDelta )| \le 2^R\), one can construct an encoding/decoding pair  , by choosing a surjection \({D : \{ 0,1 \}^R \rightarrow \mathrm {range}(\varDelta )}\), and then setting
, by choosing a surjection \({D : \{ 0,1 \}^R \rightarrow \mathrm {range}(\varDelta )}\), and then setting
which ensures that \(\Vert \mathbf {x}- D(E(\mathbf {x})) \Vert _{\mathbf {X}} \le \Vert \mathbf {x}- \varDelta (\mathbf {x}) \Vert _{\mathbf {X}}\) for all \(\mathbf {x}\in \mathcal {S}\). Thus, all our results could be rephrased in terms of such discretization maps rather than in terms of encoding/decoding pairs. For more details on this connection, see also Lemma 10. \(\blacktriangleleft \)
1.2 Our Contributions
1.2.1 Phase Transition
We improve on the dichotomy (1.3) by measuring the size of the class  of elements with compression rate s under the codec \(\mathcal {C}\). Then, a phase transition occurs: the class of elements that cannot be encoded at a “larger than optimal” rate is generic. We prove this when the signal class is a ball in a Besov- or Sobolev space, as long as this ball forms a compact subset of \(L^2(\varOmega )\) for a bounded Lipschitz domain \(\varOmega \subset \mathbb {R}^d\).
of elements with compression rate s under the codec \(\mathcal {C}\). Then, a phase transition occurs: the class of elements that cannot be encoded at a “larger than optimal” rate is generic. We prove this when the signal class is a ball in a Besov- or Sobolev space, as long as this ball forms a compact subset of \(L^2(\varOmega )\) for a bounded Lipschitz domain \(\varOmega \subset \mathbb {R}^d\).
More precisely, for each such signal class \(\mathcal {S}\), we construct a probability measure \(\mathbb {P}\) on \(\mathcal {S}\) such that the compressibility exhibits a phase transition as in the following definition.
Definition 1
A Borel probability measure \(\mathbb {P}\) on a subset \(\mathcal {S}\) of a Banach space \(\mathbf {X}\) exhibits a compressibility phase transition if it satisfies the following:

In this definition, since the set  is not necessarily measurable for
is not necessarily measurable for  , instead of the measure \(\mathbb {P}\), we use the associated outer measure \(\mathbb {P}^*\). Generally, given a measure space \((\mathcal {S}, \mathscr {A},\mu )\) the outer measure \(\mu ^*: 2^{\mathcal {S}} \rightarrow [0,\infty ]\) induced by \(\mu \) is defined as
, instead of the measure \(\mathbb {P}\), we use the associated outer measure \(\mathbb {P}^*\). Generally, given a measure space \((\mathcal {S}, \mathscr {A},\mu )\) the outer measure \(\mu ^*: 2^{\mathcal {S}} \rightarrow [0,\infty ]\) induced by \(\mu \) is defined as
In general, \(\mu ^*\) is not a measure, but it is always \(\sigma \)-subadditive, meaning that it satisfies \({\mu ^*(\bigcup _{n=1}^\infty M_n) \le \sum _{n=1}^\infty \mu ^*(M_n)}\) for arbitrary \(M_n \subset \mathcal {S}\); see [14, Section 1.4]. Furthermore, it is easy to see for \(M \in \mathscr {A}\) that \(\mu ^*(M) = \mu (M)\); that is, \(\mu ^*\) is an extension of \(\mu \).
As seen in (1.4), we are mostly interested in \(\mu ^*\)-null-sets; that is, subsets \(N \subset \mathcal {S}\) satisfying \(\mu ^*(N) = 0\). This holds if and only if there is \(N' \in \mathscr {A}\) satisfying \(N \subset N'\) and \(\mu (N') = 0\). Directly from the \(\sigma \)-subadditivity of \(\mu ^*\), it follows that a countable union of \(\mu ^*\)-null-sets is again a \(\mu ^*\)-null-set.
We note that the first implication in (1.4) is always satisfied, as a consequence of (1.3). The second part of (1.4) states that for any  and any codec \(\mathcal {C}\), almost every \(\mathbf {x}\in \mathcal {S}\) cannot be compressed by \(\mathcal {C}\) at rate s. In other words, whenever \(\mathbb {P}\) exhibits a compressibility phase transition on \(\mathcal {S}\), the property of not being compressible at a “larger than optimal” rate is a generic property.
and any codec \(\mathcal {C}\), almost every \(\mathbf {x}\in \mathcal {S}\) cannot be compressed by \(\mathcal {C}\) at rate s. In other words, whenever \(\mathbb {P}\) exhibits a compressibility phase transition on \(\mathcal {S}\), the property of not being compressible at a “larger than optimal” rate is a generic property.
Remark 2
-
(i)
We emphasize that the measure \(\mathbb {P}\) in Definition 1 is required to satisfy the second property in (1.4) universally for any choice of codec \(\mathcal {C}\).
In fact, if \(\mathbb {P}\) would be allowed to depend on \(\mathcal {C}\), one could simply choose \(\mathbb {P}= \delta _{\mathbf {x}}\), where \(\mathbf {x}= \mathbf {x}(\mathcal {C}, s) \in \mathcal {S}\) is a single element that is not approximated at rate s by \(\mathcal {C}\); for
 such an element exists under mild assumptions on \(\mathcal {S}\); see Proposition 3.
such an element exists under mild assumptions on \(\mathcal {S}\); see Proposition 3. -
(ii)
Any measure \(\mathbb {P}\) satisfying (1.4) also satisfies \(\mathbb {P}^*(\{ \mathbf {x}\}) = 0\) (and hence \(\mathbb {P}(\{ \mathbf {x}\}) = 0\)) for each \(\mathbf {x}\in \mathcal {S}\), as can be seen by taking \({\mathcal {C}= \bigl ((E_R,D_R)\bigr )_{R \in \mathbb {N}}}\) with \(D_R : \{ 0,1 \}^R \rightarrow \mathcal {S}, c \mapsto \mathbf {x}\), so that
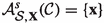 for all \({s > 0}\). Thus, any probability measure \(\mathbb {P}\) exhibiting a compressibility phase transition is atom free.
for all \({s > 0}\). Thus, any probability measure \(\mathbb {P}\) exhibiting a compressibility phase transition is atom free. -
(iii)
Measures satisfying (1.4) are quite special—in fact, Proposition 4 shows under mild assumptions on \(\mathcal {S}\) that the set of measures not satisfying (1.4) is generic in the set of atom-free probability measures. \(\blacktriangleleft \)
Our first main result establishes the existence of critical measures for all Sobolev- and Besov balls (denoted by \({{\,\mathrm{Ball}\,}}( 0 , 1; W^{k,p}(\varOmega ; \mathbb {R}))\), respectively \({{\,\mathrm{Ball}\,}}( 0 , 1; B_{p,q}^{\tau }(\varOmega ;\mathbb {R}))\); see Appendix C) that are compact subsets of \(L^2 (\varOmega )\):
Theorem 1
Let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be a bounded Lipschitz domain. Consider either of the following two settings:
-
\(\mathcal {S}:= {{\,\mathrm{Ball}\,}}\big ( 0, 1; B_{p,q}^{\tau } (\varOmega ; \mathbb {R}) \big )\) and \(s^*:= \frac{\tau }{d}\), where \(p,q \in (0,\infty ]\) and \(\tau \in \mathbb {R}\) with \({\tau > d \cdot (\frac{1}{p} - \frac{1}{2})_{+}}\), or
-
\(\mathcal {S}:= {{\,\mathrm{Ball}\,}}\bigl (0, 1; W^{k,p}(\varOmega )\bigr )\) and \(s^*:= \frac{k}{d}\), where \(p \in [1,\infty ]\) and \(k \in \mathbb {N}\) with \({k > d \cdot (\frac{1}{p} - \frac{1}{2})_+}\).
In either case,  , and there exists a Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}\) that exhibits a compressibility phase transition as in Definition 1.
, and there exists a Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}\) that exhibits a compressibility phase transition as in Definition 1.
Proof
This follows from Theorems 7, 8, and 4. \(\square \)
Since Remark 2 shows that the measure \(\mathbb {P}\) from the preceding theorem satisfies \(\mathbb {P}(M) = 0\) for each countable set \(M \subset \mathcal {S}\), we get the following strengthening of the dichotomy (1.3).
Corollary 1
Suppose the assumptions of Theorem 1 are satisfied. Then, given any codec  the set
the set  , which consists of all signals that cannot be encoded by \(\mathcal {C}\) at compression rate s for some \(s > s^*\), is uncountable.
, which consists of all signals that cannot be encoded by \(\mathcal {C}\) at compression rate s for some \(s > s^*\), is uncountable.
In words, Corollary 1 states that for every codec the set of signals in \(\mathcal {S}\) that cannot be approximated at any compression rate larger than the optimal rate for \(\mathcal {S}\) is uncountable. In contrast, previous results (such as Proposition 3) only state the existence of a single such “badly approximable” signal.
1.2.2 Quantitative Lower Bounds
The statement of Theorem 1 is purely qualitative; it shows that the set of elements that are approximable at a “better than optimal rate” forms a null-set with respect to the measure \(\mathbb {P}\). In fact, the measure \(\mathbb {P}\) constructed in (the proof of) Theorem 1 satisfies a stronger, quantitative condition: If one randomly draws a function \(f \sim \mathbb {P}\) using the probability measure \(\mathbb {P}\), one can precisely bound the probability that a given encoding/decoding pair \((E_R,D_R)\) of code-length R achieves a given error \(\varepsilon \) for f. To underline this probabilistic interpretation, we define, for any property Q of elements \(f \in \mathcal {S}\),
where \(\mathbb {P}^*\) denotes the outer measure induced by \(\mathbb {P}\).
Theorem 2
Let \(\mathcal {S}\) and \(s^*\) as in Theorem 1. Let the probability measure \(\mathbb {P}\) on \(\mathcal {S}\) as constructed in (the proof of) Theorem 1, and let us use the notation from Eq. (1.6).
Then, for any \(s > s^*\) there exist \(c, \varepsilon _0 > 0\) (depending on \(\mathcal {S},s\)) such that for arbitrary \(R \in \mathbb {N}\) and  it holds that
it holds that
Proof
This follows from Theorem 4 and (the proof of) Theorem 1. \(\square \)
Theorem 2 is interesting due to its nonasymptotic nature. Indeed, given a fixed budget of R bits and a desired accuracy \(\varepsilon \), it provides a partial answer to the question:
How likely is one to succeed in describing a random \(f \in \mathcal {S}\) to within accuracy \(\varepsilon \) using R bits?
Figure 1 provides an illustration of the phase transition behavior in dependence of \(\varepsilon \) and R; it graphically shows that the transition is quite sharp.
For \(\mathcal {S}\) a Sobolev or Besov ball, Theorem 2 provides bounds on the probability of being able to describe a random function \(f\in \mathcal {S}\) to within accuracy \(\varepsilon \) using R bits. This probability is, for every \(s > s^*\) and \(\varepsilon \in (0,\varepsilon _0)\) (\(s^*\) denoting the optimal compression rate of \(\mathcal {S}\)), upper bounded by \(E_s(R,\varepsilon ) := \min \bigl \{1,2^{R-c\cdot \varepsilon ^{-1/s}}\bigr \}\). In this figure, we show two plots of the function \(E_s\) over the \((R,1/\varepsilon )\)-plane. Both grayscale plots show \(E_s\) for \(s = 2.002 > s^*= 2\) and \(c = 1\), while the red curve indicates the critical region where \(R = (1/\varepsilon )^{1/s^*}\). We see that a sharp phase transition occurs in the sense that above and slightly below the critical curve \(R = \varepsilon ^{-1/2}\) (white area) the upper bound \(E_s\) does not rule out the possibility that it is always possible to describe \(f\in \mathcal {S}\) to within accuracy \(\varepsilon \) using R bits; but even slightly below the critical curve (dark area) the bound \(E_s\) shows that such a compression is almost impossible. The sharpness of the phase transition is more clearly shown in the zoomed part of the figure. The bottom plot further illustrates the quantitative behavior by using a logarithmic colormap. Note that in the bottom plot two different colormaps are used for the range \([-100,0]\) and the remaining range \([-1000, -100)\)
1.2.3 Lower Bounds for Neural Network Approximation
As an application, we draw a connection between the previously described results and the approximation properties of neural networks. In a nutshell, a neural network alternatingly applies affine-linear maps and a so-called activation function \(\varrho : \mathbb {R}\rightarrow \mathbb {R}\) that acts componentwise on vectors, meaning \(\varrho \bigl ( (x_1,\dots ,x_m) \bigr ) = \bigl (\varrho (x_1),\dots ,\varrho (x_m)\bigr )\). More precisely, we will use the following mathematical formalization of (fully connected, feed forward) neural networks [29].
Definition 2
Let \(d,L \in \mathbb {N}\) and \(\mathbf {N} = (N_0,\dots ,N_L) \subset \mathbb {N}\) with \(N_0 = d\). We say that \(\mathbf {N}\) is a network architecture, where L describes the number of layers of the network and \(N_\ell \) is the number of neurons in the \(\ell \)-th layer.
A neural network (NN) with architecture \(\mathbf {N}\) is a tuple
of matrices \(A_\ell \in \mathbb {R}^{N_\ell \times N_{\ell - 1}}\) and bias vectors \(b_\ell \in \mathbb {R}^{N_\ell }\). Given a function \(\varrho : \mathbb {R}\rightarrow \mathbb {R}\), called the activation function, the mapping computed by the network \(\varPhi \) is defined as
Here, we use the convention \(\varrho ( (x_1,\dots ,x_m) ) = (\varrho (x_1),\dots ,\varrho (x_m))\), i.e., \(\varrho \) acts componentwise on vectors.
The complexity of \(\varPhi \) is mainly described by the number \(L(\varPhi ) := L\) of layers, the number \(W(\varPhi ) := \sum _{\ell =1}^L \big ( \Vert A_\ell \Vert _{\ell ^0} + \Vert b_\ell \Vert _{\ell ^0} \big )\) of weights (or connections), and the number \(N(\varPhi ) := \sum _{\ell =0}^L N_\ell \) of neurons of \(\varPhi \). Here, for a matrix or vector A, we denote by \(\Vert A \Vert _{\ell ^0}\) the number of nonzero entries of A. Furthermore, we set \(d_{\mathrm {in}}(\varPhi ) := N_0\) and \(d_{\mathrm {out}}(\varPhi ) := N_L\).
In addition to the number of layers, neurons, and weights of a network, we will also be interested in the complexity of the individual weights and biases of the network, i.e., of the entries of the (weight) matrices \(A_\ell \) and the bias vectors \(b_\ell \). Thus, define
We say that \(\varPhi \) is \((\sigma ,W)\)-quantized if all entries of the matrices \(A_\ell \) and the vectors \(b_\ell \) belong to \(G_{\sigma ,W}\).
The set \(G_{\sigma ,W}\) in (1.7) contains all real numbers that belong to the grid \(2^{-\sigma \lceil \log _2 W \rceil ^2} \mathbb {Z}\) and simultaneously to the interval \(\bigl [ - W^{\sigma \lceil \log _2 W \rceil }, W^{\sigma \lceil \log _2 W \rceil } \bigr ]\); thus, the grid gets arbitrarily fine and the interval gets arbitrarily large as \(W \rightarrow \infty \), where the parameter \(\sigma \) determines how fast this happens. We note that in applications one necessarily deals with quantized NNs due to the necessity to store and process the weights on a digital computer. Regarding function approximation by such quantized neural networks, we have the following result:
Theorem 3
Let \(\varrho : \mathbb {R}\rightarrow \mathbb {R}\) be measurable and let \(d, \sigma \in \mathbb {N}\). For \(W \in \mathbb {N}\), define
Let \(\mathcal {S}\), \(s^*\), and \(\mathbb {P}\) as in Theorem 1. Then, using the notation (1.6), the following hold:
-
1.
There exists \(C = C(d,\sigma ) \in \mathbb {N}\) such that for each \(s > s^*\) there are \(c, \varepsilon _0 > 0\) satisfying
$$\begin{aligned} \mathrm {Pr} \Bigl (\, \min _{g \in \mathcal {NN}_{d,W}^{\sigma ,\varrho }} \Vert f - g \Vert _{L^2(\varOmega )} \le \varepsilon \Bigr ) \le 2^{C \cdot W \, \lceil \log _2 (1+W) \rceil ^2 - c \cdot \varepsilon ^{-1/s}} \,\, \forall \, \varepsilon \in (0,\varepsilon _0) . \end{aligned}$$(1.8)In fact, one can choose \(C = 4 + 4 \lceil \log _2(4 e d) \rceil + 8 \sigma \).
-
2.
If we define \(W_{\sigma ,\varrho } (f;\varepsilon ) \in \mathbb {N}\cup \{ \infty \}\) by
$$\begin{aligned} W_{\sigma ,\varrho } (f;\varepsilon ) := \inf \Bigl \{ W \in \mathbb {N}\,\,\, :\,\,\, \exists \, g \in \mathcal {NN}_{d,W}^{\sigma ,\varrho } \text { such that } \Vert f - g \Vert _{L^2(\varOmega )} \le \varepsilon \Bigr \} \end{aligned}$$and furthermore set
$$\begin{aligned} \mathcal {A}_{\mathcal {NN},\varrho }^*:= \bigg \{ f \in \mathcal {S}\,\,\,:\,\, \begin{array}{l} \exists \, \tau \in (0, \tfrac{1}{s^*}), \sigma \in \mathbb {N}, C > 0 \\ \forall \, \varepsilon \in (0, 1): W_{\sigma ,\varrho }(f;\varepsilon ) \le C \cdot \varepsilon ^{-\tau } \end{array} \bigg \} , \end{aligned}$$then \(\mathbb {P}^*( \mathcal {A}_{\mathcal {NN},\varrho }^*) = 0\).
Proof
The proof of this theorem is deferred to Appendix F. \(\square \)
In a nutshell, Eq. (1.8) states the following: If one draws a random function f from \(\mathbb {P}\), then with probability at least \(1 - 2^{C \cdot W \, \lceil \log _2 (1+W) \rceil ^2 - c \cdot \varepsilon ^{-1/s}}\), the function f will have \(L^2\) distance at least \(\varepsilon \) to every network from the class \(\mathcal {NN}_{d,W}^{\sigma ,\varrho }\). Consequently, Eq. (1.8) implies that the network size W has to scale at least like \(W \gtrsim \varepsilon ^{-1/s^*}\) (up to log factors) to succeed with high probability if \(\mathcal {S}\) is a Sobolev- or Besov ball with optimal exponent  . In particular, if one uses any learning procedure \(\mathrm {Learn} : \mathcal {S}\rightarrow \mathcal {NN}_{d,W}^{\sigma ,\varrho }\)— not necessarily a typical algorithm like (stochastic) gradient descent— and hopes to achieve \(\Vert f - \mathrm {Learn}(f) \Vert _{L^2(\varOmega )} \le \varepsilon \), then Eq. (1.8) provides an upper bound on the probability of success.
. In particular, if one uses any learning procedure \(\mathrm {Learn} : \mathcal {S}\rightarrow \mathcal {NN}_{d,W}^{\sigma ,\varrho }\)— not necessarily a typical algorithm like (stochastic) gradient descent— and hopes to achieve \(\Vert f - \mathrm {Learn}(f) \Vert _{L^2(\varOmega )} \le \varepsilon \), then Eq. (1.8) provides an upper bound on the probability of success.
Remark 3
(Further discussion of Theorem 3) It might seem peculiar at first sight that the depth of the approximating networks does not seem to play a role in Theorem 3, even though deeper networks should intuitively have better approximation properties. To understand how this can be, note that the theorem only provides a hardness result: it gives a lower bound on how well arbitrarily deep (quantized) networks can approximate functions from the class \(\mathcal {S}\).
Whether this lower bound is sharp (i.e., whether the critical rate \(s^*\) can be attained using suitable networks) then depends on the chosen activation function and the network depth. For instance, for approximating \(C^k\) functions, a result by Mhaskar [27] shows that shallow networks with smooth, non-polynomial activation functions already attain the optimal rates. For networks with the (non-smooth) ReLU activation function \(\varrho (x) = \max \{ 0,x \}\), on the other hand, it is known that (somewhat) deep networks are necessary to attain the optimal rates; more precisely, one needs ReLU networks of depth \(\mathcal {O}(1 + \frac{k}{d})\) to achieve the optimal approximation rates for \(C^k\) functions on \([0,1]^d\); see [29, Theorem C.6] and [31, 32].
In fact, the optimal rates predicted by Theorem 3 are attained (up to log factors) by sufficiently deep ReLU networks and domain \(\varOmega = [0,1]^d\). Precisely, there exist \(C = C(\mathcal {S}) > 0\) and \(\sigma = \sigma (\mathcal {S}) \in \mathbb {N}\) such that
where \(\tau \in (0, \frac{1}{s^*})\) is arbitrary. This follows from results in [13, 34]. Since the details are mainly technical, the proof is deferred to Appendix F. We remark that by similar arguments as in [13, 34], one can also prove the sharpness for other activation functions than the ReLU and other domains than \([0,1]^d\). \(\blacktriangleleft \)
1.3 Related Literature and Concepts
1.3.1 Minimax Optimality in Approximation Theory
Many (optimality) results in approximation theory are formulated in a minimax sense, meaning that one precisely characterizes the asymptotic decay of
where \(\mathcal {S}\subset \mathbf {X}\) is the class of signals to be approximated, and \(M_n \subset \mathbf {X}\) contains all functions “of complexity n,” for example polynomials of degree n or shallow neural networks with n neurons, etc. As recent examples of such results related to neural networks, we mention [4, 29, 41].
A minimax lower bound of the form \(d_{\mathbf {X}} (\mathcal {S}, M_n) \gtrsim n^{-s^*}\), however, only makes a claim about the possible worst case of approximating elements \(f \in \mathcal {S}\). In other words, such an estimate in general only guarantees that there is at least one “hard to approximate” function \(f^*\in \mathcal {S}\) satisfying \(\inf _{g \in M_n} \Vert f^*- g \Vert _{\mathbf {X}} \gtrsim n^{-s}\) for each \(s > s^*\), but nothing is known about how “massive” this set of “hard to approximate” functions is, or about the “average case.”
1.3.2 Results Quantifying the “mass” of Hard-To-Approximate Functions
The first paper to address this question—and one of the main sources of inspiration for the present paper—is [24]. In that paper, Maiorov, Meir, and Ratsaby consider essentially the “\(L^2\)-Besov-space type” signal class \(\mathcal {S}= \mathcal {S}_r\) of functions \(f \in L^2(\mathbb {B}_d)\) (with \({\mathbb {B}_d = \{ x \in \mathbb {R}^d :\Vert x \Vert _2 \le 1 \}}\)) that satisfy
where \( \mathscr {P}_K = \mathrm {span} \bigl \{ x^\alpha :\alpha \in \mathbb {N}_0^d \text { with } |\alpha | \le K \bigr \} \) denotes the space of d-variate polynomials of degree at most K. On this signal class, they construct a probability measure \(\mathbb {P}\) such that given the subset of functions
one obtains the minimax asymptotic \( d_{L^2}(\mathcal {S}_r, M_n) \asymp n^{-r/(d-1)}, \) but furthermore there exists \(c > 0\) such that
In other words, the measure of the set of functions for which the minimax asymptotic is sharp tends to 1 for \(n \rightarrow \infty \). In this context, we would also like to mention the recent article [23], in which the results of [24] are extended to cover more general signal classes and approximation in stronger norms than the \(L^2\) norm.
While we draw heavily on the ideas from [24] for the construction of the measure \(\mathbb {P}\) in Theorem 1, it should be noted that we are interested in phase transitions for general encoding/decoding schemes, while [23, 24] exclusively focus on approximation using the ridge function classes \(M_n\).
1.3.3 Baire Category
Extending the scale of \(C^k\) spaces (\(k \in \mathbb {N}_0\)) to the scale of Hölder-spaces \(C^\beta \), \(\beta \ge 0\), it is well-known that \(C^\beta \) is of first category (or meager) in \(C^\eta \) if \(\beta > \eta \). Similarly, under mild regularity conditions on the signal class \(\mathcal {S}\subset \mathbf {X}\), one can show for every codec  that the set
that the set  of signals \(\mathbf {x}\in \mathcal {S}\) that are encodable by \(\mathcal {C}\) at a “better than optimal” rate
of signals \(\mathbf {x}\in \mathcal {S}\) that are encodable by \(\mathcal {C}\) at a “better than optimal” rate  is meager in \(\mathcal {S}\); for instance, this holds if \(\mathcal {S}\) is compact and convex; see Proposition 3.
is meager in \(\mathcal {S}\); for instance, this holds if \(\mathcal {S}\) is compact and convex; see Proposition 3.
Thus, if one could construct a Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}\) satisfying \(\mathbb {P}^*(M) = 0\) for every set \(M \subset \mathcal {S}\) that is meager in \(\mathcal {S}\), then \(\mathbb {P}\) would automatically satisfy the phase transition (1.4). In most cases, however, it turns out that no such measure exists.
Indeed, assuming that such a measure exists and that \(\mathcal {S}\) has no isolated points, every singleton \(\{ \mathbf {x}\} \subset \mathcal {S}\) is meager in \(\mathcal {S}\), so that \(\mathbb {P}(\{ \mathbf {x}\}) = 0\) for every \(\mathbf {x}\in \mathcal {S}\). Therefore, if \(\mathcal {S}\), equipped with the topology induced by \(\Vert \cdot \Vert _{\mathbf {X}}\), has a base whose cardinal has measure zero (see below for details), then [28, Theorem 16.5] shows that one can write \(\mathcal {S}= N \cup M\), where \(M \subset \mathcal {S}\) is meager and \(N \subset \mathcal {S}\) satisfies \(\mathbb {P}(N) = 0\), leading to \(1 = \mathbb {P}(\mathcal {S}) \le \mathbb {P}^*(N) + \mathbb {P}^*(M) = 0\), a contradiction. Regarding the assumption on the existence of a base whose cardinal has measure zero, note that if \(\mathcal {S}\) is relatively compact (which always holds if  ), then \(\mathcal {S}\) is separable and hence has a countable base, whose cardinal thus has measure zero; see [28, Page 63]. In summary, if \(\mathcal {S}\subset \mathbf {X}\) is relatively compact and has no isolated points, then there does not exist a Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}\) satisfying \(\mathbb {P}^*(M) = 0\) for every set \(M \subset \mathcal {S}\) of first category.
), then \(\mathcal {S}\) is separable and hence has a countable base, whose cardinal thus has measure zero; see [28, Page 63]. In summary, if \(\mathcal {S}\subset \mathbf {X}\) is relatively compact and has no isolated points, then there does not exist a Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}\) satisfying \(\mathbb {P}^*(M) = 0\) for every set \(M \subset \mathcal {S}\) of first category.
One could further ask how “special” measures satisfying the phase transition (1.4) are; more precisely: Is the set of probability measures \(\mathbb {P}\) satisfying (1.4) generic in the set of (atom-free) probability measures? This is not the case; in fact, Proposition 4 shows under very mild assumptions that if one equips the set of atom-free probability measures on \(\mathcal {S}\) with the total variation metric, then the set of measures satisfying (1.4) is meager. In other words, the set of measures not satisfying (1.4) is generic as a subset of all atom-free Borel probability measures on \(\mathcal {S}\).
1.3.4 Small ball probabilities and Gaussian measures
An important notion that we introduce and study in this article are measures of logarithmic growth order \(s_0\), which are measures satisfying a certain small ball condition; see Eq. (1.9) below. Such small ball conditions have been extensively studied in the theory of Gaussian measures; see for instance [21, 22]. An important result in that area of research shows that the small ball probability of a Gaussian measure \(\mu \) is closely related to the behavior of the entropy numbers of the unit ball \(K_\mu \) of a certain reproducing kernel Hilbert space \(H_{\mu }\) associated with \(\mu \).
In seeming similarity, we are concerned with constructing a probability measure \(\mathbb {P}\) supported on a given set \(\mathcal {S}\) such that \(\mathbb {P}\) satisfies a certain small ball property, depending on the optimal exponent  of \(\mathcal {S}\), which is intimately related to the behavior of the entropy numbers of \(\mathcal {S}\). As far as we can tell, however, the similarity is only superficial, meaning that the main similarity is simply that both results are concerned with measures satisfying small ball properties and the relation to entropy numbers.
of \(\mathcal {S}\), which is intimately related to the behavior of the entropy numbers of \(\mathcal {S}\). As far as we can tell, however, the similarity is only superficial, meaning that the main similarity is simply that both results are concerned with measures satisfying small ball properties and the relation to entropy numbers.
To see that the questions considered in [21, 22] are different from the ones studied here, note that the Gaussian measures considered in [21, 22] are not supported on \(K_\mu \) and furthermore that the entropy numbers of \(K_\mu \) always satisfy \(H(K_\mu , \varepsilon ) \in o(\varepsilon ^{-2})\) as \(\varepsilon \rightarrow 0\), a property that is in general not shared by the signal classes \(\mathcal {S}= {{\,\mathrm{Ball}\,}}\big ( 0, 1; B_{p,q}^{\tau } (\varOmega ; \mathbb {R}) \big )\) and \(\mathcal {S}:= {{\,\mathrm{Ball}\,}}\bigl (0, 1; W^{k,p}(\varOmega )\bigr )\) that we consider.
Finally, we mention that a (non-trivial) modification of our proof shows that the measure \(\mathbb {P}\) constructed in Theorem 1 can be chosen to be (the restriction of) a suitable centered Gaussian measure.
1.3.5 Optimality Results for Neural Network Approximation
We emphasize that our lower bounds for neural network approximation consider networks with quantized weights, as in [4, 29]. The main reason is that without such an assumption, even networks with two hidden layers and a fixed number of neurons can approximate any function arbitrarily well if the activation function is chosen suitably; see [25, Theorem 4] and [40]. Moreover, even if one considers the popular ReLU activation function, it was recently observed that the optimal approximation rates for networks with quantized weights can in fact be doubled by using arbitrarily deep ReLU networks with highly complex (non-quantized) weights [41].
1.4 Structure of the Paper and Proof Ideas
In Sect. 2, we introduce and study a class of probability measures with a certain growth behavior. More precisely, we say that \(\mathbb {P}\) is of logarithmic growth order \(s_0\) on \(\mathcal {S}\subset \mathbf {X}\) if for each \(s > s_0\) there exist \(\varepsilon _0 = \varepsilon _0 (s) > 0\) and \(c = c(s) > 0\) satisfying
Here, as in the rest of the paper, \({{\,\mathrm{Ball}\,}}(\mathbf {x},\varepsilon ;\mathbf {X})\) is the closed ball around \(\mathbf {x}\) of radius \(\varepsilon \) with respect to \(\Vert \cdot \Vert _{\mathbf {X}}\). A probability measure has critical growth if its logarithmic growth order equals the optimal compression rate  . We show in particular that every critical probability measure exhibits a compressibility phase transition as in Definition 1, and we show how critical probability measures can be transported from one set to another.
. We show in particular that every critical probability measure exhibits a compressibility phase transition as in Definition 1, and we show how critical probability measures can be transported from one set to another.
Intuitively, the natural way to construct a probability measure \(\mathbb {P}\) satisfying (1.9) is to make the measure “as uniform as possible,” so that each ball \({{\,\mathrm{Ball}\,}}(\mathbf {x},\varepsilon ;\mathbf {X})\) contains roughly the same (small) volume. At first sight, it is thus natural to choose \(\mathbb {P}\) to be translation invariant. It is well-known, however, (see, e.g., [17, Page 218]) that there does not exist any non-trivial locally finite, translation invariant measure on an infinite-dimensional, separable Banach space.
Therefore, we construct a measure \(\mathbb {P}\) satisfying (1.9) in the setting of certain sequence spaces, where we can exploit the product structure of the signal class \(\mathcal {S}\) to make the measure as uniform as possible—this technique was pioneered in [24]. More precisely, in Sect. 3, we study the sequence spaces  , which are essentially the coefficient spaces associated with Besov spaces. By modifying the construction given in [24], we construct probability measures of critical growth on the unit balls
, which are essentially the coefficient spaces associated with Besov spaces. By modifying the construction given in [24], we construct probability measures of critical growth on the unit balls  of the spaces
of the spaces  , for the range of parameters for which the embedding
, for the range of parameters for which the embedding  is compact. For the case \(q = \infty \), we directly use the product structure of the spaces to construct the measure; the construction for the case \(q < \infty \) uses the measure from the case \(q = \infty \), combined with a technical trick (namely, introducing an additional weight).
is compact. For the case \(q = \infty \), we directly use the product structure of the spaces to construct the measure; the construction for the case \(q < \infty \) uses the measure from the case \(q = \infty \), combined with a technical trick (namely, introducing an additional weight).
The construction of critical measures on the unit balls of Besov and Sobolev spaces is then accomplished in Sect. 4, by using wavelet systems to transfer the critical measure from the sequence spaces to the function spaces. This makes heavy use of the transfer results established in Sect. 2.
A host of more technical proofs are deferred to the appendices.
1.5 Notation
We write \(\mathbb {N}:= \{1,2,3,\dots \}\) for the set of natural numbers, and \(\mathbb {N}_0 := \{0\} \cup \mathbb {N}\) for the natural numbers including zero. The number of elements of a set M is denoted by \(|M| \in \mathbb {N}_0 \cup \{ \infty \}\). For \(n \in \mathbb {N}_0\), we define \([n] := \{ k \in \mathbb {N}:k \le n \}\); in particular, \([0] = \emptyset \).
For \(x \in \mathbb {R}\), we write \(x_+ := \max \{ 0, x \}\) and \(x_{-} := (-x)_+ = \max \{ 0, -x \}\).
We assume all vector spaces to be over \(\mathbb {R}\), unless explicitly stated otherwise.
For a given (quasi)-normed vector space \((\mathbf {X}, \Vert \cdot \Vert )\), we denote the closed ball of radius \(r \ge 0\) around \(\mathbf {x}\in \mathbf {X}\) by
If we want to emphasize the quasi-norm (for example, if multiple quasi-norms are considered on the same space \(\mathbf {X}\)), we write \({{\,\mathrm{Ball}\,}}( \mathbf {x}, r; \Vert \cdot \Vert )\) instead.
We say that a subset \(\mathcal {S}\) of a topological space \(\mathbf {X}\) is relatively compact, if the closure \({\overline{\mathcal {S}}}\) of \(\mathcal {S}\) in \(\mathbf {X}\) is compact. If \(\mathbf {X}\) is a complete metric space with metric d, then this holds if and only if \(\mathcal {S}\) is totally bounded, meaning that for every \(\varepsilon > 0\) there exist finitely many \(\mathbf {x}_1,\dots ,\mathbf {x}_N \in \mathbf {X}\) satisfying \(\mathcal {S}\subset \bigcup _{i=1}^N \{ \mathbf {x}\in \mathbf {X}:d(\mathbf {x},\mathbf {x}_i) \le \varepsilon \}\); see [14, Theorem 0.25].
For an index set \(\mathcal {I}\) and an integrability exponent \(p \in (0,\infty ]\), the sequence space \(\ell ^p (\mathcal {I}) \subset \mathbb {R}^{\mathcal {I}}\) is
where \(\Vert \mathbf {x}\Vert _{\ell ^p} := \bigl (\sum _{i \in \mathcal {I}} |x_i|^p\bigr )^{1/p}\) if \(p < \infty \), while \(\Vert \mathbf {x}\Vert _{\ell ^\infty } := \sup _{i \in \mathcal {I}} |x_i|\).
A Comment on Measurability: Given a (not necessarily measurable) subset \(M \subset \mathbf {X}\) of a Banach space \(\mathbf {X}\), we will always equip M with the trace \(\sigma \)-algebra
of the Borel \(\sigma \)-algebra \(\mathscr {B}_{\mathbf {X}}\). A Borel measure on M is then a measure defined on \(M \Cap \mathscr {B}_{\mathbf {X}}\).
Note that if \((\varOmega , \mathscr {A})\) is any measurable space, then \({\varPhi : \varOmega \rightarrow M}\) is measurable if and only if it is measurable considered as a map \({\varPhi : \varOmega \rightarrow (\mathbf {X}, \mathscr {B}_{\mathbf {X}})}\).
2 General Results on Phase Transitions in Banach Spaces
In this section, we establish an abstract version of the phase transition considered in (1.4) for signal classes in general Banach spaces and a class of measures that satisfy a uniform growth property that we term “critical” (see Definition 3). We will show in Sect. 2.1 that such critical measures automatically induce a phase transition behavior. We furthermore show in Sect. 2.2 that criticality is preserved under pushforward by “nice” mappings. The existence of critical measures is by no means trivial; quite the opposite, their construction for a class of sequence spaces in Sect. 3—and for Besov and Sobolev spaces on domains in Sect. 4—constitutes an essential part of the present article.
2.1 Measures of Logarithmic Growth
Definition 3
Let \(\mathcal {S}\ne \emptyset \) be a subset of a Banach space \(\mathbf {X}\), and let \(s_0 \in [0,\infty )\).
A Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}\) has (logarithmic) growth order \(s_0\) (with respect to \(\mathbf {X})\) if for every \(s > s_0\), there are constants \(\varepsilon _0, c> 0\) (depending on \(s,s_0,\mathbb {P},\mathcal {S},\mathbf {X}\)) such that
We say that \(\mathbb {P}\) is critical for \(\mathcal {S}\) (with respect to \(\mathbf {X}\)) if \(\mathbb {P}\) has logarithmic growth order  , with the optimal compression rate
, with the optimal compression rate  as defined in Eq. (1.1).
as defined in Eq. (1.1).
Remark
-
(1)
If \(\mathbb {P}\) has growth order \(s_0\), then \(\mathbb {P}\) also has growth order \(\sigma \), for arbitrary \(\sigma > s_0\).
-
(2)
Instead of Property (2.1), one could equivalently only require that the measure of balls centered at points of \(\mathcal {S}\) decays rapidly. More precisely, (2.1) is valid for certain \(\varepsilon _0,c > 0\) (depending on \(s,s_0,\mathbb {P},\mathcal {S},\mathbf {X}\)) if and only if there exist \(\varepsilon _1,\omega > 0\) (depending on \(s,s_0,\mathbb {P},\mathcal {S},\mathbf {X}\)) satisfying
$$\begin{aligned} \mathbb {P}\bigl (\mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x}, \varepsilon ; \mathbf {X})\bigr ) \le 2^{- \omega \cdot \varepsilon ^{-1/s}} \qquad \forall \, \mathbf {x}\in \mathcal {S}\text { and } \varepsilon \in (0, \varepsilon _1) . \end{aligned}$$(2.2)Indeed, if (2.1) holds, then so does (2.2) (with \(\omega = c\) and \(\varepsilon _1 = \varepsilon _0\)). Conversely, suppose (2.2) holds for certain \(\varepsilon _1, \omega > 0\). Set \(c := \omega / 2^{1/s} > 0\) and \(\varepsilon _0 := \varepsilon _1 / 2\) and let \(\varepsilon \in (0,\varepsilon _0)\) and \(\mathbf {x}\in \mathbf {X}\) be arbitrary. First, if \(\mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x},\varepsilon ;\mathbf {X}) = \emptyset \), then trivially \(\mathbb {P}\bigl (\mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x},\varepsilon ;\mathbf {X})\bigr ) = 0 \le 2^{-c \cdot \varepsilon ^{-1/s}}\). Otherwise, there exists \(\mathbf {y}\in \mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x},\varepsilon ;\mathbf {X})\) and then \({{\,\mathrm{Ball}\,}}(\mathbf {x},\varepsilon ;\mathbf {X}) \subset {{\,\mathrm{Ball}\,}}(\mathbf {y}, 2\varepsilon ; \mathbf {X})\) and \(2 \varepsilon < \varepsilon _1\). Hence, (2.2) shows
$$\begin{aligned} \mathbb {P}\big ( \mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x},\varepsilon ;\mathbf {X}) \big ) \le \mathbb {P}\big ( \mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {y},2\varepsilon ;\mathbf {X}) \big ) \le 2^{-\omega \cdot (2\varepsilon )^{-1/s}} = 2^{-c \cdot \varepsilon ^{-1/s}} \end{aligned}$$by our choice of c. \(\blacktriangleleft \)
The motivation for considering the growth order of a measure is that it leads to bounds regarding the measure of elements \(\mathbf {x}\in \mathcal {S}\) that are well-approximated by a given codec; see Eq. (2.3) below. Furthermore, as we will see in Corollary 2, if \(\mathbb {P}\) is a probability measure of growth order \(s_0\), then necessarily  , so critical measures have the minimal possible growth order.
, so critical measures have the minimal possible growth order.
The following theorem summarizes our main structural results, showing that critical measures always exhibit a compressibility phase transition.
Theorem 4
Let the signal class \(\mathcal {S}\) be a subset of the Banach space \(\mathbf {X}\), let \(\mathbb {P}\) be a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(\mathbf {X}\), and set  . Then, the following hold:
. Then, the following hold:
-
(i)
Let \(s > s^*\) and let \(c= c(s) > 0\) and \(\varepsilon _0 = \varepsilon _0(s)\) as in Eq. (2.1). Then, for any
 , we have $$\begin{aligned} \mathrm {Pr}\big ( \Vert \mathbf {x}- D_R(E_R(\mathbf {x})) \Vert _{\mathbf {X}} \le \varepsilon \big ) \le 2^{R - c \cdot \varepsilon ^{-1/s}} \qquad \forall \, \varepsilon \in (0,\varepsilon _0) , \end{aligned}$$(2.3)
, we have $$\begin{aligned} \mathrm {Pr}\big ( \Vert \mathbf {x}- D_R(E_R(\mathbf {x})) \Vert _{\mathbf {X}} \le \varepsilon \big ) \le 2^{R - c \cdot \varepsilon ^{-1/s}} \qquad \forall \, \varepsilon \in (0,\varepsilon _0) , \end{aligned}$$(2.3)where we use the notation from Eq. (1.6).
-
(ii)
For every \(s > s^*\) and every codec
 , the set
, the set  is a \(\mathbb {P}^*\)-null-set:
is a \(\mathbb {P}^*\)-null-set: 
-
(iii)
For every \(0 \le s < {s^*}\), there exists a codec
 with distortion
with distortion 
for a constant \(C = C(s, \mathcal {C}) > 0\). In particular, the set of s-compressible signals
 defined in Eq. (1.2) satisfies
defined in Eq. (1.2) satisfies  and hence
and hence  .
.
Remark
-
(1)
Note that the theorem does not make any statement about the case \(s = s^*\). In this case, the behavior depends on the specific choices of \(\mathcal {S}\) and \(\mathbb {P}\).
-
(2)
As noted above, the question of the existence of a critical probability measure \(\mathbb {P}\) is nontrivial. \(\blacktriangleleft \)
The proof of Theorem 4 is divided into several auxiliary results. Part (i) is contained in the following lemma.
Lemma 1
Let \(\mathcal {S}\ne \emptyset \) be a subset of a Banach space \(\mathbf {X}\), and let \(\mathbb {P}\) be a Borel probability measure on \(\mathcal {S}\) that is of logarithmic growth order \(s_0 \ge 0\) with respect to \(\mathbf {X}\).
Let \(s > s_0\) and let \(c= c(s) > 0\) and \(\varepsilon _0 = \varepsilon _0(s)\) as in Eq. (2.1). Then, for any \(R \in \mathbb {N}\) and  , we have
, we have
Further, for any given \(s > s_0\) and \(K > 0\) there exists a minimal code-length \(R_0 = R_0(s,s_0,K,\mathbb {P},\mathcal {S},\mathbf {X}) \in \mathbb {N}\) such that every  satisfies
satisfies
Remark
The lemma states that the measure of the subset of points \(\mathbf {x}\in \mathcal {S}\) with approximation error \(\mathcal{E}_R(\mathbf {x}) := \Vert \mathbf {x}- D_R(E_R(\mathbf {x}))\Vert _\mathbf {X}\) satisfying \(\mathcal{E}_R(\mathbf {x}) \le K \cdot R^{-s}\) for some \(s > s_0\) decreases exponentially with R. In fact, the proof shows that the approximation error is decreasing asymptotically superexponentially. \(\blacktriangleleft \)
Proof
Let \(s > s_0\) and let \(c, \varepsilon _0\) as in Eq. (2.1). For \(R \in \mathbb {N}\) and \(\varepsilon \in (0, \varepsilon _0)\), define \( A (R, \varepsilon ) := \lbrace \mathbf {x}\in \mathcal {S}:\Vert \mathbf {x}- D_R (E_R(\mathbf {x})) \Vert _{\mathbf {X}} \le \varepsilon \rbrace . \) By definition,
Since \(\mathbb {P}\) is of growth order \(s_0\) and because of \(|\mathrm {range}(D_R)| \le 2^R\), we can apply (2.1) and the definition of the outer measure \(\mathbb {P}^*\) (see Eq. (1.5)) to deduce
This proves the first part of the lemma.
To prove the second part, let \(s > s_0\), and choose \(\sigma = \frac{s + s_0}{2}\), noting that \(\sigma \in (s_0, s)\). Therefore, the first part of the lemma, applied with \(\sigma \) instead of s, yields \(c, \varepsilon _0 > 0\) such that \( \mathbb {P}^*(\{ \mathbf {x}\in \mathcal {S}:\Vert \mathbf {x}- D_R(E_R(\mathbf {x})) \Vert _{\mathbf {X}} \le \varepsilon \}) \le 2^{R - c \cdot \varepsilon ^{-1/\sigma }} \) for all \(R \in \mathbb {N}\) and \(\varepsilon \in (0, \varepsilon _0)\).
Note that \(\varepsilon := K \cdot R^{-s} \le \frac{\varepsilon _0}{2} < \varepsilon _0\) holds as soon as \(R \ge \big \lceil (2 K / \varepsilon _0)^{1/s} \, \big \rceil =: R_1\). Finally, since \(s / \sigma > 1\) we can find a code-length \(R_2 = R_2 (s,s_0,\varepsilon _0,K) \in \mathbb {N}\) such that
Overall, we thus see that (2.4) holds, with \(R_0 := \max \{ R_1, R_2 \}\). \(\square \)
Proposition 1
Let \(\mathcal {S}\ne \emptyset \) be a subset of the Banach space \(\mathbf {X}\). If \(\mathbb {P}\) is a Borel probability measure on \(\mathcal {S}\) that is of growth order \(s_0 \in [0,\infty )\), then, for every \(s > s_0\) and every codec  , we have
, we have

Proof
First, note that

where \( A^{(s)}_{K,R} := \lbrace \mathbf {x}\in \mathcal {S}:\Vert \mathbf {x}- D_R (E_R(\mathbf {x})) \Vert _{\mathbf {X}} \le K \cdot R^{-s} \rbrace . \)
By \(\sigma \)-subadditivity of \(\mathbb {P}^*\), it is thus enough to show \(\mathbb {P}^*\bigl (\bigcap _{R \in \mathbb {N}} A_{K,R}^{(s)}\bigr ) = 0\) for each \(K \in \mathbb {N}\). To see that this holds, note that Lemma 1 shows
This easily implies \(\mathbb {P}^* \bigl ( \bigcap _{R \in \mathbb {N}} A_{K,R}^{(s)}\bigr ) = 0\). \(\square \)
The proof of Theorem 4 merely consists of combining the preceding lemmas.
Proof of Theorem 4
Proof of (i): This is contained in the statement of Lemma 1.
Proof of (ii): This follows from Proposition 1.
Proof of (iii): This follows from the definition of the optimal compression rate: for \(0 \le s < s^*\) there exists a codec  such that
such that
for a constant \(C > 0\) and all \(\mathbf {x}\in \mathcal {S}\). In particular, this implies  , and therefore
, and therefore  . \(\square \)
. \(\square \)
We close this subsection by showing that if \(\mathbb {P}\) is a probability measure with logarithmic growth order \(s_0\), then this growth order is at least as large as the optimal compression rate of the set on which \(\mathbb {P}\) is defined. This justifies the nomenclature of “critical measures” as introduced in Definition 3.
Corollary 2
Let \(\mathcal {S}\ne \emptyset \) be a subset of \(\mathbf {X}\), and \(\mathbb {P}\) be a Borel probability measure on \(\mathcal {S}\) of growth order \(s_0 \ge 0\). Then,  , with
, with  as defined in Eq. (1.1).
as defined in Eq. (1.1).
Proof
Suppose for a contradiction that  , and let
, and let  . By definition of
. By definition of  , there exists a codec
, there exists a codec  such that
such that  . By Proposition 1, we thus obtain the desired contradiction
. By Proposition 1, we thus obtain the desired contradiction  . \(\square \)
. \(\square \)
2.2 Transferring Critical Measures
Our main goal in this paper is to prove a phase transition as in (1.4) for \(\mathcal {S}\) being the unit ball of suitable Besov- or Sobolev spaces. To do so, we will first prove (in Sect. 3) that such a phase-transition occurs for a certain class of sequence spaces and then, transfer this result to the Besov- and Sobolev spaces, essentially by discretizing these function spaces using suitable wavelet systems. In the present subsection, we formulate a general result that allows such a transfer from a phase transition as in (1.4) from one space to another.
The precise (very general, but slightly technical) transference result reads as follows:
Theorem 5
Let \(\mathbf {X}, \mathbf {Y}, \mathbf {Z}\) be Banach spaces, and let \(\mathcal {S}_\mathbf {X}\subset \mathbf {X}\), \(\mathcal {S}_\mathbf {Y}\subset \mathbf {Y}\), and \(\mathcal {S}\subset \mathbf {Z}\). Assume that
-
1.
 ;
; -
2.
there exists a Lipschitz continuous map \(\varPhi : \mathcal {S}_\mathbf {X}\subset \mathbf {X}\rightarrow \mathbf {Z}\) satisfying \(\varPhi (\mathcal {S}_{\mathbf {X}}) \supset \mathcal {S}\);
-
3.
there exists a Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}_\mathbf {Y}\) that is critical for \(\mathcal {S}_{\mathbf {Y}}\) with respect to \(\mathbf {Y}\);
-
4.
there exists a (not necessarily surjective) measurable map \(\varPsi : \mathcal {S}_{\mathbf {Y}} \rightarrow \mathcal {S}\) that is expansive, meaning that there exists \(\kappa > 0\) satisfying
$$\begin{aligned} \Vert \varPsi (\mathbf {x}) - \varPsi (\mathbf {x}') \Vert _{\mathbf {Z}} \ge \kappa \cdot \Vert \mathbf {x}- \mathbf {x}' \Vert _{\mathbf {Y}} \qquad \forall \, \mathbf {x}, \mathbf {x}' \in \mathcal {S}_{\mathbf {Y}}. \end{aligned}$$
Then,  , and the push-forward measure \(\mathbb {P}\circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(\mathbf {Z}\).
, and the push-forward measure \(\mathbb {P}\circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(\mathbf {Z}\).
Geometric intuition behind Theorem 5. Top: An encoder/decoder pair \((E_R,D_R)\) with distortion at most \(\delta / (2L)\) corresponds to a covering of \(\mathcal {S}_{\mathbf {X}}\) by \(2^R\) balls of radius \(\delta / (2L)\), not necessarily centered inside \(\mathcal {S}_{\mathbf {X}}\) (red centers; also see Lemma 10). By doubling the radius, one can “move the centers inside \(\mathcal {S}_{\mathbf {X}}\).” Using the Lipschitz map \(\varPhi \) satisfying \(\varPhi (\mathcal {S}_{\mathbf {X}}) \supset \mathcal {S}\), this yields a covering of \(\mathcal {S}\) by \(2^R\) balls of radius \(\delta \), and hence, an encoder/decoder pair with distortion at most \(\delta \). This entails  . Bottom: Since \(\varPsi \) is expansive, the inverse image under \(\varPsi \) of a ball of radius \(\varepsilon \) is contained in a ball of radius \(2\varepsilon /\kappa \), ensuring that the push-forward measure \(\mathbb {P}\circ \varPsi ^{-1}\) is of logarithmic growth order
. Bottom: Since \(\varPsi \) is expansive, the inverse image under \(\varPsi \) of a ball of radius \(\varepsilon \) is contained in a ball of radius \(2\varepsilon /\kappa \), ensuring that the push-forward measure \(\mathbb {P}\circ \varPsi ^{-1}\) is of logarithmic growth order  on \(\mathcal {S}\), which implies
on \(\mathcal {S}\), which implies  ; see Corollary 2
; see Corollary 2
Remark
-
(1)
As mentioned in Sect. 1.5, regarding the measurability of \(\varPsi \), \(\mathcal {S}_{\mathbf {Y}}\) is equipped with the trace \(\sigma \)-algebra of the Borel \(\sigma \)-algebra on \(\mathbf {Y}\), and analogously for \(\mathcal {S}\).
-
(2)
In most practical applications of this theorem, one is given a Lipschitz continuous map \(\varPhi : \mathbf {X}\rightarrow \mathbf {Z}\) and a (not necessarily surjective) measurable, expansive map \(\varPsi : \mathbf {Y}\rightarrow \mathbf {Z}\) satisfying \(\varPhi (\mathcal {S}_{\mathbf {X}}) \supset \mathcal {S}\) and \(\varPsi (\mathcal {S}_{\mathbf {Y}}) \subset \mathcal {S}\). For greater generality, in the above theorem we only assume that \(\varPhi ,\varPsi \) are defined on \(\mathcal {S}_{\mathbf {X}}\) and \(\mathcal {S}_{\mathbf {Y}}\), respectively. \(\blacktriangleleft \)
Proof
The proof is given in Appendix A. \(\square \)
3 Proof of the Phase Transition in \(\ell ^2(\mathcal {I})\)
In this section, we provide the proof of the phase transition for a class of sequence spaces associated with Sobolev- and Besov spaces; these sequence spaces are defined in Sect. 3.1, where we also formulate the main result (Theorem 6) concerning the compressibility phase transition for these spaces. Section 3.2 establishes elementary embedding results for these spaces and provides a lower bound for their optimal compression rate; the latter essentially follows by adapting results by Leopold [20] to our setting. The construction of the critical probability measure for the sequence spaces is presented in Sect. 3.3, while the proof of Theorem 6 is given in Sect. 3.4.
3.1 Main Result
Definition 4
(d-regular partitions) Let \(\mathcal {I}\) be a countably infinite index set, and \(\mathscr {P}= (\mathcal {I}_m)_{m \in \mathbb {N}}\) be a partition of \(\mathcal {I}\); that is, \(\mathcal {I}= \biguplus _{m=1}^\infty \mathcal {I}_m\), where the union is disjoint. For \(d \in \mathbb {N}\), we call \(\mathscr {P}\) a d-regular partition, if there are \(0< a< A < \infty \) satisfying
Convention: We will always assume that \(\mathcal {I}\), \(\mathscr {P}\) and d have this meaning.
Associated with a d-regular partition, we now define the following family of weighted sequence spaces.
Definition 5
(Sequence spaces) Let \(p,q \in (0,\infty ]\) and \(\alpha , \theta \in \mathbb {R}\). For any sequence \({\mathbf {x}= (x_i)_{i \in \mathcal {I}} \in \mathbb {R}^{\mathcal {I}}}\), we define

The mixed-norm sequence space  is
is

For brevity, we also define  and
and

In the remainder of this section, we will prove the existence of a critical measure on each of the sets  , provided that \(\alpha > d \cdot (\frac{1}{2} - \frac{1}{p})_+\). In the proof, the (otherwise not really important) spaces
, provided that \(\alpha > d \cdot (\frac{1}{2} - \frac{1}{p})_+\). In the proof, the (otherwise not really important) spaces  will play an essential role. The main result of this section is thus the following theorem, the proof of which is given in Sect. 3.4 below.
will play an essential role. The main result of this section is thus the following theorem, the proof of which is given in Sect. 3.4 below.
Theorem 6
Let \(p,q \in (0,\infty ]\) and \(\alpha \in \mathbb {R}\), and assume that \(\alpha > d \cdot \big ( \frac{1}{2} - \frac{1}{p} \big )_+\). Then,  is compact and hence, Borel measurable, its optimal compression rate is given by
is compact and hence, Borel measurable, its optimal compression rate is given by  , and there exists a Borel probability measure \(\mathbb {P}_{\mathscr {P},\alpha }^{p,q}\) on
, and there exists a Borel probability measure \(\mathbb {P}_{\mathscr {P},\alpha }^{p,q}\) on  that is critical for
that is critical for  with respect to \(\ell ^2(\mathcal {I})\). In particular, the phase transition described in Theorem 4 holds.
with respect to \(\ell ^2(\mathcal {I})\). In particular, the phase transition described in Theorem 4 holds.
Remark
Explicitly, the proof shows for any \(s > s^*= \frac{\alpha }{d} - (\frac{1}{2} - \frac{1}{p})\) that

where \(\varepsilon _0 = \varepsilon _0^{(0)} \cdot (s-s^*)^{2/q} \cdot e^{-s \cdot (d+1)}\) and \(c = c^{(0)} \cdot 2^{-d} \cdot (s-s^*)^{2/(s q)}\) for constants \(\varepsilon _0^{(0)} = \varepsilon _0^{(0)} (p,q,a,A) > 0\) and \(c^{(0)} = c^{(0)}(s^*,p,q,a,A) > 0\) with a, A as in (3.1). This provides control on how fast \(c,\varepsilon _0\) deteriorate as \(s \downarrow s^*\) or \(d \rightarrow \infty \). These bounds are probably not optimal. \(\blacktriangleleft \)
3.2 Embedding Results and a Lower Bound for the Compression Rate
Having introduced the signal classes  , we now collect two technical ingredients needed to construct the measures
, we now collect two technical ingredients needed to construct the measures  on these sets: A lower bound for the optimal compression rate of
on these sets: A lower bound for the optimal compression rate of  (Proposition 2) and certain elementary embeddings between the spaces
(Proposition 2) and certain elementary embeddings between the spaces  for different choices of the parameters (Lemma 2).
for different choices of the parameters (Lemma 2).
Lemma 2
Let \(p,q,r \in (0,\infty ]\) and \(\alpha ,\theta ,\vartheta \in \mathbb {R}\). If \(q > r\) and \(\vartheta > \frac{1}{r} - \frac{1}{q}\), then  . More precisely, there exists a constant \(\kappa = \kappa (r,q,\vartheta ) \ge 1\) such that
. More precisely, there exists a constant \(\kappa = \kappa (r,q,\vartheta ) \ge 1\) such that  for all \(\mathbf {x}\in \mathbb {R}^{\mathcal {I}}\).
for all \(\mathbf {x}\in \mathbb {R}^{\mathcal {I}}\).
Proof
The claim follows by an elementary application of Hölder’s inequality; the details can be found in Appendix H. \(\square \)
The following result shows that the supremal compression rate of the class  identified in Theorem 6 is realized by a suitable codec—thus, the supremum in Eq. (1.1) is attained in this setting.
identified in Theorem 6 is realized by a suitable codec—thus, the supremum in Eq. (1.1) is attained in this setting.
Proposition 2
Let \(p,q \in (0,\infty ]\) and \(\alpha \in (0,\infty )\), and assume \({\alpha > d \cdot (\tfrac{1}{2} - \tfrac{1}{p})_+}\). Then, we have  , and the set
, and the set  is compact with
is compact with  .
.
Furthermore, there exists a codec  satisfying
satisfying

Proof
In essence, this an entropy estimate for sequence spaces; see [12]. Since the precise proof mainly consists in translating the results in [20] to our setting, it is deferred to Appendix B. \(\square \)
3.3 Construction of the Measure
We now come to the technical heart of this section—the construction of the measures  . We will provide different constructions for \(q = \infty \) and for \(q < \infty \): Since for \(q = \infty \) the class
. We will provide different constructions for \(q = \infty \) and for \(q < \infty \): Since for \(q = \infty \) the class  has a natural product structure (Lemma 3), we define the measure as a product measure (Definition 6). We then use the embedding result of Lemma 2 to transfer the measure on
has a natural product structure (Lemma 3), we define the measure as a product measure (Definition 6). We then use the embedding result of Lemma 2 to transfer the measure on  to the general signal classes
to the general signal classes  ; see Definition 7.
; see Definition 7.
We start with the elementary observation that the balls  can be written as infinite products of finite-dimensional balls.
can be written as infinite products of finite-dimensional balls.
Lemma 3
The balls of the mixed-norm sequence spaces  satisfy (up to canonical identifications) the factorization
satisfy (up to canonical identifications) the factorization

Proof
We identify \(\mathbf {x}\in \mathbb {R}^\mathcal {I}\) with  , as defined in Eq. (3.2). Set \(w_m := m^\theta \cdot 2^{\alpha m}\) for \(m \in \mathbb {N}\). The statement of the lemma then follows by recalling that
, as defined in Eq. (3.2). Set \(w_m := m^\theta \cdot 2^{\alpha m}\) for \(m \in \mathbb {N}\). The statement of the lemma then follows by recalling that

\(\square \)
With Lemma 3 in hand, we can readily define  as a product measure.
as a product measure.
Definition 6
(Measures for \(q=\infty \)) Let \(\mathscr {P}= (\mathcal {I}_m)_{m \in \mathbb {N}}\) be a d-regular partition of \(\mathcal {I}\). Let \(\mathscr {B}_{m}\) be the Borel \(\sigma \)-algebra on \(\mathbb {R}^{\mathcal {I}_m}\) and denote the Lebesgue measure on \((\mathbb {R}^{\mathcal {I}_m}, \mathscr {B}_{m})\) by \(\mu _{m}\).
For \(p \in (0,\infty ]\) and \(w_m > 0\) define the probability measure \(\mathbb {P}_{m}^{p,w_m}\) on \((\mathbb {R}^{\mathcal {I}_m}, \mathscr {B}_{m})\) by

Given \(p \in (0,\infty ]\) and \(\alpha ,\theta \in \mathbb {R}\) define \(w_m := m^\theta \cdot 2^{\alpha m}\), let \(\mathscr {B}_{\mathcal {I}}\) denote the product \(\sigma \)-algebra on \(\mathbb {R}^{\mathcal {I}}\) and define  as the product measure of the family \(\bigl (\mathbb {P}_{m}^{p, w_m}\bigr )_{m \in \mathbb {N}}\) (see, e.g., [11, Section 8.2]):
as the product measure of the family \(\bigl (\mathbb {P}_{m}^{p, w_m}\bigr )_{m \in \mathbb {N}}\) (see, e.g., [11, Section 8.2]):

With the help of the preceding results, we can now describe the construction of the measure  on
on  , also for \(q < \infty \). A crucial tool will be the embedding result from Lemma 2.
, also for \(q < \infty \). A crucial tool will be the embedding result from Lemma 2.
Definition 7
(Measures for \(q<\infty \)) Let the notation be as in Definition 6.
For given \(q \in (0,\infty ]\), choose (according to Lemma 2) a constant \(\kappa = \kappa (q) \ge 1\) (with \(\kappa = 1\) if \(q = \infty \)) such that  for all \(\mathbf {x}\in \mathbb {R}^{\mathcal {I}}\), and define
for all \(\mathbf {x}\in \mathbb {R}^{\mathcal {I}}\), and define

In the following, we verify that the measures defined according to Definitions 6 and 7 are indeed (Borel) probability measures on the signal classes  and
and  , respectively. To do so, we first show that the signal classes are measurable with respect to the product \(\sigma \)-algebra \(\mathscr {B}_{\mathcal {I}}\), and we compare this \(\sigma \)-algebra to the Borel \(\sigma \)-algebra on \(\ell ^2(\mathcal {I})\).
, respectively. To do so, we first show that the signal classes are measurable with respect to the product \(\sigma \)-algebra \(\mathscr {B}_{\mathcal {I}}\), and we compare this \(\sigma \)-algebra to the Borel \(\sigma \)-algebra on \(\ell ^2(\mathcal {I})\).
Lemma 4
Let \(\mathscr {B}_{\mathcal {I}}\) denote the product \(\sigma \)-algebra on \(\mathbb {R}^{\mathcal {I}}\) and let \(p,q \in (0,\infty ]\) and \({\alpha , \theta \in \mathbb {R}}\). Then, the (quasi)-norm  is measurable with respect to \(\mathscr {B}_{\mathcal {I}}\). In particular,
is measurable with respect to \(\mathscr {B}_{\mathcal {I}}\). In particular,  .
.
Further, the Borel \(\sigma \)-algebra \(\mathscr {B}_{\ell ^2}\) on \(\ell ^2(\mathcal {I})\) coincides with the trace \(\sigma \)-algebra \({\ell ^2(\mathcal {I}) \Cap \mathscr {B}_{\mathcal {I}}}\).
Proof
The (mainly technical) proof is deferred to Appendix H. \(\square \)
Lemma 5
-
(a)
The measure
 is a probability measure on the measurable space
is a probability measure on the measurable space  .
. -
(b)
If \(\alpha > d \cdot (\frac{1}{2} - \frac{1}{p})_+\), then
 , and the measure
, and the measure  is a probability measure on
is a probability measure on  , where \(\mathscr {B}_{\ell ^2}\) denotes the Borel \(\sigma \)-algebra on \(\ell ^2(\mathcal {I})\).
, where \(\mathscr {B}_{\ell ^2}\) denotes the Borel \(\sigma \)-algebra on \(\ell ^2(\mathcal {I})\).
Proof
For the first part, Lemma 4 implies that  , so that
, so that  is a measure on
is a measure on  . Furthermore, Lemma 3 and Definition 6 show
. Furthermore, Lemma 3 and Definition 6 show  .
.
For the second part, recall from Proposition 2 that  , so that Lemma 4 implies
, so that Lemma 4 implies  , which easily implies that
, which easily implies that  is a measure on
is a measure on  . Finally, observe that
. Finally, observe that  by choice of \(\kappa \) in Definition 7, and hence
by choice of \(\kappa \) in Definition 7, and hence

\(\square \)
3.4 Proof of Theorem 6
In this subsection, we prove that the measures  constructed in Definition 7 are critical, provided that \(\alpha > d \cdot (\frac{1}{2} - \frac{1}{p})_+\). An essential ingredient for the proof is the following estimate for the volumes of balls in \(\ell ^p ([m])\).
constructed in Definition 7 are critical, provided that \(\alpha > d \cdot (\frac{1}{2} - \frac{1}{p})_+\). An essential ingredient for the proof is the following estimate for the volumes of balls in \(\ell ^p ([m])\).
Lemma 6
Let \(m \in \mathbb {N}\) and \(p \in (0,\infty ]\). The m-dimensional Lebesgue measure of \({{\,\mathrm{Ball}\,}}(0,1;\ell ^p ([m]))\) is
For every \(p \in (0,\infty ]\), there exist constants \(c_p \in (0,1]\) and \(C_p \in [1,\infty )\), such that
Proof
A proof of (3.6) can be found, e.g., in [18, Theorem 5].
For proving (3.7), we use that in [18, Lemma 4] it is shown that for each \(p \in (0,\infty )\) there are constants \(\eta _p, \omega _p > 0\) satisfying
It is clear that this remains true also for \(p = \infty \); in fact, since \(\varGamma (1) = 1\), one can simply choose \(\eta _\infty = \omega _\infty = 1\) in this case.
By (3.6), we see that
and the estimate (3.8) implies
Hence, we can choose  and
and  . \(\square \)
. \(\square \)
We are finally equipped to prove Theorem 6.
Proof of Theorem 6
Step 1: We show for \(s^*:= \frac{\alpha }{d} - (\frac{1}{2} - \frac{1}{p})\) and arbitrary \(\theta \in [0,\infty )\) that the measure  has growth order \(s^*\) with respect to \(\ell ^2(\mathcal {I})\).
has growth order \(s^*\) with respect to \(\ell ^2(\mathcal {I})\).
To this end, let \(s > s^*\) be arbitrary, and let \(\varepsilon \in (0, \varepsilon _0)\) (for a suitable \(\varepsilon _0 > 0\) to be chosen below), and \(\mathbf {x}\in \ell ^2(\mathcal {I})\). We estimate the measure  by estimating the measure of certain finite-dimensional projections of the ball, exploiting the product structure of the measure: Recall the identification \(\mathbf {x}= (\mathbf {x}_m)_{m \in \mathbb {N}}\), where \(\mathbf {x}_m = \mathbf {x}|_{\mathcal {I}_m}\). Set \(w_m := m^\theta \cdot 2^{\alpha m}\) for \(m \in \mathbb {N}\), as in Definition 6. For arbitrary \(m \in \mathbb {N}\), we have
by estimating the measure of certain finite-dimensional projections of the ball, exploiting the product structure of the measure: Recall the identification \(\mathbf {x}= (\mathbf {x}_m)_{m \in \mathbb {N}}\), where \(\mathbf {x}_m = \mathbf {x}|_{\mathcal {I}_m}\). Set \(w_m := m^\theta \cdot 2^{\alpha m}\) for \(m \in \mathbb {N}\), as in Definition 6. For arbitrary \(m \in \mathbb {N}\), we have

Using the product structure of  (cf. Eq. (3.5)) and the constant \(C_p \ge 1\) from Lemma 6, we thus see for each \(m \in \mathbb {N}\) that
(cf. Eq. (3.5)) and the constant \(C_p \ge 1\) from Lemma 6, we thus see for each \(m \in \mathbb {N}\) that

From (3.1), we see that \(n_m = 2^{d m} \, \eta _m\) for a certain \(\eta _m \in [a,A]\) and hence  . Furthermore, a straightforward curve discussion of the function
. Furthermore, a straightforward curve discussion of the function  for \(\delta = (s - s^*) \cdot \ln 2\) shows that \(x^\theta \le \bigl (\frac{\theta }{e \cdot \ln 2 \cdot (s - s^*)}\bigr )^\theta \cdot 2^{x (s-s^*)}\) for all \(x > 0\), with the convention \(0^0 = 1\). Combining these observations, we see for \(K_1^{(1)} := (\theta / (e \ln 2))^\theta \) that
for \(\delta = (s - s^*) \cdot \ln 2\) shows that \(x^\theta \le \bigl (\frac{\theta }{e \cdot \ln 2 \cdot (s - s^*)}\bigr )^\theta \cdot 2^{x (s-s^*)}\) for all \(x > 0\), with the convention \(0^0 = 1\). Combining these observations, we see for \(K_1^{(1)} := (\theta / (e \ln 2))^\theta \) that
where \(K_1 = K_1(\theta ,p,a,A) \ge 1\).
For \(K_2^{(0)} := C_p K_1 \ge 1\) and \(K_2 := K_2^{(0)} / (s - s^*)^{\theta }\), we thus see that \(K_2^{(0)} = K_2^{(0)}(\theta ,p,a,A)\) and

A good candidate for an upper bound for  is associated with a positive integer close to
is associated with a positive integer close to
Choose a positive \(\varepsilon _0 > 0\) so small that \({\widetilde{m}}(\varepsilon ) > 1\) for all \(\varepsilon \in (0, \varepsilon _0)\). An easy calculation shows that one can choose \(\varepsilon _0 = 1/(K_2 \cdot e^{s(d+1)}) = \varepsilon _0^{(0)} \cdot (s-s^*)^\theta \cdot e^{-s(d+1)}\), where \(\varepsilon _0^{(0)} = \varepsilon _0^{(0)}(\theta ,p,a,A) > 0\).
Set \(m_0 := \lfloor \widetilde{m}(\varepsilon ) \rfloor \in \mathbb {N}\). Note that \(2^{d s \cdot \widetilde{m}(\varepsilon )} = e^{- s} / (K_2 \cdot \varepsilon )\), and hence \(K_2 \, \varepsilon \, 2^{d s \cdot m_0} \le e^{- s } < 1\). For the exponent in (3.9), observe that
where \(K_3 = K_3^{(0)} \cdot 2^{-d} \cdot (s-s^*)^{\theta /s}\) and \(K_3^{(0)} = K_3^{(0)}(s^*,\theta ,p,a,A) > 0\) is given by \(K_3^{(0)} = a \big / \bigl (e \cdot (K_2^{(0)})^{1/s^*}\bigr )\). Now, (3.9) can be estimated further, yielding

for \(K_4 := s^*\cdot K_3\), so that \(K_4 = K_4^{(0)} \cdot 2^{-d} \cdot (s-s^*)^{\theta /s}\) for a suitable constant \(K_4^{(0)} = K_4^{(0)}(s^*,\theta ,p,a,A) > 0\). Since \(s > s^*\) was arbitrary, this shows that  is of logarithmic growth order \(s^*\); see Definition 3.
is of logarithmic growth order \(s^*\); see Definition 3.
Step 2: We show that  is of growth order \(s^*\) with respect to \(\ell ^2(\mathcal {I})\) on
is of growth order \(s^*\) with respect to \(\ell ^2(\mathcal {I})\) on  .
.
To see this, let \(s > s^*\) be arbitrary and choose (by virtue of Step 1) \(\varepsilon _0, c > 0\) such that  for all \(\mathbf {x}\in \ell ^2(\mathcal {I})\) and \(\varepsilon \in (0, \varepsilon _0)\). From the explicit formulas given in Step 2, we see that \(\varepsilon _0 = \varepsilon _0^{(0)} \cdot (s-s^*)^{2/q} \cdot e^{-s(d+1)}\) for \(\varepsilon _0^{(0)} = \varepsilon _0^{(0)}(p,q,a,A) > 0\), and furthermore that \(c = c^{(0)} \cdot 2^{-d} \cdot (s-s^*)^{2/(s q)}\) for \(c^{(0)} = c^{(0)}(s^*,p,q,a,A) > 0\). Recall from Definition 7 that
for all \(\mathbf {x}\in \ell ^2(\mathcal {I})\) and \(\varepsilon \in (0, \varepsilon _0)\). From the explicit formulas given in Step 2, we see that \(\varepsilon _0 = \varepsilon _0^{(0)} \cdot (s-s^*)^{2/q} \cdot e^{-s(d+1)}\) for \(\varepsilon _0^{(0)} = \varepsilon _0^{(0)}(p,q,a,A) > 0\), and furthermore that \(c = c^{(0)} \cdot 2^{-d} \cdot (s-s^*)^{2/(s q)}\) for \(c^{(0)} = c^{(0)}(s^*,p,q,a,A) > 0\). Recall from Definition 7 that  for a suitable \(\kappa = \kappa (q) \ge 1\). Define \(\varepsilon _0' := \varepsilon _0 / \kappa \) and \(c' := c \cdot \kappa ^{-1/s^*}\).
for a suitable \(\kappa = \kappa (q) \ge 1\). Define \(\varepsilon _0' := \varepsilon _0 / \kappa \) and \(c' := c \cdot \kappa ^{-1/s^*}\).
Now, if \(\varepsilon \in (0,\varepsilon _0')\), then \(\kappa \varepsilon \in (0,\varepsilon _0)\) and hence

where the last step used that \(\kappa \ge 1\) and \(s > s^*\). Overall, we have shown that  is of growth order \(s^*\) with respect to \(\ell ^2(\mathcal {I})\).
is of growth order \(s^*\) with respect to \(\ell ^2(\mathcal {I})\).
Step 3: (Completing the proof): By Proposition 2,  is compact with
is compact with  By Step 2 and Lemma 5,
By Step 2 and Lemma 5,  is a Borel probability measure on
is a Borel probability measure on  of growth order \(s^*\) with respect to \(\ell ^2(\mathcal {I})\). Thus, Lemma 9 shows that
of growth order \(s^*\) with respect to \(\ell ^2(\mathcal {I})\). Thus, Lemma 9 shows that  and that
and that  is critical for
is critical for  with respect to \(\ell ^2(\mathcal {I})\). \(\square \)
with respect to \(\ell ^2(\mathcal {I})\). \(\square \)
Remark
The proof borrows its main idea (using the product measure structure of  to work on finite dimensional projections) from [24]. \(\blacktriangleleft \)
to work on finite dimensional projections) from [24]. \(\blacktriangleleft \)
4 Examples
4.1 Besov Spaces on Bounded Open Sets \(\varOmega \subset \mathbb {R}^d\)
For Besov spaces on bounded domains, we obtain the following consequence of Theorem 6, by using suitable wavelet bases to transport the measures  to the Besov spaces. For a review of the definition of Besov spaces (on \(\mathbb {R}^d\) and on domains), and the characterization of these spaces by wavelets, we refer to Appendices C.1 and C.2 .
to the Besov spaces. For a review of the definition of Besov spaces (on \(\mathbb {R}^d\) and on domains), and the characterization of these spaces by wavelets, we refer to Appendices C.1 and C.2 .
Theorem 7
Let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be open and bounded, let \(p,q \in (0,\infty ]\), and \(\tau \in \mathbb {R}\) with \(\tau > d \cdot (\frac{1}{p} - \frac{1}{2})_{+}\).
Then,
-
(i)
\(\mathcal {S}:= {{\,\mathrm{Ball}\,}}\big ( 0, 1; B_{p,q}^{\tau } (\varOmega ; \mathbb {R}) \big )\) is a compact subset of \(L^2(\varOmega )\), with optimal compression rate given by
 ;
; -
(ii)
there exists a Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\);
-
(iii)
there exists a codec
 satisfying
satisfying 
Remark
In the discussion following Theorem 4, we observed that the existence of a critical measure in general leaves open what happens for \(s = s^*\). In the case of Besov spaces, the above theorem shows that the compression rate \(s = s^*= \frac{\tau }{d}\) is actually achieved by a suitable codec. \(\blacktriangleleft \)
Proof
Define \(\alpha := \tau + d \cdot (\frac{1}{2} - \frac{1}{p})\), noting that
so that \(\alpha \) satisfies the assumptions of Theorem 6.
Using the wavelet characterization of Besov spaces, it is shown in Appendix C.3Footnote 1 that there are countably infinite index sets \(J^{\mathrm {ext}}, J^{\mathrm {int}}\) with associated d-regular partitions \(\mathscr {P}^{\mathrm {ext}} = \big ( \mathcal {I}_m^{\mathrm {ext}} \big )_{m \in \mathbb {N}}\) and \(\mathscr {P}^{\mathrm {int}} = \big ( \mathcal {I}_m^{\mathrm {int}} \big )_{m \in \mathbb {N}}\) and such that there are linear maps

with the following properties:
-
1.
 and
and  ; this follows from Proposition 2.
; this follows from Proposition 2. -
2.
There is some \(\gamma > 0\) such that \(\Vert Q_\mathrm {int}\, \mathbf {c}\Vert _{L^2(\varOmega )} = \gamma \cdot \Vert \mathbf {c}\Vert _{\ell ^2} < \infty \) and furthermore
 for all
for all  .
. -
3.
There is \(\varrho > 0\) such that \(\Vert Q_{\mathrm {ext}} \, \mathbf {c}\Vert _{L^2(\varOmega )} \le \varrho \cdot \Vert \mathbf {c}\Vert _{\ell ^2} < \infty \) for all
 , and
, and  (4.1)
(4.1)
Furthermore, Theorem 6 shows that

and that there exists a Borel probability measure \(\mathbb {P}_0\) on  that is critical for
that is critical for  with respect to \(\ell ^2(J^{\mathrm {int}})\). Therefore, we can apply Theorem 5 with the choices \({\mathbf {X}= \ell ^2(J^{\mathrm {ext}})}\), \(\mathbf {Y}= \ell ^2(J^{\mathrm {int}})\) and \(\mathbf {Z}= L^2(\varOmega )\) as well as
with respect to \(\ell ^2(J^{\mathrm {int}})\). Therefore, we can apply Theorem 5 with the choices \({\mathbf {X}= \ell ^2(J^{\mathrm {ext}})}\), \(\mathbf {Y}= \ell ^2(J^{\mathrm {int}})\) and \(\mathbf {Z}= L^2(\varOmega )\) as well as

and \( \mathcal {S}= {{\,\mathrm{Ball}\,}}\bigl (0,1; B_{p,q}^\tau (\varOmega ;\mathbb {R})\bigr ) , \) and finally \(\varPhi = Q_{\mathrm {ext}}\), \(\varPsi = Q_{\mathrm {int}}\), and \(\kappa = \gamma \). This theorem then shows  (in particular, \(\mathcal {S}\subset L^2(\varOmega )\) is totally bounded and hence compact, since \(\mathcal {S}\subset L^2(\varOmega )\) is closed by Lemma 14) and that \(\mathbb {P}:= \mathbb {P}_0 \circ Q_{\mathrm {int}}^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\).
(in particular, \(\mathcal {S}\subset L^2(\varOmega )\) is totally bounded and hence compact, since \(\mathcal {S}\subset L^2(\varOmega )\) is closed by Lemma 14) and that \(\mathbb {P}:= \mathbb {P}_0 \circ Q_{\mathrm {int}}^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\).
Finally, Proposition 2 yields a codec  satisfying
satisfying  . Furthermore, \(Q_{\mathrm {ext}}\) is Lipschitz (with respect to \({\Vert \cdot \Vert _{\ell ^2}}\) and \(\Vert \cdot \Vert _{L^2}\)) and satisfies (4.1). Thus, Lemma 8 shows that
. Furthermore, \(Q_{\mathrm {ext}}\) is Lipschitz (with respect to \({\Vert \cdot \Vert _{\ell ^2}}\) and \(\Vert \cdot \Vert _{L^2}\)) and satisfies (4.1). Thus, Lemma 8 shows that  for some codec
for some codec  . \(\square \)
. \(\square \)
4.2 Sobolev Spaces on Lipschitz Domains \(\varOmega \subset \mathbb {R}^d\)
Let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be an open bounded Lipschitz domain (precisely, we require \(\varOmega \) to satisfy the conditions in [33, Chapter VI, Section 3.3]). We consider the usual Sobolev spaces \(W^{k,p}(\varOmega )\) (\(k \in \mathbb {N}\) and \(p \in [1,\infty ]\)) and prove that also for the unit balls of these spaces, the phase transition phenomenon holds. To be completely explicit, we endow the space \(W^{k,p}(\varOmega )\) with the following norm:
Our phase-transition result reads as follows:
Theorem 8
Let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be an open bounded Lipschitz domain. Let \(k \in \mathbb {N}\) and \(p \in [1,\infty ]\), and define \(\mathcal {S}:= {{\,\mathrm{Ball}\,}}\big ( 0, 1; W^{k,p}(\varOmega ) \big )\). If \(k > d \cdot (\frac{1}{p} - \frac{1}{2})_{+}\), then
-
(i)
\(\mathcal {S}\subset L^2(\varOmega )\) is bounded and Borel measurable and satisfies
 ;
; -
(ii)
there is a Borel probability measure \(\mathbb {P}\) on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\);
-
(iii)
there exists a codec
 satisfying
satisfying 
Remark
-
1.
As for the case of Besov spaces, the theorem shows that the critical rate \(s = s^*= \frac{k}{d}\) is actually attained by a suitable codec.
-
2.
The condition \(k > d \cdot (\frac{1}{p} - \frac{1}{2})_{+}\) is equivalent to \(\mathcal {S}\subset L^2(\varOmega )\) being relatively compact. The sufficiency is a consequence of the Rellich–Kondrachov theorem; see [1, Theorem 6.3]. For the necessity, note that if \(k \le d \cdot (\frac{1}{p} - \frac{1}{2})_+\) then necessarily \(p < 2\) (since \(k > 0\)) and thus, \(k \le \frac{d}{p} - \frac{d}{2}\), which implies \(k p \le d - d \, \frac{p}{2} < d\) and \(2 \ge q := \frac{p d}{d - k p}\). However, [1, Example 6.12] shows that the embedding \(W^{k,p}(\varOmega ) \hookrightarrow L^q(\varOmega )\) is not compact. Since \(L^2(\varOmega ) \hookrightarrow L^q(\varOmega )\) (because of \(2 \ge q\)), this shows that \(\mathcal {S}\) is not a relatively compact subset of \(L^2(\varOmega )\), since otherwise \(W^{k,p}(\varOmega ) \hookrightarrow L^2(\varOmega ) \hookrightarrow L^q(\varOmega )\) would be a compact embedding. \(\blacktriangleleft \)
Proof of Theorem 8
We present here the proof for the case \(p \in (1,\infty )\), where we will see that the claim follows from that for the Besov spaces. For the case \(p \in \{1,\infty \}\), the proof is more involved and thus, postponed to Appendix D.
First, the Rellich–Kondrachov compactness theorem (see [1, Theorem 6.3]) shows that \(W^{k,p}(\varOmega )\) embeds compactly into \(L^2(\varOmega )\). In particular, the ball \(\mathcal {S}= {{\,\mathrm{Ball}\,}}(0,1; W^{k,p}(\varOmega )) \subset L^2(\varOmega )\) is bounded; in fact, \(\mathcal {S}\) is also compact (hence Borel measurable) by reflexivityFootnote 2 of \(W^{k,p}(\varOmega )\).
Define \(\widetilde{p} := \min \{p, 2\}\) and \(\widehat{p} := \max \{p, 2\}\), as well as \(\mathcal {S}_s := {{\,\mathrm{Ball}\,}} \big ( 0, 1; B_{p,\widetilde{p}}^k (\varOmega ) \big )\) and \(\mathcal {S}_b := {{\,\mathrm{Ball}\,}}\big ( 0, 1; B_{p,\widehat{p}}^k (\varOmega ) \big )\); here, the subscript “s” stands for “small,” while “b” stands for “big,” since \(\widetilde{p}\) is the small exponent, while \(\widehat{p}\) is the large (or big) exponent. We will prove below that there are constants \(C_1, C_2 > 0\) such that
Assuming for the moment that Equation (4.3) holds, recall from Theorem 7 that  and that there exists a Borel probability measure \(\mathbb {P}_0\) on \(\mathcal {S}_s\) that is critical for \(\mathcal {S}_s\) with respect to \(L^2(\varOmega )\). Define \(\mathbf {X}:= \mathbf {Y}:= \mathbf {Z}:= L^2(\varOmega )\) and \(\mathcal {S}_{\mathbf {X}} := \mathcal {S}_b\), \(\mathcal {S}_{\mathbf {Y}} := \mathcal {S}_s\), as well as
and that there exists a Borel probability measure \(\mathbb {P}_0\) on \(\mathcal {S}_s\) that is critical for \(\mathcal {S}_s\) with respect to \(L^2(\varOmega )\). Define \(\mathbf {X}:= \mathbf {Y}:= \mathbf {Z}:= L^2(\varOmega )\) and \(\mathcal {S}_{\mathbf {X}} := \mathcal {S}_b\), \(\mathcal {S}_{\mathbf {Y}} := \mathcal {S}_s\), as well as
Using (4.3), one easily checks that all assumptions of Theorem 5 are satisfied. An application of that theorem shows that  and that \(\mathbb {P}:= \mathbb {P}_0 \circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\).
and that \(\mathbb {P}:= \mathbb {P}_0 \circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\).
Finally, Part (iii) of Theorem 7 shows that  for a suitable codec
for a suitable codec  . Next, since \(\varPhi \) is Lipschitz continuous (with respect to \(\Vert \cdot \Vert _{L^2}\)) with \(\mathcal {S}\subset \varPhi (\mathcal {S}_b)\), Lemma 8 provides a codec
. Next, since \(\varPhi \) is Lipschitz continuous (with respect to \(\Vert \cdot \Vert _{L^2}\)) with \(\mathcal {S}\subset \varPhi (\mathcal {S}_b)\), Lemma 8 provides a codec  satisfying
satisfying  as well. This establishes Property (iii) of the current theorem.
as well. This establishes Property (iii) of the current theorem.
It remains to prove (4.3). First, a combination of [36, Theorem in Section 2.5.6] and [36, Proposition 2 in Section 2.3.2] shows for the so-called Triebel–Lizorkin spacesFootnote 3\(F^k_{p,2}(\mathbb {R}^d)\) that
Hence, there are \(C_3, C_4 > 0\) satisfying \(\Vert f \Vert _{W^{k,p}(\mathbb {R}^d)} \le C_3 \cdot \Vert f \Vert _{B_{p,\widetilde{p}}^k (\mathbb {R}^d)}\) for all \(f \in B_{p,\widetilde{p}}^k (\mathbb {R}^d)\), and \(\Vert f \Vert _{B_{p,\widehat{p}}^k (\mathbb {R}^d)} \le C_4 \cdot \Vert f \Vert _{W^{k,p}(\mathbb {R}^d)}\) for all \(f \in W^{k,p}(\mathbb {R}^d)\). Furthermore, since \(\varOmega \) is a Lipschitz domain, [33, Chapter VI, Theorem 5] shows that there is a bounded linear “extension operator” \(\mathscr {E}: W^{k,p} (\varOmega ) \rightarrow W^{k,p}(\mathbb {R}^d)\) satisfying \((\mathscr {E}f)|_{\varOmega } = f\) for all \(f \in W^{k,p} (\varOmega )\).
It is now easy to prove the inclusion (4.3), with \(C_1 := C_3\) and \(C_2 := C_4 \cdot \Vert \mathscr {E}\Vert \). First, if \(f \in \mathcal {S}_s\) and \(\varepsilon > 0\), then (by the definition of Besov spaces on domains; see Eqs. (C.1) and (C.2)) there exists \(g \in B^k_{p,\widetilde{p}}(\mathbb {R}^d)\) satisfying \(f = g|_\varOmega \) and \(\Vert g \Vert _{B^k_{p,\widetilde{p}}(\mathbb {R}^d)} \le 1 + \varepsilon \). Hence,
Since this holds for all \(\varepsilon > 0\), we see that \(\Vert C_1^{-1} \, f \Vert _{W^{k,p} (\varOmega )} \le 1\); that is, \(C_1^{-1} f \in \mathcal {S}\).
Conversely, if \(f \in \mathcal {S}\), then \(g := \mathscr {E}f \in W^{k,p}(\mathbb {R}^d) \subset B^k_{p,\widehat{p}} (\mathbb {R}^d)\) and \(f = g|_{\varOmega }\), which implies
and hence \(f \in C_2 \cdot \mathcal {S}_b\). \(\square \)
Notes
Indeed, if \((f_n)_{n \in \mathbb {N}} \subset \mathcal {S}\) is arbitrary, then since \(W^{k,p}(\varOmega )\) is reflexive (see [2, Example 8.11]), the closed unit ball in \(W^{k,p}(\varOmega )\) is weakly sequentially compact (see [2, Theorem 8.10]), so that there is a subsequence \((f_{n_\ell })_{\ell \in \mathbb {N}}\) satisfying \(f_{n_\ell } \,{{} }\, f \in \mathcal {S}\) (weak convergence in \(W^{k,p}(\varOmega )\)). Again by compactness of the embedding \(W^{k,p}(\varOmega ) \hookrightarrow L^2(\varOmega )\), this implies \(f_{n_\ell } \,{\xrightarrow {L^2}{} }\, f \in \mathcal {S}\) (see, e.g., [6, Chapter VI, Proposition 3.3]), showing that \(\mathcal {S}\subset L^2(\varOmega )\) is compact.
The precise definition of these spaces is immaterial for us. We merely remark that the identity \(F_{p,2}^k (\mathbb {R}^d) = W^{k,p}(\mathbb {R}^d)\) is only valid for \(p \in (1,\infty )\).
To prove this, fix a bijection \(\iota _R : [2^R] \rightarrow \{ 0,1 \}^R\) and define \(E_R^{(0)} : [0,1) \rightarrow \{ 0,1 \}^R\) by \(E_R^{(0)} (t) := \iota _R(k)\), where \(k = k(t)\) is the unique \(k \in [2^R]\) with \(t \in \big [ \frac{k-1}{2^R}, \frac{k}{2^R} \big )\). Furthermore, define \(E_R : \mathcal {S}\rightarrow \{ 0,1 \}^R\) by setting \(E_R (\mathbf {x}) := E_R^{(0)}(t)\) if \(\mathbf {x}\in \mathcal {S}\) is of the form \(\mathbf {x}= \mathbf {x}_0 + t (\mathbf {y}_0 - \mathbf {x}_0)\) for some \(t \in [0,1)\), and \(E_R(\mathbf {x}) := E_R^{(0)}(0)\) otherwise. Finally, define \( D_R : \{ 0,1 \}^R \rightarrow \mathcal {S}, \mathbf {c}\mapsto \mathbf {x}_0 + 2^{-R} \cdot \iota _R^{-1}(\mathbf {c}) \cdot (\mathbf {y}_0 - \mathbf {x}_0) . \) It is then easy to see \( \Vert \mathbf {x}- D_R(E_R(\mathbf {x})) \Vert _{\mathbf {X}} \le 2^{-R} \Vert \mathbf {x}_0 - \mathbf {y}_0 \Vert _{\mathbf {X}} \lesssim _s R^{-s} \) for arbitrary \(s > 0\) and all \(\mathbf {x}\in M = [\mathbf {x}_0,\mathbf {y}_0)\).
References
Adams, R., Fournier, J.: Sobolev spaces, Pure and Applied Mathematics (Amsterdam), vol. 140, second edn. Elsevier/Academic Press, Amsterdam (2003)
Alt, H.W.: Linear functional analysis. Universitext. Springer-Verlag London, Ltd., London (2016). https://doi.org/10.1007/978-1-4471-7280-2.
Berger, T.: Rate-distortion theory. Wiley Encyclopedia of Telecommunications (2003)
Bölcskei, H., Grohs, P., Kutyniok, G., Petersen, P.C.: Optimal approximation with sparsely connected deep neural networks. SIAM J. Math. Data Sci. 1, 8–45 (2019)
Carl, B., Stephani, I.: Entropy, compactness and the approximation of operators, Cambridge Tracts in Mathematics, vol. 98. Cambridge University Press, Cambridge (1990). https://doi.org/10.1017/CBO9780511897467.
Conway, J.B.: A course in functional analysis, Graduate Texts in Mathematics, vol. 96, second edn. Springer-Verlag, New York (1990)
Daubechies, I.: Orthonormal bases of compactly supported wavelets. Comm. Pure Appl. Math. 41(7), 909–996 (1988). https://doi.org/10.1002/cpa.3160410705.
Daubechies, I.: Ten lectures on wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 61. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (1992). https://doi.org/10.1137/1.9781611970104.
DeVore, R.A.: Nonlinear approximation. In: Acta numerica, 1998, Acta Numer., vol. 7, pp. 51–150. Cambridge Univ. Press, Cambridge (1998). https://doi.org/10.1017/S0962492900002816.
DeVore, R.A., Lorentz, G.G.: Constructive approximation, Grundlehren der Mathematischen Wissenschaften, vol. 303. Springer-Verlag, Berlin (1993). https://doi.org/10.1007/978-3-662-02888-9.
Dudley, R.M.: Real analysis and probability, Cambridge Studies in Advanced Mathematics, vol. 74. Cambridge University Press, Cambridge (2002). https://doi.org/10.1017/CBO9780511755347.
Edmunds, D.E., Triebel, H.: Function spaces, entropy numbers, differential operators, Cambridge Tracts in Mathematics, vol. 120. Cambridge University Press, Cambridge (1996). https://doi.org/10.1017/CBO9780511662201.
Elbrächter, D., Perekrestenko, D., Grohs, P., Bölcskei, H.: Deep Neural Network Approximation Theory. IEEE Transactions on Information Theory 67(5), 2581–2623 (2021). https://doi.org/10.1109/TIT.2021.3062161
Folland, G.: Real analysis, second edn. Pure and Applied Mathematics (New York). John Wiley & Sons, Inc., New York (1999)
Grohs, P.: Optimally sparse data representations. In: Harmonic and Applied Analysis, pp. 199–248. Springer (2015)
Haroske, D.D., Schneider, C.: Besov spaces with positive smoothness on \({\mathbb{R}}^n\), embeddings and growth envelopes. J. Approx. Theory 161(2), 723–747 (2009). https://doi.org/10.1016/j.jat.2008.12.004.
Hunt, B., Sauer, T., Yorke, J.: Prevalence: a translation-invariant “almost every” on infinite-dimensional spaces. Bull. Amer. Math. Soc. (N.S.) 27(2), 217–238 (1992). https://doi.org/10.1090/S0273-0979-1992-00328-2.
Kossaczká, M., Vybíral, J.: Entropy numbers of finite-dimensional embeddings. ArXiv preprint arXiv:1802.00572 (2018)
Leoni, G.: A first course in Sobolev spaces, Graduate Studies in Mathematics, vol. 181, second edn. American Mathematical Society, Providence, RI (2017)
Leopold, H.: Embeddings and entropy numbers for general weighted sequence spaces: the non-limiting case. Georgian Math. J. 7(4), 731–743 (2000)
Li, W.V., Linde, W.: Approximation, metric entropy and small ball estimates for Gaussian measures. Ann. Probab. 27(3), 1556–1578 (1999). https://doi.org/10.1214/aop/1022677459.
Li, W.V., Shao, Q.M.: Gaussian processes: inequalities, small ball probabilities and applications. In: Stochastic processes: theory and methods, Handbook of Statist., vol. 19, pp. 533–597. North-Holland, Amsterdam (2001). https://doi.org/10.1016/S0169-7161(01)19019-X.
Lin, S.: Limitations of shallow nets approximation. Neural Netw. 94, 96 – 102 (2017). https://doi.org/10.1016/j.neunet.2017.06.016. URL http://www.sciencedirect.com/science/article/pii/S0893608017301521
Maiorov, V., Meir, R., Ratsaby, J.: On the approximation of functional classes equipped with a uniform measure using ridge functions. J. Approx. Theory 99(1), 95–111 (1999). https://doi.org/10.1006/jath.1998.3305.
Maiorov, V., Pinkus, A.: Lower bounds for approximation by MLP neural networks. Neurocomputing 25(1), 81 – 91 (1999). https://doi.org/10.1016/S0925-2312(98)00111-8. URL http://www.sciencedirect.com/science/article/pii/S0925231298001118
Mallat, S.: A wavelet tour of signal processing, third edn. Elsevier/Academic Press, Amsterdam (2009)
Mhaskar, H.N.: Neural networks for optimal approximation of smooth and analytic functions. Neural Computation 8(1), 164–177 (1996). https://doi.org/10.1162/neco.1996.8.1.164
Oxtoby, J.C.: Measure and category, Graduate Texts in Mathematics, vol. 2, second edn. Springer-Verlag, New York-Berlin (1980)
Petersen, P., Voigtlaender, F.: Optimal approximation of piecewise smooth functions using deep ReLU neural networks. Neural Netw. 108, 296–330 (2018)
Rudin, W.: Functional analysis, second edn. International Series in Pure and Applied Mathematics. McGraw-Hill, Inc., New York (1991)
Safran, I., Shamir, O.: Depth-width tradeoffs in approximating natural functions with neural networks. arXiv preprint arXiv:1610.09887 (2016)
Safran, I., Shamir, O.: Depth-width tradeoffs in approximating natural functions with neural networks. In: International Conference on Machine Learning, pp. 2979–2987. PMLR (2017)
Stein, E.: Singular integrals and differentiability properties of functions. Princeton Mathematical Series, No. 30. Princeton University Press, Princeton, N.J. (1970)
Suzuki, T.: Adaptivity of deep ReLU network for learning in Besov and mixed smooth Besov spaces: optimal rate and curse of dimensionality. In: International Conference on Learning Representations (2019). https://openreview.net/forum?id=H1ebTsActm
Triebel, H.: Theory of function spaces. III, Monographs in Mathematics, vol. 100. Birkhäuser Verlag, Basel (2006)
Triebel, H.: Theory of function spaces. Modern Birkhäuser Classics. Birkhäuser/Springer Basel AG, Basel (2010)
Vershynin, R.: High-dimensional probability, Cambridge Series in Statistical and Probabilistic Mathematics, vol. 47. Cambridge University Press, Cambridge (2018). https://doi.org/10.1017/9781108231596.
Voigtlaender, F.: Embeddings of Decomposition Spaces into Sobolev and BV Spaces. arXiv preprints arXiv:1601.02201 (2016)
Wojtaszczyk, P.: A mathematical introduction to wavelets, London Mathematical Society Student Texts, vol. 37. Cambridge University Press, Cambridge (1997). https://doi.org/10.1017/CBO9780511623790.
Yarotsky, D.: Elementary superexpressive activations. arXiv preprint arXiv:2102.10911 (2021)
Yarotsky, D., Zhevnerchuk, A.: The phase diagram of approximation rates for deep neural networks. arXiv preprint arXiv:1906.09477 (2019)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Francis Bach.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
AK acknowledges funding from the FWF projects I 3403 and P 31887–N32.
FV acknowledges support by the German Research Foundation (DFG) in the context of the Emmy Noether junior research group VO 2594/1–1.
Appendices
Transferring Approximation Rates and Measures
In this appendix, we provide the proof of Theorem 5. Along the way, we will show that expansive maps can be used to transfer measures with a certain growth order from one set to another, while Lipschitz maps can be used to transfer estimates for the optimal compression rate from one set to another.
Lemma 7
Let \(\mathbf {X}, \mathbf {Y}\) be Banach spaces and let \(\mathcal {S}\subset \mathbf {X}\) and \(\mathcal {S}' \subset \mathbf {Y}\). Assume that there exists a (not necessarily surjective) function \(\varPhi : \mathcal {S}\rightarrow \mathcal {S}'\) which is measurable (with respect to the trace \(\sigma \)-algebras of the Borel \(\sigma \)-algebras) and expansive, in the sense that there exists \(\kappa > 0\) such that
If \(s_0 \ge 0\) and if \(\mathbb {P}\) is a Borel probability measure on \(\mathcal {S}\) of growth order \(s_0\), then the push-forward measure \(\mathbb {P}\circ \varPhi ^{-1}\) is a Borel probability measure on \(\mathcal {S}'\) of growth order \(s_0\) as well.
Proof
Since \(\varPhi : \mathcal {S}\rightarrow \mathcal {S}'\) is measurable, \(\nu := \mathbb {P}\circ \varPhi ^{-1}\) is a Borel probability measure on \(\mathcal {S}'\).
To prove that \(\nu \) has growth order \(s_0\), let \(s > s_0\) be arbitrary. Since \(\mathbb {P}\) is of growth order \(s_0\), there are \(\varepsilon _0, c> 0\) such that Eq. (2.1) is satisfied. Define \(\varepsilon _0 ' := \frac{\kappa }{2} \cdot \varepsilon _0\) and \(c' := c\cdot (2 \, \kappa ^{-1})^{-1/s} = 2^{-1/s} c\cdot \kappa ^{1/s}\). We claim that \( \nu \big ( \mathcal {S}' \cap {{\,\mathrm{Ball}\,}}(\mathbf {y}, \varepsilon ; \mathbf {Y}) \big ) \le 2^{- c' \cdot \varepsilon ^{-1/s}} \) for all \(\mathbf {y}\in \mathbf {Y}\) and all \(\varepsilon \in (0, \varepsilon _0')\); this will show that \(\nu \) has growth order \(s_0\).
The estimate is trivial if \(\varPhi (\mathcal {S}) \cap {{\,\mathrm{Ball}\,}}(\mathbf {y}, \varepsilon ; \mathbf {Y}) = \emptyset \), since then \( \varPhi ^{-1} \big ( {{\,\mathrm{Ball}\,}}(\mathbf {y}, \varepsilon ; \mathbf {Y}) \big ) = \emptyset , \) and hence \( \nu \big ( \mathcal {S}' \cap {{\,\mathrm{Ball}\,}}(\mathbf {y}, \varepsilon ; \mathbf {Y}) \big ) = \mathbb {P}\big ( \varPhi ^{-1} ( \mathcal {S}' \cap {{\,\mathrm{Ball}\,}}(\mathbf {y}, \varepsilon ; \mathbf {Y}) ) \big ) = \mathbb {P}( \emptyset ) = 0 . \) Therefore, let us assume that \(\emptyset \ne \varPhi (\mathcal {S}) \cap {{\,\mathrm{Ball}\,}}(\mathbf {y}, \varepsilon ; \mathbf {Y}) \ni \mathbf {y}'\); say \(\mathbf {y}' = \varPhi (\mathbf {x}')\) for some \(\mathbf {x}' \in \mathcal {S}\). Now, for arbitrary \( \mathbf {x}\in \varPhi ^{-1} \big ( \mathcal {S}' \cap {{\,\mathrm{Ball}\,}}(\mathbf {y}, \varepsilon ; \mathbf {Y}) \big ) \subset \mathcal {S}, \) we have
We have thus shown \( \varPhi ^{-1} (\mathcal {S}' \cap {{\,\mathrm{Ball}\,}}(\mathbf {y}, \varepsilon ; \mathbf {Y})) \subset \mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x}', \frac{2}{\kappa } \, \varepsilon ; \mathbf {X}) . \) Since \(\frac{2}{\kappa } \varepsilon < \frac{2}{\kappa } \varepsilon _0 ' = \varepsilon _0\), we see by Property (2.1) as claimed that
\(\square \)
As a kind of converse of the previous result, we now show that Lipschitz maps can be used to obtain bounds for the optimal compression rate  of a signal class \(\mathcal {S}\subset \mathbf {X}\).
of a signal class \(\mathcal {S}\subset \mathbf {X}\).
Lemma 8
Let \(\mathbf {X}, \mathbf {Y}\) be Banach spaces, and let \(\mathcal {S}\subset \mathbf {X}\) and \(\mathcal {S}' \subset \mathbf {Y}\). Assume that \(\varPhi : \mathcal {S}\rightarrow \mathbf {Y}\) is Lipschitz continuous, and that \(\varPhi (\mathcal {S}) \supset \mathcal {S}'\). Then,  .
.
In fact, given a codec  satisfying \( {\lesssim R^{-s}}\) for some \(s \ge 0\), one can construct a modified codec
satisfying \( {\lesssim R^{-s}}\) for some \(s \ge 0\), one can construct a modified codec 
 satisfying
satisfying  .
.
Proof
The claim is clear if  . Thus, let us assume
. Thus, let us assume  , and let
, and let  be arbitrary. Then, there is a codec
be arbitrary. Then, there is a codec  and a constant \(C > 0\) such that
and a constant \(C > 0\) such that  for all \(R \in \mathbb {N}\). Let \(L > 0\) denote a Lipschitz constant for \(\varPhi \).
for all \(R \in \mathbb {N}\). Let \(L > 0\) denote a Lipschitz constant for \(\varPhi \).
Now, for \(\varepsilon > 0\) and \(\mathbf {x}\in \mathbf {X}\), choose \(\varPsi _\varepsilon (\mathbf {x}) \in \mathcal {S}\) such that \(\Vert \mathbf {x}- \varPsi _\varepsilon (\mathbf {x}) \Vert _{\mathbf {X}} \le \varepsilon + {{\,\mathrm{dist}\,}}(\mathbf {x}, \mathcal {S})\), and let
Now, if \(\mathbf {y}\in \mathcal {S}' \subset \varPhi (\mathcal {S})\) is arbitrary, then \(\mathbf {y}= \varPhi (\mathbf {x})\) for some \(\mathbf {x}\in \mathcal {S}\), and hence
since \( {{\,\mathrm{dist}\,}} \big ( D_R(E_R(\mathbf {x}) \big ), \mathcal {S}) \le \Vert D_R(E_R(\mathbf {x})) - \mathbf {x}\Vert _{\mathbf {X}} \le C \cdot R^{-s} \). Therefore, if for each \(\mathbf {y}\in \mathcal {S}'\) and \(R \in \mathbb {N}\) we choose \(c_{\mathbf {y}, R} \in \{0,1\}^R\) with \( \Vert \mathbf {y}- D_R^*(c_{\mathbf {y}, R}) \Vert _{\mathbf {Y}} = \min _{c \in \{0,1\}^R} \Vert \mathbf {y}- D_R^*(c) \Vert _{\mathbf {Y}} \) and define \(E_R^*: \mathcal {S}' \rightarrow \{0,1\}^R, \mathbf {y}\mapsto c_{\mathbf {y}, R}\), then \( \Vert \mathbf {y}- D_R^*(E_R^*(\mathbf {y})) \Vert _{\mathbf {Y}} \le L \cdot (1 + 2C) \cdot R^{-s} \) for all \(\mathbf {y}\in \mathcal {S}'\) and \(R \in \mathbb {N}\), and hence  . Since
. Since  was arbitrary, this completes the proof. \(\square \)
was arbitrary, this completes the proof. \(\square \)
The following lemma shows that if a signal class \(\mathcal {S}\subset \mathbf {X}\) carries a Borel probability measure of growth order \(s_0\) and satisfies  , then in fact
, then in fact  . This is elementary, but will be used quite frequently, so that we prefer to state it as a lemma.
. This is elementary, but will be used quite frequently, so that we prefer to state it as a lemma.
Lemma 9
Let \(s_0 \in [0,\infty )\), let \(\mathbf {X}\) be a Banach space, and let \(\mathcal {S}\subset \mathbf {X}\). Assume that there exists a Borel probability measure \(\mathbb {P}\) of growth order \(s_0\) on \(\mathcal {S}\) and that  . Then,
. Then,  and \(\mathbb {P}\) is critical for \(\mathcal {S}\) with respect to \(\mathbf {X}\).
and \(\mathbb {P}\) is critical for \(\mathcal {S}\) with respect to \(\mathbf {X}\).
Proof
Corollary 2 shows that  . Since
. Since  by assumption, the claim of the lemma follows. \(\square \)
by assumption, the claim of the lemma follows. \(\square \)
We finally provide the proof of Theorem 5.
Proof of Theorem 5
Since \(\varPhi : \mathcal {S}_\mathbf {X}\rightarrow \mathbf {Z}\) is Lipschitz continuous with \(\varPhi (\mathcal {S}_\mathbf {X}) \supset \mathcal {S}\), Lemma 8 shows that  . Furthermore, since \(\varPsi : \mathcal {S}_{\mathbf {Y}} \rightarrow \mathcal {S}\) is measurable and expansive and \(\mathbb {P}\) has growth order
. Furthermore, since \(\varPsi : \mathcal {S}_{\mathbf {Y}} \rightarrow \mathcal {S}\) is measurable and expansive and \(\mathbb {P}\) has growth order  , Lemma 7 shows that \(\nu := \mathbb {P}\circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) of growth order \(s^*\) as well. Now, Lemma 9 shows that
, Lemma 7 shows that \(\nu := \mathbb {P}\circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) of growth order \(s^*\) as well. Now, Lemma 9 shows that  and that \(\nu \) is critical for \(\mathcal {S}\) with respect to \(\mathbf {Z}\). \(\square \)
and that \(\nu \) is critical for \(\mathcal {S}\) with respect to \(\mathbf {Z}\). \(\square \)
A Lower Bound for the Optimal Compression Rate 
Our goal in this appendix is to show that the optimal compression rate for the class  satisfies
satisfies  , assuming that \(\alpha > d \cdot (\tfrac{1}{2} - \tfrac{1}{p})_+\). Our proof of this fact relies on an equivalence between the optimal distortion for a set and the so-called entropy numbers of that set. By combining this equivalence with known estimates for the entropy numbers of certain embeddings between sequence spaces (taken from [20]), we will obtain the claim.
, assuming that \(\alpha > d \cdot (\tfrac{1}{2} - \tfrac{1}{p})_+\). Our proof of this fact relies on an equivalence between the optimal distortion for a set and the so-called entropy numbers of that set. By combining this equivalence with known estimates for the entropy numbers of certain embeddings between sequence spaces (taken from [20]), we will obtain the claim.
First, let us describe the equivalence between the optimal achievable distortion and the entropy numbers of a set. Following [5, 12], given a (quasi)-Banach space \(\mathbf {X}\), a set \(M \subset \mathbf {X}\), and \(k \in \mathbb {N}\), the k-th entropy number \(e_k(M) := e_k (M ; \mathbf {X})\) of M is defined as
with the convention that \(\inf \emptyset = \infty \). Note that \(e_k (M)\) is finite if and only if M is bounded. Furthermore, \(e_k(M) \xrightarrow [k\rightarrow \infty ]{} 0\) if and only if \(M \subset \mathbf {X}\) is totally bounded. Finally, if \(\mathbf {Y}\) is a further (quasi)-Banach space, and \(T : \mathbf {Y}\rightarrow \mathbf {X}\) is linear, then the entropy numbers \(e_k(T)\) are defined as \(e_k(T) := e_k \big ( T({{\,\mathrm{Ball}\,}}(0, 1; \mathbf {Y})) ; \mathbf {X}\big )\).
For proving that  , we will use the following folklore equivalence between entropy numbers and the optimal achievable distortion for a given set:
, we will use the following folklore equivalence between entropy numbers and the optimal achievable distortion for a given set:
Lemma 10
Let \(\mathbf {X}\) be a Banach space and \(\emptyset \ne \mathcal {S}\subset \mathbf {X}\). Then,

Proof
The intuition is that a covering of \(\mathcal {S}\) by \(2^R\) balls \({{\,\mathrm{Ball}\,}}(\mathbf {x}_i, \varepsilon ; \mathbf {X})\) (\(i \in \{ 1,\dots ,2^R \}\)) gives rise to an encoder/decoder pair with R bits achieving distortion \(\varepsilon \), by mapping each \(\mathbf {u}\in \mathcal {S}\) to an index \(i_{\mathbf {u}} \in \{ 1,\dots ,2^R \} \cong \{ 0,1 \}^R\) such that \(\mathbf {u}\in {{\,\mathrm{Ball}\,}}(\mathbf {x}_{i_{\mathbf {u}}},\varepsilon ; \mathbf {X})\). The reconstruction map is of the form \(i \mapsto \mathbf {x}_i\). Conversely, any encoder/decoder pair using R bits and achieving distortion \(\varepsilon \) induces a covering of \(\mathcal {S}\) by \(2^R\) balls of radius \(\varepsilon \). For more details, we refer to Remark 1 and [13, Section IV]. \(\square \)
In addition to this equivalence between entropy numbers and best achievable distortion, we will use two results from [20] about the asymptotic behavior of the entropy numbers of certain sequence spaces. The following definition introduces the terminology used in [20].
Definition 8
(see [20, Equations (10), (11), and Definition 1])
A sequence \((\beta _j)_{j \in \mathbb {N}_0} \subset (0,\infty )\) is called
-
an admissible sequence if there exist \(d_0, d_1 \in (0,\infty )\) such that \(d_0 \, \beta _j \le \beta _{j+1} \le d_1 \, \beta _{j}\) for all \(j \in \mathbb {N}_0\);
-
almost strongly increasing if there exists \(\kappa \in \mathbb {N}\) such that \( 2 \beta _j \le \beta _k \) for all \(j,k \in \mathbb {N}_0\) with \(k \ge j + \kappa \).
Given \(p,q \in (0,\infty ]\) and sequences \(\varvec{\beta } = (\beta _j)_{j \in \mathbb {N}_0} \subset (0,\infty )\) and \(\mathbf {N} = (N_j)_{j \in \mathbb {N}_0} \subset \mathbb {N}\), define \( J_{\mathbf {N}} := \{ (j,\ell ) \in \mathbb {N}_0 \times \mathbb {N}:1 \le \ell \le N_j \} \) and
as well as \( \ell ^q (\beta _j \, \ell _{N_j}^p) := \big \{ \mathbf {x}\in \mathbb {C}^{J_{\mathbf {N}}} :\Vert \mathbf {x}\Vert _{\ell ^q (\beta _j \, \ell _{N_j}^p)} < \infty \big \}. \) For the case \(\varvec{\beta } = (1)_{j \in \mathbb {N}_0}\), we simply write  instead of
instead of  .
.
Using these notions, Leopold [20] proved the following results:
Theorem 9
(see [20, Theorems 3 and 4])
Let \(p_1,p_2, q_1,q_2 \in (0,\infty ]\), and let \({\mathbf {N} = (N_j)_{j \in \mathbb {N}_0} \subset \mathbb {N}}\) and \({\varvec{\beta } = (\beta _j)_{j \in \mathbb {N}_0} \subset (0,\infty )}\) both be admissible, almost strongly increasing sequences.
Assume that either
-
(i)
\(p_1 \le p_2\); or
-
(ii)
\(p_2 < p_1\) and the sequence \(\Big ( \beta _j \cdot N_j^{\frac{1}{p_1} - \frac{1}{p_2}} \Big )_{j \in \mathbb {N}_0}\) is almost strongly increasing.
Then, the embedding  holds, and there exist \(C_1, C_2 > 0\) such that for all \(L \in \mathbb {N}\), the entropy numbers
holds, and there exist \(C_1, C_2 > 0\) such that for all \(L \in \mathbb {N}\), the entropy numbers  (see the discussion around Eq. (B.1)) satisfy
(see the discussion around Eq. (B.1)) satisfy

Remark
For what follows, only the upper bound in Theorem 9 will matter. Even though Theorem 9 pertain to spaces of complex sequences, this upper bound also holds for the real-valued case. To see this, note that if we denote by \(\mathrm {Re} \, \mathbf {x}\) the (componentwise) real part of the sequence \(\mathbf {x}\), then clearly  . Hence, defining the real-valued version of the space
. Hence, defining the real-valued version of the space  as
as

we see that if  for
for 
 , then
, then  , and hence
, and hence

Proof of Proposition 2
Let \(n_m := |\mathcal {I}_m|\) and \(N_j := n_{j+1}\) for \(m \in \mathbb {N}\) and \(j \in \mathbb {N}_0\). Further, set \({\kappa := \big \lceil d^{-1} \cdot \big ( 1 + \log _2(A / a) \big ) \big \rceil }\), where we recall from Eq. (3.1) that \({a, A > 0}\) satisfy \(a \cdot 2^{d m} \le n_m \le A \cdot 2^{d m}\). Thus, \( N_{j+1} = n_{j+2} \asymp 2^{d (j+2)} = 2^d \, 2^{d (j+1)} \asymp n_{j+1} = N_j , \) which shows that \({\mathbf {N} = (N_j)_{j \in \mathbb {N}_0}}\) is admissible. Furthermore, if \(k \ge j + \kappa \), then
which shows that \(\mathbf {N}\) is almost strongly increasing.
Next, define \(\beta _j := 2^{\alpha (j+1)}\) for \(j \in \mathbb {N}_0\), noting that \(\beta _{j+1} = 2^{\alpha } \, \beta _j\), which implies that \((\beta _j)_{j \in \mathbb {N}_0}\) is admissible. Furthermore, if \(k \ge j + \lceil \alpha ^{-1} \rceil \), then \( \beta _k \ge 2 \cdot 2^{\alpha (j+1)} = 2 \, \beta _j, \) so that \((\beta _j)_{j \in \mathbb {N}_0}\) is also almost strongly increasing. Here, we used that \(\alpha > 0\).
Finally, for each \(m \in \mathbb {N}\) pick a bijection \(\iota _m : [N_{m-1}] \rightarrow \mathcal {I}_m\) (which is possible since \(N_{m-1} = n_m = |\mathcal {I}_m|\)) and define
It is easy to see that \(\varPsi \) is a bijection, and that

for arbitrary \(p,q \in (0,\infty ]\). Here, \(\mathbf {x}_m = (x_i)_{i \in \mathcal {I}_m}\) is as defined in Eq. (3.2). In the same way, we see  and also
and also  Using these identities, it is straightforward to see that
Using these identities, it is straightforward to see that  holds if and only if
holds if and only if  , and furthermore that
, and furthermore that

There are now two cases. First, if \(p \le 2\), then Eq. (B.2) and the first part of Theorem 9 with \(p_1 = p, q_1 = q\) and \(p_2 = q_2 = 2\) show that  , and yield a constant \(C_1 > 0\) such that
, and yield a constant \(C_1 > 0\) such that

for all \(L \in \mathbb {N}\).
If otherwise \(p > 2\), then \(\frac{1}{2} - \frac{1}{p} > 0\), so that our assumptions concerning \(\alpha \) imply that \(\alpha > d \cdot (\frac{1}{2} - \frac{1}{p})_+ = d \cdot (\frac{1}{2} - \frac{1}{p})\), and hence \(\gamma := \alpha + d \cdot (\frac{1}{p} - \frac{1}{2}) > 0\). Therefore, the sequence \((K_j)_{j \in \mathbb {N}_0} := \big ( \beta _j \cdot N_j^{\frac{1}{p} - \frac{1}{2}}\big )_{j \in \mathbb {N}_0}\) is almost strongly increasing; indeed, if \( k \ge j + \big \lceil \gamma ^{-1} \cdot \big ( 1 + \log _2 [ (a / A)^{\frac{1}{p} - \frac{1}{2}}] \big ) \big \rceil , \) then we see because of \(a \cdot 2^{d (j+1)} \le N_j \le A \cdot 2^{d(j+1)}\) and \(\frac{1}{p} - \frac{1}{2} < 0\) that \( N_k^{\frac{1}{p} - \frac{1}{2}} \ge A^{\frac{1}{p} - \frac{1}{2}} \cdot 2^{d(k+1)(\frac{1}{p} - \frac{1}{2})} \) and \( N_j^{\frac{1}{p} - \frac{1}{2}} \le a^{\frac{1}{p} - \frac{1}{2}} \cdot 2^{d (j+1) (\frac{1}{p} - \frac{1}{2})} . \) Since \(\gamma > 0\), we thus see
Thus, Part (ii) of Theorem 9 and Eq. (B.2) show that  , and that there is a constant \(C_2 > 0\) such that
, and that there is a constant \(C_2 > 0\) such that

for all \(L \in \mathbb {N}\).
Define \(C_3 := \max \{ C_1, C_2 \}\) and note that the preceding estimates only yield bounds for the entropy numbers  in case of \(k = 2 N_L\) for some \(L \in \mathbb {N}\), not for general \(k \in \mathbb {N}\). This, however, suffices to handle the general case. Indeed, let \(R \in \mathbb {N}\) with \(R \ge 2 N_1\) be arbitrary, and let \(L \in \mathbb {N}\) be maximal with \(2 N_L \le R + 1\); this is possible since \(N_L \rightarrow \infty \) as \(L \rightarrow \infty \). Note \( R \le R+1 < 2 \, N_{L+1} = 2 \, n_{L+2} \le 2A \, 2^{d (L+2)} = 2^{2d+1}A \, 2^{d L} \) by maximality. Since the sequence of entropy numbers
in case of \(k = 2 N_L\) for some \(L \in \mathbb {N}\), not for general \(k \in \mathbb {N}\). This, however, suffices to handle the general case. Indeed, let \(R \in \mathbb {N}\) with \(R \ge 2 N_1\) be arbitrary, and let \(L \in \mathbb {N}\) be maximal with \(2 N_L \le R + 1\); this is possible since \(N_L \rightarrow \infty \) as \(L \rightarrow \infty \). Note \( R \le R+1 < 2 \, N_{L+1} = 2 \, n_{L+2} \le 2A \, 2^{d (L+2)} = 2^{2d+1}A \, 2^{d L} \) by maximality. Since the sequence of entropy numbers  is non-increasing, we thus see
is non-increasing, we thus see

for all \(R \ge 2 N_1\) and suitable constants \(C_4,C_5 > 0\) which are independent of R.
Now, since  is bounded (otherwise, all entropy numbers would be infinite), it is easy to see
is bounded (otherwise, all entropy numbers would be infinite), it is easy to see  for \(R \in \mathbb {N}\) with \(R < 2 N_1\). With this, the claim
for \(R \in \mathbb {N}\) with \(R < 2 N_1\). With this, the claim  and the existence of a codec
and the existence of a codec  satisfying (3.3) follow from the relation between entropy numbers and optimal distortion described in Lemma 10.
satisfying (3.3) follow from the relation between entropy numbers and optimal distortion described in Lemma 10.
Finally, since  as \(R \rightarrow \infty \), it follows that
as \(R \rightarrow \infty \), it follows that  is totally bounded. Since
is totally bounded. Since  is also easily seen to be closed (this essentially follows from Fatou’s lemma), we see that
is also easily seen to be closed (this essentially follows from Fatou’s lemma), we see that  is compact. \(\square \)
is compact. \(\square \)
A Review of Besov Spaces
In this subsection, we review the relevant properties of Besov spaces on \(\mathbb {R}^d\) and on domains, including the characterization of these spaces in terms of wavelets; see Sect. C.2.
Before we dive into the details, a word of caution is in order. In the literature, there are two common definitions of Besov spaces: A Fourier analytic definition and a definition using moduli of continuity. Here, we only consider the former definition; the reader interested in the latter is referred to [9]. It should be mentioned, however, that the two definitions do not agree in general; see for instance [16]. Nevertheless, in the regime that we are interested in, the two definitions coincide, as can be deduced from [36, Theorem in Section 2.5.12]. Since we focus on the Fourier analytic definition only, we omit the details.
1.1 The (Fourier-analytic) Definition of Besov Spaces
Our presentation here follows [36, Section 2.3] and [35, Section 1.3]. In this section, all functions are taken to be complex-valued, unless indicated otherwise. Let \(\mathscr {S}(\mathbb {R}^d)\) denote the space of Schwartz functions (see, for instance, [14, Section 8.1]), and \(\mathscr {S}' (\mathbb {R}^d)\) its topological dual space, the space of tempered distributions (see [14, Section 9.2]). We use the Fourier transform on \(L^1(\mathbb {R}^d)\) with the same normalization as in [36, 39]; that is,
where \(\langle x,\xi \rangle = \sum _{j=1}^d x_j \xi _j\) denotes the standard inner product on \(\mathbb {R}^d\). With this normalization, the Fourier transform \(\mathcal {F}: L^1(\mathbb {R}^d) \rightarrow C_0(\mathbb {R}^d)\) extends to a unitary operator \(\mathcal {F}: L^2(\mathbb {R}^d) \rightarrow L^2(\mathbb {R}^d)\) and also to linear homeomorphisms \(\mathcal {F}: \mathscr {S}(\mathbb {R}^d) \rightarrow \mathscr {S}(\mathbb {R}^d)\) and \(\mathcal {F}: \mathscr {S}'(\mathbb {R}^d) \rightarrow \mathscr {S}'(\mathbb {R}^d)\), with the latter defined by \( \langle \mathcal {F}f, \varphi \rangle _{\mathscr {S}',\mathscr {S}} := \langle f, \mathcal {F}\varphi \rangle _{\mathscr {S}', \mathscr {S}}. \) Here, as in the remainder of the paper, the dual pairing for distributions is taken to be bilinear. In any case, the inverse Fourier transform is given by (the extension of) the operator \(\mathcal {F}^{-1} f (x) = \mathcal {F}f (-x)\). All of the facts listed here can be found in [30, Chapter 7].
Fix \(\varphi _0 \in \mathscr {S}(\mathbb {R}^d)\) satisfying \(\varphi _0 (\xi ) = 1\) for all \(\xi \in \mathbb {R}^d\) such that \(|\xi | \le 1\), and \(\varphi _0 (\xi ) = 0\) for all \(\xi \in \mathbb {R}^d\) satisfying \(|\xi | \ge 3/2\). Define \(\varphi _k : \mathbb {R}^d \rightarrow \mathbb {C}, \xi \mapsto \varphi _0(2^{-k} \xi ) - \varphi _0 (2^{-k + 1} \xi )\) for \(k \in \mathbb {N}\), noting that \(\sum _{j=0}^\infty \varphi _j (\xi ) \equiv 1\) on \(\mathbb {R}^d\).
With this, the (inhomogeneous) Besov space \(B^{\tau }_{p,q}(\mathbb {R}^d)\) with smoothness \(\tau \in \mathbb {R}\) and integrability exponents \(p,q \in (0,\infty ]\) is defined (see [35, Section 1.3, Definition 1.2]) as
where
This is well-defined, since \(\varphi _j \cdot \widehat{f\,}\) is a tempered distribution with compact support, so that the Paley–Wiener theorem (see [30, Theorem 7.23]) shows that \(\mathcal {F}^{-1} (\varphi _j \cdot \widehat{f\,})\) is a smooth function of which one can take the \(L^p\) norm (which might be infinite). One can show that the definition of \(B^{\tau }_{p,q} (\mathbb {R}^d)\) is independent of the precise choice of the function \(\varphi _0\), with equivalent quasi-norms for different choices; see [36, Proposition 1 in Section 2.3.2]. Furthermore, the spaces \(B^{\tau }_{p,q} (\mathbb {R}^d)\) are quasi-Banach spaces that satisfy \(B^{\tau }_{p,q}(\mathbb {R}^d) \hookrightarrow \mathscr {S}'(\mathbb {R}^d)\); see [36, Theorem in Section 2.3.3].
Now, let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be a bounded open set, and let \(\tau \in \mathbb {R}\) and \(p,q \in (0,\infty ]\). We will use the space \(\mathcal {D}' (\varOmega )\) of distributions on \(\varOmega \); for more details on these spaces, we refer to [30, Chapter 6]. Following [35, Definition 1.95], we then define
and
Here, given a tempered distribution \(f \in \mathscr {S}'(\mathbb {R}^d)\), we write \(f|_{\varOmega }\) for the restriction of f to \(\varOmega \), given by \(f|_{\varOmega } : C_c^\infty (\varOmega ) \rightarrow \mathbb {C}, \psi \mapsto f(\psi )\). It is easy to see that \(f|_{\varOmega } \in \mathcal {D}'(\varOmega )\). The spaces \(B^{\tau }_{p,q}(\varOmega )\) are quasi-Banach spaces that satisfy \(B^{\tau }_{p,q}(\varOmega ) \hookrightarrow \mathcal {D}'(\varOmega )\); see [35, Remark 1.96].
1.2 The Wavelet Characterization of Besov Spaces
Wavelets are usually constructed using a so-called multiresolution analysis of \(L^2(\mathbb {R})\). A multiresolution analysis (see [39, Definition 2.2] or [8, Section 5.1]) of \(L^2(\mathbb {R})\) is a sequence \((V_j)_{j \in \mathbb {Z}}\) of closed subspaces \(V_j \subset L^2(\mathbb {R})\) with the following properties:
-
1.
\( V_j \subset V_{j+1}\) for all \(j \in \mathbb {Z}\);
-
2.
\( \bigcup _{j \in \mathbb {Z}} V_j\) is dense in \(L^2(\mathbb {R})\);
-
3.
\(\bigcap _{j \in \mathbb {Z}} V_j = \{0\}\);
-
4.
for \(f \in L^2(\mathbb {R})\), we have \(f \in V_j\) if and only if \(f(2^{-j} \bullet ) \in V_0\);
-
5.
there exists a function \(\psi _F \in V_0\) (called the scaling function or the father wavelet) such that \(\big ( \psi _F (\bullet - m) \big )_{m \in \mathbb {Z}}\) is an orthonormal basis of \(V_0\).
To each multiresolution analysis, one can associate a (mother) wavelet \(\psi _M \in L^2(\mathbb {R})\); see [39, Theorem 2.20]. More precisely, denote by \(W_0 \subset L^2(\mathbb {R})\) the orthogonal complement of \(V_0\) as a subset of \(V_1\), and define \(W_j := \{ f (2^j \bullet ) :f \in W_0 \}\) for \(j \in \mathbb {N}\), so that \(W_j\) is the orthogonal complement of \(V_j\) in \(V_{j+1}\). We then have \(L^2(\mathbb {R}) = V_0 \oplus \bigoplus _{j=0}^\infty W_j\), where the sum is orthogonal.
One can show (see [39, Lemma 2.19]) that there exists \(\psi _M \in W_0\) such that the family \(\big ( \psi _M (\bullet - k) \big )_{k \in \mathbb {Z}}\) is an orthonormal basis of \(W_0\). In this case, we say that \(\psi _M\) is a mother wavelet associated with the given multiresolution analysis. For each such \(\psi _M\), one can show (see [35, Proposition 1.51]) that if we define
for \(j \in \mathbb {N}_0\) and \(m \in \mathbb {Z}\), then the inhomogeneous wavelet system \((\psi _{j,m})_{j \in \mathbb {N}_0, m \in \mathbb {Z}}\) forms an orthonormal basis of \(L^2(\mathbb {R})\). Furthermore, the family \(\big ( 2^{j/2} \, \psi _M (2^j \bullet - k) \big )_{j,k \in \mathbb {Z}}\) is an orthonormal basis of \(L^2(\mathbb {R})\).
For our purposes, we will need sufficiently regular wavelet systems, as provided by the following theorem:
Theorem 10
For each \(k \in \mathbb {N}\), there is a multiresolution analysis \((V_j)_{j \in \mathbb {Z}}\) of \(L^2(\mathbb {R})\) with father/mother wavelets \(\psi _F, \psi _M \in L^2(\mathbb {R})\) such that the following hold:
-
1.
\(\psi _F, \psi _M\) are real-valued and have compact support;
-
2.
\(\psi _F, \psi _M \in C^k (\mathbb {R})\);
-
3.
\(\widehat{\psi _F} (0) = (2\pi )^{-1/2}\);
-
4.
\(\int _{\mathbb {R}} x^\ell \cdot \psi _M (x) \, d x = 0\) for all \(\ell \in \{ 0,\dots ,k \}\) (vanishing moment condition).
Proof
The existence of a multi-resolution analysis \((V_j)_{j \in \mathbb {Z}}\) with compactly supported father/mother wavelets \(\psi _F, \psi _M \in C^k (\mathbb {R})\) is shown in [39, Theorem 4.7] (while the original proof was given in [7]). It is not stated explicitly, however, that \(\psi _F, \psi _M\) are real-valued, but this can be extracted from the proof: The function \(\varPhi := \psi _F\) is constructed as \(\varPhi = (2\pi )^{-1/2} \, \mathcal {F}^{-1} \varTheta \), with \(\varTheta (\xi ) = \prod _{j=1}^\infty m(2^{-j} \xi )\) (see [39, Theorem 4.1]), where the trigonometric polynomial \({m(\xi ) = \sum _{k=0}^T a_k e^{i k \xi }}\) is obtained through [39, Lemma 4.6], so that \(a_0,\dots ,a_T \in \mathbb {R}\) and \(m(0) = 1\). Therefore, [39, Lemma 4.3] shows that \(\varPhi \) is real-valued. Finally, \(\varPsi := \psi _M\) is obtained from \(\varPhi \) as \({ \varPsi (x) = 2\sum _{k=0}^T \overline{a_k} (-1)^k \varPhi (2x + k + 1); }\) see [39, Equation (4.5)]. Since \(a_0, \dots , a_T \in \mathbb {R}\), this shows that \(\psi _M = \varPsi \) is real-valued as well.
The above construction also implies \(\widehat{\psi _F} (0) = (2\pi )^{-1/2} \, \varTheta (0) = (2\pi )^{-1/2}\), because of \(\varTheta (0) = \prod _{j=1}^\infty m(0) = 1\). Finally, the vanishing moment condition is a consequence of [39, Proposition 3.1]. \(\square \)
Wavelet systems in \(\mathbb {R}^d\) can be constructed by taking suitable tensor products of a one-dimensional wavelet system. To describe this, let \(\psi _F, \psi _M\) be father/mother wavelets, and let \(T_0 := \{F\}^d\) and \(T_j := T:= \{F,M\}^d \setminus T_0\) for \(j \in \mathbb {N}\). Now, for \(t = (t_1,\dots ,t_d) \in T\) and \(m = (m_1,\dots ,m_d) \in \mathbb {Z}^d\), define \(\varPsi _m : \mathbb {R}^d \rightarrow \mathbb {C}\) and \(\varPsi _{t,m} : \mathbb {R}^d \rightarrow \mathbb {C}\) by
Finally, set \(J := \{ (j,t,m) :j \in \mathbb {N}_0, t \in T_j , m \in \mathbb {Z}^d \}\), and
Then (see [35, Proposition 1.53]), the system \((\varPsi _{j,t,m})_{(j,t,m) \in J}\) is an orthonormal basis of \(L^2(\mathbb {R}^d)\).
Finally, we have the following wavelet characterization of the Besov spaces \(B^{\tau }_{p,q}(\mathbb {R}^d)\).
Theorem 11
(consequence of [35, Theorem 1.64])
Let \(d \in \mathbb {N}\), \(p,q \in (0,\infty ]\) and \(\tau \in \mathbb {R}\). For a sequence \(\mathbf {c}= (c_{j,t,m})_{(j,t,m) \in J} \in \mathbb {C}^J\) define
and \( b^{\tau }_{p,q} (\mathbb {R}^d) := \big \{ \mathbf {c}\in \mathbb {C}^{J} :\Vert \mathbf {c}\Vert _{b^{\tau }_{p,q}(\mathbb {R}^d)} < \infty \big \} \).
Let \(k \in \mathbb {N}\), and let \(\psi _F, \psi _M\) as provided by Theorem 10, for this choice of k. Let the d-dimensional wavelet system \((\varPsi _{j,t,m})_{(j,t,m) \in J}\) be as defined in Eq. (C.4). Finally, suppose that \( k > \max \big \{ \tau , \frac{2 d}{p} + \frac{d}{2} - \tau \big \} . \) Then, the map
is well-defined (with unconditional convergence of the series in \(\mathscr {S}'(\mathbb {R}^d)\)), and an isomorphism of (quasi)-Banach spaces. The inverse map of \(\varGamma \) will be denoted by
We will also use the real-valued Besov space
where we write \( \mathscr {S}' (\mathbb {R}^d; \mathbb {R}) := \big \{ \varphi \in \mathscr {S}' (\mathbb {R}^d) :\forall \, f \in \mathscr {S}(\mathbb {R}^d ; \mathbb {R}) : \langle \varphi , f \rangle _{\mathscr {S}',\mathscr {S}} \in \mathbb {R}\big \} \) and \(\mathscr {S}(\mathbb {R}^d ; \mathbb {R}) := \{ f : \mathbb {R}^d \rightarrow \mathbb {R}:f \in \mathscr {S}(\mathbb {R}^d) \}\). The spaces \(B_{p,q}^{\tau }(\varOmega ;\mathbb {R})\) are defined similarly. We will also use the space \( b^{\tau }_{p,q} (\mathbb {R}^d; \mathbb {R}) := b^{\tau }_{p,q}(\mathbb {R}^d) \cap \mathbb {R}^J \).
1.3 Wavelets and Besov Spaces on Bounded Domains
Note that Theorem 11 only pertains to the Besov spaces \(B^{\tau }_{p,q}(\mathbb {R}^d)\). To describe Besov spaces on domains, we will use the sequence spaces \(b^{\tau }_{p,q}(\varOmega _{\mathrm {int}};\mathbb {R})\) and \(b^{\tau }_{p,q}(\varOmega _{\mathrm {ext}};\mathbb {R})\) that we now define.
Definition 9
Let \(p,q \in (0,\infty ]\) and \(\tau \in \mathbb {R}\), and let \(k \in \mathbb {N}\) with \(k > \max \{ \tau , \frac{2d}{p} + \frac{d}{2} - \tau \}\). Let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be a bounded open set. With the father/mother wavelets \(\psi _F, \psi _M\) as in Theorem 10 (with the above choice of k) and \(\varPsi _{j,t,m}\) as in Eq. (C.4), define
Finally, set
and define \(b^{\tau }_{p,q}(\varOmega _{\mathrm {int}}; \mathbb {R})\) similarly. Both of these spaces are considered as subspaces of \(b^{\tau }_{p,q}(\mathbb {R}^d; \mathbb {R})\); they are thus equipped with the (quasi)-norm \(\Vert \cdot \Vert _{b^{\tau }_{p,q}}\).
Remark
Strictly speaking, the spaces \(b_{p,q}^{\tau }(\varOmega _{\mathrm {int}}; \mathbb {R})\) and \(b_{p,q}^{\tau }(\varOmega _{\mathrm {ext}}; \mathbb {R})\) (and the index sets \(J^{\mathrm {ext}}\) and \(J^{\mathrm {int}}\)) depend on the choice of \(k \in \mathbb {N}\) and on the precise choice of \(\psi _F, \psi _M\). We will, however, suppress this dependence. \(\blacktriangleleft \)
The next lemma describes the relation between these sequence spaces and the Besov spaces \(B_{p,q}^{\tau } (\varOmega ;\mathbb {R})\).
Lemma 11
Let \(d \in \mathbb {N}\), \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) open and bounded, \(p,q \in (0,\infty ]\) and \(\tau \in \mathbb {R}\). Let \(k \in \mathbb {N}\) with \(k > \max \{ \tau , \frac{2d}{p} + \frac{d}{2} - \tau \}\). Let \(b_{p,q}^{\tau } (\varOmega _{\mathrm {int}};\mathbb {R})\) and \(b_{p,q}^{\tau } (\varOmega _{\mathrm {ext}};\mathbb {R})\) be as in Definition 9 (for the given choice of \(k,\psi _F,\psi _M\)), and J as defined before Eq. (C.4).
Then, there exist continuous linear maps
with the following properties:
-
There is \(\gamma > 0\) such that \( \Vert T_{\mathrm {int}} \mathbf {c}\Vert _{L^2(\varOmega )} = \gamma \cdot \Vert \mathbf {c}\Vert _{\ell ^2} \) for all \(\mathbf {c}\in \ell ^2 (J) \cap b_{p,q}^{\tau }(\varOmega _{\mathrm {int}}; \mathbb {R})\), and \( \Vert T_{\mathrm {int}} \mathbf {c}\Vert _{B_{p,q}^{\tau }(\varOmega )} \le \Vert \mathbf {c}\Vert _{b_{p,q}^{\tau }} \) for all \(\mathbf {c}\in b_{p,q}^{\tau }(\varOmega _{\mathrm {int}}; \mathbb {R})\).
-
There exists \(\varrho > 0\) such that \(\Vert T_{\mathrm {ext}} \mathbf {c}\Vert _{L^2(\varOmega )} \le \varrho \cdot \Vert \mathbf {c}\Vert _{\ell ^2}\) for all \(\mathbf {c}\in b_{p,q}^{\tau } (\varOmega _\mathrm {ext}; \mathbb {R})\), and we have
$$\begin{aligned} {{\,\mathrm{Ball}\,}}\big ( 0,1;B_{p,q}^{\tau } (\varOmega ;\mathbb {R}) \big ) \subset T_{\mathrm {ext}} \Big ( {{\,\mathrm{Ball}\,}}\big ( 0,1;b_{p,q}^{\tau }(\varOmega _{\mathrm {ext}};\mathbb {R}) \big ) \Big ) . \end{aligned}$$(C.5)
Proof
With the operator \(\varGamma \) as in Theorem 11, let \(\gamma := \bigl (1 + \Vert \varGamma \Vert _{b_{p,q}^{\tau }(\mathbb {R}^d) \rightarrow B_{p,q}^{\tau }(\mathbb {R}^d)}\bigr )^{-1}\), and define
By definition of the Besov space \(B_{p,q}^{\tau }(\varOmega ;\mathbb {R})\) and its norm (see Eq. (C.2)), we then see that \(T_{\mathrm {int}}\) is a well-defined continuous linear map, with
Next, let \( \mathbf {c}= (c_{j,t,m})_{(j,t,m) \in J} \in \ell ^2(J) \cap b_{p,q}^{\tau } (\varOmega _{\mathrm {int}} ; \mathbb {R}) \) be arbitrary. By orthonormality of the family \({(\varPsi _{j,t,m})_{(j,t,m) \in J} \subset L^2(\mathbb {R}^d)}\), and since \(c_{j,t,m} = 0\) for \((j,t,m) \in J \setminus J^{\mathrm {int}}\), while \({{\,\mathrm{supp}\,}}\varPsi _{j,t,m} \subset \varOmega \) for \((j,t,m) \in J^{\mathrm {int}}\), we see
To construct \(T_{\mathrm {ext}}\), let \(\varTheta \) be as in Theorem 11, set \(\varrho := 2 \cdot \bigl (1 + \Vert \varTheta \Vert _{B_{p,q}^{\tau }(\mathbb {R}^d) \rightarrow b_{p,q}^\tau (\mathbb {R}^d)}\bigr )\), and define
Exactly as for \(T_{\mathrm {int}}\), we see that \(T_{\mathrm {ext}}\) is a well-defined continuous linear map. Furthermore, using again that the family \((\varPsi _{j,t,m})_{(j,t,m) \in J} \subset L^2(\mathbb {R}^d)\) is an orthonormal system, we see
It remains to prove the inclusion (C.5). To this end, let \(f \in {{\,\mathrm{Ball}\,}}\big ( 0,1; B_{p,q}^{\tau } (\varOmega ;\mathbb {R}) \big )\) be arbitrary. By definition, this implies \(f = g|_{\varOmega }\) for some \(g \in B_{p,q}^{\tau } (\mathbb {R}^d)\) with \(\Vert g \Vert _{B_{p,q}^{\tau }} \le 2\). Let \({\mathbf {e}:= \varTheta g \in b_{p,q}^{\tau } (\mathbb {R}^d)}\), and \( \mathbf {c}= (c_{j,t,m})_{(j,t,m) \in J} \) where \( c_{j,t,m} := \varrho ^{-1} \cdot \mathbbm {1}_{J^{\mathrm {ext}}} ( (j,t,m) ) \cdot {\text {Re}} (e_{j,t,m}). \) Clearly, \( \Vert \mathbf {c}\Vert _{b_{p,q}^{\tau }} \le \varrho ^{-1} \Vert \mathbf {e}\Vert _{b_{p,q}^{\tau }} \le 2 \Vert \varTheta \Vert / \varrho \le 1, \) which means \(\mathbf {c}\in {{\,\mathrm{Ball}\,}}\big ( 0,1; b_{p,q}^{\tau } (\varOmega _{\mathrm {ext}}; \mathbb {R}) \big )\).
Finally, for an arbitrary real-valued test function \(\varphi \in C_c^\infty (\varOmega )\), we have \(\langle \varPsi _{j,t,m}, \varphi \rangle \in \mathbb {R}\) for all \((j,t,m) \in J\) and \(\langle \varPsi _{j,t,m} , \varphi \rangle = 0\) if \((j,t,m) \notin J^{\mathrm {ext}}\). Therefore,
since \(\varTheta = \varGamma ^{-1}\) and \(f = g|_{\varOmega }\) and \(\varphi \in C_c^\infty (\varOmega )\), and since f is a real-valued distribution. Therefore, \(f = T_{\mathrm {ext}} \, \mathbf {c}\), proving (C.5). \(\square \)
Finally, we show that the sequence spaces \(b_{p,q}^{\tau }(\varOmega _{\mathrm {int}} ; \mathbb {R})\) and \(b_{p,q}^{\tau }(\varOmega _{\mathrm {ext}} ; \mathbb {R})\) are quite similar to the sequence spaces  introduced in Definition 5. In fact, the following (seemingly) weak property will be enough for our purposes.
introduced in Definition 5. In fact, the following (seemingly) weak property will be enough for our purposes.
Lemma 12
Let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be open and bounded. Let \(p,q \in (0,\infty ]\) and \(\tau \in \mathbb {R}\), and define \(\alpha := \tau + d \cdot (\frac{1}{2} - \frac{1}{p})\). Let \(k \in \mathbb {N}\) with \(k > \max \{\tau , \frac{2d}{p} + \frac{d}{2} - \tau \}\), and let \(b_{p,q}^{\tau }(\varOmega _{\mathrm {int}} ; \mathbb {R})\) and \(b_{p,q}^{\tau }(\varOmega _{\mathrm {ext}} ; \mathbb {R})\) be as in Definition 9 (for the given choice of \(k,\psi _F,\psi _M\)).
Assume that \(\alpha > d \cdot (\frac{1}{2} - \frac{1}{p})_+\). Then, the embeddings \(b_{p,q}^\tau (\varOmega _{\mathrm {int}};\mathbb {R}) \hookrightarrow \ell ^2(J^{\mathrm {int}})\) and \(b_{p,q}^\tau (\varOmega _{\mathrm {ext}};\mathbb {R}) \hookrightarrow \ell ^2(J^{\mathrm {ext}})\) hold. Furthermore,
-
(i)
There is a d-regular partition \(\mathscr {P}^{\mathrm {int}}\) of \(J^{\mathrm {int}}\) and some \(\gamma > 0\) such that if we define

where \(\mathbf {c}^{\natural } \in \mathbb {R}^J\) is obtained by extending \(\mathbf {c}\in \mathbb {R}^{J^{\mathrm {int}}}\) by zero, then \(\Vert \iota _{\mathrm {int}} \Vert \le 1\) and \(\Vert \iota _{\mathrm {int}} \, \mathbf {c}\Vert _{\ell ^2} = \gamma \, \Vert \mathbf {c}\Vert _{\ell ^2}\) for all
 .
. -
(ii)
There is a d-regular partition \(\mathscr {P}^{\mathrm {ext}}\) of \(J^{\mathrm {ext}}\) and some \(\varrho > 0\) such that if we define

where \(\mathbf {c}^{\natural } \in \mathbb {R}^J\) is obtained by extending \(\mathbf {c}\in \mathbb {R}^{J^{\mathrm {ext}}}\) by zero, then \(\Vert \iota _{\mathrm {ext}} \, \mathbf {c}\Vert _{\ell ^2} = \varrho \, \Vert \mathbf {c}\Vert _{\ell ^2}\) for all
 , and
, and 
Proof
The proof is divided into three steps.
Step 1 (Estimating \(|J_{j}^{\mathrm {int}}|\) and \(|J_j^{\mathrm {ext}}|\)): We show that there are \(j_0 \in \mathbb {N}\) and \(a, A > 0\) satisfying
First of all, we clearly have \(J_j^{\mathrm {int}} \subset J_j^{\mathrm {ext}}\) and thus \(|J_j^{\mathrm {int}}| \le |J_j^{\mathrm {ext}}|\). Next, since \(\varOmega \subset \mathbb {R}^d\) is bounded and \(\psi _F, \psi _M\) have compact support, there is \(R \in \mathbb {N}\) such that \(\varOmega \subset [-R, R]^d\) and \({{\,\mathrm{supp}\,}}\psi _F \cup {{\,\mathrm{supp}\,}}\psi _M \subset [-R, R]\). Define \(A := (8 R)^d\). In view of Eqs. (C.3) and (C.4), this implies \({{\,\mathrm{supp}\,}}\varPsi _m \cup {{\,\mathrm{supp}\,}}\varPsi _{t,m} \subset m + [-R, R]^d\), and hence \({{\,\mathrm{supp}\,}}\varPsi _{0,t,m} \subset m + [-R, R]^d\) for \(t \in T_0\) and \(m \in \mathbb {Z}^d\), and finally \({{\,\mathrm{supp}\,}}\varPsi _{j,t,m} \subset 2^{1-j} (m + [-R, R]^d)\) for \(j \in \mathbb {N}\), \(t \in T_j\), and \(m \in \mathbb {Z}^d\).
Now, it is not hard to see that if \( \emptyset \ne \varOmega \cap {{\,\mathrm{supp}\,}}\varPsi _{0,t,m} \subset [-R,R]^d \cap (m + [-R,R]^d) , \) then \(m \in [-2R,2R]^d \cap \mathbb {Z}^d = \{-2R, \dots , 2R\}^d\), and thus \(|J_0^{\mathrm {ext}}| \le (1 + 4R)^d \le A \cdot 2^{d \cdot 0}\).
Furthermore, if \(j \in \mathbb {N}\) and \({ \emptyset \ne \varOmega \cap {{\,\mathrm{supp}\,}}\varPsi _{j,t,m} \subset [-R,R]^d \cap 2^{1-j} (m + [-R,R]^d) }\), then \(2^{1-j} (m + x) = y\) for certain \(x,y \in [-R,R]^d\), and hence
Because of \(|T_j| \le 2^d\), this implies \( |J_j^{\mathrm {ext}}| \le |T_j| \cdot (1 + 2^{j+1} R)^d \le (8R)^d 2^{j d} \le A \, 2^{d j} . \)
Regarding the lower bound, recall that \(\varOmega \ne \emptyset \) is open, so that there are \(x_0 \in \mathbb {R}^d\) and \(n \in \mathbb {N}\) satisfying \({x_0 + [-r, r]^d \subset \varOmega }\), where \(r := 2^{-n}\). Choose \(j_0 \in \mathbb {N}_{\ge n + 3}\) such that \(2^{j_0 - 1} r \ge 2 R\), and note \({2^{j_0 - 3} r = 2^{j_0 - 3 - n} \in \mathbb {N}}\). Let \(j \ge j_0\). Choose \(m_0 := \lfloor 2^{j-1} x_0 \rfloor \in \mathbb {Z}^d\), with the “floor” operation applied componentwise. We have \(\Vert 2^{j-1} x_0 - m_0 \Vert _\infty \le 1\), and hence
Here, one should observe \(2^{j-3} r = 2^{j - j_0} 2^{j_0 - 3 - n} \in \mathbb {N}\). Because of \(R \le 2^{j_0 - 2} r \le 2^{j-2} r\), the above estimate implies that
for all \(m \in \{ - 2^{j-3} r, \dots , 2^{j-3} r \}^d\). Because of \({{\,\mathrm{supp}\,}}\varPsi _{j,t,m+m_0} \subset 2^{1-j}(m + m_0 + [-R, R]^d)\), this implies \(|J_j^{\mathrm {int}}| \ge (2^{j-2} r)^d = (r/4)^d \cdot 2^{dj}\), so that we can choose \(a = (r/4)^d\).
Step 2 (Constructing the partitions \(\mathscr {P}^{\mathrm {int}}, \mathscr {P}^{\mathrm {ext}}\) and showing  ): Define \(\mathcal {I}_1^{\mathrm {int}} := \bigcup _{j=0}^{j_0} (\{ j \} \times J_j^{\mathrm {int}} )\) and \(\mathcal {I}_1^{\mathrm {ext}} := \bigcup _{j=0}^{j_0} (\{ j \} \times J_j^{\mathrm {ext}} )\), as well as
): Define \(\mathcal {I}_1^{\mathrm {int}} := \bigcup _{j=0}^{j_0} (\{ j \} \times J_j^{\mathrm {int}} )\) and \(\mathcal {I}_1^{\mathrm {ext}} := \bigcup _{j=0}^{j_0} (\{ j \} \times J_j^{\mathrm {ext}} )\), as well as
for \(m \in \mathbb {N}_{\ge 2}\). As shown in Step 1, we have for \(m \in \mathbb {N}_{\ge 2}\) that
and also \( |\mathcal {I}_1^{\mathrm {ext}}| \ge |\mathcal {I}_1^{\mathrm {int}}| \ge |J_{j_0}^{\mathrm {int}}| \ge a \cdot 2^{d j_0} \ge a \cdot 2^d . \) Thus, \({ a \cdot 2^{d m} \le |\mathcal {I}_m^{\mathrm {int}}| \le |\mathcal {I}_m^{\mathrm {ext}}| \le A'' \cdot 2^{d m} }\) for all \(m \in \mathbb {N}\), where \(A'' := \max \{ A', |\mathcal {I}_1^{\mathrm {ext}}| \}\). Furthermore, we have \({J^{\mathrm {int}} = \biguplus _{m \in \mathbb {N}} \mathcal {I}_m^{\mathrm {int}}}\) and \({J^{\mathrm {ext}} = \biguplus _{m \in \mathbb {N}} \mathcal {I}_m^{\mathrm {ext}}}\), so that \(\mathscr {P}^{\mathrm {int}} := \big ( \mathcal {I}_m^{\mathrm {int}} \big )_{m \in \mathbb {N}}\) and \(\mathscr {P}^{\mathrm {ext}} := \big ( \mathcal {I}_m^{\mathrm {ext}} \big )_{m \in \mathbb {N}}\) are d-regular partitions of \(J^{\mathrm {int}}\) and \(J^{\mathrm {ext}}\), respectively.
Now, for \(J_0 \subset J\) and \(\mathbf {c}\in \mathbb {R}^{J_0}\), let \(\mathbf {c}^{\natural } \in \mathbb {R}^{J}\) be the sequence \(\mathbf {c}\), extended by zero. We claim that there are \(C_1, C_2 > 0\) such that

and similarly for \(\mathscr {P}^{\mathrm {ext}}\) and \(J^{\mathrm {ext}}\) instead of \(\mathscr {P}^{\mathrm {int}}\) and \(J^{\mathrm {int}}\). For brevity, we only prove the claim for \(\mathscr {P}^{\mathrm {int}}\).
To prove (C.6), let \(\mathbf {c}\in \mathbb {R}^{J^{\mathrm {int}}}\). For \(m \in \mathbb {N}\) and \(j \in \mathbb {N}_0\), define \( \zeta _m := 2^{\alpha m} \, \Vert (c_\kappa )_{\kappa \in \mathcal {I}_m^{\mathrm {int}}} \Vert _{\ell ^p} \) and \( \omega _j := 2^{\alpha j} \big \Vert \big ( \Vert (c_{j,t,k}^{\natural })_{k \in \mathbb {Z}^d} \Vert _{\ell ^p} \big )_{t \in T_j} \big \Vert _{\ell ^q}, \) noting that  as well as \({\Vert \mathbf {c}^{\natural } \Vert _{b_{p,q}^{\tau }} = \Vert (\omega _j)_{j \in \mathbb {N}_0} \Vert _{\ell ^q}}\). Since \(|T_j| \le 2^d\) for all \(j \in \mathbb {N}_0\), we have \(\Vert \cdot \Vert _{\ell ^p (T_j)} \asymp \Vert \cdot \Vert _{\ell ^q (T_j)}\) for all \(j \in \mathbb {N}_0\), with implied constant only depending on d, p, q.
as well as \({\Vert \mathbf {c}^{\natural } \Vert _{b_{p,q}^{\tau }} = \Vert (\omega _j)_{j \in \mathbb {N}_0} \Vert _{\ell ^q}}\). Since \(|T_j| \le 2^d\) for all \(j \in \mathbb {N}_0\), we have \(\Vert \cdot \Vert _{\ell ^p (T_j)} \asymp \Vert \cdot \Vert _{\ell ^q (T_j)}\) for all \(j \in \mathbb {N}_0\), with implied constant only depending on d, p, q.
Now, define \(J_{j,t}^{\mathrm {int}} := \{ k \in \mathbb {Z}^d :(t, k) \in J_j^{\mathrm {int}} \}\) for \(j \in \mathbb {N}_0\) and \(t \in T_j\), and note for \(m \ge 2\) that \( \mathcal {I}_m^{\mathrm {int}} = \biguplus _{t \in T_{j_0 + m - 1}} \big ( \{ j_0 + m - 1 \} \times \{ t \} \times J_{j_0 + m - 1, t}^{\mathrm {int}} \big ) , \) which implies
with implied constants only depending on \(d,p,q,j_0,\alpha \). With similar arguments, we see that
Overall, we obtain that

which proves Eq. (C.6).
Step 3 (Completing the proof): Step 2 guarantees the existence of \(\gamma > 0\) satisfying  for all
for all  . Furthermore, we clearly have \(\Vert \iota _{\mathrm {int}} \, \mathbf {c}\Vert _{\ell ^2} = \gamma \, \Vert \mathbf {c}\Vert _{\ell ^2}\).
. Furthermore, we clearly have \(\Vert \iota _{\mathrm {int}} \, \mathbf {c}\Vert _{\ell ^2} = \gamma \, \Vert \mathbf {c}\Vert _{\ell ^2}\).
Similarly, Step 2 shows that there is \(\varrho > 0\) satisfying  for all \(\mathbf {c}\in \mathbb {R}^{J^{\mathrm {ext}}}\). Now, given \(\mathbf {b}\in {{\,\mathrm{Ball}\,}}\bigl (0, 1; b_{p,q}^{\tau }(\varOmega _{\mathrm {ext}}; \mathbb {R})\bigr )\), note that \(\mathbf {b}= (\mathbf {b}|_{J^{\mathrm {ext}}})^{\natural }\) and furthermore
for all \(\mathbf {c}\in \mathbb {R}^{J^{\mathrm {ext}}}\). Now, given \(\mathbf {b}\in {{\,\mathrm{Ball}\,}}\bigl (0, 1; b_{p,q}^{\tau }(\varOmega _{\mathrm {ext}}; \mathbb {R})\bigr )\), note that \(\mathbf {b}= (\mathbf {b}|_{J^{\mathrm {ext}}})^{\natural }\) and furthermore  so that
so that  satisfies \(\mathbf {b}= \iota _{\mathrm {ext}} \mathbf {c}\). It is clear that
satisfies \(\mathbf {b}= \iota _{\mathrm {ext}} \mathbf {c}\). It is clear that  .
.
Finally, Proposition 2 shows that  and
and  . Hence, we see for \(\mathbf {c}\in b_{p,q}^{\tau }(\varOmega _{\mathrm {int}};\mathbb {R})\) that
. Hence, we see for \(\mathbf {c}\in b_{p,q}^{\tau }(\varOmega _{\mathrm {int}};\mathbb {R})\) that  and hence \(b_{p,q}^\tau (\varOmega _{\mathrm {int}}; \mathbb {R}) \hookrightarrow \ell ^2(J^{\mathrm {int}})\). Similarly, one can show that \(b_{p,q}^\tau (\varOmega _{\mathrm {ext}}; \mathbb {R}) \hookrightarrow \ell ^2(J^{\mathrm {ext}})\). \(\square \)
and hence \(b_{p,q}^\tau (\varOmega _{\mathrm {int}}; \mathbb {R}) \hookrightarrow \ell ^2(J^{\mathrm {int}})\). Similarly, one can show that \(b_{p,q}^\tau (\varOmega _{\mathrm {ext}}; \mathbb {R}) \hookrightarrow \ell ^2(J^{\mathrm {ext}})\). \(\square \)
The Phase Transition for Sobolev Spaces with \(p \in \{1,\infty \}\)
In this subsection, we provide the missing proof of Theorem 8 for the cases \(p = 1\) and \(p = \infty \). We begin with the case \(p = 1\).
1.1 The case \(p = 1\)
The proof is crucially based on the following embedding.
Lemma 13
For arbitrary \(k,d \in \mathbb {N}\) and \(1 \le p < \infty \), we have \(W^{k,p}(\mathbb {R}^d) \hookrightarrow B^{k}_{p,\infty }(\mathbb {R}^d)\).
Proof
This follows from [1, Section 7.33]. Here, the definition of Besov spaces used in [1] coincides with our definition, as can be seen by combining [36, Theorem in Section 2.5.12] with [19, Proposition 17.21 and Theorem 17.24]. \(\square \)
Using this embedding, we can now prove Theorem 8 for the case \(p = 1\)
Proof of Theorem 8 for p = 1
Let \(k \in \mathbb {N}\) with \(k > d \cdot (\frac{1}{1} - \frac{1}{2})_{+} = \frac{d}{2}\) and define \(\mathcal {S}:= {{\,\mathrm{Ball}\,}}( 0, 1; W^{k,1}(\varOmega ) )\). Our goal is to apply Theorem 5 for \(\mathbf {X}:= \mathbf {Y}:= \mathbf {Z}:= L^2(\varOmega )\), \(\mathcal {S}_{\mathbf {X}} := {{\,\mathrm{Ball}\,}}(0,1;B^k_{1,\infty }(\varOmega ))\), and \(\mathcal {S}_{\mathbf {Y}} := {{\,\mathrm{Ball}\,}}(0,1;W^{k,2}(\varOmega ))\), with suitable choices of \(\varPhi ,\varPsi ,\mathbb {P}\).
To this end, first note that since \(\varOmega \subset \mathbb {R}^d\) is bounded, there exists \(\kappa > 0\) satisfying \(\kappa \, \Vert f \Vert _{W^{k,1}(\varOmega )} \le \Vert f \Vert _{W^{k,2}(\varOmega )}\) for all \(f \in W^{k,2}(\varOmega )\). Next, Theorems 7 and 8 (the latter for \(p = 2 \in (1,\infty )\)) show that \(\mathcal {S}_{\mathbf {X}}, \mathcal {S}_{\mathbf {Y}} \subset L^2(\varOmega )\) are bounded with

and that there exists a Borel measure \(\mathbb {P}_0\) on \(\mathcal {S}_{\mathbf {Y}}\) that is critical for \(\mathcal {S}_{\mathbf {Y}}\) with respect to \(L^2(\varOmega )\).
Next, we claim that there exists \(C > 0\) satisfying \(\Vert f \Vert _{B^k_{1,\infty }(\varOmega )} \le C \, \Vert f \Vert _{W^{k,1}(\varOmega )}\) for all \({f \in W^{k,1}(\varOmega )}\). Indeed, [33, Theorem 5 in Chapter VI] shows that there exists a bounded linear extension operator \(\mathscr {E}: W^{k,1}(\varOmega ) \rightarrow W^{k,1}(\mathbb {R}^d)\) satisfying \((\mathscr {E}f)|_{\varOmega } = f\) for all \(f \in W^{k,1}(\varOmega )\). Then, Lemma 13 yields \(C_1 > 0\) satisfying
so that we can choose \(C = C_1 \cdot \Vert \mathscr {E}\Vert \). In particular, this implies that \(\mathcal {S}\subset C \cdot \mathcal {S}_{\mathbf {X}} \subset L^2(\varOmega )\) is bounded, so that Lemma 16 shows that \(\mathcal {S}= \mathcal {S}\cap L^2(\varOmega ) \subset L^2(\varOmega )\) is measurable.
Overall, we see that if we choose
then \(\varPhi ,\varPsi \) are well-defined and satisfy all assumptions of Theorem 5. This theorem then shows that  and that \(\mathbb {P}:= \mathbb {P}_0 \circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\).
and that \(\mathbb {P}:= \mathbb {P}_0 \circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\).
Finally, Part (iii) of Theorem 7 yields a codec  satisfying
satisfying  . Since \(\varPhi \) is Lipschitz with \(\varPhi (\mathcal {S}_{\mathbf {X}}) \supset \mathcal {S}\), Lemma 8 shows that there exists a codec
. Since \(\varPhi \) is Lipschitz with \(\varPhi (\mathcal {S}_{\mathbf {X}}) \supset \mathcal {S}\), Lemma 8 shows that there exists a codec  that satisfies the estimate
that satisfies the estimate  , claimed in Part (iii) of Theorem 8. \(\square \)
, claimed in Part (iii) of Theorem 8. \(\square \)
1.2 The Case \(p = \infty \)
Let \(k \in \mathbb {N}\) with \(k > d \cdot (\frac{1}{\infty } - \frac{1}{2})_+ = 0\) and define \(\mathcal {S}:= {{\,\mathrm{Ball}\,}}(0, 1; W^{k,\infty }(\varOmega ))\). Note that trivially  is bounded, so that Lemma 16 implies that \(\mathcal {S}\subset L^2(\varOmega )\) is Borel measurable. Our goal is to apply Theorem 5 for \(\mathbf {X}:= \mathbf {Y}:= \mathbf {Z}:= L^2(\varOmega )\), \(\mathcal {S}_{\mathbf {X}} := {{\,\mathrm{Ball}\,}}(0,1; W^{k,2}(\varOmega ))\), and \(\mathcal {S}_{\mathbf {Y}} := {{\,\mathrm{Ball}\,}}(0,1;B^k_{\infty ,1}(\varOmega ))\), for suitable choices of \(\varPhi ,\varPsi \) and \(\mathbb {P}\).
is bounded, so that Lemma 16 implies that \(\mathcal {S}\subset L^2(\varOmega )\) is Borel measurable. Our goal is to apply Theorem 5 for \(\mathbf {X}:= \mathbf {Y}:= \mathbf {Z}:= L^2(\varOmega )\), \(\mathcal {S}_{\mathbf {X}} := {{\,\mathrm{Ball}\,}}(0,1; W^{k,2}(\varOmega ))\), and \(\mathcal {S}_{\mathbf {Y}} := {{\,\mathrm{Ball}\,}}(0,1;B^k_{\infty ,1}(\varOmega ))\), for suitable choices of \(\varPhi ,\varPsi \) and \(\mathbb {P}\).
To this end, first note that since \(\varOmega \subset \mathbb {R}^d\) is bounded, there exists \(C > 0\) satisfying \(\Vert f \Vert _{W^{k,2}(\varOmega )} \le C \, \Vert f \Vert _{W^{k,\infty }(\varOmega )}\) for all \(f \in W^{k,\infty }(\varOmega )\).
Next, it is well-known (see for instance [38, Example 7.2]) that there is \(\kappa > 0\) such that \(\kappa \, \Vert f \Vert _{W^{k,\infty }(\mathbb {R}^d)} \le \Vert f \Vert _{B^k_{\infty ,1}(\mathbb {R}^d)}\) for all \(f \in B^k_{\infty ,1}(\mathbb {R}^d)\). Now, for \(f \in B^k_{\infty ,1}(\varOmega )\) and \(\varepsilon > 0\), by definition of the norm on \(B^k_{\infty ,1}(\varOmega )\) (see Eq. (C.2)) there is some \(g \in B^k_{\infty ,1}(\mathbb {R}^d)\) with \({\Vert g \Vert _{B^k_{\infty ,1}(\mathbb {R}^d)} \le (1 + \varepsilon ) \Vert f \Vert _{B^k_{\infty ,1}(\varOmega )}}\) and \(f = g|_{\varOmega }\). Since \(g \in B^k_{\infty ,1}(\mathbb {R}^d) \subset W^{k,\infty }(\mathbb {R}^d)\), we see \(f \in W^{k,\infty }(\varOmega )\) and \( \kappa \Vert f \Vert _{W^{k,\infty }(\varOmega )} \le \kappa \Vert g \Vert _{W^{k,\infty }(\mathbb {R}^d)} \le \Vert g \Vert _{B^k_{\infty ,1}(\mathbb {R}^d)} \le (1 + \varepsilon ) \, \Vert f \Vert _{B^k_{\infty ,1}(\varOmega )} . \) We have thus shown
Finally, Theorems 7 and 8 (the latter applied with \(p = 2 \in (1,\infty )\)) show that the respective optimal compression rates are given by  and that there exists a Borel probability measure \(\mathbb {P}_0\) on \(\mathcal {S}_{\mathbf {Y}}\) that is critical for \(\mathcal {S}_{\mathbf {Y}}\) with respect to \(L^2(\varOmega )\).
and that there exists a Borel probability measure \(\mathbb {P}_0\) on \(\mathcal {S}_{\mathbf {Y}}\) that is critical for \(\mathcal {S}_{\mathbf {Y}}\) with respect to \(L^2(\varOmega )\).
Combining these observations, it is not hard to see that all assumptions of Theorem 5 are satisfied for
This theorem thus shows that  and that \(\mathbb {P}:= \mathbb {P}_0 \circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\).
and that \(\mathbb {P}:= \mathbb {P}_0 \circ \varPsi ^{-1}\) is a Borel probability measure on \(\mathcal {S}\) that is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\).
Finally, Theorem 8 shows that there exists  satisfying
satisfying  . Since \(\varPhi \) is Lipschitz with \(\varPhi (\mathcal {S}_{\mathbf {X}}) \supset \mathcal {S}\), Lemma 8 shows that there exists a codec
. Since \(\varPhi \) is Lipschitz with \(\varPhi (\mathcal {S}_{\mathbf {X}}) \supset \mathcal {S}\), Lemma 8 shows that there exists a codec  satisfying the estimate
satisfying the estimate  , as claimed in Part (iii) of Theorem 8. \(\square \)
, as claimed in Part (iii) of Theorem 8. \(\square \)
Measurability of Besov and Sobolev Balls
In this subsection, we show for the range of parameters considered in Theorems 7 and 8 that the balls \({{\,\mathrm{Ball}\,}}\big ( 0, R; B^\tau _{p,q}(\varOmega ) \big )\) and \({{\,\mathrm{Ball}\,}}\big ( 0, R; W^{k,p}(\varOmega ) \big )\) are measurable subsets of \(L^2(\varOmega )\). We remark that for the case where \(p,q \in (1,\infty )\), easier proofs than the ones given here are possible. Yet, since the proofs for the cases where \(p \in \{ 1,\infty \}\) or \(q \in \{ 1,\infty \}\) apply verbatim for a whole range of exponents, we prefer to state and prove the more general results.
We begin with the case of Besov spaces, for which the balls are in fact closed.
Lemma 14
Let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be open and bounded and let \(p,q \in (0,\infty ]\) and \(\tau \in \mathbb {R}\) with \(\tau > d \cdot (\frac{1}{p} - \frac{1}{2})_{+}\). Then, \(B^{\tau }_{p,q}(\varOmega ) \hookrightarrow L^2(\varOmega )\), and the balls \({{\,\mathrm{Ball}\,}}(0, R; B^{\tau }_{p,q}(\varOmega )) \subset L^2(\varOmega )\) are closed for all \(R > 0\).
Proof
Let \(p_0 := \max \{ p, 2 \}\). Then, [38, Example 7.2] shows that \(B^{\tau }_{p,q} (\mathbb {R}^d) \hookrightarrow L^{p_0}(\mathbb {R}^d)\), since \(p \le p_0\) and since \(\tau > d \cdot (\frac{1}{p} - \frac{1}{p_0})\) by our assumptions on \(\tau \). This implies \(B^{\tau }_{p,q}(\varOmega ) \hookrightarrow L^2(\varOmega )\), since if \(f \in B^{\tau }_{p,q}(\varOmega )\), then by definition of this space (see Eqs. (C.1) and (C.2)) there exists some \({g \in B^{\tau }_{p,q}(\mathbb {R}^d)}\) satisfying \(\Vert g \Vert _{B_{p,q}^{\tau }(\mathbb {R}^d)} \le 2 \Vert f \Vert _{B_{p,q}^{\tau }(\varOmega )}\) and \(f = g|_{\varOmega }\), and hence
It remains to show that \({{\,\mathrm{Ball}\,}}(0, R; B^{\tau }_{p,q}(\varOmega )) \subset L^2(\varOmega )\) is closed. To see this, first note that if \((g_n)_{n \in \mathbb {N}} \subset B_{p,q}^{\tau }(\mathbb {R}^d)\) satisfies \(g_n \rightarrow g \in \mathscr {S}'(\mathbb {R}^d)\) with convergence in \(\mathscr {S}'(\mathbb {R}^d)\), then \( \Vert g \Vert _{B^{\tau }_{p,q} (\mathbb {R}^d)} \le \liminf _{n \rightarrow \infty } \Vert g_n \Vert _{B^{\tau }_{p,q}(\mathbb {R}^d)} . \) Indeed, with the family \((\varphi _j)_{j \in \mathbb {N}_0} \subset \mathscr {S}(\mathbb {R}^d)\) used in the definition of Besov spaces (see Sect. C.1), we have for \(f \in \mathscr {S}'(\mathbb {R}^d)\) and \(x \in \mathbb {R}^d\) that \( \mathcal {F}^{-1}(\varphi _j \cdot \widehat{f} \,) (x) = (2\pi )^{-d/2} \cdot \big \langle \widehat{f}, \quad e^{i \langle x, \bullet \rangle } \varphi _j \big \rangle _{\mathscr {S}', \mathscr {S}} ; \) see for instance [30, Theorem 7.23]. From this, we easily see that \(\mathcal {F}^{-1}(\varphi _j \cdot \widehat{g_n}) \rightarrow \mathcal {F}^{-1}(\varphi _j \cdot \widehat{g})\), with pointwise convergence as \(n \rightarrow \infty \). Therefore, Fatou’s lemma shows that \( \Vert \mathcal {F}^{-1}(\varphi _j \cdot \widehat{g}) \Vert _{L^p} \le \liminf _{n \rightarrow \infty } \Vert \mathcal {F}^{-1}(\varphi _j \cdot \widehat{g_n}) \Vert _{L^p} . \) By another application of Fatou’s lemma, we therefore see
as claimed.
Now, we prove the claimed closedness. Let \((f_n)_{n \in \mathbb {N}} \subset {{\,\mathrm{Ball}\,}}(0, R; B_{p,q}^{\tau }(\varOmega )) \subset L^2(\varOmega )\) such that \(f_n \rightarrow f \in L^2(\varOmega )\) with convergence in \(L^2(\varOmega )\). By definition of \(B_{p,q}^{\tau }(\varOmega )\) (see Eqs. (C.1) and (C.2)), for each \(n \in \mathbb {N}\) there exists \(g_n \in B_{p,q}^{\tau }(\mathbb {R}^d)\) satisfying \(f_n = g_n |_\varOmega \) and
As seen above, \(B_{p,q}^{\tau }(\mathbb {R}^d) \hookrightarrow L^{p_0}(\mathbb {R}^d)\), so that \((g_n)_{n \in \mathbb {N}} \subset L^{p_0}(\mathbb {R}^d) = (L^{p_0'}(\mathbb {R}^d))'\) is bounded, where \(p_0' \le 2 < \infty \), so that \(L^{p_0'}(\mathbb {R}^d)\) is separable. Thus, [2, Theorem 8.5] shows that there is a subsequence \((g_{n_k})_{k \in \mathbb {N}}\) and some \(g \in L^{p_0}(\mathbb {R}^d)\) such that \(g_{n_k} \rightarrow g\) in the weak-\(*\)-sense in \(L^{p_0}(\mathbb {R}^d) = (L^{p_0'}(\mathbb {R}^d) )'\). In particular, \(g_{n_k} \rightarrow g\) in \(\mathscr {S}'(\mathbb {R}^d)\). By what we showed above, this implies \( \Vert g \Vert _{B_{p,q}^{\tau }(\mathbb {R}^d)} \le \liminf _{k \rightarrow \infty } \Vert g_{n_k} \Vert _{B_{p,q}^{\tau }(\mathbb {R}^d)} \le R . \) Finally, we have for any \(\varphi \in C_c^\infty (\varOmega )\) that \( \langle g, \varphi \rangle = \lim _{k \rightarrow \infty } \langle g_{n_k}, \varphi \rangle = \lim _{k \rightarrow \infty } \langle f_{n_k}, \varphi \rangle = \langle f, \varphi \rangle , \) since \(f_{n_k} = g_{n_k}|_{\varOmega }\) and \(f_{n_k} \rightarrow f\) in \(L^2(\varOmega )\). Overall, we thus see that \(f = g|_{\varOmega } \in B_{p,q}^{\tau }(\varOmega )\) and \(\Vert f \Vert _{B_{p,q}^{\tau }(\varOmega )} \le \Vert g \Vert _{B_{p,q}^{\tau }(\mathbb {R}^d)} \le R\). \(\square \)
For the Sobolev spaces \(W^{k,p}(\varOmega )\) with \(p = 1\), the set \({{\,\mathrm{Ball}\,}}\big ( 0, R; W^{k,1}(\varOmega ) \big )\) is not closed in \(L^2(\varOmega )\). In order to show that this ball is nonetheless Borel measurable, we begin with the following result on \(\mathbb {R}^d\).
Lemma 15
Let \(d,k \in \mathbb {N}\) and \(p \in [1,2]\). Then, \(L^2(\mathbb {R}^d) \cap W^{k,p}(\mathbb {R}^d)\) is a Borel-measurable subset of \(L^2(\mathbb {R}^d)\).
Proof
Let \(\varphi \in C_c^\infty (\mathbb {R}^d)\) with \(\varphi \ge 0\) and \(\int _{\mathbb {R}^d} \varphi (x) \, d x = 1\) and define \(\varphi _n (x) := n^{d} \cdot \varphi (n x)\). It follows from [2, Section 4.13] that if \(f \in L^2(\mathbb {R}^d)\), then \(\varphi _n *f \in L^2(\mathbb {R}^d) \cap C^\infty (\mathbb {R}^d)\) with \(\partial ^\alpha (\varphi _n *f) = (\partial ^\alpha \varphi _n) *f\).
Step 1: Define \(\mathcal {S}:= L^2(\mathbb {R}^d) \cap W^{k,p}(\mathbb {R}^d)\). In this step, we show that
For “\(\subset \)”, note that if \(f \in \mathcal {S}\), then from the definition of the weak derivative we see
so that [2, Theorem 4.15] shows that \((\partial ^\alpha \varphi _n) *f \xrightarrow [n\rightarrow \infty ]{} \partial ^\alpha f\), with convergence in \(L^p (\mathbb {R}^d)\). This proves “\(\subset \)”.
For “\(\supset \)”, let \(f \in L^2(\mathbb {R}^d)\) such that \(\big ( (\partial ^\alpha \varphi _n) *f \big )_{n \in \mathbb {N}}\) is Cauchy in \(L^p (\mathbb {R}^d)\) for each \(\alpha \in \mathbb {N}_0^d\) with \(|\alpha | \le k\). Define \(g_\alpha := \lim _{n\rightarrow \infty } [(\partial ^\alpha \varphi _n) *f] \in L^p(\mathbb {R}^d)\) for \(|\alpha | \le k\). Since [2, Theorem 4.15] shows that \(\varphi _n *f \rightarrow f\) with convergence in \(L^2\), we get \(f = g_0 \in L^p(\mathbb {R}^d)\). Furthermore, as seen above, we have \(\varphi _n *f \in C^\infty (\mathbb {R}^d)\) with \(\partial ^\alpha (\varphi _n *f) = (\partial ^\alpha \varphi _n) *f\). Therefore, we see for arbitrary \(\psi \in C_c^\infty (\mathbb {R}^d)\) and \(\alpha \in \mathbb {N}_0^d\) with \(|\alpha | \le k\) that
which shows that \(g_\alpha \) is the \(\alpha \)-th weak derivative of f; that is, \(\partial ^\alpha f = g_\alpha \in L^p(\mathbb {R}^d)\). Since this holds for all \(|\alpha | \le k\), we see that \(f \in W^{k,p}(\mathbb {R}^d)\) and thus \(f \in \mathcal {S}\).
Step 2: For \(n,m,M \in \mathbb {N}\), define
Since \(p \le 2\), it is easy to see that \(\varGamma _{n,m,M}\) is well-defined and continuous. Furthermore, \( \Vert [(\partial ^\alpha \varphi _n) *f] - [(\partial ^\alpha \varphi _m) *f] \Vert _{L^p} = \sup _{M \in \mathbb {N}} \varGamma _{n,m,M}(f), \) which—together with the result from Step 1—implies that
is a Borel-measurable subset of \(L^2(\mathbb {R}^d)\). \(\square \)
We can now prove a similar result on bounded domains. For the convenience of the reader, we recall that \(\Vert f \Vert _{W^{k,p}} = \max _{|\alpha | \le k} \Vert \partial ^\alpha f \Vert _{L^p}\); see Eq. (4.2).
Lemma 16
Let \(p \in [1,\infty ]\), \(k \in \mathbb {N}\), \(R \in (0,\infty )\), and let \(\varOmega \subset \mathbb {R}^d\) be open and bounded. In case of \(p = 1\), assume additionally that \(\varOmega \) is a Lipschitz domain.
Then, \({L^2(\varOmega ) \cap {{\,\mathrm{Ball}\,}}\big ( 0, R; W^{k,p}(\varOmega ) \big )}\) is a Borel-measurable subset of \(L^2(\varOmega )\).
Proof
Step 1: The space \(C^k ({\overline{\varOmega }})\) (with the norm \({\Vert f \Vert _{C^k({\overline{\varOmega }})} = \max _{|\alpha | \le k} \Vert \partial ^\alpha f \Vert _{\sup }}\)) is separable; see [2, Section 4.18]. Since subsets of separable spaces are separable, there exists a sequence \((\varphi _n)_{n \in \mathbb {N}} \subset C_c^\infty (\varOmega ) \setminus \{ 0 \}\) that is dense in \(C_c^\infty (\varOmega ) \setminus \{ 0 \}\) with respect to \(\Vert \bullet \Vert _{C^k({\overline{\varOmega }})}\). For \(n \in \mathbb {N}\), define
where \(p' \in [1,\infty ]\) is the conjugate exponent to p. Since \(\partial ^\alpha \varphi _n \in C_c^\infty (\varOmega ) \subset L^2(\varOmega )\), we see that \(\gamma _n\) is continuous, so that \( \gamma : L^2(\varOmega ) \rightarrow [0,\infty ], f \mapsto \sup _{n \in \mathbb {N}} \gamma _n (f) \) is Borel measurable.
Step 2: We claim that \(\bigl |\int _\varOmega f \cdot \partial ^\alpha \varphi \, d x\bigr | \le \gamma (f) \cdot \Vert \varphi \Vert _{L^{p'}}\) for all \(f \in L^2(\varOmega )\), \(\varphi \in C_c^\infty (\varOmega )\), and \(|\alpha | \le k\). Clearly, we can assume without loss of generality that \(\gamma (f) < \infty \) and \(\varphi \ne 0\). Thus, there is a sequence \((n_\ell )_{\ell \in \mathbb {N}} \subset \mathbb {N}\) such that \(\Vert \varphi - \varphi _{n_\ell } \Vert _{C^k(\overline{\varOmega })} \rightarrow 0\), which easily implies \(\Vert \varphi _{n_\ell } \Vert _{L^{p'}} \rightarrow \Vert \varphi \Vert _{L^{p'}}\) and \(\partial ^\alpha \varphi _{n_\ell } \rightarrow \partial ^\alpha \varphi \) with convergence in \(L^2(\varOmega )\) for all \(|\alpha | \le k\). Hence, \( \bigl |\int _\varOmega f \cdot \partial ^\alpha \varphi \, d x\bigr | = \lim _{\ell \rightarrow \infty } \bigl |\int _\varOmega f \cdot \partial ^\alpha \varphi _{n_\ell } \, d x\bigr | \le \lim _{\ell \rightarrow \infty } \gamma (f) \cdot \Vert \varphi _{n_\ell } \Vert _{L^{p'}} = \gamma (f) \cdot \Vert \varphi \Vert _{L^{p'}}, \) as claimed.
Step 3: In this step, we prove for \(p > 1\) that \(\mathcal {S}:= L^2(\varOmega ) \cap {{\,\mathrm{Ball}\,}}(0, R ; W^{k,p}(\varOmega ))\) satisfies \(\mathcal {S}= \{ f \in L^2(\varOmega ) :\gamma (f) \le R \}\), which then implies that \(\mathcal {S}\) is a Borel measurable subset of \(L^2(\varOmega )\).
First, if \(f \in \mathcal {S}\), then \( \bigl |\int _\varOmega f \, \partial ^\alpha \varphi _n \, d x\bigr | = \bigl |\int _\varOmega \varphi _n \, \partial ^\alpha f \, d x\bigr | \le \Vert \partial ^\alpha f \Vert _{L^p} \cdot \Vert \varphi _n \Vert _{L^{p'}} \le R \cdot \Vert \varphi _n \Vert _{L^{p'}} \) for all \(|\alpha | \le k\) and \(n \in \mathbb {N}\), so that \(\gamma (f) \le R\).
Conversely, if \(\gamma (f) \le R\), then Step 2 shows for arbitrary \(|\alpha | \le k\) and \(\varphi \in C_c^\infty (\varOmega )\) that  so that [2, Section E6.7] implies that
so that [2, Section E6.7] implies that  ; this uses our assumption \(p > 1\). Finally, for \(\varphi \in C_c^\infty (\varOmega )\) and \(|\alpha | \le k\), we have \( \bigl |\int _\varOmega \varphi \cdot \partial ^\alpha f \, d x\bigr | = \bigl |\int _\varOmega f \cdot \partial ^\alpha \varphi \, d x\bigr | \le R \cdot \Vert \varphi \Vert _{L^{p'}} . \) Therefore, [2, Corollary 6.13] shows \(\Vert \partial ^\alpha f \Vert _{L^p} \le R\) for all \(|\alpha | \le k\). By our definition of \(\Vert \bullet \Vert _{W^{k,p}(\varOmega )}\) (see Eq. (4.2)), this implies \(f \in \mathcal {S}\).
; this uses our assumption \(p > 1\). Finally, for \(\varphi \in C_c^\infty (\varOmega )\) and \(|\alpha | \le k\), we have \( \bigl |\int _\varOmega \varphi \cdot \partial ^\alpha f \, d x\bigr | = \bigl |\int _\varOmega f \cdot \partial ^\alpha \varphi \, d x\bigr | \le R \cdot \Vert \varphi \Vert _{L^{p'}} . \) Therefore, [2, Corollary 6.13] shows \(\Vert \partial ^\alpha f \Vert _{L^p} \le R\) for all \(|\alpha | \le k\). By our definition of \(\Vert \bullet \Vert _{W^{k,p}(\varOmega )}\) (see Eq. (4.2)), this implies \(f \in \mathcal {S}\).
Step 4: We prove the claim for the case \(p = 1\). Since \(\varOmega \) is a Lipschitz domain, [33, Theorem 5 in Chapter VI] yields a linear extension operator \({E : L^1(\varOmega ) \rightarrow L^1(\mathbb {R}^d)}\) satisfying \((E f)|_\varOmega = f\) for all \(f \in L^1(\varOmega )\), and such that for arbitrary \(\ell \in \mathbb {N}_0\) and \(q \in [1,\infty ]\) the restriction \(E : W^{\ell ,q}(\varOmega ) \rightarrow W^{\ell ,q}(\mathbb {R}^d)\) is well-defined and bounded.
In particular, \(E : L^2(\varOmega ) \rightarrow L^2(\mathbb {R}^d)\) is continuous and hence measurable. By Lemma 15, this means that \(\varTheta := \{ f \in L^2(\varOmega ) :E f \in W^{k,1}(\mathbb {R}^d) \} \subset L^2(\varOmega )\) is measurable. We claim that
which then implies that \(\mathcal {S}\subset L^2(\varOmega )\) is measurable.
For “\(\subset \)”, we see as in Step 3 that \(\gamma (f) \le R\) if \(f \in \mathcal {S}\). Furthermore, by the properties of the extension operator E, we also have \(f \in \varTheta \) if \(f \in \mathcal {S}\). For “\(\supset \)”, let \(f \in \varTheta \) satisfy \(\gamma (f) \le R\). Since \(f \in \varTheta \), we have \(f = (E f)|_\varOmega \in W^{k,1}(\varOmega )\). One can then argue as at the end of Step 3 (using [2, Corollary 6.13]) to see that \(f \in {{\,\mathrm{Ball}\,}}(0, R; W^{k,1}(\varOmega ))\) and thus \(f \in \mathcal {S}\). \(\square \)
Proof of the Lower Bounds for Neural Network Approximation
In this appendix, we establish a connection between rate distortion theory and approximation by neural networks. This is based on the observation from [4, 29] that one can use the existence of approximating networks to construct a codec for a function class. This in turn relies on sharp estimates for the number of functions in the class \(\mathcal {NN}_{d,W}^{\sigma ,\varrho }\) appearing in Theorem 3.
The first ingredient for such a bound is the following “compression lemma,” showing that for each neural network \(\varPhi \), one can find a “compressed network” \(\varPsi \) with the same realization \(R_\varrho \varPsi = R_\varrho \varPhi \) and such that the number of weights, layers, and neurons of \(\varPsi \) is controlled by the number of weights of \(\varPhi \). We remark that a similar result already appears in [29, Lemma G.1]. However, the proof in [29] proceeds by removing “dead neurons;” that is, neurons that do not receive input from any other neurons. The proof then relies on the assumption \(\varrho (0) = 0\) to ensure that a “dead neuron” has trivial output. In contrast, our proof relies on removing “ignored neurons,” whose output is not used in the subsequent layer; this allows us to omit the assumption \(\varrho (0) = 0\).
Lemma 17
Let \(d,k \in \mathbb {N}\) and \(\varTheta \subset \mathbb {R}\) with \(0 \in \varTheta \). Let \(\varPhi \) be a neural network with all weights/biases contained in \(\varTheta \) and with \(d_{\mathrm {in}}(\varPhi ) = d\) and \(d_{\mathrm {out}}(\varPhi ) = k\). Then, there exists a “compressed” network \(\varPsi \) with the following properties:
-
1.
\(d_{\mathrm {in}}(\varPsi ) = d\) and \(d_{\mathrm {out}}(\varPsi ) = k\),
-
2.
all weights/biases of \(\varPsi \) are contained in \(\varTheta \),
-
3.
for every \(\varrho : \mathbb {R}\rightarrow \mathbb {R}\), we have \(R_\varrho \varPhi = R_\varrho \varPsi \),
-
4.
\(W(\varPsi ) \le W(\varPhi )\),
-
5.
\(L(\varPsi ) \le W(\varPsi ) + 1\),
-
6.
\(N(\varPsi ) \le k + d + W(\varPsi )\).
Proof
For an arbitrary neural network \(\varPhi \), define \(\mathcal {C}(\varPhi ) := L(\varPhi ) + N(\varPhi ) \in \mathbb {N}\). Furthermore, define the set of “bad” networks as
Toward a contradiction, assume that the lemma is false. Then, there exists \(\varPhi ^*\in \mathcal {B}\) satisfying \(\mathcal {C}(\varPhi ^*) = \min _{\varPhi \in \mathcal {B}} \mathcal {C}(\varPhi )\). Write \(\varPhi ^*= \big ( (A_1,b_1),\dots ,(A_L,b_L) \big )\) with \(A_\ell \in \mathbb {R}^{N_\ell \times N_{\ell -1}}\) and \(b_\ell \in \mathbb {R}^{N_\ell }\) where \(N_0 = d\) and \(N_L = k\). Note that if \(L = 1\), then \(L(\varPhi ^*) = 1 \le W(\varPhi ^*) + 1\) and \(N(\varPhi ^*) \le k + d \le k + d + W(\varPhi ^*)\), so that properties 1–6 of the lemma are satisfied for \(\varPsi = \varPhi ^*\) (and \(\varPhi ^*\) instead of \(\varPhi \)), in contradiction to \(\varPhi ^*\in \mathcal {B}\). Hence, \(L \ge 2\).
Below, we will show that
Thus, for every \(\ell \in \{ 2,\dots ,L \}\) and \(j \in [N_{\ell -1}]\), we have \(\sum _{i=1}^{N_\ell } \mathbbm {1}_{(A_\ell )_{i,j} \ne 0} \ge 1\) and hence \( W(\varPhi ^*) \ge \sum _{\ell =2}^L \sum _{j=1}^{N_{\ell -1}} \sum _{i=1}^{N_\ell } \mathbbm {1}_{(A_\ell )_{i,j} \ne 0} \ge \sum _{\ell =2}^L N_{\ell -1} . \) On the one hand, this implies \(W(\varPhi ^*) \ge L - 1\) and on the other hand
Thus, choosing \(\varPsi = \varPhi ^*\), we see that \(\varPsi \) satisfies properties 1–6 of the lemma (with \(\varPhi \) replaced by \(\varPhi ^*\)), in contradiction to \(\varPhi ^*\in \mathcal {B}\).
It remains to prove Eq. (F.1). Assume toward a contradiction that it is false. Then, there exist \(\ell ^*\in \{ 2,\dots ,L \}\) and \(j^*\in [N_{\ell ^*- 1}]\) satisfying \((A_{\ell ^*})_{-,j^*} = 0\). We distinguish two cases:
Case 1 (\(N_{\ell ^*- 1} \ge 2\)): In this case, define a new network
where \(A \in \mathbb {R}^{(N_{\ell ^*- 1} - 1) \times N_{\ell ^*- 2}}\) and \(b \in \mathbb {R}^{N_{\ell ^*- 1} - 1}\) are obtained from \(A_{\ell ^*- 1}\) and \(b_{\ell ^*- 1}\), respectively, by dropping the \(j^*\)-th row. Further, we set \(c := b_{\ell ^*} \in \mathbb {R}^{N_{\ell ^*}}\) and we choose \(B \in \mathbb {R}^{N_{\ell ^*} \times (N_{\ell ^*- 1} - 1)}\) as the result of dropping the \(j^*\)-th column of \(A_{\ell ^*}\).
Since \((A_{\ell ^*})_{-,j^*} = 0\), it is easy to see \(R_\varrho \varPhi = R_\varrho \varPhi ^*\) for every \(\varrho : \mathbb {R}\rightarrow \mathbb {R}\). Note that \(\mathcal {C}(\varPhi ) = \mathcal {C}(\varPhi ^*) - 1\), so that \(\varPhi \notin \mathcal {B}\) by “minimality” of \(\varPhi ^*\). Thus, there exists a network \(\varPsi \) satisfying properties 1–6 from the statement of the lemma. Note in particular that \(R_\varrho \varPhi ^*= R_\varrho \varPhi = R_\varrho \varPsi \) and that \(W(\varPsi ) \le W(\varPhi ) \le W(\varPhi ^*)\); hence, \(\varPsi \) also satisfies properties 1–6 of the lemma for \(\varPhi ^*\) instead of \(\varPhi \), in contradiction to \(\varPhi ^*\in \mathcal {B}\).
Case 2 (\(N_{\ell ^*- 1} = 1\)): Since \(j^*\in [N_{\ell ^*- 1}]\), this implies \(j^*= 1\). Furthermore, since \( A_{\ell ^*} \in \mathbb {R}^{N_{\ell ^*} \times N_{\ell ^*- 1}} = \mathbb {R}^{N_{\ell ^*} \times 1} \) and \((A_{\ell ^*})_{-,1} = (A_{\ell ^*})_{-,j^*} = 0\), this implies \(A_{\ell ^*} = 0\). Define \( \varPhi := \big ( (0_{N_{\ell ^*} \times d}, b_{\ell ^*}) , (A_{\ell ^*+ 1}, b_{\ell ^*+ 1}), \dots , (A_L,b_L) \big ) \) and note for any \(\varrho : \mathbb {R}\rightarrow \mathbb {R}\) and \(T_\ell \, x := A_\ell \, x + b_\ell \) that \(T_{\ell ^*} x = b_{\ell ^*}\) for all \(x \in \mathbb {R}^{N_{\ell ^*- 1}}\), which implies that

Furthermore, note that all weights/biases of \(\varPhi \) belong to \(\varTheta \cup \{ 0 \} = \varTheta \) and because of \(\ell ^*\ge 2\) that \(L(\varPhi ) = L - \ell ^*+ 1 \le L - 1 < L(\varPhi ^*)\) and \(N(\varPhi ) \le N(\varPhi ^*)\), so that \(\mathcal {C}(\varPhi ) < \mathcal {C}(\varPhi ^*)\). Now, since also \(W(\varPhi ) \le W(\varPhi ^*)\), one obtains a contradiction exactly as in Case 1. \(\square \)
Using the preceding compression result, we can now derive a sharp bound on the cardinality of the set \(\mathcal {NN}_{d,W}^{\sigma ,\varrho }\) of neural network functions that appears in Theorem 3. We mention that this result is similar to [29, Lemma B.4], but without the assumption \(\varrho (0) = 0\).
Lemma 18
Let \(\varrho : \mathbb {R}\rightarrow \mathbb {R}\) and \(d,\sigma \in \mathbb {N}\). With \(\mathcal {NN}_{d,W}^{\sigma ,\varrho }\) as defined in Theorem 3, there exists a constant \(C_0 = C_0(d,\sigma ) \in \mathbb {N}\) satisfying
In fact, one can choose \(C_0 = 4 + 4 \lceil \log _2(4 e d) \rceil + 8 \sigma \).
Proof
Fix \(W \in \mathbb {N}\).
Step 1: Recall the definition of \(G_{\sigma ,W}\) (Eq. (1.7)) and note \(|\mathbb {Z}\cap [a,b]| \le 1 + (b - a)\) for \(a \le b\). Thus, noting that \(\log _2(1 + W) \ge \log _2(2) = 1\), we easily see
Step 2: Given \(L \in \mathbb {N}\), define \(N_0 := d\) and \(N_L := 1\) and define the set of all architectures with L layers and at most W “hidden neurons” as
with the understanding that \(\mathscr {A}_1\) contains a single element, the empty tuple. Next, for fixed architecture \(\varvec{N}\in \mathscr {A}_L\), define
Finally, given subsets \(I \subset H_{\varvec{N}}\) and \(J \subset R_{\varvec{N}}\), define
for \(\ell ,i,j,k \in \mathbb {N}\). Overall, recalling the definition of \(\mathcal {NN}_{d,W}^{\sigma ,\varrho }\) and using Lemma 17, we see

Finally, note that \( |R_{\varvec{N}}| = \sum _{\ell =1}^L N_\ell \le W + 1 \le 4 d \cdot W^2 \) and
Step 3: We complete the proof by estimating \(|\mathcal {NN}_{d,W}^{\sigma ,\varrho }|\) using the inclusion from Step 2. First, note that if \(\varLambda \) is any non-empty set with \(|\varLambda | \le 4d \cdot W^2\), then a standard estimate for (sums of) binomial coefficients (see, e.g., [37, Exercise 0.0.5]) shows
where the overall estimate also holds if \(\varLambda = \emptyset \). Furthermore, using the estimate from Step 1, we see for \(I \subset H_{\varvec{N}}\) and \(J \subset R_{\varvec{N}}\) with \(|I|, |J| \le W\) that

Moreover, each \(\varvec{N}= (N_1,\dots ,N_{L-1}) \in \mathscr {A}_L\) satisfies \(N_\ell \le W\), which implies for \(L \le W+1\) that \(|\mathscr {A}_L| \le |[W]^{L-1}| \le W^W\). Overall, combining the preceding observations with the inclusion from Step 2, we conclude as claimed that
\(\square \)
Finally, using the preceding estimate for the cardinality of \(\mathcal {NN}_{d,W}^{\sigma ,\varrho }\), we can now formulate the precise connection between neural network approximation and rate distortion theory.
Lemma 19
Let \(\emptyset \ne \varOmega \subset \mathbb {R}^d\) be measurable, let \(\varrho : \mathbb {R}\rightarrow \mathbb {R}\) be measurable, and let \(\sigma \in \mathbb {N}\). For \(f \in L^2(\varOmega )\) and \(\varepsilon \in (0, 1)\), let \(W_{\sigma ,\varrho } (f;\varepsilon ) \in \mathbb {N}\cup \{ \infty \}\) be as defined in Theorem 3. For \(\tau > 0\) define
Then, there exists a codec  such that
such that

Proof
Step 1: (Constructing the codec \(\mathcal {C}\)): Let \(C_0 = C_0(d,\sigma ) \in \mathbb {N}\) as in Lemma 18. For \(R \in \mathbb {N}_{\ge C_0}\), let \(W_R \in \mathbb {N}\) be maximal with \(C_0 \cdot W_R \cdot \lceil \log _2 (1+W_R) \rceil ^2 \le R\). By Lemma 18, there exists a surjection \(D_R : \{ 0,1 \}^R \rightarrow \mathcal {NN}_{d,W_R}^{\sigma ,\varrho }\). For each \(f \in L^2(\varOmega )\), choose \(\mathbf {c}(R,f) \in \{ 0,1 \}^R\) such that
and define \({E_R : L^2(\varOmega ) \rightarrow \{ 0,1 \}^R, f \mapsto \mathbf {c}(R,f)}\).
Finally, for \(R \in \mathbb {N}\) with \(R < C_0\), define
Step 2: (Completing the proof): Let \(\tau > 0\), \(\delta \in (0,\frac{1}{\tau })\), and \(f \in \mathcal {A}_{\mathcal {NN},\sigma ,\varrho }^\tau \), so that there is \(C = C(f) > 0\) satisfying \(W_{\sigma ,\varrho } (f;\varepsilon ) \le C \cdot \varepsilon ^{-\tau }\) for all \(\varepsilon \in (0,1)\).
Since the logarithm grows slower than any positive power and since the maximality of \(W_R\) implies that \(R \le C_0 \cdot (W_R + 1) \cdot \lceil \log _2 (W_R + 2) \rceil ^2\), it is easy to see that there exists \(C_1 = C_1(\tau ,\delta ,d,\sigma ) > 0\) such that \(R \le C_1 \cdot W_R^{1/(1 - \tau \delta )}\) for all \(R \in \mathbb {N}_{\ge C_0}\). Note that if R is large enough, then \(\varepsilon := C^{1/\tau } \cdot C_1^{(1 - \delta \tau )/\tau } \cdot R^{-(\frac{1}{\tau } - \delta )}\) satisfies \(\varepsilon \in (0,1)\). For these R, we thus get
By definition of \(W_{\sigma ,\varrho }(f;\varepsilon )\) and by choice of \(D_R, E_R\), we therefore see for all sufficiently large \(R \in \mathbb {N}\) that
which easily implies that  . Since \(\tau > 0\), \(\delta \in (0, \frac{1}{\tau })\), and \(f \in \mathcal {A}_{\mathcal {NN},\sigma ,\varrho }^\tau \) were arbitrary, we are done. \(\square \)
. Since \(\tau > 0\), \(\delta \in (0, \frac{1}{\tau })\), and \(f \in \mathcal {A}_{\mathcal {NN},\sigma ,\varrho }^\tau \) were arbitrary, we are done. \(\square \)
Proof of Theorem 3
Part 1: Let \(s > s^*\). As shown in Theorems 7 and 8, the measure \(\mathbb {P}\) from Theorem 1 is critical for \(\mathcal {S}\) with respect to \(L^2(\varOmega )\). Thus (see Eq. (2.1)), there exist \(c, \varepsilon _0 > 0\) such that \(\mathbb {P}\big ( \mathcal {S}\cap {{\,\mathrm{Ball}\,}}(f,\varepsilon ; L^2(\varOmega )) \big ) \le 2^{-c \cdot \varepsilon ^{-1/s}}\) for all \(f \in L^2(\varOmega )\) and \(\varepsilon \in (0,\varepsilon _0)\). Lemma 18 shows that \(|\mathcal {NN}_{d,W}^{\sigma ,\varrho }| \le 2^{C_0 W \lceil \log _2(1+W) \rceil ^2}\) for all \(W \in \mathbb {N}\) and a suitable \(C_0 = C_0(d,\sigma )\); in fact, one can take \(C_0 = 4 + 4 \lceil \log _2 (4 e d) \rceil + 8 \sigma \). Thus, setting \(C := C_0\), we see that
for all \(\varepsilon \in (0,\varepsilon _0)\). This is precisely what is claimed in Part 1 of Theorem 3.
Part 2: For \(\ell ,\sigma \in \mathbb {N}\), define
It is not hard to see that \( \mathcal {A}_{\mathcal {NN},\varrho }^* \subset \bigcup _{\sigma \in \mathbb {N}} \bigcup _{\ell \in \mathbb {N}} \mathcal {A}_{\ell ,\sigma }, \) so that it suffices to show \({\mathbb {P}^*(\mathcal {A}_{\ell ,\sigma }) = 0}\) for all \(\sigma ,\ell \in \mathbb {N}\). To see this, let  as in Lemma 19, and note with the notation of that lemma and with \(\delta := \frac{s^*/ 2}{2\ell - 1}\) and \(\tau = \bigl (1 - \frac{1}{2 \ell }\bigr ) \big / s^*\) that
as in Lemma 19, and note with the notation of that lemma and with \(\delta := \frac{s^*/ 2}{2\ell - 1}\) and \(\tau = \bigl (1 - \frac{1}{2 \ell }\bigr ) \big / s^*\) that
where Theorem 1 shows that \( \mathbb {P}^*\Bigl ( \mathcal {A}_{\mathcal {S},L^2(\varOmega )}^{s^*\cdot \frac{2 \ell - 1/2}{2\ell - 1}} (\mathcal {C}) \Bigr ) = 0. \) \(\square \)
We close this section by proving the claim at the end of Remark 3.
Proof of Remark 3
Case 1 (Besov spaces): Here, \(\mathcal {S}= {{\,\mathrm{Ball}\,}}(0,1; B_{p,q}^{\tau } (\varOmega ; \mathbb {R}))\) and \(s^*= \tau / d\), where \(\tau > d \cdot (\frac{1}{p} - \frac{1}{2})_+\). By definition of the space \(B_{p,q}^{\tau } (\varOmega ; \mathbb {R})\) (see Eqs. (C.1) and (C.2)), each \(f \in \mathcal {S}\) extends to a function \(\tilde{f} \in B_{p,q}^{\tau } (\mathbb {R}^d; \mathbb {R})\) satisfying \(\Vert \tilde{f} \Vert _{B_{p,q}^{\tau } (\mathbb {R}^d; \mathbb {R})} \le 2\). Thanks to [36, Theorem in Section 2.5.12], this implies for a suitable \(C_1 = C_1(d,p,q,\tau ) > 0\) that \(\Vert f \Vert _{B_{p,q}^{\tau ,*} (\varOmega )} \le C_1\), where \(\Vert \cdot \Vert _{B_{p,q}^{\tau ,*}(\varOmega )}\) is the norm on the Besov space used in [34].
Now, [34, Proposition 1] yields \(C_2, C_3, N_0, \theta \in \mathbb {N}_{\ge 2}\) (all depending only on \(d,p,q,\tau \)) such that for every \(f \in \mathcal {S}\) and \(N \ge N_0\), there exists a network \({\varPhi = \varPhi (f,N)}\) satisfying \(\Vert f - R_\varrho (\varPhi ) \Vert _{L^2(\varOmega )} \le \frac{C_2}{2} \cdot N^{- s^*}\) as well as \(L(\varPhi ) \le C_3 \cdot \log _2 N\) and \({W(\varPhi ) \le C_3 \cdot N \cdot \log _2 N}\), and such that all weights of \(\varPhi \) have absolute value at most \(C_3 \cdot N^{\theta }\). This almost implies the desired estimate; the main issue is that the weights are merely bounded, but not necessarily quantized. To fix this, we will use [13, Lemma VI.8].
To make this formal, let us assume in what follows that \(\varepsilon \in (0,\frac{1}{2}) \cap (0, C_2 \cdot N_0^{-s^*})\); it is easy to see that this implies the claim of Remark 3 for general \(\varepsilon \in (0, \frac{1}{2})\). Let \({N \in \mathbb {N}}\) be minimal with \(C_2 \cdot N^{-s^*} \le \varepsilon \), noting that this entails \(N \ge N_0 \ge 2\) as well as \({\varepsilon \le C_2 \cdot (N-1)^{-s^*} \le 2^{s^*} C_2 \cdot N^{-s^*}}\), and therefore \(N \le 2 \, C_2^{1/s^*} \varepsilon ^{-1/s^*}\). Now, given \(f \in \mathcal {S}\), choose \(\varPhi = \varPhi (f, N)\) as above and note that \(\Vert f - R_\varrho (\varPhi ) \Vert _{L^2(\varOmega )} \le \frac{\varepsilon }{2}\).
Define \(W := \lceil C_3 \cdot N \cdot \log _2 N \rceil \ge N\) and choose \(k = k(p,q,d,\tau ) \in \mathbb {N}\) with \({k \ge \frac{\theta }{s^*}}\) so large that \( C_3 \cdot \bigl (2 C_2^{1/s^*}\bigr )^2 \le C_3 \cdot \bigl (2 C_2^{1/s^*}\bigr )^\theta \le 2^k . \)
Since \(\log _2 N \le N\), we then see that \( W \le C_3 N^2 \le C_3 \cdot \bigl (2 \, C_2^{1/s^*} \varepsilon ^{-1/s^*}\bigr )^2 \le (\frac{\varepsilon }{2})^{-k} \) and \( C_3 \cdot N^\theta \le C_3 \cdot \bigl (2 \, C_2^{1/s^*} \varepsilon ^{-1/s^*}\bigr )^\theta \le (\frac{\varepsilon }{2})^{-k} . \) Therefore, [13, Lemma VI.8] produces a network \(\varPhi '\) satisfying  and
and  and such that
and such that
To see that this implies the claim, first note that  and that
and that
for a suitable constant \(C_4 = C_4 (d,p,q,\tau )\). Regarding the quantization, first define \(\sigma _1 := 3 k C_3\), so that \(\sigma _0 = 3 k L(\varPhi ) \le 3 k C_3 \cdot \log _2 N \le \sigma _1 \lceil \log _2 W \rceil \). Next, note that \(\frac{2}{\varepsilon } \le \frac{C_2}{\varepsilon } \le N^{s^*} \le W^{s^*}\), meaning \((\varepsilon /2)^{-\sigma _0} \le (W^{s^*})^{\sigma _0} \le W^{\sigma \lceil \log _2 W \rceil }\) with \({\sigma := \sigma _1 \, \lceil s^*\rceil }\). Furthermore, we have  , which easily implies that
, which easily implies that
Overall, this shows that \(\varPhi '\) is \((\sigma ,W)\)-quantized, so that \(R_\varrho \varPhi ' \in \mathcal {NN}_{d,W}^{\sigma ,\varrho }\). Because of \(\Vert f - R_\varrho (\varPhi ') \Vert _{L^2 (\varOmega )} \le \varepsilon \), this implies that \(W_{\sigma ,\varrho }(f;\varepsilon ) \le W \le C_4 \cdot \varepsilon ^{-1/s^*} \log _2(1/\varepsilon )\), which is what we wanted to show.
Case 2 (Sobolev spaces): Set \(p_1 := \min \{ p, 2 \}\) and note \(\mathcal {S}\subset \mathcal {S}' := {{\,\mathrm{Ball}\,}}(0,1; W^{k,p_1}(\varOmega ))\). Since \(\varOmega = [0,1]^d\) is a Lipschitz domain, [33, Chapter VI, Theorem 5] shows that each \({f \in \mathcal {S}'}\) extends to a function \(\tilde{f} \in W^{k,p_1}(\mathbb {R}^d)\) with \(\Vert \tilde{f} \Vert _{W^{k,p_1}(\mathbb {R}^d)} \le C_1\), where \({C_1 = C_1(d,p,k)}\). Now, Lemma 13 shows that \(\tilde{f} \in B^k_{p_1,\infty }(\mathbb {R}^d)\) with \(\Vert \tilde{f} \Vert _{B^{k}_{p_1, \infty }(\mathbb {R}^d)} \le C_2\) where \({C_2 = C_2 (d,p,k)}\). Overall, this easily implies \(\mathcal {S}\subset {{\,\mathrm{Ball}\,}}(0,C_2; B^k_{p_1, \infty }(\varOmega ; \mathbb {R}))\), so that the claim follows from that for the Besov spaces. Here, we implicitly used that the condition \(k > d \cdot (\frac{1}{p} - \frac{1}{2})_+\) holds if and only if \(k > d \cdot (\frac{1}{p_1} - \frac{1}{2})_+\), since \(k \in \mathbb {N}\). \(\square \)
Optimal Compression Rate and Baire Category
In Sect. 1.3.3, it was claimed that if \(\mathcal {S}\subset \mathbf {X}\) satisfies some mild assumptions and  , then the set
, then the set  is of first category in \(\mathcal {S}\), for every codec \(\mathcal {C}\). In this appendix, we provide a proof of this fact. In particular, we will see (thanks to the Baire category theorem) that this implies existence of a “badly encodable”
is of first category in \(\mathcal {S}\), for every codec \(\mathcal {C}\). In this appendix, we provide a proof of this fact. In particular, we will see (thanks to the Baire category theorem) that this implies existence of a “badly encodable”  , meaning that \(\mathbf {x}\) is not encoded at any rate
, meaning that \(\mathbf {x}\) is not encoded at any rate  by the codec \(\mathcal {C}\).
by the codec \(\mathcal {C}\).
Proposition 3
Let \(\mathbf {X}\) be a Banach space and let \(\emptyset \ne \mathcal {S}\subset \mathbf {X}\). Assume that at least one of the following two conditions is satisfied:
-
1.
\(\mathcal {S}\) is closed, bounded, and convex; or
-
2.
\(\mathcal {S}= \{ \mathbf {x}\in \mathbf {X}:\Vert \mathbf {x}\Vert _{*} \le r \}\) for some \(r \in (0,\infty )\) and a map \(\Vert \cdot \Vert _*: \mathbf {X}\rightarrow [0,\infty ]\) with the following properties:
-
(a)
\(\Vert \cdot \Vert _*\) is a quasi-norm; that is, there exists \(\kappa \ge 1\) such that \({\Vert \alpha \, \mathbf {x}\Vert _{*} = |\alpha | \cdot \Vert \mathbf {x}\Vert _*}\) and \(\Vert \mathbf {x}+ \mathbf {y}\Vert _{*} \le \kappa \cdot (\Vert \mathbf {x}\Vert _{*} + \Vert \mathbf {y}\Vert _{*})\) for all \(\alpha \in \mathbb {R}\) and \(\mathbf {x},\mathbf {y}\in \mathbf {X}\);
-
(b)
there exists \(C \ge 1\) satisfying \(\Vert \mathbf {x}\Vert _{\mathbf {X}} \le C \cdot \Vert \mathbf {x}\Vert _{*}\) for all \(\mathbf {x}\in \mathbf {X}\);
-
(c)
\(\mathcal {S}\subset \mathbf {X}\) is closed;
-
(d)
\(\Vert \cdot \Vert _*\) is “continuous with respect to itself,” meaning that \(\Vert \mathbf {x}\Vert _*\rightarrow \Vert \mathbf {x}_0 \Vert _*\) whenever \(\Vert \mathbf {x}- \mathbf {x}_0 \Vert _*\rightarrow 0\).
-
(a)
Set  and assume \(s^*< \infty \). Then, for any codec
and assume \(s^*< \infty \). Then, for any codec  , the set
, the set  is of first category in \(\mathcal {S}\). Moreover, there exists \(\mathbf {x}= \mathbf {x}(\mathcal {C}) \in \mathcal {S}\) such that for each \(\ell \in \mathbb {N}\), we have
is of first category in \(\mathcal {S}\). Moreover, there exists \(\mathbf {x}= \mathbf {x}(\mathcal {C}) \in \mathcal {S}\) such that for each \(\ell \in \mathbb {N}\), we have
Remark
-
(1)
It is not hard to see that if \(\mathbf {x}\) satisfies (G.1), then

-
(2)
The assumptions on the quasi-norm \(\Vert \cdot \Vert _{*}\) might appear quite technical, but they are usually satisfied. Indeed, the condition \(\Vert \mathbf {x}\Vert _{\mathbf {X}} \le C \cdot \Vert \mathbf {x}\Vert _{*}\) is equivalent to \(\mathcal {S}\subset \mathbf {X}\) being bounded, which is necessary for having
 . Next, most naturally appearing quasi-norms are q-norms for some \(q \in (0,1]\), meaning that \(\Vert \mathbf {x}+ \mathbf {y}\Vert _{*}^q \le \Vert \mathbf {x}\Vert _*^q + \Vert \mathbf {y}\Vert _*^q\). In this case, it is not hard to see \(\big | \Vert \mathbf {x}\Vert _*^q - \Vert \mathbf {y}\Vert _*^q \big | \le \Vert \mathbf {x}- \mathbf {y}\Vert _*^q\), which implies that \(\Vert \cdot \Vert _*\) is “continuous with respect to itself.” Finally, most natural quasi-norms satisfy the Fatou property, meaning that if \(\mathbf {x}_n \rightarrow \mathbf {x}\) in \(\mathbf {X}\), then \(\Vert \mathbf {x}\Vert _*\le \liminf _{n\rightarrow \infty } \Vert \mathbf {x}_n \Vert _{*}\). If this is the case, then \(\mathcal {S}\subset \mathbf {X}\) is closed.
. Next, most naturally appearing quasi-norms are q-norms for some \(q \in (0,1]\), meaning that \(\Vert \mathbf {x}+ \mathbf {y}\Vert _{*}^q \le \Vert \mathbf {x}\Vert _*^q + \Vert \mathbf {y}\Vert _*^q\). In this case, it is not hard to see \(\big | \Vert \mathbf {x}\Vert _*^q - \Vert \mathbf {y}\Vert _*^q \big | \le \Vert \mathbf {x}- \mathbf {y}\Vert _*^q\), which implies that \(\Vert \cdot \Vert _*\) is “continuous with respect to itself.” Finally, most natural quasi-norms satisfy the Fatou property, meaning that if \(\mathbf {x}_n \rightarrow \mathbf {x}\) in \(\mathbf {X}\), then \(\Vert \mathbf {x}\Vert _*\le \liminf _{n\rightarrow \infty } \Vert \mathbf {x}_n \Vert _{*}\). If this is the case, then \(\mathcal {S}\subset \mathbf {X}\) is closed.
Proof
For \(R \in \mathbb {N}\), define \(M_R := \mathrm {range}(D_R) \subset \mathbf {X}\). Furthermore, for \(N,\ell \in \mathbb {N}\), let
Since \({{\,\mathrm{dist}\,}}_{\mathbf {X}} (\cdot , M_R)\) is continuous, it is not hard to see that each set \(\mathcal {G}_{N,\ell } \subset \mathcal {S}\) is closed. Denote by \(\mathcal {G}_{N,\ell }^{\circ }\) the (relative) interior of \(\mathcal {G}_{N,\ell }\) in \(\mathcal {S}\).
Step 1: (If \(\mathcal {G}_{N,\ell }^\circ \ne \emptyset \), then there exist \(\mathbf {x}_0' \in \mathbf {X}\) and \(t > 0\) such that \(\mathbf {x}_0' + t \mathcal {S}\subset \mathcal {G}_{N,\ell }\)). Choose \(\mathbf {x}_0 \in \mathcal {G}_{N,\ell }^\circ \subset \mathcal {S}\) and note that \(\mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x}_0, \varepsilon ; \mathbf {X}) \subset \mathcal {G}_{N,\ell }\) for a suitable \(\varepsilon \in (0, 1)\). We distinguish the two cases regarding the assumptions on \(\mathcal {S}\).
Case 1: \(\mathcal {S}\) is convex. Note that \(\mathcal {S}\subset {{\,\mathrm{Ball}\,}}(\mathbf {0}, C; \mathbf {X})\) for a suitable \(C \ge 1\), since \(\mathcal {S}\) is bounded. Define \(t := \frac{\varepsilon }{2 C} \in (0,1)\) and \(\mathbf {x}_0' := (1 - t) \mathbf {x}_0 \in \mathbf {X}\). With these choices, we see for arbitrary \(\mathbf {x}\in \mathcal {S}\) that \(\mathbf {x}_0' + t \mathbf {x}\in \mathcal {S}\) by convexity, and furthermore
Thus, \( \mathbf {x}_0' + t \mathcal {S}\subset \mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x}_0, \varepsilon ; \mathbf {X}) \subset \mathcal {G}_{N,\ell } \).
Case 2: \(\mathcal {S}= \{ \mathbf {x}\in \mathbf {X}:\Vert \mathbf {x}\Vert _*\le r \}\) for some \(r \in (0,\infty )\).
With \(C,\kappa \ge 1\) as in Part 2 of the assumptions of the proposition, let \(0< \sigma< \frac{\varepsilon }{2 \kappa C (1 + r)}< \varepsilon < 1\) and define \(\mathbf {x}_0' := (1 - \sigma ) \, \mathbf {x}_0\), noting that \(\Vert \mathbf {x}_0' \Vert _*< r\). By continuity of \(\Vert \cdot \Vert _*\) with respect to itself, we can choose \(0< \delta < \frac{\varepsilon \cdot \min \{ 1, r\} }{2 \kappa C}\) such that \(\Vert \mathbf {x}_0' + \mathbf {y}\Vert _*< r\) for all \(\mathbf {y}\in \mathbf {X}\) satisfying \(\Vert \mathbf {y}\Vert _*\le \delta \). Define \(t := \frac{\delta }{r}\). For arbitrary \(\mathbf {y}\in \mathcal {S}\), we then have \(\Vert t \, \mathbf {y}\Vert _*\le t r = \delta \), and hence, \(\mathbf {x}_0' + t \, \mathbf {y}\in \mathcal {S}\). Furthermore, \( \Vert (\mathbf {x}_0 ' + t \, \mathbf {y}) - \mathbf {x}_0 \Vert _{\mathbf {X}} \le C \cdot \Vert - \sigma \mathbf {x}_0 + t \, \mathbf {y}\Vert _{*} \le \kappa \sigma C r + \kappa C \delta \le \varepsilon . \) Overall, we have shown that \( \mathbf {x}_0' + t \mathcal {S}\subset \mathcal {S}\cap {{\,\mathrm{Ball}\,}}(\mathbf {x}_0, \varepsilon ; \mathbf {X}) \subset \mathcal {G}_{N,\ell } , \) as desired.
Step 2: (We have \(\mathcal {G}_{N,\ell }^\circ = \emptyset \) for all \(N,\ell \in \mathbb {N}\)). Assume toward a contradiction that \(\mathcal {G}_{N,\ell }^\circ \ne \emptyset \). By Step 1, there then exist \(\mathbf {x}_0' \in \mathbf {X}\) and \(t > 0\) satisfying \(\mathbf {x}_0' + t \mathcal {S}\subset \mathcal {G}_{N,\ell }\). Thus, for each \(\mathbf {x}\in \mathcal {S}\), we have \(\mathbf {x}_0' + t \, \mathbf {x}\in \mathcal {G}_{N,\ell }\), and therefore \({{\,\mathrm{dist}\,}}_{\mathbf {X}} \big ( \mathbf {x}_0' + t \, \mathbf {x}, M_R \big ) \le N \cdot R^{-(s^*+ \frac{1}{\ell })}\) for all \(R \in \mathbb {N}\). Because of \(M_R = \mathrm {range} (D_R)\), this implies that there exists \(c_{\mathbf {x},R} \in \{0,1\}^R\) satisfying \(\Vert (\mathbf {x}_0' + t \mathbf {x}) - D_R(c_{\mathbf {x},R}) \Vert _{\mathbf {X}} \le N \cdot R^{-(s^*+ \frac{1}{\ell })}\).
Now, we define a new codec  by
by
For arbitrary \(\mathbf {x}\in \mathcal {S}\), we then see
for all \(R \in \mathbb {N}\). By definition of the optimal exponent, this implies  , which is the desired contradiction. Hence, \(\mathcal {G}_{N,\ell }^\circ = \emptyset \) for all \(N,\ell \in \mathbb {N}\).
, which is the desired contradiction. Hence, \(\mathcal {G}_{N,\ell }^\circ = \emptyset \) for all \(N,\ell \in \mathbb {N}\).
Step 3: (Completing the proof). It is easy to see  ; see Eq. (1.2). We saw in the beginning of the proof that each \(\mathcal {G}_{N,\ell }\) is closed, and in Step 2 that each \(\mathcal {G}_{N,\ell }\) has empty interior (in \(\mathcal {S}\)) and is hence nowhere dense in \(\mathcal {S}\). By definition, this shows that \(\bigcup _{N,\ell \in \mathbb {N}} \mathcal {G}_{N,\ell }\)— and hence also
; see Eq. (1.2). We saw in the beginning of the proof that each \(\mathcal {G}_{N,\ell }\) is closed, and in Step 2 that each \(\mathcal {G}_{N,\ell }\) has empty interior (in \(\mathcal {S}\)) and is hence nowhere dense in \(\mathcal {S}\). By definition, this shows that \(\bigcup _{N,\ell \in \mathbb {N}} \mathcal {G}_{N,\ell }\)— and hence also  —is of first category in \(\mathcal {S}\).
—is of first category in \(\mathcal {S}\).
Finally, we prove the existence of \(\mathbf {x}\in \mathcal {S}\) satisfying Eq. (G.1). Assume toward a contradiction that no such \(\mathbf {x}\) exists. Then for each \(\mathbf {x}\in \mathcal {S}\) there exist \(n_\mathbf {x}, \ell _\mathbf {x}\in \mathbb {N}\) such that for every \(R \ge n_{\mathbf {x}}\), we have \({\Vert \mathbf {x}- D_R(E_R (\mathbf {x})) \Vert _{\mathbf {X}} < R^{-(s^*+ \frac{1}{\ell _\mathbf {x}})}}\). Thus, it is not hard to see that
where we defined \( N_\mathbf {x}:= 1 + \max \big \{ k^{s^*+ \frac{1}{\ell _\mathbf {x}}} \cdot \Vert \mathbf {x}- D_k (E_k (\mathbf {x})) \Vert _{\mathbf {X}} :1 \le k \le n_\mathbf {x}\big \} \).
Since \(\mathbf {x}\in \mathcal {S}\) was arbitrary, this easily implies \(\mathcal {S}= \bigcup _{N,\ell \in \mathbb {N}} \mathcal {G}_{N,\ell }\). Because \(\mathcal {S}\subset \mathbf {X}\) is a closed set, and hence a complete metric space (equipped with the metric induced by \(\Vert \cdot \Vert _{\mathbf {X}}\)), the Baire category theorem ( [14, Theorem 5.9]) shows that there are certain \(N,\ell \in \mathbb {N}\) such that \(\mathcal {G}_{N,\ell }^\circ \ne \emptyset \), in contradiction to Step 2. \(\square \)
As the second result in this appendix, we show that the preceding property does not hold for general compact sets \(\mathcal {S}\subset \mathbf {X}\), even if \(\mathbf {X}= \mathcal {H}\) is a Hilbert space. In other words, some additional regularity assumption beyond compactness—like convexity— is necessary to ensure the property stated in Proposition 3.
Example 1
We consider the Hilbert space \(\mathcal {H}:= \ell ^2(\mathbb {N})\), where we denote the standard orthonormal basis of this space by \((\mathbf {e}_n)_{n \in \mathbb {N}}\). Fix \(s > 0\), define \(\mathbf {x}_0 := \mathbf {0} \in \ell ^2 (\mathbb {N})\) and \(\mathbf {x}_n := (\log _2(n+1))^{-s} \cdot \mathbf {e}_n \in \ell ^2(\mathbb {N})\) for \(n \in \mathbb {N}\), and finally set
We claim that  , but that there is a codec
, but that there is a codec  such that
such that  for every \(\sigma > 0\); that is, every element \(\mathbf {x}\in \mathcal {S}\) is compressed by \(\mathcal {C}\) with arbitrary rate \(\sigma > 0\).
for every \(\sigma > 0\); that is, every element \(\mathbf {x}\in \mathcal {S}\) is compressed by \(\mathcal {C}\) with arbitrary rate \(\sigma > 0\).
To prove  , let \(R \in \mathbb {N}\) and
, let \(R \in \mathbb {N}\) and  . By the pigeonhole-principle, there are \(n,m \in \{1, \dots , 2^R + 1\}\) satisfying \(n \ne m\) but \(E (\mathbf {x}_n) = E(\mathbf {x}_m)\). By symmetry, we can assume that \(n < m\), so that \(n+1 \le 2^R + 1 \le 2^{R+1}\). Therefore,
. By the pigeonhole-principle, there are \(n,m \in \{1, \dots , 2^R + 1\}\) satisfying \(n \ne m\) but \(E (\mathbf {x}_n) = E(\mathbf {x}_m)\). By symmetry, we can assume that \(n < m\), so that \(n+1 \le 2^R + 1 \le 2^{R+1}\). Therefore,

Since this holds for any encoder/decoder pair  and arbitrary \(R \in \mathbb {N}\), we see
and arbitrary \(R \in \mathbb {N}\), we see  .
.
Next, we construct the codec \(\mathcal {C}\) mentioned above. To do so, for each \(n \in \mathbb {N}\), fix a bijection \(\kappa _n : \{0, \dots , 2^n - 1\} \rightarrow \{0,1\}^n\) and define
For \(m \in \mathbb {N}_0\) with \(m \le 2^n - 1\), we then have \(D_n (E_n (\mathbf {x}_m)) = \mathbf {x}_{\kappa _n^{-1} (\kappa _n (m))} = \mathbf {x}_m\), while if \(m \ge 2^n\), then \(D_n (E_n (\mathbf {x}_m)) = \mathbf {x}_{\kappa _n^{-1} (\kappa _n(0))} = \mathbf {x}_0 = \mathbf {0}\), and hence
Therefore, \(\Vert \mathbf {x}- D_n (E_n (\mathbf {x})) \Vert _{\ell ^2} \le n^{-s}\) for all \(\mathbf {x}\in \mathcal {S}\), and thus  , so that
, so that  .
.
We have now proved that  . Finally, it is easy to see that given arbitrary \(\sigma > 0\), the codec \(\mathcal {C}= \big ( (E_R, D_R) \big )_{R \in \mathbb {N}}\) constructed above approximates each fixed \(\mathbf {x}\in \mathcal {S}\) with rate \(\sigma \). Indeed, for \(m \in \mathbb {N}\) and \(\mathbf {x}= \mathbf {x}_m\), we have
. Finally, it is easy to see that given arbitrary \(\sigma > 0\), the codec \(\mathcal {C}= \big ( (E_R, D_R) \big )_{R \in \mathbb {N}}\) constructed above approximates each fixed \(\mathbf {x}\in \mathcal {S}\) with rate \(\sigma \). Indeed, for \(m \in \mathbb {N}\) and \(\mathbf {x}= \mathbf {x}_m\), we have
for all \(n \in \mathbb {N}\), while for \(\mathbf {x}= \mathbf {x}_0\) we have \(\Vert \mathbf {x}- D_n (E_n (\mathbf {x})) \Vert _{\ell ^2} = 0\) for all \(n \in \mathbb {N}\). \(\blacktriangleleft \)
Finally, we show (under suitable assumptions on \(\mathcal {S}\)) that the set of probability measures satisfying the phase transition (1.4) is meager in the set of all atom-free probability measures; this was claimed in Sect. 1.3.3.
Proposition 4
Let \(\mathbf {X}\) be a Banach space and let \(\emptyset \ne \mathcal {S}\subset \mathbf {X}\) with  . Assume that there exist \(\mathbf {x}_0, \mathbf {y}_0 \in \mathbf {X}\) satisfying \(\mathbf {x}_0 \ne \mathbf {y}_0\) and
. Assume that there exist \(\mathbf {x}_0, \mathbf {y}_0 \in \mathbf {X}\) satisfying \(\mathbf {x}_0 \ne \mathbf {y}_0\) and
Denote by \(\mathcal {P}_{\mathrm {af}}\) the set of all atom-free Borel probability measures \(\mathbb {P}\) on \(\mathcal {S}\) (i.e., satisfying \(\mathbb {P}(\{ \mathbf {x}\}) = 0\) for all \(\mathbf {x}\in \mathcal {S}\)). Furthermore, denote by \(\mathcal {G}\) the set of all \(\mathbb {P}\in \mathcal {P}_{\mathrm {af}}\) satisfying the phase transition (1.4). Then, equipping \(\mathcal {P}_{\mathrm {af}}\) with the metric \(d_{TV}\) given by \(d_{TV}(\mu ,\nu ) := \sup _{A \subset \mathcal {S}\text { Borel set}} |\mu (A) - \nu (A)|\), the set \(\mathcal {G}\subset \mathcal {P}_{\mathrm {af}}\) is closed and has empty interior; in particular, \(\mathcal {G}\) is meager in \(\mathcal {P}_{\mathrm {af}}\).
Proof
\(\mathcal {G}\) is closed: Let \((\mathbb {P}_n)_{n \in \mathbb {N}} \subset \mathcal {G}\) satisfy \(d_{TV}(\mathbb {P}_n, \mathbb {P}) \rightarrow 0\). Let \(s > s^*\) and  be arbitrary. Then, we have
be arbitrary. Then, we have  for each \(n \in \mathbb {N}\), so that there exists a Borel set
for each \(n \in \mathbb {N}\), so that there exists a Borel set  satisfying \(\mathbb {P}_n (N_n) = 0\). Define \(N := \bigcap _{n=1}^\infty N_n\), noting that N is a Borel set satisfying
satisfying \(\mathbb {P}_n (N_n) = 0\). Define \(N := \bigcap _{n=1}^\infty N_n\), noting that N is a Borel set satisfying  .
.
We then see \( 0 \le \mathbb {P}(N) = \lim _{m \rightarrow \infty } \mathbb {P}_m (N) \le \lim _{m \rightarrow \infty } \mathbb {P}_m (N_m) = 0 . \) Overall, this shows \(\mathbb {P}\in \mathcal {G}\), so that \(\mathcal {G}\) is closed.
\(\mathcal {G}\) has empty interior in \(\mathcal {P}_{\mathrm {af}}\): Assume toward a contradiction that there exists \(\mathbb {P}\in \mathcal {G}^\circ \); thus, there exists \(\varepsilon > 0\) such that \({\widetilde{\mathbb {P}}} \in \mathcal {G}\) whenever \({\widetilde{\mathbb {P}}} \in \mathcal {P}_{\mathrm {af}}\) with \(d_{TV}(\mathbb {P}, {\widetilde{\mathbb {P}}}) \le \varepsilon \). Let \(M := [\mathbf {x}_0, \mathbf {y}_0) = \{ (1-t) \mathbf {x}_0 + t \, \mathbf {y}_0 :t \in [0,1) \}\). It is easy to see that
defines an atom-free Borel probability measure on \(\mathcal {S}\) satisfying \(\mathbb {P}^\natural (M) = 1\). This easily implies \({\widetilde{\mathbb {P}}} := (1-\varepsilon ) \mathbb {P}+ \varepsilon \, \mathbb {P}^\natural \in \mathcal {P}_{\mathrm {af}}\) with \(d_{TV}(\mathbb {P}, {\widetilde{\mathbb {P}}}) \le \varepsilon \). Therefore, by choice of \(\mathbb {P}\) and \(\varepsilon \), we get \({\widetilde{\mathbb {P}}} \in \mathcal {G}\). Finally, it is easy to seeFootnote 4 that there exists a codec  satisfying
satisfying  . By definition of \(\mathcal {G}\) and since \(s^*< \infty \), this implies \({\widetilde{\mathbb {P}}}(M) = 0\). However, \({\widetilde{\mathbb {P}}}(M) \ge \varepsilon \, \mathbb {P}^\natural (M) = \varepsilon > 0\), which is the desired contradiction. \(\square \)
. By definition of \(\mathcal {G}\) and since \(s^*< \infty \), this implies \({\widetilde{\mathbb {P}}}(M) = 0\). However, \({\widetilde{\mathbb {P}}}(M) \ge \varepsilon \, \mathbb {P}^\natural (M) = \varepsilon > 0\), which is the desired contradiction. \(\square \)
Technical Results Concerning Sequence Spaces
Proof of Lemma 2
Let \(\mathbf {x}\in \mathbb {R}^{\mathcal {I}}\). Set \(u_m := m^{\theta + \vartheta } \cdot 2^{\alpha m} \cdot \Vert \mathbf {x}_m \Vert _{\ell ^p(\mathcal {I}_m)}\) and \(v_m := m^{-\vartheta }\), and observe that  and
and  .
.
Let us first consider the case \(q < \infty \). In this case, \(\frac{q}{r} \in (1,\infty )\) and \(\frac{q}{q-r} \in (1,\infty )\) are conjugate exponents, so that Hölder’s inequality shows
Here, we note \(\vartheta \cdot \frac{r q}{q - r} = \frac{\vartheta }{\frac{1}{r} - \frac{1}{q}} > 1\) and \(v_m = m^{-\vartheta }\), so that \({\kappa := \max \{ 1, \Vert (v_m)_{m \in \mathbb {N}} \Vert _{\ell ^{rq / (q-r)}}\}}\) is finite.
Finally, in case of \(q = \infty \), simply note that
where now \(\kappa := \max \bigl \{ 1, \Vert (m^{-\vartheta })_{m \in \mathbb {N}} \Vert _{\ell ^r} \bigr \}\) is finite, since \(\vartheta > \frac{1}{r} - \frac{1}{q} = \frac{1}{r}\). \(\square \)
Proof of Lemma 4
By definition of the product \(\sigma \)-algebra, each of the finite-dimensional projections \(\pi _m : \mathbb {R}^{\mathcal {I}} \rightarrow \mathbb {R}^{\mathcal {I}_m}, \mathbf {x}\mapsto \mathbf {x}_m\) is measurable. Since \(\Vert \cdot \Vert _{\ell ^p (\mathcal {I}_m)}\) is continuous on \( \mathbb {R}^{\mathcal {I}_m}\) and hence Borel measurable, \({ q_m : \mathbb {R}^{\mathcal {I}} \rightarrow [0,\infty ), \mathbf {x}\mapsto 2^{\alpha m} \, m^{\theta } \, \Vert \mathbf {x}_m \Vert _{\ell ^p(\mathcal {I}_m)} }\) is \(\mathscr {B}_{\mathcal {I}}\)-measurable for each \(m \in \mathbb {N}\).
In case of \(q < \infty \), this implies that the map

is \(\mathscr {B}_{\mathcal {I}}\)-measurable as a countable series of measurable, non-negative functions, and hence so is  . If \(q = \infty \), the (quasi) norm
. If \(q = \infty \), the (quasi) norm  is \(\mathscr {B}_{\mathcal {I}}\)-measurable as a countable supremum of \(\mathscr {B}_{\mathcal {I}}\)-measurable, non-negative functions.
is \(\mathscr {B}_{\mathcal {I}}\)-measurable as a countable supremum of \(\mathscr {B}_{\mathcal {I}}\)-measurable, non-negative functions.
For proving the final claim, let us write \(\mathcal {T}:= \ell ^2(\mathcal {I}) \Cap \mathscr {B}_{\mathcal {I}}\) for brevity. By the first part of the lemma,  is \(\mathscr {B}_{\mathcal {I}}\)-measurable. Furthermore, for arbitrary \(\mathbf {x}\in \mathbb {R}^{\mathcal {I}}\) the translation \(\mathbb {R}^{\mathcal {I}} \rightarrow \mathbb {R}^{\mathcal {I}}, \mathbf {y}\mapsto \mathbf {y}+ \mathbf {x}\) is \(\mathscr {B}_{\mathcal {I}}\)-measurable. These two observations imply that the norm \(\Vert \cdot \Vert _{\ell ^2} : \ell ^2(\mathcal {I}) \rightarrow [0,\infty )\) and the translation operator \(\ell ^2(\mathcal {I}) \rightarrow \ell ^2(\mathcal {I}), \mathbf {y}\mapsto \mathbf {y}+ \mathbf {x}\) are \(\mathcal {T}\)-measurable for any \(\mathbf {x}\in \ell ^2(\mathcal {I})\). This implies that the open ball \(\{ \mathbf {y}\in \ell ^2(\mathcal {I}) :\Vert \mathbf {y}+ (-\mathbf {x}) \Vert _{\ell ^2} < r \}\) is \(\mathcal {T}\)-measurable. But \(\ell ^2(\mathcal {I})\) is separable, so that every open set is a countable union of open balls; therefore, it follows that \(\mathscr {B}_{\ell ^2} \subset \mathcal {T}\). Conversely, \(\mathcal {T}\) is generated by sets of the form \(\{ \mathbf {x}\in \ell ^2(\mathcal {I}) :p_i(\mathbf {x}) \in M \}\), where \(M \subset \mathbb {R}\) is a Borel set and \(p_i : \mathbb {R}^{\mathcal {I}} \rightarrow \mathbb {R}, (x_j)_{j \in \mathcal {I}} \mapsto x_i\). Since \(p_i |_{\ell ^2(\mathcal {I})} : \ell ^2(\mathcal {I}) \rightarrow \mathbb {R}\) is continuous with respect to \(\Vert \cdot \Vert _{\ell ^2(\mathcal {I})}\), we see that each generating set of \(\mathcal {T}\) also belongs to \(\mathscr {B}_{\ell ^2}\), which completes the proof. \(\square \)
is \(\mathscr {B}_{\mathcal {I}}\)-measurable. Furthermore, for arbitrary \(\mathbf {x}\in \mathbb {R}^{\mathcal {I}}\) the translation \(\mathbb {R}^{\mathcal {I}} \rightarrow \mathbb {R}^{\mathcal {I}}, \mathbf {y}\mapsto \mathbf {y}+ \mathbf {x}\) is \(\mathscr {B}_{\mathcal {I}}\)-measurable. These two observations imply that the norm \(\Vert \cdot \Vert _{\ell ^2} : \ell ^2(\mathcal {I}) \rightarrow [0,\infty )\) and the translation operator \(\ell ^2(\mathcal {I}) \rightarrow \ell ^2(\mathcal {I}), \mathbf {y}\mapsto \mathbf {y}+ \mathbf {x}\) are \(\mathcal {T}\)-measurable for any \(\mathbf {x}\in \ell ^2(\mathcal {I})\). This implies that the open ball \(\{ \mathbf {y}\in \ell ^2(\mathcal {I}) :\Vert \mathbf {y}+ (-\mathbf {x}) \Vert _{\ell ^2} < r \}\) is \(\mathcal {T}\)-measurable. But \(\ell ^2(\mathcal {I})\) is separable, so that every open set is a countable union of open balls; therefore, it follows that \(\mathscr {B}_{\ell ^2} \subset \mathcal {T}\). Conversely, \(\mathcal {T}\) is generated by sets of the form \(\{ \mathbf {x}\in \ell ^2(\mathcal {I}) :p_i(\mathbf {x}) \in M \}\), where \(M \subset \mathbb {R}\) is a Borel set and \(p_i : \mathbb {R}^{\mathcal {I}} \rightarrow \mathbb {R}, (x_j)_{j \in \mathcal {I}} \mapsto x_i\). Since \(p_i |_{\ell ^2(\mathcal {I})} : \ell ^2(\mathcal {I}) \rightarrow \mathbb {R}\) is continuous with respect to \(\Vert \cdot \Vert _{\ell ^2(\mathcal {I})}\), we see that each generating set of \(\mathcal {T}\) also belongs to \(\mathscr {B}_{\ell ^2}\), which completes the proof. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grohs, P., Klotz, A. & Voigtlaender, F. Phase Transitions in Rate Distortion Theory and Deep Learning. Found Comput Math 23, 329–392 (2023). https://doi.org/10.1007/s10208-021-09546-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-021-09546-4
Keywords
- Rate distortion theory
- Phase transition
- Approximation rates
- Sobolev spaces
- Besov spaces
- Neural network approximation



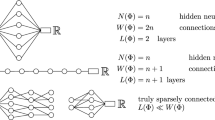
 such an element exists under mild assumptions on
such an element exists under mild assumptions on 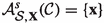 for all
for all 
 , we have
, we have  , the set
, the set  is a
is a 
 with distortion
with distortion 
 defined in Eq. (
defined in Eq. ( and hence
and hence  .
. ;
;
 is a probability measure on the measurable space
is a probability measure on the measurable space  .
. , and the measure
, and the measure  is a probability measure on
is a probability measure on  , where
, where  ;
; satisfying
satisfying 
 and
and  ; this follows from Proposition
; this follows from Proposition  for all
for all  .
. , and
, and 
 ;
; satisfying
satisfying 


 .
.
 , and
, and 

 . Next, most naturally appearing quasi-norms are q-norms for some
. Next, most naturally appearing quasi-norms are q-norms for some