Physics-lumped parameter based control oriented model of dielectric tubular actuator

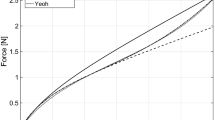
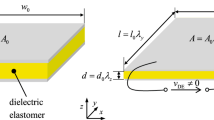
Abstract

Dielectric elastomers (DEs) deform and change shape when an electric field is applied across them. They are flexible, resilient, lightweight, and durable and as such are suitable for use as soft actuators. In this paper a physics-based and control-oriented model is developed for a DE tubular actuator using a physics-lumped parameter modeling approach. The model derives from the nonlinear partial differential equations (PDE) which govern the nonlinear elasticity of the DE actuator and the ordinary differential equation (ODE) that governs the electrical dynamics of the DE actuator. With the boundary conditions for the tubular actuator, the nonlinear PDEs are numerically solved and a quasi-static nonlinear model is obtained and validated by experiments. The full nonlinear model is then linearized around an operating point with an analytically derived Hessian matrix. The analytically linearized model is validated by experiments. Proportional–Integral–Derivative (PID) and $H_{\infty }$ control are developed and implemented to perform position reference tracking of the DEA and the controllers’ performances are evaluated according to control energy and tracking error.

Appendix

1.1 Appendix 1: derivation of equations of state

Starting with Eq. 10,

$$\begin{aligned} \delta E_H = 2\pi RH\int \delta WdX = F\delta z_B + \Phi \delta Q. \end{aligned}$$

Here,

$$\begin{aligned} \int \delta WdX=\int \left( s_1\delta \lambda _1 + s_2\delta \lambda _2 + {\bar{E}}\delta {\bar{D}}\right) dX. \end{aligned}$$

(46)

A small change in $\lambda _1$ is given by

$$\begin{aligned} \delta \lambda _1 = \frac{\partial \lambda _1}{\partial dl}\delta dl =\frac{\delta dl}{dX} \end{aligned}$$

(47)

and from Eq. 2, taking a small change in dl

$$\begin{aligned} \delta dl = \frac{dr}{dl}\delta dr + \frac{dz}{dl}\delta dz. \end{aligned}$$

Substituting Eq. 1 into this result gives

$$\begin{aligned} \delta dl = -\cos {\theta }\delta dr + \sin {\theta }\delta dz. \end{aligned}$$

Finally Eq. 47 is written as

$$\begin{aligned} \delta \lambda _1=-\cos {\theta }\frac{d(\delta r)}{dX} + \sin {\theta }\frac{d(\delta z)}{dX}. \end{aligned}$$

(48)

Also a small change in $\lambda _2$ is given by

$$\begin{aligned} \delta \lambda _2 = \frac{\partial \lambda _2}{\partial r}\delta r =\frac{\delta r}{R}. \end{aligned}$$

(49)

Finally, from Eq. 5, a small change in ${\bar{D}}$ is given by

$$\begin{aligned} \delta {\bar{D}}=\frac{\delta q}{A_0}. \end{aligned}$$

(50)

With these, Eq. 46 becomes

$$\begin{aligned} \begin{aligned} \int \left[ s_1 \left( -\cos {\theta }\frac{d(\delta r)}{dX} + \sin {\theta }\frac{d(\delta z)}{dX}\right) + s_2 \frac{\delta r}{R} + {\bar{E}}\frac{\delta q}{A_0}\right] dX\\ =\int \left[ -s_1 \cos {\theta }\frac{d(\delta r)}{dX} + s_1 \sin {\theta }\frac{d(\delta z)}{dX} + s_2 \frac{\delta r}{R} + {\bar{E}}\frac{\delta q}{A_0}\right] dX. \end{aligned} \end{aligned}$$

Integrating by parts gives

$$\begin{aligned} \begin{aligned}&s_1 (-\cos {\theta }\delta r + \sin {\theta }\delta z)\Bigr |_A^B \\&+ \int \left[ \left( \frac{d(s_1 \cos {\theta })}{dX} + \frac{s_2}{R}\right) \delta r - \frac{d(s_1 \sin {\theta })}{dX}\delta z + {\bar{E}}\frac{\delta q}{A_0}\right] dX. \end{aligned} \end{aligned}$$

By comparing the left hand side with the right hand side of the equation, the following is observed from the $\delta z$ term inside the integral

$$\begin{aligned}&\frac{d\left( s_1 \sin {\theta }\right) }{dX}=0 \nonumber \\&\quad \Longrightarrow s_1 \sin {\theta }=Constant. \end{aligned}$$

(51)

Since there is no $\delta z$ on the right hand side, physically this means that the vertical longitudinal stress component is fixed for a given applied load. This is the expected condition for the membrane in static equilibrium since the vertical force components must cancel out each other. Evaluating the boundaries gives

$$\begin{aligned} 2\pi RH \left\{ s_1\left( -\cos {\theta _B}\delta r_B + \sin {\theta _B}\delta z_B\right) \right. \\ \left. -s_1\left( -\cos {\theta _A}\delta r_A + \sin {\theta _A}\delta z_A\right) \right\} =F\delta z_B. \end{aligned}$$

The boundary conditions for the tubular actuator require that $\delta r_B=\delta r_A=\delta z_A=0$. Therefore

$$\begin{aligned} \begin{aligned} 2\pi RH s_1 \sin {\theta _B}\delta z_B=F\delta z_B \\ 2\pi RH s_1 \sin {\theta }=F. \end{aligned} \end{aligned}$$

(52)

This corresponds to Eq. 15. Moving back into the integral is Eq. 14 directly from

$$\begin{aligned} \begin{aligned} \frac{d(s_1\cos \theta )}{dX} + \frac{s_2}{R}=0 \\ \frac{d(s_1\cos \theta )}{dX}=- \frac{s_2}{R}. \end{aligned} \end{aligned}$$

(53)

This result is from the fact that there are no external forces acting on the surface of the membrane radially as would be the case if the actuator were to be under compression or tension by an applied pressure on the membrane (Son and Goulbourne 2010). Finally,

$$\begin{aligned} 2 \pi RH\int {\bar{E}}\frac{\delta q}{A_0}dX=\Phi \delta Q. \end{aligned}$$

Taking the actuator as a cylindrical capacitor, ${\bar{E}}$ does not vary along the longitudinal direction and hence is a constant with respect to the X-direction. This gives

$$\begin{aligned} H{\bar{E}} \cdot 2 \pi R\int \frac{\delta q}{A_0}dX=\Phi \delta Q. \end{aligned}$$

And from Eq. 6

$$\begin{aligned} \delta Q = 2 \pi R\int \frac{\delta q}{A_0} \end{aligned}$$

(54)

therefore

$$\begin{aligned} H{\bar{E}}=\Phi . \end{aligned}$$

(55)

1.2 Appendix 2: derivation of the governing differential equations

This is the extended derivation of Eqs. 21–23: Divide Eq. 1 by dX to get

$$\begin{aligned} \frac{dr}{dX}&=-\frac{dl}{dX}\cos {\theta },\\ \frac{dz}{dX}&=-\frac{dl}{dX}\sin {\theta }. \end{aligned}$$

But $\frac{dl}{dX}=\lambda _1$. This gives Eq. 21 which is

$$\begin{aligned} \frac{dr}{dX}&=-\lambda _1\cos \theta ,\\ \frac{dz}{dX}&=\lambda _1\sin \theta . \end{aligned}$$

Using Eqs. 14 and 51 one can get Eq. 22. Solving Eq. 14 gives

$$\begin{aligned} \frac{ds_1}{dX}\cos {\theta } = s_1\sin {\theta }\frac{d\theta }{dX} -\frac{s_2}{R} \end{aligned}$$

(56)

and solving Eq. 51 gives

$$\begin{aligned} \frac{ds_1}{dX}\sin {\theta } = -s_1\cos {\theta }\frac{d\theta }{dX}. \end{aligned}$$

(57)

Dividing Eq. 57 by Eq. 56 gives

$$\begin{aligned} \tan \theta = \frac{-s_1\cos {\theta }\frac{d\theta }{dX}}{s_1\sin {\theta }\frac{d\theta }{dX} -\frac{s_2}{R}}. \end{aligned}$$

Solving for $\frac{d\theta }{dX}$ gives

$$\begin{aligned} \begin{aligned} s_1\left( \tan \theta \cdot \sin {\theta } + \cos {\theta }\right) \frac{d\theta }{dX} = \frac{s_2}{R}\tan {\theta } \\ s_1\frac{d\theta }{dX} = \frac{s_2}{R}\sin {\theta } \end{aligned} \end{aligned}$$

Expanding $\tan \theta$ gives

$$\begin{aligned} \begin{aligned} s_1\left( \frac{\sin \theta }{\cos \theta }\cdot \sin {\theta } + \cos {\theta }\right) \frac{d\theta }{dX} = \frac{s_2}{R}\tan {\theta }, \\ s_1\left( \frac{\sin ^2\theta + \cos ^2\theta }{\cos \theta }\right) \frac{d\theta }{dX} = \frac{s_2}{R}\tan {\theta }, \end{aligned} \end{aligned}$$

and using the trigonometric identity $\sin ^2\theta + \cos ^2\theta = 1$ and multiplying through by $\frac{\cos \theta }{s_1}$ gives us Eq. 22 as

$$\begin{aligned} \frac{d\theta }{dX}=\frac{s_2}{s_1R}\sin {\theta }. \end{aligned}$$

(58)

Now the algebraic equation 23 can be derived by solving for $s_1$ in Eqs. 15 and 18 and setting the two equations equal to each other. From Eq. 15

$$\begin{aligned} s_1 = \frac{F}{2\pi RH\sin {\theta }}. \end{aligned}$$

Using the normalized load $F^*$ gives

$$\begin{aligned} s_1 = \frac{\mu F^*}{R\sin {\theta }} \end{aligned}$$

and with Eq. 18

$$\begin{aligned} \begin{aligned} s_1&= \mu \left( \lambda _1 - \frac{1}{\lambda _1^3\lambda _2^2}\right) - \frac{{\bar{D}}^2}{\epsilon \lambda _1^3\lambda _2^2} = \frac{\mu F^*}{R\sin {\theta }} \\&\frac{\mu \epsilon \lambda _1^4\lambda _2^2 - \mu \epsilon - {\bar{D}}^2}{\epsilon \lambda _1^3\lambda _2^2} = \frac{\mu F^*}{R\sin {\theta }}. \end{aligned} \end{aligned}$$

From Eq. 20, ${\bar{D}}=\epsilon \lambda _1^2\lambda _2^2{\bar{E}}$ so,

$$\begin{aligned} \begin{aligned} \frac{\mu \epsilon \lambda _1^4\lambda _2^2 - \mu \epsilon - \epsilon ^2 \lambda _1^4\lambda _2^4{\bar{E}}^2}{\epsilon \lambda _1^3\lambda _2^2} = \frac{\mu F^*}{R\sin {\theta }} \\ \lambda _1^4\left( 1 - \frac{\epsilon {\bar{E}}^2}{\mu }\lambda _2^2\big )\right) - \frac{1}{\lambda _2^2} = \frac{F^*}{R\sin {\theta }}\lambda _1^3 \end{aligned} \end{aligned}$$

From Eq. 16, ${\bar{E}}^2= \frac{\Phi ^2}{H^2}$. Substituting this in the above expression gives

$$\begin{aligned} \lambda _1^4\left( 1 - \frac{\epsilon }{\mu }\cdot \frac{{\bar{\Phi }}^2}{H^2}\lambda _2^2)\right) - \frac{1}{\lambda _2^2} = \frac{F^*}{R\sin {\theta }}\lambda _1^3 \end{aligned}$$

Using the normalized applied voltage on the membrane gives the algebraic equation

$$\begin{aligned} \left[ 1- \left( \frac{\Phi ^*r}{R}\right) ^2\right] \lambda _1^4 - \frac{F^*}{R\sin {\theta }}\lambda _1^3 - \left( \frac{R}{r}\right) ^2 = 0. \end{aligned}$$

(59)

1.3 Appendix 3: Jacobian elements

$$\begin{aligned}&\frac{\partial {\dot{x}}_1}{\partial x_1}=0, \quad \frac{\partial {\dot{x}}_1}{\partial x_2}\ =1, \quad \frac{\partial {\dot{x}}_1}{\partial x_3}&=0.\\&f_1=\frac{\partial {\dot{x}}_2}{\partial x_1}=\frac{1}{m}\Bigg \{R\cos \theta \left( \left[ 1-\left( \frac{x_3^*r}{R}\right) ^2\right] \lambda _1-\frac{R^2}{r^2\lambda _1^3}\right) \frac{\partial \theta }{\partial x_1}\\&+2R\sin \theta \left( \frac{R^2}{r^3\lambda _1}-\frac{r\lambda _1x_3^2}{R^2}\right) \frac{\partial r}{\partial x_1}\\&+R\sin \theta \left( 1-\left( \frac{x_3^*r}{R}\right) ^2+\frac{3R^2}{r\lambda _1^4}\right) \frac{\partial \lambda _1}{\partial x_1}\Bigg \},\\&f_2=\frac{\partial {\dot{x}}_2}{\partial x_2}=-\frac{c^*}{m},\\&f_3=\frac{\partial {\dot{x}}_2}{\partial x_3}=\frac{2r^2\lambda _1x_3^*}{mR}\sin \theta , \end{aligned}$$

and

$$\begin{aligned} \frac{\partial {\dot{x}}_3}{\partial x_1}&=0,&\frac{\partial {\dot{x}}_3}{\partial x_2}&=0,&\frac{\partial {\dot{x}}_3}{\partial x_3}&=-\frac{1}{RC}. \end{aligned}$$