Abstract
J-holomorphic curves in nearly Kähler \(\mathbb {CP}^3\) are related to minimal surfaces in \(S^4\) as well as associative submanifolds in \(\Lambda ^2_-(S^4)\). We introduce the class of transverse J-holomorphic curves and establish a Bonnet-type theorem for them. We classify flat tori in \(S^4\) and construct moment-type maps from \(\mathbb {CP}^3\) to relate them to the theory of \(\mathrm {U}(1)\)-invariant minimal surfaces on \(S^4\).
Similar content being viewed by others
1 Introduction
In symplectic geometry, the theory of J-holomorphic curves is a fundamental topic, which has for example led to the construction of Gromov–Witten invariants. From a Riemannian point of view, it is desirable to have examples of minimal surfaces in Einstein manifolds. One class of such examples comes from complex geometry by considering holomorphic curves in Einstein–Kähler manifolds. Nearly Kähler six-manifolds are Einstein with positive Einstein constant and J-holomorphic curves provide a class of examples of minimal surfaces inside them. However, they are neither symplectic nor complex and apart from local statements not much is known about J-holomorphic curves in general almost complex manifolds. One feature that is shared with the symplectic case is that the nearly Kähler structure equations guarantee that the volume remains constant on connected components of the moduli space of J-holomorphic curves [32]. Nevertheless, a general, in-depth theory of J-holomorphic curves in nearly Kähler manifolds seems out of reach at the moment, which is why most work has been concerned with studying them in the homogeneous examples. Historically, \(M=S^6\) has been the example studied the most, set-off by Bryant’s construction of torsion-free J-holomorphic curves as integrals of a holomorphic differential system on \(\widetilde{\mathrm {Gr}}(2,\mathbb {R}^7)\) [10]. More recently, questions about certain components of the moduli space of J-holomorphic curves have been tackled [15].
J-holomorphic curves in the twistor spaces \(\mathbb {CP}^3\) and the flag manifold \(\mathbb {F}\) are related to special submanifolds in two different geometric settings. Firstly, it is a general result that the cone of a J-holomorphic curve in a nearly Kähler manifold M gives an associative submanifold in the \(G_2\)-cone C(M). Remarkably, J-holomorphic curves in \(\mathbb {CP}^3\) and \(\mathbb {F}\) also give rise to complete associative submanifolds in the Bryant–Salamon spaces \(\Lambda ^2_-(S^4)\) and \(\Lambda ^2_-(\mathbb {CP}^2)\) [23]. Secondly, via the Eells–Salamon correspondence [14], J-holomorphic curves in the twistor spaces are in correspondence with minimal surfaces in \(S^4\) and \(\mathbb {CP}^2\). Somewhat similar to torsion-free curves in \(S^6\), the space \(\mathbb {CP}^3\) admits a particular class of J-holomorphic curves called superminimal curves. They can also be constructed via integrals of a holomorphic differential system and admit a Weierstraß parametrisation [9]. In [21], N. Hitchin developed powerful tools to reduce minimal tori in \(S^3\) to algebraic geometry in a very different way. To a minimal torus he associates a spectral curve, which is a hyperelliptic curve and whose geometry contains all information about the minimal surface. Non-superminimal tori in \(S^4\) have also been studied with methods of integrable systems [29]. The aim of this article is to describe various results on non-superminimal surfaces in \(S^4\) from the twistor perspective, building on Xu’s work on J-holomorphic curves in nearly Kähler \(\mathbb {CP}^3\) [33]. Adapting the twistor perspective means that dimension of the ambient space is increased while the second-order PDE describing a minimal surface in \(S^4\) is reduced to a first order PDE for J-holomorphic curves in \(\mathbb {CP}^3\). Since the key geometric feature we exploit is the twistor fibration \(\mathbb {CP}^3\rightarrow S^4\), it is to be expected that similar techniques can be applied to the flag manifold.
1.1 Summary of results
By Cartan–Kähler theory, J-holomorphic curves in an almost complex manifold of dimension 6 are locally described by four functions of one variable. Two functions \({\alpha _-},{\alpha _+}\) of two variables that satisfy a Laplace-type equation are parametrised by four functions of one variable too. By using an appropriate adaption of frames, we distill such two functions \({\alpha _-}\) and \({\alpha _+}\) geometrically. The twistor fibration \(\mathbb {CP}^3\rightarrow S^4\) comes with a natural connection \(T\mathbb {CP}^3=\mathcal {H}\oplus \mathcal {V}\). We will focus on J-holomorphic curves which are going to be called transverse. In particular, they have the property that they are nowhere tangent to horizontal bundle \(\mathcal {H}\) or vertical bundle \(\mathcal {V}\), see Definition 4.1. The focus of this article will be on transverse J-holomorphic tori. In fact, a compact transverse J-holomorphic curve is necessarily of genus one.
The material covered in Sect. 2 provides background and context for the subsequent sections. Section 3 establishes relationships between geometric quantities associated with a minimal surface and those of its twistor lifts, featuring a twistor interpretation of Xu’s correspondence of certain J-holomorphic curves in \(\mathbb {CP}^3\).
In Sect. 4, we define the two functions \({\alpha _-},{\alpha _+}:X\rightarrow \mathbb {R}\) for a transverse J-holomorphic curve which measure angles between different components of \(\mathrm {d}\Phi \) in \(T\mathbb {CP}^3\). They always satisfy the 2D periodic Toda lattice equation for \(\mathfrak {sp}(2)\) which are equivalent to the system
where \(\gamma ^2=({\alpha _-}{\alpha _+})^{-1/2}\) is the conformal factor of the induced metric on X and \(\Delta _0\) the Laplacian for the corresponding flat metric. Viewing the surface in the ambient space \(\mathbb {CP}^3\) means we can characterise additional data equipped to the curve, such as the first and second fundamental form in \(\mathbb {CP}^3\). It turns out that both of them can be expressed through the functions \({\alpha _-}\) and \({\alpha _+}\). As an application, we show in Theorem 5.5 that any flat J-holomorphic torus is a Clifford torus. The second fundamental form \(\mathrm {I\!I}_{\mathbb {CP}^3}\) is a complex linear tensor and its differential \(\bar{\partial } \mathrm {I\!I}_{\mathbb {CP}^3}\) can be computed neatly in terms of \({\alpha _-},{\alpha _+}\) and vanishes exactly in points where the curve is non-transverse. The normal bundle \(\nu \) of a J-holomorphic curve carries a natural holomorphic structure. We show that the normal bundles of all transverse J-holomorphic tori are isomorphic to each other, in particular all of them admit a holomorphic section.
Section 5 features a proof of a Bonnet-type theorem for J-holomorphic curves stating that the first and second fundamental form on X are determined by \({\alpha _-}\) and \({\alpha _+}\). The essence of Theorem 5.2 is that if X is simply connected then a \(\mathbb {C}^*\)-family of transverse J-holomorphic curves can be recovered from a solution to the 2D Toda lattice equation. Roughly speaking, this can be seen as a complex analogue to the statement that curves in \(\mathbb {R}^3\) are essentially classified by their curvature and torsion.
To get hold of examples of transverse J-holomorphic curves we impose an arbitrary \(\mathrm {U}(1)\)-symmetry on them in Sect. 6, given by a certain element \(\xi \in \mathfrak {sp}(2)\). Such an action commutes with a \(\mathbb {T}^2\)-action of automorphisms on \(\mathbb {CP}^3\). Given a \(\mathbb {T}^3\)-action on a torsion-free \(G_2\) manifold \(M^7\) the multi-moment maps give rise to a local homeomorphism \(M^7/{\mathbb {T}^3} \rightarrow \mathbb {R}^4\) [25, Theorem 4.5]. The only known example of a nearly Kähler manifold admitting a \(\mathbb {T}^3\)-action is \(S^3\times S^3\) whose geometry has been described with multi-moment maps by Dixon [13]. Assuming a \(\mathbb {T}^2\) symmetry on a nearly Kähler manifold \(M^6\) is less restrictive but the corresponding multi-moment map \(\nu :M^6\rightarrow \mathbb {R}\), introduced by Russo and Swann [30], is only real-valued. The question arises if there is a geometric construction of a map into \(\mathbb {R}^4\) which descends to a local homeomorphism to the \(\mathbb {T}^2\) quotient of M, at least away from a singular set. We construct a map \(p:_{\mathbb {T}^2}\backslash ^{(\mathbb {CP}^3\setminus \mathcal {S})}\rightarrow \mathbb {R}^4\) for a certain singular set \(\mathcal {S}\) and in Theorem 6.10 it is shown that p descends to a branched double cover from \( _{{{\mathbb {T}^2}} }\backslash ^{\mathbb {CP}^3\setminus \mathcal {S}}\) onto its image \(D\subset \mathbb {R}^4\). p maps \(\mathrm {U}(1)\)-invariant J-holomorphic curves in \(\mathbb {CP}^3\) to solutions of the 1D Toda lattice equation for \(\mathfrak {sp}(2)\) in D. Derived from the Lax representation of this equation one derives two preserved quantities, giving rise to a map \(u:D\rightarrow \mathbb {R}^2\).
If one equips \(\mathbb {CP}^3\) with its Kähler structure then a \(\mathbb {T}^2\)-action gives rise to a symplectic moment map whose image is a quadrilateral. Composing u with p gives rise to a \(\mathbb {T}^2\) invariant map \(P:\mathbb {CP}^3 \rightarrow \mathbb {R}^2\) whose fibres contain \(\mathrm {U}(1)\)-invariant J-holomorphic curves and whose image is a rectangle \(\bar{\mathcal {R}}\subset \mathbb {R}^2\). Just as in the symplectic case, the fibre of P degenerate over the boundary \(\partial \bar{\mathcal {R}}\) and are geometrically distinguished sets. In fact, Theorem 6.14 relates \(P^{-1}(\partial \bar{\mathcal {R}})\) to the nearly Kähler multi-moment map \(\nu \), Clifford tori and certain families of minimal tori in \(S^4\) discovered by B. Lawson [24].
2 Background
2.1 Nearly Kähler six-manifolds
Nearly Kähler manifolds are a special class of almost Hermitian manifolds (M, g, J) satisfying the equation
where \(\nabla \) is the Levi–Civita connection on M and \(\xi \) denotes any tangent vector on M. Nearly Kähler manifolds have many desirable properties from different points of view. Nearly Kähler manifolds which are not Kähler are called strictly nearly Kähler manifolds. Since Kähler and strictly nearly Kähler manifolds are very different, we will assume that M is strictly nearly Kähler. Furthermore, we assume that \(n=6\) since this case of fundamental importance for various reasons. Firstly, they are Einstein with positive Einstein constant and vanishing first Chern class [19]. Furthermore, if \(M^6\) is nearly Kähler then the Riemannian cone C(M) carries a torsion-free \(G_2\) structure. Another reason to focus on the case \(n=6\) is that they are one of the building blocks of higher-dimensional nearly Kähler manifolds, due to a result by Nagy [28]. Every nearly Kähler manifold carries a unique connection \(\overline{\nabla }\) with skew-symmetric torsion and holonomy contained in \(\mathrm {SU}(3)\), i.e. \(\overline{\nabla }g =\overline{\nabla }J =\overline{\nabla }\psi =0\).
Examples of nearly Kähler manifolds are scarce. In fact, there are only six known examples of compact nearly Kähler manifolds. If \(M=G/H\) is a homogeneous strictly nearly Kähler manifold of dimension six, then M is an element of the following list [11, Theorem 1]
-
\(G=G_2\) and \(H=\mathrm {SU}(3)\) such that \(M=S^6\)
-
\(G=S^3\times S^3 \times S^3\) and \(H=\{(g,g,g)\mid g \in S^3\}\) such that \(M=S^3\times S^3\)
-
\(G=\mathrm {Sp}(2)\) and \(H=S^1\times S^3\) such that \(M=\mathbb {CP}^3\)
-
\(G=\mathrm {SU}(3)\) and \(H=\mathbb {T}^2\) such that \(M=\mathbb {F}\) is the manifold of complete complex flags of \(\mathbb {C}^3\).
In each case, the identity component of the group of nearly Kähler automorphisms is equal to G and only for \(S^3\times S^3\) there is a finite subgroup \(\Gamma \) of G acting freely on M, giving rise to locally homogeneous examples [12]. In addition, there are two known examples of compact, simply connected nearly Kähler manifolds which are not homogeneous but admit a cohomogeneity-one action. They have been constructed by L. Foscolo and M. Haskins via cohomogeneity one actions on \(S^3\times S^3\) and \(S^6\) [17].
2.2 Twistor spaces
We briefly review a few fundamental results on four-dimensional twistor theory, see [14]. To each even-dimensional Riemannian manifold N one can associate a twistor space \(Z_{\pm }(N)\), which is a fibre bundle over N. The fibre of this bundle over x is given by
Unless specified otherwise, by twistor space Z(N) we refer to the convention of orientation reversing endomorphisms, i.e. \(Z_-(N)\). From now on, let N be four-dimensional such that the twistor space Z(N) can be identified with elements in \(\Lambda ^2_{-}(N)\) of unit length. It is a sphere bundle over N which inherits the Levi–Civita connection from \(\Lambda ^2(N)\). Hence TZ(N) splits into a vertical and horizontal subbundle \(TZ(N)=\mathcal {H}\oplus \mathcal {V}\). It turns out that Z(N) possesses a natural almost complex structure \(J_1\) known as the Atiyah–Hitchin–Singer almost complex structure. It splits into a sum of almost complex structures on \(\mathcal {H}\) and \(\mathcal {V}\). Reversing \(J_1\) on \(\mathcal {V}\) defines the Eells–Salamon almost complex structure \(J_2\). The two almost complex structures \(J_1\) and \(J_2\) are fundamentally different. It turns out that the twistor space of \(N=S^4\) with the round metric is \(\mathbb {C}\mathbb {P}^3\). The fibration \(\mathbb {C}\mathbb {P}^3\rightarrow S^4\) is constructed by composing the map
with a diffeomorphism \(\mathbb {H}\mathbb {P}^1\cong S^4\). The twistor space of \(N=\mathbb {C}\mathbb {P}^2\) is the flag manifold \(\mathrm {SU}(3)/\mathbb {T}^2\). In both cases, \(J_1\) gives rise to the well-known Kähler structures on the spaces while \(J_2\) belongs to nearly Kähler structures. The splitting \(TZ(N)=\mathcal {H}\oplus \mathcal {V}\) is parallel with respect to \(\overline{\nabla }\) when \(N=S^4\) or \(\mathbb {CP}^2\). For any immersion \(f:X \rightarrow N^4\) the differential \(\mathrm {d}f\) defines a lift, called the Gauß lift, \(\hat{\varphi }\) from X into the oriented Grassmannian bundle \(\widetilde{\mathrm {Gr}}_2(TN)\). This bundle in turn projects to Z(N) such that by composition with \(\hat{\varphi }\) one obtains a map \(\varphi :X \rightarrow Z(N)\) which is called the twistor lift of f.

There is a general relation between the Riemannian geometry of N and (almost) complex geometry of Z(N) which is exemplified by the following result.
Proposition 2.1
(Eells-Salamon)[14, Corollary 5.4] Let X be a Riemann surface and N be a four-dimensional Riemannian manifold. Then \(f:X\rightarrow N\) is a minimal branched immersion if and only if \(\varphi :X \rightarrow Z_{\pm }(N)\) is a \(J_2\)-holomorphic non-vertical curve.
Note that if \(f:X \rightarrow N\) is a branched minimal immersion, i.e. minimal immersion off a discrete set of points, then there is a rank two subbundle \(E\subset f^*(TN)\) which contains \(\mathrm {d}f(TX)\) so the Gauß lift is still well defined in this case. Furthermore, it should be mentioned that, since the domain is two-dimensional, a branched minimal immersion is the same thing as a conformal harmonic map. Via this correspondence, branched minimal surfaces in \(S^4\) are identified with \(J_2\)-holomorphic curves in the nearly Kähler twistor spaces \(\mathbb {CP}^3\).
2.3 The nearly Kähler structure on \(\mathbb {CP}^3\)
As indicated in the previous section, the nearly Kähler structure on \(\mathbb {CP}^3\) can be defined via twistor structure. For explicit computations it is convenient to define the nearly Kähler from the homogeneous space structure \(\mathbb {CP}^3=\mathrm {Sp}(2)/{S^1\times S^3}\). Identify \(\mathbb {H}^2\) with \(\mathbb {C}^4\) via \(\mathbb {H}=\mathbb {C}\oplus j \mathbb {C}\). This identification gives an action of \(\mathrm {Sp}(2)\) on \(\mathbb {C}^4\) which descends to \(\mathbb {CP}^3\) and acts transitively on that space. The stabiliser of the element (1, 0, 0, 0) is
which shows \(\mathbb {CP}^3=\mathrm {Sp}(2)/{S^1\times S^3}\). following [33], consider the Maurer–Cartan form on \(\mathrm {Sp}(2)\) which can be written in components as
Here, \(\omega _1,\omega _2,\omega _3\) and \(\tau \) are complex-valued and \(\rho _1\) as well as \(\rho _2\) are real-valued one-forms on \(\mathrm {Sp}(2)\). The equation
implies the following differential identities for the components of \(\Omega _{MC}\)
Let furthermore
so one obtains
Let finally \(\kappa _{33}=2i\rho _1\) which satisfies \(\mathrm {d}\kappa _{33}=-\omega _1\wedge \overline{\omega _1}-\omega _2\wedge \overline{\omega _2}+2\omega _3\wedge \overline{\omega _3}\). The nearly Kähler structure on \(\mathbb {CP}^3\) is defined by declaring the forms \(s^*(\omega _1),s^*(\omega _2)\) and \(s^*(\omega _3)\) to be unitary (1, 0) forms for any local section s of the bundle \(\mathrm {Sp}(2)\rightarrow \mathbb {CP}^3\). The resulting almost complex structure and metric do not depend on the choice of s. The matrix \(A_{\omega }\) is in fact the connection matrix of the nearly Kähler connection \(\overline{\nabla }\) in the frame dual to the local co-frame \((\omega _1,\omega _2,\omega _3)\). Note that the forms \((\omega _1,\omega _2,\omega _3,\tau )\) are complex-valued invariant forms on \(\mathrm {Sp}(2)\) and as such they can be seen as elements in \(\mathfrak {sp}(2)^\vee \otimes \mathbb {C}\). They span different root spaces with respect to the maximal torus \(S^1\times S^1\), see Fig. 1.
3 Properties of twistor lifts
As seen in Eq. (2.1), there is a notion of a negative and positive twistor space for a Riemannian four-manifold \(N^4\). In general, they can be different fibre bundles over \(N^4\) and Proposition 3.1 expresses how the second fundamental form of a surface in \(N^4\) is related to the lift into both twistor spaces. However, for \(N=S^4\) both twistor space are isomorphic as fibre bundles which we exploit to give a twistor interpretation of Xu’s correspondence.
3.1 Encoding the second fundamental form
Since the second fundamental form will be considered in different ambient spaces, we use the notation \(\mathrm {I\!I}_Y\) where Y is the ambient space or an ambient bundle. Let \(N^4\) be a Riemannian manifold and \(f :X^2\rightarrow N^4\) be an isometric immersion. The second fundamental form \(\mathrm {I\!I}_N\) encodes local geometric information about f. The aim of this section is to relate the norm of \(\mathrm {I\!I}_N\) to quantities defined for the twistor lift of f. Let \(\nu \) be the normal bundle of TX in \(f^*(TN)\). Locally, fix an oriented orthonormal frame \(\{e_1,e_2,e_3,e_4\}\) such that \(\{e_1,e_2\}\) is an oriented basis of \(f^*(TX)\). Denote by \(\omega _{ij}(v)=g(\nabla _v e_i,e_j)\) the locally defined connection one-forms of the Levi–Civita connection \(\nabla \) on N. Furthermore, let \(\omega _{ijk}=\omega _{ij}(e_k)\). Then \(\omega _{ijk}=-\omega _{jik}\) and if \(i,k\in \{1,2\}\) and \(j\in \{3,4\}\) then \(\omega _{ijk}=\omega _{kji}\) holds by torsion-freeness. The vertical component of the twistor lift can be computed in the following way [18]
Here \(\{y_5,y_6\}\) is a local orthonormal basis for the vertical space of Z, induced from the choice of \(\{e_1,\dots ,e_4\}\). One can regard \((\mathrm {d}\varphi )^\mathcal {V}\) as a one-form with values in \(\mathrm {Hom}_{\mathbb {C}}(TX,\nu )\). Under this identification,
The almost complex structures \(J_1\) and \(J_2\) act by \(J_1(y_5,y_6)=(-y_6,y_5)\) and \(J_2(y_5,y_6)=(y_6,-y_5)\) on the vertical bundle. Let \(f:X\rightarrow N\) be an immersion. Changing between \(\varphi _-\) and \(\varphi _+\) amounts to changing the orientation of N, i.e. swapping the indices \(3\leftrightarrow 4\). This gives the analogous formula
Proposition 3.1
Furthermore, if f is minimal then \(\Vert \mathrm {d}\varphi _-^{\mathcal {V}}\Vert =\Vert \mathrm {d}\varphi _+^{\mathcal {V}}\Vert \) if and only if \(\mathrm {I\!I}_N\) takes values in a real line bundle contained in \(\nu \).
Proof
As a consequence of Eqs. (3.1) and (3.2) we have
which implies the first statement. Hence, \(\Vert \mathrm {d}\varphi _-^{\mathcal {V}}\Vert =\Vert \mathrm {d}\varphi _+^{\mathcal {V}}\Vert \) if and only if
This condition is satisfied if and only if \(\mathrm {I\!I}_3\) and \(\mathrm {I\!I}_4\) commute. Here,
This in turn is equivalent to \(\mathrm {I\!I}_3\) and \(\mathrm {I\!I}_4\) being simultaneously diagonalisable. So, assume that \(\{e_1,e_2\}\) is a positive local frame in which \(\mathrm {I\!I}_3\) and \(\mathrm {I\!I}_4\) are diagonal, i.e. \(\mathrm {I\!I}_3=\mathrm {diag}(\omega _{131},-\omega _{131})\) and \(\mathrm {I\!I}_4=\mathrm {diag}(\omega _{141},-\omega _{141})\) due to minimality. Hence \(\mathrm {I\!I}_N\) takes values in the real line bundle which is contained in \(\nu \) and locally spanned by \(\omega _{131} \otimes e_3 + \omega _{141} \otimes e_4.\) \(\square \)
The condition that \(\mathrm {I\!I}_N\) takes values in a real line is equivalent to the ellipse of curvature being degenerate, which has been studied in [20].
Corollary 3.2
Let \(x\in X\), then f is totally geodesic in x if and only if both twistor lifts are horizontal.
Corollary 3.3
If f takes values in a totally geodesic submanifold then \(\Vert \mathrm {d}\varphi _-^{\mathcal {V}}\Vert =\Vert \mathrm {d}\varphi _+^{\mathcal {V}}\Vert \).
The relationship between \(\mathrm {I\!I}_N\) and \(\Vert \mathrm {d}\varphi _{\pm }^{\mathcal {V}}\Vert \) is expressed more explicitly in the following lemma.
Lemma 3.4
For a minimal immersion \(f:X\rightarrow N\) and \(x\in X\) there is an orthonormal frame \((e_1,e_2,e_3,e_4)\) of \(f^*(T_x N)\) such that the only nonzero components of the second fundamental form are \(-\omega _{232}=\omega _{131}=\frac{1}{\sqrt{2}}(\Vert \mathrm {d}\varphi _-^{\mathcal {V}}\Vert +\Vert \mathrm {d}\varphi _+^{\mathcal {V}}\Vert ), \quad \omega _{142}=\frac{1}{\sqrt{2}}(\Vert \mathrm {d}\varphi _-^{\mathcal {V}}\Vert -\Vert \mathrm {d}\varphi _+^{\mathcal {V}}\Vert )\).
If \(\Vert \mathrm {d}\varphi _-^{\mathcal {V}}\Vert = \Vert \mathrm {d}\varphi _+^{\mathcal {V}}\Vert \) at x we choose \(e_1,e_2\) as in the proof of Proposition 3.1 and let \(e_3\) be equal to \(\mathrm {I\!I}(e_1,e_1)\). If \(\Vert \mathrm {d}\varphi _-^{\mathcal {V}}\Vert \ne \Vert \mathrm {d}\varphi _+^{\mathcal {V}}\Vert \) then the ellipse of curvature does not degenerate and there is a frame \(e_1,\dots ,e_4\) such that \(\omega _{141}=0, \omega _{132}=0\) and \(\omega _{142}\ge \omega _{131}\ge 0\). The vectors \(e_3\) and \(e_4\) span the semi-axes of the curvature ellipse [20]. Equation 3.3 simplifies to \(\sqrt{2} \Vert \mathrm {d}\varphi _-^{\mathcal {V}}\Vert =\omega _{131}+\omega _{142}\) and \(\sqrt{2} \Vert \mathrm {d}\varphi _+^{\mathcal {V}}\Vert =-\omega _{142}+\omega _{131}\) which proves the statement.
Lemma 3.5
Let \(X\subset Y\subset Z\) all be compact with Y totally geodesic and let G act by isometries X and Z. Then Y is also G-invariant.
Proof
Let \(\nu \) be the normal bundle of X in Y. Since X, Y are compact, Y is the image of \(\exp :\nu \rightarrow Z\). \(\exp \) is G-invariant since G acts by isometries, which implies the statement. \(\square \)
3.2 Twistor interpretation of Xu’s correspondence
We give a brief overview of Xu’s work on J-holomorphic curves in \(\mathbb {CP}^3\) and provide a twistor interpretation of his correspondence of superminimal curves and curves with vanishing torsion [33]. A superminimal curve is a J-holomorphic curve \(\varphi :X\rightarrow \mathbb {CP}^3\) which is tangent to \(\mathcal {H}\), i.e. \(\mathrm {d}\varphi \) maps TX to \(\varphi ^*\mathcal {H}\). These curves are special since are holomorphic for \(J_1\) too and R. Bryant found a Weierstraß parametrisation for them, i.e. each of them is a projective line or parametrised by
for f, g meromorphic functions on X with g being non-constant [9, Theorem F]. For a general J-holomorphic curve \(\varphi \) there is a unique holomorphic line bundle \(L\subset \varphi ^*\mathcal {H}\) which contains the projection of \(\mathrm {d}{\varphi }(TX)\) to \(\varphi ^*\mathcal {H}\). Let N be the quotient bundle \(\varphi ^*\mathcal {H}/L\), which naturally carries a holomorphic structure. Define
which is an \(S^1\times S^1\) sub-bundle of \(\varphi ^* \mathrm {Sp}(2)\). The bundle P can be equipped with a connection such that the forms \(\tau \) and \(\omega _2\) restrict to basic forms on P. By multiplying \(\bar{\tau }\) by an appropriate section in \(L^\vee \otimes N\) one obtains the form \(\mathrm {I\!I}_{\mathcal {H}}\in \Omega ^{1,0}(X,L^\vee \otimes N)\).
Proposition 3.6
In \(\mathbb {CP}^3\), there is a one-to-one correspondence between horizontal holomorphic curves and \(J_2\)-holomorphic curves on which \(\mathrm {I\!I}_{\mathcal {H}}\) vanishes.
Let \(I_{\mathcal {H}}\in \Omega ^{1,0}(X,L)\) and \(I_{\mathcal {V}}\in \Omega ^{1,0}(X,\mathcal {V})\) be \(\mathrm {d}\varphi \) composed orthogonal projections onto \(\mathcal {H}\) and \(\mathcal {V}\). Then \(I_{\mathcal {H}}\), \(I_{\mathcal {V}}\) and \(\mathrm {I\!I}_{\mathcal {H}}\) are all holomorphic sections and if neither of them vanishes everywhere and X is compact with genus g and \(\varphi \) simple (in the sense of [26]), then
where \(r_{\mathcal {H}},r_{\mathcal {V}},r_{\mathrm {I\!I}}\) denote the number of zeros of \(I_{\mathcal {H}}\), \(I_{\mathcal {V}}\) and \(\mathrm {I\!I}_{\mathcal {H}}\), counted with multiplicities [33, Remark 4.11.]. The correspondence of Proposition 3.6 can be entirely described in terms of twistor lifts. All statements from Sect. 2.2 apply to the negative as well as to the positive twistor space. The twistor theory of \(S^4\) has the particularity that both the negative and the positive twistor space can be identified with \(\mathbb {CP}^3\). To distinguish the two spaces as bundles over \(S^4\) we denote them by \(\mathbb {CP}^3_{\pm }\). Both spaces are quotients of \(\mathrm {Sp}(2)\) by different but conjugate subgroups.

For a \(J_2\)-holomorphic curve \(\varphi _-:X\rightarrow \mathbb {CP}^3_-\) Xu constructs a lift \(\tilde{\varphi }_-:X \rightarrow Sp(2)/{S^1\times S^1}\) and then considers the projection onto \(\mathbb {CP}^3_+\) which yields a map \(X \rightarrow \mathbb {CP}^3_+\). He constructs a similar lift \(\tilde{\varphi }_+\) when starting with a curve in \(\mathbb {CP}^3_+\) and shows that both constructions are inverse to each other. Observe that \(Sp(2)/{S^1\times S^1}\) is nothing but \(\widetilde{\mathrm {Gr}}_2(S^4)\). Let \(\pi _{\pm }\) be the projection of \(\mathbb {CP}^3_{\pm }\) onto \(S^4\). It turns out that the lifts \(\varphi _{\pm }\) equal the Gauß lift of \(\pi _{\pm }\circ \varphi \) into \(\mathrm {Sp}(2)/{S^1\times S^1}\). This immediately shows that the two constructions are inverse to each other since the transformation leaves the underlying map into \(S^4\) unchanged. In fact, this procedure gives a way to pass between \(J_2\)-holomorphic curves in \(\mathbb {CP}^3_+\) and \(\mathbb {CP}^3_-\) due to Proposition 2.1. However, when starting with a horizontal \(J_2\)-holomorphic curve in \(\mathbb {CP}^3_-\) the resulting curve in \(\mathbb {CP}^3_+\) need not be horizontal. In fact the tangent bundle of F admits a natural splitting
which is a connection of the fibration \(Sp(2)/{S^1\times S^1}\rightarrow S^4\) such that
If \(\{f_1,f_2,f_3,f_4\}\) denotes a frame dual to \(\{\omega _1,\omega _2,\omega _3,\tau \}\) then \(\mathbf{H} \) is locally spanned by \(f_1\) and \(f_2\), \(V_-\) by \(f_3\) and \(V_+\) by \(f_4\). Consider a \(J_2\)-holomorphic curve \(\varphi _-:X \rightarrow \mathbb {CP}^3_-\) and the Gauß lift \(\hat{\varphi }_-:X \rightarrow \mathrm {Sp}(2)/{S^1\times S^1}\). The curve is horizontal if the lift does not have a component in \(V_-\). Equation (3.7) describes the splitting of \(\mathfrak {sp}(2)/{\mathfrak {t}^2}\) into root spaces. In fact, Eq. (2.2) reveals that the component in \(V_+\) vanishes if and only if
on X which proves Proposition 3.6. Finally, observe that Eq. (2.3) implies that \(\mathrm {I\!I}_{\mathcal {H}}\) is equal to the second fundamental form of L in \(\varphi ^*\mathcal {H}\) which is an element in \(\Omega ^{1,0}(X,\mathrm {Hom}(L,N))\) because L is a holomorphic sub bundle of \(\varphi ^*\mathcal {H}\). The holomorphicity of \(\mathrm {I\!I}_{\mathcal {H}}\) can then be related to properties of the curvature tensor of \(\varphi ^*\mathcal {H}\).
4 Adapting frames on J-holomorphic curves
Recall from Sect. 2.3 that there are three distinguished classes of J-holomorphic curves in \(\mathbb {CP}^3\). The first are curves which are always tangent to the vertical bundle \(\mathcal {V}\). They are twistor lines and are parametrised by elements in \(S^4\). Since the horizontal bundle \(\mathcal {H}\) is of complex rank two it is less restrictive to require a curve being tangent to \(\mathcal {H}\). These curves are called superminimal and classified in Eq. (3.5). There is a third class of curves, namely those on which \(\mathrm {I\!I}_{\mathcal {H}}\) vanishes identically. Such curves are in one to one correspondence with superminimal curves by Proposition 3.6. Since all of these classes are relatively well understood we are interested in studying J-holomorphic curves which do not belong to any of these three classes and are defined as follows.
Definition 4.1
A J-holomorphic curve \(\varphi :X\rightarrow \mathbb {CP}^3\) is called transverse if one of the equivalent conditions is satisfied
-
\(\mathrm {I\!I}_{\mathcal {H}}\ne 0\) everywhere and \(\varphi \) is nowhere tangent to the horizontal bundle \(\mathcal {H}\) or the vertical bundle \(\mathcal {V}\)
-
Both twistor lifts of \(\pi _-\circ \varphi :X\rightarrow S^4\) are nowhere horizontal or vertical
-
The Gauß lift of \(\pi _-\circ \varphi \) into \(\mathrm {Sp}(2)/{S^1\times S^1}\) is nowhere tangent to either bundle \(\mathbf {H}\),\(\mathbf {V}_-\) or \(\mathbf {V}_+\).
If X is homeomorphic to a two-sphere then the curve is superminimal or satisfies \(\mathrm {I\!I}_{\mathcal {H}}\equiv 0\) [34]. If X is a torus then the curve is automatically transverse if it is not superminimal or satisfies \(\mathrm {I\!I}_{\mathcal {H}}\equiv 0\). If X is compact with genus \(g\ge 2\) there are non-transverse points, see Eq. (3.6). For this reason, we are mainly interested in the case when X has genus one. However, the set of non-transverse points is discrete and in the end of Sect. 4.3 we will describe the behaviour of the curve near these points.
In the case of the nearly Kähler \(S^3\times S^3\), the almost product structure gives a natural choice of an \(\mathrm {SU}(3)\) frame along any J-holomorphic curve. This allows to study the structure equations in terms of a reduced set of functions, classify and identify sub-classes of J-holomorphic curves in \(S^3\times S^3\) [6]. The aim of this section is to provide a similar analysis for J-holomorphic curves in \(\mathbb {CP}^3\). Instead of an almost product structure, the parallel splitting \(T\mathbb {CP}^3=\mathcal {H}\oplus \mathcal {V}\) plays a key role in this case. By an appropriate frame adaption we will describe transverse J-holomorphic curves by two functions \({\alpha _-},{\alpha _+}:X\rightarrow \mathbb {R}\) which carry local geometric information such as the curvature and second fundamental form of the curve.
4.1 The action of H on \(\mathfrak {sp}(2)\)
Consider the embedding \(i:\mathrm {U}(2)\rightarrow \mathrm {SU}(3)\) via \(A\mapsto \begin{pmatrix} A &{} 0 \\ 0 &{} \mathrm {det}(A^{-1}) \end{pmatrix}\). Let \((v_1,v_2,v_3)^T\in \mathbb {C}^3\) with \(|v_1|^2+|v_2|^2 \ne 0\) and \(|v_3|^2 \ne 0\). Then there is \(A\in \mathrm {U}(2)\) such that if \((w_1,w_2,w_3)^T=A (v_1,v_2,v_3)^T\) then \(w_2=0\) and \(w_3/w_1\in \mathbb {R}^{>0}\). The choice of such an A is unique up to multiplication by an element in the subgroup \(K'=\{\mathrm {diag}(e^{i\vartheta },e^{-2i\vartheta },e^{i\vartheta })\}\subset \mathrm {SU}(3)\). Define the double cover \(u:H=\mathrm {U}(1)\times \mathrm {Sp}(1) \rightarrow \mathrm {U}(2)\) where \(u(\lambda ,q)\) acts on \(\mathbb {C}^2=\mathbb {C}\oplus j \mathbb {C}=\mathbb {H}\) by \(h\mapsto q h \lambda ^{-1}\). Let \(\rho \) be the action of \(\mathrm {U}(1)\times \mathrm {Sp}(1)\) on \(V_1=\mathbb {C}^3\) coming from \(i\circ u\). Consider the adjoint action of \(H\subset \mathrm {Sp}(2)\) on \(\mathfrak {sp}(2)\). It splits as
The action of H on \(\mathfrak {h}\) is the adjoint action while H acts on \(V_1\) by \(\rho \). Here \(V_1\) embeds into \(\mathfrak {sp}(2)\) as follows
Note that \(K=\rho ^{-1}(K')=\{\mathrm {diag}(e^{i\theta },e^{i 3 \theta })\}\) and define \(W=\{(v_1,0,v_3)\in V_1 \mid v_3/{v_1}>0\}\). We have proven the following.
Lemma 4.2
For any \(\zeta =\eta +(v_1,v_2,v_3)\in \mathfrak {h} \oplus \mathbb {C}^3\) with \((v_1,v_2)\ne (0,0)\) and \(v_3 \ne 0\) there is \(h\in H\) such that \(h\zeta h^{-1}\) lies in W. Such an h is unique up to an element in K.
The adjoint action of K on \(\mathfrak {h}\) splits into one-dimensional subspaces. Let
The action of K on \(V_3\) is trivial while it acts on \(V_2\) by multiplication of \(e^{-6i \theta }\). On the other hand, K acts on \((z_1,0,z_3)\in W\) by multiplication of \(e^{2i\theta }\) in each component. Define
We conclude
Lemma 4.3
Let \(v=(z_1,z_2,z_3,w,x_1,x_2) \in \mathfrak {sp}(2)\) with \((z_1,z_2)\ne (0,0), w\ne 0\) and \(z_3\ne 0\). Then there is always an element \(A\in K\) such that \(Av\in \mathfrak {r}\). The choice of such an element A is unique up to multiplication of an element of the subgroup \(K_F:=\{\mathrm {diag}(e^{i\theta },e^{i 3 \theta })\mid e^{8i\theta }=1\}\cong \mathbb {Z}_8.\)
4.2 Transverse J-holomorphic curves in \(\mathbb {CP}^3\)
Consider a general J-holomorphic curve \(\varphi :X\rightarrow \mathbb {CP}^3\). Denote by g the nearly Kähler metric on \(\mathbb {CP}^3\) which splits as \(g_{\mathcal {H}}+g_{\mathcal {V}}\) since the splitting \(T\mathbb {CP}^3=\mathcal {H}\oplus \mathcal {V}\) is orthogonal. We will consider the pull-back metrics of \(g,g_{\mathcal {H}},g_{\mathcal {V}}\) to X via \(\varphi \) and denote them with the same symbols. The metric \(2 g_{\mathcal {H}}\) is equal to the induced metric from \(\pi \circ \varphi :X\rightarrow S^4\). Note that \(\mathrm {Sp}(2)\) pulls back to an \(S^1\times S^3\) bundle over X. The structure equations are formulated with respect to differential forms on \(\mathrm {Sp}(2)\). To simplify matters, one reduces the \(S^1\times S^3\) bundle \(\varphi ^*(\mathrm {Sp}(2))\) which ensures that additional relations of the differential forms are satisfied. To begin with, one can reduce the bundle \(\varphi ^*(\mathrm {Sp}(2))\) to an \(S^1\times S^1\) bundle P by imposing the equation \(\omega _2=0\), see [33]. This gives a lift of \(\varphi \) into \(\mathrm {Sp}(2)/{S^1\times S^1}\). On this reduction, \(\tau \) becomes a basic form of type (1, 0). Since \(\varphi \) is J-holomorphic \(\mathrm {d}\varphi (T^{1,0})\) takes values in the subbundle corresponding to the root spaces \(\{(2,0),(0,-2),(-1,1)\}\) which are associated with \((\omega _3,\tau ,\omega _1)\) under the isomorphism \(\Omega ^1(\mathrm {Sp}(2),\mathbb {C})^{\mathrm {Sp}(2)}\cong \mathfrak {sp}(2)^\vee \otimes \mathbb {C}\), see Fig. 2. Given a semi-simple Lie group with maximal torus T the flag manifold G/T carries a natural m-symmetric structure \(\tau \) where m is the height of the Lie algebra of G. \(\tau \) gives rise to a splitting \(T_{\mathbb {C}}(G/T)=\oplus [\mathcal {M}_k]\) and a map \(\psi :X \rightarrow G/T\) is called \(\tau \)-primitive if it satisfies a compatibility condition between the complex structure on X and \(\tau \), see [8]. In the case of \(G=\mathrm {Sp}(2)\), \(\{(2,0),(0,-2),(-1,1)\}\) is a basis of \([\mathcal {M}_1]\).
Proposition 4.4
Any J-holomorphic curve \(\varphi :X \rightarrow \mathbb {CP}^3\) admits a lift into \(\mathrm {Sp}(2)/{S^1\times S^1}\) which is \(\tau \)-primitive in the sense of [8]. Conversely, composing any \(\tau \)-primitive map \(X\rightarrow \mathrm {Sp}(2)/{S^1\times S^1}\) with the projection \(\mathrm {Sp}(2)/{S^1\times S^1}\rightarrow \mathbb {CP}^3\) gives a J-holomorphic curve \(X\rightarrow \mathbb {CP}^3\).
Note that under this identification, the formula [34, Remark 4.11.] becomes an application of the more general Plucker formula for \(\tau \)-primitive maps [7].
We will now explain how \(\varphi ^*(\mathrm {Sp}(2))\) can in fact be reduced to a discrete bundle for a transverse J-holomorphic curve \(\varphi :X \rightarrow \mathbb {CP}^3\). We can define the function \({\alpha _-}:X \rightarrow \mathbb {R}^{>0}\) by
where \(\xi \) is any nonzero vector in \(T_xX\). Here \(|\cdot |_{\mathcal {H}}\) and \(|\cdot |_{\mathcal {V}}\) denote the norms with respect to the metric \(g_{\mathcal {H}}\) and \(g_{\mathcal {V}}\) on X. The value of \({\alpha _-}\) does not depend on this choice because \(\varphi \) is J-holomorphic. The function \({\alpha _-}\) is a measure for the angle in which TX lies between \(\mathcal {H}_X\) and \(\mathcal {V}_X\). In accordance with Lemma 4.2 we now adapt frames in the following way. Over X, define the principal bundle Q by the relations
The bundle Q has structure group \(K\cong S^1\). From now on, we will consider the restrictions of all differential forms to Q without changing the notation. Note that, since the structure group of Q is K, the forms \(\tau ,3\rho _1-\rho _2\) and \(\omega _1\wedge {\overline{\omega _1}}\) become basic, i.e. they descend to forms on \(\mathbb {CP}^3\). The structure equations then yield
Combining all of the equations gives that \(\tau \) and \(-\mathrm {d}\mathrm {log}({\alpha _-})+i(-3\rho _1+\rho _2)\) are (1, 0)-forms since their wedge product with \(\omega _1\) vanishes. Since \(\rho _1\) and \(\rho _2\) and \(-\mathrm {d}\mathrm {log}({\alpha _-})\) are real-valued we get that
for any tangent vector \(\xi \). In other words,
Note that a-priori this is an equation on Q but it also holds on X since \(-3\rho _1+\rho _2\) is a basic form. Equation (4.4) implies that
Here, \(\Delta \) denotes the positive definite Laplace operator \(\Omega ^0(X)\rightarrow \Omega ^2(X)\).
4.3 Further reduction of the structure group
Since \(\varphi \) is assumed to be transverse, \(\tau \) is nowhere vanishing. On Q, both \(\tau \) and \(\omega _1\) reduce to forms on X with values in the same line bundle. So we can define
for any \(\xi \in T_xX\) which does not depend on \(\xi \in T_x X\) since \(\tau \) is a (1, 0)-form. In fact, by Proposition 4.4 transverse J-holomorphic curves correspond to \(\tau \)-primitive maps \(\hat{\varphi }:X\rightarrow \mathrm {Sp}(2)/{S^1\times S^1}\). As seen in Eq. (3.7)
Note that \({\alpha _-}\) is a measure of the angle of TX between \(\hat{\varphi }^*(H)\) and \(\hat{\varphi }^*(V_-)\) while \({\alpha _+}\) is a measure of the angle of TX between \(\hat{\varphi }^*(H)\) and \(\hat{\varphi }^*(V_+)\). This is why we will refer to \({\alpha _-}\) and \({\alpha _+}\) as angle functions. By Lemma 4.2, we can adapt frames further. The bundle Q restricts to a \(K_F\) bundle R which is characterised by the equation \(\tau ={\alpha _+} \omega _1\). From the structure equations we now get
Combining Eqs. (4.7) and (4.6) one infers that \(-\mathrm {d}\mathrm {log}({\alpha _+})+i(-\rho _1+3\rho _2)\) is a (1, 0)-form. As before, we get
This implies
Let us summarise the results so far
Lemma 4.5
Let \(\varphi :X \rightarrow \mathbb {CP}^3\) be a transverse J-holomorphic curve. Then the bundle \(\varphi ^*(\mathrm {Sp}(2))\) restricts to a \(K_F\) bundle R on which the following equations hold
Reducing the bundle \(\mathrm {Sp}(2)\) over a transverse J-holomorphic curve can be summarised in Table 1.
By the uniformisation theorem, any metric on a Riemann surface is (globally) conformally equivalent to a constant curvature metric which is being made explicit by the following proposition.
Proposition 4.6
The metrics \(g_{\mathcal {H}}\) and g are globally conformally flat for any transverse J-holomorphic curve \(\varphi :X\rightarrow \mathbb {CP}^3\). The conformal factor is given by \(\gamma ^2=({\alpha _-} {\alpha _+})^{-1/2}\)
Proof
Since the metrics \(g_{\mathcal {H}}\) and g only differ by the conformal factor \((1+{\alpha ^2_-})\) it suffices to prove this statement for \(g_{\mathcal {H}}\). First assume that X is simply connected, i.e. \(X\cong \mathbb {D}\) or \(\mathbb {C}\). In this case, the bundle R admits a global section s. Then \(s^*\omega _1\) is a unitary (1, 0)-form on X, satisfying the equation
Hence
since \(\mathrm {d}(\gamma ^{-1})-i d^C(\gamma ^{-1})\) is a (1, 0)-form. This means that the metric \(\gamma ^{-2} g_{\mathcal {H}}\) has a closed, unitary (1, 0)-form \(\gamma ^{-1} s^* \omega _1\), hence it is flat. If X is not simply connected we can show the statement by passing to the universal cover. \(\square \)
Putting Eqs. (4.5), (4.9), (4.7) and (4.8) together gives
If we equip X with the metric \(g_\mathcal {H}\) then \(-\frac{1}{2i} \omega _1\wedge \overline{\omega _1}\) becomes the volume form \(\mathrm {vol}_{\mathcal {H}}\) on X and we may rewrite the equations as
The curvature form on X is then given by
Let \(\gamma =({\alpha _-}{\alpha _+})^{-1/4}\) as in Proposition 4.6, i.e. \(\gamma ^{-2} g_\mathcal {H}\) is flat. Denote by \(\Delta _0\) the Laplace operator on functions with respect to \(\gamma ^{-2} g_\mathcal {H}\).
Theorem 4.7
Let \(\varphi :X\rightarrow \mathbb {CP}^3\) be a transverse J-holomorphic curve. Then the functions \({\alpha _-},{\alpha _+}\) satisfy
These equations are equivalent to the affine 2D Toda lattice equations for \(\mathfrak {sp}(2)\). The induced Gauß curvature on X is
Proof
Equation 4.13 is a direct consequence of the discussion preceding the theorem. The formula for the Gauß curvature follows from Eq. (4.12) since \(-i\kappa _{11}\) is the Levi–Civita connection form of X. If we define \({\hat{\alpha }_{\pm }}=\gamma {\alpha _{\pm }}\) such that \(\gamma =(\hat{\alpha }_- \hat{\alpha }_+)^{1/2}\) and Eq. (4.13) becomes
So if we let \(\hat{\alpha }^2_-=\frac{1}{\sqrt{2}}\exp (\Omega _1)\) and \(\hat{\alpha }^2_+=\frac{1}{\sqrt{2}}\exp (-\Omega _2)\) these equations are equivalent to the 2D affine Toda equations for \(\mathfrak {sp}(2)\). \(\square \)
Note the metric induced from \(\pi \circ \varphi :X\rightarrow S^4\) equals \(2g_\mathcal {H}\) and has hence Gauß curvature equal to \(1-{\alpha ^2_-}-{\alpha ^2_+}\).
Remark 4.8
Note that the result is consistent with Proposition 4.4 since a \(\tau \)-primitive map into G/T is described by the Toda lattice equations for \(\mathfrak {g}\) [8]. Furthermore, the relationship between Toda lattice equations and minimal surfaces in \(S^4\) has already been observed in [29].
From Sect. 2.3 recall that \(I_{\mathcal {H}},I_{\mathcal {V}}, \mathrm {I\!I}_{\mathcal {H}}\) are all holomorphic sections in different line bundles over X. If one of these sections vanishes in a point, then the curve is not transverse in this point and \(\alpha _-\) or \(\alpha _+\) becomes singular. In Proposition 4.10 we will show how the defining equations for \(\alpha _{\pm }\) Eq. (4.13) can locally be extended to the singular set. To this aim, we will make use of the following observation.
Lemma 4.9
Let L be a line bundle equipped with a Hermitian metric over a Riemann surface X with holomorphic section s. Then for each point \(x\in X\) there is a neighbourhood U such that \(|s|=|z|^{k_x} u\) with u positive and smooth, \(z:U \rightarrow \mathbb {C}\) biholomorphic onto its image, \(z(0)=x\) and \(k_x\) a nonnegative integer.
Proof
For \(x\in X\) choose a local non-vanishing section \(s':U\rightarrow L\) and write \(s=f s'\) for a holomorphic function \(f:U\rightarrow \mathbb {C}\). Then \(k_x\) is the order of the pole of f at x, possibly 0 and the statement follows. \(\square \)
This lemma can now be applied to study the singularities of \(\alpha _{\pm }\).
Proposition 4.10
Let \(\varphi :X \rightarrow \mathbb {CP}^3\) be a J-holomorphic curve with neither \(I_{\mathcal {H}},I_{\mathcal {V}},\mathrm {I\!I}_{\mathcal {H}}\) vanishing everywhere. Then there is a discrete set S such that \(\varphi |_{X\setminus S}\) is transverse with angle functions \(\alpha _{\pm }:X\setminus S \rightarrow (0,\infty )\) satisfying Eq. (4.13). For each point \(x\in S\) there are integers \(k_{\pm }\), not both zero, a neighbourhood \(U\subset \mathbb {CP}^3\) of x and a chart \(z:U\rightarrow \mathbb {C}\) with \(z(x)=0\) such that \(\alpha _{\pm }=\hat{\alpha }_{\pm }|z|^{k_{\pm }}\) for \(\hat{\alpha }_{\pm }\) smooth and positive on U. The metric \(g \hat{\gamma }^{-2}\) for \(\hat{\gamma }=(\hat{\alpha }_- \hat{\alpha }_+)^{-1/4}\) is flat on U. The functions \(\hat{\alpha }_{\pm }\) satisfy the equations
which are defined on all of U. Here \(\hat{\Delta }_0\) is the Laplace operator for \(g \hat{\gamma }^{-2}\).
Proof
Observe that
with the norms on the different line bundles induced from the metric on \(\varphi ^*T\mathbb {CP}^3\). Hence S is the discrete set where \(I_{\mathcal {H}}, I_{\mathcal {V}}\) or \(\mathrm {I\!I}_{\mathcal {H}}\) vanish. By Lemma 4.9 we can locally write \(\alpha =\hat{\alpha }|z|^{k_{\pm }}\) for \(k\in \mathbb {Z}\). The rest of the statement follows from the fact that \(\mathrm {log}|z|\) is harmonic since z is holomorphic. \(\square \)
4.4 The second fundamental form of transverse curves
As a nearly Kähler manifold, \(\mathbb {CP}^3\) comes equipped with two natural connections. The Levi–Civita connection \(\nabla \) and the nearly Kähler connection \(\overline{\nabla }\). It turns out that the second fundamental form of a J-holomorphic curve is the same for \(\nabla \) and \(\overline{\nabla }\). Despite \(\overline{\nabla }\) having torsion it is the connection that is easier to work with since it preserves the almost complex structure J. For a fixed J-holomorphic curve \(\varphi :X \rightarrow \mathbb {CP}^3\) consider the map \(\Theta _{\varphi }:TX\rightarrow \nu \) which is defined as \(\Theta =-{\alpha ^2_-}\mathrm {Id}_{\mathcal {H}}+\mathrm {Id}_{\mathcal {V}}\). Observe that \(\Theta \) is injective and let \(N_1=\Theta (TX)\). Denote by \(N_2\) the orthogonal complement of \(N_1\) in \(\nu \). It turns out that \(N_2\) is in fact equal to the kernel of the orthogonal projection \(\nu \rightarrow \mathcal {V}_X\). In other words, \(\varphi ^*(T\mathbb {CP}^3)\) splits into an orthogonal sum of complex line bundles
where \(N_1\cong TX\) and \(N_2\cong (TX)^{-2}\). This splitting is related to the reduction of \(\varphi ^*(\mathrm {Sp}(2))\) to Q. If
and s is a (local) section \(s:X \rightarrow Q\), \(s^*(u_1,u_2,u_3)\) is a unitary frame as well. Let \((f_1,f_2,f_3)\) be the dual frame of \(s^*(u_1,u_2,u_3)\). Then \(f_1\) always takes values in TX, \(f_2\) in \(N_1\) and \(f_3\) in \(N_2\). A frame with this property will be called a Q-adapted frame from now on. The connection matrix \(A_u\) for the frame \(\{f_1,f_2,f_3\}\) is then computed via applying the base change Eq. (4.16) to the connection matrix \(A_{\omega }\) in Eq. (2.3) and using Eq. (4.4)
Lemma 4.11
For a Q-adapted frame \(f_1,f_2,f_3\) and co-frame \(u_1,u_2,u_3\), the second fundamental form of X is equal to
for \(\mathrm {I\!I}_1=-\frac{2}{{\alpha ^2_-} +1} \mathrm {d}^{1,0}{\alpha _-}\) and \(\mathrm {I\!I}_2=\frac{\tau }{\sqrt{{\alpha ^2_-} +1}}=\frac{{\alpha _+} \omega _1}{\sqrt{{\alpha ^2_-} +1}}\). We see that transverse points of a J-holomorphic curve are never totally geodesic. Conversely, the frame \(\{f_1,f_2,f_3\}\) and the first and second fundamental form of a transverse curve determine \({\alpha _-}\) and \({\alpha _+}\).
Proof
The expression for \(\mathrm {I\!I}_{\mathbb {CP}^3}\) can be read off from Eq. (4.17). For the last statement, note that \(\mathrm {I\!I}_1=-2\mathrm {d}^{1,0}\mathrm {arctan}({\alpha _-})\). Assume that \({\alpha _-},{\alpha _+}\) and \({\alpha '_-},{\alpha '_+}\) are two pairs of functions inducing the same first and second fundamental form. Then \(\mathrm {arctan}({\alpha _-})\) and \(\mathrm {arctan}({\alpha '_-})\) differ by a real constant. Equivalently,
for a constant \(C\in \mathbb {R}\). Furthermore, the equation for \(\mathrm {I\!I}_2\) implies that
Putting all together gives that
which is a constant by Proposition 4.6. However, this is only possible if \(C=0\) or if \({\alpha _-}\) is constant. But solutions with \({\alpha _-}\) constant force \({\alpha ^2_-}={\alpha ^2_+}=1/2\) and hence \(C=0\). \(\square \)
Different Q-adapted frames are related by an action of \(K\cong S^1\). To work out tensors which are invariant under this action, let \(\lambda =(e^{i\theta },e^{3i\theta })\) be an element in K and denote \(-2\theta =\vartheta \). The action of \(\lambda \) introduces a gauge transformation leading to a transformed set of tensors \((\omega _1',\omega _2',\omega _3',\tau ')\) on Q. Note that
which leads to
and hence
Consequently, the tensors \(\tau \otimes u_{i} \otimes f_3, u_i\otimes f_j, u_3\otimes f_3\) for \(i,j=1,2\) are all invariant under K and hence correspond to tensors on X. Regard the second fundamental form \(\mathrm {I\!I}_{\mathbb {CP}^3}\) as a section in \(\Omega ^{1,0}(X,\mathrm {Hom}(TX,\nu ))\). The connection \(\overline{\nabla }\) induces connections \(\overline{\nabla }^T\) and \(\overline{\nabla }^\perp \) on TX and \(\nu \) and thus there is a well-defined object \(\bar{\partial }_{\overline{\nabla }} \mathrm {I\!I}_{\mathbb {CP}^3}=\mathrm {d}_{\overline{\nabla }} \mathrm {I\!I}_{\mathbb {CP}^3}\in \Omega ^{1,1}(X,\mathrm {Hom}(TX,\nu ))\). We have seen that a transverse J-holomorphic curve has no points which are totally geodesic. Having holomorphic second fundamental form is a natural generalisation of being totally geodesic.
Theorem 4.12
The differential of the second fundamental form is equal to
In particular, there is no transverse J-holomorphic curve with holomorphic second fundamental form.
Proof
Using Eq. (4.18), the differential of \(\mathrm {I\!I}_{\mathbb {CP}^3}\) is computed by
This expression takes values in \(\Omega ^{1,1}(X,TX^{\vee }\otimes \nu )\) and we compute the components in \(u_1\otimes f_2\) and \(u_1\otimes f_3\) separately. Note that
and
Furthermore, the \(u_1\otimes f_2\) component of \(-\mathrm {I\!I}_1\wedge \overline{\nabla }^T u_1 \otimes f_2-u_1\otimes \mathrm {I\!I}_1\wedge \overline{\nabla }^\perp f_2\) is equal to
Finally, the \(u_1\otimes f_2\) component of \(-u_1\otimes \mathrm {I\!I}_2\wedge \overline{\nabla }^\perp f_3\) is equal to
Observe that various terms cancel and that the \(u_1 \otimes f_2\) component of \(\mathrm {d}_{\overline{\nabla }} \mathrm {I\!I}_{\mathbb {CP}^3}\) is
The \(u_1\otimes f_3\) component is computed in an analogous way and equal to
since both \(\mathrm {I\!I}_2\) and \(\mathrm {d}{\alpha _-} -i\mathrm {d}^C {\alpha _-}\) are (1, 0) forms. This proves the formula
For a transverse J-holomorphic curve, \({\alpha _-}\) is always positive. So the second fundamental form is holomorphic if and only if \({\alpha _-}\) is constant to \(\sqrt{2/3}\). However, no such solution exists for Eq. (4.13). \(\square \)
Remark 4.13
Let \(f:X\rightarrow S^4\) be a minimal immersion with twistor lift \(\varphi :X \rightarrow \mathbb {CP}^3\) and associated angle functions \(\alpha _{\pm }\). Then f induces the metric \(2g_{\mathcal {H}}\) on \(S^4\) and \(\alpha _{\pm }=2 \Vert \mathrm {d}\varphi _{\pm }^{\mathcal {V}}\Vert \). In this setting, we have defined the second fundamental forms \(\mathrm {I\!I}_{S^4},\mathrm {I\!I}_{\mathcal {H}}\) and \(\mathrm {I\!I}_{\mathbb {CP}^3}\), depending on the ambient space or bundle. Curves with \(\mathrm {I\!I}_{\mathcal {H}}\equiv 0\) are in one-to-one correspondence with superminimal curves while
In fact, by Lemmas 3.4 and 4.11 each of \(\alpha _{\pm }\), \(\mathrm {I\!I}_{\mathbb {CP}^3}\) and \(\mathrm {I\!I}_{S^4}\) determines the other two.
4.5 Holomorphic structure of the normal bundle
The nearly Kähler connection \(\overline{\nabla }\) preserves J and \(\nu \) is a complex subbundle of \(T\mathbb {CP}^3\). Hence \(\overline{\nabla }^\perp \) gives rise to a holomorphic structure on \(\nu \). Let \(\varphi :X \rightarrow \mathbb {CP}^3\) be a transverse torus. The degree of \(\nu \) is zero since the first Chern class of any nearly Kähler manifold vanishes, i.e.
Let \(\mathrm {Bun}(r,d)\) be the space of indecomposable holomorphic bundles of rank r and degree d over X. By Atiyah’s classification of holomorphic vector bundles over elliptic curves [2], \(\mathrm {Bun}(2,0)\) is isomorphic to a two-torus. For any element \(E\in \mathrm {Bun}(2,0)\) the line bundle \(\Lambda ^2(E)\) is trivial. This is consistent with the fact that \(\Lambda ^2(\nu )=TX\). The space \(\mathrm {Bun}(2,0)\) has a distinguished element \(E_0\), the unique non-trivial extension of the sequence
Based on this, there are a-priori three possibilities for \(\nu \). Either \(\nu \) is decomposable, isomorphic to \(E_0\) or another element in \(\mathrm {Bun}(2,0)\). In the following we will see that for a transverse J-holomorphic torus in \(\mathbb {CP}^3\), \(\nu \) is always isomorphic to \(E_0\). Let \(\sigma _{ij}\) be the components of the connection matrix \(A_u\). Assume that the frame \(\{f_1,f_2,f_3\}\) is R-adapted, such that Eq. (4.10) hold. Then \(s=s_2 f_2+s_3f_3\) describes a general section in the normal bundle for \(s_2,s_3\in \Omega (X,\mathbb {C})\). By the Leibniz rule for \(\bar{\partial }\), holomorphic sections are solution of the equation
Since \(\sigma _{32}\) is of type (1, 0) it annihilates \(\frac{\partial }{\partial \bar{z}}\). Note that on X, \(u_1=\sqrt{1+{\alpha ^2_-}}\omega _1\) and hence by Proposition 4.6 we can find a local coordinate z on X such that
Then Eq. (4.21) reduces to
and
Hence, all solutions of Eq. (4.21) are given by
for a constant \(c\in \mathbb {C}\). Furthermore, we have
So, define \(s_2'=s_2 {\alpha ^{1/4}_+}{\alpha ^{-3/4}_-}\sqrt{1+{\alpha ^2_-}}\) which makes Eq. (4.22) equivalent to
and this in turn results in
But the function \({\alpha ^{-1/2}_-} {\alpha ^{1/2}_+}\) is non-vanishing which forces \(c=0\) and \(s_2'\) to be a constant. This computation implies the following two lemmas.
Lemma 4.14
Let X be a transverse torus then \(h^0(X,\nu )=1\)
Lemma 4.15
The holomorphic section \(s_2'f_2\) induces an exact sequence of holomorphic bundles
Proof
Since \(s_2\) is non-vanishing the section gives an injection \(\mathbb {C}\rightarrow \nu \). The quotient bundle admits a non-vanishing holomorphic section because \(\sigma ^{0,1}_{33}\) is \(\bar{\partial }\)-exact. Hence the quotient is trivial. \(\square \)
Summarising the two statements above gives
Proposition 4.16
As a holomorphic bundle, the normal bundle \(\nu \) of a transverse torus is the unique non-trivial extension of the sequence
5 A Bonnet-type theorem
The uniqueness part of the classical Bonnet theorem says that two surfaces \(\Sigma ,\Sigma '\subset \mathbb {R}^3\) with the same first and second fundamental form I and \(\mathrm {I\!I}\) necessarily differ by an isometry of \(\mathbb {R}^3\). The existence part states that given a simply connected surface \(\Sigma \) with the tensors \(I,\mathrm {I\!I}\) defined on \(\Sigma \) satisfying the Gauß and Codazzi equation there is an immersion \(\Sigma \rightarrow \mathbb {R}^3\) with induced first and second fundamental form equal to I and \(\mathrm {I\!I}_{\mathbb {R}^3}\). One way how to prove this statement is via the theorem of Maurer–Cartan: Let G be a Lie Group with Maurer–Cartan form \(\Omega _{MC}\), let N be connected and simply connected, equipped with \(\eta \in \Omega ^1(N,\mathfrak {g})\) satisfying \(\mathrm {d}\eta +\frac{1}{2}[\eta ,\eta ]=0.\) Then there exists a smooth map \(f:N\rightarrow G\), unique up to left translation in G, such that \(f^*\Omega _{MC}=\eta \). In this section we will show, also using the theorem of Maurer–Cartan, an analogue of Bonnet’s theorem for J-holomorphic curves in \(\mathbb {CP}^3\).
We have seen that given a transverse J-holomorphic curve \(\varphi :X\rightarrow \mathbb {CP}^3\) there are functions \({\alpha _-},{\alpha _+},\gamma \) that satisfy Eq. (4.13), where \(\gamma \) is determined by \({\alpha _-}\) and \({\alpha _+}\). Up to a constant factor, the functions \(({\alpha _-},{\alpha _+},\gamma )\) determine the first and second fundamental form of X. Composing \(\varphi \) with an element in an automorphism in \(\mathrm {Sp}(2)\) leaves the quantities \(({\alpha _-},{\alpha _+})\) invariant since they are defined via components of \(\Omega _{MC}\). Besides, the data \(({\alpha _-},{\alpha _+})\) determines the first and second fundamental form up to a constant.
If a Bonnet-theorem holds for J-holomorphic curves in \(\mathbb {CP}^3\) then the first and second fundamental form determine the curve up to isometries. Furthermore it would say that such a curve exists if the Gauß and Codazzi equations are satisfied. In our setting, system Eq. (4.11) plays the role of these equations. This raises the following question. Are the solutions of Eq. (4.11) in one to one correspondence to transverse J-holomorphic curves up to isometries? Later, we will see that the answer to this question is no because there are periodic solutions of Eq. (4.11) which do not descend to a two-torus. However, there is a positive result for when X is simply connected.
Lemma 5.1
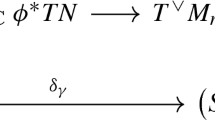
Let X be a simply connected Riemann surface equipped with a metric k. Let furthermore \({\alpha _-},{\alpha _+} :X\rightarrow \mathbb {R}^{>0}\) such that Eq. (4.13) are satisfied for \(\gamma =({\alpha _-} {\alpha _+})^{-1/4}\) and that \(\gamma ^{-2}k\) is flat. Then there is a J-holomorphic immersion \(\varphi :X \rightarrow \mathbb {CP}^3\) such that the induced metric satisfies \(g_{\mathcal {H}}=k\). The angle functions of \(\varphi \) are exactly \({\alpha _-}\) and \({\alpha _+}\). The immersion is unique up to isometries of \(\mathbb {CP}^3\) and an element in \(S^1/{\mathbb {Z}_4}\cong S^1\) which parametrises a choice of a unitary (1, 0)-form \(\omega _0\) on X such that \(\mathrm {d}(\gamma ^{-1} \omega _0)=0\).
Proof
Since X is simply connected and globally conformally flat, it is isomorphic to \(\mathbb {C}\) as a complex manifold by the uniformisation theorem. In particular, \(\Omega ^{1,0}(X)\) is trivial as a bundle, let \(\omega _0\) be a unitary (1, 0)-form on X. Arguing similarly as in the proof of Proposition 4.6 we see that, since \(\gamma ^{-2}k\) is flat,
Now, define a \(\mathfrak {sp}(2)\)-valued one-form on X by
And observe that
is equivalent to Eqs. (4.13) and (5.1). Hence, by Cartan’s theorem, there is an immersion \(\Phi :X\rightarrow \mathrm {Sp}(2)\) such that \(\Phi ^*(\Omega _{MC})=\eta \) which is unique up to left multiplication in \(\mathrm {Sp}(2)\). Note that \(\varphi ^*(\Omega _{MC})=\eta \) is equivalent to the equations
Consider the map \(\varphi =\pi \circ \Phi :X\rightarrow \mathbb {CP}^3\)

Then \(\varphi \) is also an immersion because \(v\in \mathrm {ker}(\mathrm {d}\varphi )\subset T^{1,0}(X)\) is equivalent to \(\Phi ^*\omega _i(v)=\omega _i(\mathrm {d}\Phi (v))=0\) for \(i=1,2,3\). By Eq. (5.2), this implies that \(\omega _0(v)=0\) and hence \(v=0\). Furthermore, \(\varphi \) is J-holomorphic since \(\Phi \) pulls back the forms \(\omega _i\) to multiples of \(\omega _0\). Since \(\omega _1\) is unitary for \(g_{\mathcal {H}}\), \(\omega _0\) for k and \(\Phi ^*(\omega _1)=\omega _0\) the metric \(g_{\mathcal {H}}\) induced by \(\varphi \) is equal to k. Since left-multiplication on \(\mathrm {Sp}(2)\) acts on \(\mathbb {CP}^3\) by isometries it remains to prove that choosing \(e^{i\vartheta } \omega _0\) as unitary (1, 0)-form on X yields, up to isometries, the same immersion \(\varphi :X\rightarrow \mathbb {CP}^3\) as \(\omega _0\) if \(e^{4i\vartheta }=1\). Let \(R_\lambda \) be the right multiplication of an element \(\lambda =(e^{i\vartheta },e^{i\vartheta })\) on \(\mathrm {Sp}(2)\). Then \(R_{\lambda }^*(\Omega _{MC})=\mathrm {Ad}_{\lambda ^{-1}}(\Omega _{MC})\). From our knowledge of the adjoint action of K on \(\mathfrak {sp}(2)\) we infer that
Hence, if \(e^{4i\vartheta }=1\) then \(\omega _1\) and \(\tau \) transform in the same way. This means that in this case if \(\varphi \) satisfies \(\varphi ^*{\Omega _{MC}}=\eta _{\omega _0}\) then \((\varphi \circ R_{\lambda })^*(\Omega _{MC})=\eta _{e^{i\vartheta }\omega _0}\). But right multiplication on \(\mathrm {Sp}(2)\) does not affect the immersion \(\varphi :X \rightarrow \mathbb {CP}^3\). \(\square \)
Note that Lemma 5.1 as it is stated requires X to be equipped with a fixed metric. However, it is more natural to let the metric be one of the quantities to be determined, such as \({\alpha _-}\) and \({\alpha _+}\). Think of X as equipped with a flat metric and consider a solution of Eq. (4.13) with \(\gamma =({\alpha _-}{\alpha _+})^{-1/4}\). Then \(({\alpha _-},{\alpha _+})\) is a solution of Eq. (4.11) with the metric \(g=\gamma ^2 g_0\). However, we could also have chosen the metric \(\lambda ^2 g_0\) for a constant \(\lambda >0\). In general, Lemma 5.1 will produce a different immersion \(\varphi _{\lambda } :X\rightarrow \mathbb {CP}^3\). The following theorem is then a reformulation of Lemma 5.1.
Theorem 5.2
Let X be a simply connected Riemann surface and let \(({\alpha _-},{\alpha _+})\) be solutions of Eq. (4.13) for some flat metric on X. Then there is a J-holomorphic immersion \(\varphi :X \rightarrow \mathbb {CP}^3\) such that the angle functions \(\varphi \) are exactly \({\alpha _-}\) and \({\alpha _+}\). The immersion is unique up to isometries of \(\mathbb {CP}^3\), a choice \(\lambda >0\) and an element in \(S^1/{\mathbb {Z}_4}\cong S^1\) which parametrises a choice of a unitary (1, 0)-form \(\omega _0\) on X such that \(\mathrm {d}(\gamma ^{-1} \omega _0)=0\).
In other words, a solution \(({\alpha _-},{\alpha _+})\) of Eq. (4.13) specifies the immersion up to isometries and a choice of a constant \((\lambda , \omega _0)\in \mathbb {C}^*\). In the case when the solutions \(({\alpha _-},{\alpha _+})\) and hence g have symmetries, the different embeddings \(\varphi _{\lambda , \gamma }\) might come from reparametrisations of X. Consider for example, \(X=\mathbb {C}\) and let \(L_\lambda :\mathbb {C}\rightarrow \mathbb {C}\) be the multiplication by \(\lambda \). Define furthermore \({\alpha _-}_{\lambda }={\alpha _-} \circ L_{\lambda },{\alpha _+}_{\lambda }={\alpha _+} \circ L_{\lambda },g_{\lambda }=g\circ L_{\lambda }\). If \(({\alpha _-},{\alpha _+})\) solves Eq. (4.11) for a metric g on \(\mathbb {C}\) then \(({\alpha _-}_\lambda ,{\alpha _+}_\lambda )\) is a solution of Eq. (4.11) for the metric \(\lambda ^{2} g_{\lambda }\). This solution comes from the J-holomorphic curve \(\varphi \circ L_{\lambda }\). In particular, if \(g_\lambda =g\) then the different immersions \(\varphi _{\lambda }\) come from reparametrisations of X by \(L_\lambda \). Similarly, if the induced g has radial symmetry, different choices of \(\omega _0\) correspond to reparametrisations by rotations.
5.1 Special solutions of the Toda equations
Note that Eq. (4.13) are symmetric in \({\alpha _-}\) and \({\alpha _+}\), meaning a distinguished set of solutions is of the form \(\alpha ={\alpha _-}={\alpha _+}\). This reduces Eq. (4.13) to
which becomes the Sinh–Gordon equation after rescaling the metric with a constant factor. This is somewhat similar to the situation in \(S^3\times S^3\) where J-holomorphic curves with \(\Lambda =0\) are locally described by the same equation. In particular,
Proposition 5.3
Transverse J-holomorphic curves in \(\mathbb {CP}^3\) with \({\alpha _-}={\alpha _+}\) are locally described by the same equation as constant mean curvature tori in \(\mathbb {R}^3\).
Geometrically, the condition \({\alpha _-}={\alpha _+}\) is satisfied for a J-holomorphic curve if the corresponding minimal surface \(X\rightarrow S^4\) lies in a totally geodesic \(S^3\), see Corollary 3.3. Hence the twistor lifts of the surfaces \(T_{k,m}\subset S^3\subset S^4\) from Sect. 6.1 give rise to examples of J-holomorphic tori with \({\alpha _-}={\alpha _+}\). The Clifford torus \(T_{1,1}\) plays a special because it is a \(\mathbb {T}^2\) group orbit. Any J-holomorphic curve which is isometric to the twistor lift of \(T_{1,1}\) will be referred to as Clifford torus. Since isometries leave \({\alpha _-}\) and \({\alpha _+}\) invariant this means that \({\alpha _-}\) and \({\alpha _+}\) are constant on Clifford tori. Observe, that there is in fact only one solution for \({\alpha _-}\) and \({\alpha _+}\) constant.
Lemma 5.4
If either \({\alpha _-}\) or \({\alpha _+}\) is constant then both must be constant and equal to \(1/\sqrt{2}\).
Theorem 5.5
Let \(\varphi :X \rightarrow \mathbb {CP}^3\) be a transverse J-holomorphic curve such that the induced metric \(g_{\mathcal {H}}\) is flat and X is equal to \(\mathbb {T}^2\) or \(\mathbb {C}\) as a complex manifold. Then \(\varphi \) parametrises a Clifford torus for \(X=\mathbb {T}^2\) and its universal cover if \(X=\mathbb {C}\).
Proof
By passing to the universal cover it suffices to assume \(X=\mathbb {C}\). Furthermore, by Eq. (4.12), flatness of \(g_\mathcal {H}\) is equivalent to \(1={\alpha ^2_-}+{\alpha ^2_+}\) and so Eq. (4.13) implies that \(\log ({\alpha ^2_-}(1-{\alpha ^2_-}))\) is harmonic. It is also bounded because \({\alpha ^2_-},{\alpha ^2_+}>0\) and hence constant. Since \({\alpha _-}\) and \({\alpha _+}\) must be constant on Clifford tori it follows from Lemma 5.4 that \({\alpha ^2_-}={\alpha ^2_+}=1/2\). Now, Theorem 5.2 can be applied to prove uniqueness. Note that since \(\mathbb {C}\) carries the flat metric, a different choice of \((\omega _0,\lambda )\) amounts to applying an isometry of X. \(\square \)
Consider \(\mathbb {T}^2=\mathbb {R}^2/{(2\pi \mathbb {Z})^2}\) equipped with the metric \(g_{m,k}=\mathrm {d}x^2+f_{m,k}(x) \mathrm {d}y^2\) for \(f_{m,k}(x)=m^2 \cos (x)^2 + k^2 \sin (x)^2\) and \(k,m\in \mathbb {R}\setminus \{0\}\). Let \(\hat{f}_{m,k}=\frac{\sqrt{8}}{k m} f_{m,k}\) and \(\alpha _-=\alpha _+=2\hat{f}_{m,k}^{-1}\), which implies \(\gamma =\alpha _-^{-1/2}\) and \(\gamma ^{-2} g=g_0\) is a flat metric with Laplace operator
Observe that these \(\alpha _\pm \) and g are a solution of Eq. (5.3) and hence give rise to transverse J-holomorphic curves in \(\mathbb {CP}^3\). In fact, they correspond to the minimal surfaces \(\Psi _{m,k}\) described in the following section.
The case when X is superminimal can be regarded as the limit \(\alpha _-\rightarrow 0\). In fact, a similar frame adaption gives
and Gauß curvature \(2(1-{\alpha ^2_+})\) for \( g_\mathcal {H}\). The solution \(\alpha _+^2=2/3\) results in constant curvature 1/3. The induced metric from the immersion in \(S^4\) is \(2g_{\mathcal {H}}\), i.e. the corresponding minimal surface has constant curvature 1/3, volume \(12 \pi \) and corresponds to the Veronese surface. If \(\varphi \) is superminimal it is also a holomorphic curve for the standard Kähler structure on \(\mathbb {CP}^3\). Similarly to Eq. (3.6) one derives for a simple superminimal curve
where \(\deg (\varphi )\) is the algebraic degree of \(\varphi \). Since \(\varphi \) is tangent to \(\mathcal {H}\), \(r_{\mathcal {H}}\) is the number of branching points of \(\varphi \) and by Proposition 3.1, \(r_{\mathrm {I\!I}}\) is the number of totally geodesic points of the corresponding minimal branched immersion in \(S^4\). To obtain an explicit solution of Eq. (5.4), consider the superminimal curve \(\Theta =\Theta (f,g)\) parametrised via Eq. (3.5), for \(f(z)=z^k\) and \(g(z)=z\) regarded as maps \(\mathbb {CP}^1\rightarrow \mathbb {CP}^1\). This example has been considered by Friedrich [18], who computed the degree of \(\Theta \), which equals k for \(k\ge 3\). The induced metric, curvature and \(\alpha _+^2\) on X can then be computedFootnote 1 by pulling back the Fubini-Study Kähler potential on \(\mathbb {CP}^3\) resulting in
for \(r=|z|\). We see that \(\alpha _+^2\) vanishes everywhere if \(k=0,1,2\), assume from now on \(k\ge 3\). Then \(\alpha _+\) has a zero of order \(k-3\) at both \(z=0\) and \(z=\infty \), yielding \(r_{\mathrm {I\!I}}=2k-6\). This confirms \(\mathrm {deg}(\Theta )=k\) since \(\Theta \) is an immersion, which implies \(r_{\mathcal {H}}=0\).
6 \(\mathrm {U}(1)\)-invariant J-holomorphic curves
\(\mathrm {U}(1)\)-actions on the nearly Kähler \(\mathbb {CP}^3\) have been studied on the resulting \(G_2\)-cone by Atiyah and Witten in the context of dimensional reductions of M-theory [3]. Closed expressions for the induced metric, curvature and the symplectic structure on \(\mathbb {R}^6\) have recently been found by Acharya, Bryant and Salamon [1] for one particular \(\mathrm {U}(1)\)-action.
While superminimal curves can be parametrised very explicitly our description of transverse curves has been, with the exception of Clifford tori, rather indirect so far. Imposing \(\mathrm {U}(1)\)-symmetry on the curves reduces a system of PDE’s to a system of ODE’s. In terms of \({\alpha _-}\) and \({\alpha _+}\), the 2D Toda lattice equation will reduce to the 1D Toda lattice equation. Killing vector fields on \(\mathbb {CP}^3\) are in one to correspondence with Killing vector fields on \(S^4\). We will provide a twistor perspective on the work of \(\mathrm {U}(1)\)-invariant minimal surfaces [16]. The geodesic equation on \(S^3\) for the Hsiang–Lawson metric is replaced by the computationally less involved 1D Toda equation. The twistor perspective establishes relationship between \(\mathrm {U}(1)\)-invariant curves and the toric nearly Kähler geometry of \(\mathbb {CP}^3\).
6.1 \(\mathrm {U}(1)\)-invariant minimal surfaces in \(S^3\)
In [24], Lawson developed a rich theory of minimal surfaces in \(S^3\). For \(m,k \in \mathbb {R}\setminus \{0\}\) there is a minimal immersion
with induced metric \(g_{m,k}\) from Sect. 5.1. Assume that k, m are coprime integers, such that \(T_{m,k}=\mathrm {Im}(\Psi _{km})\) represent Klein bottles 2|(mk) and tori otherwise. The surface \(T_{1,1}\) is the Clifford torus T. They are geodesically ruled and are invariant under the \(\mathrm {U}(1)\)-action \(\rho \) given by
It is furthermore shown that closed minimal surfaces invariant under this action are in one to one correspondence with closed geodesics in the orbit space \(S^3/\mathrm {U}(1)\) equipped with an ovaloid metric. By studying this metric explicitly, a rationality condition on the initial values for the geodesic to be closed is obtained. This gives rise to a countable family of tori \((T_{k,m,a})_{a\in A_{k,m}}\) where \(A_{k,m}\) is a certain countable dense subset of \((0,\pi /2)\). This family is bounded by \(T_{k,m}\) corresponding to the boundary case \(a=0\) and the Clifford torus T for \(a=\pi /2\). Similarly, for either \(m=0,k=0\) or \(m=\pm k\) there is a countable family \(C_a\) of minimal tori bounded by the Clifford torus and a totally geodesic two-sphere [22, Theorem 8].
Any cohomogeneity-one minimal surface in \(S^3\) belongs to the families \(C_a\) or \(T_{k,m,a}\) [22, Theorem 9]. Furthermore, Lawson constructs for any minimal surface in \(S^3\) an associated minimal surface in \(S^5\) which he calls bipolar surface. For the family \(T_{k,m}\) the bipolar surfaces lie in \(S^4\) but not in a totally geodesic \(S^3\). Extend \(\rho \) to an action on \(S^4\subset \mathbb {C}^2\oplus \mathbb {R}\) by letting \(\mathrm {U}(1)\) act trivially on the \(\mathbb {R}\) component. The Hsiang–Lawson family \(T_{k,m,a}\) is contained in the totally geodesic three sphere \(x=0\). Furthermore, the corresponding surfaces of this family are also \(\mathrm {U}(1)\)-invariant but under the modified action \((\tilde{k}, \tilde{m})=(m-k,m+k)\). Denote by \(\widetilde{T}_{k,m,a}\) the family of bipolar surfaces constructed from \(T_{\tilde{k},\tilde{m},a}\). The two families \(T_{k,m,a}\) and \(\widetilde{T}_{k,m,a}\) will play a special role in the following discussion.
6.2 Killing vector fields
Since the nearly Kähler \(\mathbb {CP}^3\) has isometry group \(\mathrm {Sp}(2)\) any element \(\xi \in \mathfrak {sp}(2)\) gives rise to the Killing vector field
Assume that there is \(t>0\) such that \(\exp (t \xi )\) equals the identity \(e\in \mathrm {Sp}(2)\), i.e. \(\xi \) corresponds to an action \(\rho \) of \(\mathrm {U}(1)\) on \(\mathbb {CP}^3\). Acting via \(\rho \) on integral curves of \(JK^{\xi }\) gives rise to \(\mathrm {U}(1)\)-invariant J-holomorphic curves in \(\mathbb {CP}^3\). Another way of stating this is that \([K^{\xi },JK^{\xi }]=0\) and that the span of \(K^{\xi }\) and \(JK^{\xi }\) defines an integrable distribution \(V_{\xi }\) on \(M=\mathbb {CP}^3\setminus ({K^{\xi }})^{-1}(0)\). The integral submanifold are exactly the \(\rho \) invariant J-holomorphic curves in \(\mathbb {CP}^3\) which foliate M. Due to the isomorphism between \(\mathfrak {sp}(2)\cong \mathfrak {so}(5)\), the element \(\xi \) also gives rise to a Killing vector field \(K^{\xi }_{S^4}\). This results in a uniqueness statement for minimal surfaces in \(S^4\).
Lemma 6.1
Let \(x\in S^4\) such that \(V \subset T_x S^4\) be a two-dimensional subspace containing \(K_{S^4}^{\xi }(x)\) and let \(p \in \pi ^{-1}(x)\subset \mathbb {CP}^3\) be the twistor lift of V. If \(K_p^{\xi }\) is non-vertical there is a locally unique minimal surface \(\Sigma \) with \(x\in \Sigma \) and \(V=T_x\Sigma \).
Let X be an integral submanifold of the distribution \(V_{\xi }\). Since it is a J-holomorphic curve the bundle \(\mathrm {Sp}(2)|_X\) reduces to the \(\mathbb {Z}_8\) bundle \(R_X\), see Lemma 4.5. There is an \(\mathbb {Z}_8\) bundle R over M which restricts to \(R_X\) on each integral submanifold. Note that the construction of R is linked to the subspace \(\mathfrak {r}\subset \mathfrak {sp}(2)\) which becomes apparent in the following lemma.
Lemma 6.2
If a section \(s:\mathbb {CP}^3\supset U \rightarrow \mathrm {Sp}(2)\) lies in R then \(s^*(\Omega _{MC})(K^{\xi })=s^{-1} \xi s \in \mathfrak {r}\).
Proof
Let s be a section of R. Consider the section \(s'=L_g \circ s \circ L_{g^{-1}}\) where \(g=\exp (t \xi )\) for some \(t\in \mathbb {R}\). Then \(s'^*(\Omega _{MC})(K_x^{\xi })=\Omega _{MC}(K_{gx}^{\xi })\in \mathfrak {r}\). In other words, \(s'\) satisfies Eq. (4.10) and hence \(s'\) also has values in R. Since the sections s and \(s'\) are joined by a continuous path and R has discrete structure group it follows that \(s'=s\), i.e.
This implies
\(\square \)
The point of the previous lemma is that it gives a more explicit description of the bundle R. Over U, define the \(K_F\) bundle \(R'=\{g\in \mathrm {Sp}(2) \mid g^{-1} \xi g \in \mathfrak {r}\}\). By Lemma 6.2, \(R=R'\). The point of the previous lemma is that it gives a more explicit description of the bundle R.
Corollary 6.3
A section \(s:U \rightarrow \mathrm {Sp}(2)\) takes values in R if and only if \(s^{-1} \xi s \in \mathfrak {r}\).
The presence of the vector field \(K^{\xi }\) means we can define the functions \(h=\Vert K^{\xi }\Vert _{\mathcal {H}}^2\), \(v_-=\Vert K^{\xi }\Vert _{\mathcal {V}}^2\). Furthermore, if we restrict \(\tau \) to R the quantity \(v_+=|\tau (K^{\xi })|^2\) is well-defined. This gives
Let X be a transverse integral submanifold. Since \(K^{\xi }\) and \(JK^{\xi }\) commute, these vector fields give rise to coordinates (u, t) such that \(\frac{\partial }{\partial u}=K^{\xi }\) and \(\frac{\partial }{\partial t}=JK^{\xi }\). The induced metric \(g_{\mathcal {H}}\) on X is equal to \(h (\mathrm {d}u^2+\mathrm {d}t^2)\). In particular, due to Proposition 4.6 and since h is the conformal factor of the metric, the quantity \(C=h\sqrt{{\alpha _-} {\alpha _+}}=h^{1/2}(v_-v_+)^{1/4}\) is constant along X. Hence, Eq. (4.13) reduces to
It is clear that the equations of Lemma 4.5 hold when the forms are restricted to R. However, the fact that \(K^{\xi }\) is a Killing vector field guarantees that the following additional equations are satisfied
for a constant \(\lambda \in S^1\). Note that Eq. (6.3) are satisfied because isometries preserve the quantities \({\alpha _-}\) and \({\alpha _+}\). Equation (6.4) holds because (u, t) are isothermal coordinates for \(g_{\mathcal {H}}\) on integral submanifold. Lastly, Eq. (6.5) and Eq. (6.6) follow from (6.4) and the definition of \(v_-,v_+\), i.e. Eq. (6.1) as well as the equations defining R, i.e. Eq. (4.10). Note that we have abused notation slightly here. By how \(K_F\) acts on \(\mathfrak {r}\) the forms \(\omega _1,\dots ,\omega _3\) are basic on R but take values in a possibly non-trivial line bundle on X whose structure group reduces to \(K_F\). In other words, \(\lambda \) is only well-defined up to multiplication of a fourth root of unity. However, this poses no problem since the results which follow will only depend on \(\mu =\lambda ^4\).
6.3 Lax Representation and Toda Lattices
Since a general transverse curve satisfies the 2D periodic Toda lattice equation, \(\mathrm {U}(1)\)-invariant curves will satisfy the 1D periodic Toda lattice equations for the same Lie algebra, i.e. Eq. (6.2). These equations admit a Lax representation [5]. In the following, we will work out this Lax representation directly from the formalism of adapted frames. Consider the restriction of \(\Omega _{MC}\) to the reduced bundle R, which will still be denoted by \(\Omega =\Omega _{MC}\). We have
Consequently, \(K^{\xi }(\Omega (JK^{\xi }))=0\) because \(h,v_-,v_+\) are constant along \(K^{\xi }\). With this in mind, let us evaluate both two-forms at \(K^{\xi }\wedge JK^{\xi }\)
Evaluating the right-hand side of Eq. (6.9) gives
Hence, Eq. (6.9) is equivalent to Eq. (6.2). In other words, we have found a Lax representation of the ODE system. This proves the following lemma.
Lemma 6.4
The eigenvalues of \(\Omega (K^{\xi })\in \mathfrak {sp}(2)\subset \mathfrak {su}(4)\) are constant along \(JK^{\xi }\).
Introduce the variables
where the dot denotes the derivative with respect to \(\frac{\mathrm {d}}{\mathrm {d}t}\), i.e. along \(JK^{\xi }\). Then Eq. (6.2) is equivalent to
This system is Hamiltonian with
The Hamiltonian is in the form of [5, Theorem 1]. In other words, Eq. (6.10) are the equations for a generalised, periodic Toda lattice for the Lie algebra \(\mathfrak {sp}(2)\). Bogoyavlensky’s Lax representation for such a system coincides with Eq. (6.9). Thus we have proven
Proposition 6.5
Simply connected, embedded, transverse J-holomorphic curves with a one-dimensional symmetry give rise to solutions to the 1D periodic Toda lattice equations for the Lie algebra \(\mathfrak {sp}(2)\) with Lax representation
Define
Then one can check explicitly that the eigenvalues of \(\Omega (K^{\xi })\) are given by
We have seen that a choice of a Killing vector field on \(\mathbb {CP}^3\) gives rise to the above ODE system. The converse statement is also true.
Proposition 6.6
Let \(X\cong \mathbb {C}\) be a Riemann surface equipped with coordinates (u, t) a metric \(k=C \gamma ^2 (\mathrm {d}u^2+\mathrm {d}t^2)\) and \({\alpha _-},{\alpha _+}:X\rightarrow \mathbb {R}^{>0}\) satisfy the ODE system Eq. (6.2) for some \(C>0\). Then there is an element \(\xi \in \mathfrak {sp}(2)\) such that X is an integral manifold of the distribution \(V_{\xi }\) and such that \({\alpha _-},{\alpha _+}\) are the angle functions and the tautological embedding \(X\rightarrow \mathbb {CP}^3\) is J-holomorphic and isometric.
Proof
Let \(({\alpha _-},{\alpha _+})\) be a solution of Eq. (6.2) with \(C>0\). We will now give a \(\xi \in \mathfrak {sp}(2)\) such that the integral submanifold through \([e]=[1,0,0,0]\in \mathbb {CP}^3\) has exactly the angle functions \({\alpha _-},{\alpha _+}\). We have already seen that such integral submanifolds satisfy Eq. (6.2). System Eq. (6.2) itself does not depend on the choice of \(\xi \). In fact, \(\xi \) will determine its initial condition. Hence, it suffices to show that a \(\xi \) with the desired properties can be found for any \(C>0\) and fixed initial conditions for \(\alpha _-(0),\alpha _+(0),\dot{\alpha }_-(0),\dot{\alpha }_+(0)\). Let \(h_0=C{\alpha _-}(0)^{1/2}{\alpha _+}(0)^{1/2},{v_-}_0=C {\alpha _-}(0)^{3/2}{\alpha _+}(0)^{-1/2},{v_+}_0=C {\alpha _+}(0)^{3/2}{\alpha _-}(0)^{-1/2}\) and
Consider the integral manifold of \(V_{\xi }\) passing through the point \([e]=[1,0,0,0]\in \mathbb {CP}^3\). By construction, since at the point \(e\in \mathrm {Sp}(2)\) we have \(\Omega _{MC}(K^{\xi })=\xi \) and so \(e\in \mathrm {Sp}(2)\) lies in the reduced bundle \(R_X\). Hence, we can apply Lemma 4.5 and evaluate \(\rho _1\) and \(\rho _2\) at \(K^{\xi }([e])\) to see that the angle functions \({\alpha _-},{\alpha _+}\) of X satisfy the given initial conditions. \(\square \)
6.4 The \(\mathbb {T}^2\)-action
In this subsection, we will investigate describe the geometry of a general \(\mathrm {U}(1)\)-action on \(\mathbb {CP}^3\) with respect to the vector field \(JK^{\xi }\) and make use of the fact that such an action commutes with a subgroup of \(\mathrm {Sp}(2)\), which is generically a two-torus. To that end, we fix
which integrates to the \(\mathrm {U}(1)\)-action \(\rho (e^{i\vartheta }[Z_0,Z_1,Z_2,Z_3])= [e^{k i\vartheta } Z_0,e^{-k i\vartheta } Z_1,e^{m i\vartheta }Z_2,e^{-m i\vartheta } Z_3]\) on \(\mathbb {CP}^3\). We fix an isomorphism \(\mathfrak {sp}(2)\cong \mathfrak {so}(5)\) which maps \(\xi \) to the element \((k+m,-k-m,k-m,m-k,0)\in \mathfrak {so}(5)\) and thus corresponds to the \(\mathrm {U}(1)\)-action with weights \((\tilde{k}=m-k,\tilde{m}=m+k)\) on \(S^4\subset \mathbb {C}\oplus \mathbb {C}\oplus \mathbb {R}\). The Lawson torus \(T_{\tilde{k},\tilde{m}}\) and the bipolar torus \(\tilde{T}_{\tilde{k},\tilde{m}}\) admit J-holomorphic twistor lifts which are invariant under \(\rho \) and will be denoted by \(\tau _{k,m}\) and \(\tilde{\tau }_{k,m}\), respectively. Let \(\mathrm {Stab}(\xi )=\{g\in \mathrm {Sp}(2)\mid g^{-1} \xi g=\xi \}\), observe that
We will refer to the first two cases as degenerate and to the last case as non-degenerate. Due to the presence of a larger symmetry group, the degenerate cases are simpler and have been treated by the author elsewhere. This is why, in this article, we restrict ourselves to the degenerate case in which \(\mathrm {Stab}(\xi )\) is equal to the standard two-torus in \(\mathrm {Sp}(2)\) i.e. \(\{\mathrm {diag}( e^{i \theta }, e^{i\phi })\}\) to which we will simply refer as \(\mathbb {T}^2\) unless stated otherwise. Let \(\xi _1,\xi _2\) be the elements in \(\mathfrak {sp}(2)\) corresponding to the action of \(e^{i\theta }\) and \(e^{i\phi }\), respectively. This torus action gives rise to the multi-moment map \(\nu =\omega (K^{\xi _1},K^{\xi _2})\), introduced in [30].
Proposition 6.7
The nearly Kähler multi-moment map on \(\mathbb {CP}^3\) is given in homogeneous coordinates by
There are two Clifford tori which arise as orbits of \(\mathbb {T}^2\) and are equal to the preimages of the extremal values of \(\nu \). Hence they are \(\mathbb {T}^2\) orbits of the points [1, 1, 1, i] and \([1,1,1,-i]\). When investigating \(\rho \)-invariant J-holomorphic curves, it proves worthwhile to study lower-dimensional subsets Y of \(\mathbb {CP}^3\) which are both invariant under \(\rho \) and the flow of \(JK^{\xi }\). In other words, the distribution \(V_{\xi }\) is then tangent to Y and the problem of finding \(\rho \)-invariant J-holomorphic curves can be done separately on each such Y. Since \(\mathrm {d}\nu =\psi ^+(K^{\xi _1},K^{\xi _2},\cdot )\), \(V_{\xi }\) is tangent to each preimage \(\nu ^{-1}(c)\). The value 0 as well as extrema of \(\nu \) have a distinguished geometrical importance, there are the following sets which arise in a natural geometric way and to which \(V_{\xi }\) is tangent
-
\(\mathcal {C}=\nu ^{-1}(\{\nu _{\mathrm {min}}, \nu _{\mathrm {max}} \})\)
-
\(\mathcal {B}=\nu ^{-1}(0)\).
-
\(\mathcal {Q}\), the quadric associated with \(\xi \) under the identification \(\mathfrak {sp}(2)\) with the real part of \(S^2(\mathbb {C}^4)\)
-
\(\mathcal {S}\), the set where \(\mathbb {T}^2\) does not act freely
-
\(\mathcal {T}\), a distinguished \(S^1\) bundle over \(S^3_0\subset \mathbb {R}^4\oplus \{0\}\) (for (k, m) non-degenerate)
-
\(\tilde{\mathcal {T}}\), a four-dimensional submanifold constructed from \(\mathcal {T}\) via Lawson’s bipolar construction.
In the following we will define and outline the properties of each of the subsets.
The four points \(\{[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]\}\) are the fixed points of the \(\mathbb {T}^2\)-action. It turns out that \(\mathbb {T}^2\) acts on the projective line going through any two of them with cohomogeneity one. More specifically, let
Observe that
The action of \(\mathbb {T}^2\) on \(\mathbb {CP}^3\) is free away from the projective lines \(L_1,\dots ,L_6\), i.e. \(\mathcal {S}=L_1 \cup \dots \cup L_6\). Note that \(L_1\) and \(L_6\) are twistor lines, i.e. \(h=0\), while \(L_2,\dots ,L_5\) are superminimal, i.e. \(v_-=0\). Since \(L_2,\dots ,L_5\) project to totally geodesic two-spheres they furthermore satisfy \(v_+=0\), see Proposition 3.1. Via the isomorphism \(\mathfrak {sp}(2)\otimes \mathbb {C}\cong S^2(\mathbb {C}^4)\), \(\xi \) is identified with the polynomial
Furthermore, since \(\mathfrak {sp}(2)\cong \mathfrak {so}(5)\), \(\xi \) defines a vector field \(K_{S^4}^\xi \) on \(S^4\). Since it is a Killing vector field, \(\nabla (K_{S^4}^\xi )\) can be identified with a two form on \(S^4\). Its anti-self-dual part satisfies the twistor equation and gives thus rise to a quadric on \(\mathbb {CP}^3=Z_-(S^4)\), holomorphic with respect to \(J_1\), see [4, ch. 13]. This quadric is given by
and coincides with the vanishing set of the quadratic expression Eq. (6.13). For \(x\in \mathbb {CP}^3\), let \(X_x\) be the unique \(\rho \)-invariant embedded J-holomorphic curve containing x and \(\Sigma _x\) be the corresponding minimal surface in \(S^4\). Define
Lemma 6.8
If \(k=m\) then \(\mathcal {T}=\mathbb {CP}^3\).
Proof
For \(k=m=1\) the action on \(S^4\) only rotates the first two components of \(\mathbb {R}^2\oplus \mathbb {R}^3\). This action commutes with \(\mathrm {SO}(2)\times \mathrm {SO}(3)\). Let \(\Sigma \) be a minimal surface containing the orbit \(\mathcal {O}_x\) for some x. Let \(\nu \) be the normal bundle of \(\mathcal {O}_x\) in \(\Sigma \) and \(v\in \nu _x\). By an action of \(\mathrm {SO}(2)\times \mathrm {SO}(3)\) we can assume that x and v lie in \(\mathbb {R}^4\oplus \{0\}\). In particular, x is contained in \(S_0^3\subset \mathbb {R}^4\oplus \{0\}\) and v is tangent to it. Because \(\nu \) and \(S^3\) are \(\rho \)-invariant we have that \(\mathcal {O}_x\subset S^3\) and \(\nu _x \subset TS^3\). By [31], there is an embedded, \(\rho \)-invariant minimal surface \(\Sigma '\) such that \(\mathcal {O}_x \subset \Sigma '\subset S^3\). Now, Lemma 6.1 implies that \(\Sigma =\Sigma '\), i.e. \(\Sigma \subset S^3_0\). \(\square \)
Lemma 6.9
If \(k\ne m\) and \(\Sigma \) is a \(\rho \)-invariant minimal surface which is contained in a totally geodesic \(N\cong S^3\) then \(N=S_0^3=\mathbb {R}^4\oplus \{0\} \cap S^4\).
Proof
One can check that \(\mathbb {R}^4\oplus \{0\} \cap S^4\) is the only totally geodesic \(S^3\) on which \(\rho \) acts. The statement follows from Lemma 3.5.
From now on, assume \(k\ne m\). Over the totally geodesic \(S^3_0\) we introduce the reduced Grassmannian bundle
and notice that \(\mathrm {Gr}(K^\xi ,S_0^3)\) is in fact an \(S^1\)-bundle over \(S_0^3\) which is mapped diffeomorphically to \(\mathcal {T}\subset \mathbb {CP}^3=Z_-(S^4)\) by the projection \(\widetilde{\mathrm {Gr}_2}(S^4)\rightarrow Z_-(S^4)\). Note that \(\mathcal {T}\) is also invariant under \(\rho \) and \(JK^{\xi }\) is tangent to \(\mathcal {T}\). For a minimal surface \(\Sigma \) denote by \(\tilde{\Sigma }\) the bipolar surface from Sect. 6.1. Let
For both \(\mathcal {T}\) and \(\tilde{\mathcal {T}}\) we obtain explicit expressions in Sect. 6.7.
6.5 Separating \(\mathbb {T}^2\)-orbits
As highlighted in the introduction, it is desirable to have a geometric construction of a map into \(\mathbb {R}^4\) which descends to a local homeomorphism to the \(\mathbb {T}^2\) quotient of \(\mathbb {CP}^3\), at least away from a singular set. In general, one candidate for such a map is \((\nu ,\Vert K^{\xi _1}\Vert , \Vert K^{\xi _2}\Vert ,g(K^{\xi _1},K^{\xi _2}))\). For \(S^3\times S^3\) such a map cannot have four-dimensional image however, due to the presence of a unit Killing vector field on \(S^3\times S^3\). This is a special case, because \(S^3\times S^3\) is the only nearly Kähler manifold admitting a unit Killing vector field [27]. Nevertheless, it seems difficult to compute the differentials of \(g(K^{\xi _i},K^{\xi _j})\) in a general setting.
For the case \(M=\mathbb {CP}^3\) we use a variant p of this map, based on the splitting \(T\mathbb {CP}^3=\mathcal {H}\oplus \mathcal {V}\). It turns out that, up to a sign, the multi-moment map \(\nu \) can be expressed as a function of \(\nu \), Corollary 6.17. The quotient \(_{\mathbb {T}^2}\backslash ^{\mathbb {CP}^3\setminus \{L_1\cup \dots \cup L_6\}}\) is smooth and will be denoted by \(M_F\). Note that the functions \((v_+,v_-,r_+,r_-)\) are all \(\mathbb {T}^2\)-invariant.
Theorem 6.10
The functions
map to a bounded set \(D\subset \mathbb {R}^4\) over which p is a branched double cover. The two different points in the fibres of p are complex conjugates of each other and the branch locus is equal to \(\mathcal {B}=\nu ^{-1}(0)\).
Proof
Let
and \(\mathfrak {r}_F=\mathfrak {r}\cap \mathfrak {sp}(2)_F\). The aim is to define a smooth map \(M_F \rightarrow D\subset \mathbb {R}^6\) as a composition of
We will now define each of the maps individually and establish its properties.
\(c_F\):
Consider the map \(c:\mathrm {Sp}(2)\rightarrow \mathfrak {sp}(2),\quad g\mapsto g^{-1} \xi g\). Denote the image of c by \(\mathcal {O}^{\xi }\). Note that c descends to a diffeomorphism from \(_{\mathbb {T}^2}\backslash ^{\mathrm {Sp}(2)}\) onto its image. Quotienting both spaces by the right action of \(S^1 \times S^3\) gives a homeomorphism between \(_{\mathbb {T}^2}\backslash ^{\mathbb {CP}^3}\) and \(\mathcal {O}^{\xi }/{S^1\times S^3}\). Denote the restriction of this map to \(M_F\) by \(c_F\) and observe that \(c_F\) maps \(M_F\) diffeomorphically onto
for \(\mathcal {O}_{F}^{\xi }=\mathcal {O}^{\xi }\cap \mathfrak {sp}(2)_F\).
\(\Pi \):
If \(x\in \mathfrak {sp}(2)_F\) then the orbit of x under the action of \(S^1\times S^3\) intersects \(\mathfrak {r}_F\) in a \(K_F\) orbit. In other words, there is an injective map \(\Pi :\mathfrak {sp}(2)_F/{S^1\times S^3}\rightarrow \mathfrak {r}_F/{K_F}\). On the other hand, the inclusion \(\mathfrak {r}_F\subset \mathfrak {sp}(2)_F\) induces \(\iota :\mathfrak {r}_F/{K_F} \rightarrow \mathfrak {sp}(2)_F/{S^1\times S^3}\) and \(\Pi \circ \iota =\mathrm {Id}\). This implies that \(\Pi \) is in fact a diffeomorphism from \(\mathfrak {sp}(2)_F/{S^1\times S^3}\) to \(\mathfrak {r}_F/{K_F}\).
\(\bar{\zeta }\):
Consider the map
which is \(K_F\) invariant. On \(\mathbb {R}_+^3\times \mathbb {R}^2 \times [-1,1]\ni (v_-,v_+,r_-,r_+,h,\mu )\), motivated by Eq. (6.11), we define the functions
Denote by \(\bar{D}\subset \mathbb {R}^6\) the set defined by the equations
The image of \(\mathfrak {r}_F\) under \(\bar{\zeta }\) is \(\bar{D}\). This follows because Eq. (6.15) describe how eigenvalues of elements in \(\mathfrak {r}\) are calculated, i.e. Eq. (6.12). Furthermore, since \(\mathfrak {sp}(2)\) is semi-simple, conjugacy classes are uniquely characterised by their eigenvalues. Note that \(\bar{\zeta }\) descends to a double cover \(\mathfrak {r}/{K_F}\), branched over \(\mathbb {R}_+^3\times \mathbb {R}^2 \times \{-1,1\}\). The two preimages are obtained by switching between \(\lambda \) and \(\overline{\lambda }\).
\(\mathrm {pr}\):
Since Eq. (6.15) can be solved uniquely for h and \(\mu \) the projection \(\mathrm {pr}\) from \(\mathbb {R}_+^3\times \mathbb {R}^2 \times [0,1]\) to the first four components maps \(\bar{D}\) diffeomorphically onto its image
We have shown that Eq. (6.14) restricts to
and that \(\bar{\zeta }\) is a branched double cover while each other map is a diffeomorphism. Hence, p is a branched double cover. By Eq. (6.7) and Lemma 6.2, \(p=(v_-,v_+,r_-,r_+)\). Observing that p stays invariant under the map \(\delta :[Z_0,Z_1,Z_2,Z_3]\mapsto [\overline{Z_0},\overline{Z_1},\overline{Z_2},\overline{Z_3}]\) completes the proof. \(\square \)
The proof of Theorem 6.10 gives an explicit description of the branch locus of \(\zeta \). The involution \(\delta \) preserves the metric and reverses the almost complex structure on \(\mathbb {CP}^3\). The fixed point set of \(\delta \) is the standard \(\mathbb {RP}^3\) which is hence a special Lagrangian submanifold for the nearly Kähler structure [34].
Lemma 6.11
The set \(\mathbb {RP}^3\) is special Lagrangian for the nearly Kähler structure on \(\mathbb {CP}^3\).
Given a nearly Kähler manifold with a \(\mathbb {T}^2\)-action the possibly singular space \(_{\mathbb {T}^2}\backslash ^{\nu ^{-1}(0)}\) arises naturally. In the case of \(\mathbb {CP}^3\) this space is an orbifold.
Lemma 6.12
The set \(_{\mathbb {T}^2}\backslash ^{\nu ^{-1}(0)}\) is homeomorphic to \(\mathbb {RP}^3/\{\pm 1\}\) where the action of \(-1\) is given by \([X_0,X_1,X_2,X_3]\mapsto [-X_0,-X_1,X_2,X_3].\)
6.6 A torus fibration of D
The image of p is equal to D and explicitly described by Eq. (6.16). To understand the set more conceptually, we show that D itself admits a two-torus fibration over a rectangle \(\mathcal {R}\) in \(\mathbb {R}^2\). The torus fibres degenerate over the edges of the rectangle. Consider \((H_2,64C^2)\) as a map from D to \(\mathbb {R}^2\). Recall that (ik, im) are purely imaginary and equal to
Since \(\mu \in [-1,1]\) we obtain the inequalities
In fact, the image of \(u=(H_2,64C^2)\) is equal to the rectangle, with one corner point missing
Note that \(\mathcal {R}\) is bounded by the following line segments.
Motivated by the Toda lattice treatment, define the symplectic form
Let \(\mathcal {R}_0=\mathcal {R}\setminus \{l_1\cup \cdots \cup l_4\}\) the interior of \(\mathcal {R}\) and \(D_0=u^{-1}(\mathcal {R}_0)\). Using this symplectic form one can apply the Liouville–Arnold theorem to prove.
Proposition 6.13
On \(D_0\), u is a submersion and its fibres are homeomorphic to \(\mathbb {T}^2\). Around any \(x\in D_0\) there are local coordinates
such that the angles \(\vartheta _1,\vartheta _2\) are coordinates on \(u^{-1}\{x\}\) and \(I_1,I_2\) only depend on \(H_2\) and \(C^2\). In these coordinates Eq. (6.2) is transformed to
While the previous proposition shows that fibres over \(\mathcal {R}_0\) are regular it is to be expected that the preimages of the boundary of \(\mathcal {R}\) correspond to subsets with special geometric properties. In Sect. 6.4, we have considered the distinguished subsets \(\mathcal {S},\mathcal {T},\tilde{\mathcal {T}},\mathcal {C}\) and \(\mathcal {B}\). The following proposition is visualised in Fig. 3 and summarises how the preimages of \(l_1\cup \cdots \cup l_4\) are related to these subsets.
Theorem 6.14
The special subsets \(\mathcal {S},\mathcal {T},\tilde{\mathcal {T}},\mathcal {C}\) and \(\mathcal {B}\) are related to the edges of \(\mathcal {R}\)
-
\(u^{-1}(l_2)=p(\mathcal {T})\cong \mathbb {D}^2\), see Fig. 4
-
\(u^{-1}(l_3)=p(\widetilde{\mathcal {T}})\cong \mathbb {D}^2\)
-
\(u^{-1}(l_1\cup l_4)=p(\mathcal {B}\setminus \mathcal {S})\)
while the corner points of \(\mathcal {R}\) are related to the Clifford torus \(\tau _{1,1}\), Lawson torus \(\tau _{k,m}\) and the bipolar torus \(\tilde{\tau }_{k,m}\) by
-
\(u^{-1}(l_3 \cap l_4)=p(\tilde{\tau }_{k,m})\cong S^1\)
-
\(u^{-1}(l_1\cap l_2)=p(\tilde{\tau }_{k,m})\cong S^1\)
-
\(u^{-1}(Q)=p(\mathcal {C})\cong \{*\}\).
In the case \(k=m\) the rectangle \(\mathcal {R}\) degenerates to the line \(l_2\), which is a manifestation of Lemma 6.8. If \(m=0\) then \(\mathcal {R}\) degenerates to the line \(l_3\).
Note that the map \(u\circ p\) extends to the singular set, i.e. to the map
mentioned in the introduction and P maps \(_{\mathbb {T}^2}\backslash ^\mathcal {S}\) to the point \((16(k^2-m^2)^2,0)\). To prove Theorem 6.14 we first establish a more explicit understanding of the map p.
6.7 Relation between p and moment maps
If one is just interested in a homeomorphism or cover \(_{\mathbb {T}^2}\backslash ^{\mathbb {CP}^3}\rightarrow \mathbb {R}^4\) the functions \((v_-,v_+,r_-,r_+)\) are an unnecessarily complicated choice from a topological point of view. The reason for using these functions is that \(JK^{\xi }\) takes a simple form
To get an idea of what the functions \((v_-,v_+,r_-,r_+,h)\) look like in homogeneous coordinates consider the following set of \(\mathbb {T}^2\) invariant functions
Clearly, \(1=f_1+f_3\) and the functions are also invariant under \(\delta \). Note that the Kähler structure on \(\mathbb {CP}^3\) admits a \(\mathbb {T}^3\) action and after choosing an appropriate basis for \({\mathfrak {t}^3}^\vee \), \((f_1,f_2,f_4)\) are multiples of the symplectic moment map on \(\mathbb {CP}^3\). We can furthermore deduce the relation between the functions \(f_1,\dots ,f_5\) and \(\nu \). Note that \(\nu \) is not invariant under \(\delta \) but satisfies \(\nu \circ \delta =-\nu \) and can thus not be expressed in terms of \(f_1,\dots ,f_5\). However, observe that the square of \(\nu \) can be expressed in terms of the \(f_i\) via
Denote by \(D_f\) the image of \((f_1,f_2,f_4,f_5)\) in \(\mathbb {R}^4\). By writing down an explicit section one can prove that away from the branch locus \(\mathcal {B}\) the \(\mathbb {T}^2\times \{\pm 1\}\) principal bundle \((f_1,f_2,f_4,f_5):\mathbb {CP}^3\rightarrow \mathbb {R}^4\) is trivial. Our aim is to express \(p=(v_-,v_+,r_-,r_+)\) in terms of the functions \(f_1,\dots ,f_5\). For a quaternion \(q=z+jw\in \mathbb {C}\oplus j\mathbb {C}\) let \(q_{\mathbb {C}}=z\) and \(q_{j\mathbb {C}}=w\).
Lemma 6.15
\((v_-,r_-,v_+,r_+)=\zeta \circ \Pi :\mathfrak {sp}(2)_F \rightarrow D\) is given by
where \(Q_3=q_2^{-1} q_3 q_2\).
Proof
The functions \((v_-,r_-,v_+,r_+)\) can be computed by conjugating \(\sigma \) with an element in \(S^1\times S^3\) to an element in \(\mathfrak {r}\). Note that \(\mathfrak {r}_F/K_F=\mathfrak {f}^1/K\) for
Furthermore, p is invariant under the group K so it suffices to find \(g\in \mathrm {Sp}(2)\) such that \(g^{-1} \sigma g \in \mathfrak {f}^1.\) Hence, we can conjugate \(\sigma \) with the element \(\mathrm {diag}(1,\frac{q_2}{|q_2|})\) and the result follows from the definition of \(\bar{\zeta }\). \(\square \)
We now pick a section
with
Consequently,
Let
Combining Eq. (6.19) with Lemma 6.15 we can compute
Denote by \(\pi _{\mathbb {T}^2}\) the quotient map \(\mathbb {CP}^3\setminus {\mathcal {S}}\rightarrow M_F\) by the \(\mathbb {T}^2\)-action. Equation (6.20) can in fact be solved for \((f_1,f_2,f_4,f_5)\). This implies together with the triviality of the bundle \(f:\mathbb {CP}^3\setminus {\mathcal {S}} \rightarrow D_f\) the following proposition.
Proposition 6.16
There is a homeomorphism \(D_f\rightarrow D\) which is a diffeomorphism in the smooth points such that the following diagram commutes

In particular \(p\circ \pi _{\mathbb {T}^2}\) is a trivial \(\mathbb {T}^2 \times \{\pm 1\}\) bundle when restricted to \(\mathbb {CP}^3\setminus (\mathcal {S}\cup \mathcal {B})\).
Note that Eq. (6.18) yields the following corollary of Proposition 6.16.
Corollary 6.17
The square of the multi-moment map \(\nu \) is a function of \((v_-,v_+,p_-,p_+)\)
The rest of the subsection consists of proofs of some of the statements of Theorem 6.14. Note that the preimage of \(l_1,l_2\) in \(\bar{D}\) are exactly all points with \(\mu =1\) or \(\mu =-1\), respectively. Hence, the preimage of \(l_1\cup l_2\) is equal to the branch locus of \(\zeta \). We can check explicitly
Note that on \(u^{-1}(l_3)\) the equation \(2h=\sqrt{E_+E_-}\) is satisfied.
Lemma 6.18
The set \(\mathcal {T}\) can be explicitly described as \(\{f_1=1/2, \quad f_4k=f_2m\}\subset \mathbb {CP}^3\).
Proof
This follows from Eq. (6.20) by setting \(E_-=E_+\) and \(r_-=r_+\). \(\square \)
Note that on D we have \(C^2=(k^2+m^2-v_-v_+-1/4r_-^2-1/4 r_+^2)(\sqrt{vs})\). The maximum value of \(C^2\) on D is attained for \(r_-=0,r_+=0\) and \(v_-=v_+=\frac{1}{4}(k^2+m^2)\) resulting in \(C^2_{\max }=\frac{1}{8}(k^2+m^2)^2\). Furthermore we have \(h=\frac{1}{2}(k^2+m^2)\) which means \({\alpha _-}={\alpha _+}=\frac{1}{2}\) and is consistent with Lemma 5.4. These solutions describe the two \(\mathbb {T}^2\) invariant Clifford tori. In particular, if \(k,m\ne 0\) then the \(\mathbb {T}^2\) invariant tori never lie in \(\mathcal {B}\). Furthermore, we have \(f_1=1/2, f_2=0,f_4=0,f_5=0\) and in particular \(\frac{1}{16}(f_1^2-f_2^2)(f_3^2-f_4^2)-f_5^2=\frac{1}{256}\) which means \(\nu =\pm 3/4\). That means that the two Clifford tori are equal to \(\nu ^{-1}(\pm 3/4)\) which are the extremal values of \(\nu \).
The other special point on \(l_4\) is the intersection point \(l_1\cap l_4\). Its preimage under \(p\circ u\) is identified with the subset of points in \([X_0,X_1,X_2,X_3]\in \mathbb {RP}^3/{\pm 1}\) that satisfy \(f_1=1/2\) and \(f_4k=f_2m\), i.e.
Hence, \({p\circ u}^{-1}(l_1\cap l_4)\) and thus \({p\circ u}^{-1}(l_1\cap l_4)\) is homeomorphic to two copies of \(\mathbb {RP}^1\cong S^1\).
Lemma 6.19
The preimage \(u^{-1}(l_4)\) is homeomorphic to a closed two-disk in D.
Proof
Inserting \(v_-=v_+\) and \(r_-=r_+\) into the inequalities describing \(\mathcal {R}\) impose
which is homeomorphic to a disk in the \((v_-,r_-)\) coordinates. \(\square \)
The flowlines of \(JK^\xi \) in \((p\circ u)^{-1}(l_4)\) are mapped to closed curves in \(u^{-1}(l_4)\) which are plotted in Fig. 4.
6.8 Superminimal \(\mathrm {U}(1)\)-invariant curves
The focus of this article has been on transverse J-holomorphic curves. But the computations carried out in Sect. 6.7 give a framework for classifying \(\mathrm {U}(1)\)-invariant superminimal curves too. From Eq. (6.20) we can deduce that \(v_-=4|kZ_0Z_1+mZ_2Z_3|^2\) which implies
Lemma 6.20
The vector field \(K_x^{\xi }\) is horizontal in \(x \in \mathbb {CP}^3\) if and only if x lies on the quadric \(\mathcal {Q}\).
In the case \(k=m\) this has already been observed in [1, Corollary 6.3] where this quadric has been described in more detail. Remarkably, \(\mathcal {Q}\) is constructed from \(\xi \) in three different ways, via \(\mathfrak {sp}(2)\otimes \mathbb {C}\cong S^2(\mathbb {C}^4)\), via the anti-selfdual part of \(\nabla (K^{\xi })\), as explained after Eq. (6.13), and via Lemma 6.20. If a \(\rho \) invariant J holomorphic curve intersects \(\mathcal {Q}\) it will lie in \(\mathcal {Q}\) entirely. In other words, \(\mathcal {Q}\) is invariant under \(\rho \) and \(J K^{\xi }\) is tangent to \(\mathcal {Q}\). Furthermore, it follows that \(\mathcal {Q}\) is traced out by superminimal \(\rho \)-invariant J-holomorphic curves. The following proposition then follows from Eq. (3.5).
Proposition 6.21
All superminimal curves invariant under \(\rho \) are given by
for \(C\in \mathbb {C}\). Furthermore,
for \(X_C=\mathrm {Im}(\varphi _C)\subset \mathbb {CP}^3\) and \(Y_C=\mathrm {Im}(\psi _C)\subset \mathbb {CP}^3\).
Observe that \(X_L\) is totally geodesic if and only if \(L=0\). This is equivalent to saying that \(v_+\) vanishes on the curve as well. \(X_0\) is part of the singular set of the torus action.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
see https://github.com/deepfloe/superminimal-curves for an implementation in Mathematica
References
Acharya, B.S., Bryant, R.L., Salamon, S.: A circle quotient of a G2 cone. Differ. Geom. Appl. 73, 101681 (2020)
Atiyah, M. F.: Vector bundles over an elliptic curve. In: Proceedings of the London Mathematical Society 3.1, 414–452 (1957)
Atiyah, M., Witten, E.: M-Theory dynamics on a manifold Of G2-holonomy. In: Advances in Theoretical and Mathematical Physics, pp. 1–106 (2002)
Besse, A.L.: Einstein Manifolds. Springer Science & Business Media, Berlin (2007)
Bogoyavlensky, O.I.: On perturbations of the periodic Toda lattice. Commun. Math. Phys. 51(3), 201–209 (1976)
Bolton, J., Dillen, F., Dioos, B., Vrancken, L., et al.: Almost complex surfaces in the nearly Kähler \(S^{3} \times S^{3}\). Tohoku Math. J. 67(1), 1–17 (2015)
Bolton, J, Woodward, LM: Some geometrical aspects of the 2-dimensional Toda equations. In: Geometry, topology and physics (Campinas, 1996), pp. 69–81 (2011)
Bolton, J, MWoodward, L, : The affine Toda equations and minimal surfaces. In: Harmonic Maps and Integrable Systems, pp. 59–82. Springer (1994)
Bryant, R.L.: Conformal and minimal immersions of compact surfaces into the 4- sphere. J. Differ. Geom. 17(3), 455–473 (1982)
Bryant, R.L.: Submanifolds and special structures on the octonians. J. Differ. Geom. 17(2), 185–232 (1982)
Butruille, J.-B.: Homogeneous nearly Kähler manifolds. In: Handbook of Pseudo- Riemannian Geometry and Supersymmetry, 399–423 (2010)
Cortés, V., Vásquez, J.J.: Locally homogeneous nearly Kähler manifolds. Ann. Glob. Anal. Geom. 48(3), 269–294 (2015)
Dixon, K.: The multi-moment map of the nearly Kähler \(S^{3} imes S^{3}\). In: Geom Dedicata 200, 351–362 (2019)
Eells, J., Salamon, S.: Twistorial construction of harmonic maps of surfaces into four-manifolds. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze 12(4), 589–640 (1985)
Fernández, L.: The space of almost complex 2-spheres in the 6-sphere. Trans. Am. Math. Soc. 367(4), 2437–2458 (2015)
Ferus, D., Pedit, F.: \(S^{1}\)-equivariant minimal tori in \(S^{4}\) and \(S^{1}\)-equivariant Willmore tori in S3. Math. Z. 204(1), 269–282 (1990)
Foscolo, L.: Haskins, M.: New G2-holonomy cones and exotic nearly KKähler structures on \(S^{6} \text{and} S^{3} \times S^{3}\). Ann. Math. 59–130 (2017)
Friedrich, T.: On surfaces in four-spaces. Ann. Glob. Anal. Geom. 2(3), 257–287 (1984)
Gray, A.: The structure of nearly Kähler manifolds. Math. Ann. 223(3), 233–248 (1976)
Guadalupe, I., Rodríguez, L.: Normal curvature of surfaces in space forms. Pac. J. Math. 106, 95–103 (1983)
Hitchin, N.J.: Harmonic maps from a 2-torus to the 3-sphere. J. Differ. Geom. 31(3), 627–710 (1990)
Hsiang, W., Lawson, B.: Minimal submanifolds of low cohomogeneity. J. Differ. Geom. 5(1–2), 1–38 (1971)
Karigiannis, S., Min-Oo, M.: Calibrated subbundles in noncompact manifolds of special holonomy. Ann. Glob. Anal. Geom. 28(4), 371–394 (2005)
Lawson, B.: Complete minimal surfaces in S3. Ann. Math 92(2), 335–374 (1970)
Madsen, T.B., Swann, A.: Multi-moment maps. Adv. Math. 229(4), 2287–2309 (2012)
McDuff, D., Salamon, D.: J-Holomorphic Curves and Symplectic Topology, vol. 52. American Mathematical Soc, Providence (2012)
Moroianu, A., Paul-Andi, N., Semmelmann, U.: Unit Killing vector fields on nearly Kähler manifolds. Int. J. Math. 16(03), 281–301 (2005)
Nagy, P.-A.: Nearly Kähler geometry and Riemannian foliations. Asian J. Math 6(3), 481–504 (2002)
Perus, D., Pedit, F., Pinkall, U., Sterling, L.: Minimal tori in S4. J. Reine Angew. Math. 429, 1–47 (1992)
Russo, G., Swann, A.: Nearly Kähler six-manifolds with two-torus symmetry. J. Geom. Phys. 138, 144–153 (2019)
Uhlenbeck, K.: Equivariant Harmonic Maps into Spheres, pp. 146–158. Harmonic Maps. Springer, Berlin (1982)
Verbitsky, M.: Pseudoholomorphic curves on nearly Kähler manifolds. Commun. Math. Phys. 324(1), 173–177 (2013)
Xu, F.: Pseudo-holomorphic curves in nearly Kähler \(\text{ CP}^{3}\). Differ. Geom. Appl. 28(1), 107–120 (2010)
Xu, F.: SU(3)-structures and special Lagrangian geometries. In: arXiv preprint math/0610532 (2006)
Acknowledgements
The author is grateful to his PhD supervisors Jason Lotay and Simon Salamon for their advice and support. This work was supported by the Engineering and Physical Sciences Research Council [EP/L015234/1], the EPSRC Centre for Doctoral Training in Geometry and Number Theory (The London School of Geometry and Number Theory), University College London.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aslan, B. Transverse J-holomorphic curves in nearly Kähler \(\mathbb {CP}^3\). Ann Glob Anal Geom 61, 115–157 (2022). https://doi.org/10.1007/s10455-021-09806-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10455-021-09806-0