Effect of density dependence on coinfection dynamics: part 2

Abstract

In this paper we continue the stability analysis of the model for coinfection with density dependent susceptible population introduced in Andersson et al. (Effect of density dependence on coinfection dynamics. arXiv:2008.09987, 2020). We consider the remaining parameter values left out from Andersson et al. (Effect of density dependence on coinfection dynamics. arXiv:2008.09987, 2020). We look for coexistence equilibrium points, their stability and dependence on the carrying capacity K. Two sets of parameter value are determined, each giving rise to different scenarios for the equilibrium branch parametrized by K. In both scenarios the branch includes coexistence points implying that both coinfection and single infection of both diseases can exist together in a stable state. There are no simple explicit expression for these equilibrium points and we will require a more delicate analysis of these points with a new bifurcation technique adapted to such epidemic related problems. The first scenario is described by the branch of stable equilibrium points which includes a continuum of coexistence points starting at a bifurcation equilibrium point with zero single infection strain #1 and finishing at another bifurcation point with zero single infection strain #2. In the second scenario the branch also includes a section of coexistence equilibrium points with the same type of starting point but the branch stays inside the positive cone after this. The coexistence equilibrium points are stable at the start of the section. It stays stable as long as the product of K and the rate ${\bar{\gamma }}$ of coinfection resulting from two single infections is small but, after this it can reach a Hopf bifurcation and periodic orbits will appear.

1 Introduction

In this paper we continue on the work of [2] where we studied the equilibrium dynamics for a continuous compartmental model of two infectious diseases with the ability to co-infect individuals. In the model we assume that only the susceptibles can give birth and that the reproductive rate depends on the density of the susceptibles. This dependence is modelled with a parameter $K>0$ which is the carrying capacity of the population. Recall that by an (equilibrium) branch we understand any continuous in $K\ge 0$ family of equilibrium points of a dynamic system which are locally stable for all but finitely many threshold values of K.

In [2] it was established that for a certain set of parameters (except of K) there exists such an equilibrium branch parameterized by $K>0$. Furthermore, in all cases considered in [2], such a branch can be expressed explicitly.

In this paper we will show that the same holds for the rest of the parametric choices. The main difficulty compared to [2] is that for our parameters the equilibrium branch consists of coexistence equilibrium where single infection of each disease and coinfection both occurs. There are no simple explicit expression for these equilibrium points and we will require a more delicate analysis of these points with a new bifurcation technique adapted to such epidemic related problems.

1.1 The model

As in [2], we assume that the single infection cannot be transmitted by the contact with a coinfected person. This process gives rise to the model:

$$\begin{aligned} \begin{aligned} S'&=\left( r\left( 1-\frac{S}{K}\right) -\alpha _1I_1-\alpha _2I_2-\alpha _3I_{12}\right) S,\\ I_1'&=(\alpha _1S - \eta _1I_{12}-\gamma _1I_2 - \mu _1)I_1,\\ I_2'&=(\alpha _2S - \eta _2I_{12}-\gamma _2I_1- \mu _2)I_2,\\ I_{12}'&=(\alpha _3S+ \eta _1I_1+\eta _2I_2-\mu _3)I_{12}+{\overline{\gamma }}I_1I_2, \\ R'&=\rho _1 I_1+\rho _2I_2+\rho _3 I_{12}-\mu _4' R, \end{aligned} \end{aligned}$$

(1)

where we use the following notation:

• S represents the susceptible class,

• $I_1$ and $I_2$ are the infected classes from strain 1 and strain 2 respectively,

• $I_{12}$ represents the co-infected class,

• R represents the recovered class.

Following [1, 3, 11], we assume that the reproduction rate depends on the density of population that allows us to obtain a limited population growth. We also consider the recovery of each infected class [see the last equation in (1)]. The fundamental parameters of the system are:

• $r=b-d_0$ is the intrinsic rate of natural increase, where b is the birthrate and $d_0$ is the death rate of S-class,

• K is the carrying capacity (see also the next section),

• $\rho _i$ is the recovery rate from each infected class ($i=1,2,3$),

• $d_i$ is the death rate of each class, $( i=1,2,3,4)$, where $d_3$ and $d_4$ correspond $I_{12}$ and R respectively,

• $\mu _i=\rho _i+d_i, i=1,2,3.$

• $\alpha _1$, $\alpha _2$, $\alpha _3$ are the rates of transmission of strain 1, strain 2 and both strains (in the case of coinfection),

• $\gamma _i$ is the rate at which infected with one strain get infected with the other strain and move to a coinfected class ($i=1,2$),

• $\eta _i$ is the rate at which infected from one strain getting infection from a co-infected class $( i=1,2)$;

We only consider the case when the reproduction rate of susceptibles is not less than their death rate since we know that the population will go extinct in that case. The system is considered under the natural initial conditions $S(0)>0$, $I_1(0)\ge 0$, $I_2(0)\ge 0$, $I_{12}(0)\ge 0$ and we denote the total population by $N=S+I_1+I_2+I_{12}+R$.

Since the variable R is not present in the first four equations, without loss of generality, we may consider only the first four equations of system (1). It is convenient to introduce the notation

$$\begin{aligned} \sigma _i{:}{=}\frac{\mu _i}{\alpha _i}, \qquad 1\le i\le 3. \end{aligned}$$

(2)

And similarly to the first part [2] we make the following assumption

$$\begin{aligned} \sigma _1< \sigma _2 < \sigma _3. \end{aligned}$$

(3)

We shall also assume that (1) satisfies the non-degenerate condition

$$\begin{aligned} \varDelta _\alpha =\left| \begin{array}{cc} \eta _1 &{}\quad \alpha _1 \\ \eta _2 &{}\quad \alpha _2 \\ \end{array} \right| =\eta _1\alpha _2-\eta _2\alpha _1\ne 0. \end{aligned}$$

(4)

This condition have a natural biological explanation: the virus strains 1 and 2 have different (co)infections rates. We use the notation

$$\begin{aligned} {\bar{\gamma }}= \gamma _1+\gamma _2,\;\;\gamma =(\gamma _1,\gamma _2), \end{aligned}$$

and

$$\begin{aligned} A_1= & {} \frac{\alpha _1\alpha _3}{r}(\sigma _3-\sigma _1), \eta _1^*\,{:=}\,\frac{\eta _1}{A_1} \\ A_2= & {} \frac{\alpha _2\alpha _3}{r}(\sigma _3-\sigma _2), \eta _2^*\,{:=}\,\frac{\eta _2}{A_2} \\ A_3= & {} \frac{\alpha _1\alpha _2}{r}(\sigma _2-\sigma _1), \gamma ^*\,{:=}\,\frac{\gamma _1}{A_3}. \end{aligned}$$

Notice that by (3) one has $A_1,A_2,A_3>0$. We have

$$\begin{aligned} \alpha _2A_1=\alpha _3A_3+ \alpha _1A_2. \end{aligned}$$

(5)

The determinants $\varDelta _\alpha$ and $\varDelta _\mu =\eta _1\mu _2-\eta _2\mu _1$ are related to each other by

$$\begin{aligned} \varDelta _\mu =\frac{\eta _1r}{\alpha _1}A_3+\sigma _1\varDelta _\alpha = \frac{\eta _2r}{\alpha _2}A_3+\sigma _2\varDelta _\alpha , \end{aligned}$$

hence $A_3>0$ implies

$$\begin{aligned} \varDelta _\mu>\sigma _1\varDelta _\alpha \qquad \varDelta _\mu >\sigma _2\varDelta _\alpha . \end{aligned}$$

(6)

This implies an inequality which will be useful in the further analysis:

$$\begin{aligned} \sigma _2(\varDelta _\alpha +\gamma _2\alpha _3)<\varDelta _\mu +\gamma _2\mu _3. \end{aligned}$$

(7)

We shall also make use of the following relations:

$$\begin{aligned} \eta _1^* -\eta _2^*&< \eta _1\frac{\alpha _2}{\alpha _1A_2}-\eta _2^* = \frac{\varDelta _\alpha }{\alpha _1A_2}. \end{aligned}$$

(8)

A consequence of (8) and (6) is that for $\eta _1^*>\eta _2^*$ we have $\varDelta _\alpha ,\;\varDelta _\mu >0$. On the other hand, one has

$$\begin{aligned} \eta _1^*- \eta _2^* = \frac{(\varDelta _\alpha \sigma _3-\varDelta _\mu )\alpha _3}{rA_1A_2} \end{aligned}$$

(9)

1.2 The main result

It is elementary to see that except for the trivial equilibrium state $G_1=(0,0,0,0)$ and the disease free equilibrium $G_{000}=(K, 0,0,0)$, there exist only 6 possible types of equilibrium points $G_{100}$, $G_{010}$, $G_{001}$, $G_{101}$, $G_{011}$, $G_{111}$ determined by their non-zero compartments (see Table 1 and Proposition 1 below for explicit representations). Here, the equilibrium points $G_{100}$, $G_{010}$, $G_{001}$ have two non-zero components and represent points where only one of the diseases are present or where the diseases only exist together as coinfection. At the points $G_{101},G_{011}$ one of the diseases are only present in coinfected individuals while the other disease also occurs as single infections. The point $G_{111}$ is the coexistence equilibrium were both types of single infection is present as well as coinfection. Our main results extends the results of [6] and [7] on the case of small values of $\gamma _i$. More precisely, we have only four possible scenarios of developing of a locally stable equilibrium point as a continuous function of increasing carrying capacity K, see Theorem 1 below.

Table 1 The types of equilibrium states of (1), where $\star$ denotes a non-zero coordinate

Theorem 1

Let all parameters $\alpha _i,\mu _i,\eta _i,\gamma _i$ of (1) be fixed with ${\bar{\gamma }}$ sufficiently small. Then one has exactly one locally stable nonnegative equilibrium point depending on $K>0$. Furthermore, changing the carrying capacity K from zero to infinity, the type of this locally stable equilibrium point changes according to one of the following alternative scenarios:

• (i) $G_{000}\rightarrow G_{100}$;

• (ii) $G_{000}\rightarrow G_{100}\rightarrow G_{101}\rightarrow G_{001}$;

• (iii) $G_{000} \rightarrow G_{100}\rightarrow G_{101}\rightarrow G_{111}\rightarrow G_{011}\rightarrow G_{001}$;

• (iv) $G_{000}\rightarrow G_{100}\rightarrow G_{101}\rightarrow G_{111}$.

The first two scenarios are considered in our paper [2]. In this paper we consider the remained two scenarios, (iii) and (vi). These cases require a more nontrivial bifurcation analysis with application of methods similar to the principle of the exchange of stability developed in [8], see also [2, 9] for recent applications in population analysis. In our context, this requires a delicate analysis of the inner equilibrium state $G_{111}$, as well as a new bifurcation technique.

2 Equilibrium points

We note that the last equation in (1) can be solved explicitly with respect to R:

$$\begin{aligned} R(t)=e^{-\mu '_4t}R(0)+\int _0^t e^{\mu '_4(\tau -t)}(\rho _1I_1+\rho _2I_2+\rho _3I_{12})(\tau ) d\tau \end{aligned}$$

therefore it suffices to study the dynamics of the first four equations in (1). If $I_1,I_2$ and $I_{12}$ have limits ${\hat{I}}_1$, ${\hat{I}}_2$ and ${\hat{I}}_{12}$ respectively as $t\rightarrow \infty$ then R will have the limit

$$\begin{aligned} {\hat{R}}= \frac{\rho _1{\hat{I}}_1+\rho _2{\hat{I}}_2+ \rho _3 {\hat{I}}_{12}}{\mu _4} \end{aligned}$$

Let us turn to the first four equations in (1). The equilibrium points satisfy the following system

$$\begin{aligned} \begin{aligned}&\left( b\left( 1-\frac{S}{K}\right) -\alpha _1I_1-\alpha _2I_2-\alpha _3I_{12}-\mu _0\right) S=0,\\&(\alpha _1S - \eta _1I_{12}-\gamma _1I_2 - \mu _1)I_1=0,\\&(\alpha _2S - \eta _2I_{12}-\gamma _2I_1- \mu _2)I_2=0,\\&(\alpha _3S+ \eta _1I_1+\eta _2I_2-\mu _3)I_{12}+{\overline{\gamma }}I_1I_2=0. \end{aligned} \end{aligned}$$

(10)

and in [2] we had the following proposition

Proposition 1

Except for the trivial equilibrium $G_1=(0,0,0,0)$ and the disease free equilibrium $G_{000}=(K, 0,0,0)$ there exist only the following equilibrium states:

$$\begin{aligned} G_{100}= & {} \left( \sigma _1, \frac{r}{K\alpha _1}(K-\sigma _1), 0,0\right) ,\\ G_{010}= & {} \left( \sigma _2,0,\frac{r}{K\alpha _2}(K-\sigma _2), 0\right) ,\\ G_{001}= & {} \left( \sigma _3,0,0,\frac{r}{K\alpha _3}(K-\sigma _3)\right) ,\\ G_{101}= & {} \left( S^*,\frac{\alpha _3}{\eta _1}(\sigma _3-S^*),0,\frac{\alpha _1}{\eta _1}(S^*-\sigma _1)\right) , \quad \text {where}\quad S^*=K\left( 1-\frac{1}{\eta _1^*}\right) , \,\, \\ G_{011}= & {} \left( S^*,0,\frac{\alpha _3}{\eta _2}(\sigma _3-S^*),\frac{\alpha _2}{\eta _2}(S^*-\sigma _2)\right) , \quad \text {where}\quad S^*=K\left( 1-\frac{1}{\eta _2^*}\right) ,\,\, \\ G_{111}= & {} (S^*,I_1^*,I_2^*,I_{12}^*). \end{aligned}$$

All needed information about equilibrium points $G_1$ – $G_{101}$ can be found in [2]. Here we consider only points $G_{111}$ and $G_{011}$. To highlight the dependence of the equilibrium points on K we will write sometimes $G_j(K)$.

2.1 Coexistence equilibria

The coordinates of coexistence equilibrium points satisfy

$$\begin{aligned} \left\{ \begin{array}{l} r\left( 1-\frac{S}{K}\right) -\alpha _1I_1-\alpha _2I_2-\alpha _3I_{12}=0,\\ \alpha _1S - \eta _1I_{12}-\gamma _1I_2 - \mu _1=0,\\ \alpha _2S - \eta _2I_{12}-\gamma _2I_1- \mu _2=0,\\ \alpha _3S+\eta _1I_1+\eta _2I_2-\mu _3+\frac{{\overline{\gamma }}I_1I_2}{I_{12}}=0 \end{array} \right. \end{aligned}$$

(11)

Furthermore, as it is shown in [2], Sect. 3.2, the S coordinate of an inner equilibrium point (coexistence equilibrium) satisfies $P(S)=0$ where

$$\begin{aligned} P(S)\,{:=}\,P_{\gamma ,K}(S)\,{:=}\, \begin{vmatrix} \mu _1&\quad \mu _2&\quad \mu _3&\quad \frac{r}{ K}(S- K)S \\ \alpha _1&\quad \alpha _2&\quad \alpha _3&\quad \frac{r}{ K}(S- K) \\ 0&\quad \gamma _1&\quad \eta _1&\quad \mu _1-\alpha _1S \\ \gamma _2&\quad 0&\quad \eta _2&\quad \mu _2-\alpha _2S \\ \end{vmatrix}. \end{aligned}$$

One can verify that

$$\begin{aligned} P(S)=p_2S^2+p_1S+p_0, \end{aligned}$$

where

$$\begin{aligned} p_0= & {} r(-A_3\varDelta _\mu - \theta + \gamma _1\mu _2A_1+\gamma _2\mu _1A_2), \\ p_1= & {} r(A_3\varDelta _\alpha + \frac{\theta }{ K}+\rho -\gamma _1\alpha _2A_1-\gamma _2\alpha _1A_2), \\ p_2= & {} -\frac{r}{ K}\rho . \end{aligned}$$

Here

$$\begin{aligned}&\rho {:}{=} \begin{vmatrix} \alpha _1&\quad \alpha _2&\quad \alpha _3 \\ 0&\quad \gamma _1&\quad \eta _1 \\ \gamma _2&\quad 0&\quad \eta _2 \\ \end{vmatrix}= \gamma _1 \alpha _1\eta _2+\gamma _2 \alpha _2 \eta _1 -\gamma _1 \gamma _2\alpha _3,\\&\theta {:}{=} \begin{vmatrix} \mu _1&\quad \mu _2&\quad \mu _3 \\ 0&\quad \gamma _1&\quad \eta _1 \\ \gamma _2&\quad 0&\quad \eta _2 \\ \end{vmatrix}= \gamma _1 \mu _1\eta _2+\gamma _2 \mu _2 \eta _1 -\gamma _1 \gamma _2\mu _3, \end{aligned}$$

If the S component is known the other components can easily be founded from the linear system of equations that results from the first three equations of (10).

Let us introduce the Jacobian matrix of the right hand side of (1), with the redundant last row removed, computed at an inner equilibrium point $G_{111}=(S,I_1,I_2,I_{12})$:

$$\begin{aligned} J_8=\mathrm{diag}(S,I_1,I_2,I_{12})B,\;\;\;B=\left( \begin{matrix} -\frac{r}{ K} &{}\quad -\alpha _1 &{}\quad -\alpha _2 &{}\quad -\alpha _3 \\ \alpha _1 &{}\quad 0 &{}\quad -\gamma _1 &{}\quad -\eta _1 \\ \alpha _2 &{}\quad -\gamma _2 &{}\quad 0 &{}\quad -\eta _2 \\ \alpha _3 &{}\quad \eta _1+{\overline{\gamma }}r_2 &{}\quad \eta _2+{\overline{\gamma }}r_1 &{}\quad -{\overline{\gamma }}r_1r_2 \end{matrix} \right) , \end{aligned}$$

where

$$\begin{aligned} r_1=\frac{I_1}{I_{12}},\;\;\;r_2=\frac{I_2}{I_{12}}. \end{aligned}$$

(12)

Adding the first three rows of $J_8$ to its last row one obtains applying systematically (10) that

$$\begin{aligned} \det B&=\frac{\det (J_8)}{SI_1I_2I_{12}} =\frac{1}{I_{12}}\begin{vmatrix} \frac{r}{ K}&\quad \alpha _1&\quad \alpha _2&\quad \alpha _3 \\ -\alpha _1&\quad 0&\quad \gamma _1&\quad \eta _1 \\ -\alpha _2&\quad \gamma _2&\quad 0&\quad \eta _2 \\ \frac{r}{ K}(2S- K)&\quad \mu _1&\quad \mu _2&\quad \mu _3 \end{vmatrix}\\&=\frac{1}{I_{12}}\begin{vmatrix} \mu _1&\quad \mu _2&\quad \mu _3&\quad \frac{r}{K}(2S- K) \\ \alpha _1&\quad \alpha _2&\quad \alpha _3&\quad \frac{r}{ K} \\ 0&\quad \gamma _1&\quad \eta _1&\quad -\alpha _1 \\ \gamma _2&\quad 0&\quad \eta _2&\quad -\alpha _2 \end{vmatrix} =\frac{1}{I_{12}}\,\frac{\partial P(S)}{\partial S}. \end{aligned}$$

The last equality is verified directly by using the definition of P(S). This implies an important property

$$\begin{aligned} \det B=\frac{1}{I_{12}}\frac{\partial P(S)}{\partial S}. \end{aligned}$$

(13)

We assume that

$$\begin{aligned} \frac{\partial P_{\gamma ,K}(S)}{\partial S}>0\;\;\hbox {for any coexistence equilibrium point}. \end{aligned}$$

(14)

Remark 1

Inequality (14) together with (13) implies, in particular, that the Jacobian matrix is invertible at every coexistence equilibrium and so there exists a curve G(K) through this point, parameterized by K and consisting of equilibrium points satisfying (14). Moreover (14) implies that the product of all eigenvalues of the Jacobian matrix at a coexistence eq. point is positive which provides a necessary condition for local stability of the corresponding equilibrium point. By Lemma 4 and (8) we have that $\varDelta _\alpha >0$ if the condition (14) is valid and the set of coexistence equilibria is non empty. Then since

$$\begin{aligned} \frac{\partial P(S)}{\partial S}=\alpha _1\alpha _2(\sigma _2-\sigma _1)\varDelta _\alpha +O(\bar{\gamma }), \end{aligned}$$

inequality (14) is a priori true for small $\bar{\gamma }$.

Lemma 1

Let $G(K)=(S(K),I_1(K),I_2(K),I_{12}(K))$ be a curve consisting of coexistence equilibrium points satisfying (14). Let also $(K_1,K_2)$ be the maximal interval of existence of such curve. Then

• (i) $\frac{\partial S}{\partial K}<0$ and $\frac{\partial I_{12}}{\partial K}<0$ for $K\in (K_1,K_2)$.

• (ii) $K_1\ge \sigma _1$ and there exists a limit $\lim _{K\rightarrow K_1}G(K)$ which is an equilibrium point with at least one zero component.

• (iii) if $K_2<\infty$ then there exists a limit $\lim _{K\rightarrow K_2}G(K)$ which is an equilibrium point with at least one zero component.

• (iv) if $K_2=\infty$ then there is a limit $\lim _{K\rightarrow \infty }G(K)$ which is an equilibrium point of the limit system.

Proof

Differentiating (11) with respect to K, we get

$$\begin{aligned} B\left( \begin{array}{l} \frac{\partial S}{\partial K} \\ \frac{\partial {{I}_{1}}}{\partial K} \\ \frac{\partial {{I}_{2}}}{\partial K} \\ \frac{\partial {{I}_{12}}}{\partial K} \end{array}\right) = \left( \begin{array}{l} -\frac{rS}{K^2} \\ 0 \\ 0 \\ 0 \end{array}\right) . \end{aligned}$$

Therefore

$$\begin{aligned} \frac{\partial {S}}{\partial K}=-(B^{-1})_{11}\frac{rS}{K^2}=-\frac{rSI_{12}}{K^2\frac{\partial P(S)}{\partial S}}\cdot (\gamma _1\gamma _2{\overline{\gamma }}r_1r_2 +\gamma _1\eta _2(\eta _1+{\overline{\gamma }}r_2)+\eta _1\gamma _2(\eta _2+{\overline{\gamma }}r_1)) \end{aligned}$$

and

$$\begin{aligned} \frac{\partial {{I}_{12}}}{\partial K}=-(B^{-1})_{41}\frac{rS}{ K^2}=-\frac{rSI_{12}}{ K^2\frac{\partial P(S)}{\partial S}}\cdot ({\alpha _1\gamma _2(\eta _2+{\overline{\gamma }}r_1)+\gamma _1\alpha _2(\eta _1+{\overline{\gamma }}r_2)+\gamma _1\gamma _2\alpha _3}). \end{aligned}$$

which proves (i).

To prove (ii) we note first that the equilibrium point $G_{000}$ is globally stable for $K\in (0,\sigma _1)$ according to [2], Proposition 2, and therefore $K_1\ge \sigma _1$. Next, since S and $I_{12}$ components are monotone according to (i), and bounded there is a limit

$$\begin{aligned} S^{(1)}=\lim _{K\rightarrow K_1}S(K)\;\;\text{ and }\;\;I_{12}^{(1)}=\lim _{K\rightarrow K_1}I_{12}(K). \end{aligned}$$

The $I_1$ and $I_2$ components satisfying equations

$$\begin{aligned} \gamma _1I_2= & {} \alpha _1S - \eta _1I_{12} - \mu _1,\\ \gamma _2I_1= & {} \alpha _2S - \eta _2I_{12}- \mu _2, \end{aligned}$$

which implies convergence of these components to $I_{1}^{(1)}$ and $I_{2}^{(1)}$ respectively as $K\rightarrow K_1$. Clearly $G^{(1)}=(S^{(1)},I_{1}^{(1)},I_{2}^{(1)},I_{12}^{(1)})$ is an equilibrium point which must be on the boundary of the positive orthant, otherwise one can continue the branch G(K) outside the maximal interval of existence. This argument proves (ii). Proof of (iii) and (iv) are the same up to some small changes as the proof of (ii). $\square$

To exclude from our analysis the equilibrium point $G_{010}$ we will require in this text that

$$\begin{aligned} \gamma ^*<1. \end{aligned}$$

(15)

Under this condition $G_{010}$ is always unstable. Since we are interested only in locally stable equilibrium point the point $G_{010}$ will not appear in our forthcoming analysis.

2.2 The equilibrium state $G_{011}$

Let us consider the equilibrium point $G_{011}$. The components are given by Proposition 1 as

$$\begin{aligned} G_{011}&=(S^*,0,I_2^*,I_{12}^*),\\ S^*&=K\left( 1-\frac{1}{\eta _2^*}\right) ,\\ I_2^*&=\frac{\alpha _3}{\eta _2}(\sigma _3-S^*),\\ I_{12}^*&=\frac{\alpha _2}{\eta _2}(S^*-\sigma _2). \end{aligned}$$

This point has type $G_{011}$ (i.e. three positive components) if and only if

$$\begin{aligned} \sigma _2<S^*<\sigma _3\quad \text {and}\quad \eta _2^*>1, \end{aligned}$$

where the first relation is equivalent to

$$\begin{aligned} \frac{\sigma _2\eta _2^*}{\eta _2^*-1}<K<\frac{\sigma _3\eta _2^*}{\eta _2^*-1}. \end{aligned}$$

(16)

Similarly to above we find the Jacobian matrix evaluated at $G_{011}$ as

$$\begin{aligned} J_7= \begin{bmatrix} -r\frac{S^*}{K} &{}\quad -\alpha _1S^* &{}\quad -\alpha _2S ^*&{}\quad -\alpha _3S^* \\ 0 &{}\quad \alpha _1S^*-\eta _1I_{12}^*-\gamma _1I_2^*-\mu _1 &{}\quad 0 &{}\quad 0 \\ \alpha _2I_2^* &{}\quad -\gamma _2I_2^* &{}\quad 0 &{}\quad -\eta _2I_2^* \\ \alpha _3I_{12}^* &{}\quad \eta _1I_{12}^*+{\overline{\gamma }}I_2^*&{}\quad \eta _2I_{12}^* &{}\quad 0 \end{bmatrix}. \end{aligned}$$

where $S,I_2,I_{12}$ are given by Proposition 1. Since the submatrix

$$\begin{aligned} {\tilde{J}}= \begin{bmatrix} -r\frac{S^*}{K} &{}\quad -\alpha _2S^* &{}\quad -\alpha _3S^* \\ \alpha _2I_2^* &{}\quad 0 &{}\quad -\eta _2I_2^* \\ \alpha _3I_{12}^* &{}\quad \eta _2I_{12}^* &{}\quad 0 \end{bmatrix} = \begin{bmatrix} S^* &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad I_2^* &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad I_{12}^* \end{bmatrix} \begin{bmatrix} -\frac{r}{K} &{}\quad -\alpha _2 &{}\quad -\alpha _3 \\ \alpha _2 &{}\quad 0 &{}\quad -\eta _2 \\ \alpha _3 &{}\quad \eta _2 &{}\quad 0 \end{bmatrix}, \end{aligned}$$

is stable by Routh-Hurwitz criteria, we conclude that the matrix $J_7$ is stable whenever

$$\begin{aligned} \alpha _1S^*-\eta _1I_{12}^*-\gamma _1I_2^*-\mu _1 <0. \end{aligned}$$

(17)

Using Proposition 1, we can rewrite (17) as

$$\begin{aligned} S^*(\varDelta _\alpha -\gamma _1\alpha _3)>\varDelta _\mu -\gamma _1\mu _3. \end{aligned}$$

(18)

If $\varDelta _\alpha -\gamma _1\alpha _3=0$ then the linear stability holds whenever $\varDelta _\mu -\gamma _1\mu _3<0$. For $\varDelta _\alpha -\gamma _1\alpha _3\ne 0$, let us define

$$\begin{aligned} {\hat{S}}_2=\frac{\varDelta _\mu -\gamma _1\mu _3}{\varDelta _\alpha -\gamma _1\alpha _3}\;\;\text{ and }\;\;\hat{K}_2=\hat{S}_2\frac{\eta _2^*}{\eta _2^*-1} \end{aligned}$$

then (18) can be written

$$\begin{aligned} \left\{ \begin{aligned} S^*>{\hat{S}}_2\quad \text { if }\varDelta _\alpha -\gamma _1\alpha _3>0 \\ S^*<{\hat{S}}_2\quad \text { if }\varDelta _\alpha -\gamma _1\alpha _3<0 \end{aligned}\right. \end{aligned}$$

It can be verified also that

$$\begin{aligned} {\hat{S}}_2-\sigma _1&=\frac{rA_1A_3(\eta _1^*-\gamma ^*)}{(\varDelta _\alpha -\gamma _1\alpha _3)\alpha _1}\nonumber \\ {\hat{S}}_2-\sigma _2&=\frac{rA_2A_3(\eta _2^*-\gamma ^*)}{(\varDelta _\alpha -\gamma _1\alpha _3)\alpha _2}\nonumber \\ {\hat{S}}_2-\sigma _3&=\frac{rA_1A_2(\eta _2^*-\eta _1^*)}{(\varDelta _\alpha -\gamma _1\alpha _3)\alpha _3} \end{aligned}$$

(19)

This readily yields the (local) stability criterion:

Proposition 2

The equilibrium point $G_{011}$ is nonnegative and locally stable if and only if $\eta _2^*>1$ and exactly one of the following conditions holds:

• (i) $\frac{\sigma _2\eta _2^*}{\eta _2^*-1}<K<\frac{\min ({\hat{S}}_2,\sigma _3)\eta _2^*}{\eta _2^*-1}$ when $\varDelta _\alpha -\gamma _1\alpha _3<0$ and $\eta _2^*<\gamma ^*$,

• (ii) $\frac{\max ({\hat{S}}_2,\sigma _2)\eta _2^*}{\eta _2^*-1}<K<\frac{\sigma _3\eta _2}{\eta _2-1}$ when $\varDelta _\alpha -\gamma _1\alpha _3>0$ and $\eta _1^*>\eta _2^*$,

• (iii) K subject to (16) when $\varDelta _\alpha -\gamma _1\alpha _3=0$ and $\varDelta _\mu -\gamma _1\mu _3<0$

By (19) we get that for small values of $\gamma _1$ one has the following refinement of the above proposition.

Corollary 1

Let $\eta _2^*>1$ and

$$\begin{aligned} 0\le \gamma ^*< \eta _2^*. \end{aligned}$$

(20)

Then the equilibrium point $G_{011}$ is nonnegative and linearly stable if and only if

• (i) $\eta _1^*>\eta _2^*>1$ and $\frac{\hat{S}_2\eta _2^*}{\eta _2^*-1}<K<\frac{\sigma _3\eta _2^*}{\eta _2^*-1}$,

  or

• (ii) K subject to (16), $\varDelta _\alpha -\gamma _1\alpha _3=0$ and $\varDelta _\mu -\gamma _1\mu _3<0$.

  Therefore the bifurcation point $\hat{K}_2$ appears here only in the case (i).

Proof

By the made assumption, the case (i) in Proposition 2 is impossible. So it is sufficient to prove (i). It is thus required that $\eta ^*_1>\eta _2^*>1$. If $\eta ^*_1>\eta _2^*>1$ then

$$\begin{aligned}&\varDelta _\alpha -\gamma _1\alpha _3=\eta _1^*A_1\alpha _2-\eta ^*_2A_2\alpha _1-\gamma ^*A_3\alpha _3 \\&\quad >\eta _1^*( A_1\alpha _2-A_2\alpha _1-A_3\alpha _3)=0 \end{aligned}$$

where we used equation (5) in the last equality. Furthermore, since (20) and $\varDelta _\alpha -\gamma _1\alpha _3>0$ holds for this case we also obtain from (19) that $\hat{S}_2-\sigma _2>0$, therefore $\max ({\hat{S}}_2,\sigma _2)=\hat{S}_2$, and we arrive at the desired conclusion. $\square$

In what follows we will assume that

$$\begin{aligned} \gamma ^*<1\;\;\text{ and }\;\;\gamma _1<\alpha _3^{-1}\varDelta _\alpha . \end{aligned}$$

(21)

We note that the first inequality guarantees (20) since the equilibrium point $G_{011}$ exists only if $\eta _2^*>1$.

3 Branches of coexisting equilibria

3.1 Bifurcation of $G_{101}$

From [2] we know that the equilibrium point $G_{101}$ with the only zero component $I_2$ has the form

$$\begin{aligned} G_{101}=\left( S^*,\frac{\alpha _3}{\eta _1}(\sigma _3-S^*),0,\frac{\alpha _1}{\eta _1}(S^*-\sigma _1)\right) \end{aligned}$$

(22)

where

$$\begin{aligned} S^*=K\left( 1-\frac{1}{\eta ^*_1}\right) . \end{aligned}$$

We also know that it has positive components (except $I_2$) when $\eta ^*_1>1$ and

$$\begin{aligned} \sigma _1<S^*<\sigma _3\;\;\text{ or } \text{ equivalently }\;\;\frac{\sigma _1\eta ^*_1}{\eta _1^*-1}< K<\frac{\sigma _3\eta ^*_1}{\eta _1^*-1} \end{aligned}$$

The bifurcation point (the point where the Jacobian is zero) corresponds to

$$\begin{aligned} K={\hat{K}}_1=\frac{\varDelta _\mu +\mu _3\gamma _2}{\varDelta _\alpha +\alpha _3\gamma _2}\frac{\eta _1^*}{\eta _1^*-1}\;\;\text{ and }\;\; S^{*}={\hat{S}}_{1}=\frac{\varDelta _\mu +\mu _3\gamma _2}{\varDelta _\alpha +\alpha _3\mu _2}. \end{aligned}$$

(23)

and is denoted ${\hat{G}}_{101}=G({\hat{K}}_1)$.

Stability analysis of $G_{101}$ is given in the next proposition.

Proposition 3

The equilibrium point $G_{101}$ is nonnegative if $\eta _1^*>1$ and it is stable if the following conditions hold:

$$\begin{aligned} \frac{\sigma _1\eta _1^*}{\eta _1^*-1}<K<\frac{Q\eta _1^*}{\eta _1^*-1} \end{aligned}$$

where

$$\begin{aligned} Q=\left\{ \begin{array}{ll} \sigma _3&{} \text { if }\eta _2^*> \eta _1^*;\\ \hat{S}_1&{} \text { if }\eta _2^*<\eta _1^*. \end{array} \right. \end{aligned}$$

The case $\eta _2^*> \eta _1^*$ (when we have no bifurcation) is considered in our paper [2]. Here we will assume that

$$\begin{aligned} \eta ^*_1>\eta ^*_2. \end{aligned}$$

(24)

By (8) the last inequality implies that

$$\begin{aligned} \varDelta _\alpha>(\eta ^*_1-\eta _2^*)A_2\alpha _1>0. \end{aligned}$$

By using (6), one verifies straightforward that

$$\begin{aligned} \sigma _2<\frac{\varDelta _\mu }{\varDelta _\alpha }<{\hat{S}}_{1}<\sigma _3. \end{aligned}$$

Notice a useful identity [the last equality is by (9)]

$$\begin{aligned} \hat{S}_1-\hat{S}_2= & {} \frac{\alpha _3{\bar{\gamma }} (\sigma _3\varDelta _\alpha -\varDelta _\mu )}{(\varDelta _\alpha -\gamma _1\alpha _3)(\varDelta _\alpha +\gamma _2\alpha _3)}\nonumber \\= & {} \frac{{\bar{\gamma }} r A_1A_2(\eta _1^*- \eta _2^*)}{(\varDelta _\alpha -\gamma _1\alpha _3)(\varDelta _\alpha +\gamma _2\alpha _3)}. \end{aligned}$$

(25)

As a result of Corollary 1 and Proposition 3 we get that ${\hat{S}}_1,{\hat{S}}_2$ only exist as parts of equilibrium points when $\varDelta _\alpha -\gamma _1\alpha _3>0$ and $\eta _1^*>\eta _2^*>1$. In this case we see from (25) that ${\hat{S}}_1>{\hat{S}}_2$.

We will now prove the following lemma.

Lemma 2

Let (24) be valid and $\frac{\partial P}{\partial S}|_{S={\hat{S}}_1}>0$. Then there exists a smooth branch of equilibrium points $G_{111}(K)=(S,I_1,I_2,I_{12})(K)$ defined for small $|K- {\hat{K}}_1|$ with the asymptotics

$$\begin{aligned} S(K)= & {} {\hat{S}}_1+{\mathcal {O}}(K-{\hat{K}}_1)\nonumber \\ I_1(K)= & {} \frac{\alpha _3}{\eta _1}(\sigma _3-{\hat{S}}_1)+{\mathcal {O}}(K-{\hat{K}}_1) \nonumber \\ I_2(K)= & {} \frac{\eta _1r(\varDelta _\mu +\gamma _2\mu _3)I_{12}({\hat{K}}_1)}{\frac{\partial P(S)}{\partial S}|_{K={\hat{K}}_1} {\hat{K}}_1^2}(K-{\hat{K}}_1) +{\mathcal {O}}((K-{\hat{K}}_1)^2)\nonumber \\ I_{12}(K)= & {} \frac{\alpha _1}{\eta _1}({\hat{S}}_1-\sigma )+{\mathcal {O}}(K-{\hat{K}}_1). \end{aligned}$$

(26)

Furthermore this equilibrium point is locally stable for ${\hat{K}}_1<K\le {\hat{K}}_1+\varepsilon$, where $\varepsilon$ is a small positive number. Moreover all equilibrium points in a small neighborhood of $G_{101}(\hat{K}_1)$ are exhausted by two branches $G_{101}(K)$ and $G_{111}(K)$.

Remark 2

The constant $\varepsilon$ does not depend on $\gamma _i$ but it does depend on $\alpha _i$, $\mu _i$ and $\eta _i$.

Proof

In order to use results of Appendix B we write system (10) in the following form

$$\begin{aligned}&F(x;s)=0,\nonumber \\&x_4f(x')=0, \end{aligned}$$

(27)

where

$$\begin{aligned} x=(x',x_4)=(x_1,x_2,x_3,x_4)=(S,I_1,I_{12},I_2), \end{aligned}$$

where $s=K-{\hat{K}}_1$,

$$\begin{aligned} F(x,s)=\left( \begin{array}{l} \Big (\frac{r}{K}(K-x_1)-\alpha _1x_2-\alpha _2x_4-\alpha _3x_3\Big )x_1 \\ (\alpha _1x_1-\eta _1x_3-\gamma _1x_4-\mu _1)x_2 \\ (\alpha _3x_1+\eta _1x_2+\eta _2x_4-\mu _3)x_3+\bar{\gamma }x_2x_4 \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} f(x')=\alpha _2x_1-\eta _2x_3-\gamma _2x_2-\mu _2. \end{aligned}$$

By the definition of the bifurcation point (23) and (22), we have that

$$\begin{aligned} x^*=\left( {\hat{S}}_1,\frac{\alpha _3}{\eta _1}(\sigma _3-{\hat{S}}_1),\frac{\alpha _1}{\eta _1}({\hat{S}}_1-\sigma _1)\right) \end{aligned}$$

solves the equation $F(x^*,0;0)=0$ and $f(x^*)=0$. Futhermore, the vector

$$\begin{aligned} \xi (s)=x^*+s\Big (1-\frac{1}{\eta _1^*}\Big )\Big (1,\frac{-\alpha _3}{\eta _1},\frac{\alpha _1}{\eta _1}\Big ) \end{aligned}$$

solves $F(\xi (s),0;s)=0$. The matrix $A=(\partial _{x_j}F_k(x^*,0,0))_{1\le j,k\le 3}$ is explicitly given by

$$\begin{aligned} A=\mathrm{diag}(x_1^*,x_2^*,x_3^*)\hat{A},\;\;\quad \hat{A}=\left( \begin{matrix} -\frac{r}{{\hat{K}}_2} &{}\quad -\alpha _1 &{}\quad -\alpha _3 \\ \alpha _1 &{}\quad 0 &{}\quad -\eta _1 \\ \alpha _3 &{}\quad \eta _1 &{}\quad 0 \end{matrix} \right) . \end{aligned}$$

Using the Routh–Hurwitz stability criterion we can deduce that $A(x^*,0)$ is stable and invertible. Since

$$\begin{aligned} \nabla _{x'} f(x^*)=(\alpha _2,-\gamma _2,\eta _2),\;\;\partial _{x_4}F(x^*,0;0)= (-\alpha _2x^*_1,-\gamma _1x^*_2,\eta _2x^*_3+\bar{\gamma }x^*_2)^T, \end{aligned}$$

we get

$$\begin{aligned} \varTheta =\nabla _{x'} f \cdot A^{-1}\partial _{x_4}F|_{x=(x^*,0),s=0}=(\alpha _2,-\gamma _2,\eta _2)\hat{A}^{-1} (-\alpha _2,-\gamma _1,\eta _2+\bar{\gamma }x^*_2/x_3^*)^T. \end{aligned}$$

Let us evaluate $\varTheta$ and check that $\varTheta \ne 0$. First we observe the equality

$$\begin{aligned} \left( \begin{array}{llll} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \end{array} \right) B(y^*,K_1) \left( \begin{array}{llll} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \end{array} \right) = \left( \begin{array}{llll} &{} \quad &{} \quad &{}\quad -\alpha _2 \\ &{}\quad {\hat{A}} &{}\quad &{}\quad -\gamma _1 \\ &{} \quad &{} \quad &{}\quad \eta _2+\bar{\gamma }x^*_2/x_3^* \\ \,\alpha _2 \,&{}\quad -\gamma _2\,&{}\quad \eta _2\, &{}\quad 0 \end{array} \right) \nonumber \\ \end{aligned}$$

(28)

By (13)

$$\begin{aligned} \det (\text{ left-hand } \text{ side } \text{ of } (28))=\frac{1}{I_{12}}\frac{\partial P(S)}{\partial S}\Big |_{S=S_1}. \end{aligned}$$

(29)

Let us show that

$$\begin{aligned} \det (\text{ right-hand } \text{ side } \text{ of } (28))=\varTheta \det \hat{A}\,. \end{aligned}$$

(30)

For this purpose consider the equation

$$\begin{aligned} \left( \begin{matrix} {\hat{A}} &{}\quad (-\alpha _2,-\gamma _1,\eta _2+\bar{\gamma }x^*_2/x_3^*)^T \\ (\alpha _2,-\gamma _2,\eta _2) &{}\quad 0 \end{matrix} \right) \left( \begin{matrix} X \\ x \end{matrix}\right) = \left( \begin{matrix} {\bar{0}} \\ 1 \end{matrix} \right) \end{aligned}$$

(31)

where $X\in {\mathbb {R}}^{3}$, $x\in {\mathbb {R}}$ and ${\bar{0}}=(0,0,0)^T$. We denote by $\hat{B}$ the matrix in the left-hand side of (31) and using the expression for the matrix inverse, we get

$$\begin{aligned} x=\frac{\det ({\hat{A}})}{\det ({\hat{B}})}. \end{aligned}$$

(32)

Solving (31) as a linear system by finding first X and then x from the last equation, we obtain $-\varTheta x=1$. The last relation together with (32) gives (30). Now the relations (29) and (30) imply

$$\begin{aligned} \varTheta =-\frac{\frac{\partial P(S)}{\partial (S)}\big |_{S={\hat{S}}_1}}{\det ({\hat{A}})I_{12}}, \end{aligned}$$

which along with

$$\begin{aligned} \det ({\hat{A}}({\hat{K}}_1))=\frac{1}{{\hat{S}}_1 I_1^* I_{12}^*}\left| \begin{matrix} -\frac{r}{{\hat{K}}}{\hat{S}}_1 &{}\quad -\alpha _1{\hat{S}}_1 &{}\quad -\alpha _3{\hat{S}}_1 \\ \alpha _1I_1^* &{}\quad 0 &{}\quad -\eta _1I_1^* \\ \alpha _3I^*_{12} &{}\quad \eta _1I^*_{12} &{}\quad 0 \end{matrix} \right| =-\frac{r}{{\hat{K}}_1}\eta _1^2 \end{aligned}$$

gives

$$\begin{aligned} \varTheta ={\hat{K}}_1\frac{\frac{\partial P(S)}{\partial (S)}\big |_{S={\hat{S}}_1}}{r\eta _1^2I_{12}}>0. \end{aligned}$$

Next, since $f(x^*,0;0)=0$, we have

$$\begin{aligned} f(\xi (s),0;s)=\frac{s}{\eta _1}\Big (1-\frac{1}{\eta _1^*}\Big )\Big (\varDelta _\alpha +\gamma _2\alpha _3\Big ). \end{aligned}$$

Now applying (72) in the appendix we get

$$\begin{aligned} x_4=\frac{1}{\eta _1}\Big (1-\frac{1}{\eta _1^*}\Big )\Big (\varDelta _\alpha +\gamma _2\alpha _3\Big )\frac{1}{\varTheta }s+O(s^2), \end{aligned}$$

which is equivalent to (26).

To prove local stability let us consider the matrix

$$\begin{aligned} {{\mathcal {B}}}=\left( \begin{matrix} A &{}\quad \partial _{x_n}F(x^*,0;0) \\ 0 &{}\quad 0 \end{matrix}\right) . \end{aligned}$$

Since the matrix A is stable the matrix ${{\mathcal {B}}}$ has three eigenvalues with negative real parts and one eigenvalue equals zero. The eigenvalues of the Jacobian matrix

$$\begin{aligned} {{\mathcal {J}}}(s)=\left( \begin{matrix} \nabla _{x'}F(\hat{x}(s);s) &{}\quad \partial _{x_n}F(\hat{x}(s);s) \\ \nabla _{x'}(x_nf(x'))|_{x=\hat{x}(s)} &{}\quad f(\hat{x}') \end{matrix}\right) \end{aligned}$$

are small perturbation of the eigenvalue of ${{\mathcal {B}}}={{\mathcal {J}}}(s)$. Therefore three of them have negative real part for small s and the last one $\lambda (\hat{x}(s))$ is perturbation of zero eigenvalue of ${{\mathcal {B}}}$, and it has the following asymptotics (see relation (73) in the Appendix)

$$\begin{aligned} \lambda (\hat{x}(s))= & {} -\frac{d}{ds}f(\xi (s),0;s)|_{s=0}s+O(s^2)\\= & {} -\frac{s}{\eta _1}\Big (1-\frac{1}{\eta _1^*}\Big )\Big (\varDelta _\alpha +\gamma _2\alpha _3\Big )+O(s^2) \end{aligned}$$

and hence it is negative for small positive s. This proves the local stability of the coexistence equilibrium point. $\square$

3.2 Bifurcation of $G_{011}$

We will assume in this section that

$$\begin{aligned} \eta ^*_1>\eta ^*_2>1 \end{aligned}$$

(33)

From [2] we know that the equilibrium point $G_{011}$ with only zero component $I_1$ has the form

$$\begin{aligned} G_{011}=\left( S^*,0,\frac{\alpha _3}{\eta _2}(\sigma _3-S^*),\frac{\alpha _2}{\eta _2}(S^*-\sigma _2)\right) \end{aligned}$$

(34)

where $S^*=K (1-\frac{1}{\eta ^*_2})$. We also know that it has positive components (except $I_1$) when $\eta ^*_2>1$ and

$$\begin{aligned} \sigma _2<S^*<\sigma _3\text { or equivalently } \frac{\sigma _2\eta ^*_2}{\eta _2^*-1}<K<\frac{\sigma _3\eta ^*_2}{\eta _2^*-1} \end{aligned}$$

As in Sect. 3.1 we obtain

$$\begin{aligned} \varDelta _\alpha >0 \end{aligned}$$

The bifurcation point (the point where the Jacobian is zero) corresponds to

$$\begin{aligned} K={\hat{K}}_2=\frac{\varDelta _\mu -\gamma _1\mu _3}{\varDelta _\alpha -\gamma _1\alpha _3}\frac{\eta ^*_2}{\eta _2^*-1}\text { and } S^*={\hat{S}}_2=\frac{\varDelta _\mu -\gamma _1\mu _3}{\varDelta _\alpha -\gamma _1\alpha _3} \end{aligned}$$

(35)

and is denoted ${\hat{G}}_{011}=G_{011}({\hat{K}}_2)$.

For $\gamma _1^*<\eta _2^*$ we have that ${\hat{S}}_2>\sigma _2$ and that $G_{011}$ is stable for K in the interval

$$\begin{aligned} \frac{{\hat{S}}_2\eta ^*_2}{\eta ^*_2-1}<K<\frac{\sigma _3\eta _2^*}{\eta ^*_2-1} \end{aligned}$$

We will now prove the following lemma

Lemma 3

Let (33) be valid and $\frac{\partial P}{\partial S}\big |_{S={\hat{S}}_2}>0$. Then there exists a smooth branch of equilibrium points $G_{111}=(S,I_1,I_2,I_{12})(K)$ defined for small $|K-{\hat{K}}_2|$ with the asymptotics

$$\begin{aligned} S(K)&={\hat{S}}_2+{\mathcal {O}}(K-{\hat{K}}_2) \nonumber \\ I_1(K)&=-\frac{\eta _2r(\varDelta _\mu -\gamma _1\mu _3)I_{12}}{\frac{\partial P(S)}{\partial S}{\hat{K}}_2^2}(K-{\hat{K}}_2) +{\mathcal {O}}((K-{\hat{K}}_2)^2) \nonumber \\ I_2(K)&=\frac{\alpha _3}{\eta _2}(\sigma _3-{\hat{S}}_2)+{\mathcal {O}}(K-{\hat{K}}_2) \nonumber \\ I_{12}(K)&=\frac{\alpha _1}{\eta _2}({\hat{S}}_2-\sigma _2)+{\mathcal {O}}(K-{\hat{K}}_2). \end{aligned}$$

(36)

These equilibrium points are locally stable for ${\hat{K}}_2-\varepsilon \le K< {\hat{K}}_2$, where $\varepsilon$ is a small positive number. Moreover all equilibrium points in a small neighborhood of $G_{011}(\hat{K}_2)$ are exhausted by two branches $G_{011}(K)$ and $G_{111}(K)$.

Remark 3

The constant $\varepsilon$ does not depend on $\gamma$ but it does depend on $\alpha$, $\mu$ and $\eta$.

Proof

We write system (10) in the form

$$\begin{aligned}&F(x;s) \\&f(x')=0, \end{aligned}$$

where

$$\begin{aligned} x=(x',x_4)=(x_1,x_2,x_3,x_4)=(S,I_2,I_{12},I_1) \end{aligned}$$

where $s=K-{\hat{K}}_2$,

$$\begin{aligned} F(x,s)=\left( \begin{array}{l} \Big (\frac{r}{K}(K-x_1)-\alpha _1x_4-\alpha _2x_2-\alpha _3x_3\Big )x_1 \\ (\alpha _2x_1-\eta _2x_3-\gamma _2x_4-\mu _2)x_2 \\ (\alpha _3x_1+\eta _1x_4+\eta _2x_2-\mu _3)x_3+\bar{\gamma }x_4x_2 \end{array}\right) \end{aligned}$$

and

$$\begin{aligned} f(x')=\alpha _1x_1-\eta _1x_3-\gamma _1x_2-\mu _1 \end{aligned}$$

By the definition of the bifurcation point (35) and (34), we have that

$$\begin{aligned} x^*=\left( {\hat{S}}_2,\frac{\alpha _3}{\eta _2}(\sigma _3-{\hat{S}}_2), \frac{\alpha _{12}}{\eta _2}({\hat{S}}_2-\sigma _2)\right) \end{aligned}$$

solves the equation $F(x^*,0;0)=0$ and $f(x^*)=0$. Furthermore, the vector

$$\begin{aligned} \xi (s)=x^*+s\left( 1-\frac{1}{\eta _2^*}\right) \left( 1,\frac{-\alpha _3}{\eta _2},\frac{\alpha _2}{\eta _2}\right) \end{aligned}$$

solves the equation $F(\xi (s),0,s)=0$. The matrix $A=(\partial _{x_j}F_k(x^*,0,0))^3_{j,k=1}$ is evaluated as

$$\begin{aligned} A=\text {diag}(x_1^*,x_2^*,x_3^*){\hat{A}},\; {\hat{A}}=\left( \begin{matrix} -\frac{r}{K} &{}\quad -\alpha _" &{}\quad -\alpha _3 \\ \alpha _2 &{}\quad 0 &{}\quad -\eta _2 \\ \alpha _3 &{}\quad \eta _2 &{}\quad 0 \end{matrix}\right) \end{aligned}$$

with the help of Routh–Hurwitz stability criterion we can deduce that A is stable and invertible. Since

$$\begin{aligned} \nabla _{x'}f(x^*)=(\alpha _1,\gamma _1,\eta _1),\;\partial _{x_4}F(x^*,0,;0)=(-\alpha _1x_1^*,-\gamma _2x^*_2, \eta _1x_3+{\bar{\gamma }} x_2)^T \end{aligned}$$

we get

$$\begin{aligned} \varTheta =\nabla _{x'}f\cdot A^{-1}\partial _{x_4}F\big |_{x=(x^*,0)}=(\alpha _1,\gamma _1,\eta _1){\hat{A}}^{-1}(-\alpha _1x_1^*,-\gamma _2x^*_2, \eta _1x_3+{\bar{\gamma }} x_2)^T \end{aligned}$$

Let us evaluate $\varTheta$ and check that $\varTheta \ne 0$. First we observe the equality

$$\begin{aligned} \left( \begin{array}{llll} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \end{array} \right) B(y^*,{\hat{K}}_2) \left( \begin{array}{llll} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \end{array} \right) = \left( \begin{array}{llll} &{} \quad &{}\quad &{}\quad -\alpha _1 \\ &{}\quad {\hat{A}} &{} \quad &{}\quad -\gamma _2 \\ &{} \quad &{}\quad &{}\quad \eta _1+\bar{\gamma }x^*_2/x_3^* \\ \,\alpha _1 \,&{}\quad -\gamma _1\,&{}\quad \eta _1\, &{}\quad 0 \end{array} \right) \nonumber \\ \end{aligned}$$

(37)

In the same way as in Sect. 3.1 we get

$$\begin{aligned} \varTheta ={\hat{K}}_2 \frac{\frac{\partial P(S)}{\partial S}\big |_{S={\hat{S}}_2}}{\det ({\hat{A}})I_{12}} \end{aligned}$$

which along with

$$\begin{aligned} \det ({\hat{A}}({\hat{K}}_2))=\left| \begin{matrix} -\frac{r}{{\hat{K}}_2} &{}\quad -\alpha _2 &{}\quad -\alpha _3 \\ \alpha _2 &{}\quad 0 &{}\quad -\eta _2 \\ \alpha _3 &{}\quad \eta _2 &{}\quad 0 \end{matrix} \right| =-\eta _2^2\frac{r}{{\hat{K}}_2} \end{aligned}$$

Next, since $f(x^*,0;0)=0$, we have

$$\begin{aligned} f(\xi (s),0;s)=\frac{s}{\eta _2}\Big (1-\frac{1}{\eta _2^*}\Big )\Big (\varDelta _\alpha -\gamma _1\alpha _3\Big ). \end{aligned}$$

Now applying (72) we get

$$\begin{aligned} x_4=\frac{1}{\eta _2}\Big (1-\frac{1}{\eta _2^*}\Big )\Big (\varDelta _\alpha -\gamma _1\alpha _3\Big )\frac{1}{\varTheta }s+O(s^2), \end{aligned}$$

which is equivalent to (36). To prove local stability let us consider the matrix

$$\begin{aligned} {{\mathcal {B}}}=\left( \begin{matrix} A &{} \partial _{x_n}F(x^*,0;0) \\ 0 &{} 0 \end{matrix}\right) . \end{aligned}$$

Since the matrix A is stable the matrix ${{\mathcal {B}}}$ has three eigenvalues with negative real part and one eigenvalue zero. The eigenvalues of the Jacobian matrix

$$\begin{aligned} {{\mathcal {J}}}(s)=\left( \begin{matrix} \nabla _{x'}F(\hat{x}(s);s) &{} \partial _{x_n}F(\hat{x}(s);s) \\ \nabla _{x'}(x_nf(x'))|_{x=\hat{x}(s)} &{} f(\hat{x}') \end{matrix}\right) \end{aligned}$$

are small perturbation of the eigenvalue of ${{\mathcal {B}}}={{\mathcal {J}}}(s)$. Therefore three of them have negative real part for small s and the last one $\lambda (\hat{x}(s))$, which is a perturbation of the zero eigenvalue of ${{\mathcal {B}}}$, has the following asymptotics (see (73) in Appendix B)

$$\begin{aligned} \lambda (\hat{x}(s))=-\frac{d}{ds}f(\xi (s),0;s)|_{s=0}s+O(s^2) =-\frac{s}{\eta _2}\Big (1-\frac{1}{\eta _2^*}\Big )\Big (\varDelta _\alpha -\gamma _1\alpha _3\Big )+O(s^2) \end{aligned}$$

and hence it is negative for small positive s. This proves the local stability of the coexistence equilibrium point. $\square$

3.3 Equilibrium transition for coexistence equilibrium points

Lemma 4

Let the assumption (14) be valid. If there exists a coexistence equilibrium point then

• (i)
  $$\begin{aligned} \eta _1^*>\eta _2^*\;\;\text{ and }\;\; \eta _1^*>1 \end{aligned}$$

  and this point lies on the branch of coexistence eq. points which starts at $K={\hat{K}}_1$ at the bifurcation point $\hat{G}_6$. Moreover

• (ii) if additionally $\eta _1^*>\eta _2^*>1$ then the above branch is finished at $K={\hat{K}}_2$ at the point $\hat{G}_7$.

• (iii) If $\eta _1^*>1>\eta _2^*$ then the above branch can be continued up to $K=\infty$.

Proof

Let us assume that there is a coexistence eq. point $G^*_8$ for $K=K^*$. Let $(K_1,K_2)$ be the maximal existence interval for existence of the branch $G_{111}(K)$ of coexistence equilibrium points containing $K^*$ and $G_{111}(K^*)=G^*_8$. According to Lemma 1 there exists a limit $G^*=\lim _{K\rightarrow K_1}G_{111}(K)$ and this limit is an equilibrium with at least one zero component. According Lemma 2 in [2] the only possible scenarios are either that $G^*=G_{101}$ and $\alpha _2S^* - \eta _2I_{12} - \gamma _2 I_1 - \mu _2 =0$ or that $G^*=G_{011}$ and $\alpha _1S-\eta _1I_{12}-\gamma _1 I_2-\mu _1=0$. This happens only if $G^*={\hat{G}}_{101}$ or $G^*={\hat{G}}_{011}$. The case $G^*=G_{010}$ is disregarded due to assumption (15). According to (25) with its associated comment we have that ${\hat{S}}_1>{\hat{S}}_2$ and $\eta ^*_1>\eta _2^*$. Since ${\hat{S}}_1>S_2$ and $\frac{\partial S}{\partial K}<0$ according to Lemma 1 deduce that $G^*={\hat{G}}_{101}$. From existence of ${\hat{G}}_{101}$ it follows that $\eta _1^*>1$ and we obtain (i).

If ${\hat{K}}_2$ is finite then there is a limit of $G_{111}(K)$ as $K\rightarrow {\hat{K}}_2$ and this limit lies on the boundary. Simple modification of the above arguments shows that this limit is $\hat{G}_7$ which gives (ii).

In the case (iii) there are no $\hat{G}_6$ or $\hat{G}_7$ and hence the branch can be continued for all $K>\hat{K}_1$. $\square$

When considering coexistence equilibrium points we assume that:

Assumption 2

• If $\eta _1^*>\eta _2^*$ and $\eta _1^*>1$ then $\partial _SP(\hat{S}_1)>0$ when $K=\hat{K}_1$;

• If $\eta _1^*>\eta _2^*>1$ then additionally to (i) it is supposed that $\partial _SP(\hat{S}_2)>0$ when $K=\hat{K}_2$.

Lemma 5

• (i) Let $\eta _1^*>\eta _2^*>1$ and $\partial _SP(\hat{S}_i)>0$ when $K=\hat{K}_i$, $i=1,2$. Then there is a branch of coexistence equilibrium points starting at $\hat{G}_6$, $K=\hat{K}_1$, and ending at $\hat{G}_7$, $K=\hat{K}_2$. All possible coexistence equilibrium points lies on this branch.

• (ii) Let $\eta _1^*>1>\eta _2^*$ and $\partial _SP(\hat{S}_1)>0$ when $K=\hat{K}_1$. There is a branch of coexistence equilibrium points starting at $\hat{G}_6$, $K=\hat{K}_1$, and defined for all $K>\hat{K}_1$. All possible coexistence equilibrium points lies on this branch.

Proof

• (i) By Lemma 3 there is a branch of coexistence equilibrium points ending at $\hat{G}_7$, $K=\hat{K}_2$ and defined for small $\hat{K}_2-K>0$. By Lemma 4 it can be continued to the interval $(\hat{K}_1,\hat{K}_2)$ and the limit when $K\rightarrow \hat{K}_1$ is equal to $\hat{G}_6$. If we take any coexistence equilibrium then by Lemma 4 it must lie on an equilibrium curve starting at $\hat{G}_6$. Then by uniqueness in Lemma 2 this curve must coincide with the coexistence equilibrium branch constructed in the beginning.

• (ii) In this case there is no bifurcation point $\hat{G}_7$ and the proof repeats with some simplifications the proof of (i).

$\square$

4 Stability of coexistence equilibrium points

4.1 Auxiliary assertion

Let Q and q be two positive constants. We introduce the set of $Y=(Y_1,Y_2,Y_3,Y_4)$

$$\begin{aligned} {{\mathcal {Y}}}=\{Y:Y_k\le Q \, \min ( Y_1,Y_4)\ge q,Y_2+Y_3\ge q,\;\min (Y_2, Y_3)\ge 0\}. \end{aligned}$$

Consider the matrix depending on the parameters Y and K:

$$\begin{aligned} {{\mathcal {M}}}={{\mathcal {M}}}(Y,K)=\mathrm{diag}(Y_1,Y_2,Y_3,Y_4)M,\;\;M=\left( \begin{matrix}-\frac{r}{K}&{}\quad -\alpha _1&{}\quad -\alpha _2&{}\quad -\alpha _3\\ \alpha _1&{}\quad 0&{}\quad 0&{}\quad -\eta _1\\ \alpha _2&{}\quad 0&{}\quad 0&{}\quad -\eta _2\\ \alpha _3&{}\quad \eta _1&{}\quad \eta _2&{}\quad 0 \end{matrix}\right) . \end{aligned}$$

Let also $\lambda _k=\lambda _k(Y,K)$, $k=1,2,3,4$, be their eigenvalues numerated according to the order $|\lambda _1|\ge |\lambda _2|\ge |\lambda _3|\ge |\lambda _4|$.

In the next lemma we give some more information about the first three eigenvalues.

Lemma 6

Let $0<K_1<K_2$. Then

$$\begin{aligned} \varXi =\max _{j=1,2,3}\max _{Y\in {{\mathcal {Y}}}}\max _{K_1\le K\le K_2} \mathfrak {R}\lambda _j(Y,K)<0. \end{aligned}$$

(38)

Proof

First assume that all components of Y are non-zero. Let $\lambda \in \mathbb {C}$ be an eigenvalue of ${{\mathcal {M}}}$, i.e.

$$\begin{aligned} {{\mathcal {M}}}X=\lambda X,\;\;X=(X_1,X_2,X_3,X_4)^T\in \mathbb {C}^4,\;\;X\ne 0. \end{aligned}$$

(39)

This implies

$$\begin{aligned} \mathfrak {R}({{\mathcal {M}}}X,D^{-1} X)=-\frac{r}{K}|X_1|^2=\mathfrak {R}\lambda (D^{-1}X,X), \end{aligned}$$

where $D=\mathrm{diag}(Y_1,Y_2,Y_3,Y_4)$ and $(\cdot ,\cdot )$ is the inner product in $\mathbb {C}^4$. Therefore

$$\begin{aligned} \mathfrak {R}\lambda =-\frac{r}{K}\frac{|X_1|^2}{(D^{-1}X,X)}. \end{aligned}$$

This gives $\mathfrak {R}\lambda \le 0$. Assume now that $\lambda =i\tau$, $\tau \in \mathbb {R}$, which implies $X_1=0$. Then (39) implies

$$\begin{aligned}&\alpha _1X_2+\alpha _2X_3+\alpha _3X_4=0\nonumber \\&\quad -\eta _1Y_2X_4=\lambda X_2,\;\;-\eta _2Y_3X_4=\lambda X_3\nonumber \\&Y_4(\eta _1X_2+\eta _2X_3)=\lambda X_4. \end{aligned}$$

(40)

If $\lambda =0$ then $X_4=0$ and from the first and last equations in (40) we get that $X_2=X_3=0$. If $X_4=0$ and $\lambda \ne 0$ then from the middle equations in (40) we obtain $X_2=X_3=0$. Consider the case when $\lambda \ne 0$ and $X_4\ne 0$. Expressing $X_2$ and $X_3$ through $X_4$ from the middle equations in (40) and putting them in the first equation, we get

$$\begin{aligned} X_4\Big (-\frac{\alpha _1\eta _1Y_2+\alpha _2\eta _2Y_3}{\lambda }+\alpha _3\Big )=0, \end{aligned}$$

which implies $X_4=0$. Thus we have shown that there are no eigenvalues of ${{\mathcal {M}}}$ on the imaginary line, i.e. $\mathfrak {R}\lambda _j<0$, $j=1,2,3,4$, provided all $Y_j$ ar positive.

Next consider the case $Y_2=0$. Then one eigenvalue of ${{\mathcal {M}}}$ is zero and the remaining three can be found from the eigenvalue problem

$$\begin{aligned} \mathbf{diag}(Y_1,Y_3,Y_4)\left( \begin{matrix}-\frac{r}{K}&{}\quad -\alpha _2&{}\quad -\alpha _3\\ \alpha _2&{}\quad 0&{}\quad -\eta _2\\ \alpha _3&{}\quad \eta _2&{}\quad 0 \end{matrix}\right) (X_1,X_3,X_4)^T=\lambda (X_1,X_3,X_4)^T. \end{aligned}$$

(41)

Similar to the eigenvalue problem (39) one can show that $\mathfrak {R}\lambda <0$ for (41).

The argument in the case $Y_3=0$ is the same as in the case $Y_2=0$. Thus we have shown that for all $(Y,K)\in {{\mathcal {Y}}}$, $\mathfrak {R}\lambda _j(Y,K)<0$, $j=1,2,3$. Since the eigenvalues continuously depend on (Y, K) and the set ${{\mathcal {Y}}}$ is compact, we arrive at (38). $\square$

4.2 Local stability in the case $\eta _1^*>\eta _2^*>1$

The main stability result for the equilibrium points branch in Lemma 6 is the following

Proposition 4

Let $\eta _1^*>\eta _2^*>1$ and $G_{111}(K)$, $\hat{K}_1\le K\le \hat{K}_2$ be the branch constructed in Lemma 5 (i). Then there exists a constant $\delta$ depending only on $\alpha _j$, $j=1,2,3$, and $\eta _1$, $\eta _2$ such that if $\bar{\gamma }\le \delta$ then all points on this branch for $\hat{K}_1< K<\hat{K}_2$ are locally stable.

Proof

Consider equilibrium points $G_{111}(K)=(S(K),I_1(K),I_2(K),I_{12}(K))$, $K\in [\hat{K}_1,\hat{K}_2]$. By Corollary 2 of [2] and Lemma 5 all of the components are non-negative and bounded by a certain constant independent of K and $\gamma _1,\,\gamma _2$. Solving for S and $I_{12}$ in the second and third of (11) gives

$$\begin{aligned} S(K)=\frac{\varDelta _\mu }{\varDelta _\alpha }+O(\bar{\gamma }),\;\;I_{12}(K)=\frac{\alpha _1\alpha _2(\sigma _2-\sigma _1)}{\varDelta _\alpha } +O(\bar{\gamma }). \end{aligned}$$

(42)

Furthermore, from the last equation in (11) we get

$$\begin{aligned} \eta _1I_1+\eta _2I_2=\alpha _3(\sigma _3-S)-\bar{\gamma }\frac{I_1I_2}{I_{12}} \end{aligned}$$

which implies due to (42)

$$\begin{aligned} \eta _1I_1+\eta _2I_2=\frac{rA_1A_2(\eta _1^*-\eta _2^*)}{\alpha _3\varDelta _\alpha }+O(\bar{\gamma }). \end{aligned}$$

We will keep the notation ${{\mathcal {Y}}}$ for our case ($Y=(S,I_1,I_2,I_{12})$), where

$$\begin{aligned} q= & {} \frac{1}{2}\min \Bigg (\frac{\varDelta _\mu }{\varDelta _\alpha },\frac{\alpha _1\alpha _2(\sigma _2-\sigma _1)}{\varDelta _\alpha }, \frac{1}{\min (\eta _1,\eta _2)}\frac{rA_1A_2(\eta _1^*-\eta _2^*)}{\alpha _3\varDelta _\alpha }\Bigg ), \\ Q= & {} \max \Big (\sigma _3,\frac{r}{\sigma _1}\Big ), \end{aligned}$$

and $\bar{\gamma }$ is kept sufficiently small. Then we can use Lemma 6, where $K_j=\hat{K}_j$, $j=1,2$.

We introduce two subsets of ${{\mathcal {Y}}}\times [\hat{K}_1,\hat{K}_2]$. The first one $\hat{{\mathcal {Y}}}_1$ consists of all $(Y;K)\in {{\mathcal {Y}}}\times [\hat{K}_1,\hat{K}_2]$ such that $\mathfrak {R}\lambda _1\ge \varXi /2$, where $\varXi$ is the constant from Lemma 6 (in our case it depends only on $\alpha _j$, $j=1,2,3,$ and $\eta _1$, $\eta _2$. The second set $\hat{{\mathcal {Y}}}_2$ consists of all $(Y;K)\in {{\mathcal {Y}}}\times [\hat{K}_1,\hat{K}_2]$ such that $\mathfrak {R}\lambda _1\le \varXi /2$. Introduce the contours

$$\begin{aligned} \varGamma _1=\{\lambda \in \mathbb {C}:\mathfrak {R}\lambda =\varXi /4, |\mathfrak {I}\lambda |\le C,\;\lambda -\varXi /4=Ce^{i\varphi },\varphi \in (\pi /2,3\pi /2)\} \end{aligned}$$

and

$$\begin{aligned} \varGamma _2=\{\lambda \in \mathbb {C}:\mathfrak {R}\lambda =3\varXi /4, |\mathfrak {I}\lambda |\le C,\;\lambda -3\varXi /4=Ce^{i\varphi },\varphi \in (\pi /2,3\pi /2)\}, \end{aligned}$$

where C is sufficiently large. Put

$$\begin{aligned} a_k=\max _{\hat{{\mathcal {Y}}}_k}\max _{\lambda \in \varGamma _k}||({{\mathcal {M}}}-\lambda )^{-1}||,\;\;k=1,2. \end{aligned}$$

By Lemma 6 there are at least 3 eigenvalues of ${\mathcal {M}}$ with $\mathfrak {R}\lambda \le \varXi$ Consider two cases (i) the remaining eigenvalue satisfies $\mathfrak {R}\lambda <\frac{5}{8}\varXi$ or (ii) it satisfies $\mathfrak {R}\lambda \ge \frac{5}{8}\varXi$. Since the norm of the matrix

$$\begin{aligned} {\mathcal {N}}=\mathrm {diag}(S,I_1,I_2,I_{12})\left( \begin{matrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\gamma _1 &{}\quad 0 \\ 0 &{}\quad -\gamma _2 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {\bar{\gamma }} r_2 &{}\quad {\bar{\gamma }} r_1 &{}\quad -{\bar{\gamma }} r_1 r_2 \end{matrix}\right) \end{aligned}$$

is estimated by $C_1{\bar{\gamma }}$ with $C_1$ independent on $\gamma$ and K we conclude that by Rouche’s theorem the number of eigenvalues inside $\varGamma _2$ of the matrix ${\mathcal {M}}$ and $\mathcal {M+N}$ is the same for small ${\bar{\gamma }}$ in the case (i). Similarly we have that in the case (ii) the number of eigenvalues of ${\mathcal {M}}$ and $\mathcal {M+N}$ is the same inside the contour $\varGamma _1$ for small ${\bar{\gamma }}$ and this number is equal to 4.

This implies that for small $\bar{\gamma }$ there are at least three eigenvalues of the Jacobian matrix $J_8$ with negative real part on the branch $G_{111}(K)$. Since

$$\begin{aligned} \det J_8(G_{111}(K))>0 \quad \text { for }K\in (\hat{K}_1,\hat{K}_2) \end{aligned}$$

we conclude that all eigenvalues of $J_8(G_{111}(K))$ must have negative real part. This proves the proposition. $\square$

4.3 Instability for large K

In this section we assume that

$$\begin{aligned} \eta _1^*>1>\eta _2^*. \end{aligned}$$

(43)

According to Lemma 5 there exists a branch $G_{111}(K)$, $K\in [\hat{K}_1,\infty )$, of coexistence equilibrium points starting from $G_{111}( \hat{K}_1)=\hat{G}_6$. For $K=\infty$ and $\gamma =0$ the interior point has the coordinates

$$\begin{aligned} G_{111} (\infty )|_{\gamma =0}= (S^*,I_1^*,I^*_2,I^*_{12})=\Big (\frac{\varDelta _\mu }{\varDelta _\alpha },\frac{r}{\varDelta _\alpha }(A_2-\eta _2), \frac{r}{\varDelta _\alpha }(\eta _1-A_1),\frac{r}{\varDelta _\alpha }A_3\Big ). \end{aligned}$$

All eigenvalues of the corresponding Jacobian matrix lie on the imaginary axis.

For $K=\infty$ and small $\gamma >0$ the interior point has the coordinates $G_\infty (\gamma )= G_\infty (0)+O(|\gamma |)$, where $\gamma =(\gamma _1,\gamma _2)$. Our goal is to analyze the location of eigenvalues of the Jacobian matrix when $\gamma$ is small.

The characteristic polynomial of the Jacobian matrix of the interior point is (up to a positive factor)

$$\begin{aligned} \frac{1}{SI_1I_2I_{12}} \det (J_8-\lambda I)=p(\lambda ){:}{=}\left| \begin{matrix} -\frac{\lambda }{S} &{} -\alpha _1 &{} -\alpha _2 &{} -\alpha _3 \\ \alpha _1 &{} -\frac{\lambda }{I_1} &{} -\gamma _1 &{} -\eta _1 \\ \alpha _2 &{} -\gamma _2 &{} -\frac{\lambda }{I_2} &{} -\eta _2 \\ \alpha _3 &{}\quad \eta _1+{\bar{\gamma }} r_2 &{}\quad \eta _2+{\bar{\gamma }} r_1 &{}\quad -{\bar{\gamma }} r_1r_2-\frac{\lambda }{I_{12}} \end{matrix}\right| \end{aligned}$$

where $r_i$ are defined in (12). It is clear that the polynomial p is monic. The necessary condition for stability of the polynomial p is the positivity of all its coefficients. Let us evaluate the coefficient $p_1$ of the $\lambda$ term and show that it can be negative for certain choice of parameters (we note that for $\gamma =0$ this coefficient is zero). This will imply that some of all eigenvalues must have positive real part. We have

$$\begin{aligned} p_1&=- \left( \frac{1}{S} \left| \begin{matrix} 0 &{} -\gamma _1 &{} -\eta _1 \\ -\gamma _2 &{} 0 &{} -\eta _2 \\ \eta _1+{\bar{\gamma }} r_2 &{}\quad \eta _2+{\bar{\gamma }} r_1 &{}\quad -{\bar{\gamma }} r_1r_2 \end{matrix}\right| +\frac{1}{I_1} \left| \begin{matrix} 0 &{} -\alpha _2 &{} -\alpha _3 \\ \alpha _2 &{} 0 &{} -\eta _2 \\ \alpha _3 &{}\quad \eta _2+{\bar{\gamma }} r_1 &{}\quad -{\bar{\gamma }} r_1r_2 \end{matrix} \right| \right. \\&\qquad \left. +\frac{1}{I_2}\left| \begin{matrix} 0 &{} -\alpha _1 &{} -\alpha _3 \\ \alpha _1 &{} 0 &{}-\eta _1 \\ \alpha _3 &{}\quad \eta _1+{\bar{\gamma }} r_2 &{}\quad -{\bar{\gamma }} r_1r_2 \end{matrix} \right| +\frac{1}{I_{12}} \left| \begin{matrix} 0 &{}\quad -\alpha _1 &{}\quad -\alpha _2 \\ \alpha _1 &{} 0 &{} -\gamma _1 \\ \alpha _2 &{} -\gamma _2 &{} 0 \end{matrix} \right| \right) \\&\quad ={\bar{\gamma }}\left( -\frac{ \eta _1\eta _2}{S} + \frac{ r_1\alpha _2(\alpha _3+\alpha _2r_2)}{I_1} +\frac{ \alpha _1r_2(\alpha _1r_1+\alpha _3)}{I_2}-\frac{ \alpha _1\alpha _2}{I_{12}} \right) +O({\bar{\gamma }}^2) \\&\quad ={\bar{\gamma }}\left( -\frac{ \eta _1\eta _2}{S} + \frac{ \alpha _2(\alpha _3+\alpha _2r_2)+\alpha _1(\alpha _1r_1+\alpha _3)-\alpha _1\alpha _2}{I_{12}} \right) +O({\bar{\gamma }}^2) \end{aligned}$$

Plugging in the values of $S,I_{12},r_1,r_2,$ for $K=\infty$ and $\gamma =0$ we continue the above equalities

$$\begin{aligned} p_1&= {\bar{\gamma }}\varDelta _\alpha \left( -\frac{\eta _1\eta _2 }{\varDelta _\mu }+\frac{(\alpha _2+\alpha _1)\alpha _3-\alpha _1\alpha _2}{rA_3}+\frac{\alpha _2^2(\eta _1-A_1)+\alpha _1^2(A_2-\eta _2)}{rA_3^2}\right) +O(\gamma ^2) \\&= {\bar{\gamma }}\varDelta _\alpha \left( -\frac{\eta _1\eta _2}{\varDelta _\mu }+\frac{\alpha _2^2\eta _1-\alpha _1^2\eta _2}{rA_3^2}+\frac{(\alpha _2+\alpha _1)\alpha _3-\alpha _1\alpha _2}{rA_3}+\frac{\alpha _1^2A_2-\alpha _2^2A_1}{rA_3^2}\right) +O(\gamma ^2) \end{aligned}$$

with

$$\begin{aligned}&b-\mu _0=1\\&\mu _i=1\\&\alpha _1=10,\;\alpha _2=9.9,\;\alpha _3=1, \end{aligned}$$

(2) and (4) is satisfied and we get

$$\begin{aligned} A_1&=9 \\ A_2&=0.1 \\ A_3&=8.9. \end{aligned}$$

We can now choose $\eta _1$ and $\eta _2$ such that $\eta _1*>1>\eta _2^*$ and $\eta _1^*,\eta _2^*\approx 1$. For these values Lemma 4 tells us that there exists a coexistence equilibrium branch defined for infinitely large K. On the other hand the coefficient of the $\lambda ^1$ term is approximately

$$\begin{aligned} SI_1I_2I_{12}\gamma \varDelta _\alpha \left( -\frac{10*9.9}{0.1}+\frac{19.9-9.9}{0.1}+0\right) =SI_1I_2I_{12}\gamma \varDelta _\alpha (-890)<0 \end{aligned}$$

and so when K is sufficiently large and $\gamma$ is sufficiently small this equilibrium branch is unstable.

4.4 Hopf bifurcation

In this section we assume that (43) is satisfied. Thus there exists a branch of coexistence equilibrium points $G_{111}(K)$ defined for $K>\hat{K}_1$. We assume also that the parameters $\alpha _1,\,\alpha _2,\,\alpha _3$ and $\eta _1,\,\eta _2$ are chosen such that the stability is lost when $K{\bar{\gamma }}$ is large. Since the point $G_{111}(K)$ is stable when K is close to ${\hat{K}}_1$ there exists a point $K=K_c$ where the local stability of $G_{111}$ is lost. Since the trace of the Jacobian matrix is always negative the eigenvalues can only reach the imaginary axis in pairs. If we assume that the derivative of their real part at $K=K_c$ is positive then there is a simple Hopf bifurcation so for K close to $K_c$ there are periodic oscillations, see [9]. We also mention that the loss of stability by the positive equilibrium when the carrying capacity of the resource is increased is a well-established ecological phenomenon called the paradox of enrichment dating back to the works of Rosenzweig [10]. We discuss this in more details in a forthcoming work.

4.5 Local stability in the case $\eta _1^*>1>\eta _2^*$

Theorem 2

Let $\eta _1^*>1>\eta _2^*$ and let $G_{111}(K)$, $K\in (\hat{K}_1,\infty )$ be the branch of equilibrium points starting at $\hat{G}_6$. There exists a constant $\omega >0$ depending on $\alpha _1,\alpha _2,\alpha _3$ and $\eta _1,\eta _2$ such that if $K{\bar{\gamma }}\le \omega$ for $K\in (\hat{K}_1,\infty )$, then the inner equilibrium points $G_{111}(K)$ are locally stable.

Proof

In what follows in the proof we will denote by c and C, possibly with indexes, various positive constants depending on $\alpha _1,\,\alpha _2,\,\alpha _3$ and $\eta _1,\,\eta _2$. The Jacobian matrix is equal to $J_8(K)=D(A+K+\varGamma )$, where $D=\mathrm{diag}(S,I_1,I_2,I_{12})$,

$$\begin{aligned}&K\!=\!\left( \begin{matrix} -\frac{r}{K} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -{\bar{\gamma }} r_1r_2 \end{matrix}\right) ,\;\; A\!=\!\left( \begin{matrix} 0 &{}\quad -\alpha _1 &{}\quad -\alpha _2 &{}\quad -\alpha _3 \\ \alpha _1 &{}\quad 0 &{}\quad 0 &{}\quad -\eta _1 \\ \alpha _2 &{}\quad 0 &{}\quad 0 &{}\quad -\eta _2 \\ \alpha _3 &{}\quad \eta _1 &{}\quad \eta _2 &{}\quad 0 \end{matrix} \right) ,\\&\varGamma \!=\!\left( \begin{matrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -\gamma _1 &{}\quad 0 \\ 0 &{}\quad -\gamma _2 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {\bar{\gamma }} r_2 &{}\quad {\bar{\gamma }} r_1 &{}\quad 0 \end{matrix} \right) \end{aligned}$$

Consider the eigenvalue problem

$$\begin{aligned} D(A+K+\varGamma )u=\lambda u. \end{aligned}$$

(44)

If $\gamma =0$ then the eigenvalue of this problem lie in the half-plane $\mathfrak {R}\lambda <0$. If we show that the are no eigenvalues of (44) with $\lambda =i\tau$, $\tau \in \mathbb {R}$, for all $\gamma$ and K satisfying $K\bar{\gamma }\le \omega$ then by continuity argument for eigenvalues we obtain the required result. Therefore let us assume that one of eigenvalues has the form $\lambda =i\tau ,\;\tau \in {\mathbb {R}}$ and that no eigenvalue has positive real part. We will now show that the problem (44) has only the trivial solution. For large K and small $\gamma$ (say $K\ge K_*$ and $\bar{\gamma }\le \bar{\gamma _*}$) we have

$$\begin{aligned} G_{111}(K)=\Big (\frac{\varDelta _\mu }{\varDelta _\alpha },\frac{r}{\varDelta _\alpha }(A_2-\eta _2), \frac{r}{\varDelta _\alpha }(\eta _1-A_1),\frac{r}{\varDelta _\alpha }A_3\Big )+O(\bar{\gamma } +K^{-1}). \end{aligned}$$

(45)

Therefore

$$\begin{aligned} c\le S\le C,\,\;c\le I_1\le C,\;\;c\le I_2\le C,\;\;c\le I_{12}\le C, \end{aligned}$$

(46)

where C and c are positive constants depending on $\alpha$ and $\eta$. Furthermore, the Jacobian matrix at the point (45) is

$$\begin{aligned} D\left( \begin{matrix}0&{}\quad -\alpha _1&{}\quad -\alpha _2&{}\quad -\alpha _3\\ \alpha _1&{}\quad 0&{}\quad 0&{}\quad -\eta _1\\ \alpha _2&{}\quad 0&{}\quad 0&{}\quad -\eta _2\\ \alpha _3&{}\quad \eta _1&{}\quad \eta _2&{}\quad 0 \end{matrix}\right) +O(\bar{\gamma }+K^{-1}) \end{aligned}$$

and therefore,

$$\begin{aligned} \det J_8(K)=SI_1I_2I_{12}\varDelta _\alpha ^2+O(\bar{\gamma }+K^{-1}). \end{aligned}$$

Thus we may assume that $\det J_8(K)\ge c_1>0$. This fact together with (46) gives

$$\begin{aligned} 0<c_2\le | \lambda _j(K){|\le c_3},\;\;j=1,2,3,4,\;\;K\ge K_*\;\;{{\bar{\gamma }} \le {\bar{\gamma }}_*}, \end{aligned}$$

where $\lambda _j(K)$, $j=1,2,3,4$, are eigenvalues of $J_8(K)$.

Assume that $\lambda =i\tau ,$ $c_2\le \tau \le c_3$ is an eigenvalue to $J_8$. We will now show that this leads to a contradiction. Multiplying both sides of (44) by $D^{-1}{\bar{u}}$ and taking the real part and using that $\mathfrak {R}(Au,u)=0$ we get $=\mathfrak {R}((K+\varGamma )u,u)=0$ or

$$\begin{aligned} -\frac{r}{K}|u_1|^2&-{\bar{\gamma }} r_1r_2|u_4|^2 -\gamma _1\mathfrak {R}(u_3{\bar{u}}_2)-\gamma _2 \mathfrak {R}(u_2{\bar{u}}_3)\nonumber \\&+ {\bar{\gamma }}\mathfrak {R}\{(r_2u_2+r_1u_3){\bar{u}}_4\}=0 \end{aligned}$$

(47)

Let us derive some relations between $u_1,u_2,u_3$ and $u_4$. From the first three equations in (44) we obtain

$$\begin{aligned}&S\left( -\frac{r}{K}u_1-\alpha _1u_2-\alpha _2u_3-\alpha _3u_4\right) =i\tau u_1 \nonumber \\&I_1(\alpha _1u_1-\gamma _1u_3-\eta _1u_4)=i\tau u_2 \nonumber \\&I_2(\alpha _2u_1-\gamma _2u_2-\eta _2u_4)=i\tau u_3 \end{aligned}$$

(48)

We rewrite the last two equations as

$$\begin{aligned} i\tau u_2+\gamma _1I_1u_3&=\alpha _1I_1u_1-\eta _1I_1u_4 \\ i\tau u_3+\gamma _2I_2u_2&=\alpha _2I_2u_1-\eta _2I_2u_4 \end{aligned}$$

and solving them we obtain

$$\begin{aligned}&u_2=\frac{(-i\tau \alpha _1I_1+\alpha _2\gamma _1I_1I_2)u_1-(\eta _2\gamma _1I_1I_2-i\tau \eta _1I_1)u_4}{\tau ^2+\gamma _1\gamma _2I_1I_2} \end{aligned}$$

(49)

$$\begin{aligned}&u_3=\frac{(\alpha _1\gamma _2I_1I_2-i\tau \alpha _2I_2)u_1 -(\eta _1\gamma _2I_1I_2-i\tau \eta _2I_2)u_4}{\tau ^2+\gamma _1\gamma _2I_1I_2}. \end{aligned}$$

(50)

Inserting these relations in (48) we get

$$\begin{aligned}&u_1\left( \frac{i\tau }{S}+\frac{r}{K}+\alpha _1\frac{-i\tau \alpha _1I_1+\alpha _2\gamma _1I_1I_2}{\tau ^2+\gamma _1\gamma _2I_1I_2}+ \alpha _2\frac{\alpha _1\gamma _2I_1I_2-i\tau \alpha _2I_2}{\tau ^2+\gamma _1\gamma _2I_1I_2}\right) \\&\quad =u_4\left( -\alpha _3+\alpha _1\frac{-i\tau \eta _1I_1+\eta _2\gamma _1I_1I_2}{\tau ^2+\gamma _1\gamma _2I_1I_2}+\alpha _2\frac{\eta _1\gamma _2I_1I_2-i\tau \eta _2I_2}{\tau ^2+\gamma _1\gamma _2I_1I_2}\right) \end{aligned}$$

This leads to

$$\begin{aligned} |u_4|\le C_3|u_1| \end{aligned}$$

(51)

The relations (49) and (50) together with (51) gives

$$\begin{aligned} |u_2|,\;|u_3|\le C_4|u_1| \end{aligned}$$

Now (47) implies that

$$\begin{aligned} -\frac{r}{K}|u_1|^2+C_1\bar{\gamma }|u_1|^2=0. \end{aligned}$$

This is impossible if $C_1$ is sufficiently small. Thus the local stability of $G_{111}(K)$, ${K}\ge K_*$, is proved.

The local stability of $G_{111}(K)$ for $K\in (\hat{K}_1,K_*]$ is proved in the same manner as in the proof of Proposition 4. $\square$

5 Equilibrium transition with increasing K

In this section we finalize our results in two theorems describing the equilibrium branch for the sets of parameter $\eta _1^*>\eta ^*_2>1$ and $\eta _1^*>1>\eta ^*_2$.

5.1 Equilibrium transition when $\eta _1^*>\eta _2^*>1$

In this section we will prove that there exist an equilibrium branch $G_{000}\rightarrow G_{100} \rightarrow G_{101} \rightarrow G_{111} \rightarrow G_{011}\rightarrow G_{001}$ in the case $\eta _1^*>\eta _2^*>1$. By Corollary 5 in [2] we know that for these parameters there is an equilibrium branch

$$\begin{aligned} G_{000}\rightarrow G_{100} \rightarrow G_{101} \rightarrow \ldots \end{aligned}$$

Furthermore from Sect. 3.1 we know the this branch continues onto $G_{111}$ at $K=K_1$. From Sects. 2.2 and 3.2 in this paper as well as Theorem 1 from [2], we get that there exist an equilibrium branch

$$\begin{aligned} \ldots \rightarrow G_{111}\rightarrow G_{011}\rightarrow G_{001}. \end{aligned}$$

One could suspect that these two equilibrium branches are the two parts of a complete equilibrium branch. We shall now prove that indeed that is the case.

Theorem 3

Let (14), (21) and Assumption 2 hold and let $\eta _1^*>\eta _2^*>1$. Then there exists a unique branch of equilibrium points $G^*(K)$ parameterised by $K\in (0,\infty )$:

(a):

For $0< K\le \sigma _1$ the point $G^*(K)$ is of type $G_{000}$

(b):

For $\sigma _1<K\le \frac{\sigma _1\eta _1^*}{\eta ^*_1-1}$ the point $G^*(K)$ is of type $G_{100}$;

(c):

For $\frac{\sigma _1\eta ^*_1}{\eta ^*_1-1}<K\le \frac{{\hat{S}}_1\eta _1^*}{\eta ^*_1-1}$ the point $G^*(K)$ is of type $G_{101}$;

(d):

For $\frac{{\hat{S}}_1\eta _1^*}{\eta _1^*-1}< K<\frac{{\hat{S}}_2\eta _2^*}{\eta _2^*-1}$ the point $G^*(K)$ is of type $G_{111}$;

(e):

For $\frac{{\hat{S}}_2\eta _2^*}{\eta _2^*-1}\le K<\frac{\sigma _3\eta _2^*}{\eta _2^*-1}$ the point $G^*(K)$ is of type $G_{011}$;

(f):

For $K\ge \frac{\sigma _3\eta _2^*}{\eta _2^*-1}$ the point $G^*(K)$ is of type $G_{001}$.

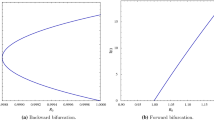
we display this schematically as (see Fig. 1)

$$\begin{aligned} G_{000}\rightarrow G_{100} \rightarrow G_{101} \rightarrow G_{111} \rightarrow G_{011} \rightarrow G_{001}. \end{aligned}$$

(52)

The point $G^*(K)$ is locally stable whenever it is not a coexistence point. It is also locally stable near the end on the interval ${\hat{K}}_1<K< {\hat{K}}_2$ and it is locally stable on the whole interval if ${\bar{\gamma }}$ is small

Proof

This theorem follow from Lemma 4 and Proposition 4 in Sect. 4.2$\square$

Fig. 1

This graphs gives the idea of how the $S^*$ component of the equilibrium branch changes with K and shows the type of the equilibrium point. The function $S^*(K)$ is a piecewise linear function except in the interval $\frac{S_1\eta ^*_1}{\eta ^*_1-1}<K<\frac{S_1\eta ^*_2}{\eta ^*_2-1}$ where it is strictly decreasing. Note that the order of the elements on both axis is correct

5.2 Equilibrium transition when $\eta _1^*>1>\eta _2^*$

In this section we will prove that there exist an equilibrium branch ${\hat{G}}_{000}\rightarrow {\hat{G}}_{100} \rightarrow {\hat{G}}_{101} \rightarrow {\hat{G}}_{111}$ in the case $\eta _1^*>1>\eta _2^*$. By Corollary 5 in [2] we know that for these parameters there is an equilibrium branch

$$\begin{aligned} {\hat{G}}_{000}\rightarrow {\hat{G}}_{100} \rightarrow {\hat{G}}_{101} \rightarrow \ldots \end{aligned}$$

Furthermore from Sect. 3.1 we know the this branch continues onto $G_{111}$ at $K={\hat{K}}_1$. We are left to prove that this equilibrium does persists.

Theorem 4

Let (14), (21) and Assumption 2 hold and let $\eta _1^*>1>\eta _2^*$. Then there exists a unique branch of equilibrium points $G^*(K)$ parameterised by $K\in (0,\infty )$:

(a):

For $0<K\le \sigma _1$ the point $G^*(K)$ is of type $G_{000}$

(b):

For $\sigma _1<K\le \frac{\sigma _1\eta _1^*}{\eta ^*_1-1}$ the point $G^*(K)$ is of type $G_{100}$

(c):

For $\frac{\sigma _1\eta ^*_1}{\eta ^*_1-1}<K\le \frac{{\hat{S}}_1\eta _1^*}{\eta ^*_1-1}$ the point $G^*(K)$ is of type $G_{101}$;

(d):

For $K>\frac{{\hat{S}}_1\eta _1^*}{\eta _1^*-1}$ the point $G^*(K)$ is of type $G_{111}$;

We display this schematically as (see Fig. 2)

$$\begin{aligned} {\hat{G}}_{000}\rightarrow {\hat{G}}_{100} \rightarrow {\hat{G}}_{101} \rightarrow {\hat{G}}_{111}. \end{aligned}$$

(53)

The point $G^*(K)$ is locally stable whenever it is not a coexistence point. It is also locally stable near the left end on the interval ${{\hat{K}}}_1<K<\infty$ and it is locally stable if $K{\overline{\gamma }}$ is small.

Proof

This theorem follow from Lemma  4 and Theorem 2 in Sect. 4.5. $\square$

Fig. 2

This graphs gives the idea of how the $S^*$ component of the equilibrium branch changes with K and shows the type of the equilibrium point. The function $S^*(K)$ is a piecewise linear function except when $K>\frac{S_1\eta ^*_1}{\eta ^*_1-1}$ where it is strictly decreasing and converging to a value between ${\hat{S}}_1$ and ${\hat{S}}_2$. Note that the order of the elements on both axis is correct

6 Some concluding remarks

Below we briefly comment on our results from the biological point of view. We start from $K=0$ and reason how the dynamics changes as K increases. For small carrying capacity K the susceptible population will be kept so low that the likelihood of an infected individual spreading its disease will be too low (below 50% ) for any disease to spread. As K increases the stable susceptible population increase.

When the stable susceptible population reaches $\sigma _1$, any increase in $S^*$ due to increased K will result in the disease 1 with highest transmission rate to be able to spread. But it can only spread until the susceptible population is equal to $\sigma _1$. So from now on $S^*=\sigma _1$ and an increases in K gives an increase of $I^*_1$ . Disease 2, with lower transmission rates then disease 1, can not spread since it is outcompeted by disease 1.

The disease 2 can however spread through the population of infected with disease 1. Under the condition $\frac{\sigma _1\eta _1^*}{\eta _1^*-1}<K<\frac{\min (\sigma _2,{{\hat{S}}_1})\eta _1^*}{\eta _1^*-1}$ the sum of susceptibles and infected of disease 1 will be so high that disease 2 can spread. However disease 2 will only occur as a coinfection in the stable state. This is a result of the fact that we assume that coinfected individuals can only spread both disease simultaneously. The single infections of disease 2 are either outcompeted by disease 1 or they become part of the coinfected compartment. For these K the compartment of single infected of disease 1 will decrease with K. This does however not mean that disease 1 becomes less prevalent, only that it occurs more as a coinfection. The susceptibles increase for these K. This is a consequence of the assumption of the coinfection being less transmissible then single infection. When the coinfection rises the average transmission rate of the diseases decrease allowing the susceptible population to increase.

For the parameters dealt with in this paper ($\eta ^*_1>1$) it will happen that as the average transmission rate of the disease decrease eventually single infection of disease 2 will be more transmissible then disease 1 and the coinfection and will thus be able to spread as a single infection giving rise to a stable coexistence point. From there either the equilibrium point stays as a coexistence point for all large K or the single infections starts to only occur in coinfections, with disease 1 being the first to stop occurring as a single infection. The susceptible population can only increase to $\sigma _3$ at which point any increase in susceptibles would even be absorbed be the least transmittable compartment (coinfection). The sick population can by assumption not reproduce and so it must also have an upper bound. If this upper bound is large compared to $\sigma _3$ we will have a situation where a large proportion of the population is sick making coinfection far more likely to occur then single infections resulting in the diseases only occuring as coinfection. while the overall sick population can increase indefinitely. So when K is large enough the number of sick individuals will be far more then the susceptibles making coinfections far more likely to occur then single infection leading to a stable state of coinfection with no single infections.

Appendices

Implicit function theorem

Let

$$\begin{aligned} {{\mathcal {F}}}:\mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}^n \end{aligned}$$

be a $C^2$ mapping. Let us consider the equation

$$\begin{aligned} {{\mathcal {F}}}(x,y)=0. \end{aligned}$$

(54)

We assume that

$$\begin{aligned} {{\mathcal {F}}}(0,0)=0\;\;\text{ and } \text{ that } \text{ the } \text{ matrix }\;\; A\,{:=}\,D_x{{\mathcal {F}}}(0,0)\;\;\text{ is } \text{ invertible }. \end{aligned}$$

Our aim is to find a solution to (54) $x=x(y)$ such that $x(0)=0$ and estimate the region where such solution exists. We fix positive numbers a and b and put

$$\begin{aligned} \varLambda =\varLambda _{a,b}=\{ (x,y)\,:\, |x|\le a,\;|y|\le b\}. \end{aligned}$$

Let also

$$\begin{aligned} B_a=\{x\,:\, |x|\le a\}. \end{aligned}$$

We introduce the quantities

$$\begin{aligned} M=\max _{\varLambda }||D_xD_x{{\mathcal {F}}}(x,y)||,\;\;M_1=\max _{\varLambda }||D_yD_x{{\mathcal {F}}}(x,y)||. \end{aligned}$$

Here the above norms are understood in the following sense

$$\begin{aligned} ||D_xD_x{{\mathcal {F}}}(x,y)||=\max _{|\zeta |,|\xi |=1}\left| \sum _{i,j=1}^n\partial _{x_i}\partial _{x_j}{{\mathcal {F}}}(x,y)\zeta _i\xi _j\right| \end{aligned}$$

Here $|\cdot |$ is the usual euclidian norm. We also introduce

$$\begin{aligned} L=\max _{\varLambda }||D_y{{\mathcal {F}}}(x,y)||, \end{aligned}$$

where

$$\begin{aligned} ||D_y{{\mathcal {F}}}(x,y)||=\max _{|\xi |=1}|D_y{{\mathcal {F}}}(x,y)\xi |. \end{aligned}$$

The following result is a well known implicit function theorem. We supply it with a short proof since we want to include in the formulation a quantitative information about the solution.

Theorem 5

If the constants a and b satisfies

$$\begin{aligned} ||A^{-1}||(Ma+M_1b)\le q\;\;\text{ and }\;\;||A^{-1}||\Big (Ma+M_1b+L\frac{b}{a}\Big )\le 1, \end{aligned}$$

(55)

where $q<1$ and $||A^{-1}||$ is the usual operator-norm of $A^{-1}$. Then there exists a $C^2$-function $x=x(y)$ defined for $|y|\le b$ which delivers all solutions to (54) from $\varLambda$.

Proof

We write (54) as a fixed point problem

$$\begin{aligned} x=F(x,y),\;\;\;\text{ where }\;\;F(x,y)=A^{-1}\big ( Ax-{{\mathcal {F}}}(x,y)\big ). \end{aligned}$$

(56)

Let us check that F maps $B_a$ into itself and that it is a contraction operator there.

To show the first property we note that

$$\begin{aligned} {{\mathcal {F}}}(x,y)=\int _0^1\frac{d}{dt}{{\mathcal {F}}}(tx,ty)dt=\int _0^1\sum _{i=1}^n \partial _{x_i}{{\mathcal {F}}}(tx,ty)x_i+\sum _{k=1}^m \partial _{y_k}{{\mathcal {F}}}(tx,ty)y_kdt. \end{aligned}$$

Therefore

$$\begin{aligned} F(x,y)=A^{-1}\int _0^1\Bigg (\sum _{i=1}^n(\partial _{x_i}{{\mathcal {F}}}(0,0)- \partial _{x_i}{{\mathcal {F}}}(tx,ty))x_i-\sum _{k=1}^m\partial _{y_k}{{\mathcal {F}}}(tx,ty)y_k\Bigg )dt. \end{aligned}$$

Since

$$\begin{aligned}&\partial _{x_i}{{\mathcal {F}}}(0,0)- \partial _{x_i}{{\mathcal {F}}}(tx,ty)=-\int _0^1 \frac{d}{d\tau }(\partial _{x_i}{{\mathcal {F}}})(\tau tx,\tau ty)d\tau \\&\quad =-\int _0^1\Bigg ( \sum _{j=1}^n\partial _{x_j}\partial _{x_i}{{\mathcal {F}}}(\tau tx,\tau ty)tx_j +\sum _{k=1}^m\partial _{y_k}\partial _{x_i}{{\mathcal {F}}}(\tau tx,\tau ty)y_k\Bigg )d\tau , \end{aligned}$$

we get

$$\begin{aligned}&|F(x,y)|\le |A^{-1}\int _0^1\int _0^1\sum _{i=1}^n\Bigg (-\sum _{j=1}^n\partial _{x_j}\partial _{x_i}{{\mathcal {F}}}(\tau tx,\tau y)tx_j\\&\quad +\sum _{k=1}^m\partial _{y_k}\partial _{x_i}{{\mathcal {F}}}(\tau tx,\tau y)y_k\Bigg )x_id\tau dt\\&\quad +\Big |\int _0^1\sum _{k=1}^m\partial _{y_k}F(tx,ty)y_kdt\Big | \le ||A^{-1}||\left( Ma+M_1b+L\frac{b}{a}\right) |a|<a, \end{aligned}$$

which guarantees that F maps $B_a$ on to itself.

For checking the contraction property we write

$$\begin{aligned}&|F(x_1,y)-F(x_2,y)|\\&\quad =|A^{-1}(A(x_1-x_2)-\int _0^1\frac{d}{dt}{{\mathcal {F}}}((x_2+t(x_1-x_2),y)dt| \\&\quad \le ||A^{-1}||\cdot \Big |\int _0^1\sum _{i=1}^n\partial _{x_i}{{\mathcal {F}}}(0,0)- \partial _{x_i}{{\mathcal {F}}}(x_2+t(x_1-x_2),y))(x_1-x_2)_idt\Big | \\&\quad \le ||A^{-1}||\int _0^1\Bigg ( \sum _{i,j}|\partial _{x_j}\partial _{x_i}{{\mathcal {F}}}(\tau (x_2+t(x_1-x_2),\tau y)tx_j(x_1-x_2)_i| \\&\qquad +|\sum _{i,k}\partial _{y_k}\partial _{x_i}{{\mathcal {F}}}(\tau (x_2+t(x_1-x_2),\tau y)y_k(x_1-x_2)_i|\Bigg )d\tau )dt \le q|x_1-x_2|, \end{aligned}$$

so F is a contraction and by the Banach fixed point theorem we can conclude that there exists a unique $c^1$-function $x=x(y)$ defined for $|y|\le b$. Since ${{\mathcal {F}}}\in C^2$ the same is true for x(y). $\square$

In the next assertion we present estimates of the derivatives of the solution x(y).

Theorem 6

The matrix $D_x{{\mathcal {F}}}(x,y)$ is invertible for all $(x,y)\in \varLambda$ and

$$\begin{aligned} |D_x{{\mathcal {F}}}(x,y)^{-1}|\le \frac{||A^{-1}||}{1-q}. \end{aligned}$$

(57)

Furthermore

$$\begin{aligned} |D_yx(y)|\le \frac{||A^{-1}||L}{1-q}, \end{aligned}$$

(58)

and

$$\begin{aligned} ||D_yD_yx||\le \frac{||A^{-1}||}{1-q}\left( M\frac{||A^{-1}||^2L^2}{(1-q)^2}+2N\frac{||A^{-1}||L}{1-q}+M_2\right) , \end{aligned}$$

(59)

where

$$\begin{aligned} N=\max _{\varLambda }||D_yD_xF(x,y)||,\;\;M_2=\max _{\varLambda }||D_yD_yF(x,y)||. \end{aligned}$$

Proof

With $B=D_x{{\mathcal {F}}}(x,y)$ we have $B^{-1}=A^{-1}(I+(B-A)A^{-1})^{-1})$, which gives (57) because

$$\begin{aligned} ||A^{-1}||||B-A||\le ||A^{-1}||(Ma+M_2b)\le q. \end{aligned}$$

Since

$$\begin{aligned} {{\mathcal {F}}}_{x_k}x^k_{y_i}+{{\mathcal {F}}}_{y_i}=0, \end{aligned}$$

(60)

we arrive at (58) by using (57) and definition of L.

Derivating once again (60) with respect to y we obtain with Einsteins summation index

$$\begin{aligned} \frac{\partial ^2}{\partial y_i\partial y_j}{{\mathcal {F}}}={{\mathcal {F}}}_{x_kx_l}x^k_{y_i}x^l_{y_j}+{{\mathcal {F}}}_{y_ix_l}x^l_{y_j}+{{\mathcal {F}}}_{x_py_j}x^p_{y_i}+{{\mathcal {F}}}_{x_p}x^{p}_{y_iy_j}+{{\mathcal {F}}}_{y_iy_j}=0. \end{aligned}$$

Solving for $x_{y_iy_j}$ we get

$$\begin{aligned} x_{y_iy_j}=-(F_x)^{-1}(F_{x_kx_l}x^k_{y_i}x^l_{y_j}+F_{y_ix_l}x^l_{y_j}+F_{x_py_j}x^p_{y_i}+F_{y_iy_j}). \end{aligned}$$

Using the definitions of norms we obtain (59). $\square$

Corollary 2

Let $\varLambda _b=\{(x,y):|x|\le \sqrt{b}, |y|\le b\}$ and let

$$\begin{aligned} {\hat{M}}=\sum _{1\le |\alpha |+k\le 2}\max _{\varLambda _b}||D^\alpha _{x}D_y^\beta {{\mathcal {F}}}(x,y)||. \end{aligned}$$

(61)

If

$$\begin{aligned} ||A^{-1}||{\hat{M}} (\sqrt{b}+b)\le c_{n,m}, \end{aligned}$$

(62)

where $c_{n,m}$ is a positive constant depending only on n and m, then there exists a $C^2$-function $x=x(y)$ defined for $|y|\le b$ and such that $|x|\le \sqrt{b}$, which delivers all solution to (54) from $\varLambda _b$. Moreover, the matrix $D_xF(x,y)$ is invertible for all $(x,y)\in \varLambda$ and

$$\begin{aligned} |D_xF(x,y)^{-1}|\le & {} C||A^{-1}||,\;\;\\ |D_yx(y)|\le & {} C||A^{-1}||{\hat{M}}, \\ ||D_yD_yx(y)||\le & {} C{\hat{M}} ||A^{-1}||(1+{\hat{M}}||A^{-1}||+{\hat{M}}^2||A^{-1}||^2), \end{aligned}$$

where C depends only on n and m.

Bifurcation from a degenerate bifurcation point

The results of the following section can not be considered as new. They can be deduced from the classical results from [4, 5], see also [8] for more complete a presentation and related references. Here we give another direct presentation which is more suitable for application to models appearing in biological applications. First, systems here are finite dimensional and have a special structure, which essentially simplifies the proofs. Second, the bifurcation parameter is fixed from the beginning and we are interesting in bifurcation with respect to this parameter. Therefore we present here proofs which are more adapted to our situation.

1.1 Interior equilibrium point

Let $x'=(x_1,\ldots ,x_{n-1})$ and $x=(x',x_n)$. Consider the problem

$$\begin{aligned} {{\mathcal {F}}}(x;s)=0,\;\;x\in {\mathbb {R}}^n,\;\;s\in {\mathbb {R}}, \end{aligned}$$

(63)

where ${{\mathcal {F}}}=({{\mathcal {F}}}_1,\ldots ,{{\mathcal {F}}}_n)^T$. We put $F(x;s)=({{\mathcal {F}}}_1,\ldots ,{{\mathcal {F}}}_{n-1})^T$ and assume that ${{\mathcal {F}}}_n(x;s)=f(x;s)x_n$, where $({{\mathcal {F}}}_1,\ldots ,{{\mathcal {F}}}_{n-1})$ and f are real valued function of class $C^2$ with respect to all variables. Then the problem (63) can be written as

$$\begin{aligned}&F(x;s)=0, \end{aligned}$$

(64)

$$\begin{aligned}&x_nf(x;s)=0. \end{aligned}$$

(65)

It is assumed that there exists $x^*\in \mathbb {R}^{n-1}$ such that

$$\begin{aligned} F(x^*,0;0)=0 \end{aligned}$$

and that the $(n-1)\times (n-1)$-matrix

$$\begin{aligned} A=\{A_{kj}\}_{k,j=1}^{n-1}=\{\partial _{x_j}{{\mathcal {F}}}_k(x^*,0;0)\}_{j,k=1}^{n-1} \end{aligned}$$

(66)

is invertible. This implies, in particular, that the equation

$$\begin{aligned} F(\xi ,0;s)=0 \end{aligned}$$

(67)

has a solution $\xi (s)\in C^2([-b,b])$ such that $\xi (0)=x^*$. Here b is a positive number satisfying (62), where ${\hat{M}}$ is given by (61) with ${{\mathcal {F}}}$ replaced by F.

This is a single solution to (67) in $\varLambda _b$ according to Corollary 2. Moreover this solution is of the class $C^2$ and estimates of the derivatives are presented in the same corollary. One can easily verify that ${\check{x}}(s)=(\xi (s),0)$ solves system (64), (65) for $s\in [-b,b]$.

We assume that $f(x^*,0;0)=0$ and our goal is to construct a solution to Eqs. (64), (65) different from ${\check{x}}(s)$. This will be achieved if we solve the problem

$$\begin{aligned} F(x;s)= & {} 0, \end{aligned}$$

(68)

$$\begin{aligned} f(x;s)= & {} 0. \end{aligned}$$

(69)

instead of (64), (65). We denote the Jacobian matrix of the right-hand side at the point $(x^*,0;0)$ by ${{\mathcal {A}}}$. Direct calculations show that

$$\begin{aligned} {{\mathcal {A}}}=\begin{bmatrix} A&{}\quad \partial _{x_n}F(x^*,0;0)\\ \nabla _{x'}f(x^*,0;0)&{}\quad \partial _{x_n}f(x^*,0;0) \end{bmatrix}. \end{aligned}$$

To find the inverse of the matrix consider the equation

$$\begin{aligned} {{\mathcal {A}}}(X',X_n)^T=(Y',Y_n). \end{aligned}$$

Then

$$\begin{aligned} \varTheta X_n=\nabla _{x'}f\cdot A^{-1}Y'-Y_n\;\;\text{ and }\;\;X'=A^{-1}(Y'-\partial _{x_n}F X_n), \end{aligned}$$

(70)

where and in what follows we assume that

$$\begin{aligned} \varTheta {:}{=}\nabla _{x'}fA^{-1}\partial _{x_n}F(x^*,0;0)-\partial _{x_n}f(x^*,0;0)\ne 0. \end{aligned}$$

So the matrix ${{\mathcal {A}}}$ is invertible if A is invertible and $\varTheta \ne 0$. From (70) it follows the estimates

$$\begin{aligned} |X_n|\le \frac{||A^{-1}||}{|\varTheta |}\,|\nabla _{x'}f|\,|Y'|+\frac{1}{|\varTheta |}|Y_n| \end{aligned}$$

and

$$\begin{aligned} |X'|\le&||A^{-1}||\,(|Y'|+|\partial _{x_n}F|\,|X_n|)\le ||A^{-1}||\Bigg (1+\frac{||A^{-1}||\,|\partial _{x_n}F|\,||\nabla _{x'}f||}{|\varTheta |}\Bigg )|Y'|\\&+\frac{||A^{-1}||\,|\partial _{x_n}F|}{|\varTheta |}Y_n. \end{aligned}$$

Therefore

$$\begin{aligned} ||{{\mathcal {A}}}^{-1}||\le C\Big (||A^{-1}||+\frac{1}{|\varTheta |}\big (1+|\partial _{x_n}F|\,||A^{-1}||\big )\big (1+|\nabla _{x'}f|\,||A^{-1}||\big )\Big ), \end{aligned}$$

where C is a positive constant depending only on n.

Let us introduce the quantity

$$\begin{aligned} \mathcal {{\hat{M}}}=\sum _{1\le |\alpha |+k\le 2}\max _{\varLambda _b}(||D^\alpha _{x}\partial _s^kF(x;s)||+|D^\alpha _{x}\partial _s^kf(x;s)|), \end{aligned}$$

Then according to Corollary 2 there exists a solution $\hat{x}(s)=(\hat{x}'(s),\hat{x}_n(s))$ to (64)–(65) belonging to $C^2([-b,b])$ such that $\hat{x}(0)=(x^*,0)$. Here b is a positive number satisfying (62), where $\hat{M}$ is replaced by $\hat{{\mathcal {M}}}$.

Let us evaluate the derivative $\frac{d\hat{x}(s)}{ds}$. Differentiating (68) and setting $s=0$, we have

$$\begin{aligned} A\frac{d}{ds}\hat{x}'(0)+\partial _{x_n}F(x^*,0;0)\frac{d}{ds}\hat{x}_n(0)+\partial _sF(x^*,0;0)=0. \end{aligned}$$

Differentiating $F(\xi (s),0;s)=0$ with respect to s we get $\partial _sF(x^*,0;0)=-A\frac{d}{ds}\xi (0)$. Therefore

$$\begin{aligned} A\frac{d}{ds}(x'-\xi )(0)+\partial _{x_n}F(x^*,0;0)\frac{d}{ds}\hat{x}_n(0)=0. \end{aligned}$$

(71)

Writing Eq. (69) as $f(\hat{x}(s);s)-f({\check{x}}(s);s)+f({\check{x}}(s);s)=0$ and differentiating it at $s=0$, we get

$$\begin{aligned} \nabla _{x'}f(x^*,0;0)\frac{d}{ds}(\hat{x}'-\xi )(0)+\partial _{x_n}f(x^*,0;0)\frac{d}{ds}\hat{x}_n(0)+\frac{d}{ds}f({\check{x}};s)\Big |_{s=0}=0. \end{aligned}$$

Therefore

$$\begin{aligned} \hat{x}_n(s)=\frac{\frac{d}{ds}f(\xi (s),0;s)|_{s=0}}{\varTheta }s+O(s^2), \end{aligned}$$

(72)

where $O(s^2)$ is estimated by $Cs^2$, where C depends only on n, $||{{\mathcal {A}}}^{-1}||$ and $\hat{{\mathcal {M}}}$. Other components are not important for us in this paper so we write only that

$$\begin{aligned} \hat{x}'(s)=y^*+O(|s|) \end{aligned}$$

with similar comment on O(s) as above. From (71) we can derive a similar formula for the derivative

$$\begin{aligned} \frac{d}{ds}\hat{x}'(s)=\frac{d}{ds}\xi (0)-A^{-1}\partial _{x_n}F(x^*,0;0)\frac{d}{ds}\hat{x}_n(0)+O(|s|). \end{aligned}$$

1.2 On smallest eigenvalue of the Jacobian

The Jacobian matrix for system (64), (65) is

$$\begin{aligned} {{\mathcal {J}}}={{\mathcal {J}}}(x;s)=\begin{bmatrix} \partial _{x'}F(x;s)&{}\quad \partial _{x_n}F(x;s)\\ \partial _{x'}(x_nf)&{}\quad \partial _{x_n}(x_nf) \end{bmatrix}. \end{aligned}$$

The Jacobian matrix

$$\begin{aligned} {{\mathcal {J}}}(x^*,0;0)=\begin{bmatrix} A &{}\quad \partial _{x_n}F\\ 0&{}\quad 0 \end{bmatrix}\;\;\text{ at }\;\;(x;s)=(x^*,0;0) \end{aligned}$$

has a simple eigenvalue 0. Let us denote the perturbation of this eigenvalue at the point (x; s) by $\lambda =\lambda (x;s)$. The smallest eigenvalue of ${{\mathcal {J}}}({\check{x}}(s);s)$ is

$$\begin{aligned} \lambda ({\check{x}}(s);s)=f({\check{x}}(s);s)=\frac{d}{ds}f(\xi (s),0;s)|_{s=0}s+O(s^2). \end{aligned}$$

(73)

Our aim is to find smallest eigenvalue of ${{\mathcal {J}}}(\hat{x}(s);s)$ corresponding to the solution $\hat{x}(s)$. The eigenvalue equation for the Jacobian at the point $\hat{x}(s)$ is

$$\begin{aligned} {{\mathcal {A}}}\begin{bmatrix} X'\\ X_n \end{bmatrix}=\lambda \begin{bmatrix} X'\\ X_n \end{bmatrix} \end{aligned}$$

Without lost of generality we can put $X_n=1$. Solving this system with respect to $X'$ and putting the result in the last equation, we get

$$\begin{aligned} -x_n\nabla _{x'}f\cdot \Big (D_{x'}F+x_n\partial _{x'}G(\hat{x};s)-\lambda \Big )^{-1}\partial _{x_n}(F)+\partial _{x_n}(x_nf)=\lambda . \end{aligned}$$

Which implies $\lambda (s)=-\hat{x}(s)\varTheta +O(s^2)$ or, using (72), we get

$$\begin{aligned} \lambda (\hat{x}(s);s)=-\frac{d}{ds}f(\xi (s),0;s)|_{s=0}s+O(s^2). \end{aligned}$$

(74)

Comparing (73) and (74), we see that the first derivative of smallest eigenvalue corresponding to solutions ${\check{x}}$ and $\hat{x}$ has opposite sign.

Remark 4

If we assume that the function $s\rightarrow f(\xi (s),0;s)$ is strongly monotone on the interval $[-b,b]$ then all solution to (64), (65) in the set $|s|\le b$, $|x'-x^*|^2+x_n^2\le b$ are exhausted by ${\check{x}}(s)$ and $\hat{x}(s)$, where b corresponds to $\mu {:}{=}\max (||A^{-1}||\hat{M},||{{\mathcal {A}}}^{-1}||\hat{{\mathcal {M}}})$ in (62). Moreover derivatives of first and second order of this solutions are estimated by constant depending on $\mu$ and n only.