AXISYMMETRIC WAVE PROPAGATION IN FUNCTIONALLY GRADE CYLINDER WITH SMOOTH RADIAL DISTRIBUTION OF PHYSICAL PARAMETERS

Abstract—

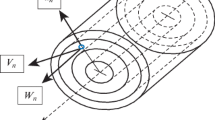
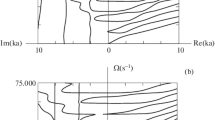
Novel approximate methods of wave propagation analysis are developed for functionally graded cylinders with mass and elastic parameters described by continuously differentiable functions of radius. Two of these methods relate to embedding of boundary value problems into corresponding initial value problems and the third method demonstrates methodology of discretization of the physical parameters over cylinder’s cross-section. Frequency spectra diagrams of dilatational and shear waves are plotted for travelling and evanescent regimes. Diagrams of phase and group velocities are plotted for dilatational travelling waves.

APPENDIX

System of axisymmetric dilatational vibration of cylinder with radial dependence of its physical (mass density and elastic) parameters is as follows:

$$\begin{array}{*{20}{c}} {\rho \left( r \right)\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} = \frac{{\partial \sigma _{{rr}}^{{}}}}{{\partial r}} + \frac{{\partial \sigma _{{rz}}^{{}}}}{{\partial z}} + \frac{{\sigma _{{rr}}^{{}} - \sigma _{{zz}}^{{}}}}{r}} \\ {\rho \left( r \right)\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = \frac{{\partial \sigma _{{rz}}^{{}}}}{{\partial r}} + \frac{{\partial \sigma _{{zz}}^{{}}}}{{\partial z}} + \frac{{\sigma _{{rz}}^{{}}}}{r},} \end{array}$$

(A.1)

where $u = u\left( {t,r,z} \right)$, ${v} = 0$, $w = w\left( {t,r,z} \right)$ are the radial and axial displacements correspondingly, t is time, r is radial coordinate and z is axial coordinate; ρ(r) is mass density; ${{\sigma }_{{rr}}}$, ${{\sigma }_{{\theta \theta }}}$, ${{\sigma }_{{zz}}}$, ${{\sigma }_{{rz}}}$ are stresses which are linearly dependent on strains due to Hook’s law:

$$\begin{gathered} \begin{array}{*{20}{c}} {\sigma _{{rr}}^{{}} = \lambda \left( r \right)\left( {{{\varepsilon }_{{rr}}} + {{\varepsilon }_{{\theta \theta }}} + {{\varepsilon }_{{zz}}}} \right) + 2\mu \left( r \right){{\varepsilon }_{{rr}}},} \\ {\sigma _{{\theta \theta }}^{{}} = \lambda \left( r \right)\left( {{{\varepsilon }_{{rr}}} + {{\varepsilon }_{{\theta \theta }}} + {{\varepsilon }_{{zz}}}} \right) + 2\mu \left( r \right){{\varepsilon }_{{\theta \theta }}},} \\ {\sigma _{{zz}}^{{}} = \lambda \left( r \right)\left( {{{\varepsilon }_{{rr}}} + {{\varepsilon }_{{\theta \theta }}} + {{\varepsilon }_{{zz}}}} \right) + 2\mu \left( r \right){{\varepsilon }_{{zz}}}} \end{array} \\ \sigma _{{rz}}^{{}} = \mu \left( r \right){{\varepsilon }_{{rz}}}, \\ \end{gathered} $$

(A.2)

where $\lambda \left( r \right)$, $\mu \left( r \right)$ are Lame’s elastic factors and ${{\varepsilon }_{{rr}}} = {{\varepsilon }_{{rr}}}\left( {t,r,z} \right)$, ${{\varepsilon }_{{\theta \theta }}} = {{\varepsilon }_{{\theta \theta }}}\left( {t,r,z} \right)$, ${{\varepsilon }_{{zz}}} = {{\varepsilon }_{{zz}}}\left( {t,r,z} \right)$, ${{\varepsilon }_{{rz}}} = {{\varepsilon }_{{rz}}}\left( {t,r,z} \right)$ are linearized strains:

$${{\varepsilon }_{{rr}}} = \frac{{\partial u}}{{\partial r}},\quad {{\varepsilon }_{{\theta \theta }}} = \frac{u}{r},\quad {{\varepsilon }_{{zz}}} = \frac{{\partial w}}{{\partial z}},\quad {{\varepsilon }_{{rz}}} = \frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial r}}$$

(A.3)

Substituting (A.2) in (A.1), we obtain the following we obtain the following system of axisymmetric dilatational vibration of the cylinder:

$$\begin{array}{*{20}{c}} {\rho \left( r \right)\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}}& = &{\left[ {\lambda \left( r \right) + 2\mu \left( r \right)} \right]\frac{{\partial {{\varepsilon }_{{rr}}}}}{{\partial r}} + \lambda \left( r \right)\left( {\frac{{\partial {{\varepsilon }_{{\theta \theta }}}}}{{\partial r}} + \frac{{\partial {{\varepsilon }_{{zz}}}}}{{\partial r}}} \right) + \mu \left( r \right)\left[ {\frac{{\partial {{\varepsilon }_{{rz}}}}}{{\partial r}} + \frac{2}{r}\left( {{{\varepsilon }_{{rr}}} - {{\varepsilon }_{{\theta \theta }}}} \right)} \right]} \\ {}&{}&{ + \frac{{d\lambda \left( r \right)}}{{dr}}\left( {{{\varepsilon }_{{rr}}} + {{\varepsilon }_{{\theta \theta }}} + {{\varepsilon }_{{zz}}}} \right) + 2\frac{{d\mu \left( r \right)}}{{dr}}{{\varepsilon }_{{rr}}},} \end{array}$$

$$\rho (r)\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = \lambda (r)\left( {\frac{{\partial {{\varepsilon }_{{zz}}}}}{{\partial z}} + \frac{{\partial {{\varepsilon }_{{\theta \theta }}}}}{{\partial z}}} \right) + \left[ {\lambda (r) + 2\mu (r)} \right]\frac{{\partial {{\varepsilon }_{{zz}}}}}{{\partial z}} + \mu (r)\left( {\frac{{\partial {{\varepsilon }_{{rz}}}}}{{\partial r}} + \frac{{{{\varepsilon }_{{rz}}}}}{r}} \right) + \frac{{d\mu (r)}}{{dr}}{{\varepsilon }_{{rz}}}.$$

(A.4)

In the case of axisymmetric torsional vibration, the governing equation is:

$$\rho \left( r \right)\frac{{{{\partial }^{2}}{v}}}{{\partial {{t}^{2}}}} = \frac{{\partial \sigma _{{r\theta }}^{{}}}}{{\partial r}} + \frac{{\partial \sigma _{{\theta z}}^{{}}}}{{\partial z}} + \frac{{2\sigma _{{r\theta }}^{{}}}}{r},$$

(A.5)

where ${v} = {v}\left( {t,r,z} \right)$, $u = w = 0$, and stresses are:

$$\sigma _{{r\theta }}^{{}} = \mu \left( r \right)\varepsilon _{{r\theta }}^{{}},\quad \sigma _{{\theta z}}^{{}} = \mu \left( r \right)\varepsilon _{{\theta z}}^{{}},$$

(A.6)

where strains are:

$$\varepsilon _{{r\theta }}^{{}} = \frac{{\partial {v}}}{{\partial r}} - \frac{{v}}{r},\quad \varepsilon _{{\theta z}}^{{}} = \frac{{\partial {v}}}{{\partial z}}.$$

(A.7)

Substituting (A.7) in (A.6) and further in (A.5), we obtain the following equation of axisymmetric shear vibration of the cylinder:

$$\rho \left( r \right)\frac{{{{\partial }^{2}}{v}}}{{\partial {{t}^{2}}}} = \mu \left( r \right)\left( {\frac{{\partial {{\varepsilon }_{{r\theta }}}}}{{\partial r}} + \frac{{\partial {{\varepsilon }_{{\theta z}}}}}{{\partial z}} + \frac{{2{{\varepsilon }_{{r\theta }}}}}{r}} \right) + \frac{{d\mu \left( r \right)}}{{dr}}{{\varepsilon }_{{r\theta }}}.$$

(A.8)