Minimizing the makespan on a single machine subject to modular setups

Abstract

Single machine scheduling with sequence-dependent setup times is one of the classical problems of production planning with widespread applications in many industries. Solving this problem under the min-makespan objective is well known to be strongly NP-hard. We consider a special case of the problem arising from products having a modular design. This means that product characteristics, (mass-)customizable by customers, are realized by separate components that can freely be combined. If consecutive products differ by a component, then a setup is necessary. This results in a specially structured setup matrix that depends on the similarities of product characteristics. We differentiate alternative problem cases where, for instance, the setup operations for multiple components either have to be executed sequentially or are allowed to be conducted in parallel. We analyze the computational complexity of various problem settings. Our findings reveal some special cases that are solvable in polynomial time, whereas most problem settings are shown to remain strongly NP-hard.

1 Introduction

We consider a production scheduling problem where jobs are to be sequenced on a single machine subject to sequence-dependent setup times under the min-makespan objective. This problem, which according to the famous 3-field notation introduced by Graham et al. (1979) is denoted by $[1|s_{ij}|C_{\max }]$, is closely related to the traveling salesman problem (TSP). The processing times of jobs merely constitute a constant portion of the makespan, and minimizing the makespan is thus equivalent to minimizing the total setup time. Processing jobs and setup times in the scheduling problem then directly correspond to visiting customers and distances in the TSP. A wide range of results for the TSP with special structures of distance matrices is documented by the survey papers of Boysen and Stephan (2016), Burkard et al. (1998), and Oda and Ota (2001) as well as Stephan and Boysen (2017).

While the scheduling problem with sequence-dependent setup times is strongly NP-hard in general, this paper considers special structures of setup times arising in the context of modular product architectures. We address the question whether under this special structure the problem is still hard to solve or can be solved in polynomial time.

Fig. 1

A modular product and its production process

The relevance of specially structured setup matrices in the context of modular products came to our mind when visiting a production plant of Germany’s market leader for sectional garage doors (see Fig. 1a). The sections of garage doors, (mass-)customizable by customers selecting the interior and exterior surface coating as well as the kind of polyurethane (PU) foam insulation, are produced in the continuous production process schematically depicted in Fig. 1b. Since interior and exterior steel coatings are unrolled from their coils and continuously pulled along the three main production stages, the whole process can be modeled by a single machine. Sequence-dependent setups occur whenever two subsequent jobs, which correspond to customer orders for garage doors, vary in their individual specification according to insulation, interior, and/or exterior coating, so that one or both of the steel coils and/or the cartridge of the PU foam is to be changed. Vice versa, our three resources (i.e., insulation, interior, and exterior coating) remain unchanged if subsequent jobs share the specific product characteristic. Thus, we have a specially structured setup matrix that depends on the similarity of product characteristics of subsequent jobs.

Modular product architectures, providing “a one-to-one mapping from functional elements in the function structure to the physical components of the product” with “de-coupled interfaces between components” (Ulrich 1995) are widely aspired “to provide customized products or services through flexible processes in high volumes and at reasonably low costs” (Da Silveira et al. 2001) in mass-customization environments. Typically, there is also a one-to-one mapping not only from product characteristic to component, but also to a resource required for the assembly of the respective component. Whenever the resource required depends on the product and needs to be exchanged if products differ in the resource, modular products share the peculiarities of our garage door manufacturer, and we have specially structured setup times that depend on the similarity of product characteristics.

For these modular setups, we want to investigate whether the specially structured setup matrices allow solving problem $[1|s_{ij}|C_{\max }]$ in polynomial time. In doing so, we differentiate problem variants according to three features:

• Setup operations of resources to be altered between two successive jobs can be executed in parallel, so that the maximum time over all current resource setups is to be considered, or sequentially, so that the sum of single resource setups constitutes the setup time.

• While we always consider operations equipping the machine with a resource type, removal operations caused by removing the resource type required by the previous job may be relevant or not.

• Setup times per resource can all be equal, e.g., changing any type of exterior steel coil, interior steel coil, and PU cartridge always takes the same amount of time, characteristic-dependent, e.g., changing any type of exterior steel coil takes identical setup time, which may, however, differ from the constant setup time for changing any type of PU cartridges, or value-dependent, e.g., each specific type of steel coil and PU cartridge may require a different setup time.

We combine all manifestations of these features and, hence, have twelve problem variants in total. We determine the computational complexity of all but one of these variants.

There are several other papers that provide polynomial time algorithms for special single machine scheduling problems with setups when minimizing makespan $C_{\max }$. They arise in case of family setups where products are subdivided into families and only changes between families cause setup operations, e.g., see Bai et al. (2012), Huang et al. (2011), Lee and Wu (2010), Wang et al. (2008, 2012), Wu and Lee (2008), Xu et al. (2014), Yang (2011), and Yang and Yang (2010) and if setups are applied to model learning effects and their duration decreases with increasing cumulated production time, e.g., see Cheng et al. (2010), Huang et al. (2013), Koulamas and Kyparisis (2008), Lai et al. (2011), Soroush (2012) and Yin et al. (2010, 2012). However (to the best of the authors’ knowledge), none of these existing approaches considers our case of modular setups where the similarity of product characteristics influences setup times. Our own finding (after a thorough literature search) is also supported by the manifold and up-to-date survey papers on scheduling with setups provided in Allahverdi (2015), Allahverdi et al. (1999), Allahverdi et al. (2008) and Stefansdottir et al. (2017) where modular setups are not mentioned.

The remainder of the paper is structured as follows. Section 2 defines the problem setting and classifies the different problem cases investigated in this paper. Our complexity results are presented in Sect. 3, and finally, Sect. 4 concludes the paper.

2 Problem definition and classification

We have a modular product, which is mass-customizable by customers specifying a given set $C=\{c_1,\ldots ,c_m\}$ of m different product characteristics. For each characteristic $c \in C$, a customer can select from a given set of integer values $V_c$ reflecting the alternative options. For our garage door example, the insulation is a product characteristic c and there is a set $V_c$ of alternative insulation types the customers may choose from. All jobs, each corresponding to an order for a specific product customized according to a customer’s demand, are unified in job set $J=\{1,\ldots ,n\}$. Each job $j\in J$ is defined by its processing time $p_j$ and a value $v_{j,c}\in V_c$ for each characteristic $c\in C$. Let $K_c$ be the number of distinct values for characteristic c among the set of jobs, and let $K=\max \left\{ K_c\mid c\in C\right\}$.

From now on, a characteristic $c \in C$ with value $v \in V_c$ refers to the product characteristic (e.g., the interior coating of a garage door) and its value (e.g., a specific kind of coating), but also to the specific resource (e.g., a steel coil) required by the machine and its specific resource type (e.g., a specific type of coil) to realize the value of the characteristic. Thus, we say processing job j with $v_{j,c}\in V_c$, $c\in C$, requires the machine to have value $v_{j,c}$ of characteristic c. For each value $v\in V_c$, $c\in C$, we have a setup time $s^e_{v,c}\ge 0$ for equipping characteristic c with value v and a setup time $s^r_{v,c}\ge 0$ for removing value v from characteristic c.

A schedule is a sequence $\sigma$ of jobs with $\sigma (k)$ being the kth job in $\sigma$. For processing a job j, we have to configure the machine by setting each characteristic $c\in C$ to $v_{j,c}\in V_c$. The actual setup time $s_{i,j}$ between two jobs i and j depends on the values required by both jobs for each characteristic. The setup time $s_{i,j,c}$ for characteristic c of job j immediately following i amounts to $s^r_{v_{i,c},c}+s^e_{v_{j,c},c}$, if $v_{j,c}\ne v_{i,c}$ and to 0 otherwise. If setups for characteristics are conducted sequentially, then $s_{i,j}=\sum _{c\in C}s_{i,j,c}$. If setups for characteristics are conducted in parallel, then $s_{i,j}=\max \left\{ s_{i,j,c}\mid c\in C\right\}$. The setup time $s_{0,j}$ before the first job $j=\sigma (1)$ amounts to $s_{0,j}=\sum _{c\in C}s^e_{v_{j,c},c}$ or $s_{0,j}=\max \left\{ s^e_{v_{j,c},c}\mid c\in C\right\}$. The setup time $s_{j,0}$ after the last job $j=\sigma (n)$ amounts to $s_{j,0}=\sum _{c\in C}s^r_{v_{j,c},c}$ or $s_{j,0}=\max \left\{ s^r_{v_{j,c},c}\mid c\in C\right\}$.

The makespan $C_{\max }(\sigma )$ of a schedule $\sigma$ is

$$\begin{aligned} C_{\max }(\sigma )=s_{0,\sigma (1)}+\sum _{k=1}^{n-1}s_{\sigma (k),\sigma (k+1)}+s_{\sigma (n),0}+\sum _{j\in J}p_j. \end{aligned}$$

The goal in problem ModSetup-Seq and ModSetup-Par is to find a minimum makespan schedule when setups are conducted sequentially and in parallel, respectively.

In order to improve intuition about the problem setting, we discuss a small example in the following. We consider job set $J=\{1,2,3\}$, characteristics $c_1$ and $c_2$, value sets $V_{c_1}=\{1,2\}$ and $V_{c_2}=\{3,4\}$, values for jobs and characteristics as given in Table 1, and setup times for equipping and removing as given in Table 2. Each job $j \in J$ has unit processing time $p_j=1$.

Table 1 Values for jobs and characteristics

Table 2 Setup times

Figures 2, 3, 4 and 5 depict schedules corresponding to schedules (1, 3, 2) and (1, 2, 3) with parallel and sequential setups, respectively. The gray blocks represent jobs with the topmost entry referring to the job number j, the second entry representing $v_{j,c_1}$, and the third entry representing $v_{j,c_2}$. Setups are depicted as white blocks immediately before or after the job they belong to. The line a setup is depicted in refers to the corresponding characteristic. The entry of the white blocks reflects the length of the corresponding setup.

Fig. 2

$C_{\max }=17$ for schedule (1, 3, 2) with parallel setups

Fig. 3

$C_{\max }=18$ for schedule (1, 2, 3) with parallel setups

Fig. 4

$C_{\max }=25$ for schedule (1, 3, 2) with sequential setups

Fig. 5

$C_{\max }=22$ for schedule (1, 2, 3) with sequential setups

As we can see in the example, schedule (1, 3, 2) yields a smaller makespan for parallel setups, while schedule (1, 2, 3) finds better results for sequential setups.

In general, it is easy to see that the total processing time is a constant, so that, from now on, we will assume that $p_j=0$ and neglect processing times. In the following, we elaborate how the different problem variants investigated in this paper are derived.

• Setup aggregation Our first distinction addresses the aggregation of setup times required for altering the divergent characteristics of two successive jobs. Here, we distinguish the two problem versions ModSetup-Seq (e.g., a single worker executes all setups for the different characteristics sequentially) and ModSetup-Par (e.g., each characteristic is serviced by a separate worker, so that all relevant setups are executed in parallel) elaborated above.

• Removing time Furthermore, we distinguish whether or not there are special setup times for removing values from characteristics required by the previous job. An extra removing time is to be considered, for instance, if removing the steel coils required by the previous jobs takes different amounts of time, e.g., due to varying weights or sizes. Once all removing times for the different values of a characteristic are equal, they can simply be added to the setup times related with equipping the machine for the subsequent job. Note that the removing time of the last job, then, is covered by the setup time for equipping of the first job. Note, furthermore, that due to symmetry the problem setting with setup times for equipping but without setup times for removing is equivalent to the problem setting with setup times for removing but without setup times for equipping.

• Setup time differences We call the standard case value-dependent setup time. Here, equipping any value v for characteristic c may take individual setup times $s^e_{v,c}\ge 0$. Analogously, individual setup times $s^r_{v,c}\ge 0$ for removing v from c can occur. Furthermore, we distinguish the following special cases. We investigate the special case where setup times are only characteristic-dependent; that is, we have $s^e_{v,c}=s^e_{c}$ and $s^r_{v,c}=s^r_{c}$ for each characteristic $c\in C$ and each value $v\in V_c$. Furthermore, we analyze the special case where $s^e_{c}=1$ and $s^r_{c}=1$ for each characteristic $c\in C$, so that all setup times are equal.

Given these distinctions, we receive twelve different problem settings to be investigated in the following section.

3 Analysis of computational complexity

This section analyzes the computational complexity of the problem variants defined in Sect. 2. The main results are summarized in Table 3.

Table 3 Subproblems and their complexity status

We first establish the following properties, which justify a simplifying assumption concerning all problem variants to be treated later on.

Lemma 1

In both ModSetup-Seq and ModSetup-Par, setup times satisfy the triangle inequality.

Proof

Let us first consider setup times $s_{i,j,c}$ and $s_{j,k,c}$ for an arbitrary job triplet $i\in J$, $j\in J$, and $k\in J$ and an arbitrary characteristic $c\in C$. We have

$$\begin{aligned} s_{i,j,c}+s_{j,k,c}= {\left\{ \begin{array}{ll} s^r_{v_{i,c},c}+s^e_{v_{j,c},c}+s^r_{v_{j,c},c}+s^e_{v_{k,c},c}\ge s^r_{v_{i,c},c}+s^e_{v_{k,c},c} &{} \text{ if } v_{i,c}\ne v_{j,c} \text{ and } v_{j,c}\ne v_{k,c}\\ s^r_{v_{j,c},c}+s^e_{v_{k,c},c}=s^r_{v_{i,c},c}+s^e_{v_{k,c},c} &{} \text{ if } v_{i,c}=v_{j,c} \text{ and } v_{j,c}\ne v_{k,c}\\ s^r_{v_{i,c},c}+s^e_{v_{j,c},c}= s^r_{v_{i,c},c}+s^e_{v_{k,c},c} &{} \text{ if } v_{i,c}\ne v_{j,c} \text{ and } v_{j,c}=v_{k,c}\\ 0=s_{i,k,c} &{} \text{ if } v_{i,c}=v_{j,c}=v_{k,c}. \end{array}\right. } \end{aligned}$$

Note that the above carries over to setups before the first job j and between the first two jobs j and k in a schedule as well as to setups after the last job j and between the last two jobs i and j in a schedule. To see this, in the former case we can set $s^r_{v_{i,c},c}=0$ and in the latter case, we can set $s^e_{v_{k,c},c}=0$.

Now, we consider setup times $s_{i,j}=\sum _{c\in C}s_{i,j,c}$ and $s_{j,k}=\sum _{c\in C}s_{j,k,c}$ for an arbitrary job triplet i, j, and k in ModSetup-Seq. We obtain

$$\begin{aligned} s_{i,j}+s_{j,k}&=\sum _{c\in C}s_{i,j,c}+\sum _{c\in C}s_{j,k,c}\\&=\sum _{c\in C}\left( s_{i,j,c}+s_{j,k,c}\right) \ge \sum _{c\in C}s_{i,k,c}=s_{i,k} . \end{aligned}$$

Finally, we consider setup times $s_{i,j}=\max \left\{ s_{i,j,c}\mid c\in C\right\}$ and $s_{j,k}=\max \left\{ s_{j,k,c}\mid c\in C\right\}$ for an arbitrary job triplet i, j, and k in ModSetup-Par. We obtain

$$\begin{aligned} s_{i,j}+s_{j,k}= & {} \max \left\{ s_{i,j,c}\mid c\in C\right\} +\max \left\{ s_{j,k,c}\mid c\in C\right\} \\\ge & {} \max \left\{ s_{i,j,c}+s_{j,k,c}\mid c\in C\right\} \ge \max \left\{ s_{i,k,c}\mid c\in C\right\} =s_{i,k}. \end{aligned}$$

Again, this result carries over to setups before the first job j and between the first two jobs j and k in a schedule as well as to setups after the last job j and between the last two jobs i and j in a schedule. $\square$

The fact that the triangle inequality is satisfied, hence, means that the approximability results by Svensson et al. (2017, 2018) and Traub and Vygen (2020) for the asymmetric TSP (with the triangle inequality being satisfied) carry over to both ModSetup-Seq and ModSetup-Par. Svensson et al. (2018) show that the asymmetric TSP can be approximated within a factor of 5,500 in polynomial time, and Svensson et al. (2017) refine this result to a factor of 506. Most recently, Traub and Vygen (2020) further reduced the factor to $22+\epsilon$ for any $\epsilon >0$.

Lemma 2

There is an optimal schedule for ModSetup-Seq (ModSetup-Par) where jobs coinciding in the value of each characteristic are scheduled consecutively.

Proof

Consider an arbitrary optimal schedule and the first job i that does not immediately follow the previous job j with identical values for each characteristic. If there is no such job, we are done. Due to Lemma 1, we do not increase total setup time by removing i from its current position and inserting it immediately after j. By repeating this step, we find an optimal schedule where jobs coinciding in the value of each characteristic are scheduled consecutively. $\square$

Corollary 1

Both ModSetup-Seq and ModSetup-Par can be solved in $\mathcal {O}(n\cdot m\cdot K+(m\cdot K)!)$ time and, thus, in $\mathcal {O}(n)$ time, if m and K are fixed.

Proof

We can cluster jobs with identical values for each characteristic by sorting in $\mathcal {O}(n\cdot m\cdot K)$ time using radix sort. We then have a fixed number $m\cdot K$ of clusters to be sequenced. Evaluating each of the $(m\cdot K)!$ sequences can be done in constant time, if m and K are fixed. $\square$

In the following, we will assume that we do not have jobs coinciding in all values of characteristics. We can ensure this by a preprocessing step that clusters jobs accordingly. Such a preprocessing step clustering jobs with identical values for all characteristics can be conducted in $\mathcal {O}(n\cdot m\cdot K)$ time using radix sort or in $\mathcal {O}((n\log n)\cdot m)$ time with comparison-based sorting. After the preprocessing step, we handle clusters as jobs.

3.1 Sequential setups

This section analyzes the computational complexity of those problem cases where setups are executed sequentially, i.e., we have $s_{i,j}=\sum _{c\in C}s_{i,j,c}$ for all $i,j \in J$ with $i \ne j$. Unfortunately, the problem turns out to be strongly NP-hard not only in the most restricted case, but also if we additionally restrict the setting to no more than $m=2$ characteristics. We show NP-hardness by reduction from the problem to find a Hamiltonian path in a cubic graph, abbreviated to Ham-Cube, which is strongly NP-complete, see Garey and Johnson (1979).

Theorem 1

ModSetup-Seq with $s^e_{v,c}=1$ for each characteristic $c\in C$ and each value $v\in V_c$ and without setups for removing is strongly NP-hard even if $m=2$.

Proof

We consider an arbitrary instance I of Ham-Cube given by a cubic graph $G=(V,E)$. Let $v_j^1$, $v_j^2$, and $v_j^3$ be the three nodes adjacent to $j\in V$. We first construct another instance $I'$ of Ham-Cube specified by a graph $G'=(V',E')$ as follows.

We replace each node in V by a triangle in $G'$ where each of the nodes in a triangle establishes the connection to one other triangle. Connections among triangles correspond to edges in E. Let $j^i\in V'$ be the node in the triangle replacing $j\in V$ that connects its triangle to the triangle replacing $i\in V$. Furthermore, we define ${\widetilde{E}}$, the set of edges between different triangles. Punnim et al. (2007) show that there exists a Hamiltonian cycle in $G'$, if and only if there exists one in G. The idea of the proof can be easily adapted to show that there is a Hamiltonian path in $G'$, if and only if there is one in G.

Now, we construct an instance $I''$ of ModSetup-Seq. We set $J=V'$ and $m=2$. Jobs $j^{k_1}$, $j^{k_2}$, and $j^{k_3}$ have $v_{j^{k_1},1}=v_{j^{k_2},1}=v_{j^{k_3},1}=j$ for each $j\in J$. Jobs $j^i$ and $i^j$ have $v_{j^i,2}=v_{i^j,2}=\{j,i\}$ for each $\{j^i,i^j\}\in {\widetilde{E}}$. Finally, we have $s^e_{v,c}=1$ for each value v of each characteristic c and do not consider setups for removing. This completes the reduction which is pseudo-polynomial, see Garey and Johnson (1979, p. 101).

Summarizing, we have a job for each node in $V'$. Two jobs coincide in the value of the first characteristic, if they belong to the same triangle in $G'$ (and, therefore, correspond to the same node in G). Two jobs coincide in the value of the second characteristic, if they belong to different triangles and are connected by an edge in $G'$ (and, therefore, correspond to an edge in G).

We claim that there is a schedule with makespan of at most $|V'|+1$ for $I''$, if and only if there is a Hamiltonian path in $G'$.

• If there is a Hamiltonian path in $G'$, then we can construct a schedule for $I''$ by having the jobs in the same order as the corresponding nodes in the Hamiltonian path in $G'$. We, then, have setup time of 2 prior to the first job. Furthermore, we have a setup time of 1 between each pair of consecutive jobs. This is true, because two jobs differ in exactly one characteristic’s value, if the corresponding nodes in $G'$ are adjacent. Hence, there is a schedule for $I''$ with makespan of at most $2+(|V'|-1)=|V'|+1$.

• Now, assume there is a schedule with a makespan of at most $|V'|+1$. We have a setup time of 2 prior to the first job, which leaves $|V'|-1$ total setup time for setups between pairs of consecutive jobs. Since there are no identical jobs, we have a setup time of at least 1 for each such pair. Hence, each pair of consecutive jobs corresponds to adjacent nodes in $G'$, since non-adjacent nodes in $G'$ incur a setup time of 2.

Hence, there is schedule with a makespan of at most $|V'|+1$ for $I''$, if and only if there is a Hamiltonian path in G. $\square$

Fig. 6

Example instances I, $I'$, and $I''$ in the proof of Theorem 1

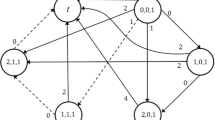
To illustrate the relation between instances I, $I'$, and $I''$ in the proof, we provide an example in the following. Figure 6a depicts an example instance I with $V=\{1,\ldots ,6\}$. The modified graph $G'$ specifying instance $I'$ is depicted in Fig. 6b. Here, we have a triangle of nodes for each node in G. Two triangles are connected by an edge in $E'$, if and only if the corresponding nodes in V are connected by an edge in E. Each node in a triangle connects its triangle to exactly one other triangle.

The Hamiltonian path (1, 6, 5, 2, 3, 4) in G corresponds to, e.g., the Hamiltonian path

$$\begin{aligned} (1^4,1^5,1^6,6^1,6^3,6^5,5^6,5^1,5^2,2^5,2^4,2^3,3^2,3^6,3^4,4^3,4^2,4^1) \end{aligned}$$

in $G'$. The other way round, the Hamiltonian path

$$\begin{aligned} (1^4,4^1,4^2,4^3,3^4,3^2,3^6,6^3,6^5,6^1,1^6,1^5,5^1,5^6,5^2,2^5,2^4,2^3) \end{aligned}$$

in $G'$, where nodes $1^4$, $1^5$, and $1^6$ belonging to the same triangle are not visited consecutively, implies a Hamiltonian path

$$\begin{aligned} (4^1,4^2,4^3,3^4,3^2,3^6,6^3,6^5,6^1,1^6,1^4,1^5,5^1,5^6,5^2,2^5,2^4,2^3) \end{aligned}$$

in $G'$, where nodes of each triangle are visited consecutively. The latter Hamiltonian path in $G'$ implies Hamiltonian path (4, 3, 6, 1, 5, 2) in G.

Figure 6c highlights for each job corresponding to a node in $G'$ the values of the characteristics in instance $I''$. We can see that the first value coincides with the corresponding node in G, while the second value reflects the corresponding edge in G.

Let us once more consider Hamiltonian path

$$\begin{aligned} (4^1,4^2,4^3,3^4,3^2,3^6,6^3,6^5,6^1,1^6,1^4,1^5,5^1,5^6,5^2,2^5,2^4,2^3) \end{aligned}$$

in $G'$. If we have the corresponding schedule for $I''$, then we obtain a total setup time of $2+(|V'|-1)=2+(18-1)=19$ since two consecutive jobs coincide in exactly one characteristic’s value.

Note that Theorem 1 states strong NP-hardness for the most restricted version of ModSetup-Seq with $s^e_{v,c}=1$ for each characteristic $c\in C$ and each value $v\in V_c$ and without setups for removing. Hence, all other problem cases ModSetup-Seq share this complexity status. However, we add another complexity result that proves strong NP-hardness, if instead the maximum number K of distinct values over all characteristics is restricted. Again, we show NP-hardness by reduction from the problem to find a Hamiltonian path in a cubic graph, abbreviated to Ham-Cube.

Theorem 2

ModSetup-Seq with $s^e_{v,c}=1$ for each characteristic $c\in C$ and each value $v\in V_c$ and without setups for removing is strongly NP-hard even if $K=2$.

Proof

We consider an arbitrary instance I of Ham-Cube given by a cubic graph $G=(V,E)$ and construct an instance $I'$ of ModSetup-Seq as follows. We set $J=V$ and $m=|E|$. We consider a one-to-one relationship between edges in E and characteristics. We refer to the characteristic associated with $e\in E$ as $c_e$. For each $j\in J$ and each $e\in E$, we have $v_{j,e}=1$ if e is incident to j, and $v_{j,e}=0$ otherwise. Finally, we have $s^e_{1,c}=s^e_{0,c}=1$ for each characteristic c and do not consider setups for removing. This completes the reduction which is pseudo-polynomial.

Summarizing, we have a job for each node in V. Two distinct jobs j and $j'$ have $v_{j,e}=v_{j',e}=1$ for a characteristic $c_e$, if and only if nodes j and $j'$ are adjacent in G and e is the connecting edge. Since G is cubic, each job j has $v_{j,e}=1$ for exactly three characteristics, and we denote the set of these characteristics as $C_j$. We refer to them as the characteristics of job j.

We claim that there is a schedule with a makespan of at most $5.5\cdot |V|-4$ for $I'$, if and only if there is a Hamiltonian path in G.

We, first, have a look at the total setup time for characteristic $c_{e}$ with $e=\{j,j'\}$ in a given schedule. Note that a setup time of 1 is due before the first job in any schedule. Without loss of generality, we assume that j is scheduled before $j'$.

• If j and $j'$ are scheduled in the first two positions or in the last two positions, then total setup time for $c_e$ is 2.

• If j and $j'$ are scheduled in consecutive positions p and $p+1$, respectively, with $p=2,\ldots ,n-2$ or in positions 1 and n, then total setup time for $c_e$ is 3.

• If j and $j'$ are scheduled in non-consecutive positions p and $p'$, respectively, with $p=1$ and $2<p'<n$ or $1<p<n-1$ and $p'=n$, then total setup time for $c_e$ is 4.

• If j and $j'$ are scheduled in non-consecutive positions p and $p'$, respectively, with $1<p<p'-1<n'-1$, then total setup time for $c_e$ is 5.

Now, we analyze the total setup time in a given schedule $\sigma$ and distinguish two cases.

• If there is a characteristic $c_e\in C_{\sigma (1)}\cap C_{\sigma (n)}$, then the total setup time for characteristics in $C_{\sigma (1)}\cup C_{\sigma (n)}$ is at least

  $$\begin{aligned}&LB_1=\underbrace{1\cdot 3}_{c_e}\nonumber \\&\quad +\underbrace{2\cdot 2}_{LB'_1}+2\cdot 4=15. \end{aligned}$$

  Obviously, the total setup time for $c_e$ is 3. If and only if $C_{\sigma (1)}\cap C_{\sigma (2)}\ne \emptyset$ ($C_{\sigma (n-1)}\cap C_{\sigma (n)}\ne \emptyset$), the total setup time for the characteristic in $C_{\sigma (1)}\cap C_{\sigma (2)}$ (in $C_{\sigma (n-1)}\cap C_{\sigma (n)}$) is 2 leading to partial lower bound $LB'_1$. The total setup time for at least one characteristic of $\sigma (1)$ and at least one characteristic of $\sigma (n)$ is 4 leading to the last term in $LB_1$. Hence, total setup time for characteristics in $C_{\sigma (1)}\cup C_{\sigma (n)}$ equals 15, if $C_{\sigma (1)}\cap C_{\sigma (2)}\ne \emptyset$ and $C_{\sigma (n-1)}\cap C_{\sigma (n)}\ne \emptyset$ and exceeds 15 otherwise.

  Among the $1.5\cdot |V|-5$ other characteristics at most $|V|-3$ can have total setup time of 3. In fact, if $C_{\sigma (k)}\cap C_{\sigma (k+1)}\ne \emptyset$, $k=2,\ldots ,n-2$, then total processing time of $c_e$ with $e=\{\sigma (k),\sigma (k+1)\}$ is 3. This leads to a total setup time for the $1.5\cdot |V|-5$ remaining characteristics of

  $$\begin{aligned} S_1(q)&=3\cdot (|V|-3-q)+5\cdot (0.5\cdot |V|-2+q)\nonumber \\&=5.5\cdot |V|-19+2\cdot q. \end{aligned}$$

  with q being the number of pairs of consecutive jobs in $\sigma (2),\ldots ,\sigma (n-1)$ having no characteristic in common. We, thus, obtain a lower bound of the total setup time for all characteristics of

  $$\begin{aligned} LB(q)&=LB_1+S_1(q)=15+5.5\cdot |V|-19+2\cdot q\nonumber \\&=5.5\cdot |V|-4+2\cdot q. \end{aligned}$$

  Furthermore, a total setup time of $LB(0)=5.5\cdot |V|-4$ is achieved, if and only if $C_{\sigma (k)}\cap C_{\sigma (k+1)}\ne \emptyset$ for each $k=1,\ldots ,n-1$.

• If $C_{\sigma (1)}\cap C_{\sigma (n)}=\emptyset$, then the total setup time for characteristics in $C_{\sigma (1)}\cup C_{\sigma (n)}$ is at least

  $$\begin{aligned} LB_2=\underbrace{2\cdot 2}_{LB'_2}+4\cdot 4=20. \end{aligned}$$

  Partial lower bound $LB'_2$ is motivated as $LB'_1$ above. The total setup time for the two remaining characteristics of $\sigma (1)$ and $\sigma (n)$, respectively, is 4 leading to the last term in $LB_2$. Hence, the total setup time for the characteristics in $C_{\sigma (1)}\cup C_{\sigma (n)}$ equals 20, if $C_{\sigma (1)}\cap C_{\sigma (2)}\ne \emptyset$ and $C_{\sigma (n-1)}\cap C_{\sigma (n)}\ne \emptyset$ and exceeds 20 otherwise.

  For the $1.5\cdot |V|-6$ remaining characteristics, we can derive a total setup time of

  $$\begin{aligned} S_2(q)\!=\!3\cdot (|V|\!-\!3\!-\!q)\!+\!5\cdot (0.5\cdot |V|\!-\!3\!+\!q)\!=\!5.5\cdot |V|\!-\!24\!+\!2\cdot q. \end{aligned}$$

  We, thus, obtain a lower bound

  $$\begin{aligned} LB(q)\!=\!LB_2\!+\!S_2(q)\!=\!20\!+\!5.5\cdot |V|\!-\!24\!+\!2\cdot q\!=\!5.5\cdot |V|\!-\!4\!+\!2\cdot q. \end{aligned}$$

  Furthermore, a total setup time of $LB(0)=5.5\cdot |V|-4$ is achieved, if and only if $C_{\sigma (k)}\cap C_{\sigma (k+1)}\ne \emptyset$ for each $k=1,\ldots ,n-1$.

For both cases, we see that the lower bound of $5.5\cdot |V|-4$ of the total setup time (and thus of the makespan) is achieved, if and only if $C_{\sigma (k)}\cap C_{\sigma (k+1)}\ne \emptyset$ for each $k=1,\ldots ,n-1$. Hence, a schedule with makespan $5.5\cdot |V|-4$ implies a Hamiltonian path in G and vice versa. This completes the proof. $\square$

Summarizing, the most restricted version of ModSetup-Seq considered in this paper is strongly NP-hard, even if either $m=2$ or $K=2$. Since ModSetup-Seq can be solved in polynomial time if both m and K are fixed, see Corollary 1, this completes the picture.

3.2 Parallel setups

This section analyzes the computational complexity of those problem cases where setups are executed in parallel, i.e., we have $s_{i,j}=\max \left\{ s_{i,j,c}\mid c\in C\right\}$ for all $i,j \in J$ with $i \ne j$.

First, we develop a positive result for the special case with $s^e_{v,c}=s^e_{c}$ and $s^r_{v,c}=s^r_{c}$ for each characteristic $c\in C$ and each value $v\in V_c$. Without loss of generality, we assume that $s^e_{c_k}+s^r_{c_k}\ge s^e_{c_{k+1}}+s^r_{c_{k+1}}$ for each $k=1,\ldots ,m-1$.

Lemma 3

There is an optimal schedule to ModSetup-Par with $s^e_{v,c}=s^e_{c}$ and $s^r_{v,c}=s^r_{c}$, where all jobs having the same value for $c_1$ are scheduled consecutively.

Proof

Consider an optimal schedule where some jobs with the same value for $c_1$ are not scheduled consecutively. Let j be the first job, which is followed by an immediate successor s(j) with $v_{j,c_1}\ne v_{s(j),c_1}$ although there is a (non-immediate) successor $j'$ with $v_{j,c_1}=v_{j',c_1}$. If there is more than one such successor, we assume that $j'$ is the first one. Let $p(j')$ be the immediate predecessor of $j'$.

We modify the schedule as follows. We postpone the subsequence of jobs $(s(j),\ldots ,p(j'))$ and move it to the end of the schedule. Now, $j'$ immediately follows j. The total setup time changes as follows.

• In the original schedule, the setup time between s(j) and its immediate predecessor j and between $j'$ and its immediate predecessor $p(j')$ is $2(s^r_{c_1}+s^e_{c_1})$. The last job in the schedule causes $\max \left\{ s^r_{c}\mid c\in C\right\}$ setup time for removing.

• In the new schedule, the setup time between s(j) and its immediate predecessor is at most $s^r_{c_1}+s^e_{c_1}$ and the setup time between $j'$ and its immediate predecessor j is at most $s^r_{c_2}+s^e_{c_2}\le s^r_{c_1}+s^e_{c_1}$. Here, also, the last job in the schedule causes $\max \left\{ s^r_{c}\mid c\in C\right\}$ setup time for removing.

Since the total setup time does not increase, the makespan does not increase either. Hence, the modification yields an optimal schedule. By repeating this step, we can achieve an optimal schedule as specified in the lemma. $\square$

To illustrate the basic idea of the proof of Lemma 3, we consider job set $J=\{1,\ldots ,6\}$, characteristics $c_1$, $c_2$, and $c_3$, and value sets $V_{c_1}=\{1,2,3\}$, $V_{c_2}=\{4,5,6\}$, and $V_{c_3}=\{7,8,9\}$. The values for these jobs and characteristics are given in Table 4, and the setup times for equipping and removing are given in Table 5. Note that we have $s^e_{v,c}=s^e_{c}$ and $s^r_{v,c}=s^r_{c}$.

Table 4 Values for jobs and characteristics

Table 5 Setup times

Figure 7 depicts a schedule where not all jobs having the same value for $c_1$ are scheduled consecutively. In this example, we have $j=3$ and $j'=6$.

Fig. 7

Schedule with jobs having the same value for $c_1$ not scheduled consecutively

The schedule in Fig. 8 is obtained from the schedule in Fig. 7 by applying the modification used in the Proof of Lemma 3. We postpone the subsequence $(s(j),\ldots ,p(j'))$, which consists of jobs 4 and 5, and move it to the end of the schedule. This modification reduces the makespan by one time unit.

Fig. 8

Schedule with jobs having the same value for $c_1$ scheduled consecutively

Theorem 3

ModSetup-Par with $s^e_{v,c}=s^e_{c}$ and $s^r_{v,c}=s^r_{c}$ for each characteristic $c\in C$ and each value $v\in V_c$ can be solved in $\mathcal {O}(n\cdot m\cdot K)$.

Proof

Lemma 3 allows to cluster jobs according to their values of $c_1$. We refer to these clusters as $c_1$-clusters. Note that between each pair of $c_1$-clusters we have a total setup time of $s^r_{v,c_1}+s^e_{v,c_1}$. Before the first $c_1$-cluster, we have a setup time of $\max \left\{ s^e_{c_k}\mid c_k\in C\right\}$ and after the last $c_1$-cluster, we have a setup time of $\max \left\{ s^r_{c_k}\mid c_k\in C\right\}$. Hence, we can sequence $c_1$-clusters in an arbitrary order. Then, jobs in each $c_1$-cluster can be sequenced independently.

Note that within each $c_1$-cluster, we can apply Lemma 3 with respect to $c_2$ instead of $c_1$. Hence, we arrange $c_2$-clusters within each $c_1$-cluster that can be sequenced in arbitrary order. At this point, we can assume that there is no setup before the first job and after the last job in each $c_1$-cluster, because the maximum possible time has been considered already between $c_1$-clusters (and before the first and after the last $c_1$ cluster). Following this line of argument, we arrange $c_{k+1}$ within $c_k$-cluster for $k=1,\ldots ,m-1$. Due to Lemma 3, this yields an optimal schedule. We can implement this cluster schedule by sorting jobs lexicographically using radix sort in $\mathcal {O}(n\cdot m\cdot K)$. $\square$

For the instance depicted in Figs. 7 and 8, we have an optimal schedule derived by sorting jobs lexicographically illustrated in Fig. 9.

Fig. 9

Optimal schedule

The most general case of ModSetup-Par, however, turns out to be NP-hard. We show this result by a transformation from the path version of the geometric traveling salesman problem with maximum metric, abbreviated to PATH-TSP-MAX. Note that the geometric traveling salesman problem with maximum metric is strongly NP-hard, see Garey and Johnson (1979). It follows easily that the problem to find a shortest path with a given start point u and a given end point v that visits all other points exactly once is strongly NP-hard, as well.

${{{\mathbf {{\small {\uppercase {PATH-TSP-MAX}}}}}}:}$ Given a set $P\subseteq Z\times Z$ of (integer) points in the plane, two specified points $u,v\in P$, and a positive integer B, is there a simple path of length B or less (with respect to the maximum metric) that starts in u, ends in v, and visits every point exactly once?

Theorem 4

ModSetup-Par is strongly NP-hard, even if $m=6$.

Proof

For an arbitrary instance I of PATH-TSP-MAX, e.g., a set P of points, a start point $u\in P$, an end point $v\in P$, and an integer B, we construct an instance $I'$ of ModSetup-Par with $m=6$ characteristics $c_1$ to $c_6$ as follows. Without loss of generality, we assume the smallest coordinates in I in both dimensions to be zero. Additionally, we assume that coordinates are not larger than B, since otherwise the answer to I trivially is no. Summarizing, we assume $0\le p_x\le B$ and $0\le p_y\le B$ for each $p=(p_x,p_y)\in P$.

For each point $p\in P$, we introduce a job p requiring unique values $v_{p,c_1}=p_1$, $v_{p,c_2}=p_2$, $v_{p,c_3}=p_3$, $v_{p,c_4}=p_4$, $v_{p,c_5}=p_5$, and $v_{p,c_6}=p_6$ for characteristics $c_1, c_2, c_3, c_4, c_5$, and $c_6$, respectively. For each job p, $p\ne u$ and $p\ne v$, the resulting setup times for equipping and removing are

• $s^e_{p_1,c_1}=p_x$ and $s^r_{p_1,c_1}=B-p_x$ for characteristic $c_1$,

• $s^e_{p_2,c_2}=B-p_x$ and $s^r_{p_2,c_2}=p_x$ for $c_2$,

• $s^e_{p_3,c_3}=p_y$ and $s^r_{p_3,c_3}=B-p_y$ for $c_3$,

• $s^e_{p_4,c_4}=B-p_y$ and $s^r_{p_4,c_4}=p_y$ for $c_4$,

• $s^e_{p_5,c_5}=B$ and $s^r_{p_5,c_5}=0$ for $c_5$ and

• $s^e_{p_6,c_6}=0$ and $s^r_{p_6,c_6}=B$ for $c_6$.

For jobs u and v, setup times for equipping and removing are

• $s^e_{u_1,c_1}=0$, $s^e_{v_1,c_1}=v_x$, $s^r_{u_1,c_1}=B-u_x$, and $s^r_{v_1,c_1}=0$ for $c_1$,

• $s^e_{u_2,c_2}=0$, $s^e_{v_2,c_2}=B-v_x$, $s^r_{u_2,c_2}=u_x$, and $s^r_{v_2,c_2}=0$ for $c_2$,

• $s^e_{u_3,c_3}=0$, $s^e_{v_3,c_3}=v_y$, $s^r_{u_3,c_3}=B-u_y$, and $s^r_{v_3,c_3}=0$ for $c_3$,

• $s^e_{u_4,c_4}=0$, $s^e_{v_4,c_4}=B-v_y$, $s^r_{u_4,c_4}=u_y$, and $s^r_{v_4,c_4}=0$ for $c_4$,

• $s^e_{u_5,c_5}=0$, $s^e_{v_5,c_5}=B$, $s^r_{u_5,c_5}=0$, and $s^r_{v_5,c_5}=0$ for $c_5$ and

• $s^e_{u_6,c_6}=0$, $s^e_{v_6,c_6}=0$, $s^r_{u_6,c_6}=B$, and $s^r_{v_6,c_6}=0$ for $c_6$.

This completes the reduction which is pseudo-polynomial. The question we ask is whether there is a schedule with a total setup time of at most $|P|\cdot B$.

A parallel setup of characteristics $c_1$ and $c_2$ from a job p ($p\ne v$) to a job q ($q\ne u$) requires $\max \{B-p_x+q_x;p_x+B-q_x\}=B+\max \{q_x-p_x;p_x-q_x\}$ time units. Analogously, a parallel setup of $c_3$ and $c_4$ from p ($p\ne v$) to q ($q\ne u$) requires $B+\max \{q_y-p_y;p_y-q_y\}$. Thus, a parallel setup of all characteristics $c_1$ to $c_6$ from p ($p\ne v$) to q ($q\ne u$) requires $B+\max \{q_x-p_x;p_x-q_x;q_y-p_y;p_y-q_y;0\}=B+d_\infty (p,q)$ time units with $d_\infty (p,q)$ denoting the distance between the corresponding points p and q in I. Consequently, a YES-certificate of I with a length at most B directly corresponds to a YES-certificate of $I'$ with the total setup time of $|P|\cdot B$.

For the opposite direction, suppose an arbitrary schedule for $I'$ with a total setup time of at most $|P|\cdot B$. We, first, establish that this schedule necessarily starts with u and ends with v. The total setup time for both $c_5$ and $c_6$ is $(|P|-1)\cdot B$. Hence, we have a total setup time for $c_5$ and $c_6$ combined of at least $|P|\cdot B$ (and, thus a total setup time of more than $|P|\cdot B$ since setup times between jobs for $c_1$ to $c_4$ exceed B) unless the positive setup times for $c_5$ and $c_6$ occur in the same $|P|-1$ gaps between jobs. The latter can only be achieved when having u and v in the first and the last position, respectively.

Thus, the schedule directly corresponds to a path from u to v and due to the analogy between setup times between jobs and distances between points the path has a length of at most B. This completes the proof. $\square$

Next, we add another complexity result that proves strong NP-hardness, if instead the maximum number K of distinct values over all characteristics is restricted. We show NP-hardness by a reduction from the problem to find a Hamiltonian path in a graph, abbreviated to Ham, which is strongly NP-complete, see Garey and Johnson (1979).

Theorem 5

ModSetup-Par is strongly NP-hard, even if $K=3$ and $s^e_{v,c}=s^r_{v,c}$ for all $c\in C$ and $v\in V_c$.

Proof

We consider an arbitrary instance I of Ham given by a graph $G=(V,E)$ with $V=\{1,\ldots ,|V|\}$. We construct an instance $I'$ of ModSetup-Par as follows.

• For each vertex $i\in V$, we have a job i in $I'$.

• For each pair (j, k) of vertices with $j<k$ of I, we introduce a characteristic $c_{j,k}$ in $I'$. In the following, we call these characteristics edge-characteristics.

  • The set of values for edge-characteristic $c_{j,k}$ is $V_{j,k}=\{j,k,0\}$.

  • For edge-characteristic $c_{j,k}$, job j receives value $v_{j,c_{j,k}}=j$, job k has value $v_{k,c_{j,k}}=k$, and each other job i, $i\ne j$ and $i\ne k$, has value $v_{i,c_{j,k}}=0$.

  • We set $s^e_{j,c_{j,k}}=s^r_{j,c_{j,k}}=s^e_{k,c_{j,k}}=s^r_{k,c_{j,k}}=0$, that is equipping edge-characteristic $c_{j,k}$ with j or k or removing j or k from $c_{j,k}$ takes no time, if $\{j,k\}\in E$. If $\{j,k\}\not \in E$, we set $s^e_{j,c_{j,k}}=s^r_{j,c_{j,k}}=s^e_{k,c_{j,k}}=s^r_{k,c_{j,k}}=1$. Finally, we set $s^e_{0,c_{j,k}}=s^r_{0,c_{j,k}}=0$.

• For each vertex $i\in V$, we introduce a characteristic $c_i$ in $I'$. In the following, these characteristics are called vertex-characteristics.

  • The set of values for vertex-characteristics $c_{i}$ is $V_{i}=\{i,0\}$.

  • For vertex-characteristic $c_i$, job i receives value $v_{i,c_{i}}=i$, whereas each other job j, $j\ne i$, has value $v_{j,c_{i}}=0$.

  • We set $s^e_{0,c_i}=s^r_{0,c_i}=0$, that is equipping vertex-characteristic $c_{i}$ with value 0 or removing value 0 from $c_{i}$ takes no time. Furthermore, we set $s^e_{i,c_i}=s^r_{i,c_i}=1$.

Thus, we have |V| jobs and $0.5\cdot |V|\cdot (|V|-1)+|V|$ characteristics each having at most 3 values. The reduction is pseudo-polynomial.

The question we ask is whether there is a schedule with a makespan of at most $|V|+1$. For each job i, we have at least a setup time of $s^e_{i,c_i}=1$ for equipping characteristic $c_i$ with value i and, for the last job $i'$, we have at least a setup time of $s^r_{i',c_{i'}}=1$ for removing $i'$ from $c_{i'}$. Thus, $|V|+1$ is a lower bound for the makespan in $I'$ due to the vertex-characteristics.

We can achieve a makespan of $|V|+1$ only if we do not have two consecutive jobs j and k, such that $\{j,k\}\not \in E$. These jobs would incur a total setup time of $s^r_{j,c_{j,k}}+s^e_{k,c_{j,k}}=2$ in between. However, for a pair of consecutive jobs j and k, such that the corresponding nodes are adjacent in I, we have a total setup time of 0 for each edge-characteristic. This completes the proof. $\square$

Summarizing, similar as for ModSetup-Seq problem ModSetup-Par is strongly NP-hard, even if either m or K are fixed. On the other hand, ModSetup-Par can be solved in polynomial time if both m and K are fixed, see Corollary 1, or setup times are not value-dependent, see Theorem 3.

4 Conclusions and outlook

This paper investigates the well-known machine scheduling problem $[1|s_{ij}|C_{\max }]$ for the special case of modular products. In a mass-customization environment, modular products allow customers to individually specify their products by selecting a specific value (e.g., a specific PU foam) for different product characteristics (e.g., the insulation of a garage door) and each value is realized by a dedicated component assembled into the product. If each component requires a specific resource (e.g., the cartridge containing the selected PU foam) during the assembly process, which need not be changed whenever two subsequent jobs share the respective value of the product characteristic, then the setup matrix becomes specially structured and depends on the similarity of products. We provide an in-depth analysis of computational complexity for different problem cases with modular products. Specifically, we distinguish whether resource setups are executed sequentially or in parallel and consider removal operations as well as special setup times. We show that for some cases with parallel setups, our detailed view on the special structure of setups is worthwhile and provides an algorithm finding optimal solutions in polynomial time. Other problem cases are shown to be strongly NP-hard, so that the complexity status compared to $[1|s_{ij}|C_{\max }]$ remains unaltered. Note that the producer of sectional garage doors that brought the peculiarities of modular setups to our attention applies a single worker for setups, so that the sequential setups render their machine scheduling problem strongly NP-hard.

Future research should investigate the leftover problem case, whose complexity status is still open. This case considers parallel resource setups, no removal operations $s^r_{v,c}=0$, and general setup times $s^e_{v,c}\ge 0$. Furthermore, developing exact and heuristic solution procedures for the strongly NP-hard problem cases is a valid task for future research. Such procedures should exploit the special structure of the setup matrices and could, for instance, apply our efficiently solvable problem case as a bounding argument.