Phase diagram of YbZnGaO₄ in applied magnetic field

Abstract

Recently, Yb-based triangular-lattice antiferromagnets have garnered significant interest as possible quantum spin-liquid candidates. One example is YbMgGaO₄, which showed many promising spin-liquid features, but also possesses a high degree of disorder owing to site-mixing between the non-magnetic cations. To further elucidate the role of chemical disorder and to explore the phase diagram of these materials in applied field, we present neutron scattering and sensitive magnetometry measurements of the closely related compound, YbZnGaO₄. Our results suggest a difference in magnetic anisotropy between the two compounds, and we use key observations of the magnetic phase crossover to motivate an exploration of the field- and exchange parameter-dependent phase diagram, providing an expanded view of the available magnetic states in applied field. This enriched map of the phase space serves as a basis to restrict the values of parameters describing the magnetic Hamiltonian with broad application to recently discovered related materials.

Introduction

Recent years have seen renewed interest in triangular-lattice antiferromagnets featuring anisotropic interactions and other traits conducive to exotic quantum ground states, particularly in the hunt for experimental realizations of quantum spin liquids. Mapping the phase diagrams of these materials is thus of paramount importance, as the variation in magnetic anisotropy, relative exchange coupling strengths, and corresponding magnetic Hamiltonians offered by different materials are fundamentally important to the pursuit of such states.

One system that sparked an explosion of experimental and theoretical interest is the triangular-lattice antiferromagnet YbMgGaO₄, which has led to a broad research effort that currently involves a number of related compounds^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}. There are two important physical aspects of this group of materials that have become clear due to recent insights. Because of the localized nature of the f-orbitals, the ranges of the effective spin-spin interactions in these insulating materials are strongly limited, implying that all of the Kramers-ion-based materials are expected to be closely described by the same nearest-neighbor anisotropic-exchange model with the parameters that are permitted by triangular-lattice symmetry^17,18,19,20. This reasonably compact model should provide a consistent interpretation of the current and future experiments and give important new insights into fundamental properties of these materials²¹.

The second generic feature is the strong effect of disorder observed in some of the well-studied representatives of these compounds. It has been argued theoretically that even a benign form of bond disorder necessarily generates perturbations that are relevant in the Imry-Ma sense^22,23,24, making a consideration of the defects an inevitable and essential part of a realistic description of most anisotropic-exchange magnets. Empirically, many of the newly synthesized materials seem to show no magnetic ordering^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}. Then, given the strong disorder effects, it is a question whether the non-magnetic ground states of these materials are due to a genuine quantum-disordered spin-liquid (SL) phase, or due to a scenario similar to the disorder-induced “spin-liquid mimicry,” suggested for YbMgGaO₄²³.

There is also an intriguing broader question on whether the disorder-induced spin-liquid-like behavior retains any of the unique and desired properties of the intrinsic spin liquids, thus potentially turning disorder into a feature rather than an obstacle^25,26,27. A counterintuitive example of the role of disorder in a related material is the case of NaYbO₂, where introducing Na⁺ site vacancies leads to an antiferromagnetic transition at a few Kelvin and thus disorder supports an ordered phase²⁸. Further understanding and insight into the role of disorder are needed to make progress in this direction.

One of the persistent issues in the studies of the anisotropic-exchange magnets in general and of the rare-earth family in particular is the identification of their model parameters²⁹. In the case of the disorder-induced pseudo-SL state, this problem is further aggravated, as it is not clear what state the disorder-free system would have assumed. In this work, we propose that the experimental and theoretical investigations of the field-induced phases offers a powerful instrument to significantly narrow the allowed parameter space to a region that is consistent with the material’s phenomenology.

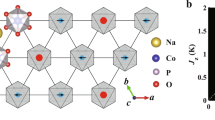
In YbMgGaO₄ and YbZnGaO₄, the source of disorder is due to the $R\bar{3}m$ symmetry, leading to fifty–fifty site-mixing of the non-magnetic cations Mg²⁺ or Zn²⁺ with the Ga³⁺. Efforts to determine the exchange parameters for placing YbMgGaO₄ in proposed phase diagrams and otherwise comparing to the numerous theoretical investigations to affirm or deny a QSL state were obstructed by the various broadening effects and consequentially enhanced uncertainty in the measurements. Several studies concentrated their efforts on further refining measurements of the exchange parameters^30,31.

In this work, we provide a detailed study of the field-induced effects and characteristics of YbZnGaO₄ and offer comparison with the results in YbMgGaO₄³¹. Informed by measurements from high-resolution magnetometry and a variety of neutron scattering techniques, we put forward a theoretical analysis of the structure of their field-induced phase diagram and propose a parameter region for both materials that is compatible with our empirical findings.

Results

Preliminary characterization

Susceptibility measurements on a 1.81 mg single-crystal sample of YbZnGaO₄ conducted using an in-house Cryogenic S700X SQUID magnetometer (with 3He probe) yield low-temperature fits, suggesting Curie-Weiss temperatures of Θ_CW = −2.67 K and Θ_CW = −2.62 K for parallel and perpendicular to the sample c axis, respectively (see Supplementary Fig. 4). These values are more isotropic than those reported for YbMgGaO₄ or for YbZnGaO₄ in earlier works (though YbZnGaO₄ was also more isotropic than YbMgGaO₄ in those measurements)³².

We emphasize that while the difference in the Curie-Weiss temperature for the in-plane vs out-of-plane field has initially suggested a rather strong easy-plane character of YbMgGaO₄³³, the subsequent spectroscopic studies have hinted at a rather moderate XXZ anisotropy, yielding a nearly Heisenberg value of Δ = 0.8–0.9³⁰. In the case of YbZnGaO₄, Curie-Weiss temperatures for the in-plane and out-of-plane fields from our measurements and those of earlier works³² are much closer to the Heisenberg limit. Given the trend, this indicates that the anisotropy in YbZnGaO₄ may, in fact, be of the easy-axis type. A more direct demonstration of that is offered by the results that are discussed in Sec. “Tunnel diode oscillator technique and SQUID magnetization”.

A unique opportunity afforded by a close comparison between YbMgGaO₄ and YbZnGaO₄ is the qualitative contrast of the effect of the cation substitution on the disorder between the two materials. One obvious consideration is the differing ionic radii of the Mg²⁺ and Zn²⁺, which are ~72 and 74 pm, respectively (a 2.7% difference). This small difference yields slightly smaller lattice parameters for YbMgGaO₄ when compared to YbZnGaO₄, as shown by comparison of parameters given by refs. ³⁴ and ³², respectively, which, in turn, may yield marginally stronger exchange for YbMgGaO₄, also explaining the smaller Curie-Weiss temperatures and lower field onset for the anomaly discussed in Sec. “Tunnel diode oscillator technique and SQUID magnetization” for YbZnGaO₄. This is consistent with the observation that the related compound NaYbO₂, with an in-plane lattice parameter smaller by only about 1.8% from YbMgGaO₄, shows a significantly larger Curie-Weiss temperature (Θ_CW = −10.38 K¹² as opposed to −4 K for YbMgGaO₄)³¹. Furthermore, both Zn²⁺ and Ga³⁺ have d¹⁰ electronic configurations, whereas Mg²⁺ is p⁶. While the displacement of Yb³⁺ can still be expected based on the charge difference between the cations, leading to the observed broadening in inelastic neutron scattering studies of the single-magnon dispersion and crystal electric field levels³⁵, the local environment may be more homogeneous for YbZnGaO₄, and may be related to the difference in anisotropic response under field. However, further studies will be required to compare the effective role of disorder between the two systems.

Tunnel diode oscillator technique and SQUID magnetization

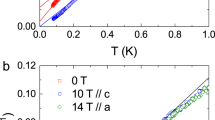
The first indications of the magnetic transitions in YbZnGaO₄, which are similar to the ones we have previously identified in YbMgGaO₄³¹, were found using the tunnel diode oscillator (TDO) technique (see methods). As the applied magnetic field is changed, the sample magnetization M(H) with respect to field is altered, thus changing the inductance of the coil and the measured resonant frequency of the circuit, yielding a signal proportional to χ(H). From Figure 1a, where the change in resonant frequency is plotted versus the applied field, a clear nonlinearity is apparent beginning just below 1 T. This nonlinearity persists to at least 2 T for the field parallel to sample c axis. Upon raising the temperature, the feature is completely suppressed at about 4 K, affirming its magnetic origin. This behavior is also consistent with a similar feature in YbMgGaO₄³¹. As the sample orientation is rotated with respect to the field, the anisotropic response is made apparent, with the feature encompassing a broader range of the field for H⊥c. This feature is confirmed by more conventional magnetization and susceptibility measurements carried out using the in-house SQUID magnetometer with a 3He probe in temperatures down to 300 mK. The same distinct plateau-like feature is apparent in the χ(H) in both TDO and SQUID measurements, as is clear from Fig. 1d, e. Integrating the change in frequency with respect to applied field yields a curve consistent with magnetization as measured in SQUID (see Fig. 1c). We note that the anomaly in YbZnGaO₄ measured via TDO and SQUID magnetization occurs at a slightly lower field compared to the analogous feature measured in YbMgGaO₄³¹ (see Supplementary Fig. 5).

Fig. 1: Tunnel diode oscillation (TDO) frequency and ac susceptibility.

a TDO (Δf/f ∝ ΔM/ΔH) shows an anomaly for H∥c, which weakens as temperature increases b The anomaly shows anisotropic response in applied field, and is more pronounced for H∥c (curves offset for clarity in b). c M(H) measured with SQUID corroborates TDO measurement when Δf is integrated with respect to field. d,e dM/dH from SQUID compares very favorably with TDO signal. f Frequency-dependent cusps measured with low-temperature ac susceptibility. g Comparison of critical temperatures measured in this work for YbZnGaO₄ to earlier measurements by Ma et al.³².

The features in the magnetization derivative and tunnel diode oscillator technique (TDO) measurements in both in-plane and out-of-plane fields are reminiscent of the plateau-like behavior that is expected in the canonical Heisenberg or XXZ nearest-neighbor triangular-lattice magnets³⁶. Importantly, the TDO and magnetization measurements in YbZnGaO₄ and YbMgGaO₄, together with the Curie-Weiss extrapolations from the susceptibility mentioned above, suggest an important distinction between the two materials. The effects of the in-plane and the out-of-plane field directions show different behavior as a function of the field orientation—compare Fig. 1b of this work and Figure 1c in ref. ³¹. Specifically, the relative severity of the anomaly in TDO data in YbZnGaO₄ in H∥c are resemblant of that in H⊥c data of YbMgGaO₄, and vice versa. This suggests that YbZnGaO₄ and YbMgGaO₄ correspond to different types of the XXZ anisotropy, the easy-axis and the easy-plane, respectively.

ac susceptibility and disorder

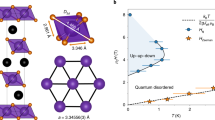
From our measurements of ac susceptibility of YbZnGaO₄ (see Fig. 1f), we find critical temperatures corresponding to the characteristic cusps of the ac susceptibility occur at substantially lower temperatures than previously measured³². Indeed, our characteristic temperatures are around 20%−30% lower for all comparable frequencies—see Fig. 1g. Consequently, for our measurement of ${{\Delta }}P=\frac{{{\Delta }}{T}_{{{{\rm{f}}}}}}{{T}_{{{{\rm{f}}}}}{{\Delta }}{{\mathrm{log}}}\,(\omega )}$, a quantitative measure of the freezing temperatures per decade of frequency, we find a value of ΔP = 0.139(4), substantially larger than the ΔP = 0.053(4) of previous work. This value of ΔP is typically associated with superparamagnetic behavior³⁷ as opposed to spin glasses. That being said, insulating spin glasses typically show greater frequency dependence³⁷. If this ΔP is interpreted as indicative of superparamagentic behavior, it may be understood as a consequence of many microscopic domains with insignificant cooperative freezing. This phenomenon is likely due to disorder, but further suppression of the freezing temperature could be attributed to the high degree of frustration as well as disorder. The percentage of frozen spins is estimated to be ~16% (see Supplementary Fig. 9), comparable to the previous study³² and to the case of YbMgGaO₄³³.

General questions about the effects of disorder in spin systems persist, especially in light of its aforementioned potential relationship to QSL states for some materials^25,26,27. The origin and effects of disorder related to the observed spin-liquid features of YbMgGaO₄ have been addressed earlier^23,35.

Neutron scattering

For this work, diffuse neutron scattering data were collected at CORELLI at Oak Ridge National Laboratory in total-scattering mode (see Fig. 2). The sample was aligned with the [h, k, 0] scattering plane, and applied field along the sample c axis. Data were collected at 130 mK for 0, 1, 1.5, 2, 3, 4, and 5 T. Color maps of the neutron scattering intensity after subtracting the 20 K as background reveal the evolution of the magnetic structure, which is qualitatively comparable to the YbMgGaO₄ data. With no applied field, the intensity largely resides at the high-symmetry M points on the edges of the Brillouin zone. At 1 T the scattering intensity is almost completely uniform along the zone edge, while at 1.5 T the intensity is found predominantly at the high-symmetry K-points. Intensity at the M points is well established to correspond to stripe-ordered states in long-range ordered triangular systems, while intensity at the K-point is generally suggestive of 120 °-type ordering or other three-sublattice states²⁰. As in the case of YbMgGaO₄, this migration of the scattering intensity with applied field corresponds to the anomaly observed in the magnetometry data. The changes in intensity were further confirmed by measurements with the triple-axis spectrometer at spin polarized inelastic neutron spectrometer (SPINS; see Supplementary Fig. 7).

Fig. 2: Diffuse neutron scattering in applied field.

a–g show evolution of diffuse neutron scattering with increasing applied field for H∥c for data integrated over 0.5 < L < 0.5. h Integrations of line cuts across the first BZ edge, where the uncertainty represents one standard deviation. Sample temperature was 130 mK and a 20 K background was subtracted to isolate magnetic contributions.

We further measured inelastic neutron scattering (INS) from a YbZnGaO₄ single-crystal sample at Cold Neutron Chopper Spectrometer (CNCS)³⁸ in applied field (see Fig. 3) at Oak Ridge National Laboratory. Here, we again see a clear evolution of the intensity as a function of energy and Q with increasing applied field. We note that at low field the intensity is notably concentrated on the M points. The intensity has no clear dispersion up to about 3 T, but instead consists of a broad continuum, similar to the 0 T with weakening intensity as the spins are presumably canted further from the scattering plane with increased field. At 4 T, the scattering remains broad in energy, but a dispersion is faintly visible at low energy along the zone edge. This dispersion has minima at the zone edges and rises as it approaches the Γ points. The shape of this dispersion closely resembles what is measured in the polarized state measured at 8 T, indicating that the system is approaching polarization. At 8 T the system is nearly completely polarized, and a clear dispersion is evident. As in the case of YbMgGaO₄³³, the dispersion is broadened, likely due to the disorder and the resulting distribution of exchange parameters and g-factors.

Fig. 3: Inelastic neutron scattering in applied field.

Panels a–e show evolution of inelastic neutron scattering with increasing applied field for H∥c for integer fields from 0 to 4 T, where the 8 T data (where magnetic excitations have been lifted to above 1.2 meV) has been used for background subtraction). Panels f and g are calculated using SpinW for 0 T (stripe yz) and 2.5 T (V-state), respectively, with a summation from three possible magnetic domain orientations related by 2π/3 rotation. to best compare to the short-range order observed in experiment. Parameters used for SpinW calculations are (in meV) J = 0.15, J_±± = − 0.0045, J_z± = 0.045, J_zz = 0.165, J² = 0.0075, ${J}_{zz}^{2}=0.00825$, g_∥ = 3.82, such that J_±±/J = − 0.03, and J_z±/J = 0.3. The dashed lines of f and g indicate the minimum and maximum energies for the 2-magnon dispersion for the domains. h shows 8 T dispersion, and a dotted line indicating the calculated curve from LSWT for the parameters described above. Experimental data are shown for an integration perpendicular to the path direction of width Q = 0.36 Å⁻¹. Cuts for experimental data were generated using Horace⁶¹.

Additional measurements to characterize YbZnGaO₄’s response to applied field were conducted using polarized neutrons at BT7³⁹ at the National Institute of Standards and Technology, with a vertical guide field set up (see Supplementary Fig. 8). After subtracting background measurements (40 K) from base (0.3 K) and correcting for the polarization rate, comparison of the spin flip (SF, measuring the in-plane component) shows a stronger in-plane component along the zone edge at 0 T, compared to 2 T, with particularly high intensity in the vicinity of the high-symmetry M point, likely affirming increased canting of the spins with increasing field, but also possibly indicating a reduced spin component parallel to the zone edge (pointing to nearest neighbors in real space). This greater intensity near the zone edge for the SF scattering at 0 T can also be seen in the orthogonal cut from M to Γ.

Measurements at disk-chopper spectrometer (DCS) time-of-flight spectrometer⁴⁰ (see Supplementary Fig. 6, which shows an equivalent cut at 0 T to that in Fig. 3a) and SPINS triple-axis spectrometer (see Supplementary Fig. 7, which shows constant Q scans at high-symmetry points) at the National Institute of Standards and Technology, confirm the features shown in Fig. 3 in a diversity of backgrounds and instrument setups. Thus, these INS measurements collectively show a consistent picture—a broad continuum at the zone edge that evolves with increasing applied field, while the diffuse neutron scattering data collected using CORELLI at Oak Ridge National Laboratory (see Fig. 2) reveals a field-induced transition in the underlying short-range spin correlations.

Model and zero-field phases

The interplay of the crystal field and spin–orbit coupling on the magnetic moment of the Kramers-ion results in the splitting of its levels into a well-separated doublet structure built from a mix of various spin and orbital states. The exchange interactions of the lowest doublets (pseudo-spins-$\frac{1}{2}$) are constrained only by the discrete lattice symmetry. For the triangular lattice of YbMgGaO₄ and YbZnGaO₄, this general anisotropic-exchange nearest-neighbor model is given by

$$\begin{array}{lll}{{{\mathcal{H}}}}\,=\,\mathop{\sum}\limits_{\langle ij\rangle }\left\{J\left({S}_{i}^{x}{S}_{j}^{x}+{S}_{i}^{y}{S}_{j}^{y}+{{\Delta }}{S}_{i}^{z}{S}_{j}^{z}\right)\right.\\ \qquad\,\,+\,2{J}_{\pm\! \pm }\!\left[\left({S}_{i}^{x}{S}_{j}^{x}-{S}_{i}^{y}{S}_{j}^{y}\right)\cos {\tilde{\varphi }}_{\alpha }-\left({S}_{i}^{x}{S}_{j}^{y}+{S}_{i}^{y}{S}_{j}^{x}\right)\sin {\tilde{\varphi }}_{\alpha }\right]\\ \qquad\,\,+\,\left.{J}_{z\pm }\!\left[\left({S}_{i}^{y}{S}_{j}^{z}+{S}_{i}^{z}{S}_{j}^{y}\right)\cos {\tilde{\varphi }}_{\alpha }-\left({S}_{i}^{x}{S}_{j}^{z}+{S}_{i}^{z}{S}_{j}^{x}\right)\sin {\tilde{\varphi }}_{\alpha }\right]\right\},\end{array}$$

(1)

where bond angles ${\tilde{\varphi }}_{\alpha }$ are that of the primitive vectors of the lattice with the x axis, ${\tilde{\varphi }}_{\alpha }\,=\,\{0,2\pi /3,-2\pi /3\}$. The J_±± and J_z± bond-dependent terms are due to the strong spin–orbit coupling¹⁷.

The zero-field phase diagram of the model (1) with an additional second-nearest-neighbor exchange J₂ has been studied extensively^{17,19,20,41,42,43,44}, and its three-dimensional (3D) classical version is shown in Fig. 4 in the J₂-J_±±-J_z± axes for Δ = 1, with all couplings in units of J > 0.

Fig. 4: A simplified classical zero-field J₂-J_±±-J_z± phase diagram of the model (1).

Dashed red line marks a representative value of the J₂ term used for all panels of Fig. 5.

There are three main ordered states in the antiferromagnetic limit of the XXZ interaction: a coplanar three-sublattice 120° state, which corresponds to the ordering vector at K-points, a collinear stripe-x two-sublattice state with spins pointing along the nearest-neighbor bonds and the ordering vector at M points, and a second collinear stripe-yz state with the same ordering vector but spins tilted out of the lattice plane and perpendicular to the nearest-neighbor bonds.

We should note that the phase diagram in Fig. 4 is simplified. The simplification comes from only taking the single-Q spiral ansatz that does not include more complicated multi-Q states^42,44. Moreover, the quantum version of the phase diagram also has a spin-liquid phase^19,20, which is located along the tricritical boundary between stripe and 120° states for a limited range of the XXZ anisotropy near the Heisenberg limit.

Exploring the XXZ parameter space

One of the puzzling features observed in some of the first experiments in YbMgGaO₄³⁴ was an indication of the field-induced phase crossovers seen in magnetic susceptibility. Recent susceptibility and TDO measurements of YbMgGaO₄ have further supported these observations³¹. Here, we present a variety of measurements on high-quality single-crystal samples to show that very similar features, indicating field-induced crossovers for both H∥c and H⊥c, also occur in YbZnGaO₄.

The neutron scattering measurements in the out-of-plane magnetic field H∥c³¹, also indicated a field-induced crossover and brought another piece of evidence to light. Neutron diffraction has showed that the field-induced crossover is accompanied by a shift of magnetic intensity from the M-points at the lower fields to K-points at the higher fields. In an ordered state, such an intensity shift would correspond to a transition from a four-sublattice to a three-sublattice state. Our key finding is that this feature alone allows one to put strong boundaries on the exchange parameters of the system when the phase diagram of relevant parameters is considered.

From the susceptibility data presented above and as established by earlier work in the case of YbMgGaO₄, YbZnGaO₄ can be characterized as easy-axis anisotropy while YbMgGaO₄ is easy-plane. Therefore, in the following we use two representative values of XXZ anisotropy for the model (1), the easy-plane case Δ = 0.8 that is related to YbMgGaO₄, and the easy-axis case Δ = 1.1 as related to YbZnGaO₄.

First, we explore the parameter region that would allow for a transition from the four-sublattice to the three-sublattice state at some finite value of the out-of-plane magnetic field H_c using classical energy minimization. We fix the second-nearest-neighbor coupling J₂ to the value 0.05J (red line in Fig. 4) and the XXZ anisotropy in the model (1) to the two values discussed above. That leaves the bond-dependent anisotropies J_±± and J_z± and the field as the parameters to scan through. We highlight our findings in Fig. 5a, b in the form of an intensity plot of the field H_c of such a four-to-three-sublattice transition in units of the saturation field, H_c/H_s, and in the J_±±–J_z± axes (in units of J). The 120° phase is a three-sublattice state already at zero-field and remains such for all the fields, while most of the stripe phase regions remain four-sublattice throughout the entire field range.

Fig. 5: Phase diagrams in zero-field as a function of bond-dependent parameters and applied field.

a Intensity plot of H_c/H_s in J_z±−J_±± axes for Δ = 1.1, J₂ = 0.05J. H_c is the critical field of the transition from the four- to three-sublattice state, H_s is the saturation field. Dot represents parameter set used in SpinW calculations. H was scanned in steps of 0.1 and units of gμ_BJ, equivalent to steps of 0.021 in terms of H_c/H_s for H_s = 4.815. b Same as in a for Δ = 0.8, where step size in H_c/H_s was 0.026 corresponding to H_s = 3.87. c Intensity plot of the magnetic susceptibility, χ = dM/dH, in the J_z±−H plane for Δ = 1.1, J₂ = 0.05J, and J_±± = 0. Singularities correspond to phase transitions. d Same as in c for Δ = 0.8.

Our key finding is illustrated by the gradient-color regions interpolating between the only-three- and only-four-sublattice regions in Fig. 5a, b. They demonstrate that already at the level of our classical energy analysis, the four-to-three-sublattice transition indeed takes place at some value of H_c < H_s in a surprisingly extended region that emanates from the 120° part of the phase diagram into the stripe-yz phase and extends up to J_z± ~ J in both cases, with the intensity emphasizing how far this transition is from the saturation field H_s.

It should be noted that for S = 1/2, quantum effects in zero-field are known to broaden the stability region of the 120° phase beyond the boundaries of the classical model consideration¹⁹. Therefore, one may also expect the region of the four-to-three-sublattice transition to extend beyond the classical predictions in this work.

While one can expect that quantum effects will further stabilize and extend the field-induced three-sublattice states, we note that experimentally the 4-to-3 (or M-to-K) transition in both YbMgGaO₄ and YbZnGaO₄ occurs at a rather low field, H_c < 0.5H_s, which provides further restrictions on the possible parameter ranges. At the level of our approximations, this constraint puts YbMgGaO₄ and YbZnGaO₄ in a close proximity to the 120° phase boundary, giving the upper bound J_z±/J ≲ 0.4.

As one can see in Fig. 5a, there is a narrow region inside the stripe-x phase where the transition of interest also occurs, but it involves another transition back to the four-sublattice state at higher fields, so we do not consider it as a relevant region to the materials in question here.

Field-induced states

To provide further insights into the effects of the field, we explore the phases it can produce. In some cases, the field-induced transformation of the spin structures involves simple canting toward the field until a full saturation is reached at some H_s. However, in frustrated spin systems, or systems with anisotropic interactions, the field-evolution is more complicated. The case of the triangular-lattice Heisenberg antiferromagnet is paradigmatic in this respect³⁶, showcasing a well-known and much-studied sequence of transitions from Y to up-up-down (UUD) plateau and V states in its field-evolution toward saturation. The XXZ extension of the same model also includes noncoplanar umbrella and coplanar fan states⁴⁵. Next-nearest-neighbor interactions and anisotropies also introduce a wider variety of four-sublattice field-induced states^46,47.

However, the field-evolution of the phases of the anisotropic-exchange model (1), which combines frustration from the bond-dependent terms with that of the triangular-lattice geometry, remains largely unexplored. In this work, we offer some essential understanding and make significant steps of such an exploration.

We use the same representative values of J₂ = 0.05J and of the easy-axis and easy-plane XXZ anisotropies Δ = 1.1 and Δ = 0.8 as in Fig. 5a, b to provide an insight into the rich phase diagram of the model (1) in a field. In Fig. 5c, d, we present intensity plots of the magnetic susceptibility χ = dM/dH in the J_z±–H plane. They are obtained from the classical energy minimization of the four- and three-sublattice states in a field for the two values of the XXZ anisotropy and for J_±± = 0. Since singularities in χ correspond to the phase transitions, these figures, in fact, constitute the 2D J_z±–H phase diagrams of the model (1) at fixed Δ and J₂ along the constant-J_±± cut shown in Fig. 5a, b. Similar vertical cuts along J_z± for the other values of J_±± and J₂ are also presented below to provide an understanding of the field-evolution of different states across the other dimensions of the phase diagram.

In case of the easy-axis XXZ anisotropy in Fig. 5c, at the lower values of J_z± one can observe the expected canonical sequence of the Y-UUD-V phase transitions of the three-sublattice states in the triangular-lattice XXZ model^36,45. Their corresponding spin structures are sketched in the figure.

The field-induced behavior of the stripe states also includes multiple transitions. At the lowest field, the collinear stripe-yz spin configuration, in which spins are tilted off the basal plane of the lattice, is deformed into a noncoplanar four-sublattice state with all four spins on the elementary plaquette having different tilt angles. There is a broad crossover from this state to a structure with three spins forming an umbrella and the fourth strictly antiparallel to the magnetic field, see the sketches of the spin order in Fig. 5c. This latter state is stable in a wide field region. As the field increases further, at not too small J_z± there is a spin-flop-like transition to a similar state, umbrella with a fourth spin parallel to the field. For the yet larger values of J_z±, transition to the saturation occurs directly from this umbrella+up state via a first-order transition.

The main feature in both Fig. 5c, d, which is also our key finding, is that the region of stability of the three-sublattice states, related to the experimentally observed intensity at the K-point, expands at the larger values of the magnetic field. Therefore, there is a region of the model parameters where an evolution from the four-sublattice to the saturated state necessarily proceeds via a high-field three-sublattice state.

For the easy-axis case of Fig. 5c, this high-field state is a coplanar V state. For the easy-plane XXZ anisotropy case of Fig. 5d, the four-sublattice phases and all the discussed trends are the same, while the three-sublattice region, classically, is a single noncoplanar umbrella state, which is a canted 120° structure. We note that in the quantum case and for not too small XXZ anisotropy Δ, this umbrella state is replaced by the same sequence of Y-UUD-V phases as in Fig. 5c⁴⁵. In contrast with the large-J_z± first-order transition from the four-sublattice state to saturation, the transition from both V and umbrella states to saturation is second-order. We note that the discussed transitions agree with the prior classical Monte-Carlo simulations³¹ conducted in the context of the parameter search for YbMgGaO₄ for a narrower range of parameters.

Further evolution of the phases

Here we present further details on the field-evolution of various phases of the model (1) for different choices of J₂ and J_±±. Our Figs. 6 and 7 show the intensity plots of the magnetic susceptibility in the J_z±–H plane for the same choices of the XXZ anisotropy Δ = 1.1 and Δ = 0.8 as in Fig. 5c, d, respectively. Each row of the graphs corresponds to a different constant-J_±± cut of Fig. 5a, b and each column corresponds to a different constant-J₂ cut of the 3D phase diagram in Fig. 4.

Fig. 6: Intensity plots of the magnetic susceptibility for the easy-axis case, Δ = 1.1 and for various J₂ and J_±±.

The axes and color-scale are the same as in Fig. 5c, which is also the central panel here.

While the variations of the J_±± term simply give an elaborate dissection of what happens underneath the projected view of the intensity plots of Fig. 5a, b for J_±± = ± 0.05J cuts, it is clear that the next-nearest-neighbor interaction J₂ works strongly against the field-induced three-sublattice states. This is in accord with Fig. 4, which shows that at J₂ ≈ 0.125J the 120° state is completely eliminated from the zero-field phase diagram. The sets of parameters where no three-sublattice state is observed at any field are highlighted with a red frame in Fig. 7. There are other changes that include shrinking or expanding of the phases already described and the appearance of a canted stripe state for large J₂ and negative J_±± that occur at J_z± ≲ 0.2J and larger fields for Δ = 1.1 and for all fields for Δ = 0.8, see upper right panels of Figs. 6 and 7.

Fig. 7: Same as in Figure 6 for Δ = 0.8.

Phase diagrams without three-sublattice states are marked with the red frame.

The main takeaway from Figs. 6 and 7 is that the region of the four- to three-sublattice transition is limited by the extent of J_±± already shown in Fig. 5a, b and more strongly by the next-nearest-neighbor interaction J₂. Therefore, the experimental observations that the critical field of such a transition H_c ≲ H_s in both YMGO and YZGO put strong bounds on the anisotropic-exchange parameters. This analysis also limits next-nearest-neighbor interactions to J₂ ≲ 0.1J as only four-sublattice states survive for larger J₂.

S(Q, ω) for select parameters

In order to relate the above theoretical analysis to our experimental results for YbZnGaO₄ and YbMgGaO₄, we used SpinW⁴⁸ to calculate linear spin-wave theory (LSWT) S(Q, ω) for representative sets of parameters from the identified regions of the phase diagram that are shown by dots in Fig. 5a, b. Since the phase diagrams are for the parameters in units of the overall scale J, the latter is set to match LSWT dispersion in high fields. Comparison of the data to calculations from SpinW is inherently challenging owing to the implicit assumption in the SpinW calculations of the absence of disorder (which is necessary to reproduce the broadening in energy and Q observed in experiment). Nonetheless, for the parameters indicated in Fig. 5a we find very good qualitative agreement between calculations and data (see Fig. 3) in the absence of disorder. The SpinW optimization algorithm optmagsteep was used with iterative manual adjustment of the spin state until the stable spin state (free of imaginary modes) was found. We should note that the V state spectrum is unstable for 2.5 T near the Γ point for the chosen set of parameters. The instability is weak and may signify a transition to a more complicated multi-Q state. While the manual tweaking allows us to find a quasi-stable state with the gapped spectrum, the stable V state spectrum is gapless as any three-sublattice state of (1) with broken continuous symmetry, see also ref. ²⁰ for the 120° state spectrum.

In particular, comparing the diffuse scattering from Fig. 3a 0 T and the resolution-convolved dispersion calculated from SpinW in Fig. 3f, we note the enhanced intensity in the vicinity of M and K clearly present in both. Furthermore, the greater intensity residing in a range of energy from near the elastic line to about 0.2 meV in the calculation is clearly present, albeit undoubtedly broadened by disorder, in the experimental data. As discussed in previous works^32,33,35, disorder smears the intensity in Q and E, which would also account for the intensity visible at higher energies in the INS data.

In Fig. 3g we show the calculated dispersion using SpinW at 2.5 T, where the spins reside in the V state. The dispersion has again been convolved with the resolution of the instrument (using data available at https://rez.mcvine.ornl.gov/) for best comparison to the experimental data. Note that the intensity at the Γ point (though suppressed as discussed below) is at ~0.5 meV, as expected from comparison to the 2 and 3 T data. Furthermore, the modes above the Brillouin zone edge (which we emphasize follow from the superposition of three domains in the clean limit) offer a hint as to the the origins of the the broad continuum apparent in the data. As the field is raised, the contributions from modes above the zone edge in the SpinW calculation are reduced (compare the intensity from modes above M and K at 0 and 2 T). When the system is fully saturated, and the V-state gives way to the field-induced ferromagnetic state, the modes above the zone edge are completely absent (see the curve calculated from the analytic expression following from linear spin-wave theory superimposed on the 8 T INS data in Fig. 3h). This evolution of intensity is qualitatively consistent with that observed in the data, where broadening due to disorder smears out the modes. That is, the modes residing above the zone edge contribute to the continuum at low to intermediate field, but are reduced in intensity as the system enters the (subject-to-disorder) V-state, and are replaced by the broadened, otherwise singular mode when the system is fully polarized.

We also point out that an apparent visibility of the magnon modes in LSWT S(Q, ω) in the vicinity of the Γ point at low fields, Fig. 3f, g, and lack thereof in the experimental data, Fig. 3(a–c), can be explained by a significant interaction of the single-magnon branch with the two-magnon continuum. While the quantitative calculation of such effects in the anisotropic-exchange models is quite involved^49,50 and is beyond the scope of the present work, we, nevertheless, provide an intuitive insight into it by showing the bottom of the two-magnon continuum for three magnetic domains in Fig. 3f, g. As shown by the dashed lines in Fig. 3 for both 0 T and 2.5 T, the bottom of the continuum has lower energy than one magnon modes at the large portion of the Brillouin zone, including the Γ point. For S = 1/2 systems, such an overlap can lead to strong decays and near-complete disappearance of the well-defined magnon excitations in the corresponding range of momenta together with the other phenomena such as strong renormalization of the single-magnon branches^51,52. These effects require significant coupling between one- and two-magnon sectors—an inevitable consequence of the anisotropic-exchange terms in (1), which are allowed by the presence of strong spin–orbit coupling in the rare-earth-based and some transition-metal compounds^29,49,53.

We also note that, generally, and especially due to the presence of multiple domains, the INS signal necessarily contains not only the transverse single-magnon fluctuations, LSWT simulations of which are shown in Fig. 3f, g, but also the longitudinal component (S^zz(Q, ω) in the local spin axes). It corresponds to the two-magnon intensity in the SWT language and is not shown in the theory plots, which explains the lack of intensity in the two-magnon energy range in theoretical results relative to that observed in experiment. The role of the longitudinal response can be instead illustrated by the two-magnon density of states, shown in Supplementary Figs. 10 and 11, which are calculated for the zero-field stripe-yz state and 2.5 T V state, respectively. These results faithfully demonstrate the missing two-magnon intensity in a broad agreement with the experimental data. To demonstrate the expected extent of the two-magnon signal, we have also provided the upper boundary of the two-magnon continuum in Fig. 3f, g.

We have also calculated the 0 T S(Q, ω) for the parameters identified as appropriate for the easy-plane character of YbMgGaO₄, identified by a dot in Fig. 5b, (see Supplementary Fig. 12), which is in excellent qualitative agreement with Figure 2a of ref. ³³. We further calculated the S(Q, ω) for the field-induced polarized state, where the overall scaling of the model (given by J) was chosen for best agreement. Within the uncertainty of the broad scattering observed in experiment, this calculation also yields a very good qualitative agreement (Supplementary Fig. 13).

Discussion

The hunt for the QSL state has yielded numerous studies of interesting new compounds and underlying physical phenomena, even though the ultimate goal may remain elusive. The search for a QSL state in the context of YbZnGaO₄ and YbMgGaO₄ materials seems likely nearing its end, although one cannot claim yet with absolute certainty that the issue is completely settled⁵⁴. In the present work, we have established a potentially close description of YbZnGaO₄ and YbMgGaO₄ in a hypothetical clean limit, allowing for the implications of the disordered, real-world materials to follow. While possibly denied the coveted QSL state, a deeper understanding of the rich and diverse phase diagram of the triangular-lattice antiferromagnets is still a highly satisfying reward that will likely serve as a roadmap for future studies, in particular for designing new materials or advancing these studies to explore this rich phase diagram.

The present work seeks to advance our understanding of the phase diagram describing YbMgGaO₄, YbZnGaO₄, and many related systems. We note that our specific conclusions about these materials are a part of a greater effort to narrow down possible magnetic exchange parameters in these systems^30,31,55,56, and provide a guideline on how to address the issue of chemical disorder in real-world materials. In a very recent work³¹ by some of the same authors, the phase crossovers similar to those shown in Figs. 1 and 2 were used to constrain parameters of YbMgGaO₄, with the focus on reproducing them in the disorder-free limit, but without a broader map of the phase diagram beyond the observations offered by an optimization algorithm. Indeed, the methods used in that prior work suggest a general approach to find exchange parameters for disordered systems. By contrast, the goal of this work is to provide an expanded context of the phase diagram in which the observed crossovers can occur in principle, offering a common description for the phenomena observed in both systems.

Reflecting on what has been learned from many theoretical and experimental studies of these two compounds and related QSL candidates in the past few years, and also looking to the future pursuit of QSL materials, a few key aspects pertaining to recent rare-earth-based materials stand out. First, the rare-earth-based materials will continue to be of interest as QSL candidates for some time. Encouragingly, several numerical techniques, including exact diagonalization⁵⁴, Density Matrix Renormalization Group²³, and variational Monte-Carlo⁴⁴ have identified the presence and even the range in the parameter space of a QSL state in the phase diagram of the nearest-neighbor Hamiltonian of Equation (1), relevant to all Kramers’ ion rare-earth triangular-lattice compounds. Furthermore, the rare-earth-based materials have advantages over past QSL candidate systems, thanks to their localized f-shells that suppress longer-range exchanges, which tend to stabilize ordered states, thus requiring a less delicate parameter tuning to realize a QSL state compared to, for example, the J₁ − J₂ model⁵⁷. While there is some difficulty presented by their sensitivity to the effects of disorder, as YbMgGaO₄ and YbZnGaO₄ have shown, rare-earth- and especially Yb-based compounds continue to emerge as promising QSL candidates. For example, consider the ytterbium-based chalcogenides, which show promising QSL features and numerous phase transitions induced by an applied magnetic field^{2,7,8,9,10,11}. The precise nature of these transitions, and the locations of these materials in the phase diagram of the model of Equation (1), are not yet known. This is particularly intriguing in the context of the present study, which demonstrates that strong constraints on the parameter space may be imposed by field-induced transitions. As such, the present work will serve as a guide of the parameter space in the search of QSLs and other intriguing phenomena in frustrated triangular-lattice compounds, and will importantly benefit the materials design efforts in this field.

Altogether, we have demonstrated the power of the experimental and theoretical insights in identifying relevant parameter spaces of YbMgGaO₄ and YbZnGaO₄ and, potentially, other related materials. We have investigated their field-induced phases and have shown that despite their disorder-induced pseudo-SL ground states, we can significantly narrow the allowed regions of their phase diagram that are compatible with the phenomenologies of these materials. Similar consideration can be applied to the other materials such as chalcogenides. More experimental and theoretical investigations, such as targeted materials design, neutron scattering for the in-plane field directions augmented by analytical and numerical studies for this setting, and utilizing alternative tuning parameters such as external pressure, all could be useful for exploring the diverse phase diagram of this group of compounds and shedding further light on their rich physics.

Methods

Synthesis

Samples were synthesized from finely mixed Yb₂O₃ (99.9%), ZnO (99.9%), and Ga₂O₃ (99.999%) powders at 1350 °C. High-quality single-crystals (such as pictured in Supplementary Fig. 2) were grown using the optical floating zone technique. A typical growth was conducted in 1 MPa O₂ atmosphere with a speed ranging from 4 to 10 mm/hour. Single-crystal quality was confirmed via laue X-ray diffraction (Supplementary Fig. 3), while powder X-ray diffraction (PXRD) was used to confirm the correct phase at every step of synthesis (see Supplementary Fig. 1).

High-resolution magnetization measurements

High-resolution measurements of magnetization were achieved with the complimentary tunnel diode oscillator (TDO) technique³¹. In a TDO measurement, a tunnel diode is biased to operate in the negative resistance region of the IV-curve. This provides power that maintains the resonance of a LC-circuit at a frequency range between 10 and 50 MHz. A nearly single-crystal sample with dimensions of 2 mm in length and 1 mm in diameter was wound inside a detection coil, with the c axis of the sample aligned with the coil axis. The sample and coil constitute the inductor of the LC circuit. With the application of field, the sample magnetization change induces a change in the inductance, and thus shifts the resonance frequency. This technique enables highly sensitive detection of changes of magnetic moments ~ 10⁻¹⁵ Am²⁵⁸.

Magnetization was also directly measured via an in-house Cryogenic S700X SQUID magnetometer in temperatures down to 300 mK using a 3He probe. A 1.81 mg sample was mounted on a silver straw with vacuum grease in H∥c and H⊥c orientations.

ac-susceptibility measurements were carried out on a long, approximately rectangular sample with field perpendicular to the sample c axis in a dilution refrigerator with a base temperature of 20 mK.

Neutron scattering

Diffuse neutron scattering data were collected at the CORELLI spectrometer at Spallation Neutron Source, Oak Ridge National Laboratory⁵⁹. This instrument is a quasi-Laue TOF instrument equipped with a 2D detector, with a –20° to +150° in-plane coverage. The incident neutron energy was between 10 meV and 200 meV. A superconducting magnet was used to provide a vertical magnetic field up to 5 T, which constrained the out-of-plane coverage to ± 8°. A 0.8 g single-crystal was mounted on a Cu plate in a dilution refrigerator. The sample was aligned with the (h, k, 0) plane horizontal and the magnetic field along the [0, 0, l] direction. Neutron-absorbing Cd was used to shield the sample holder to reduce the background scattering. Experiments were conducted with applied fields at the base temperature of 130 mK by rotating the crystal through 180° in 3° steps, and then at 20 K in the same fields for background subtraction. The data were reduced using Mantid for the Lorentz and spectrum corrections⁶⁰.

To account for the temperature factor in our background subtraction in total-scattering mode, we compared the ratio of integrated intensities of a rectangular volume of reciprocal space at 5 T for both temperatures. The region was bounded by −0.45 < h < −0.35, 0.5 < k < 0.6, and −2 < l < 2. We used this region, away from the zone edge, and our 5 T data to ensure the comparison was unaffected by diffuse magnetic scattering. This integration approximates the ratio of Bose population factors—our scaling factor was 1.01 ± 0.005. To improve statistics, we used symmetry operations. All analysis and visualization were performed using Mantid and Python.

We conducted inelastic neutron scattering experiments at the CNCS³⁸ at Oak Ridge National Laboratory, and the DCS⁴⁰ and SPINS at the National Institute of Standards and Technology. The same 1.4 g single-crystal sample was aligned to use the [h, k, 0] scattering plane and with the field parallel to the sample c-axis (along the [001] direction). All measurements were carried out in dilution refrigerators, with sample mounted on copper sample mounts such as pictured in Supplementary Fig. 2.

The base temperatures for CNCS, DCS, and SPINS measurements were 50, 70, and 60 mK, respectively. For CNCS and DCS, the sample was rotated through ~180 degrees. The incident energy used at CNCS, DCS, and SPINS was 3.9, 3.55, and 3.7 meV, respectively.

Analysis of CNCS data was carried out in large part using the HORACE software package⁶¹. Analysis of DCS data was carried out in large part using the DAVE software package⁶².

We measured using polarized neutrons at the BT7³⁹ beamline at the National Instistute of Standards and Technology. We measured with a fixed final energy of 14.7 meV at about 0.5 meV such that the FWHM of the collimated beam was 1.08 meV and encompassed the energy range of the continuum as pictured for low fields in Fig. 3. Samples were again aligned to use the [h, k, 0] scattering plane, and measurements were conducted using a vertical guide field (parallel to the sample c-axis). A 3He cryostat was used. 0 T measurements were performed in the absence of a magnet, and then a 7 T magnet was added to perform measurements at 2 T. Flipping ratios ranged from 19 to 33 for the 0 T measurements and from 17 to 28 for the 2 T measurements. Polarization correction was performed using pbcor software.

Theory

For the LSWT S(Q, ω) we used SpinW calculations⁴⁸. The global phase diagram was obtained using classical energies for the single-Q states, see refs. ^19,20, and for the field-induced phases, classical energy minimization of the three- and four-sublattice structures was used.