Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-19T10:24:41.563Z Has data issue: false hasContentIssue false
  • English
  • Français

Qualitative properties of singular solutions to fractional elliptic equations

Part of: Theory of singularities and catastrophe theory Miscellaneous topics - Partial differential equations Singularities

Published online by Cambridge University Press:  14 September 2021

Shuibo Huang ,
Zhitao Zhang  and
Zhisu Liu
Shuibo Huang
Affiliation:
School of Mathematics and Computer Science, Northwest Minzu University, Lanzhou, Gansu 730030, P. R. China Key Laboratory of Streaming Data Computing Technologies and Application, Northwest Minzu University, Lanzhou, Gansu 730030, P. R. China (huangshuibo2008@163.com)
Zhitao Zhang*
Affiliation:
School of Mathematical Sciences, Jiangsu University, Zhenjiang 212013, P. R. China HLM, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, P. R. China School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, P. R. China (zzt@math.ac.cn)
Zhisu Liu
Affiliation:
Center for Mathematical Sciences, China University of Geosciences, Wuhan, Hubei 430074, P. R. China (liuzhisu183@sina.com)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, by the moving spheres method, Caffarelli-Silvestre extension formula and blow-up analysis, we study the local behaviour of nonnegative solutions to fractional elliptic equations

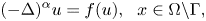\begin{align*} (-\Delta)^{\alpha} u =f(u),~~ x\in \Omega\backslash \Gamma, \end{align*}
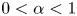where $0<\alpha <1$, 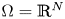$\Omega = \mathbb {R}^{N}$ or 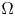$\Omega$ is a smooth bounded domain, 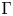$\Gamma$ is a singular subset of 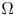$\Omega$ with fractional capacity zero, 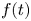$f(t)$ is locally bounded and positive for 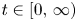$t\in [0,\,\infty )$, and 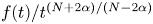$f(t)/t^{({N+2\alpha })/({N-2\alpha })}$ is nonincreasing in 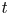$t$ for large 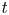$t$, rather than for every 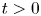$t>0$. Our main result is that the solutions satisfy the estimate
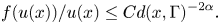\begin{align*} f(u(x))/ u(x)\leq C d(x,\Gamma)^{{-}2\alpha}. \end{align*}
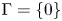 This estimate is new even for $\Gamma =\{0\}$. As applications, we derive the spherical Harnack inequality, asymptotic symmetry, cylindrical symmetry of the solutions.

Keywords

Fractional elliptic equationsMoving spheres methodBlow-up analysisLocal behaviourSingular solutions

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 58K55: Asymptotic behavior 32S05: Local singularities
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 5 , October 2022 , pp. 1155 - 1190
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexandrov, A. D.. A characteristic property of the spheres. Ann. Mat. Pura. Appl. 58 (1962), 303–354.CrossRefGoogle Scholar
Ao, W., DelaTorre, A., González, M. and Wei, J.. A gluing approach for the fractional yamabe problem with prescribed isolated singularities. J. Reine. Angew. Math. 163 (2020), 25–78.CrossRefGoogle Scholar
Berestycki, H. and Nirenberg, L.. On the method of moving planes and the sliding method. Bol. Soc. Bras. Mat. Nova. Ser. 22 (1991), 1–37.CrossRefGoogle Scholar
Cabre, X. and Sire, Y.. Nonlinear equations for fractional Laplacians I: regularity maximum principles, and Hamiltonian. estimates. Ann. Inst. H. Poincaré Anal. Non. Linéaire. 31 (2014), 23–53.CrossRefGoogle Scholar
Caffarelli, L., Gidas, B. and Spruck, J.. Asymptotic symmetry and local behavior of semilinear elliptic equations with critical Sobolev growth. Commun. Pure. Appl. Math. 42 (1989), 271–297.CrossRefGoogle Scholar
Caffarelli, L., Jin, T., Sire, Y. and Xiong, J.. Local analysis of solutions of fractional semi-linear elliptic equations with isolated singularities. Arch. Ration. Mech. Anal. 213 (2014), 245–268.CrossRefGoogle Scholar
Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Comm. Partial. Differential Equations. 32 (2007), 1245–1260.CrossRefGoogle Scholar
Cao, D. and Li, Y.. Results on positive solutions of elliptic equations with a critical Hardy-Sobolev operator. Methods Appl. Anal. 15 (2008), 81–95.CrossRefGoogle Scholar
Chang, S.-Y. A. and González, M.. Fractional Laplacian in conformal geometry. Adv. Math. 226 (2011) 1410–1432.CrossRefGoogle Scholar
Chen, W., Li, C. and Li, Y.. A direct method of moving planes for the fractional Laplacian. Adv. Math. 308 (2017), 404–437.CrossRefGoogle Scholar
Chen, W., Li, Y. and Zhang, R.. A direct method of moving spheres on fractional order equations. J. Funct. Anal. 272 (2017), 4131–4157.CrossRefGoogle Scholar
Chen, C. and Lin, C.. Local behavior of singular positive solutions of semilinear elliptic equations with Sobolev exponent. Duke. Math. J. 78 (1995), 315–334.CrossRefGoogle Scholar
Chen, C. and Lin, C.. Estimates of the conformal scalar curvature equation via the method of moving planes. Comm. Pure. Appl. Math. 50 (1997), 971–1017.3.0.CO;2-D>CrossRefGoogle Scholar
Chen, C. and Lin, C.. Estimate of the conformal scalar curvature equation via the method of moving planes II. J. Differential Geom. 49 (1998), 115–178.CrossRefGoogle Scholar
Chen, C. and Lin, C.. A spherical Harnack inequality for singular solutions of nonlinear elliptic equations. Ann. Scuola. Norm. Sup. Pisa. Cl. Sci. 30 (2001), 713–738.Google Scholar
Chen, Y., Liu, C. and Zheng, Y.. Existence results for the fractional Nirenberg Problem. J. Funct. Anal. 270 (2016), 4043–4086.CrossRefGoogle Scholar
DelaTorre, A. and González, M.. Isolated singularities for a semilinear equation for the fractional Laplacian arising in conformal geometry. Rev. Mat. Iberoam. 34 (2018), 1645–1678.CrossRefGoogle Scholar
DelaTorre, A., Pino, M., González, M. and Wei, J.. Delaunay-type singular solutions for the fractional Yamabe problem. Math. Ann. 369 (2017), 597–626.CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker's guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573.CrossRefGoogle Scholar
Dipierro, S., Montoro, L., Peral, I. and Sciunzi, B.. Qualitative properties of positive solutions to nonlocal critical problems involving the Hardy-Leray potential. Calc. Var. Partial. Differential Equations 55 (2016), 99.CrossRefGoogle Scholar
Esposito, F., Montoro, L. and Sciunzi, B.. Monotonicity and symmetry of singular solutions to quasilinear problems. J. Math. Pures Appl. 126 (2019), 214–231.CrossRefGoogle Scholar
Gidas, B., Ni, W. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Comm. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
González, M., Mazzeo, R. and Sire, Y.. Singular solutions of fractional order conformal Laplacians. J. Geom. Anal. 22 (2012), 845–863.CrossRefGoogle Scholar
Guo, Z., Li, J. and Wan, F.. Asymptotic behavior at the isolated singularities of solutions of some equations on singular manifolds with conical metrics. Comm. Partial. Differential Equations 45 (2020), 1647–1681.CrossRefGoogle Scholar
Guo, Z., Wan, F. and Yang, Y.. Asymptotic expansions for singular solutions of $\Delta u+e^{u}=0$ in a punctured disc. Calc. Var. Partial. Differential Equations 60 (2021), 51.CrossRefGoogle Scholar
Han, Q., Li, X. and Li, Y.. Asymptotic expansions of solutions of the Yamabe equation and the $\sigma _k$-Yamabe equation near isolated singular points. Comm. Pure. Appl. Math. 74 (2021), 1915–1970.CrossRefGoogle Scholar
Han, Z., Li, Y. Y. and Teixeira, E.. Asymptotic behavior of solutions to the $k$-Yamabe equationnear isolated singularities. Invent. Math. 182 (2010), 635–684.CrossRefGoogle Scholar
Huang, S. and Tian, Q.. Harnack-type inequality for fractional elliptic equations with critical exponent. Math. Methods Appl. Sci. 43 (2020), 5380–5397.CrossRefGoogle Scholar
Jin, T., Li, Y. Y. and Xiong, J.. On a fractional Nirenberg problem part. I: blow up analysis and compactness of solutions. J. Eur. Math. Soc. 16 (2014), 1111–1171.CrossRefGoogle Scholar
Jin, T., Li, Y. Y. and Xiong, J.. The Nirenberg problem and its generalizations: a unified approach. Math. Ann. 369 (2017), 109–151.CrossRefGoogle Scholar
Jin, T., Queiroz, O., Sire, Y. and Xiong, J.. On local behavior of singular positive solutions to nonlocal elliptic equations. Calc. Var. Partial. Differential Equations 56 (2017), 9.CrossRefGoogle Scholar
Korevaar, N., Mazzeo, R, Pacard, F. and Schoen, R.. Refined asymptotics for constant scalar curvature metrics with isolated singularities. Invent. Math. 135 (1999), 233–272.CrossRefGoogle Scholar
Leung, M.. Refined estimates for simple blow-ups of the scalar curvature equation on $S^{n}$. Trans. Amer. Math. Soc. 370 (2018), 1123–1157.CrossRefGoogle Scholar
Li, C.. Local asymptotic symmetry of singular solutions to nonlinear elliptic equations. Invent. Math. 123 (1996), 221–231.CrossRefGoogle Scholar
Li, Y. and Zhang, L.. Liouville-type theorems and Harnack-type inequalities for semilinear elliptic equations. J. Anal. Math. 90 (2003), 27–87.CrossRefGoogle Scholar
Lin, C. and Prajapat, J.. Harnack type inequality and a priori estimates for solutions of a class of semilinear elliptic equations. J. Differential Equations 244 (2008), 649–695.CrossRefGoogle Scholar
Lin, C. and Prajapat, J.. Asymptotic symmetry of singular solutions of semilinear elliptic equations. J. Differential Equations 245 (2008), 2534–2550.CrossRefGoogle Scholar
Montoro, L., Punzo, F. and Sciunzi, B.. Qualitative properties of singular solutions to nonlocal problems. Annali di Matematica 197 (2018), 941–964.CrossRefGoogle Scholar
Oliva, F., Sciunzi, B. and Vaira, G.. Radial symmetry for a quasilinear elliptic equation with a critical Sobolev growth and Hardy potential. J. Math. Pures Appl. 140 (2020), 89–109.CrossRefGoogle Scholar
Schoen, R.. The existence of weak solutions with prescribed singular behavior for a conformally invariant scalar equation. Commun. Pure Appl. Math. 41 (1988), 317–392.CrossRefGoogle Scholar
Schoen, R. and Yau, S. T.. Conformally flat manifolds, Kleinian groups and scalar curvature. Invent. Math. 92 (1988), 47–71.CrossRefGoogle Scholar
Sciunzi, B.. On the moving plane method for singular solutions to semilinear elliptic equations. J. Math. Pures Appl. 108 (2017), 111–123.CrossRefGoogle Scholar
Serena, D., Xavier, R. and Enrico, V.. Nonlocal problems with Neumann boundary conditions. Rev. Mat. Iberoam. 33 (2017), 377–416.Google Scholar
Serrin, J.. A symmetry problem in potential theory. Arch. Ration. Mech. Anal. 43 (1971), 304–318.CrossRefGoogle Scholar
Silvestre, L.. Regularity of the obstacle problem for a fractional power of the Laplace operator. Comm. Pure. Appl. Math. 60 (2007), 67–112.CrossRefGoogle Scholar
Tan, J. and Xiong, J.. A Harnack inequality for fractional Laplace equations with lower order terms. Discrete Contin. Dyn. Syst. 31 (2011), 975–983.CrossRefGoogle Scholar
Wu, L. and Chen, W.. The sliding methods for the fractional $p$-Laplacian. Adv. Math. 361 (2020), 106933.CrossRefGoogle Scholar
Xiong, J.. The critical semilinear elliptic equation with isolated boundary singularities. J. Differential Equations 263 (2017), 1907–1930.CrossRefGoogle Scholar
Yang, H. and Zou, W.. Exact asymptotic behavior of singular positive solutions of fractional semi-linear elliptic equations. Proc. Amer. Math. Soc. 147 (2019), 2999–3009.CrossRefGoogle Scholar
Yang, H. and Zou, W.. On isolated singularities of fractional semi-linear elliptic equations. Ann. Inst. H. Poincar. Anal. Non. Linéaire. 38 (2021), 403–420.CrossRefGoogle Scholar
Yang, H. and Zou, W.. Sharp blow up estimates and precise asymptotic behavior of singular positive solutions to fractional Hardy-Hénon equations. J. Differential Equations 278 (2021), 393–429.CrossRefGoogle Scholar
Zhang, L.. Refined asymptotic estimates for conformal scalar curvature equation via moving sphere method. J. Funct. Anal. 192 (2002), 491–516.CrossRefGoogle Scholar