Introduction

Technological1 and fundamental2 difficulties with the continued downscaling of field-effect transistors have motivated the development of alternative beyond-Moore and beyond-CMOS (complementary metal–oxide–semiconductor) energy-efficient computing systems. At the device level, both conventional CMOS and many new transistor technologies require a high drive current, low off current, and the ability to scale device sizes even smaller. To the extent that these demands can be passed down to the material level, they translate into the search for a highly conductive, highly confined material system that still allows precise control over the electric current. The high system’s conductivity is necessary for fast transistor charging/discharging, while the high degree of the electrostatic confinement in nano-switches3 is necessitated by both the high density of nanodevices and the need to control each nanodevice channel. With the emergence of atomically precise techniques to produce planar dopant-based structures in semiconductors, a particular interest has been paid to the δ-layer structures, when the dopant atoms form a mono or several atomic layers with the dopant densities much higher than the solid solubility limit4. Such structures have been shown to possess very high current densities5,6 and thus have a strong potential for beyond-Moore applications.

Electronic structure and conductive properties of Si:P δ-layer systems, which consists of a thin, highly phosphorous (P) doped 2D sheet layer embedded in lightly doped silicon, as shown in Fig. 1a, have been a subject of active studies for the last several decades7,8,9,10,11,12,13,14,15,16,17,18 leading to applications in quantum computing19,20 and advanced microelectronic devices6,21,22. Recent angle-resolved photoemission spectroscopy (ARPES) measurements23,24,25,26,27 revealed the existence of shallow conductive states that determines the conductive properties of these systems. Mazzola et al.25 revealed the quantization of the conduction band and the valence band near the Fermi level. Most recently, based on high-resolution ARPES experiments, the presence of three sub-bands has been observed: 1Γ, 2Γ and the shallow 3Γ for the δ-layer donor density of 9.0 × 1013 cm−2 in Holt et al.26, and for a donor density of 1.7 × 1014 cm−2 in Mazzola et al.27, that could not be explained by the existing theoretical models without the need to adjust the value of Si dielectric constant to ϵ ≈ 40 for high-density phosphorus regions. However, it is easy to see that a charge self-consistent solution of the Poisson-Schrodinger equation already takes into account the increase of the effective dielectric constant, by directly accounting for the free electrons, and thus the adjustment of ϵ in the Poisson equation itself can lead to double-counting of the screening effect. The existence of Δ-band was also observed by Holt et al.26 for thicker δ-layer systems.

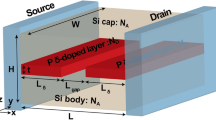
Fig. 1: Geometry of the δ-layer system and corresponding computational model.
figure 1

The Si:P δ-layer device shown in a consists of a source, drain, and channel. The channel is composed of a Si body, Si cap, and P δ-layer. The source and drain represent an extension of the channel to the infinity along the x-axis, with the same properties along the z-axis as the channel. The dimension of the device along the y-axis is infinite. The Si cap and Si body are doped with a doping density of acceptors of NA, whereas the P δ-layer is doped with a doping density of donors of ND. b the 2D computational model used in the simulations, which represents a cross-section of the xz-plane of the device (see panel (a)).

Full size image

Naturally, particular attention has also been given to numerical studies of the electronic structure of δ-layer systems. Previous computational studies of these systems based on either effective mass16, tight-binding15,18,28 or density functional theory13,14,17 formalisms can be classified into two categories: truly closed-system approaches, with the Dirichlet-type boundary conditions for the wave-function, and approaches with periodic boundary conditions along the propagation direction. However, in both cases, if the conductive properties of the system need to be extracted, this principally cannot be done directly from the quantum-mechanical flux. Indeed, the current density, j, is proportional to Ψ ∇ Ψ* − Ψ* ∇ Ψ, which is zero for any closed-system wave-function Ψ or is simply proportional to the wave-vector for the case of periodic boundary condition, which cannot be used to compute the flux in most non-trivial cases. Thus, most typically, a classical or semi-classical Drude–Sommerfeld29,30 approximation assuming that the current density is proportional to the electron density, j ~ n, has to be additionally employed to extract the conductive properties from the closed-system solution. Periodic boundary conditions allow conductivity extraction in the case of idealized metallic nanowires in semiconductor28, however, the corresponding assumption that the transmission coefficient equals unity for each propagating mode ignores the influence of discrete charged impurities and interface roughness. The use of truly open-system boundary conditions allows direct computation of conductive properties from the quantum-mechanical flux and can be readily extended to simulate more complex structures such as tunnel junctions, gated devices, and transistors.

In the following, we present an application of an open-system non-equilibrium green function (NEGF) Keldysh formalism31 that enables a systematic quantum-mechanical study of conductive properties of semiconductor δ-layer systems in the low-temperature regime32. We demonstrate that this open-system treatment allows us to explain the origin of shallow conducting sub-bands recently observed in high-resolution ARPES experiments and accurately reproduces the sheet resistance values obtained by different experimental groups for a wide range of the δ-layer donor densities. Further analysis reveals two main effects: (1) the existence of spatially separated layers of free electrons with different average energies that are formed around the δ-layer and (2) significant quantum-mechanical dependence of conductivity on the δ-layer thickness for a fixed charge sheet density.

Results and discussion

Our device consists of a semi-infinite source and drains (represented by the NEGF open boundary conditions), in contact with the channel of length L, which is composed of a lightly doped Si cap, a very highly P-doped layer, and a lightly doped Si body (see Fig. 1a). By using the NEGF open boundary conditions, the source and drain represent a way to extend the channel into infinity along the x-axis. Therefore, the source and drain have the same properties as the channel. The length of the channel along the x-axis is assumed to be L = 50 nm to avoid the boundary effect (between the source and drain contacts). The length along the y-direction is assumed to be infinite with a flat electrostatic potential, corresponding to plane-wave solutions of the Schrödinger equation along the y-axis. This ansatz allows us to seek the numerical solution of the Poisson-open-Schrödinger equation in 2D. It is achieved by analytically integrating the Schrödinger equation over the y-axis momentum, which results in the effective 2D Fermi–Dirac distribution functions33. The resulting 2D computational model for our device is shown in Fig. 1b. In all simulations, we assume a temperature of 4 K.

First, we investigate the density of states (DOS) induced by an embedded P δ-layer in Si and its dependence on the layer depth, D, from the Si cap/body surfaces. For conceptual simplicity, we analyze symmetric configurations, where D in the Si cap/body is the same. We start by considering the concentration of donors of 1.0 × 1014 cm−2 in the δ-layer and the δ-layer thickness is set to 0.2 nm to approximate a monolayer of phosphorous atoms. We note that the nearest-neighbor distance between atoms in Silicon is approximately 0.23 nm. The doping density in the δ-layer is given by units of cm−2 to be consistent with the experiments’ nomenclature, i.e., \({N}_{D}^{2D}=t\times {N}_{D}^{3D}\), where t is the δ-layer thickness, \({N}_{D}^{2D}\) is the doping density of the δ-layer in cm−2 and \({N}_{D}^{3D}\) is the doping density in cm−3. Throughout this work, the doping concentration of acceptors of 1.0 × 1017 cm−3 in the Si body/cap is assumed. The results of the corresponding open-system quantum-mechanical treatment are shown in Fig. 2a, where the DOS are computed for D = 10, 20, and 40 nm. As expected in the open-system quantum-mechanical formulation, the DOS is a continuous function of energy. The sharp peaks in the DOS correspond to the propagation modes (of energies Em) that exist due to the confinement along the z-axis. The assumed source/drain geometry produces a one-dimensional flux, therefore these modes have only one degree of freedom which explains their (\(1/\sqrt{E-{E}_{m}}\))-like shape. Below the Fermi level, there are two distinct occupied sub-bands referred to in the traditional band structure formulations as 1Γ and 2Γ, corresponding to the two peaks in the DOS approximately at the energies of −190 and −20 meV. Importantly, Fig. 2a demonstrates that these occupied states are independent of the depth distance D of the δ-layer from the surfaces. Our calculations show that these states change only once they are shallow enough that D approaches the effective thickness of the electron cloud. This result is in agreement with the ARPES measurements of Mazzola et al.25 that show that the quantized conduction band states are largely independent of the dopant depth D, while strongly depending on the dopant density. As we will see later the number of occupied states and their respective energies are strongly dependent on both the δ-layer thickness t and doping level ND. On the other hand, the unoccupied states above the Fermi level are strongly dependent on the δ-layer depth D, since they come from the conventional geometric device confinement. The number of these modes increases with the encapsulation distance of the δ-layer, transitioning into the continuum mode in the limit of large D.

Fig. 2: Conduction band structure of δ-layer systems.
figure 2

a Total density of states, DOS(E), per unit length along the y-axis for Si:P δ-layer systems for distinct δ-layer depths, D. b Local density of states, LDOS(E,z), for a Si:P δ-layer system of D = 10 nm in the function of the energy and z position; the gray line indicates the corresponding charge self-consistent potential. c Transmission coefficient for each mode m for Si:P δ-layer system of D = 10 nm. d LDOS(E,z) for a Si:P δ-layer system of D = 20 nm. The δ-layer doping density is ND = 1.0 × 1014 cm−2, the Si cap, and Si bod doping densities are NA = 1.0 × 1017 cm−3, and the δ-layer thickness is t = 0.2 nm. Parts of panels (a) and (b) are reproduced with permission from Mendez et al.49, IEEE.

Full size image

As we will demonstrate in the following, in order to understand the electronic transport mechanism in highly conductive δ-layer systems, it is essential to analyze the electron distribution along the confinement direction in real space (LDOS). Figure 2b shows the LDOS(E,z) computed using our open-system treatment for the considered Si:P δ-system with D = 10 nm. In addition to the energy quantization of the occupied states, they are also separated in space and with a distinct structure: the lowest energy mode, around −190 meV, is centered around the δ-layer (z = 0.0 nm); the highest energy mode, around −20 meV, is located off-center around ±1 nm from the δ-layer on both sides. These occupied states remain spatially invariant with the depth of the δ-layer as well, as illustrated in Fig. 2d showing the LDOS for D = 20 nm.

In general, LDOS(E,z) in such semiconductor δ-layer systems takes a peculiar shape that we term “quantum menorah” as shown in Fig. 2b. We note that a “binary” (occupied/unoccupied) version of such LDOS was previously predicted using the traditional closed-system approximations for an abstract semiconductor9. A particular balance of donor/acceptor concentrations and the thickness value of the δ-layer determine the specific “menorah” shape and the exact location of the Fermi level, thus determining the system’s conducting properties. For instance, the increase of the acceptor cap/body doping results in vertical stretching of the structure, while the decrease of the donor concentration results in the compression. The corresponding transmission coefficient for each mode shown in Fig. 2c is a consequence of a quantum-mechanical relation T(E) = ∑mΓmm(E)Amm(E), where Γmm(E) and Amm(E) are the Hermitian form of the system’s self-energy and the spectral function respectively, with both matrices written in the mode representation34.

Next, we evaluate the influence of the δ-doping profile on the conduction sub-band structure. Our simulations reveal that the number of conduction sub-bands and their corresponding energy splittings are strongly influenced by both the δ-layer thickness t and the doping density ND. Figure 3 shows the free electron distribution (i.e., the DOS weighted with the Fermi–Dirac distribution) for a fixed 2 nm δ-layer thickness with diverse doping densities, and for a constant sheet doping density of 2 × 1014 cm−2 with different δ-layer thicknesses, respectively. For a fixed δ-layer thickness, the increment of the sheet doping increases the number of conducting modes, as well as the splitting energy between them, passing from a sole sub-band (1Γ) to two sub-bands (1Γ and 2Γ), and from two sub-bands to three sub-bands (1Γ, 2Γ, and 3Γ), as shown in Fig. 3a. In contrast, for a fixed sheet doping, the increment of the δ-layer thickness increases the number of modes, but decreases the energy splitting between them, particularly between 1Γ and 2Γ for t = 4 nm, as reflected in Fig. 3b. We note that this may be an indication that previously reported low (<50 meV) energy splitting between these sub-bands27 is only true for relatively thick (>5 nm) δ-layers. The highly P-doped δ-layer creates an electrostatic potential well (see Fig. 2b, gray line), which becomes sharper for smaller δ-layer thicknesses and higher doping densities. A sharper confinement potential leads to an increased energy splitting between sub-bands, causing a larger average energy difference between the electrons in the distinct parallel layers. The energy splitting between sub-bands is proportional to the sheet doping density, which is in agreement with previous tight-binding calculations15.

Fig. 3: Free electron energy distribution and current spectrum.
figure 3

Influence of the δ-layer thickness, t, and the donor doping density in the δ-layer, ND, on the free electron energy distribution per unit length along the y-axis (i.e., the DOS per unit length weighted with the Fermi–Dirac distribution) and current spectrum for an applied low voltage (1 mV): a for a fixed δ-layer thickness of t = 2 nm, and b for a fixed sheet doping density of ND = 1.2 × 1014 cm−2.

Full size image

The current spectrum is also shown in Fig. 3. Even though more carriers are allocated in the lowest-energy sub-bands for high confinement potentials, the electrical current is carried out equally among the conductive sub-bands. For example, for the 0.2 nm δ-layer thickness with a doping density of 1.2 × 1014 cm−2 in Fig. 3b, the free electron distribution between sub-bands is approximately 90%(1Γ) and 10%(2Γ), but the current contribution of each sub-band is similar (about 50%). However, the contribution of higher-energy sub-bands on the current becomes more significant as the confinement potential becomes weaker, i.e. electrons at the outer layers will start to carry the majority of the current. For instance, the 4 nm δ-layer thickness with a doping density of 1.2 × 1014 cm−2 in Fig. 3b, the electron distribution between sub-bands is approximately 35%(1Γ), 45%(2Γ), and 20%(3Γ), however, the current contribution of each sub-band is around 10%(1Γ), 25%(1Γ), and 65%(3Γ).

The effective electron cloud thickness as a function of the sheet doping density ND and the δ-layer thickness t is shown in Fig. 4. For low doping densities, below ND = 1013 cm−2, the electron cloud thickness is almost independent of the δ-layer thickness and is only determined by the doping value (the weak confinement regime). However, for high doping densities, above ND = 5 × 1013 cm−2, the effective electron thickness becomes independent of the doping value itself and is determined only by the δ-layer thickness value (the strong confinement regime).

Fig. 4: Effective electron cloud thickness around the δ-layer plane.
figure 4

This result reveals that the dependence of the effective electron cloud on the δ-layer doping ND and thickness t is highly nonlinear.

Full size image

Next, we validate our calculations against experimental data by several groups5,35,36,37 by comparing the macroscopic conductive properties of the system. To carry out this, we first need to introduce a heuristic elastic defect scattering model for meso- and macroscopic scale into our quantum transport framework (see Supplementary Method 2 for further details). In this work, we neglect the effects of inelastic scattering, since in Si:P-δ systems the phase-relaxation length lψ is larger than the mean free path lm at low temperatures5. There are two kinds of elastic scattering events that we consider in our open-system treatment: (1) scattering due to channel geometry and confinement due to a specific doping profile, which we refer to as geometry scattering, and (2) defect scattering (e.g., vacancies, dislocations, and impurities). The geometry scattering is already taken into account by our charge self-consistent quantum transport framework that also accounts for electron-electron interaction (via local density approximation exchange-correlation potentials). We can simulate defect scattering via abstract coherence-breaking scatterers represented as a linear density ν per transmission mode m along the channel of length L. The linear defect density is defined as ν = N/L, where N is the total number of elastic scatterers per transmission mode. Then the effective transmission function per mode along the channel can be expressed as32

$$\frac{1-{T}_{mm}^{\,{{{{\mathrm{eff}}}}}}(E)}{{T}_{mm}^{{{{{\mathrm{eff}}}}}\,}(E)}=\frac{1-{T}_{mm}(E)}{{T}_{mm}(E)}+\mathop{\sum }\nolimits_{i = 1}^{N}\frac{1-{t}_{mm}^{^{\prime} (i)}(E)}{{t}_{mm}^{^{\prime} (i)}(E)},$$
(1)

where Tmm(E) is the transmission function per mode without defect scatterers across the channel, and \({t}_{mm}^{{\prime} (i)}(E)\) is the transmission probability per mode due to a scatterer i. In other words, the first term of the right side of Eq. (1) takes into account the geometry scattering, whereas the second term encompasses the defects. Assuming that all scatterers have identical transmission probabilities \({t}_{mm}^{{\prime} (i)}={t}_{mm}^{{\prime}}\), the effective transmission function results as

$${T}_{mm}^{\,{{{{\mathrm{eff}}}}}\,}(E)=\frac{1}{1+\frac{1-{T}_{mm}(E)}{{T}_{mm}(E)}+L\nu \frac{1-{t}_{mm}^{\prime}(E)}{{t}_{mm}^{\prime}(E)}}.$$
(2)

The term \(\nu \frac{1-{t}_{mm}^{\prime}}{{t}_{mm}^{\prime}}\) can either be assumed to be constant for all modes and energies or as being inversely proportional to the characteristic mean free path lm32. To account for the reported increase of lm for very high δ-layer densities5 we assume that \(\nu \frac{1-{t}_{mm}^{\prime}}{{t}_{mm}^{\prime}} \approx \frac{{\alpha}}{{l}_{m}(N_{2D})^{\prime}}\), where α is proportional to the linear defect density in the system. We note the conductance obtained from the effective transmission in Eq. (2) is analogous (equivalent in the limit of low voltages) to the conductance calculated using previous elastic scattering models28,38,39.

By applying the described scattering model in our quantum transport simulations, we compute the sheet resistance for a wide range of δ-layer thickness (from 0.2 to 5 nm) and doping densities (from 4 × 1011 to 7.5 × 1014 cm−2). The computed sheet resistances are shown in Fig. 5 for α = 1.0 and 2.0 and compared against experimental data5,35,36,37. The open-system quantum-mechanical simulations generally reproduce the experimental data for the entire doping range and from diverse sources by only adjusting the defect linear density parameter α. It is important to point out that all systematic electrical measurements5,36,37 performed for a wide range of densities can be reproduced very well with our model with a particular value of the linear defect density α, as reflected in Fig. 5. Moreover, the shown experimental results can be classified into the distinct groups based on their samples impurity density: as the data in Fig. 5 suggest, the earlier samples5 had twice higher linear impurity density α = 2, while more recent samples36,37 had the lower impurity density as α = 1 for them. Figure 6 shows the computed sheet conductance for the system as a function of the sheet doping density ND and the δ-layer thickness t. It is evident that the complex sub-band structure has a significant effect on the system’s conductive properties that manifests itself in the conduction decrease for the sharper confining potentials. Indeed, semi-classically the conductivity can only depend on the sheet δ-layer density, but not on the δ-layer thickness, unless it is assumed that the mobility strongly depends on the distance from the δ-layer and properly reflects the difference in average energies of electrons in different occupied sub-bands. Thus, the predicted strong dependence of the conductivity on the δ-layer thickness presented in Fig. 6 is a direct consequence of the fully quantum-mechanical open-system treatment.

Fig. 5: Sheet resistance for δ-layer systems.
figure 5

Comparison of the computed sheet resistance R□ for two values of the linear impurity density α vs. experimental data5,35,36,37 in the function of the doping density in the δ-layer ND. Figure reproduced with permission from Mendez et al.49, IEEE.

Full size image
Fig. 6: Sheet electrical conductance for Si:P δ-layer systems.
figure 6

The sheet conductance, G□, is shown as a function of δ-layer thickness, t, and donor doping density in the δ-layer, ND (for the linear impurity density α = 1). The significant deviation from the classical result, where the current, j, is proportional to the electron density, n, i.e., j ~ n (which would correspond to perfectly horizontal color bands) is due to the quantum-mechanical resistivity increase for sharper δ-profiles.

Full size image

Conclusion

We have presented an open-system quantum transport treatment for semiconductor δ-layer systems that revealed a quantized conduction sub-band structure that we termed “quantum menorah”. The structure predicts the existence of spatially separated layers of free electrons with significantly different average energies. With the rapidly advancing atomically precise manufacturing techniques, this property could be used for thermoelectric applications40, when free electrons of particular energy would be “mechanically” blocked or allowed to pass through, e.g., by the means of the appropriately located, thin dielectric or acceptor-δ layer(s). Together with the high δ-layer systems conductivity, the ability to selectively filter charge carriers based on their kinetic energy could be used to design thermoelectric systems with a high figure of merit41.

Our simulation results for Si:P δ-systems suggest that the quantized sub-band structure manifests itself in two main effects: (1) the highly non-linear dependence of the electron cloud on the confining δ-layer doping profile and (2) the general quantum-mechanical resistivity increase for sharper δ-layer doping profiles. Understanding the dependence of the electron cloud thickness on the δ-layer doping profile is especially important for designing qubits, ultra-scaled field-effect transistors and beyond CMOS devices, when the device critical dimensions are already shrunk to the nm-scale.

Finally, we point out that the non-trivial results presented in this work, particularly the strong deviation from the semiclassical j ~ n dependence for high donor densities shown in Fig. 6, indicate the general necessity of the fully quantum-mechanical open-system treatment for highly confined and conductive systems, which were previously studied only with the band-structure approaches based on the closed-system approximation(s).

Methods

We concentrate our analysis on the free electron properties in Si:P δ-layer systems obtained through the charge self-consistent solution in the “jellium approximation”16 of the Poisson equation and the single-band (Γ-valley) effective mass Schrödinger equation with the open-system boundary conditions (obtained using the non-equilibrium Green’s functions \(G(r,r^{\prime} ,E)\)32). In this model, the influence of the Si nuclei, and the core and valence electrons is introduced only through the Si effective mass tensor, while the main effect is being determined by the process of establishing the global Fermi level for the open system, which we numerically emulate by finding the charge self-consistent real-space solution using the Hartree potential augmented with the exchange-correlation corrections42. Then the resulting quantum-mechanical open-system quantities of interest, such as the local DOS \(LDOS(r,E)=-\frac{1}{\pi }\,{{\mbox{Im}}}\,[G(r,r,E)]\) and the transmission function T(E) = Tr[ΓL(E)G(E)ΓR(E)G†(E)] are used to compute the current spectrum j(E) and the macroscopic conductive properties such as the sheet resistance. For an efficient implementation of this rather demanding computational scheme we utilized the Contact Block Reduction method34,43 and the open-system predictor–corrector method44 augmented with Anderson mixing scheme45 (see Supplementary Method 1 for further details). The accuracy and reliability of the contact block reduction method have been established in numerous publications34,43,44,46,47,48. We justify the use of the simple single-band approximation by (1) the desire to simplify the free-electron Hamiltonians to reduce the computational burden for the first open-system treatment of these systems and (2) the recent report26, where the relative contribution of Γ and Δ bands have been studied using high-resolution ARPES measurements, demonstrating that only the Γ band is occupied for the monoatomic δ-layers (see Table I within26). We note that no fitting parameters of any kind were used in the charge-self consistent calculations of this work. We also note that the sheet resistance/conductance computing model contains a single parameter, the linear defect density, as described in the discussion of Eq. (2). The standard values of electron effective masses ml = 0.98 × me, mt = 0.19 × me, and the dielectric constant ϵSi = 11.7 of Si were used. The use of the bulk effective masses has been proven to give very accurate results for Si:P δ-layer systems when compared to both tight-binding and density functional theory calculations16.