Simulation of slot-coating of nanocellulosic material subject to a wall-stress dependent slip-velocity at die-walls

Abstract

Bio-based nanocellulosic materials are non-toxic, renewable, exhibit excellent barrier properties, and are suitable candidates for sustainable food packaging applications. Sizing and designing coating parameters for slot-coating process using nanocellulose suspensions is challenging due to complex shear-thinning rheology and the presence of a water-rich boundary layer, effecting significant apparent slip at the wall. Previous studies have shown that the flow inside the coating bead can be complex, with occasional stagnation regions and a rheological model incorporating yield stress which should be considered while analyzing slot coating of nanocellulosic flows. This work extends earlier investigations by including the effects of the particle depleted water-rich boundary layer. The suspension is modeled as a Casson fluid with a shear-thinning viscosity, and the particle depletion at the wall is represented by an infinitely thin layer modeled as a local shear-dependent nonlinear slip law. The resulting two-phase flow equations are solved using a Finite Volume Method (FVM) coupled with the Volume of Fluid (VoF) method for tracking the free surface interface. It is observed that slip alters the flow’s dynamics in the coating bead, and the effect of slip cannot be ignored, especially at high shear rates. For thin films, the presence of slip enhances the flow, leading to more material coated on the substrate. In contrast, for thicker coatings, apparent slip leads to an augmentation in stagnant, non-yielded regions, potentially generating uneven surfaces.

Introduction

Widespread industrial and academic interest in nanocellulosic materials1 as a bio-based alternative for food packaging2 is driven due to renewability, the abundance of cellulose, and proven barrier properties against oxygen,3 mineral oils,4 and grease.5 From an operative perspective, a thorough understanding of the flow and rheological properties of nanocellulosic materials is essential to control and optimize high throughput manufacturing and efficient automation of coating processes.6 In coating applications, where the desired product is a thin film (either free-standing or on a substrate), control of rheological properties is directly relevant to the final product properties. For example, in slot coating, the suspension rheology is critical for favorable coating processing conditions and will control the drying energy requirements, whereas the resulting spatial and orientation distribution of nanocellulosic particles will influence the final product characteristics. The distribution of nanocellulose fibrils in an aqueous suspension is extremely complex and leads to distinct rheological characteristics. Recent studies from our group7,8 show the processing viability of slot-die coating and the applicability in multi-layer packaging barriers for gases and grease.

Rheological data of nanocellulose depends on the morphology of the fibrils, including fibrillation, aspect-ratio, length, shape,9 and flexural properties.10 Apart from that, the fibrils’ surface charge can influence the rheology to a certain extent.11 These factors are dictated by the process life cycle that is utilized to prepare the material.12 In general, nanocellulosic suspensions are non-Newtonian yield-stress materials and are usually analyzed in the purview of standard models such as Herschel–Bulkley13 or a power law model14,15,16. However, at high shear rates generated in slot-coating processes, the viscosity field predicted by these models may not be necessarily physically accurate.17 One of the most prominent causes of inaccuracy in predicting the coating conditions is the presence of apparent slip at the walls, due to the presence of a thin wall-bounded particle-depleted layer on the order of a few microns where the shear is highly nonuniform.16,18 One study19 suggests that apparent slip may arise due to particle migration as a result of the random Brownian motion and two competing forces: hydrodynamic interactions between the fibrils and the wall, and fibril–fibril interactions, while other studies argue that fibrils migrate from the high shear rate, near-wall regions toward lower-shear bulk flow until the shear-rate gradients are balanced by the concentration gradients.20 Although the effect of apparent wall slip may not be directly relevant and can be neglected in lower concentrations, the contribution of nonlinear wall slip becomes more critical as the solid content is increased and must be addressed along with other essential modeling challenges stemming from the presence of yield stress and highly shear-thinning behavior.21,22

Various approaches for modeling the effective deficit in momentum transfer resulting from the apparent slip layer have been suggested in the past; including molecular dynamics (MD)23 method and Lattice Boltzmann method (LBM).24 However, the most effective mode is to employ the traditional flow solving techniques, which discretize and solve the macroscopic Navier–Stokes (NS) equations on a continuum mechanics framework. As a first approximation, the particle-depleted layer can be modeled as an infinitely thin layer and can be effectively applied by replacing the no-slip boundary condition in the wall-parallel direction by a wall-shear stress-dependent nonlinear Navier slip condition. This approach is motivated by the knowledge that, provided there is an empirical model of the slip behavior from standard experiments, the model can provide accurate stress and velocities at the wall without calculating the small-scale particle interactions, which can be prohibitively cumbersome for a slot-coating setup at industrial production rates. The current work aims to provide a study of the mechanisms on how slip can influence the flow of nanocellulosic materials in realistic industrially applicable conditions and continues our recent works in the same area.17,25 Precisely, herein, the simulation results of slot-die flow for a 3% micro fibrillated cellulose (MFC) is presented with the knowledge of previously reported experimental data.16

The article is organized as follows. A physical description of the slot-die coating setup, the computational method, the rheology model along with the boundary conditions, are described in “Definition of the physical problem” section. The results of the numerical simulations are presented in “Results and discussion” section, followed with a summary of the work and concluding remarks.

Definition of the physical problem

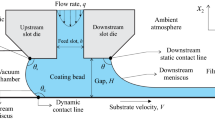
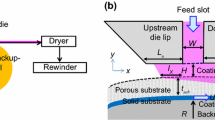
In the pilot coating setup developed by Kumar et al.26, micro-fibrillated cellulose is pumped into the slot-die through an elongated distribution chamber, which distributes the suspension along the narrow slot gap channel to generate a uniform flow. As shown in Fig. 1, the coating head is installed at a 3 o’clock position about the backup roller and is offset ($L_o$) 7 mm downward from its centre. The radius (R) of the backup roller is 56.7 mm, the slot length ($L_s$) is 34 mm, and slot-gap (h) is kept fixed at 500$\ \mu m$. Upon exiting the slot-gap, the suspension spans the gap between the adjacent die lips and the coating substrate, which is translating past with a velocity $V_s$, attached to the backup roller. To simplify the computational setup, the region comprising the coating bead and the slot gap excluding the distribution chamber (highlighted region with dashed lines in Fig. 1) is adopted as domain of interest, and a uniform inlet velocity is prescribed at the feed-slot inlet. Both the upstream lip length ($L_u$) and the downstream lip length ($L_d$) are fixed at 5 mm. The upstream length ($L_{uu}$) is sufficiently extended to 15 mm in order to reduce the influence of artificial outlet boundary conditions into the domain, while the downstream length, $L_{dd}$, is prolonged to 5 mm to assure the flow field is fully developed along the coating direction.

Fig. 1

Illustration of the slot-coater geometry used in this study. The computational domain is highlighted using dashed lines along with the boundary conditions

Table 1 Operating parameters

The minimum slot web gap (SWG) between the substrate and the downstream lip is varied, as shown in Table 1. A relative offset position of the roller creates a converging geometry in the coating gap along the downstream direction, allowing the coat weight to be controlled independently of the slot die feed flow rate by adjusting the SWG. The idea for operating the slot-coater in an unconventional metering mode is to decouple the slot inflow rate from the coat weight. However, the process in this slot-die setup is based on the forced rejection of the coating liquid, similar to knife or bar coating, and is usually classified as a post-metered method.27,28 In other words, the unconventional metering described earlier can also be characterized as a slot-fed knife coating system. Such a setup generates high enough shear rates inside the slot to fluidize the material, thereby facilitating low process viscosities. The excess coating material falls down due to gravity along the upstream opening and is collected for reuse. If the coating layer is very thin or the drying capacity of the equipment is adequate, the entire material fed to the slot die can be converted to coating. In this case, the coat weight is controlled by the ratio of the substrate speed to the inlet velocity ($V_{s}/V_{in}$).

Mathematical formulation

The fluid flow is considered as two-phase, laminar and isothermal. The governing equations are the conservation of mass and the unsteady Navier–Stokes equations, and is assumed to be without mass-transfer across the gas–liquid interface.

Fig. 2

Casson rheology model fitted for 3% microfibrillated cellulose (MFC) with the existing experimental data 16

The incompressible mass conservation equation is represented as:

$$\begin{aligned} \nabla \cdot \mathbf {u}= 0 \end{aligned}$$

(1)

where $\mathbf {u}$ is the velocity vector. The conservation of linear momentum is expressed as:

$$\begin{aligned} \frac{\partial \rho \mathbf {u}}{\partial t} + \nabla \cdot \left( {\rho \mathbf {uu}} \right) = - \nabla p + \rho \mathbf {g} + \nabla \cdot \mathbf {T} + \mathbf {F}_{b} \end{aligned}$$

(2)

Above, t, p, $\rho$, and $\mathbf {T}$ are the time, pressure, density, and viscous stress-tensor, respectively. Acceleration due to gravity is denoted by $\mathbf {g}$. The force due to surface tension can be incorporated as a source term per unit volume and is denoted here as $\mathbf {F}_{b}$. The viscous stress tensor follows $\mathbf {T}= \mu \left( \nabla \mathbf {u}+ \nabla \mathbf {u}^{T} \right)$, for dynamic viscosity, expressed as $\mu$. To capture the free-surface interface, the Volume of Fluid (VoF)29 method introduces the indicator field ($\alpha$), describing volume fraction of either of the fluids, bounded by $0\le \alpha \le 1$. The physical properties are calculated using the weighted average function. For example, if $\alpha _l$ indicates the liquid volume fraction, and the corresponding liquid/gas density and viscosity are denoted as $\rho _l$/$\rho _g$ and $\mu _l$/$\mu _g$, respectively, then the average density and viscosity are defined as

$$\begin{aligned} \rho= & {} \alpha _l \rho _l+(1-\alpha _l)\rho _g \end{aligned}$$

(3)

$$\begin{aligned} \mu= & {} \alpha _l \mu _l+(1-\alpha _l)\mu _g \end{aligned}$$

(4)

The free surface of the suspension is tracked by solving the transport equation for the volume fraction as,

$$\begin{aligned} \frac{{\partial \alpha _{l} }}{\partial t} + \nabla \cdot \left( {\alpha _{l} u} \right) = 0 \end{aligned}$$

(5)

The geometric VoF isoAdvector scheme by Roenby et al.30 was employed for interface reconstruction due to its superior results in interface sharpness, boundedness, and shape preservation, compared to the conventional artificial surface compression method. In equation (2), the surface tension term is considered as a volumetrically distributed force active only in the cells containing the interface as,

$$\begin{aligned} \mathbf {F}_b=\sigma \kappa \left( \nabla \alpha \right) \end{aligned}$$

(6)

Here $\sigma$ is the surface tension and $\kappa$ is the local curvature of the interface determined using the phase-fraction field distribution as,

$$\begin{aligned} \kappa = \nabla \cdot \left( \frac{\nabla \alpha }{|\nabla \alpha |} \right) \end{aligned}$$

(7)

Rheology model

In this study, the rheology of MFC suspension is numerically described using a Casson model31, where shear stress (${\tau }$) can be expressed as a function of shear rate ($\dot{\gamma }$) as,

$$\begin{aligned} \sqrt{\tau } = \sqrt{\tau _0}+\sqrt{\eta _p \dot{\gamma }} \end{aligned}$$

(8)

A Casson model is preferred here over a power law or a Herschel–Bulkley model to numerically describe the constitutive equation because the former includes the yield stress ($\tau _0$) and the asymptotic viscosity ($\eta _p$) at high shear rates. Furthermore, a reasonable assumption is made so that the rheology of the suspension is free of time-dependent fluctuations. The bi-viscosity regularization model32 was employed to deal with the discontinuous material behavior of unyielding regions in the flow domain. Finite viscosity ($\mu _0$) is assumed when the fluid functions as a solid ($\tau < \tau _0$). As the flow yields, the local viscosity is estimated using the Casson model using equation (8). To mimic the particle-depleted slip layer, the wall slip velocity is modeled as a function of wall shear stress, and the relationship between the two quantities is prescribed as a nonlinear power law:

$$\begin{aligned} U_{slip}= S\tau _w^m \end{aligned}$$

(9)

The parameters for the Casson model, viz. the yield stress ($\tau _0=255.4$ Pa) and the asymptotic viscosity ($\eta _p=9.55$ mPas), and for the slip model ($S=3.31$ and $m=4.63$) were computed from the rotational and slot viscometry measurements reported for 3% concentration of mechanically produced MFC.16 These parameters were obtained by performing an optimized set of CFD studies of the slot-viscometer setup by systematically varying the slot gap, so that the differences in the experimental and predicted numerical pressure drops were minimal. From Fig. 2, we can see that the effect of nonlinear slip becomes prominent at high shear rates and the experimental data deviates from the Casson fit. Similar deviations of the experimental fitted model at high shear-region are also observed in earlier studies16,33

Equations (2) to (7) are solved subject to the boundary conditions as given below. Here $\mathbf {n}$ and $\mathbf {t}$ denote the local normal and tangent to the boundary surface, respectively.

• BC-1: Along the velocity inlet boundary plane, a fixed uniform velocity profile ($V_{in}$) is prescribed.

• BC-2: Along the artificial outflow boundary plane in the downstream, the flow is assumed to be fully developed ($\mathbf {n} \cdot \nabla \mathbf {u} =0$), with fixed ambient pressure ($p=p_0$).

• BC-3: Along the upstream boundary plane, a direction-specific inlet-outlet velocity condition is prescribed, if the direction of flow is pointed out of the domain, a zero-gradient boundary condition is implemented, while a prescribed velocity based on the flux in the boundary normal direction is assigned in case of reverse flow. In addition, the pressure along the boundary is prescribed to be at ambient pressure ($p=p_0$).

• BC-4: At solid walls, for the reference no-slip case, the no-slip and no-penetration conditions are applied. ($\mathbf {u} =0$), for the cases where slip is accounted for, the no-slip boundary conditions are replaced by the nonlinear slip law given in equation (9).

• BC-5: For the moving substrate, the velocity component parallel to the moving wall is set to the prescribed substrate velocity ($\mathbf {u} \cdot \mathbf {t} =V_s$), while the surface normal velocity component is set to zero ($\mathbf {u} \cdot \mathbf {n} =0$).

Numerical solution

The governing system of equations is solved in a segregated method employing the pressure implicit method for pressure linked equations (PIMPLE) algorithm for pressure-velocity coupling using OpenFOAM.34 The accuracy of the implementation of the nonlinear slip boundary condition was validated against analytical solutions known in the literature.25 For the computations, a Crank-Nicolson temporal scheme with a blending coefficient of 0.9 was adopted. For computing the gradients, a Gauss linear scheme was adopted, while the Laplacian operators were discretized using a Gauss linear corrected scheme. The convective terms in the momentum equation were estimated using a limited Gauss linear scheme, with the scheme switching to an upwind scheme in the regions of high velocity gradients. Additional details on the implementation of the numerical schemes can be found in the OpenFOAM user’s guide.35 The system of linear equations appearing in the discretization of the pressure terms was solved adopting the generalized geometric algebraic multigrid (GAMG) solver, along with the combined DIC Gauss–Seidel smoother. A self-adapting time step based on the maximum Courant number ($Co_{max} = 0.5$) has been used for the time step computations. A relatively small maximum Courant number criteria ensure small time steps and guarantee that the discretization errors due to the time scheme are minimal. Additionally, to ensure the proper velocity-pressure coupling, a momentum predictor was enabled with the isoAdvector scheme as it was essential for maintaining the accuracy of the simulations.

All simulations were performed at a fixed substrate velocity to inlet-velocity ratio of $(V_s/V_{in}=0.83)$, so that the only parameters that were varied in this work are substrate velocity $V_s$ and the slot web gap (SWG), as depicted in Table 1. To clarify and compare the role of the depleted layer, all cases were run with the nonlinear slip along with the reference no-slip condition. For resolving the dynamic behavior of the moving contact line present on the backup roller, a dynamic contact angle boundary condition present in the existing framework of OpenFOAM is applied. A grid independence test for the case with slot web gap SWG = $150\ \mu m$ and substrate speed $V_s=0.5$ m/s was conducted to ensure that the numerical simulations were not dependent on the grid resolution. Three different meshes with a total element count of 50234, 21840, and 15698 were analyzed. The generated numerical results varied within 3% and were considered independent of the grid resolution. In all cases investigated, the finest mesh with 50234 elements was selected.

Results and discussion

The converging geometry ensures a more favorable pressure-gradient downstream as the flow resistance in a pressure-driven flow scales with the third power of the gap distance. The impact of slip on the pressure drop can be illustrated using Fig. 3, where pressure contours of the coating bead in the downstream gap at SWG = $600\ \mu m$ are compared for the prescribed substrate speeds of $V_s= 0.167$ m/s and $V_s= 0.5$ m/s, respectively. As expected, the pressure drop is attenuated appreciably in the presence of slip, compared to the no-slip case. A similar behavior is noticed for the other slot web gaps as well.

Fig. 3

Representation of pressure contours of the coating bead at SWG = $600\ \mu m$

Fig. 4

Comparison of the predicted average pressure at the inlet (BC-1) in bars for different substrate velocities: no-slip with $V_s=0.167$ m/s (Red triangle overline); slip with $V_s=0.167$ m/s (Red asterisk overline); no-slip with $V_s=0.333$ m/s (Green triangle overline); slip with $V_s=0.333$ m/s (Green asterisk overline); no-slip with $V_s=0.5$ m/s (Blue triangle overline); slip with $V_s=0.5$ m/s (Blue asterisk overline)

The average pressure predicted by the numerical model at the inlet boundary indicates a measure of pressure drop inside the slot as the outlet boundaries are kept at ambient pressure. Fig. 4 depicts the relative difference in pressure drops between the corresponding slip and no-slip cases, and the effect of slip is more prominent at lower substrate speeds. As the substrate velocity is increased, the contribution from the pressure-driven flow is much less than that from the shear-driven flow. From Fig. 4, for the case $V_s=0.5$, it can be seen that among different SWGs, the difference in inlet pressure remains small, as the suspension is already fluidized due to high shear rate. In addition to that, higher substrate speeds at narrower SWGs are found to lead to large fluctuations in the pressure fields, especially near to the moving substrate, as shown in Fig. 3b, leading to abrupt disruptions at the moving contact-line in the upstream meniscus, letting air entrainment into the coating bead. Such disturbances are undesirable as they may eventually lead to variations in the coating thickness causing coating defects.

In Fig. 5, we examine the slip velocity generated at the downstream die-wall, scaled by the substrate velocity (the lip boundary from $y=16$ mm to $y=21$ mm in Fig. 3). A representative case for $V_s=0.5$ m/s is only shown here as the behavior of the profiles are closely matched for the lower substrate velocities. The difference in slip velocities at the wall for the cases with SWG = $300\ \mu m$ and SWG = $450\ \mu m$ is marginal among them except near the slot exit ($y>5$). However, for the SWG = $150\ \mu m$ we observe that the slip velocities at the gap entrance are much lower, as the shear from the substrate drives the flow entirely. Additionally, as the pressure-driven flow dominates, the slip layer at the die-wall develops very quickly and at the die-lip exit, the velocities reach $~90\%$ of the substrate velocity, yielding a full plug-like profile. It is to be noted that for the largest SWG, the slip-influenced region remains confined to a narrow layer as the resulting slip velocities are less than $~60\%$ of the substrate speed. This may not be desirable as some of the regions inside the gap may remain unyielded, and the flocculated structures inside the MFC suspensions continue intact, possibly leading to inhomogeneous coatings.

Fig. 5

Variation of the slip velocity scaled by the substrate velocity along the downstream die-lip wall for the case $V_s=0.5$ m/s

Understanding the development of the upward flow in the coating bead inside the converging gap enables us to further elucidate the role of slip. Figure 6 represents the non-dimensional vertical component of velocity scaled with the substrate velocity (U(y)/U(s)) as a function of the local non-dimensional horizontal position ($x/x_{max}$) sampled at three different sections in the converging geometry, viz. 1 mm and 3 mm above the slot gap exit, and at the die lip exit (at $y=17$ mm, $y=19$ mm and at $y=21$ mm, respectively, in Fig. 3). In the case of SWG = $150\ \mu m$, the low-viscosity zone generated alongside the moving substrate due to the shear-thinning nature of the suspension reduces its ability to transfer momentum away from the substrate. Consequently, a high-viscosity, stagnant region is formed at the downstream gap entrance along the lip wall. However, as the fluid moves along the gap, the pressure-driven flow dominates, leading to a fully developed profile at the flow exit. This, in turn, generates velocities higher than the moving substrate in the bulk of the flow.

Fig. 6

Evolution of velocity profile along the converging gap. Here, the profiles shown in are for the prescribed substrate velocity, $V_s=0.5$ m/s. The solid lines are predicted by the no-slip model, while the dashed line shows the profiles denoted by the slip model

As the SWG is increased, low shear rates mean higher momentum from the substrate is transferred across the gap by the fluid and the velocities at the lip exit are comparable to the substrate velocity. Notice that the slip velocity generated at the upstream die wall lowers the local shear stresses and leads to a more plug-like velocity profile at the exit, and the influence of the slip layer becomes limited, with just $20\%$ of the gap for the case with SWG = $600\ \mu m$. For lower substrate velocities, the pattern appears similar and is not shown here for brevity, but the slip layer’s influence is much more diminished. For instance, for the case with SWG = $600\ \mu m$ and $V_s=0.333$ m/s, the slip layer extends to $15\%$ of the slot gap, while for the case with $V_s=0.167$ m/s, the slip layer stretches just $8\%$ of the slot gap.

Fig. 7

Variation of wet coating thickness at different slot web gaps and coating speeds

Figure 7 compares the model predictions for the final wet coating layer thickness at the lip exit for the investigated slot web gaps at different substrate speeds. The wet coating layer thicknesses for the no-slip at SWG = $150\ \mu m$ is controlled by the SWG at the lip exit, except for the lowest substrate velocity, at 156 $\ \mu m$. However, as we employ slip at the boundary, the wet layer thickness increases by ca. $12-15 \%$. For instance, at $V_s=0.167$ m/s and $3\%$ consistency of MFC, slip at the wall results in an increase in dry coating layer thickness from $4.7\ \mu m$ to $5.3\ \mu m$. This excess material might cause runnability issues due to bleeding, i.e., accumulation of coating material outside the top lip. However, with an increase in the substrate speed, the wet-layer thickness approaches that of the SWG, for no-slip cases. Furthermore, the percentage difference between the final wet coating thickness for the slip and no-slip cases, by and large, remains constant.

Fig. 8

Comparison of percentage unyielded area at different slot web gaps

Increasing the SWG to $450\ \mu m$ shows a similar trend but the difference in the final wet layer thicknesses between the slip and no-slip cases is $6 - 8 \%$, whereas for SWG = $600\ \mu m$, the influence of slip in the final coating thickness is hardly perceivable (less than 1.5%). In contrast to the larger ones, for small SWGs, the slip at the wall could considerably change the final amount of suspension coated on the substrate. Also, the marginal decrease in the coat weight with increasing substrate speed could be resulting from the weakened ability to pull the material downstream at higher shear rates. Due to the shear-thinning behavior of suspension, the downstream shear-flow induced by the moving substrate cannot overcome the pressure-driven flow.

Fig. 9

Comparison of the effect of slip on the local shear stress and the predicted unyielded region for different slot web gaps (SWG). Here, the results shown are for the prescribed substrate velocity, $V_s=0.5$ m/s

At high consistencies, processing MFC suspension through narrow slots becomes challenging due to the presence of yield stress. We expect the flocculated fluid to be fully fluidized as it flows through the narrow slot gap. However, earlier investigations16,36,37 suggest that there is a presence of non-deforming plugs in pipe flows and narrow slots. It will be useful to investigate non-yielded, stagnant regions ($\tau < \tau _0$) for the flows inside a coating bead. The challenge of mitigating the non-yielded regions (recalling that yield-stress strongly depends on the fiber concentration, $\tau _0 \sim \mathcal {O}(Conc^3)$22) is even more acute when trying to increase the nanocellulose concentration to minimize the amount of water to be dried. To get a quantitative picture of the stagnant regions in the flow, the region in the downstream gap from the slot gap exit to the die lip exit is chosen, and the estimated percentage unyielded area is shown in Fig. 8. At lower SWGs, the percentage unyielded area is reduced considerably as the overall shear stress level rises in the coating bead gap bridged between the substrate and the coating head. However, at a fixed SWG, increasing the substrate speeds leads to only marginal reduction in the unyielded area. Additionally, the presence of slip leads to a considerable increase in the unyielded regions, accentuated at faster coating speeds and larger SWGs. This is further explained in Fig. 9, where the regions in the flow domain where the local shear stresses lower than the yield stress are highlighted. Close to the die-lip exit, a non-yielding region is formed, adjacent to the moving substrate as the local velocity gradients shift closer to zero. This phenomenon occurs when the flow component from the pressure-driven flow remains comparable to the component of the shear driven flow from the moving substrate. For the case of SWG = $600\ \mu m$ and with the presence of slip at the walls, there is a net reduction in the local velocity gradient, increasing the local viscosity. Large unyielded regions inside the slot die emphasize the need to coat at faster coating speeds so that a high enough shear rate is generated within the slot die, and the material is completely fluidized. However, retaining the coating meniscus stable poses a challenge at high coating speeds. At lower SWGs than presented here, getting stable results from the simulations proved difficult as the air entrainment from the unstable bottom meniscus spans the whole gap and the coatings were not continuous.

Conclusions

Production of nanocellulose films using slot coating is one of the favored coating methods due to its potential scalability for large-scale commercial production. However, coating very thin films at relatively large substrate speeds is challenging as the suspension exhibits complex boundary phenomena, such as particle depleted boundary layer, leading to apparent slip at the wall. In this study, a model describing the rheological behavior of nanocellulose suspension, incorporating the particle depletion at the wall is proposed. The model is implemented in an open-source CFD program and numerically modeled for an existing mini-pilot slot coating setup operating with an unconventional metering mode. The model analyzed here is for a 3% consistency suspension of microfibrillated cellulose (MFC), described as shear thinning, yield stress, Casson fluid. The resulting set of governing equations were solved using a two-phase Volume of Fluid method using OpenFOAM. The results reveal that the slip at the wall leads to an increase in the wet coating thickness, especially at smaller slot gaps. The flow dynamics in the coating bead and the evolution of the velocity profile through the coating gap strongly depend on the slot web gap. For wider slot web gaps, the slip velocities generated in the downstream gap are relatively lower and the region influenced by slip is limited. On the other hand, as the slot web gap decreases, an increased shear rate favorably improves the viscosity field downstream, mitigating unyielded regions. The numerical results suggest that the presence of slip at the wall marginally enhances the coatability of the nanocellulose suspension using the slot coater for thinner films, but may lead to an increase in unyielded regions for thicker films due to the reduced shear rates, augmenting local viscosities.