Compressible and nonisothermal viscoelastic flow between eccentrically rotating cylinders

Abstract

A Taylor–Galerkin finite element time marching scheme is derived to numerically simulate the flow of a compressible and nonisothermal viscoelastic liquid between eccentrically rotating cylinders. Numerical approximations to the governing flow and constitutive equations are computed over a custom refined unstructured grid of piecewise linear Galerkin finite elements. An original extension to the DEVSS formulation for compressible fluids is introduced to stabilise solutions of the discrete problem. The predictions of two models: the extended White–Metzner and FENE-P-MP are presented. Comparisons between the torque and load bearing capacity predicted by both models are made over a range of viscoelastic parameters. The results highlight the significant and interacting effects of elasticity and compressibility on journal torque and resultant load, and the stability of the journal bearing system.

1 Introduction

Lubricants reduce wear and vibration in bearing systems by preventing contact between moving parts. The physical characteristics of lubricants are a crucial determining factor in the performance and longevity of lubricated systems such as car engines and axles. As a consequence, lubrication theory is of particular interest to the automotive industry. The flow between eccentrically rotating cylinders is of particular interest in the mathematical modelling of journal bearing lubrication [30] since it is an idealised problem that retains important elements of the engineering problem.

Journal bearing systems are an intricate part of a large number of industrial and commercial mechanical devices. The working temperature of bearing systems can vary widely within the flow and has a huge impact on the overall performance of the system [20]. Thermal analysis of dynamically loaded bearings (journal bearings) is an invaluable tool in the design of bearing systems and lubricants [20]. Polymers are added to mineral oils to make multigrade oils. The reason for doing this is to weaken the dependence of viscosity on temperature [30]. The addition of elastic polymer chains in Newtonian lubricants results in a viscoelastic mixture. The effect of viscoelasticity on journal bearing performance has been a subject of interest in many investigations. Real journal bearing systems operate at high rates of rotation where the flow Mach number is large enough to be in a weakly compressible regime. Furthermore, the compressibility of a lubricant has been shown to play a significant role in the load bearing capacity of a journal bearing [6].

From a mathematical standpoint, the flow between eccentrically rotating cylinders is an attractive benchmark problem because of its closed geometry, free from sharp and moving boundaries [30]. Several comprehensive numerical investigations of the statically and dynamically loaded bearing problem have been performed by Phillips, Bollada and Davies [5,6,7, 19, 20, 30], and is a commonly visited benchmark problem in CFD. Phillips and Roberts [32] showed that at high eccentricities the predicted reaction forces exerted on the journal by a UCM fluid during rotation are significantly larger than for Newtonian fluids.

Beris et al. [2, 3] calculated the flow between eccentrically rotating cylinders for UCM and PTT fluids using spectral/finite element methods. The method used was based on a formulation of the governing equations in terms of a stream function and extra-stress tensor. Solutions were obtained for $De=90$ for an eccentricity ratio of 0.1. Davies and Li [13] investigated the effects of temperature thinning and pressure thickening using an incompressible White–Metzner model. They found that, at high eccentricities, pressure thickening dominates the viscosity behaviour due to the enormous pressure gradients generated across the narrow gap region of the flow [13].

The first comprehensive study into the effect of fluid compressibility in Newtonian lubricants in journal bearing systems was performed by Bollada and Phillips [5]. In their investigation, they used a log density formulation, in which the governing equations for mass and momentum were rewritten in terms of log density and then solved using a semi-Lagrangian discretisation in time and spectral elements in space. The numerical results showed that even at Mach numbers as low as 0.02 compressibility had a significant effect on the resultant load bearing capacity. Despite these findings, only a small percentage of papers in the literature have considered the fully nonisothermal and compressible problem. To the authors’ knowledge, no investigations have been carried out assessing the numerical predictions of compressible, nonisothermal and viscoelastic flows between eccentrically rotating cylinders.

In this paper, we will focus solely on the statically loaded bearing problem in which a cylinder, radius $R_J$ rotates under a time-dependent load inside a cylindrical container with radius $R_B$ ($R_B-R_J>0$). The centre of the journal is fixed at a distance, e, to the left of the centre of the bearing. The concentric configuration of this problem ($e=0$) is known as the Taylor–Couette problem, which is one of the classical problems in fluid mechanics (Fig. 1).

For a Newtonian fluid, Taylor [34] showed that the purely azimuthal shearing flow that occurs at low speeds becomes unstable as the inertial forces increase. The flow then becomes fully 3D with steady toroidal roll cells forming. As a consequence, an upper limit exists to the Reynolds number if the assumption of 2D flow is to be used. Taylor [34] proposed a parameter, now commonly known as the Taylor number, T, to characterise this critical condition for instability. In the concentric case, this parameter is defined by $T = (Re)^2 (R_B-R_J) / R_J$ when the outer cylinder is stationary. The critical value of Taylor number for primary instability obtained using linear stability analysis is $T=1708$ and this agrees with the experiments that Taylor [34] performed. For the values of $R_B$ and $R_J$ considered in this paper, the value of Re that corresponds to the critical Taylor number is $Re=58$ for the concentric configuration. Cole [9] performed extensive experiments to explore the influence of eccentricity on the critical Taylor number. He showed that for an eccentricity ratio of 0.8 the critical Taylor number increases by between 100 and 200%. This means that for the configuration considered here the Reynolds number corresponding to the critical Taylor number lies in the range [116, 174]. The inclusion of viscoelasticity and nonisothermality is likely to lead to an earlier onset of instabilities. However, to the best of our knowledge the impact of eccentricity ratio in these settings has not been explored.

Fig. 1

Taylor–Couette problem. At lower Reynolds numbers, the flow is steady and azimuthal (Image: Magasjukur2, 2011)

Significant contributions to the development of continuum models for viscoelastic fluids were made in the middle of the last century by Truesdell, Coleman and Noll [10, 11, 35] and Oldroyd [29]. Oldroyd [29] derived a constitutive equation suitable for modelling the behaviour of dilute polymer solutions under quite general flow conditions. The Oldroyd-B model generalised the equations of linear viscoelasticity by expressing the stress/strain relationship in tensorial form and ensuring certain admissibility criteria are satisfied.

The inability of many macroscopic constitutive models to predict the flow of viscoelastic fluids in complex flows prompted the development of kinetic theory models (Bird et al. [4]) based on the coarse-grained concept of an elastic dumbbell immersed in a Newtonian solvent. However, many problems in engineering and industry require the prediction of nonisothermal compressible flows and so models that are fit for this purpose need to be constructed.

In this paper, numerical predictions are generated using constitutive models for compressible nonisothermal viscoelastic fluids. A suitable theoretical framework for modelling such complex fluids is provided by nonequilibrium thermodynamics. In particular, the generalised bracket framework of Dressler et al. [14] and Beris and Edwards [15, 16] provides a general structure for deriving models that are consistent with the laws of thermodynamics. In this paper, two thermodynamically derived viscoelastic models are considered: the extended White–Metzner (EWM) model (Souvaliotis and Beris, [33]) and the FENE-P-MP model (Mackay and Phillips, [26]). Viscometric analysis shows that both models are shear thinning whilst the FENE-P-MP model displays strong extensional strain hardening.

The EWM model of Souvaliotis and Beris [33] is a differential-type phenomenological viscoelastic fluid model that closely resembles the White–Metzner model [36] in which the relaxation time is considered as a scalar function of an internal structural tensorial parameter rather than the rate of deformation tensor. The EWM model retains an important advantage of the WM model in that it can accurately predict the viscosity and first normal stress difference of any polymeric fluid in a simple shear flow using only a single relaxation time. In addition, it guarantees the evolutionary character of the flow field and a nonnegative entropy production by the fluid. Because the EWM model is thermodynamically admissible, it is possible to extract thermodynamic (and statistical) information about the fluid from its predictions. Germann et al. [17] were the first to solve one of the benchmark problems in computational rheology using the EWM model when they studied eccentric Taylor–Couette flow.

Numerical solutions are obtained by discretising the governing equations in time using a two-step Taylor–Galerkin method and in space using Galerkin finite elements. In order to combat numerical instability phenomena, the computations are stabilised using both SUPG and a novel adaptation of DEVSS for compressible flow.

This paper is organised as follows. The general set of governing equation domain and boundary conditions are presented in Sec. 2. The numerical scheme used to generate results is given in Sec. 3. In Sec. 4, the numerical scheme for incompressible flow is benchmarked and numerical results are compared to those from the literature for an incompressible Oldroyd-B fluid. In Sec. 5, the compressible flow of an (i) extended White–Metzner and (ii) FENE-P-MP fluid is analysed. Measurements of the reaction forces and torque on the rotating journal are assessed for $0\le {We}\le 1.0$, $10\le {Re}\le {200}$ and $0\le {Ma}\le 0.1$. A discussion of the parameter values used in the compressible flow simulations is also given. Some concluding remarks are provided in Sec. 6.

2 Mathematical formulation

The flow is bounded between two cylinders of different radii. The inner cylinder (or journal) of radius $R_J$ rotates with a constant angular velocity $\omega$ within a hollow outer cylinder (or bearing) of radius $R_B$ that remains stationary. We assume that the viscoelastic liquid completely fills the region between the two cylinders. Both cylinders are assumed to be of infinite extent in the axial z-direction so that the long bearing approximation can be invoked. The distance between the axes of rotation of the journal and bearing is known as the eccentricity, e, where

$$\begin{aligned} \epsilon = \frac{e}{R_B-R_J}, \end{aligned}$$

(2.1)

so that the eccentricity ratio $\epsilon$ is in the range $0 \le \epsilon \le 1$. The computational domain is the two-dimensional region between the two cylinders,

$$\begin{aligned} \Omega =\{(x,y):x^2+y^2\le {R^2_B} \text{ and } {(x+e)}^2+y^2\ge {R^2_J}\} \end{aligned}$$

(2.2)

with boundaries

$$\begin{aligned} \Gamma _J=\{(x,y): (x+e)^2+y^2=R_J^2\}\qquad \Gamma _B=\{(x,y): x^2+y^2=R_B^2\} \end{aligned}$$

(2.3)

A diagram of the computational domain is shown in Fig. 2.

Fig. 2

Schematic diagram of the computational domain $\Omega$

The governing equations comprise the conservation of mass, momentum and energy written in the following form

$$\begin{aligned} \begin{aligned}&\frac{\partial \rho }{\partial {t}}+\nabla \cdot (\rho {\mathbf{u }})=0,\\&\rho \frac{D{\mathbf{u }}}{Dt}=-\nabla {p}+\mu _s\Bigg (\nabla ^2{\mathbf{u }}+\frac{1}{3}\nabla (\nabla \cdot {\mathbf{u }})\Bigg )+\nabla \cdot \varvec{\tau }_p+{\mathbf{F }},\\&\rho {C}_p\frac{D\theta }{Dt}=-\nabla \cdot {\mathbf{q }}+\varvec{\sigma }:\nabla {\mathbf{u }},\\ \end{aligned} \end{aligned}$$

(2.4)

where $\rho$ is the density, ${\mathbf {u}}$ is the velocity, p is the pressure, $\varvec{\tau }_p$ is the polymeric contribution to the extra-stress tensor, $\theta$ is absolute temperature, $\varvec{\sigma }=-p{\mathbf{I }}+2\mu _s {\mathbf {D}}+\varvec{\tau }_p$ is the Cauchy stress tensor, ${\mathbf{q }}=-\kappa \nabla {\theta }$ is the heat flux vector and ${\mathbf{F }}$ is the applied force. The material parameters are $\mu _s$, the solvent viscosity, $C_p$, the specific heat at constant pressure and $\kappa$ the heat conduction coefficient. The solvent viscosity is assumed to be constant. The eccentrically rotating cylinder problem is a prototype for journal bearing lubrication. In automotive engineering mineral oils are formulated to minimise the dependence of viscosity on temperature. This is achieved by adding polymers to mineral oils to formulate a multigrade oil. With the addition of polymers, the oil becomes non-Newtonian. Thus, we have implemented a constant solvent viscosity to describe the behaviour of the base mineral oil and a polymeric viscosity that depends on temperature to model the polymer additives.

The stress tensor $\varvec{\tau }_{p}$ is a function of both ${\mathbf{C }}$ and $\theta$

$$\begin{aligned} \varvec{\tau }_{p}={\mathbf{g }}_1({\mathbf{C }}, \theta ), \end{aligned}$$

(2.5)

where ${\mathbf{C }}$ is the conformation tensor satisfying the constitutive equation

$$\begin{aligned} {\mathbf{C }}+{\lambda }(\theta )({\mathop {{\mathbf{C }}}\limits ^{\triangledown }}+(\nabla \cdot {\mathbf{u }}){\mathbf{C }}) + {\mathbf{g }}_2({\mathbf{C }},{\mathbf{D }})={\mathbf{I }}, \end{aligned}$$

(2.6)

and ${\mathbf{D }}$ is the rate of deformation tensor. In equations (2.5) and (2.6), ${\mathbf{g }}_1$ and ${\mathbf{g }}_2$ are model-dependent tensor functions. Finally, an equation of state is required to relate pressure and density. Here we use the equation

$$\begin{aligned} \frac{\partial {p}}{\partial \rho }=c^2_0\Bigg (1+\alpha \frac{(\theta -\theta _0)}{\theta _0}\Bigg ), \end{aligned}$$

(2.7)

where $c_0$ is the speed of sound and $\theta _0$ is a reference temperature. The parameter $\alpha$ is related to the expansion of the fluid at $\theta =\theta _0$. A value $\alpha =0$ corresponds to isothermal flow and $\alpha =1$ to an ideal gas equation.

On $\Gamma _J$, no-slip boundary conditions and constant temperature are imposed

$$\begin{aligned} {\mathbf{u }}=\frac{\phi (t)}{\root \of {x^2+y^2}}(y,-x),\qquad \theta =\theta _0, \end{aligned}$$

where the ramp function $\phi$ is defined by

$$\begin{aligned} \phi (t)=\frac{\omega }{2}(1+\tanh (8({t}-0.5))), \end{aligned}$$

(2.8)

and $\omega$ is the maximum angular velocity of the journal. The hyperbolic tangent function was chosen so that the rotational speed of the journal increases smoothly to approximately $\omega$ over the time interval [0, 2]. On $\Gamma _B$, a Dirichlet (no-slip) condition for the velocity and a Robin condition for the temperature are imposed

$$\begin{aligned} {\mathbf{u }}={\mathbf{0 }},\quad \frac{\partial {\theta }}{\partial {\mathbf{n }}}=-\frac{Bi}{h_c} \theta , \end{aligned}$$

where $h_c$ is a characteristic thickness and the Biot number, Bi, is a nondimensional measure of the heat transfer at the outward facing boundary of the journal bearing. The relative thickness, $\upsilon$, is defined by

$$\begin{aligned} \upsilon =\frac{R_B-R_J}{R_J}. \end{aligned}$$

(2.9)

Note the relative thickness is a measure of the ratio gap to journal radius, whereas $h_c$ is a dimensional parameter related to convective heat transfer through the outer boundary. Let L, U and $(\theta _h-\theta _0)$ denote characteristic length, velocity and temperature scales, respectively. We introduce the dimensionless variables

$$\begin{aligned} \begin{aligned}&{\mathbf{u }}^*=\frac{{\mathbf{u }}}{U},\quad {\mathbf{x }}^*=\frac{{\mathbf{x }}}{L}\quad t^*=\frac{tU}{L},\quad \\ \rho ^*=\frac{\rho }{\rho _0},\quad&{p}^*=\frac{pL}{\mu _0U},\quad \theta ^*=\frac{\theta -\theta _0}{\theta _h-\theta _0},\quad \varvec{\tau }^*_p=\frac{L \varvec{\tau }_p}{\mu _0 U}. \end{aligned} \end{aligned}$$

(2.10)

The system of equations (2.4), (2.6), (2.7) can be written in the following nondimensional form

$$\begin{aligned} \begin{aligned}&\frac{\partial \rho }{\partial {t}}+\nabla \cdot (\rho {\mathbf{u }})=0,\\&{Re}\rho \frac{D{\mathbf{u }}}{Dt}=-\nabla {p}+\Bigg [\beta _v\Bigg (\nabla ^2{\mathbf{u }}+\frac{1}{3}\nabla (\nabla \cdot {\mathbf{u }})\Bigg )+\nabla \cdot \varvec{\tau }_{p}\Bigg ]+{\mathbf{F }},\\&\rho \frac{D\theta }{Dt}= Di \nabla \cdot \tilde{{\mathbf{q }}}+V_{h}\varvec{\sigma }:\nabla {\mathbf{u }},\\&{\mathbf{C }}+We{\tilde{\psi }}(\theta )({\mathop {{\mathbf{C }}}\limits ^{\triangledown }}+(\nabla \cdot {\mathbf{u }}){\mathbf{C }}) + {\mathbf{g }}_2({\mathbf{C }},{\mathbf {D}})={\mathbf{I }},\\&\frac{\partial {\rho }}{\partial {p}}=\frac{Ma^2}{Re(1+{\tilde{\alpha }}\theta )}, \end{aligned} \end{aligned}$$

(2.11)

where Re is the Reynolds number, We is the Weissenberg number, Ma is the Mach number, $\beta _v$ is the viscosity ratio, Di is the diffusion number and $V_h$ is the viscous heating number with definitions

$$\begin{aligned} \begin{aligned} Re=\frac{\rho _0UL}{\mu _0},\qquad&\qquad {We}=\frac{\lambda {U}}{L},\\ Ma=\frac{U}{c_0},\qquad&\qquad \beta _{v}=\frac{\mu _s}{\mu _0},\qquad {Bi}=\frac{h}{k_B}L,\\ {Di}=\frac{\kappa }{\rho _0C_pUL},\quad&\quad {V_h}=\frac{U\mu _0}{\rho _0C_pL(\theta _h-\theta _0)}.\\ \end{aligned} \end{aligned}$$

(2.12)

In the above definitions, h and $k_B$ are the heat transfer coefficient and the thermal conductivity of the outer boundary, respectively. We define $h_c=L$ so that the thermal boundary condition on $\Gamma _B$ can be expressed purely in terms of the Biot number,

$$\begin{aligned} \frac{\partial {\theta }}{\partial {\mathbf{n }}}=-{Bi}\; \theta . \end{aligned}$$

2.1 Constitutive models

2.1.1 Extended White–Metzner (EWM) model

The generalisation of the Oldroyd-B model to account for variable relaxation time was proposed by White and Metzner [36]. The extended White–Metzner (EWM) model [33] is a thermodynamically derived constitutive equation suitable for modelling viscoelastic fluids with variable relaxation time. Importantly the dependence of $\lambda$ on the conformation tensor and not the strain rate and pressure avoids the potential loss of evolutionarity that can occur with the White–Metzner model ([1] p. 230). The polymeric viscosity and relaxation time depend on both temperature and conformation stress. The nondimensional form of the EWM model is given by (2.5)–(2.6) with

$$\begin{aligned} {\mathbf{g }}_1({\mathbf{C }},\theta )=\frac{(1-\beta _v){\hat{\psi }}({\mathbf{C }},\theta )}{We{\tilde{\psi }}({\mathbf{C }},\theta )}({\mathbf{C }}-{\mathbf{I }})\qquad {\mathbf{g }}_2({\mathbf{C }},{\mathbf{D }})={\mathbf{0 }}. \end{aligned}$$

(2.13)

Combining both the EWM stress thinning and temperature dependence, we obtain the following functions for the viscosity and relaxation time

$$\begin{aligned} {\hat{\psi }}({\mathbf{C }},\theta )=\frac{1}{2}I_1({\mathbf{C }})^k \exp (-A_{p,0}\theta ), \end{aligned}$$

(2.14)

and

$$\begin{aligned} {\tilde{\psi }}({\mathbf{C }},\theta )=\frac{1}{2}I_1({\mathbf{C }})^k \left( \frac{\theta }{\theta _s}+1\right) \exp (-A_{p,0}\theta ), \end{aligned}$$

(2.15)

where we define

$$\begin{aligned} \theta _s = \theta _0/(\theta _h-\theta _0), \end{aligned}$$

$A_{p,0}$ is the activation energy and k is a power law index.

Note that the coefficient of 1/2 appears in the 2D formulation to ensure that $\varvec{\psi }=1$ when ${\mathbf{C }}={\mathbf{I }}$ and $\theta =0$. For the 3D case, the coefficient is 1/3 as presented in the literature [17, 33]. The values of the various parameters used in the simulations of the EWM model are given in Table 1. The value for k has been chosen to represent moderate shear thinning and is equal to the value chosen by Germann et. al [17] for ‘fluid 1’ in their study of the same problem. The value of the viscosity ratio, $\beta _v$, is a standard choice in computational rheology. The parameters $\theta _s$ and $A_{p,0}$ have been chosen to represent moderate temperature dependence of the fluid’s elastic response.

Table 1 Nondimensional parameters in the viscosity relations for the EWM model

2.1.2 FENE-P-MP model

The second model considered is the FENE-P-MP model (Mackay and Phillips [26]), described by (2.5)–(2.6) with

$$\begin{aligned} \begin{aligned} {\mathbf{g }}_1({\mathbf{C }},\theta )&=\frac{(1-\beta _v){\hat{\psi }}({\mathbf{C }},\theta )}{We{\tilde{\psi }}({\mathbf{C }},\theta )}({\mathbf{f }}(\text {tr}{\mathbf{C }}){\mathbf{C }}-{\mathbf{I }}),\\ {\mathbf{g }}_2({\mathbf{C }},{\mathbf{D }})&= ({\mathbf{f }}(\text {tr}{\mathbf{C }})-1){\mathbf{C }}+We\phi ({\dot{\epsilon }})[{\mathbf{C }}\cdot {\mathbf{D }}+{\mathbf{D }}\cdot {\mathbf{C }}],\\ \end{aligned} \end{aligned}$$

(2.16)

where

$$\begin{aligned} {\mathbf{f }}(\text {tr}{\mathbf{C }})=\frac{b^2}{b^2-\text {tr}{\mathbf{C }}}, \end{aligned}$$

(2.17)

and

$$\begin{aligned} \phi ({\dot{\epsilon }})=\frac{\cosh (\lambda _D{\dot{\epsilon }})-1}{2}, \end{aligned}$$

(2.18)

where $\lambda _D$ is the dissipation parameter, ${\dot{\epsilon }}$ is the generalised strain rate and b is the maximum extension of the spring in the FENE model.

3 Numerical approximation

3.1 Time discretisation: Taylor–Galerkin method

The governing equations are temporally discretised using a Taylor–Galerkin method. Taylor–Galerkin methods were initially developed for solving convective transport problems for which the governing equations are hyperbolic [30]. The motivation for Taylor–Galerkin methods stems from the desire to derive high-order accurate time-stepping schemes which can be used in conjunction with spatial discretisation methods. A two-step Taylor–Galerkin algorithm for computing nonisothermal and (weakly) compressible viscoelastic flow is given by

$$\begin{aligned}&\mathbf{Step 1a } \quad \qquad \Bigg (\frac{\rho ^{n+\frac{1}{2}}-\rho ^{n}}{\Delta t/2}\Bigg ) = -{\mathbf{u }}^{n} \cdot \nabla \rho ^{n} - \rho ^{n} (\nabla \cdot {\mathbf{u }}^{n})\nonumber \\&\mathbf{Step 1b }\qquad {Re}\Bigg (\frac{\rho ^{n+\frac{1}{2}}{\mathbf{u }}^{n+\frac{1}{2}}-\rho ^{n}{\mathbf{u }}^n}{\Delta {t}/2}\Bigg )=\beta _v\Bigg (\nabla ^2{\mathbf{u }}^{n}+\frac{1}{3}\nabla (\nabla \cdot {\mathbf{u }}^n)\Bigg )-Re{\mathbf{u }}^n\cdot \nabla {\mathbf{u }}^n+\nabla \cdot \varvec{\tau }_p^n-\nabla {p}^n\nonumber \\&\mathbf{Step 1c }\qquad We{\tilde{\psi }}(\theta )\Bigg (\frac{{\mathbf{C }}^{n+\frac{1}{2}}-{\mathbf{C }}^n}{\Delta {t}/2}\Bigg )=[{\mathbf{I }}-{\mathbf{C }}-We {\widetilde{\psi }}(\theta )({\mathbf{u }}\cdot \nabla {\mathbf{C }}-{\mathbf{C }}\nabla {\mathbf{u }}+\nabla {\mathbf{u }}^T{\mathbf{C }}+\nabla \cdot {\mathbf{u }}{\mathbf{C }})-{\mathbf{g }}_2({\mathbf{C }},{\mathbf{D }})]^{n}\nonumber \\&\mathbf{Step 1d }\quad \qquad \rho ^n \left( \frac{\theta ^{n+\frac{1}{2}}-\theta ^n}{\Delta {t}/2}\right) =Di\nabla ^2\theta ^{n}- \rho ^n{\mathbf{u }}^n\cdot \nabla \theta ^{n}+V_h(\varvec{\sigma }^{n}:\nabla {\mathbf{u }}^{n}-p^n\nabla \cdot {\mathbf{u }}^n)\nonumber \\&\mathbf{Step 2 }\quad \qquad {Re}\rho ^{n}\Bigg (\frac{{\mathbf{u }}^*-{\mathbf{u }}^n}{\Delta {t}}\Bigg )=\frac{1}{2}\beta _v\Bigg (\nabla ^2{\mathbf{u }}^{n}+\frac{1}{3}\nabla (\nabla \cdot {\mathbf{u }}^n)\Bigg )-Re{\mathbf{u }}^{n+\frac{1}{2}}\cdot \nabla {\mathbf{u }}^{n+\frac{1}{2}}+\nabla \cdot \varvec{\tau }_p^{n+\frac{1}{2}}-\nabla {p}^n\nonumber \\&\mathbf{Step 3 } \quad \qquad \Bigg (\frac{\rho ^{n+1}-\rho ^{n}}{\Delta t}\Bigg ) = -{\mathbf{u }}^{n+\frac{1}{2}} \cdot \nabla \rho ^{n+\frac{1}{2}} - \rho ^{n+\frac{1}{2}} (\nabla \cdot {\mathbf{u }}^{n+\frac{1}{2}})\nonumber \\&\mathbf{Step 4 }\qquad \qquad \qquad p^{n+1}-p^n = \frac{Re(1+{\tilde{\alpha }}\theta ^n)}{Ma^2} (\rho ^{n+1}-\rho ^{n})\nonumber \\&\mathbf{Step 5 }\qquad {Re}\Bigg (\frac{\rho ^{n+1}{\mathbf{u }}^{n+1}-\rho ^{n}{\mathbf{u }}^*}{\Delta {t}}\Bigg )=-\frac{1}{2}\nabla (p^{n+1}-p^{n})+\frac{1}{2}\beta _v\Bigg (\nabla ^2{\mathbf{u }}^{n+1}+\frac{1}{3}\nabla (\nabla \cdot {\mathbf{u }}^{n+1})\Bigg )\nonumber \\&\mathbf{Step 6 }\qquad We{\tilde{\psi }}(\theta )\Bigg (\frac{{\mathbf{C }}^{n+1}-{\mathbf{C }}^n}{\Delta {t}}\Bigg )+{\mathbf{C }}^{n+1}=[{\mathbf{I }}-We{\widetilde{\psi }}(\theta )({\mathbf{u }}\cdot \nabla {\mathbf{C }}-{\mathbf{C }}\cdot \nabla {\mathbf{u }}+\nabla {\mathbf{u }}^T\cdot {\mathbf{C }}+(\nabla \cdot {\mathbf{u }}){\mathbf{C }})\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad -{\mathbf{g }}_2({\mathbf{C }},{\mathbf{D }})]^{n+\frac{1}{2}}\nonumber \\&\mathbf{Step 7 }\quad \qquad \left( \frac{\rho ^{n+1}\theta ^{n+1}-\rho ^n\theta ^n}{\Delta {t}}\right) =Di\nabla ^2\theta ^{n+1}- \rho ^{n+\frac{1}{2}}{\mathbf{u }}^{n+\frac{1}{2}}\cdot \nabla \theta ^{n+\frac{1}{2}}+V_h(\varvec{\sigma }^{n+\frac{1}{2}}:\nabla {\mathbf{u }}^{n+\frac{1}{2}}-p^n\nabla \cdot {\mathbf{u }}^n) \end{aligned}$$

(3.1)

where $\hat{{\mathbf {D}}}={\mathbf {D}}-\frac{1}{2}(\nabla \cdot {\mathbf{u }}){\mathbf{I }}$. Equation (3.1) represents a second-order (in time) discretisation for the system of equations for weakly compressible viscoelastic flow (Eq. (2.11)).

Step 1 represents an explicit discretisation of the continuity, momentum, constitutive and energy equations over a half time step. An intermediate velocity is computed in Step 2, and together with Step 5, these represent a second-order Crank–Nicolson discretisation of the momentum equation. Step 3 is a discretisation of the continuity equation using the mid-point rule. Step 4 is a discretisation of the equation of state in which the temporal derivative of density is replaced by the temporal derivative of pressure using the chain rule

$$\begin{aligned} \frac{\partial \rho }{\partial t} = \frac{Ma^2}{Re(1+{{\tilde{\alpha }}} \theta )} \frac{\partial p}{\partial t}. \end{aligned}$$

(3.2)

Steps 5, 6 and 7 represent discretisations of the momentum, constitutive and energy equations, respectively, in which the nonlinear terms are evaluated using the mid-point rule and the linear terms are treated implicitly.

3.2 Weak formulation

The weak formulation of the semi-discrete problem 3.1 is discretised using the finite element method. In order to write the weak form of the problem, we introduce appropriate function spaces. The space of square integrable functions in a domain, $\Omega$, is denoted $L^2(\Omega )$ and the space of functions whose first-order partial derivatives are square integrable is denoted by $H^1(\Omega )$. We define the function spaces for the velocity, pressure, stress and temperature as follows

$$\begin{aligned} {\mathcal {V}}=&\left\{ {\mathbf{v }}\in {H}^1(\Omega )^2: {\mathbf{v }}={\mathbf{v }}_J \text{ on } \Gamma _J, {\mathbf{v }}={\mathbf{0 }} \text{ on } \Gamma _B \right\} , \end{aligned}$$

(3.3)

$$\begin{aligned} {\mathcal {Q}}=&\left\{ q\in {L}^2(\Omega )\right\} , \end{aligned}$$

(3.4)

$$\begin{aligned} {\mathcal {Z}}=&\left\{ {\mathbf{R }}: \quad {R}_{ij}\in {H}^1(\Omega ),\quad {R}_{ij}={R}_{ji}, i,j=1,2 \right\} , \end{aligned}$$

(3.5)

$$\begin{aligned} {\mathcal {Q}}^T=&\left\{ \theta \in {H}^1(\Omega ): \theta =\theta _0 \text{ on } \Gamma _J \right\} . \end{aligned}$$

(3.6)

Similarly, we define the corresponding test spaces for velocity and temperature as follows

$$\begin{aligned} {\mathcal {V}}_0=&\left\{ {\mathbf{v }}\in {H}^1(\Omega )^2:{\mathbf{v }}=0\,\text{ on }\,\partial \Omega \right\} , \end{aligned}$$

(3.7)

$$\begin{aligned} {\mathcal {Q}}^T_0=&\left\{ \theta \in {H}^1(\Omega ): \theta =0 \text{ on } \Gamma _J \right\} . \end{aligned}$$

(3.8)

The weak formulation of each step in Eq. 3.1 is derived by multiplying each equation by a test function from an appropriate test space and integrating over $\Omega$. By applying Green’s theorem, we are able to express the second-order derivatives appearing in Eq. 3.1 in terms of first-order derivatives of the weak solution and test functions.

3.3 Numerical stabilisation

3.3.1 DEVSS and DEVSS-G

The governing equations can be expressed in a modified but mathematically equivalent form to improve the ellipticity of the momentum equation and to stabilise the corresponding numerical approximation. The success of schemes introducing additional ellipticity into the momentum equation arises from the explicit form of the viscous operator in the momentum equation, which results in solving an elliptic saddle point problem. For viscoelastic fluids, this viscous term is scaled with the ratio of Newtonian to total viscosity, $\beta$. As our interest is predominantly in flow configurations with dominant viscoelastic effects, $\beta \approx 0.1$. In this case, the elastic stress contribution can dominate the viscous term and this can lead to instabilities. Perera and Walters [31] introduced the idea of introducing ellipticity through a change of variable. This approach was first employed in the elastic viscous split stress (EVSS) formulation by Mendolson et al. [28] for flows of second-order fluids. The change of variables performed in EVSS-type methods may be impossible for some constitutive equations. This motivated Guénette and Fortin [18] to propose the discrete EVSS (DEVSS) formulation, which does not require a change of variables and the viscous term in the momentum equation is introduced only in an approximate sense.

In the case of incompressible flow, the rate of deformation tensor ${\mathbf{D }}=(\nabla {\mathbf{u }}+\nabla {\mathbf{u }}^{T})$ is introduced as an additional variable and the momentum equation is expressed in the form

$$\begin{aligned} Re\frac{D{\mathbf{u }}}{Dt}+\nabla {p}+\gamma _u(\nabla ^2{\mathbf{u }}-\nabla \cdot {\mathbf{D }})+\beta _v\nabla ^2{\mathbf{u }}-\nabla \cdot \varvec{\tau }_p=0, \end{aligned}$$

(3.9)

where $\gamma _u$ is the DEVSS stabilisation parameter. At the continuous level, it is clear that the term multiplied by $\gamma _u$ is equal to zero because $\nabla \cdot {\mathbf{D }}=\nabla ^2{\mathbf{u }}$. This is not true when the approximation space for ${\mathbf{D }}$ does not contain the gradient of the approximation space for velocity. As a result, in regions of high deformation rate where stress gradients are largest the DEVSS term stabilises the solution.

In the case of compressible flow, we propose the following extension to the DEVSS formulation (3.9) in which the momentum equation is now expressed in the form

$$\begin{aligned} Re \frac{D{\mathbf{u }}}{Dt}+\nabla {p}+\gamma _u\Bigg (\nabla ^2{\mathbf{u }}+\frac{1}{3}\nabla (\nabla \cdot {\mathbf{u }})-\nabla \cdot {\mathbf{D }}\Bigg )+\beta _v\Bigg (\nabla ^2{\mathbf{u }}+\frac{1}{3}\nabla (\nabla \cdot {\mathbf{u }})\Bigg )-\nabla \cdot \varvec{\tau }_p=0, \end{aligned}$$

(3.10)

where the expression for ${\mathbf{D }}$ is given by

$$\begin{aligned} {\mathbf{D }}=\Bigg (\nabla {\mathbf{u }}+\nabla {\mathbf{u }}^{T}-\frac{2}{3}(\nabla \cdot {\mathbf{u }}){\mathbf{I }}\Bigg ). \end{aligned}$$

(3.11)

In both cases, $\varvec{\tau }_p$ is determined by the constitutive equation.

Brown et al. [8] used the velocity gradient tensor, ${\mathbf {G}}= \nabla {\mathbf {u}}$, as an additional unknown, instead of using the rate of deformation tensor, ${\mathbf {D}}$. In this method, called the EVSS-G method, the additional unknown, ${\mathbf {G}}$, is computed by means of an $L^2$ projection of $\nabla {\mathbf {u}}$. In analogy to the EVSS-G method, the DEVSS-G method (Liu et al. [22]) may be defined, where a projection of the velocity gradient tensor is made instead of the rate of deformation tensor. In this formulation, the velocity gradient projection tensor is used in the constitutive equation as well as in the momentum equation. We choose the solution space for the velocity gradient tensor as $[L^2(\Omega )]^{2 \times 2}$, to be consistent with the spaces for pressure and polymeric stress, which are chosen to be $L^2_0(\Omega )$ and $[L^2(\Omega )]^{2 \times 2}_s$, respectively.

3.3.2 SUPG

The first application of streamlined upwind methods to viscoelastic flows was performed by Marchal and Crochet [27]. The authors used both the SUPG method and streamlined upwind (SU) method for computing the stress; however, they found that the consistent SUPG integration of the constitutive equation produced errors in the calculation of stick–slip flow and flow through an abrupt contraction. Crochet and Legat [12] concluded that the failure of SUPG to prevent numerical breakdown was due to errors occurring at the sharp corners within the flow. They substantiated this claim by illustrating that SUPG was both stable and accurate when used to solve the flow of a UCM fluid around a sphere and through a corrugated tube. A review of SUPG methods for viscoelastic flows by Phillips and Owens can be found here [30].

The weak formulation of the constitutive equation (2.11) is modified using SUPG augmented test functions $\hat{{\mathbf{R }}}_h$ and ${\hat{q}}_h$ defined by

$$\begin{aligned} \hat{{\mathbf{R }}}_h={\mathbf{R }}_h+h\frac{{\mathbf{u }}_h}{|{\mathbf{u }}_h|}\cdot \nabla {\mathbf{R }}_h, \end{aligned}$$

(3.12)

and

$$\begin{aligned} {\hat{q}}_h=q_h+h\frac{{\mathbf{u }}_h}{|{\mathbf{u }}_h|}\cdot \nabla {q}_h, \end{aligned}$$

(3.13)

where h is the cell diameter of the finite element. The weak formulation of the constitutive and continuity equations becomes

$$\begin{aligned} \int _{\Omega }\left( {\mathbf{C }}_h+We({\mathop {{\mathbf{C }}}\limits ^{\triangledown }}_h+(\nabla \cdot {\mathbf{u }}_h){\mathbf{C }}_h) +{\mathbf{g }}_2({\mathbf{C }}_h,{\mathbb {D}}_h)-{\mathbf{I }}\right) :\hat{{\mathbf{R }}}_h\,d\Omega =0, \end{aligned}$$

(3.14)

and

$$\begin{aligned} \int _{\Omega }\left( \frac{\partial \rho }{\partial {t}}+\nabla \cdot (\rho {\mathbf{u }})\right) {\hat{q}}_h\,d\Omega =0, \end{aligned}$$

(3.15)

respectively.

For problems with smooth boundaries, high-order accuracy and stability for the stress and density solutions can be obtained. For problems with singularities, the augmented test functions collapse to the standard Galerkin test function near the boundary and spurious oscillations can occur.

Fig. 3

a Piecewise linear P1, b piecewise quadratic P2 and c piecewise constant P0 elements

3.4 Discretised problem

The computational domain, $\Omega$, is partitioned into triangular finite elements. On each element, each dependent variable is approximated using a low-order polynomial in which the unknowns are the coefficients of the basis functions. These are the degrees of freedom of the problem and are typically approximations to the dependent variables at the nodes. A set of algebraic equations is then derived by choosing appropriate test functions and evaluating or approximating the integrals that appear in the weak formulation of Eq. (3.1). Essentially a test function is associated with each unknown in the problem. In this paper, we restrict ourselves to three types of compatible finite elements suitable for modelling viscoelastic flow, namely P1 piecewise linear continuous Lagrangian elements for pressure, density and temperature, P2 piecewise quadratic for velocity and P1 discontinuous Lagrangian elements for stress (see Fig. 3). In the implementation of DEVSS-G stabilisation, we make use of the space of discontinuous functions over $\Omega$ constructed using P0 elements for approximating ${\mathbf {G}}$.

We can construct conforming finite element spaces ${\mathcal {V}}_h\subset {\mathcal {V}}$, ${\mathcal {Q}}_h\subset {\mathcal {Q}}$ and ${\mathcal {Z}}_h\subset {\mathcal {Z}}$ in the usual manner

$$\begin{aligned} {\mathcal {V}}_h=&\left\{ {\mathbf{v }}_h\in {H}^1(\Omega )^2: {\mathbf{v }}={\mathbf{v }}_J \text{ on } \Gamma _J, \quad {\mathbf{v }}_h={\mathbf{0 }} \text{ on } \Gamma _B \right\} , \end{aligned}$$

(3.16)

$$\begin{aligned} {\mathcal {Q}}_h=&\left\{ q_h\in {L}^2(\Omega )\right\} , \end{aligned}$$

(3.17)

$$\begin{aligned} {\mathcal {Z}}_h=&\left\{ {\mathbf{R }}: \quad {R}_{h,ij}\in {H}^1(\Omega ),\quad {R}_{h,ij}={R}_{h,ji},\quad i,j=1,2 \right\} , \end{aligned}$$

(3.18)

$$\begin{aligned} {\mathcal {Q}}_h^T=&\left\{ \theta _h \in {H}^1(\Omega ): \theta =\theta _0 \text{ on } \Gamma _J \right\} . \end{aligned}$$

(3.19)

This combination of discrete function spaces ensures that the Ladyzhenskaya–Babuška–Brezzi (LBB) or inf-sup condition is satisfied.

Analogous to Eq. (3.1), the fully discrete problem can be expressed in terms of the following steps in which each step requires the solution of a linear system of equations:

$$\begin{aligned} \begin{aligned}&\mathbf{Step 1a } \quad \qquad 2{\mathbf{M }}^{Q}\varvec{\Gamma }^{n+\frac{1}{2}}=2{\mathbf{M }}^{Q}\varvec{\Gamma }^{n}-\Delta {t}\left( {\mathbf{H }}^{1,{\mathbf{u }}}+{\mathbf{H }}^{2,{\mathbf{u }}}\right) \varvec{\Gamma }^n \\&\mathbf{Step 1b } \quad \qquad \left( \begin{array}{cc} {2Re}{\mathbf{M }}^{V}+\Delta {t}\gamma _v{\mathbf{A }} &{} -\Delta {t}\gamma _v{\mathbf{C }} \\ -\Delta {t}\hat{{\mathbf{E }}} &{} \Delta {t}{\mathbf{M }}^{Z} \end{array} \right) \left( \begin{array}{c} {\mathbf{U }}^{n+\frac{1}{2}} \\ {\mathbf{D }}^{n+\frac{1}{2}} \end{array}\right) = \left( \begin{array}{c} \tilde{\varvec{{\mathcal {F}}}}_1^u \\ 0 \end{array}\right) \\&\mathbf{Step 1c } \quad \qquad 2We{\mathbf{M }}^{Z}{\mathbf{T }}^{n+\frac{1}{2}}=[(2We-\Delta {t}){\mathbf{M }}^{Z}-We{{\mathbf{F }}}^n]{\mathbf{T }}^{n}+\hat{{\mathbf{I }}}\\&\mathbf{Step 1d } \quad \qquad 2{\mathbf{M }}^{Q}\Theta ^{n+\frac{1}{2}}=[2{\mathbf{M }}^{Q}-{\mathbf{M }}+\Delta {t}Di{{\mathbf{G }}}^n]\Theta ^{n}+{{\mathbf{L }}^{n}}{\mathbf{U }}^{n}\\&\mathbf{Step 2 } \quad \qquad \left( \begin{array}{cc} {Re}{\mathbf{M }}^{V}+\Delta {t}\gamma _v{\mathbf{A }} &{} -\Delta {t}\gamma _v{\mathbf{C }} \\ -\Delta {t}\hat{{\mathbf{E }}} &{} \Delta {t}{\mathbf{M }}^{Z} \end{array}\right) \left( \begin{array}{c} {\mathbf{U }}^{*} \\ {\mathbf{D }}^{*} \end{array} \right) = \left( \begin{array}{c} \tilde{\varvec{{\mathcal {F}}}}_2^u \\ 0 \end{array}\right) \\&\mathbf{Step 3 } \quad \qquad {\mathbf{M }}^{Q}\varvec{\Gamma }^{n+1}={\mathbf{M }}^{Q}\varvec{\Gamma }^{n}-\Delta {t}\left( {\mathbf{H }}^{1,{\mathbf{u }}}+{\mathbf{H }}^{2,{\mathbf{u }}}\right) \varvec{\Gamma }^{n+\frac{1}{2}}\\&\mathbf{Step 4 } \quad \qquad \Bigg (\frac{Ma^2}{\Delta {t}}{\mathbf{M }}_{\vartheta }^Q+\frac{\Delta {t}}{2}{\mathbf{G }}\Bigg )P^{n+1}=\Bigg (\frac{Ma^2}{\Delta {t}}{\mathbf{M }}_{\vartheta }^Q+\frac{\Delta {t}}{2}{\mathbf{G }}\Bigg )P^{n}-\Bigg ({\mathbf{H }}^{1,\rho }+{\mathbf{H }}^{2,\rho }\Bigg ){\mathbf{U }}^* \\&\mathbf{Step 5 } \quad \qquad \left( \begin{array}{cc} {Re}{\mathbf{M }}^{V}+\Delta {t}\gamma _v{\mathbf{A }} &{} -\Delta {t}\gamma _v{\mathbf{C }} \\ -\Delta {t}\hat{{\mathbf{E }}} &{} \Delta {t}{\mathbf{M }}^{Z} \end{array}\right) \left( \begin{array}{c} {\mathbf{U }}^{n+1} \\ {\mathbf{D }}^{n+1} \end{array}\right) = \left( \begin{array}{c} \tilde{\varvec{{\mathcal {F}}}}_3^n \\ 0 \end{array}\right) \\&\mathbf{Step 6 } \quad \qquad (We+\Delta {t}){\mathbf{M }}^{Z}{\mathbf{T }}^{n+\frac{1}{2}}=[We{\mathbf{M }}^{Z}-We{{\mathbf{F }}}^{n+\frac{1}{2}}]{\mathbf{T }}^{n+\frac{1}{2}}+\hat{{\mathbf{I }}}\\&\mathbf{Step 7 } \quad \qquad 2{\mathbf{M }}^{Q_T}\Theta ^{n+1}=[2{\mathbf{M }}^{Q_T}-{\mathbf{M }}+\Delta {t}Di{{\mathbf{G }}}]\Theta ^{n+\frac{1}{2}}+{{\mathbf{L }}^{n+1/2}}{\mathbf{U }}^{n+1/2} \end{aligned} \end{aligned}$$

(3.20)

where $\tilde{\varvec{{\mathcal {F}}}}^u_i$ $i=1,2,3$ represent the discretised form of the explicit terms in Steps 1b, 2 and 5, respectively, in Eq. (3.1).

The matrices appearing in Eq. (3.20) are defined by the following expressions

$$\begin{aligned}&M^V_{ij}=\int _{\Omega }\Gamma _j\varvec{\phi }_j\cdot \varvec{\phi }_i\,d\Omega ,\qquad {}M^Z_{ij}=\int _{\Omega }\varvec{\xi }_j:\varvec{\xi }_i\,d\Omega \nonumber \\&M^Q_{ij}=\int _{\Omega }{\zeta }_j{\zeta }_i\,d\Omega ,\qquad {}M^{Q_T}_{ij}=\int _{\Omega }\Gamma _j{\zeta }_j{\zeta }_i\,d\Omega ,\nonumber \\&A_{ij}=\int _{\Omega }\nabla \varvec{\phi }_j:\nabla \varvec{\phi }_i\,d\Omega ,\nonumber \\&B^{n}_{ij}=\int _{\Omega }\hat{{\mathbf{u }}}^n\cdot \nabla \varvec{\phi }_j\cdot \varvec{\phi }_i\,d\Omega ,\qquad {}C_{ij}=-\int _{\Omega }\varvec{\xi }_j:\nabla \varvec{\phi }_i\,d\Omega ,\nonumber \\&D_{ij}=\int _{\Omega }\nabla \zeta _j\cdot \varvec{\phi }_i\,d\Omega =-\int _{\Omega }\zeta _j\nabla \cdot \varvec{\phi }_i\,d\Omega ,\nonumber \\&E_{ij}=\int _{\Omega }\frac{1}{2}(\nabla \varvec{\phi }_j+\nabla \varvec{\phi }_j^T):\varvec{\xi }_i\,d\Omega ,\nonumber \\&{F}_{ij}=\int _{\Omega }{\mathbf{U }}_l(\varvec{\phi }_l\cdot \nabla \varvec{\xi }_j-\varvec{\xi }_j\cdot \nabla \varvec{\phi }_l^T-\nabla \varvec{\phi }_l\cdot \varvec{\xi }_j+(\nabla \cdot \varvec{\phi })\varvec{\xi }_j):\varvec{\xi }_i\,d\Omega ,\nonumber \\&G_{ij}=\int _{\Omega }\nabla {\zeta }_j\cdot \nabla {\zeta }_i\,d\Omega ,\qquad {}M_{ij}=\int _{\Omega }\left( {\mathbf{U }}_j\varvec{\phi }_j\cdot \nabla \zeta _j\right) \zeta _i\,d\Omega ,\nonumber \\&H^{\rho ^n_h,1}_{ij}=\int _{\Omega }\Gamma _j\zeta _j\nabla \cdot \varvec{\phi }_j{\zeta }_i\,d\Omega ,\qquad {}H^{\rho ^n_h,2}_{ij}=\int _{\Omega }\Gamma _j\varvec{\phi }_j\cdot \nabla {\zeta }_i\,d\Omega \nonumber \\&L^n_{ij}=\int _{\Omega }[\varvec{\Sigma }_j\varvec{\xi }_j:\nabla {\phi }_j]{\zeta }_i\,d\Omega . \end{aligned}$$

(3.21)

where $\{\phi _i\}$ are velocity basis functions, $\{\varvec{\xi }_i\}$ are stress basis functions and $\{\zeta _i\}$ are pressure basis functions.

4 Numerical scheme validation for incompressible Oldroyd-B fluid parameters

The numerical scheme presented in the previous section is benchmarked by performing numerical simulations of incompressible flow and comparing results with the predictions of Li et al. [21] based on a spectral element approximation and analytical predictions based on a combination of lubrication theory and the long bearing approximation. The study of Li et al. [21] used the dimensional form of the governing equations, which is also adopted in this section so that direct and meaningful numerical comparisons can be made between the approaches. The governing equations are given by (2.4)–(2.6) with

$$\begin{aligned} {\mathbf{g }}_1({\mathbf{C }})=\frac{\mu _p}{\lambda _0}({\mathbf{C }}-{\mathbf{I }}),\qquad {\mathbf{g }}_2({\mathbf{C }},{\mathbf{D }})=0. \end{aligned}$$

(4.1)

In addition, we assume that the flow is incompressible and isothermal, and therefore, in these equations we set $\rho =\rho _0$, $\nabla \cdot {\mathbf{u }}=0$, $\lambda (T)=\lambda _0$ and $\mu _p(T)=\mu _p$. The parameters in the numerical scheme are chosen as follows: $\Delta {t}=h^2_\mathrm{min}$, $c_1=0.1$, $c_2=0.05$ and $\gamma _u=1-\beta _v$. The computational domain is defined by $R_J=0.03125$m, $R_B=0.03129$m. A finite element mesh with 3448 elements and 216,272 degrees of freedom is used.

In the case of a Newtonian fluid, the load on the journal is in the direction orthogonal to the line joining the centres of the journal and bearing. When the gap $c=R_B-R_J\ll {R}_B$, it is possible to perform an order of magnitude analysis on the full Navier–Stokes equations. This analysis gives rise to Reynolds’ equation. In the long bearing approximation to Reynolds’s equation, it is assumed that the pressure is constant in the z-direction, and thus, the effects of the side boundary conditions are negligible.

4.1 Comparison with long bearing theory

Analytical solutions for the journal bearing problem can be obtained by invoking the lubrication approximation. In the thin bearing approximation, Reynolds’ equation can be solved analytically to obtain the following expression for the pressure field

$$\begin{aligned} p=p_0+\frac{6\mu \omega {R}^2_J}{c^2}\frac{\epsilon {\sin {\theta }}(2+\epsilon \cos {\theta })}{(2+\epsilon ^2)(1+\epsilon \cos \theta )^2}, \end{aligned}$$

(p. 292 [30]) from which the load and torque can be computed

$$\begin{aligned} F_y=\frac{24\pi \mu \omega {n}R_J^4\epsilon }{c^2((1-\epsilon ^2)(2+\epsilon ^2))^\frac{1}{2}},\quad C=\frac{4\pi \mu \omega {n}R_J^4}{c(1-\epsilon ^2)^\frac{1}{2}}+\frac{F_ye}{2}, \end{aligned}$$

where $n>1$ is the ratio of the length of the bearing to its diameter [21, 30]. This allows the load and torque to be calculated explicitly as a function of the viscosity, rotation speed and eccentricity.

4.2 Benchmark results

Solutions are generated using the nondimensionalised scheme and so the appropriate dimensional factors are included in order to compare with predictions from the literature. Load and torque are calculated using the following formulae

$$\begin{aligned} {\mathbf{F }} =&\begin{pmatrix} F_x\\ F_y \end{pmatrix}=\left( \frac{L^3}{\mu U}\right) \int _{\Gamma _J}\varvec{\sigma }\cdot {\mathbf{n }}\,dS, \end{aligned}$$

(4.2)

$$\begin{aligned} C =&\left( \frac{L^4}{\mu U}\right) \int _{\Gamma _J}{\mathbf{n }}^T\cdot \varvec{\sigma }\cdot {\mathbf{t }}\,dS, \end{aligned}$$

(4.3)

where ${\mathbf {n}}$ and ${\mathbf {t}}$ are unit vectors normal and tangent to $\Gamma _J$. The characteristic length and velocity scales are chosen to be

$$\begin{aligned} L=R_J,\qquad {U}={\omega }R_J, \end{aligned}$$

(4.4)

Table 2 Comparison of load and torque on the journal calculated using the present method, SEM calculations and long bearing theory for Newtonian flow: $\omega =25$ rad/s, $\mu _p=\lambda =0$, $\mu _s=\mu =5\times {10}^{-3}$ Pa s, $R_J = 1 \times 10^{-2}$m ($Re = 50$)

Table 3 Dependence of the load and torque on the relaxation time with $\omega =25$ rad/s, $\mu _s=\mu _p=2.5\times {10}^{-3}$ Pa s, $\mu =5\times {10}^{-3}$ Pa s, $R_J = 1 \times 10^{-2}$m $t=10$s

Tables 2 and 3 compare the approximations to F and C generated using the numerical scheme in Sect. 3 to the prediction of long bearing theory and the numerical predictions of Li et al. [21]. In Table 2, the influence of the load and torque on $\epsilon$ is presented for a Newtonian fluid. Both F and C increase with increasing $\epsilon$. Good agreement between the different approaches is obtained for $\epsilon < 0.95$. In Table 3, the influence of the load and torque on $\lambda$ is presented for a viscoelastic fluid. When $\lambda =0$, the horizontal force component, $F_x=0$. For $\lambda >0$, $F_x \ne 0$ and $F_x \ll F_y$. However, for the range of relaxation times considered there is negligible effect on F and C. The difference between the LBT and numerical predictions for high eccentricities is almost certainly due to resolution problems in the narrow gap due to the large velocity gradients that occur in that region.

5 Weakly compressible and nonisothermal viscoelastic flow

5.1 Geometrical data and fluid parameters

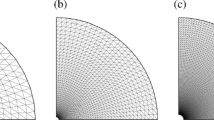
In order to establish a clear relationship between the effects of viscoelasticity and compressibility, we consider a fixed geometry and keep most of the fluid parameters constant. Simulations are computed over a range of values of Re, Ma and We, and the results allow for both qualitative and quantitative analysis of the effects on the flow characteristics of two important variables: the journal rotation rate, $\omega$, and the relaxation time, $\lambda$. Three finite element meshes M1–M3 were used with increasing refinement, from the coarsest mesh M1 to the finest mesh M3, to ensure the mesh independence of the numerical approximations (see Fig. 4). The mesh characteristics are given in Table 4. The computational domain is specified by the following choice of geometric parameters: $R_J = 1 \times 10^{-2}$m, $R_B = 2 \times 10^{-2}$m, $e = 8 \times 10^{-3}$m.

Chosen fluid parameters are given in Table 5. The influence of the angular velocity of the journal and the fluid relaxation time on the behaviour/stability of the journal bearing is investigated. The angular velocity is allowed to vary in the interval [100, 1000] rad/s. The fluid density and viscosity were chosen to be that of 15W40 engine oil (data from Anton Paar Ltd). The journal bearing of radii 1 cm (journal) and 2 cm (bearing) was chosen so that empirical measurements of the same flow problem can be easily obtained. The eccentricity is kept fixed at $\epsilon =0.8$ as this was near the upper limit of the range of $\epsilon$ values where the incompressible scheme produced reliable results. The dimensionless groups for this problem have been defined earlier.

To reduce the large number of nondimensional variables, we set the fluid and experimental parameters to those given in Table 5. In this case, Re and Ma are directly proportional to the angular frequency of the bearing, $\omega$, and due to the choice of characteristic velocity, We is proportional to $\omega \lambda$.

Note that for the generation of results for compressible flow we only consider the nondimensional equations and solutions without re-dimensionalising. The input data given in Table 5 are used to guide the range of nondimensional parameters used. In a real experiment, the Reynolds, Mach and Weissenberg number would not be independent, and instead would be directly dependent on the angular velocity of the inner cylinder. However, in order to gain insight into the effects of compressible viscoelasticity we will vary Re, We and Ma independently.

Table 4 Flow between eccentrically rotating cylinders: Mesh characteristics and degrees of freedom M1–M3

Fig. 4

Finite element meshes for the flow between eccentrically rotating cylinders: a Coarse mesh (M1), b medium (M2) and c fine (M3)

Table 5 Fluid parameters

5.2 Results and discussion

Results were generated on a single CPU machine, and the numerical method was implemented using the FEniCS finite element [23] library. Python modules used to generate the following results can be found here [24]. Typical simulations had a run time of between 4 and 8 hours depending on mesh resolution. Throughout the computations, DEVSS (Sec. 3.3.1) parameters were set to $\gamma _u=1-\beta _v$. The key measurements of the efficiency and effectiveness of a journal bearing lubricant are the torque and resultant load on the journal. Pressure is the dominant contribution to the force around the journal. In the numerical simulation of an incompressible Newtonian fluid, the pressure is antisymmetric about the narrow gap [5, 30]. When either We or Ma is nonzero, this asymmetry is broken leading to an inevitable nonzero component of force in the x direction.

The ratio of the magnitude of horizontal and vertical forces, denoted by $\chi$, can be used as a measurement of rotational stability [6]

$$\begin{aligned} \chi = \frac{F_x}{|F_y|}. \end{aligned}$$

(5.1)

When $F_x > 0$, there is a component of the load that acts along the line joining the centres of the journal and bearing and in a direction away from the smallest gap. In a dynamic setting, this would ensure that the journal is pushed away from the bearing, thereby contributing to journal stability. Clearly, if $F_x \gg F_y$ then the axial component of the load dominates the perpendicular component, and so increasing stability is characterised by the limit $\chi \rightarrow \infty$ (Fig. 5).

Fig. 5

Flow between eccentrically rotating cylinders: the resultant force acting on the journal calculated using Eq. (4.2)

5.2.1 Mesh convergence

First we demonstrate the temporal and spatial mesh convergence by analysing the kinetic and elastic energy profile with flow parameters $Re=50$, $We=0.25$ and $Ma=0.001$ and solutions generated over the coarse (M1), medium (M2) and fine (M3) meshes. Figure 6 shows the evolution of kinetic and elastic energy using each of these three meshes. Spatial convergence is demonstrated and the near overlapping of the solutions, especially for meshes M2 and M3, is observed. The steady-state values of both the kinetic and elastic energy are attained rapidly at $t \approx 2$ in all cases.

Fig. 6

Mesh convergence analysis: evolution of a kinetic energy, b elastic energy for an extended White–Metzner fluid with $Re=50$, $We=0.25$, $Ma=0.001$

Fig. 7

Mesh convergence analysis: torque profile in the range $0\le {t}\le 4$ using mesh M1, M2 and M3. The parameter values are shown in Table 6 with $Re=50$, $We=0.25$ and $Ma=0.001$

Figure 7 shows the convergence behaviour of the torque on meshes M1, M2 and M3 for $Re=50$, $We=0.25$ and $Ma=0.001$. All three meshes predict the location and height of the initial overshoot and undershoot. There is a slight variation in the passage to the steady-state value of the torque. However, the behaviour on meshes M2 and M3 agrees as shown in the zoomed region in this figure.

5.2.2 Extended White–Metzner model

The results in the previous section demonstrated that convergence was obtained on mesh M2. Therefore, all results in this section are generated on this mesh. The compressible version of the extended White–Metzner model is used.

As the journal begins to rotate a film of fluid close to the journal is dragged around the journal. The dominant flow feature is a recirculation region in the wider gap in which the fluid recirculates with the centre of rotation just below the centre line. Thus, the majority of the fluid is not dragged around the cylinder as in the concentric case leading to a mechanism for greater journal efficiency [6]. The kinetic energy grows as the flow accelerates, reaches a maximum as the journal reaches its maximum speed and then reduces significantly as the elastic energy grows. The steady-state kinetic energy decreases as the Weissenberg number increases in contrast to the elastic energy which decreases.

Table 6 Nondimensional parameters

Table 7 Flow between eccentrically rotating cylinders

Table 8 Flow between eccentrically rotating cylinders

A quantitative comparison with the literature is made with respect to the maximum value of the stream function in the case $\epsilon =0.8$. In particular, this value is compared to the value reported by Germann et al. [17]. For this specific simulation, we set $\upsilon =1$ and not the value provided in Table 6. The maximum value of the stream function obtained for this simulation was 0.0622 compared with a value of 0.0627 obtained by Germann et al. [17].

Fig. 8

Extended White–Metzner flow between eccentrically rotating cylinders: steady-state a pressure, b temperature and c $\rho {\mathbf{u }}$. The parameter values are shown in Table 6 with $We=0.1$, $Re=100$, $Ma=0.1$ and $t=20$

Fig. 9

Extended White–Metzner flow between eccentrically rotating cylinders: steady-state a pressure, b temperature and c $\rho {\mathbf{u }}$. The parameter values are shown in Table 6 with $We=1$, $Re=100$, $Ma=0.1$ and $t=20$

Fig. 10

Flow between eccentrically rotating cylinders: steady-state (extended White–Metzner fluid) $\varvec{\sigma }_{xx}$ for a $We=1.0$, $Re=100$ b $We=0.1$, $Re=100$ and c $We=0.1$, $Re=25$ (the parameter values are shown in Table 6 with $Ma=0.1$)

Fig. 11

Flow between eccentrically rotating cylinders: influence of the evolution of We on a kinetic energy, b elastic energy in extended White–Metzner flow (the parameter values are shown in Table 6 with $Re=100$ and $Ma=0.01$)

Fig. 12

Influence of We, Re and Ma on the evolution of the torque, C, and vertical load, $F_y$, for an extended White–Metzner fluid: a C for $Ma=0.05$; b $F_y$ for $Ma=0.05$; c C for $Ma=0.1$; d $F_y$ for $Ma=0.1$ (remaining parameters defined in Table 6)

In Table 7, the values of the stability factor, $\chi$, are tabulated for the extended White–Metzner fluid for $Re=50$. The influence of compressibility and viscoelasticity on $\chi$ is explored. For a fixed value of Ma, $\chi$ increases as We increases. This highlights the growing contribution of $F_x$ to the force on the journal as the viscoelasticity of the fluid increases producing a resultant force that increasingly aligns with the line joining the centres of the journal and bearing. For a fixed value of We, $\chi$ increases slowly with increasing Ma. Local increases in density in the narrow gap generate an additional resistance.

In Table 8, the values of the stability factor, $\chi$, are tabulated for a slightly compressible extended White–Metzner fluid with $Ma=0.01$. The influence of inertia and viscoelasticity on $\chi$ is explored. For a fixed value of Re, $\chi$ increases as We increases. Again viscoelasticity is responsible for moving the direction of the resultant force away from a direction perpendicular to the line joining the centres of the journal and bearing to one that has a greater component in the x-direction. For a fixed value of We, the behaviour of $\chi$ as a function of Re is not so uniform. The greatest change, an increase in the value of $\chi$, takes place from $Re=100$ to $Re=200$. However, this increase diminishes as We increases so that for $We=1$ there is hardly any difference between the values of $\chi$ obtained for $Re=25$ and $Re=200$. Note that although some of the computations for $Re=200$ have not reached steady-state values they are converging in a damped oscillatory manner and the computations are terminated when the amplitude of the oscillations falls below 0.005.

Figures 8 and 9 show the steady-state pressure, temperature and density profiles of the flow for $We=0.1$ and $We=1$, respectively, with $Ma=0.1$ and $Re=100$. There is a region of high pressure as the fluid is forced through the narrow gap by the rotating journal. As the fluid emerges from this region, there is a region of low pressure with the lowest value of pressure attained on the journal wall. For a Newtonian fluid, i.e. $We=0$, it is well known that the pressure distribution is asymmetric about the line joining the centres of the journal and bearing. This gives rise to a load with zero horizontal component. When $We \ne 0$, the asymmetry in the pressure distribution is broken giving rise to a nonzero horizontal component of the load which grows in magnitude as We increases. The load then increasingly acts in a direction which moves the journal away from the region of smallest gap as the viscoelasticity of the fluid as measured by We is increased.

Figure 10 shows the influence of We and Re on the behaviour of the axial normal stress component, $\sigma _{xx}$ for $Ma=0.1$. Whilst for a Newtonian fluid the extra-stress components are antisymmetric about the line $y=0$ giving rise to a vanishing component of force in the x-direction, both viscoelasticity and compressibility break this symmetry. For $We>0$, there is a concentration of elastic stress in the narrow gap region of the geometry that increases with increasing We. This results in a nonzero force component $F_x$. As We is increased, the stress concentration that occurs downstream of the narrow gap and the asymmetry of this stress component around the journal about the line $y=0$ increases. The increased values of $F_x$ result in increased values of $\chi$ and hence increased stability characteristics.

The temperature of the fluid is maximum near the journal and in the region around the narrow gap. Larger temperature gradients can be found in the narrow gap when the eccentricity or viscous heating parameter, $V_h$, are increased. The influence of this parameter will be explored fully in future work.

Figure 11 shows the influence of We on the evolution of the kinetic and elastic energies for $\beta _v=0.5$, $Re=100$ and $Ma=0.01$. For $Re=100$, the evolution of the energies is largely independent of We so inertia rather than elasticity is the dominating influence. When $Re=25$, elasticity becomes more important giving rise to a sharp increase in the kinetic energy. The elastic energy increases dramatically for $We=1$ for both $Re=25$ and $Re=100$ compared with $We=0$ and $We=0.1$ as one would expect with increased levels of viscoelasticity. For $We=1$, the steady-state elastic energy dominates the kinetic energy by almost two orders of magnitude.

Figure 12 demonstrates the competing influence of Re, We and Ma on the torque, C, and normal load, $F_y$. Compressibility has very little effect on C as can be seen from Fig. 12a, c. For $Re=100$, there is an initial large overshoot in C independent of the value of We. In the case $We=1$ and $Re=25$, there is a much smaller overshoot in C due to the reduced influence of inertia followed by a slight undershoot before the steady-state value is attained. There is a slightly enhanced steady-state value of the torque for $We=1$ for both $Re=25$ and $Re=100$. The transient behaviour of the normal load is characterised by a series of overshoots and undershoots, the amplitudes of which are larger for the more compressible fluid, i.e. for $Ma=0.1$, and take longer to decay. For $We=1$ and $Re=25$, the normal load rapidly reaches the steady-state value. Varying Re has a much larger influence on the maximum torque value reached within the first two seconds of the flow. However, for each set of simulations the steady-state torque value increased with increases in We. For nonzero Ma, increasing Re results in larger temporal oscillations in both $F_y$ and torque spanning the initial ten second flow phase. Ma has little influence on the torque profiles in the range $0<Ma<0.1$ as is shown by the similarity between 12a, c.

In Fig. 13, the dependence of the stability parameter, $\chi$, on We is presented. In Fig. 13a, the dependence of $\chi$ on We is plotted for different values of Re for a fixed value $Ma=0.05$. For intermediate values of Re, there is little influence of $\chi$ on We and the behaviour is almost independent of We. For $Re=200$, there is a large initial increase in the value of $\chi$ until a value of $We \approx 0.25$ followed by a more gradual increase for $0.25 \le We \le 1$. For $Re=25$, the behaviour of $\chi$ is similar to that for intermediate values of $\chi$ except for $We=1$ when there is a large uplift in its value which agrees with its value for $Re=200$. In Fig. 13b, the dependence of $\chi$ on We is plotted for different values of Ma for a fixed value $Re=50$.

There is a weak relationship between Mach number and rotational stability. For Mach numbers in the range $0\le {Ma}\le 0.05$, the stability factor increases with Re for $We<0.5$ whilst for $We>0.5$ this trend is reversed. The Weissenberg number has a much stronger influence on the stability factor. In the range $0\le {}We\le 1$, the value of $\chi$ increases from around 0.02 to 0.4 ($Re=50$). However, at higher Ma values ($>0.05$) the resultant force starts to display unsteady behaviour (as displayed in Fig. 12), and therefore, accurate steady-state stability factors cannot be obtained. Figure 13 illustrates the interacting effects of Re, Ma and We on $\chi$.

In cases where the flow did not reach a steady state, the reaction forces, and by implication the stability factor itself, oscillated around steady mean values. Flow solutions were computed over $0<t\le {40}$ and the mean value of the stability factor over the time interval $35 \le t \le {40}$ was computed and this value is provided in the tables.

Fig. 13

Flow between eccentrically rotating cylinders: extended White–Metzner flow values of the stability factor, $\chi$ against We for a varying Re ($Ma=0.05$) and b varying Ma ($Re=50$)

5.2.3 FENE-P-MP model

We now turn our attention to numerical results generated using the FENE-P-MP constitutive model. In Fig. 14, the effect of the dissipation parameter $\lambda _D$ on the evolution of the torque and normal load is presented for the following parameter values: $We=0.5$, $Re=50$ and $Ma=0.01$. In Fig. 14a, we observe that the overshoot and steady-state value of the torque increases with $\lambda _D$. We recall that $\lambda _D=0$ corresponds to the FENE-P model. We observe a similar trend in Fig. 14b with heightened values of the normal load with increasing values of $\lambda _D$. There is also an initial overshoot which is larger for larger values of $\lambda _D$ followed by a series of undershoots and overshoots which damp out over time. This behaviour is typical of viscoelastic fluids.

In Fig. 15, the stream function and the divergence of the velocity field are plotted for the following parameter values: $We=0.5$, $Re=10$, $Ma=0.05$, $\beta =0.9$, $\lambda _D=0.1$. As shown in Fig. 15b, the flow is largely incompressible and exhibits slight compressibility in the narrow gap and in the converging and diverging part of the journal boundary. The maximum absolute value of $\nabla \cdot {\mathbf {u}}$ is approximately $10^{-2}$. The value of $\lambda _D$ has a considerable effect on rotational stability $\chi$. When $\lambda _D=0$, there is a quasidependence of $\chi$ on We. For $\lambda _D \ne 0$, there is a sharp increase in the value of $\chi$ for $0.25 \le We \le 0.5$ followed by a slightly less sharp decrease for $We \ge 0.5$. This demonstrates the stabilising effect of viscoelasticity on the stability of the system.

In Table 9, the influence of We and the dissipation parameter $\lambda _D$ on the stability factor $\chi$ is explored for a FENE-P-MP fluid with $Ma=0.05$ and $Re=50$. For a fixed value of We, $\chi$ increases as $\lambda _D$ increases. For $\lambda _D=0$, $\chi$ increases monotonically with increasing We. For $\lambda _D \ne 0$, $\chi$ initially increases with We until $We=0.5$ before decreasing as We increases further (Fig. 16).

Figure 14 shows a sample of the numerical results for the FENE-P-MP model with Ma and Re fixed at $Re=50$, $We=0.5$. The dissipation parameter, $\lambda _D$, has a very significant impact on the journal torque, C, and the stability factor ranges from $\chi =0.81$ to 21.25. The steady-state value of $F_y$ and range of values for $F_y$ achieved during transient flow reduces as $\lambda _D$ is increased within the range $0\le \lambda _D\le {0.2}$. The transient behaviour of $F_y$ is oscillatory after the initial flow acceleration ($0\le {t}\le {1}$) and this influences the behaviour of $\chi$ as well. For parameter values satisfying $\lambda _D>0$, $We>0.5$, $Ma>0.01$, $Re>50$, the unsteady flow behaviour continued up until the numerical simulation ceased at $t=20$ and hence are noted in Table 9. However, in all of the numerical experiments the frequency and amplitude of the oscillations decreased over time and either converged to steady-state values or were terminated once the amplitude fell below 0.005. In the latter case, this was always within the time range $0<t<20$.

In a steady-state FENE-P-MP flow, the influence of We on $\varvec{\sigma }$ is such that the vertical component of F reverses in the range $0.5\le {We}\le 1.0$. [25] Hence, a sample of stability factor values on this range show that a maximum value occurs in the range $0.5\le {We}\le 1.0$. When $F_y=0$, there is no component of the force perpendicular to the line joining the centres of the journal and bearing and since $F_x>0$ in these calculations the journal is stabilised. In the case of the dynamic problem in which the journal is free to translate as well as rotate, the force would cause the journal to move away from the narrow gap in the direction in which the clearance is greatest.

Fig. 14

Flow between eccentrically rotating cylinders: the effect of dissipation parameter $\lambda _D$ on a torque and b $F_y$ for FENE-P-MP flow ($We=0.5$, $Re=50$ $Ma=0.01$)

Fig. 15

Flow between eccentrically rotating cylinders: FENE-P-MP model. Contours of a stream functions, b $\nabla \cdot {\mathbf{u }}$ for $We=0.5$, $Re=10$, $Ma=0.05$, $\beta =0.9$, $\lambda _D=0.1$)

Table 9 Flow between eccentrically rotating cylinders

Fig. 16

Flow between eccentrically rotating cylinders: FENE-P-MP values of the stability factor, $\chi$ against We ($Ma=0.05$, $Re=50$)

Fig. 17

Contour plots of the steady-state generalised shear rate, ${\dot{\gamma }}$ for a EWM, b FENE-P-MP, for $Re=50$, $We=0.5$, $Ma=0.01$ with other parameter values taken from Table 6

The maximum values of the generalised shear rate, defined by

$$\begin{aligned} {\dot{\gamma }} = \sqrt{\frac{1}{2}\dot{\varvec{\gamma }}:\dot{\varvec{\gamma }}} \end{aligned}$$

(5.2)

where $\dot{\varvec{\gamma }}$ is the rate of strain tensor, are shown in Table 10 for a range of We values for both FENE-P-MP and EWM models and contour plots of the generalised shear rate are shown in Fig. 17 for both models considered in this paper for Re = 50, Ma = 0.01.

Table 10 Dependence of the maximum value and location of the generalised shear rate, ${\dot{\gamma }}$, for the EWM and FENE-P-MP models for $Re=50$, $Ma=0.01$, $\lambda _D=0.05$ (FENE-P-MP only)

6 Summary

Recent developments in the derivation of mathematical models have facilitated the description of the behaviour of compressible nonisothermal viscoelastic fluids. For example, Mackay and Phillips [26] derived a class of models based on the FENE-P model using the generalised bracket formulation. This formulation ensures that the derived models are thermodynamically consistent. A class of dissipative models for Boger fluids, developed by Mackay and Phillips [26] within the bracket framework, complements the class of phenomenological models that already exist in the literature. There are many examples of compressible nonisothermal models in the literature that are ad hoc in the sense that they are modifications of existing incompressible isothermal models formed by suitably adjusting material functions or adding additional terms in the governing equations. For any flow problem concerning non-Newtonian liquids under nonisothermal conditions, thermodynamically consistent modelling of the fluid permits a more accurate analysis of the flow and predicts behaviour that cannot be captured with simpler, parametrised models.

A Taylor–Galerkin finite element scheme is used as the basis of the numerical simulations presented in this paper. Numerical results for the flow of a viscoelastic fluid or lubricant between eccentrically rotating cylinders have been presented. This problem is sometimes referred to as the statically loaded journal bearing problem. Both incompressible and compressible flows have been considered, and the scheme presented is validated using numerical results in the literature and compared with those obtained using lubrication theory under the long bearing assumption.

Analysing the flow using the (incompressible) Oldroyd-B model suggests that viscoelasticity (as measured by We) has little influence on the load bearing characteristics of the journal. A nonzero value of the relaxation time introduces a nonzero component of the force in the axial direction, but this is significantly smaller than the component in the perpendicular direction and there is almost no variation in either the load or the torque when the relaxation time is increased by over two orders of magnitude. However, significant stabilisation of the journal bearing system is found when both the EWM and FENE-P-MP models are used. The separate and combined effects of compressibility and viscoelasticity stabilise the system as quantified using the stability parameter. Although both models predict shear thinning behaviour, the FENE-P-MP model predicts increases in both torque and rotational stability as We is increased. This can be explained by the hidden extensional flow behaviour which is introduced by the journal’s rotational eccentricity. Although the flow is shear-dominated, the nip or narrow gap region creates a significant extensional component to the flow. Hence, the FENE-P-MP model, which predicts extensional strain hardening demonstrates a large increase in effective viscosity which in turn affects the forces on the journal bearing.

This paper has focussed on the statically rotating journal bearing or eccentrically rotating cylinder problem in which the journal or inner cylinder rotates about its axis but does not translate in response to the force it is subjected to by the fluid. One extension of this work is to consider the dynamic problem in which the journal is permitted to move in response to the load. Whilst the current paper has focussed on the effects of the narrow gap on viscosity and heat transfer, the dynamic problem would enable further exploration of the physics of an eccentrically rotating cylinder.