Abstract
We consider a recently introduced geometrically nonlinear elastic Cosserat shell model incorporating effects up to order \(O(h^{5})\) in the shell thickness \(h\). We develop the corresponding geometrically nonlinear constrained Cosserat shell model, we show the existence of minimizers for the \(O(h^{5})\) and \(O(h^{3})\) case and we draw some connections to existing models and classical shell strain measures. Notably, the role of the appearing new bending tensor is highlighted and investigated with respect to an invariance condition of Acharya (Int. J. Solids Struct. 37(39):5517–5528, 2000) which will be further strengthened.







Similar content being viewed by others
Notes
They may be written in terms of the Poisson ratio of the isotropic and homogeneous material \(\nu =\frac{\lambda }{2\,(\lambda +\mu )} \).
These conditions are equivalent to \(\mu >0\) and \(2\,\lambda +\mu > 0\), which assure the positive definiteness of the quadratic form \(W_{\mathrm{shell}}( X) = \mu \,\lVert \mathrm{sym}\,X\rVert ^{2} + \mu _{\mathrm{c}}\lVert \mathrm{skew}\,X\rVert ^{2} + \dfrac{\lambda \,\mu }{\lambda +2\,\mu }\,\big [ \mathrm{tr} (X)\big ]^{2} = \mu \, \lVert \mathrm{ dev \,sym} \,X\rVert ^{2} + \mu _{\mathrm{c}} \lVert \mathrm{skew} \,X\rVert ^{2} +\, \dfrac{2\,\mu \,(2\,\lambda +\mu )}{3(\lambda +2\,\mu )}\,[ \mathrm{tr} (X)]^{2}\).
In our assertion, the square root of a positive semidefinite matrix \(X\) is the unique positive semidefinite matrix \(Y\), denoted by \(\sqrt{X}\), such that \(Y^{2}=X\). If \(X\) is positive definite, then its square root is also positive definite. For an idempotent positive semidefinite matrix \(A\), meaning \(A^{2}=A\), by the definition, its square root is the matrix itself \(\sqrt{A}=A\).
Since \(\mathrm{SO}(3)\) is compact, a property that does not transfer to the linearized problem.
For shells with little initial regularity. Classical shell models typically need to assume that \(y_{0}\in {\mathrm{C}}^{3}(\overline{\omega },\mathbb{R}^{3})\).
By \(c\) and \(c_{i}\), \(i\in \mathbb{N}\), we will denote (positive) constants that may vary from estimate to estimate but will remain independent of \(m\), \(\nabla m\) and \({Q}_{ \infty }\).
It does add nothing to the shell model itself.
For shells with little initial regularity. Classical shell models typically need to assume that \(y_{0}\in {\mathrm{C}}^{3}(\overline{\omega },\mathbb{R}^{3})\).
However, in the modified constrained Cosserat shell model presented in Sect. 4.1 the energy density is expressed in terms of
$$\begin{aligned} {\mathrm{sym}}(\mathcal{R}_{\infty } -\mathcal{G}_{\infty } \,\mathrm{L}_{y_{0}}) \in {\mathrm{Sym}}(2)\qquad \text{and}\qquad \mathrm{sym}[(\mathcal{R}_{\infty } -\mathcal{G}_{\infty } \,\mathrm{L}_{y_{0}})\,\mathrm{L}_{y_{0}}]\in {\mathrm{Sym}}(2). \end{aligned}$$(5.11)Tambača [41, page 4, Definition of the set \(\mathcal {A}^{f}\)] also requires \({Q}_{ \infty } \nabla y_{0}=\nabla m\), in order to arrive at the pure bending shell model. In this case \(\mathcal{G}_{\infty }=0\) and
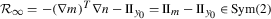 .
.Indeed, the biaxial stretching of a cylinder [1, Sect. 6.2] satisfies (6.10b) with \(a=\beta =0\) (see [1, Eq. (34)]) and for the uniform normal deflection [1, Sect. 6.1] we have \(m=y_{0}+ c\, n_{0}\) where \(c\in \mathbb{R}\) is a fixed factor. Hence,
$$ \partial _{x_{1}}m=\partial _{x_{1}}y_{0}+c\,\partial _{x_{1}}n_{0} \quad \text{and}\quad \partial _{x_{2}}m=\partial _{x_{2}}y_{0}+c\, \partial _{x_{2}}n_{0}. $$So that, \(a\,\|\partial _{x_{1}}y_{0}\|^{2} \overset{\text{(6.10a)}}{=} \langle \partial _{x_{2}}m, \partial _{x_{1}}y_{0}\rangle = c\,\langle \partial _{x_{2}}n_{0}, \partial _{x_{1}}y_{0}\rangle \overset{(\ast )}{=} c\,\langle \partial _{x_{1}}n_{0},\partial _{x_{2}}y_{0}\rangle = \langle \partial _{x_{1}}m,\partial _{x_{2}}y_{0}\rangle \overset{\text{(6.10a)}}{=}\beta \,\|\partial _{x_{2}}y_{0}\|^{2}\) where in \((\ast )\) we made use of the symmetry of the second fundamental form. Furthermore, since \(\|n_{0}\|^{2}=1\) implies that \(\langle \partial _{x_{i}}n_{0},n_{0}\rangle =0\) we have \(\partial _{x_{1}}n_{0}=\theta _{1}\ \partial _{x_{1}}y_{0}+\theta _{2} \ \partial _{x_{2}}y_{0}\) and \(\partial _{x_{2}}n_{0}=\vartheta _{1}\ \partial _{x_{1}}y_{0}+ \vartheta _{2}\ \partial _{x_{2}}y_{0}\) so that \(\partial _{x_{1}}m\times \partial _{x_{2}}m=((1+c\,\theta _{1})(1+c \,\vartheta _{2})-c^{2}\,\theta _{2}\vartheta _{1})\,\partial _{x_{1}}y_{0} \times \partial _{x_{2}}y_{0} \), implying that the range of the fixed value \(c\) should be adjusted in such a way that the prefactor is positive and \(1+c\,\theta _{1}\ge c\,\theta _{2}\ge 0\) as well as \(1+c\,\vartheta _{2}\ge c\,\vartheta _{1}\ge 0\), which are exactly the requirements for the positive-definiteness improved in (6.10b).
References
Acharya, A.: A nonlinear generalization of the Koiter–Sanders–Budiansky bending strain measure. Int. J. Solids Struct. 37(39), 5517–5528 (2000)
Adams, R.A.: Sobolev Spaces, 1st edn. Pure and Applied Mathematics, vol. 65. Academic Press, London (1975)
Anicic, S.: Du modèle de Kirchhoff-Love exact à un modèle de coque mince et á un modèle de coque pliée. PhD thesis, Université Joseph Fourier (Grenoble 1) (2001)
Anicic, S.: Polyconvexity and existence theorem for nonlinearly elastic shells. J. Elast. 132(1), 161–173 (2018)
Anicic, S.: Existence theorem for a first-order Koiter nonlinear shell model. Discrete Contin. Dyn. Syst., Ser. S 12(6), 1535–1545 (2019)
Anicic, S., Léger, A.: Formulation bidimensionnelle exacte du modèle de coque 3D de Kirchhoff-Love. C. R. Acad. Sci. Paris, Ser. Math. 329(8), 741–746 (1999)
Bîrsan, M.: Derivation of a refined 6-parameter shell model: Descent from the three-dimensional Cosserat elasticity using a method of classical shell theory. Math. Mech. Solids 25(6), 1318–1339 (2020)
Bîrsan, M., Neff, P.: Existence of minimizers in the geometrically non-linear 6-parameter resultant shell theory with drilling rotations. Math. Mech. Solids 19(4), 376–397 (2014)
Bîrsan, M., Neff, P.: Shells without drilling rotations: A representation theorem in the framework of the geometrically nonlinear 6-parameter resultant shell theory. Int. J. Eng. Sci. 80, 32–42 (2014)
Budiansky, B., Sanders, J.L. Jr.: On the “best” first-order linear shell theory. Tech. Rept. No. 14, Contract No. 1886(02), Division of Engineering and Applied Physics, Harvard University (1962)
Budiansky, B., Sanders, J.L. Jr.: On the “best” first-order linear shell theory. In: Progress in Applied Mechanics, the Prager Anniversary Volume (1963)
Chróścielewski, J., Makowski, J., Pietraszkiewicz, W.: Statics and Dynamics of Multifold Shells: Nonlinear Theory and Finite Element Method. Wydawnictwo IPPT PAN, Warsaw (2004) (in Polish)
Chróścielewski, J., Pietraszkiewicz, W., Witkowski, W.: On shear correction factors in the non-linear theory of elastic shells. Int. J. Solids Struct. 47, 3537–3545 (2010)
Ciarlet, Ph.G.: Mathematical Elasticity, Vol. III: Theory of Shells, 1st edn. North-Holland, Amsterdam (2000)
Ciarlet, Ph.G.: An Introduction to Differential Geometry with Applications to Elasticity. Springer, Berlin (2005)
Ciarlet, Ph.G., Mardare, C.: Nonlinear Korn inequalities. J. Math. Pures Appl. 104(6), 1119–1134 (2015)
Ciarlet, Ph.G., Mǎlin, M., Mardare, C.: New estimates of the distance between two surfaces in terms of the distance between their fundamental forms. Anal. Appl. 17(03), 363–392 (2019)
Cosserat, E., Cosserat, F.: Théorie des corps déformables. Hermann et Fils, Paris (1909) (reprint 2009)
Eremeyev, V.A., Pietraszkiewicz, W.: Local symmetry group in the general theory of elastic shells. J. Elast. 85, 125–152 (2006)
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: The isotropic Cosserat shell model including terms up to \({O}(h^{5})\). Part I: Derivation in matrix notation. J. Elast. 142, 201–262 (2020). https://doi.org/10.1007/s10659-020-09796-3. arXiv:2003.00549
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: The isotropic elastic Cosserat shell model including terms up to order \(O(h^{5})\) in the shell thickness. Part II: Existence of minimizers. J. Elast. 142, 263–290 (2020). https://doi.org/10.1007/s10659-020-09795-4. arXiv:2003.08594
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: Linear Cosserat-shell models including terms up to \({O}(h^{5})\). In preparation
Girault, V., Raviart, P.A.: Finite Element Approximation of the Navier-Stokes Equations. Lect. Notes Math., vol. 749. Springer, Heidelberg (1979)
Koiter, W.T., Simmonds, J.G.: Foundations of shell theory. In: Theoretical and Applied Mechanics, pp. 150–176. Springer, Berlin (1973)
Korn, A.: Zwei Anwendungen der Methode der sukzessiven Annäherungen. In: Carathéodory, C., Hessenberg, G., Landau, E., Lichtenstein, L. (eds.) Mathematische Abhandlungen Hermann Amandus Schwarz, pp. 215–229. Springer, Berlin (1914)
Leis, R.: Initial Boundary Value Problems in Mathematical Physics. Teubner, Stuttgart (1986)
Libai, A., Simmonds, J.G.: The Nonlinear Theory of Elastic Shells, 2nd edn. Cambridge University Press, Cambridge (1998)
Malin, M., Mardare, C.: Nonlinear Korn inequalities on a hypersurface. Chin. Ann. Math., Ser. B 39(3), 513–534 (2018)
Mardare, C.: On the derivation of nonlinear shell models from three-dimensional elasticity. Rev. Roum. Math. Pures Appl. 53, 499–522 (2008), hal-00392028
Neff, P.: A geometrically exact Cosserat-shell model including size effects, avoiding degeneracy in the thin shell limit. Part I: Formal dimensional reduction for elastic plates and existence of minimizers for positive Cosserat couple modulus. Contin. Mech. Thermodyn. 16, 577–628 (2004)
Neff, P.: A geometrically exact viscoplastic membrane-shell with viscoelastic transverse shear resistance avoiding degeneracy in the thin-shell limit. Part I: The viscoelastic membrane-plate. Z. Angew. Math. Phys. 56(1), 148–182 (2005)
Neff, P.: Local existence and uniqueness for a geometrically exact membrane-plate with viscoelastic transverse shear resistance. Math. Methods Appl. Sci. 28, 1031–1060 (2005)
Neff, P.: A geometrically exact planar Cosserat shell-model with microstructure: Existence of minimizers for zero Cosserat couple modulus. Math. Models Methods Appl. Sci. 17, 363–392 (2007)
Neff, P., Münch, I.: Curl bounds Grad on \(\mathrm{SO}(3)\). ESAIM Control Optim. Calc. Var. 14, 148–159 (2008)
Neff, P., Lankeit, J., Madeo, A.: On Grioli’s minimum property and its relation to Cauchy’s polar decomposition. Int. J. Eng. Sci. 80, 207–217 (2014)
Pietraszkiewicz, W.: Consistent second approximation to the elastic strain energy of a shell. Z. Angew. Math. Mech. 59, 206–208 (1979)
Pietraszkiewicz, W.: Refined resultant thermomechanics of shells. Int. J. Eng. Sci. 49, 1112–1124 (2011)
Pietraszkiewicz, W., Konopińska, V.: Drilling couples and refined constitutive equations in the resultant geometrically non-linear theory of elastic shells. Int. J. Solids Struct. 51, 2133–2143 (2014)
Šilhavỳ, M.: Curvature measures in linear shell theories. Preprint No. 22-2020, Institute of Mathematics, The Czech Academy of Sciences (2020)
Steigmann, D.J.: Koiter’s shell theory from the perspective of three-dimensional nonlinear elasticity. J. Elast. 111, 91–107 (2013)
Ljulj, M., Tambača, J.: A Naghdi type nonlinear model for shells with little regularity. J. Elast. 142, 447–494 (2020). https://doi.org/10.1007/s10659-020-09802-8
Toupin, R.A.: Elastic materials with couple stresses. Arch. Ration. Mech. Anal. 11, 385–413 (1962)
Toupin, R.A.: Theories of elasticity with couple-stresses. Arch. Ration. Mech. Anal. 17, 85–112 (1964)
Weinberg, K., Neff, P.: A geometrically exact thin membrane model-investigation of large deformations and wrinkling. Int. J. Numer. Methods Eng. 74(6), 871–893 (2008)
Zhilin, P.A.: Applied Mechanics – Foundations of Shell Theory. State Polytechnical University Publisher, Sankt Petersburg (2006) (in Russian)
Acknowledgements
The work of I.D. Ghiba was supported by a grant of the Romanian Ministry of Research and Innovation, CNCS–UEFISCDI, Project no. PN-III-P1-1.1-TE-2019-0348, Contract No. TE 8/2020, within PNCDI III. This research has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project no. 415894848 (M. Bîrsan, P. Lewintan and P. Neff).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 A.1 Useful Identities
We provide some properties of the tensors in the variational formulation of the shell models from [20, 21]:
Remark A.1
The following identities are satisfied:
-
(i)
\(\mathrm{tr}[{\mathrm{A}}_{y_{0}}]\,=\,2\), \({\det }[{\mathrm{A}}_{y_{0}}]\,=\,0;\quad \) \(\mathrm{tr}[{\mathrm{B}}_{y_{0}}]\,=\,2\,\mathrm{H}\), \({\det }[{\mathrm{B}}_{y_{0}}]\,=\,0\),
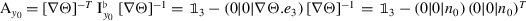 ,
,\(\mathrm{B}_{y_{0}} = [\nabla \Theta ]^{-T}\; \mathrm{II}_{y_{0}}^{\flat }\; [ \nabla \Theta ]^{-1}\)
-
(ii)
\(\mathrm{B}_{y_{0}}\) satisfies the equation of Cayley-Hamilton type \(\mathrm{B}_{y_{0}}^{2}-2\,\mathrm{H}\, \mathrm{B}_{y_{0}}+\mathrm{K}\, \mathrm{A}_{y_{0}} \,=\,0_{3}\);
-
(iii)
\(\mathrm{A}_{y_{0}}{\mathrm{B}}_{y_{0}}\,=\,\mathrm{B}_{y_{0}}{\mathrm{A}}_{y_{0}}\,= \,\mathrm{B}_{y_{0}}\), \(\mathrm{A}_{y_{0}}^{2}\,=\,\mathrm{A}_{y_{0}}\), \(\mathrm{C}_{y_{0}}\in \mathfrak{so}(3)\), \(\quad \mathrm{C}_{y_{0}}^{2}\,=\,-\mathrm{A}_{y_{0}}\), \(\lVert {\mathrm{C}}_{y_{0}}\rVert ^{2}=2\);
-
(iv)
 ;
; -
(v)
\(\mathrm{C}_{y_{0}} \mathcal{K}_{e,s} {\mathrm{A}}_{y_{0}}\,\,=\,\,\mathrm{C}_{y_{0}} \mathcal{K}_{e,s} \), \(\mathcal{E}_{m,s} {\mathrm{A}}_{y_{0}}\,\,=\,\,\mathcal{E}_{m,s} \).
Further, in view of \(\mathrm{I}_{y_{0}}^{-1} {\mathrm{II}}_{y_{0}}= \mathrm{L}_{y_{0}} \) and considering also the third fundamental form defined by \(\mathrm{III}_{y_{0}}= \mathrm{II}_{y_{0}} {\mathrm{L}}_{y_{0}}\), we note the relations
1.2 A.2 The Classical Nonlinear Koiter Shell Model in Cartesian Matrix Notation
In this subsection, we consider the variational problem for the geometrically nonlinear Koiter energy for a nonlinear elastic shell [15, page 147] and we rewrite it in matrix format. The problem written in tensor format [15, page 147], [40, Eq. (1) and Eq. (101)] is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \):

where the fourth order constitutive tensor \(\mathbb{C}_{\mathrm{shell}}^{\mathrm{iso}}:\mathrm{Sym}(2)\to {\mathrm{Sym}}(2)\) for isotropic elastic shells in the Koiter model is given by [14]
Since our model is completely written in matrix format, we also transform the above classical minimization problem in matrix format. To this aim, let us remark that in (A.2), for a second order symmetric tensor \(X \,=\,X_{\alpha \beta } e _{\alpha }\otimes e _{\beta }\), we have
A little calculation shows
where \(P\,=\, \nabla \Theta \), and similarly
If we substitute (A.5) and (A.6) into (A.4), we obtain
which holds for any symmetric tensor \(X \,=\,X_{\alpha \beta } e _{\alpha }\otimes e _{\beta }\).
Writing the equation (A.7) for the symmetric matrix \(X\,=\, \frac{1}{2}(\mathrm{I}_{m}-\mathrm{I}_{y_{0}})\) and respectively the matrix \(X\,=\, \mathrm{II}_{m}-\mathrm{II}_{y_{0}}\), then we obtain the following relations

Hence, putting all together, in matrix format and for a nonlinear elastic shell, the variational problem for the Koiter energy is to find a deformation of the midsurface \(m:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing on \(\omega \)
The main feature of the classical Koiter model is that it is just the sum of the correctly identified membrane term and bending terms (under inextensional deformation).
1.3 A.3 Thickness Versus Invertibility and Coercivity
1.3.1 A.3.1 Invertibility Conditions for the Parametrized Initial Surface \(\Theta \)
We note that \(\det \nabla \Theta (x_{3})= 1-2\, H\,x_{3}+K\, x_{3}^{2}=(1-\kappa _{1} \,x_{3})(1-\kappa _{2}\, x_{3})>0\)  if and only if \(1-\kappa _{1}\,x_{3}\) and \(1-\kappa _{2}\, x_{3}\) have the same sign. However, \(1-\kappa _{1}\,x_{3}\) cannot be negative, since for \(\kappa _{1}<0\) this will imply that \(1<\kappa _{1}\,x_{3}\)
if and only if \(1-\kappa _{1}\,x_{3}\) and \(1-\kappa _{2}\, x_{3}\) have the same sign. However, \(1-\kappa _{1}\,x_{3}\) cannot be negative, since for \(\kappa _{1}<0\) this will imply that \(1<\kappa _{1}\,x_{3}\)  which is not true if \(x_{3}>0\), while for \(\kappa _{1}\geq 0\) this will imply that \(1<\kappa _{1}\,x_{3}\)
which is not true if \(x_{3}>0\), while for \(\kappa _{1}\geq 0\) this will imply that \(1<\kappa _{1}\,x_{3}\)  which is not true if \(x_{3}<0\). Therefore, \(1-2\, H\,x_{3}+K\, x_{3}^{2}>0\)
which is not true if \(x_{3}<0\). Therefore, \(1-2\, H\,x_{3}+K\, x_{3}^{2}>0\)  if and only if \(1>\kappa _{1}\,x_{3}\) and \(1>\kappa _{2}\, x_{3}\)
if and only if \(1>\kappa _{1}\,x_{3}\) and \(1>\kappa _{2}\, x_{3}\)  . These conditions are equivalent with
. These conditions are equivalent with  and
and  , i.e., equivalent with (1.18).
, i.e., equivalent with (1.18).
1.3.2 A.3.2 Coercivity for the \(O(h^{5})\) Model
The decisive point in the proof of the existence where the condition on the thickness is used is only in the proof of the coercivity of the internal energy density. Therefore, in this appendix, we extend the result regarding the coercivity of the internal energy to the following result:
Proposition A.2
Coercivity in the theory including terms up to order \(O(h^{5})\)
For sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients satisfying \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\), the energy density
is coercive in the sense that there exists a constant \(a_{1}^{+}>0\) such that \(W(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\,\geq \, a_{1}^{+}\, \big ( \lVert \mathcal{E}_{m,s}\rVert ^{2} + \lVert \mathcal{K}_{e,s}\rVert ^{2} \,\big )\), where \(a_{1}^{+}\) depends on the constitutive coefficients.
Proof
From the assumptions \(h\, |\kappa _{1}|<\alpha \), \(\ h\, |\kappa _{2}|<\alpha \), it follows that
Therefore, for \(\alpha <\sqrt{\frac{20}{3}}\) it follows \(h-\mathrm{K}\,\frac{h^{3}}{12}> h-\,\frac{h}{12}\alpha ^{2}>0 \ \ \textrm{and} \ \ \frac{h^{3}}{12}\,-\frac{h^{3}}{80}\alpha ^{2}>0\). On the other hand, from [21, Proposition 3.1.] we have
Using the inequalities (A.12), we deduce
Let us remark for \(0<\alpha <\sqrt{\frac{20}{3}}\), if there exist \(\delta >\frac{20}{3}\) and \(\varepsilon >\frac{40\, \alpha }{20-3\, \alpha ^{2}}\) such that
then \(\alpha <\sqrt{\frac{2}{3}(29-\sqrt{761})}\simeq 0.97083\). Since the map \((\delta , \varepsilon )\mapsto \delta + 2\,\varepsilon \,\alpha \) is linear, it increases in gradient direction and hence, the condition \(\alpha <\sqrt{\frac{2}{3}(29-\sqrt{761})}\simeq 0.97083\) is also sufficient for the existence of \(\delta >\frac{20}{3}\) and \(\varepsilon >\frac{40\, \alpha }{20-3\, \alpha ^{2}}\) such that (A.15) is satisfied.

In view of (A.14) and (2.10), we see that there exist positive constants \(b_{1}^{+}, b_{2}^{+},b_{3}^{+}>0\) such that

The desired constant \(a_{1}^{+}\) from the conclusion can be chosen as \(a_{1}^{+}\,{=}\,\min \big \{\dfrac{h}{12}\,b_{1}^{+}\, \min \{c_{1}^{+}, \mu _{\mathrm{c}}\}, \dfrac{h}{12}\,b_{2}^{+}\,\min \{c_{1}^{+},\mu _{\mathrm{c}} \}, h\,b_{3}^{+}\, { c_{2}^{+}} \big \}\). □
1.3.3 A.3.3 Coercivity for the \(O(h^{3})\) Model
In this subsection we investigate if the conditions which assure the existence of the solution may be relaxed in the Cosserat shell model up to \(O(h^{3})\), too. In fact, as in the previous subsection, it is enough to prove some new coercivity results under weakened conditions on the thickness. We recall that in the Cosserat shell model up to \(O(h^{3})\) the shell energy density \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\) is given by (3.65).
Proposition A.3
The first coercivity result in the theory including terms up to order \(O(h^{3})\)
For sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients satisfying the constitutive coefficients are such that \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\) and where \(c_{2}^{+}\) denotes the smallest eigenvalue of \(W_{\mathrm{curv}}( S )\), and \(C_{1}^{+}>0\) denotes the largest eigenvalues of the quadratic form \(W_{\mathrm{shell}}^{\infty }( S)\), the total energy density \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\) is coercive, in the sense that there exists a constant \(a_{1}^{+}>0\) such that \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\,\geq \, a_{1}^{+} \, \big ( \lVert \mathcal{E}_{m,s}\rVert ^{2} + \lVert \mathcal{K}_{e,s} \rVert ^{2}\,\big ) \), where \(a_{1}^{+}\) depends on the constitutive coefficients.
Proof
Similarly as in the proof presented in [21, Proposition 4.1], we obtain the estimate

which after imposing the conditions \(-h^{2} |K|>-\alpha ^{2}\) and \(-h\, |H|>-\alpha \), using (A.12), (2.10) and since the Frobenius norm is sub-multiplicative and \(\lVert C_{y_{0}}\rVert ^{2}=2 \), leads to

for all \(\alpha , \delta , \varepsilon >0\) such that \(12-\alpha ^{2}- \varepsilon -2\,\alpha \, \delta >0\) and \(12-\alpha ^{2}>0\). Since \(\lVert B_{y_{0}}\rVert ^{2}=4\, \mathrm{H}^{2}-2\,\mathrm{K}\), it follows
Using again that \(h\) is small, we obtain \(-h^{2}\,(4\, \mathrm{H}^{2}-2\,\mathrm{K})\geq -h^{2}\,(4\, \mathrm{H}^{2}+2 \,|{\mathrm{K}}|)\geq -6\,\alpha ^{2} \) and
We consider \(\delta =\gamma \, \varepsilon \) and we choose \(\epsilon >0\) and \(\gamma >0\) such that
This choice of the variable \(\varepsilon >0\) is possible if and only if \(\frac{(12-\alpha ^{2})^{2}\gamma }{4\,(a+2\,\alpha \gamma )\,(\alpha +3\, \alpha ^{2}\gamma )}> \frac{h^{2}\,\max \{C_{1}^{+},\mu _{\mathrm{c}}\} }{c_{2}^{+}}\). At this point we use that
and this maximum value is attained for \(\gamma =\frac{1}{\sqrt{6}\,a}\). Hence, we arrive at the following condition on the thickness \(h\):
which proves the coercivity if the condition from the hypothesis is satisfied. □
The condition (A.18) on the thickness does not represent a relaxation of the condition imposed in [21, Proposition 4.1], i.e., not in the sense of the relaxed condition (A.10) which is found for the \(O(h^{5})\) Cosserat shell model. Indeed, since the map \(\alpha \mapsto \frac{(5-2\sqrt{6})(\alpha ^{2}-12)^{2}}{4\, \alpha ^{2}} \frac{ {c_{2}^{+}}}{\max \{C_{1}^{+},\mu _{\mathrm{c}}\} }\) is monotone decreasing on \([0,2]\) (the interval of the values of the parameter \(\alpha \) for which the construction of the model has sense), a large value for \(\alpha \) will relax the first condition (A.18)1 while the other condition (A.18)2 on the thickness will become more restrictive. Since the second condition (A.18)2 is expressed in terms of all constitutive parameters, through \(c_{2}^{+}\) and \(\max \{C_{1}^{+},\mu _{\mathrm{c}}\} \), while the first condition (A.18)1 depends on the curvatures of the referential configuration, the largest value of the parameter \(\alpha \) in the coercivity result would be chosen as the best compromise between the conditions (A.18)1 and (A.18)2. In conclusion, in comparison to the conditions imposed in [21, Proposition 4.1], for a specific material and a specific referential configuration the new condition (A.18) would offer a largest interval of values for the upper bound of the thickness.
We also note that in [21, Proposition 4.1], because the condition of the form (A.18)2 from the hypothesis of Proposition A.3 depends on the length scale \(L_{c}\), we have proved another coercivity result which avoids this aspect:
Proposition A.4
The second coercivity result in the theory including terms up to order \(O(h^{3})\)
For sufficiently small values of the thickness \(h\) such that
and for constitutive coefficients satisfying the constitutive coefficients are such that \(\mu >0, \,\mu _{\mathrm{c}}>0\), \(2\,\lambda +\mu > 0\), \(b_{1}>0\), \(b_{2}>0\) and \(b_{3}>0\) and let \(c_{1}^{+}\) and \(\max \{C_{1}^{+},\mu _{\mathrm{c}}\} >0\) denote the smallest and the largest eigenvalues of the quadratic form \(W_{\mathrm{shell}}^{\infty }( S)\), the total energy density \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\) is coercive, in the sense that there exists a constant \(a_{1}^{+}>0\) such that \(W^{(h^{3})}(\mathcal{E}_{m,s}, \mathcal{K}_{e,s})\,\geq \, a_{1}^{+} \, \big ( \lVert \mathcal{E}_{m,s}\rVert ^{2} + \lVert \mathcal{K}_{e,s} \rVert ^{2}\,\big )\), where \(a_{1}^{+}\) depends on the constitutive coefficients.
1.4 A.4 Acharya’s Bending Tensor in Cartesian Matrix Notation
For comparison purpose, let us mark all the vectors and tensors defined by Acharya [1, Page 5520] with the subscript \(A\) (e.g., \(\boldsymbol{f}_{A} \), \(\boldsymbol{b}^{*}_{A} \), \((\boldsymbol{E}_{\alpha })_{A} \)). We express them using our notations as follows:
Let us denote by \([ \boldsymbol{T}_{A}] \) the \(3\times 3 \) matrix of the components in the basis \(\{ e_{i}\otimes e_{j}\} \) for any tensor \(\boldsymbol{T} \) defined by Acharya [1, Page 5519]. Then, we have
and
so that
Furthermore, we have
and using (A.41) we get
By virtue of (A.28) and (A.29), the classical bending strain measure can be written as [1, Eq. 3]
For the tensor \(\boldsymbol{U}_{A} \) we obtain using equation (A.28) the expression
Thus, the bending tensor defined by Acharya [1, Eq. 8] is given by
Inserting here the relations (A.28), (A.29) and (A.31), we obtain that the bending tensor \(\widetilde{\boldsymbol{K}}_{A} \) defined in the paper by Acharya [1, Eq. 7 and 8] can be written in our matrix notation as follows:

Since  and
and  , the following relation between the nonlinear bending tensor \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) introduced by Acharya and our nonlinear bending tensor \(\mathcal{R}_{\infty }^{\flat }\) holds
, the following relation between the nonlinear bending tensor \(\widetilde{\mathcal{R}}_{\mathrm{Acharya}}\) introduced by Acharya and our nonlinear bending tensor \(\mathcal{R}_{\infty }^{\flat }\) holds

where we have used  and (6.2).
and (6.2).
1.5 A.5 A Direct Proof of the Fact That \(\mathcal{R}_{\infty }^{\flat }\) Satisfies AR1, AR2 and AR3 ∗
It is obvious that the tensor (6.1) satisfies condition AR2, see Sect. 6.2. Moreover, using similar calculations as in Sect. 6.2, for a rigid deformation, we have

so that we conclude

which means that \(\mathcal{R}_{\infty }^{\flat }\) satisfies AR1.
In order to show that \(\mathcal{R}_{\infty }^{\flat }\) satisfies AR3∗, using
we deduce that

where we have used that \(\mathrm{U_{e}}\) is positive-definite. Together with the definition of the symmetric matrix \(\mathrm{U_{e}}\) we get

Again, using the intermediate steps (6.16) and (A.38) in the expression (6.2) we obtain \(\mathcal{R}_{\infty }^{\flat }=0_{3}\) since

so that also \(\mathcal{R}_{\infty }^{\flat }\) satisfies AR1, AR2 and AR3∗.
1.6 A.6 Alternative Representation of Energy in Terms of the New Strain Tensors
We present in the following an alternative formulation of the unconstrained Cosserat-shell model from (3.21). In this section, for a matrix of the form \(X\,=\,(X^{S}\, |\, 0)\; [\nabla \Theta \,]^{-1}\in \mathbb{R}^{3 \times 3}\), we consider the matrix \(X^{C} \,=\, [\nabla \Theta \,]^{T} X^{S}\in \mathbb{R}^{3\times 2}\), i.e.,
For the bilinear form \(W_{\mathrm{shell}}( X, Y) \) given in (2.6) we have then the transformations
where, e.g.,
We note that the last relation can be written using the first fundamental form \(\mathrm{I}_{y_{0}} \) and its square root in the following alternative ways:
Moreover, if we decompose the matrix \(X^{C} \in \mathbb{R}^{3\times 2}\) in two block matrices (the matrix  and the matrix \(e_{3}^{T}\, X^{C} \in \mathbb{R}^{1\times 2}\)), then we can write the bilinear form as
and the matrix \(e_{3}^{T}\, X^{C} \in \mathbb{R}^{1\times 2}\)), then we can write the bilinear form as

where we define for any \(X, Y\in \mathbb{R}^{2\times 2} \) the bilinear form
Analogous results hold for the quadratic form \(W_{\mathrm{curv}}( X, X) \).
We can decompose the \(3\times 2 \) matrices in two block matrices (\(2 \times 2 \) and \(1\times 2 \)) and express the strain energy densities \(W_{\mathrm{memb}} \) and \(W_{\mathrm{memb,bend}}\) as functions of the matrices \(\mathcal{G}_{\infty }\) and \(\mathcal{R}_{\infty }\) (we have used that \(\mathcal{T}_{\infty }\) vanishes) in the following form
where  , \(W_{\mathrm{inplane}} \) is given by (A.45) and we have denoted
, \(W_{\mathrm{inplane}} \) is given by (A.45) and we have denoted
We can see in the expression (A.46) the different parts of the energy corresponding to in-plane deformation, transverse shear, or coupling terms with bending.
Finally, the bending-curvature energy density \(W_{\mathrm{bend,curv}} \) can be written as function of \(\mathcal{R}_{\infty }\) and \(\mathcal{N}_{\infty }\) as follows
where we have denoted for any \(2\times 2 \) matrix \(X \) the quadratic form (positive definite)

Thus, the model can be expressed entirely in terms of the change of metric tensor \(\mathcal{G}_{\infty }\), the bending strain tensor \(\mathcal{R}_{\infty }\) and the vector of drilling bendings \(\mathcal{N}_{\infty }\), through the relations (A.46) and (A.48).
Rights and permissions
About this article
Cite this article
Ghiba, ID., Bîrsan, M., Lewintan, P. et al. A Constrained Cosserat Shell Model up to Order \(O(h^{5})\): Modelling, Existence of Minimizers, Relations to Classical Shell Models and Scaling Invariance of the Bending Tensor. J Elast 146, 83–141 (2021). https://doi.org/10.1007/s10659-021-09851-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-021-09851-7
Keywords
- Geometrically nonlinear Cosserat shell
- 6-parameter resultant shell
- In-plane drill rotations
- Constrained Cosserat elasticity
- Isotropy
- Existence of minimizers
- Scaling invariance
- Bending tensor



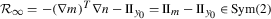 .
.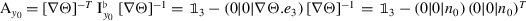 ,
, ;
;