1 Introduction

In a modern social context requiring increasing possibilities to move fast and on long distances, vehicle safety is of vital importance to considerably reduce the number of fatal accidents. To respond to these urgent societal challenges, in 2011 the European Commission adopted an ambitious Road Safety Programme aiming to halve the chances of deaths in Europe in the following decade. The programme set out a mix of initiatives, both at European and national level, focusing on a considerable improvement of active safety (onboard vehicle controls), passive safety (structural and infrastructural enhancements) and preventive safety (analysing and detecting road users' behavior) [1].

In the specific context of active safety, the future of the mobility on wheels is going towards the development of advanced control algorithms for enhancing vehicle interaction both with the road and with the vehicle network. A full and accurate knowledge of the vehicle states is required for onboard control logics to guarantee a correct and effective performance. Current vehicle control systems of passenger cars rely on available measurements such as longitudinal velocity, lateral/longitudinal accelerations, yaw rate. That is the case of, e.g., the Electronic Stability Control (ESC), nowadays installed in all passenger cars.

The availability of additional vehicle states would allow the development of more advanced active vehicle controllers, further enhancing vehicle safety. That is the case of vehicle sideslip angle, a vehicle state defined as the angle between the vehicle longitudinal axis and the direction of the vehicle velocity at the center of mass [2]. The availability of this state would be dramatically helpful [3,4,5]. However, the possibility to measure sideslip angle directly on board is limited. Optical and GPS-based sensors, usually employed to this purpose, are expensive and quite uncomfortable for a large-scale adoption. Alternatively, the sideslip angle can be estimated via real-time software modeling techniques. Several observers have been developed to this aim, yet sideslip angle estimation is still an open issue in the automotive field [6, 7]. Three modeling categories can be identified in the literature: kinematic models, dynamic models and combined models. Most of the proposed methods to estimate sideslip angle need only signals that are easily measurable within the integrated set of sensors already available in a standard passenger car.

The first category is based on kinematic relationships involving yaw rate, lateral and longitudinal velocities and their derivatives. No vehicle or tire parameters are involved. However, kinematic-based estimators become unobservable when the yaw rate approaches zero, and usually provide noisier estimations. Nevertheless, kinematic models are more suitable for transient maneuvers and they work well in the nonlinear region of the tire [8]. Some examples of kinematic models are shown in [9], where a simple yet effective logic is adopted to correct the unobservability and prevent possible sideslip angle drifting in straight roads due to yaw rate and lateral acceleration sensor offsets (which are unavoidable). Selmanaj et al. [9] correct the approach presented in [8] with a heuristically calculated term. An heuristic function is evaluated through the use of bivariate Gaussian distributions and a set of three signals (steering angle, yaw rate and sideslip rate) with their derivatives. Because of their disadvantages, it is infrequent to come across estimators purely based on kinematic models. Instead, either a dynamic model is used, or a combination of kinematic and dynamic models.

The second category is very frequently adopted in the literature, as it is based on the equilibrium equations of the vehicle, often described by means of a single-track model [8, 10,11,12,13,14,15,16,17,18]. However, examples with a four-wheel configuration vehicle model can also be found [19,20,21,22,23,24]. Often an Extended Kalman filter [25] is used, but in [22,23,24] the Unscented version of the Kalman filter is applied when the model becomes strongly nonlinear. Dynamic approaches are very sensitive to the tire model adopted within the estimator. Some papers choose a linear tire model [10, 11, 13, 14], while others use Pacejka's Magic Formula [12, 15, 23] and a significant group adopt even different tire models such as the Dugoff tire model [19, 22, 24] and the Rational tire model [21, 26]. In [10,11,12,13,14,15,16,17,], an extended adaptive Kalman filter is used, integrated with an estimation/adaptation algorithm for the tire parameters. On the other hand, [21] proposes a dual extended Kalman filter, where two Kalman filters are used in a recursive way. The first one estimates vehicle parameters that are fed to the second Kalman filter which estimates the vehicle state. In [13] another interesting two-stage structure is investigated. The first stage is an Extended Kalman filter which provides information about the vehicle state, and the second one employs the Extended Kalman filter results to obtain an estimation of the tire parameters. In [23], a new approach for the vehicle state estimation based on a detailed vehicle model and an Unscented Kalman filter is presented. The mathematical model relies on a planar two-track model extended by an advanced vertical tire force calculation method. Doumiati et al. [22] and [24] also apply the Unscented version of the Kalman filter, but [22] also employs a set of deflection sensors installed on the suspension system, which is not a common sensor set for a passenger vehicle. [24] estimates the tire-road friction coefficient by introducing it in the state vector. The authors of [15] employ the Magic Formula in an innovative way, coupled with an Extended Kalman filter and with the addition of new tuning parameters which control the shape of lateral tire forces. Interestingly, [26] introduces cornering stiffnesses directly in the state vector, hence obtaining their real-time estimation. [27] applies the same idea to the parameters of the Rational tire model.

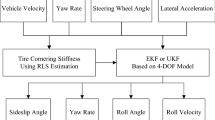
The third category features a mixed approach, employing a well-thought combination of kinematic and dynamic modeling. The study presented in [28] combines a kinematic approach with a dynamic formulation to overcome the problem of the unobservability when the yaw rate is around zero. In [29] the kinematic and dynamic models are cleverly combined to make the most of each formulation, and a steady-state index is defined to properly weight the outputs of the two models. Moreover, a simple cornering stiffness identification method is proposed. The authors of [30] apply their model to an electric vehicle featuring multi-sensing hub units, which are sensor units able to provide a very accurate measurement in terms of tire lateral forces. The authors also estimate sideslip and roll angles with a coupled approach including a Recursive Least Squares (RLS) method and a Kalman filter. In [31] a mixed approach is applied, with a mostly kinematic-based model: an algorithm to estimate tire-road friction is presented, that is activated only if the lateral velocity derivative is sufficiently high and the yaw rate is above a predefined threshold, or when the ESC is on.

This paper proposes a new method to estimate vehicle sideslip angle, with the following novelties:

  • the development of an innovative combination of kinematic and dynamic modeling, denoted as cross-combined approach, which introduces a mutual influence between the two approaches;

  • the development of an Unscented Kalman filter framework based on the cross-combined approach and a modified Dugoff tire model;

  • the validation of the proposed approach on a large set of experimental data acquired on a rear-wheel-drive motorsport car equipped with an optical sensor for the measurement of sideslip angle, along with an Inertial Measurement Unit (IMU), wheel speed sensors, and a steering wheel sensor;

  • a comparison between the proposed method and a traditional method for sideslip angle estimation.

The remainder of the paper is organized as follows. Section 2 provides a description of the Kalman filter and its main variants. Section 3 describes the proposed estimator with specific focus on the kinematic filter, the dynamic filter, and the concept of cross-combination. Section 4 presents results based on experimental tests in which the proposed approach is compared to a traditional one. Section 5 draws the main conclusions.

2 The Kalman filter (KF)

The Kalman filter is named after Rudolph E. Kalman, who first described a new solution to the discrete-data linear filtering problem in 1960 [25]. Theoretically, the Kalman filter is an estimator for the linear quadratic Gaussian problem, i.e. estimating the instantaneous state of a linear dynamic system perturbed by Gaussian white noise, by using measurements linearly related to the state, also corrupted by Gaussian white noise. The resulting estimator is statistically optimal with respect to any quadratic function of the estimation error [32]. The name “filter” derives from the fact that, practically, it allows to remove the known and unknown noise components in the measurements and in the description of the system. Several versions of the KF exist. Some of the most important versions are described here, including versions that allow to deal with nonlinear systems, as is the case of vehicle dynamics.

2.1 The basic Kalman filter (KF) for linear systems

The original Kalman filter formulation is designed to deal with linear systems, estimating the state \(\boldsymbol{x}\in {\mathbb{R}}^{N}\) of the observed system. The generic linear process can be described in discrete-time form by means of process and measurement equations, respectively:

$$\begin{aligned} {\varvec{x}}_{\varvec{k}} = {\varvec{Ax}}_{{{\varvec{k}} - 1}} + {\varvec{Bu}}_{\varvec{k}} + {\varvec{Ww}}_{{{\varvec{k}} - 1}} \\ {\varvec{z}}_{\varvec{k}} = {\varvec{Hx}}_{\varvec{k}} + {\varvec{Vv}}_{\varvec{k}} \\ \end{aligned}$$
(1)

where \({\varvec{x}}_{\varvec{k}}\) and \({\varvec{u}}_{\varvec{k}}\) are respectively the state vector and the input at the generic time step \(k\), \({\varvec{A}}\) the dynamic matrix, \({\varvec{B}}\) the control matrix, \({\varvec{H}}\) the measurement matrix, \({\varvec{W}}\) the process noise matrix, \({\varvec{V}}\) the measurement noise matrix. \({\varvec{x}}_{\varvec{k}}\) is a column vector with \(N\) elements. \({\varvec{w}}_{\varvec{k}}\) and \({\varvec{v}}_{\varvec{k}}\) represent the process and measurement noise with \({\varvec{Q}}\) and \({\varvec{R}}\) being the correspondent covariance matrices. The matrices \({\varvec{A}},{\varvec{B}},{\varvec{H}},{\varvec{W}},{\varvec{V}}\) allow to relate state, input, and noises to the subsequent (propagated) state and to the measurements. The equations of the recursive algorithm are divided into time update equations and measurement update equations. The time update equations describe the evolution of the system a-priori, i.e., only based on the model of the system:

$$\begin{aligned} {\hat{\varvec{x}}}_{\varvec{k}}^{ - } &= {\varvec{A}}{\hat{\varvec{x}}}_{{{\varvec{k}} - 1}} + {\varvec{Bu}}_{\varvec{k}} \\ {\varvec{P}}_{\varvec{k}}^{ - } &= {\varvec{AP}}_{{{\varvec{k}} - 1}} {\varvec{A}}^{\varvec{T}} + {\varvec{WQW}}^{\varvec{T}} \\ \end{aligned}$$
(2)

where \({\hat{\varvec{x}}}_{\varvec{k}}^{ - }\) indicates the a-priori estimated state at time step \(k\), \({\varvec{P}}_{{\varvec{k} - 1}}\) the state covariance at time step (\(k - 1\)), \({\varvec{P}}_{\varvec{k}}^{ - }\) the a-priori state covariance at time step \(k\).

The measurement update equations allow to correct the a-priori estimation based on the gathered measurement, hence providing the a-posteriori estimation of the state:

$$\begin{aligned} {\varvec{K}}_{\varvec{k}} & = {\varvec{P}}_{\varvec{k}}^{ - } {\varvec{H}}^{\varvec{T}} \left( {{\varvec{HP}}_{\varvec{k}}^{ - } {\varvec{H}}^{\varvec{T}} + {\varvec{VRV}}^{\varvec{T}} } \right)^{{ - 1}} \\ {\hat{\varvec{x}}}_{\varvec{k}} &= {\hat{\varvec{x}}}_{\varvec{k}}^{ - } + {\varvec{K}}_{\varvec{k}} \left( {{\varvec{z}}_{\varvec{k}} - {\varvec{H}}{\hat{\varvec{x}}}_{\varvec{k}}^{ - } } \right) \\ {\varvec{P}}_{\varvec{k}} & = \left( {{\varvec{I}} - {\varvec{K}}_{\varvec{k}} {\varvec{H}}} \right){\varvec{P}}_{\varvec{k}}^{ - } \\ \end{aligned}$$
(3)

where \({\hat{\varvec{x}}}_{\varvec{k}}\) is the estimated state at time step \(k\), \({\varvec{P}}_{\varvec{k}}\) the covariance at time step \(k\), and \({\varvec{K}}_{\varvec{k}}\) is denoted as Kalman gain. Note that covariance matrices \({\varvec{P}}\), \({\varvec{W}}\) and \({\varvec{V}}\) are semi-positive definite.

2.2 Extended Kalman filter (EKF) and Unscented Kalman filter (UKF)

The main drawback of the basic Kalman filter is its suitability for the estimation of the state of a process governed only by a linear set of stochastic difference equations. Yet, it is well known that real processes are often far from linear. For nonlinear systems, the so-called Extended Kalman filter can be adopted [25, 33, 34]. Equation (1) can be generalized as:

$$\begin{aligned} &{\varvec{x}}_{\varvec{k}} = {\varvec{f}}\left( {{\varvec{x}}_{{{\varvec{k}} - 1}} ,{\varvec{u}}_{{{\varvec{k}} - 1}} ,{\varvec{w}}_{{{\varvec{k}} - 1}} } \right) \\ &{\varvec{z}}_{\varvec{k}} = {\varvec{h}}\left( {{\varvec{x}}_{\varvec{k}} ,{\varvec{v}}_{\varvec{k}} } \right) \\ \end{aligned}$$
(4)

which entails generic functions \({\varvec{f}}\) and \({\varvec{h}}\). The key idea of the EKF is to linearize the system, at each time step, around the estimated state of the system at the previous time step:

$$\begin{aligned} A_{{k\left[ {i,j} \right]}} &= \frac{{\partial f_{{\left[ i \right]}} }}{{\partial x_{{\left[ j \right]}} }}\left( {{\hat{\varvec{x}}}_{{{\varvec{k}} - 1}} ,{\varvec{u}}_{{{\varvec{k}} - 1}} ,\mathbf{0}} \right) \\ W_{{k\left[ {i,j} \right]}} &= \frac{{\partial f_{{\left[ i \right]}} }}{{\partial w_{{\left[ j \right]}} }}\left( {{\hat{\varvec{x}}}_{{{\varvec{k}} - 1}} ,{\varvec{u}}_{{{\varvec{k}} - 1}} ,\mathbf{0}} \right) \\ H_{{k\left[ {i,j} \right]}} &= \frac{{\partial h_{{\left[ i \right]}} }}{{\partial x_{{\left[ j \right]}} }}\left( {{\hat{\varvec{x}}}_{\varvec{k}}^{ - } ,\mathbf{0}} \right) \\ V_{{k\left[ {i,j} \right]}} &= \frac{{\partial h_{{\left[ i \right]}} }}{{\partial v_{{\left[ j \right]}} }}\left( {{\hat{\varvec{x}}}_{\varvec{k}}^{ - } ,\mathbf{0}} \right) \\ \end{aligned}$$
(5)

where \(A_{{k\left[ {i,j} \right]}}\), \(W_{{k\left[ {i,j} \right]}}\), \(H_{{k\left[ {i,j} \right]}}\), \(V_{{k\left[ {i,j} \right]}}\) represent the generic element of, respectively, \({\varvec{A}}_{\varvec{k}}\), \({\varvec{W}}_{\varvec{k}}\), \({\varvec{H}}_{\varvec{k}}\), \({\varvec{V}}_{\varvec{k}}\), on row i and column j, and \(f_{{\left[ i \right]}}\), \(h_{{\left[ i \right]}}\), \(x_{{\left[ i \right]}}\), \(v_{{\left[ i \right]}}\), \(w_{{\left[ i \right]}}\) represent the i-th element of, respectively, \({\varvec{f}}\), \({\varvec{h}}\), \({\varvec{x}}\), \({\varvec{v}}\), \({\varvec{w}}\). Essentially Eq. (5) contains the Jacobian matrices of the partial derivatives of the process and measurement functions with respect to the state and the noise. As a result, the following time update equations can be used for the a-priori evolution of the EKF (note that in these expressions the two covariance matrices are also assumed non-constant, for more generality):

$$\begin{aligned} {\hat{\varvec{x}}}_{\varvec{k}}^{ - } &= {\varvec{f}}\left( {{\hat{\varvec{x}}}_{{{\varvec{k}} - 1}} ,{\varvec{u}}_{{{\varvec{k}} - 1}} ,\mathbf{0}} \right) \\ {\varvec{P}}_{\varvec{k}}^{ - } &= {\varvec{A}}_{\varvec{k}} {\varvec{P}}_{{{\varvec{k}} - 1}} {\varvec{A}}_{\varvec{k}}^{\varvec{T}} + {\varvec{W}}_{\varvec{k}} {{\varvec{Q}}_{{{\varvec{k}} - 1}}} {\varvec{W}}_{\varvec{k}}^{\varvec{T}} \\ \end{aligned}$$
(6)

and the a-posteriori equations are:

$$\begin{aligned} {\varvec{K}}_{\varvec{k}} &= {\varvec{P}}_{\varvec{k}}^{ - } {\varvec{H}}_{\varvec{k}}^{\varvec{T}} \left( {{\varvec{H}}_{\varvec{k}} {\varvec{P}}_{\varvec{k}}^{ - } {\varvec{H}}_{\varvec{k}}^{\varvec{T}} + {\varvec{V}}_{\varvec{k}} {\varvec{R}}_{\varvec{k}} {\varvec{V}}_{\varvec{k}}^{\varvec{T}} } \right)^{{ - 1}} \\ {\hat{\varvec{x}}}_{\varvec{k}} &= {\hat{\varvec{x}}}_{\varvec{k}}^{ - } + {\varvec{K}}_{\varvec{k}} \left( {\varvec{z}_{\varvec{k}} - {\varvec{h}}\left( {{\hat{\varvec{x}}}_{\varvec{k}}^{ - } ,\mathbf{0}} \right)} \right) \\ {\varvec{P}}_{\varvec{k}} &= \left( {{\varvec{I}} - {\varvec{K}}_{\varvec{k}} {\varvec{H}}_{\varvec{k}} } \right){\varvec{P}}_{\varvec{k}}^{ - } \\ \end{aligned}$$
(7)

Despite the EKF is an elegant, efficient and recursive way to estimate the state of a nonlinear system, it has important flaws:

  • The calculation of Jacobian matrices may be computationally expensive, especially in situations where the partial derivatives are to be calculated online at each time step.

  • The linearized transformation provides good results only when the error propagation can be relatively well approximated by a linear model. This problem is deeply discussed in [35, 36].

To overcome the drawbacks related to the linearization process, many studies have been carried out. Attempts include the development of high-order Kalman filters [37] and more sophisticated versions of the EKF [38]. A widely appreciated solution is the Unscented Kalman filter (UKF), which provides a relatively simple and immediate way to propagate mean and covariance variables of random signals through a nonlinear transformation, without the need for linearization. The UKF is founded on the intuition that it is easier to approximate a probability distribution than it is to approximate an arbitrary nonlinear function or transformation [39]. The state distribution is represented with a set of deterministically chosen sample points, denoted as “sigma-points”. The sigma-points are a set of \(2N + 1\) potential guesses of the state of the system, with a given mean and covariance reflecting the same characteristics of the state to be estimated. In case of additive process and measurement noise, the \(2N + 1\) sigma-points can be obtained as:

$$\begin{aligned} {\varvec{X}}_{{{\varvec{k}} - 1}}^{{\left( 0 \right)}} = {\hat{\varvec{x}}}_{{{\varvec{k}} - 1}} \\ {\varvec{X}}_{{{\varvec{k}} - 1}}^{{\left( {\varvec{i}} \right)}} = {\hat{\varvec{x}}}_{{{\varvec{k}} - 1}} + \left( {\sqrt {\left( {N + \psi } \right){\varvec{P}}_{{{\varvec{k}} - 1}} } } \right)_{i} \quad \;for\; i = 1, 2, \ldots , N \\ {\varvec{X}}_{{{\varvec{k}} - 1}}^{{\left( {\varvec{i}} \right)}} = {\hat{\varvec{x}}}_{{{\varvec{k}} - 1}} - \left( {\sqrt {\left( {N + \psi } \right){\varvec{P}}_{{{\varvec{k}} - 1}} } } \right)_{{i - N}} \quad \;for\;i = N + 1, N + 2, \ldots , 2N \\ \end{aligned}$$
(8)

where in general \({\varvec{X}}_{\varvec{k}}^{{\left( {\varvec{i}} \right)}}\) represents the i-th sigma-point (\(i = 0, 1, 2, \ldots , 2N\)) at time step \(k\), which is a column vector with \(N\) elements—just as the state vector, for which a sigma-point is a potential guess. The notation \(\left( {\sqrt {\left( {N + \psi } \right) {\varvec{P}_{{k - 1}}^{{}} }} } \right)_{i}\) stands for the i-th column of the argument, which is calculated through the Cholesky decomposition. The UKF parameter \(\psi\) is defined as \(\psi = \sigma ^{2} \left( {N + \kappa } \right) - N\) where \(\sigma\) and \(\kappa\) are further UKF parameters, discussed below. At each time step, every sigma-point is propagated through the nonlinear dynamic function \({\varvec{f}}\):

$$\hat{\varvec{X}}_{\varvec{k}}^{\left({\varvec{i}} \right) - } = {\varvec {f}}\left( {\varvec{X}}_{{\varvec{k}} - {\mathbf{1}}}^{\left( {\varvec{i}} \right)}, {\varvec{u}}_{{\varvec{k}} - {\mathbf{1}}} ,{\mathbf{0}} \right)\quad for\;i = 0, 1, 2, \ldots , 2N$$
(9)

where \({\hat{\varvec{X}}}_{\varvec{k}}^{{\left( {\varvec{i}} \right) - }}\) is the i-th a-priori propagated sigma-point, so it is also a column vector with \(N\) elements. Thus, the a-priori estimated mean and covariance can be computed as [40,41,42]:

$$ \begin{aligned} \hat{\varvec{x}}_{\varvec{k}}^{ - } &= \mathop{\sum}\limits_{{i = 0}}^{{2N}} W_{m}^{{\left( i \right)}} \hat{\varvec{X}}_{\varvec{k}}^{{\left({\varvec{ i}} \right) - }} \\ {\varvec{ P}}_{\varvec{k}}^{ - } &= \mathop{\sum}\limits_{{i = 0}}^{{2N}} W_{c}^{{\left( i \right)}} \left\{ {\hat{\varvec{X}}_{\varvec{k}}^{{\left( {\varvec{i}} \right)- }} - {\hat{\varvec{{x}}}}_{\varvec{k}}^{ - } } \right\}\left\{ {{\hat{\varvec{{X}}}}_{\varvec{{k}}}^{{\left({\varvec{ i}} \right) - }} - {\hat {\varvec{{x}}}}_{\varvec{{k}}}^{ - } } \right\}^{T} +\; {\varvec{Q}} \\ \end{aligned} $$
(10)

based on the appropriate weights

$$\begin{aligned} W_{m}^{{\left( 0 \right)}} = \frac{\psi }{{\psi + N}} \\ W_{c}^{{\left( 0 \right)}} = \frac{\psi }{{\psi + N}} + \left( {1 - \sigma ^{2} + \gamma } \right) \\ W_{m}^{{\left( i \right)}} = W_{c}^{{\left( i \right)}} = \frac{1}{{2\left( {\psi + N} \right)}} \quad for\;i = 1, 2, \ldots , 2N \\ \end{aligned}$$
(11)

For the calibration phase of the filter:

  • \(\kappa\) represents the tailedness of the probability distribution, a default starting point can be \(\kappa = 0\) [43];

  • \(0 < \sigma < 1\);

  • \(\gamma > 0\) (for a Gaussian distribution the optimal value is \(\gamma = 2 \) [41]).

The measurement update equation set is:

$$\begin{aligned} &\hat{\varvec{Z}}_{\varvec{k}}^{{\varvec {\left( i \right)} - }}= {\varvec{h}}\left( \hat{\varvec{X}}_{\varvec{k}}^{\left({\varvec{i}} \right) - } ,{\mathbf{0}} \right)\quad for\;i = 0, 1, 2, \ldots ,2N \\ &\hat{\varvec{z}}_{\varvec{k}}^{ - } = \mathop \sum \limits_{{i = 0}}^{{2N}} W_{m}^{{\left( i \right)}} \hat{\varvec{Z}}_{\varvec{k}}^{\left({\varvec{i}} \right) - } \\ &{{\varvec{P}}_{{\varvec{z}_{\varvec{k}} }}} = \mathop \sum \limits_{{i = 0}}^{{2N}} W_{c}^{{\left( i \right)}} \left\{ \hat{\varvec{Z}}_{\varvec{k}}^{\left({\varvec{i}} \right) - } - \hat{\varvec{z}}_{\varvec{k}}^{ - } \right\}\left\{ \hat{\varvec{Z}}_{\varvec{k}}^{\left({\varvec{i}} \right) - } - \hat{\varvec{z}}_{\varvec{k}}^{ - } \right\}^{T} +\; {\varvec {R}} \\ &{\varvec{P}}_{{\varvec{x}}_{\varvec{k}} {\varvec{z}}_{\varvec{k}}} = \mathop \sum \limits_{{i = 0}}^{{2N}} W_{c}^{{\left( i \right)}} \left\{ \hat{\varvec{X}}_{\varvec{k}}^{\left({\varvec{i}} \right) - } - \hat{\varvec{x}}_{\varvec{k}}^{ - } \right\}\left\{ \hat{\varvec{Z}}_{\varvec{k}}^{ - } - \hat{\varvec{z}}_{\varvec{k}}^{ - } \right\}^{T} \\ &{{\varvec {K}}}_{k} = {{\varvec {P}}_{{\varvec{x}_{\varvec{k}} \varvec{z}_{\varvec{k}} }}} {{\varvec {P}}_{{\varvec{z}_{\varvec{k}} }}^{{ - 1}}} \\& \hat{\varvec{x}}_{\varvec{k}} = \hat{\varvec{x}}_{\varvec{k}}^{ - } + {{\varvec{K}}_{\varvec{k}}} \left( { {{\varvec {z}}_{\varvec{k}}} - \hat{\varvec{z}}_{\varvec{k}}^{ - } } \right) \\ &{\varvec {P}}_{\varvec{k}} = {\varvec{P}}_{\varvec{k}}^{ - } - {\varvec{K}}_{\varvec{k}} {\varvec {P}}_{{\varvec{z}_{\varvec{k}} }} {\varvec {K}}_{\varvec{k}}^{\varvec{T}} \\ & \end{aligned}$$
(12)

where \({\hat{\varvec{Z}}}_{\varvec{k}}^{{\left( {\varvec{i}} \right) - }}\) is the i-th a-priori measurement vector corresponding to the i-th a-priori propagated sigma-point \({\hat{\varvec{X}}}_{\varvec{k}}^{{\left( {\varvec{i}} \right) - }}\), and \({\varvec{P}}_{{\varvec{z}_{\varvec{k}} }}\) and \({\varvec{P}}_{{{\varvec{x}}_{\varvec{k}} {\varvec{z}}_{\varvec{k}} }}\) are the measurement covariance matrix and the cross-covariance matrix, respectively. The above version of the UKF is exploited in this paper. However, for completeness, it is worth noting that in the general case of non-additive process and measurement noise, the UKF entails an augmented state vector \({\varvec{x}}_{\varvec{k}}^{\varvec{a}}\) and covariance matrix \({\varvec{P}}_{\varvec{k}}^{\varvec{a}}\), defined as:

$$\begin{aligned} &{\varvec{x}_{\varvec{k}}^{\varvec{a}}} = \left[ {\begin{array}{*{20}c} {\varvec{x}_{\varvec{k}} } \\ {\varvec{w}_{\varvec{k}} } \\ {\varvec{v}_{\varvec{k}} } \\ \end{array} } \right] \\ &{\varvec{P}_{\varvec{k}}^{\varvec{a}}} = \left[ {\begin{array}{*{20}c} {\varvec{P}_{\varvec{k}} } & {\mathbf {0} }& {\mathbf {0}} \\ {\mathbf {0}} & {\varvec {Q}} & {\mathbf {0}} \\ {\mathbf {0}} & {\mathbf {0}} & {\mathbf {R}} \\ \end{array} } \right] \\ \end{aligned}$$
(13)

The corresponding state update and measurement update equations are reported in [44].

3 Design of the estimator

The proposed estimator is based on an innovative combination of a standard kinematic filter and a novel dynamic filter. The following subsections describe in detail: (1) the kinematic filter; (2) the dynamic filter; (3) the cross-combined method to merge kinematic and dynamic filters.

3.1 Kinematic filter

The kinematic filter only exploits kinematic quantities related to vehicle motion, so that no tire model is needed to estimate the lateral velocity, hence the sideslip angle. By simply manipulating the expressions of longitudinal and lateral acceleration as functions of longitudinal velocity, lateral velocity, and yaw rate, and by choosing the state as \({\varvec{x}} = \left[ {v_{x} \quad v_{y} } \right]^{T}\), the ideal (noise-free) process is described by [7]:

$$\left[ {\begin{array}{*{20}c} {\dot{v}_{\mathbf{x}} } \\ {\dot{v}_{y} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & r \\ { - r} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{\mathbf{x}} } \\ {v_{y} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{\mathbf{x}} } \\ {a_{y} } \\ \end{array} } \right]$$
(14)

Regarding the description of the noise, the insightful yet simple approach described in [28] was chosen since it allows to include directly (in \({\varvec{Q}}\)) the measurement noise covariances of yaw rate, lateral and longitudinal acceleration. As a result, the process is described by:

$$\left[ {\begin{array}{*{20}c} {\dot{v}_{x} } \\ {\dot{v}_{y} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & r \\ { - r} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{x} } \\ {v_{y} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{x} } \\ {a_{y} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} - v_{y} &- 1 &0 \\ v_{x} &0& - 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {w_{r} } \\ {w_{{a_{x} }} } \\ {w_{{a_{y} }} } \\ \end{array} } \right]$$
(15)

which uses the measurement of yaw rate directly in the dynamic matrix, and the measurements of longitudinal and lateral accelerations as inputs. The actual measurement equation of the filter is straightforward:

$${\varvec {z}} = {\varvec{Hx} }= \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{x} } \\ {v_{y} } \\ \end{array} } \right]$$
(16)

Because both the process and the measurement equations are linear, the state can be estimated with the basic KF (2–3) using the matrices:

$$\begin{aligned} &{\varvec {A}} = \left[ {\begin{array}{*{20}c} 0 & r \\ { - r} & 0 \\ \end{array} } \right] \\ &{\varvec {B}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] \\& {\varvec {H}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right] \\& {\varvec {W}} = \left[ {\begin{array}{*{20}c} -v_{y} &-1 & 0 \\ v_{z} & 0 & -1 \\ \end{array} } \right] \\ \end{aligned}$$
(17)

The forward Euler method is applied to perform the calculation in discrete time. As already assessed in [8], kinematic approaches are unobservable when the yaw rate is close to zero. A simple reset logic is applied to correct lateral velocity estimation, by forcing \(v_{y}\) to zero when the magnitude of \(r\) is sufficiently small.

Finally, at each time step, the sideslip angle is calculated, by definition, as \(\beta = \arctan \left( {v_{y} /v_{x} } \right)\).

3.2 Dynamic filter

A dynamic filter is based on the equilibrium equations of the vehicle, which need a constitutive law (tire model) to explicitly express the tire forces as functions of relevant parameters. The subsequent paragraphs describe respectively: i) vehicle model and tire model; ii) the UKF implementation of the filter.

3.2.1 Vehicle model and tire model

A double-track vehicle model is adopted, as shown in Fig. 1. The lateral equilibrium equation and the yaw balance equation for this model are:

$$\begin{aligned} ma_{y} = m\left( {\dot{v}_{y} + v_{x} r} \right) = F_{{y11}} \cos \left( \delta \right) + F_{{y12}} \cos \left( \delta \right) + F_{{y21}} + F_{{y22}} \\ J_{z} \dot{r} = F_{{y11}} \cos \left( \delta \right)a + F_{{y11}} \sin \left( \delta \right)\frac{{t_{{w1}} }}{2} + F_{{y12}} \cos \left( \delta \right)a - F_{{y12}} \sin \left( \delta \right)\frac{{t_{{w1}} }}{2} - F_{{y21}} b - F_{{y22}} b \\ \end{aligned}$$
(18)
Fig. 1
figure 1

Double track vehicle model (adapted from [2])

Full size image

Note that the steering angles of the front left and front right wheels are assumed to be the same (\(\delta\)) and that because longitudinal interactions typically have small effects, these are neglected in the lateral dynamics equations. On the other hand, the proposed double-track schematization allows to consider effects such as individual wheel slip angles and lateral load transfers. These effects help grasping a fairly accurate vehicle behavior, benefiting the estimator accuracy, unlike the single-track vehicle model adopted in many other estimators.

The lateral forces are expressed by a nonlinear tire model, considering key aspects of tire behavior such as nonlinearity, saturation, and dependency on the vertical load. In particular, the version of the Dugoff tire model presented in [45] is chosen, as it presents a very similar behavior to the well-known—yet more complex—Magic Formula. For a single wheel, the tire lateral force can be expressed as:

$$F_{y} = C_{\alpha } (\tan {\alpha}) p\left( \lambda \right)G_{\alpha }$$
(19)

where \(p\left( \lambda \right)\) is a nonlinear function defined as:

$$\begin{aligned} p\left( \lambda \right) = \left\{ {\begin{array}{*{20}l} \left( {2 - \lambda } \right)\lambda & \lambda < 1 \\ 1 & \lambda \ge 1 \\ \end{array} } \right. \\ {\text{with}}\;\lambda = \frac{{\mu _{{max}} F_{z} }}{{2\left| {C_{\alpha } \tan \alpha } \right|}} \\ \end{aligned}$$
(20)

and \({G}_{\alpha }\) is a correction term, function of the wheel slip angle and the tire-road friction coefficient:

$$G_{\alpha } = \left( {\mu _{{max}} - 1.6} \right)\tan \alpha + 1.155$$
(21)

However, with this formulation of \(G_{\alpha }\) [45], same values of \(\alpha\) but with opposite signs would not result in the same magnitude of lateral force (note that this formulation does not account for camber). To correct that, in this paper Eq. (21) is modified as follows:

$$G_{\alpha } = \left( {\mu _{{max}} - 1.6} \right)|\tan \alpha | + 1.155$$
(22)

which ensures a symmetrical behavior for positive and negative values of \(\alpha .\)

The selected tire model also requires the vertical load on each tire:

$$\begin{aligned} F_{{z_{{11}} }} = \frac{{mgb}}{{2l}} - \frac{{ma_{x} h}}{{2l}} - mB_{1} a_{y} + \frac{1}{4}\rho v_{x}^{2} C_{{z_{1} }} S_{a} \\ F_{{z_{{12}} }} = \frac{{mgb}}{{2l}} - \frac{{ma_{x} h}}{{2l}} + mB_{1} a_{y} + \frac{1}{4}\rho v_{x}^{2} C_{{z_{1} }} S_{a} \\ F_{{z_{{21}} }} = \frac{{mga}}{{2l}} + \frac{{ma_{x} h}}{{2l}} - mB_{2} a_{y} + \frac{1}{4}\rho v_{x}^{2} C_{{z_{2} }} S_{a} \\ F_{{z_{{22}} }} = \frac{{mga}}{{2l}} + \frac{{ma_{x} h}}{{2l}} + mB_{2} a_{y} + \frac{1}{4}\rho v_{x}^{2} C_{{z_{2} }} S_{a} \\ \end{aligned}$$
(23)

Each expression in Eq. (23) includes, in order: static load contribution; longitudinal load transfer contribution; lateral load transfer contribution; downforce contribution. For the lateral load transfer, according to [46], it is:

$$\begin{aligned} B_{1} = \frac{1}{{t_{{w1}} }}\left( {\frac{b}{l}d_{1} + \frac{{K_{{r1}} }}{{K_{{r1}} + K_{{r2}} }}\left( {h - \left( {d_{1} + \frac{{\left( {d_{2} - d_{1} } \right)a}}{l}} \right)} \right)} \right) \\ B_{2} = \frac{1}{{t_{{w2}} }}\left( {\frac{a}{l}d_{2} + \frac{{K_{{r2}} }}{{K_{{r1}} + K_{{r2}} }}\left( {h - \left( {d_{1} + \frac{{\left( {d_{2} - d_{1} } \right)a}}{l}} \right)} \right)} \right) \\ \end{aligned}$$
(24)

where \(K_{{r1}}\) and \(K_{{r2}}\) are the roll stiffness values of, respectively, the front and rear axle, and \(d_{1}\) and \(d_{2}\) are the heights of the roll centers of, respectively, the front and rear axle.

Finally, the congruence equations [2] provide the relationship between kinematic quantities and slip angles:

$$\begin{aligned} &\alpha _{{11}} = \delta - \arctan \left( {\frac{{v_{y} + ra}}{{v_{x} - rt_{{{\text{w}}1}} /2}}} \right) \\ &\alpha _{{12}} = \delta - \arctan \left( {\frac{{v_{y} + ra}}{{v_{x} + rt_{{{\text{w}}1}} /2}}} \right) \\ &\alpha _{{21}} = - \arctan \left( {\frac{{v_{y} - rb}}{{v_{x} - rt_{{{\text{w}}2}} /2}}} \right) \\ &\alpha _{{22}} = - \arctan \left( {\frac{{v_{y} - rb}}{{v_{x} + rt_{{{\text{w}}2}} /2}}} \right) \\ \end{aligned}$$
(25)

From the above equations, it is clear that the vehicle longitudinal velocity is required. That is estimated based on measurements including wheel speed sensors and accelerometers, as discussed in Sect. 4.

3.2.2 UKF filter implementation

Based on the vehicle model in Eq. (18), the state vector is chosen as \({\varvec{x}} = \left[ {v_{y} \quad r} \right]^{T}\), so \(N = 2\). The input vector is \({\varvec{u}} = \left[ \delta \right]\) and the measurement vector is \({\varvec{z}} = \left[ {r \quad a_{y} } \right]^{T}\) (both variables can be easily measured with standard sensors). By discretizing Eq. (18) with the forward Euler method, the system dynamics is expressed as:

$$\begin{aligned} v_{{y_{k + 1}}} =\, & v_{{y_k}} + \left[ {\frac{{\left( {F_{{y11_k}} + F_{{y12_k}} } \right)\cos \left( {\delta _{k} } \right) + F_{{y21_k}} + F_{{y22_k}} }}{m} - v_{{x_k}} r_{k} } \right]\Delta t \\ r_{{k + 1}} =\, & r_{k} + \left[ {\left( {F_{{y11_k}} + F_{{y12_k}} } \right)\cos \left( {\delta _{k} } \right)a + \left( {F_{{y11_k}} - F_{{y12_k}} } \right)\sin \left( {\delta _{k} } \right)\frac{{t_{{w1}} }}{2} - \left( {F_{{y21_k}} + F_{{y22_k}} } \right)b} \right]\frac{{\Delta t}}{{J_{z} }} \\ \end{aligned}$$
(26)

together with Eqs. (19–25). Regarding the relationships between \({\varvec {z}}\) and \({\varvec {x}}\), \(r\) is straightforward because it appears directly both in \({\varvec {z}}\) and \({\varvec {x}}\), while \(a_{y}\) can be related to the vehicle state at each time step through:

$$a_{{y_{k} }} = \frac{1}{m}\left[ {F_{{y_{{21_{k} }} }} + F_{{y_{{22_{k} }} }} + \left( {F_{{y_{{11_{k} }} }} + F_{{y_{{12_{k} }} }} } \right)\cos \left( {\delta _{k} } \right)} \right]$$
(27)

together with Eqs. (19–25). The matrices \({\varvec{Q}}\) and \({\varvec{R}}\) are:

$${\varvec {Q}} = \left[ {\begin{array}{*{20}c} {v_{y,s}^{2} } & 0 \\ 0 & {r_{s}^{2} } \end{array} } \right]$$
(28)
$${\varvec {R}} = \left[ {\begin{array}{*{20}c} {r_{m,s}^{2} } & 0 \\ 0 & {a_{y,m,s}^{2} } \end{array} } \right]$$
(29)

where \(v_{{y,s}}\) is the standard deviation of the process noise on \(v_{y}\), \(r_{s}\) is the standard deviation of the process noise on \(r\), \(r_{{m,s}}\) is the standard deviation of the measurement noise on \(r\), and \(a_{{y,m,s}}\) is the standard deviation of the measurement noise on \(a_{y}\).

Based on Eq. (8), the \(2N + 1 = 5\) sigma-points are:

$$\begin{aligned} {\varvec{ X}}_{{\mathbf{k - 1}}}^{{\mathbf{\left( 0 \right)}}} &= \hat{\varvec{x}}_{{\mathbf{k - 1}}} \\ {\varvec{X}}_{{\mathbf{k - 1}}}^{{\mathbf{\left( 1 \right)}}}& = \hat{\varvec{x}}_{{\mathbf{k - 1}}} + \left( {\sqrt {\left( {N + \psi } \right) {\varvec{P}_{{\mathbf{k - 1}}}} } } \right)_{1} \\ {\varvec{X}}_{{\mathbf{k - 1}}}^{{\mathbf{\left( 2 \right)}}} &= \hat{\varvec{x}}_{{\mathbf{k - 1}}} + \left( {\sqrt {\left( {N + \psi } \right) {\varvec{P}}_{{\mathbf{k - 1}}} }} \right)_{2} \\ {\varvec{ X}}_{{\mathbf{k - 1}}}^{{\mathbf{\left( 3 \right)}}} &= \hat{\varvec{x}}_{{\mathbf{k - 1}}} - \left( {\sqrt {\left( {N + \psi } \right) {\varvec{P}}_{{\mathbf{k - 1}}} } } \right)_{3} \\ {\varvec {X}}_{{\mathbf{k - 1}}}^{{\mathbf{\left( 4 \right)}}} &= \hat{\varvec{x}}_{{\mathbf{k - 1}}} - \left( {\sqrt {\left( {N + \psi } \right) {\varvec{P}}_{{\mathbf{k - 1}}} } } \right)_{4} \\ \end{aligned}$$
(30)

where the square root of a matrix can be calculated with the Cholesky factorization. The estimated state vector at each time step can then be obtained using Eqs. (9–12), noting that for each sigma-point Eq. (9) is Eq. (26), while Eq. (27) is used in the first of Eq. (12). Finally, at each time step, again \(\beta = \arctan \left( {v_{y} /v_{x} } \right)\).

3.3 Cross-combination

The described kinematic filter and dynamic filter run at the same time. The final estimate of the sideslip angle is calculated as a weighted average of the sideslip angle obtained through the two filters according to the following procedure (Fig. 2): (1) the measured value of ay is stored in a 0.1 s buffer; (2) a steady-state index is calculated, mainly depending on the Root Mean Square (RMS) of the stored samples of \(a_{y}\); (3) the steady-state index is used to compute a weight for the kinematic contribution, \(w_{{kin}}\), and a weight for the dynamic contribution, \(w_{{dyn}}\), with \(w_{{kin}} + w_{{dyn}} = 1\). The rationale is that, as suggested in [29], kinematic and dynamic models are better suited for, respectively, transient and steady-state conditions.

Fig. 2
figure 2

(top) Schematic of the methodology used to calculate the weights of the kinematic and the dynamic filter; (bottom) Detail of the membership functions

Full size image

For \(\left| {a_{y} } \right| \ge 1\), the root mean square (RMS) value of the lateral acceleration is computed over the 0.1 s buffer (e.g., 10 samples for a frequency of 100 Hz). A membership function is used to calculate the value of the steady-state index: if the computed RMS value is lower than 0.4 m/s2, meaning that \(a_{y}\) does not vary significantly, the steady-state index is set equal to 1; between 0.4 m/s2 and 0.6 m/s2 the membership function produces a linearly variable output from 1 to 0; for values larger than 0.6 m/s2 the maneuver is assumed to be in transient conditions, thus the steady-state index is set to 0. Instead, if \(a_{y}\) is within ± 1 m/s2, the steady-state index is set to 1, to prevent possible fluctuations of the sideslip angle estimation in nearly straight-line conditions due to the kinematic filter. \(w_{{dyn}}\) is 1 when the steady-state index is 1, while it varies linearly from 1 to 0.7 corresponding to values of the steady-state index from 1 to 0.

This paper also proposes, for the first time, to cross-combine the variables in common between the output of one filter and the input of the other. Precisely the variables in common are \(r\) and \(v_{x}\), in that:

  • the kinematic filter needs \(r\) as input and produces \(v_{x}\) as output;

  • the dynamic filter needs \(v_{x}\) as input and produces \(r\) as output.

Normally, for the kinematic filter, \(r\) is taken directly from a sensor, and for the dynamic filter, \(v_{x}\) is calculated as a function of the measured wheel speeds. While both values are affected by sensor noise, the values for the same quantities obtained as output of each filter are expected to be more accurate. The kinematic filter should produce a better estimation of \(v_{x}\) than the value calculated through wheel speed sensors, and the dynamic filter should produce a better estimation of \(r\) than the measured value obtained through the sensor – note that unmodeled effects, such as pitch and roll motion, do affect the accuracy of the yaw rate measurement. So, these values of \(v_{x}\) and \(r\) can be used as inputs of the kinematic and dynamic filter, respectively. This new idea, denoted as cross-combination and shown in Fig. 3, has the potential to improve the accuracy of the estimation of \(v_{y}\) and thus of the sideslip angle.

Fig. 3
figure 3

Schematic of the proposed filtering approach with cross-combination

Full size image

4 Results

The proposed cross-combined filter was tested on a large set of data obtained through a performance-oriented rear-wheel-drive car, mounting front tires 30/68 (tread band width in cm/external tire diameter in cm) on an R18 (radius in inches) rim, and rear tires 31/71 mounted on an R18 rim. The vehicle (Fig. 4) was equipped with:

  • an Inertial Measurement Unit (IMU) OXTS 3000 [48], providing longitudinal acceleration, lateral acceleration, yaw rate, with the following main specifications: accelerometer, bias stability 2 µg, Servo technology, range 10 g; gyroscope, bias stability 2°/h, MEMS technology, range 100°/s;

  • four wheel speed sensors Bosch HA-M [49] with the following main specifications: max frequency 4.2 kHz, accuracy repeatability of the falling edge of tooth < 4%;

  • a steering angle sensor Bosch LWS [50] with the following main specifications: range \(\pm\) 780°, absolute physical resolution 0.1°;

  • a Correvit S-Motion Type 2055A sensor [51], providing vehicle longitudinal velocity and sideslip angle, with the following main specifications: range 400 km/h, linear velocity measurement accuracy <|0.2%| (%FSO—Full Span Output), angle resolution < 0.01°.

The main vehicle parameters are reported in Table 1.

Fig. 4
figure 4

Test vehicle

Full size image
Table 1 Vehicle parameters
Full size table

Starting from the wheel speed sensor data, two options were considered to calculate the longitudinal vehicle velocity. A simple and straightforward option was to calculate the average speed of the front wheels, because for a rear-wheel-drive car the front wheels undergo lower slip values than the rear wheels. A more sophisticated solution was actually implemented. Denoting with \(v_{{M,ij}}\) the measured speed at wheel ij, estimates of the vehicle longitudinal velocity, \(\hat{v}_{{x,ij}}\), can be obtained from each wheel based on rigid body kinematics [47] as follows:

$$\begin{aligned} \hat{v}_{{x,11}} &= v_{{M,11}} \cos \delta + \frac{{rt_{{w1}} }}{2} \\ \hat{v}_{{x,12}} &= v_{{M,12}} \cos \delta - \frac{{rt_{{w1}} }}{2} \\ \hat{v}_{{x,21}} &= v_{{M,21}} + \frac{{rt_{{w2}} }}{2} \\ \hat{v}_{{x,22}} &= v_{{M,22}} - \frac{{rt_{{w2}} }}{2} \\ \end{aligned}$$
(31)

Compared to the calculation of the average of \(\hat{v}_{{x,ij}}\), this allows to depurate: (1) the yaw rate effect due to the wheels being located with a lateral offset with respect to the vehicle longitudinal axis; (2) the steering angle effect, as the measured wheel speed is aligned with the wheel and not necessarily the vehicle longitudinal axis. Then, the following logic is implemented to identify, among the four wheels, the one with the lowest slip, based on the measurement of \(a_{x}\):

  • if \(a_{x} > 0.5\) m/s2, i.e. the vehicle accelerates, wheel speeds are larger than the longitudinal vehicle speed so the lowest value is the closest to the actual vehicle speed: the vehicle longitudinal speed is estimated as \(min\left( {\hat{v}_{{x,11}} ,\hat{v}_{{x,12}} ,\hat{v}_{{x,21}} ,\hat{v}_{{x,22}} } \right)\)

  • if \(a_{x} < - 0.5\) m/s2, i.e. the vehicle decelerates, wheel speeds are smaller than the longitudinal vehicle speed so the largest value is the closest to the actual vehicle speed: the vehicle longitudinal speed is estimated as \(max\left( {\hat{v}_{{x,11}} ,\hat{v}_{{x,12}} ,\hat{v}_{{x,21}} ,\hat{v}_{{x,22}} } \right)\)

  • for low values of acceleration, i.e. if \(\left| {a_{x} } \right| \le 0.5\) m/s2, the vehicle longitudinal speed is estimated through a weighted average of \(\hat{v}_{{x,ij}}\)., with weights calculated according to [9].

Thanks to the availability of the sideslip angle measurement, the root mean square error (RMSE) method was selected as the performance index for assessing the quality of the estimation:

$$\beta _{e} = \sqrt {\frac{1}{n}\mathop \sum \limits_{{k = 1}}^{n} \left( {\hat{\beta }_{k} - \beta _{k} } \right)^{2} }$$
(32)

where \(n\) is the number of time samples. The proposed filtering technique was also compared to a traditional technique using a linear dynamic model, for which equations are reported in the Appendix. In the following figures, the two techniques are referred to as, respectively, KF (Kalman filter, linear dynamic) and UKF-CC (Cross-combined kinematic and UKF dynamic).

Figures 5 and 6 depict the measured and estimated sideslip angle along four race tracks. Each figure corresponds to a single lap, which is representative of the corresponding track since each filter behaved consistently along all laps. These experimental tests include a variety of testing conditions: multiple runs were carried out, with the same vehicle, tires, and equipment, in European and Asian race tracks, in different seasons of the year, on dry tarmac. For all of the tracks, the KF is able to follow the general trend but with significant discrepancies all round, up to around 5 deg. Instead, the UKF + CC provides a much more reliable and smooth tracking. In terms of RMSE, the KF is normally above 1 deg, while the UKF + CC settles on an average value of 0.53 deg, with an improvement of around 50% with respect to the KF (Table 2).

Fig. 5
figure 5

Measured and estimated sideslip angle for one lap of: (left) Track 1; (right) Track 2

Full size image
Fig. 6
figure 6

Measured and estimated sideslip angle for one lap of: (left) Track 3; (right) Track 4

Full size image
Table 2 Performance comparison of a traditional filter (linear dynamic) and the proposed filter
Full size table

Figure 7 compares different methods to estimate \({v}_{x}\), against the measured value. While all of the methods perform fairly well—because wheel speeds are rather informative measurements anyway—important remarks can be made. For the method using the average speed of the front wheels, the rationale was to pick the wheels with lower slips for a rear-wheel-drive car. However, that is no longer ideal in braking scenarios, when the front wheels undergo significant slips, even more than for the rear wheels. This is evident in Fig. 7 just before 296 s. On the other hand, the method using all of the wheel speeds and \({a}_{x}\) provides a more reliable result, though sometimes affected by discontinuities due to the rule-based nature of the method. The \({v}_{x}\) output of the kinematic filter, instead, is the smoothest signal and is the closest to the measured profile. This further supports the idea of the cross-combination, because a better \({v}_{x}\) is given as input to the dynamic filter, contributing to the quality of the estimation of the sideslip angle.

Fig. 7
figure 7

Comparison of longitudinal vehicle speed estimation methods, Track 4: measured speed through optical sensor (blue), average of the front wheel speeds (red), technique inspired to [9] explained at the beginning of Sect. 4 (yellow), kinematic filter used in the proposed method (purple). Left: entire lap; Right: detail

Full size image

5 Conclusion

This paper presented a novel approach for the estimation of vehicle sideslip angle. The analyses presented in this paper lead to the following main conclusions:

  • the kinematic and dynamic models for the estimation of sideslip angle can be cross-combined, by feeding part of the output of each filter as input to the other filter;

  • the cross-combination allows to further improve the estimation of the vehicle longitudinal velocity compared to current state-of-the-art techniques, in turn benefiting the precision of the sideslip angle estimation;

  • the modified Dugoff tire model is a simple yet effective constitutive model and produces the same lateral force—slip angle behavior regardless of the sign of the slip angle;

  • the proposed cross-combined kinematic and UKF dynamic filter allows to estimate the vehicle sideslip angle with an average RMSE of around 0.5 deg on experimental data.

Future developments will deal with: (1) tire longitudinal dynamics and combined interactions; (2) effects of roll and bank angles; (3) effects of tire temperature; (4) the potential investigation of methodologies for coping with variable road friction conditions; (5) further experimental tests with possible real-time implementation of the filter.