Guaranteed lower bounds on eigenvalues of elliptic operators with a hybrid high-order method

Abstract

This paper introduces a novel hybrid high-order (HHO) method to approximate the eigenvalues of a symmetric compact differential operator. The HHO method combines two gradient reconstruction operators by means of a parameter $0<\alpha <~1$ and introduces a novel cell-based stabilization operator weighted by a parameter $0<\beta <\infty$. Sufficient conditions on the parameters $\alpha$ and $\beta$ are identified leading to a guaranteed lower bound property for the discrete eigenvalues. Moreover optimal convergence rates are established. Numerical studies for the Dirichlet eigenvalue problem of the Laplacian provide evidence for the superiority of the new lower eigenvalue bounds compared to previously available bounds.

1 Introduction

The eigenvalue problem for symmetric compact differential operators is a fundamental task in the numerical analysis with a well-understood a priori error analysis for conforming finite element methods (FEM) leading to optimal asymptotic convergence rates [4, 5]. The Rayleigh–Ritz min–max principle shows that the discrete FEM eigenvalues are also guaranteed upper bounds of the exact eigenvalues, even in the pre-asymptotic range of coarse triangulations. In practice, guaranteed lower bounds (GLBs) can be even more important in a safety analysis in computational mechanics or for the detection of spectral gaps. The computation of lower eigenvalue bounds has been achieved based on the solution of nonconforming finite element schemes followed by a simple post-processing in [15, 16]. In particular, letting $\kappa ^2:={{\pi ^{-2}}+({2n(n+1)(n+2)})^{-1}}$ in nD, and if $\lambda _{CR }(j)$ is the j-th discrete eigenvalue computed with the Crouzeix–Raviart FEM, [16] proves (without extra conditions; the linear independency condition in [15, 16] can be neglected [19, 27]) that

$$\begin{aligned} GLBCR (j):=\frac{\lambda _{CR }(j)}{1+\kappa ^2h_{\max }^2\lambda _{CR }(j)}\le \lambda (j), \end{aligned}$$

(1.1)

thereby delivering a GLB on the j-th continuous Dirichlet eigenvalue $\lambda (j)$ for the Laplacian. Several other contributions [10, 11, 27,28,29, 34, 37, 38] derived GLBs using the maximal mesh-size $h_{\max }$ as a global parameter as in (1.1). This results in a possible underestimation for locally refined triangulations.

This motivated the design of novel schemes for the direct computation of GLBs without a global post-processing. The first example can be found in [20] for a hybridizable discontinuous Galerkin (HDG) method with Lehrenfeld–Schöberl stabilization, also studied under the label weak Galerkin scheme. The scheme proposed in [20] requires the fine tuning of skeletal-based stabilization terms. The main contribution of the present work is to introduce a new scheme which leads to GLBs on the eigenvalues under a simplified tuning of the stabilization terms. To achieve our goal, we rely on the framework of hybrid high-order (HHO) methods. HHO methods have been introduced in [23, 24] for linear diffusion and locking-free linear elasticity and have been bridged to HDG and nonconforming virtual element methods (ncVEM) in [12]. Recall that in HHO methods the discrete unknowns are polynomials of degree $k\ge 0$ attached to the mesh faces and polynomials of degree $\ell \in \{k-1,k,k+1\}$, $\ell \ge 0$, attached to the mesh cells. In the present setting, we consider the degree $\ell =k+1$ for the cell unknowns. Moreover the two key ingredients in HHO methods are a local gradient reconstruction operator and a local stabilization operator. The HHO method devised herein introduces two novelties with respect to the literature. The first novelty is that the gradient reconstruction combines an operator mapping to piecewise Raviart–Thomas functions of degree k and an operator mapping to the piecewise gradient of piecewise polynomials of degree at most ${(k+1)}$. Although Raviart–Thomas reconstructions were considered previously in [1, 21], it is the first time that they are combined with another reconstruction. Note that the present analysis cannot employ the single Raviart–Thomas reconstruction. The second novelty is that the stabilization operator is not skeletal-based but cell-based.

The weak formulation of the continuous Laplace eigenvalue problem seeks $(\lambda ,u)\in {\mathbb {R}}^+\times H^1_0(\Omega )$ such that

$$\begin{aligned} a(u,v)= \lambda b(u,v)\quad \text { for all }v\in H^1_0(\Omega )\qquad \text { and }\qquad b(u,u)=1. \end{aligned}$$

(1.2)

The discrete eigenvalue problem seeks $(\lambda _h,u_h)\in {\mathbb {R}}^+\times V_h$ with

$$\begin{aligned} a_h(u_h,v_h)=\lambda _h b_h(u_h,v_h) \quad \text { for all }v_h\in V_h\qquad \text { and }\qquad b_h(u_h,u_h)=1. \end{aligned}$$

(1.3)

While the bilinear form $b_h$ represents the $L^2(\Omega )$ scalar product b, the gradient-like approximations in the bilinear form $a_h$ involve two reconstructions R and $G_{RT}$ of the discrete unknowns in $V_h:=P_{k+1}({\mathcal {T}})\times P_k({\mathcal {F}})$ with the space of piecewise polynomials of degree at most $(k+1)$ on each simplex in the triangulation $P_{k+1}({\mathcal {T}})$ and the space of piecewise polynomials of degree at most k on each face $P_k({\mathcal {F}})$. The precise definition of the linear maps $R:V_h\rightarrow L^2(\Omega ;{\mathbb {R}})$ and $G_{RT}: V_h\rightarrow L^2(\Omega ;{\mathbb {R}}^n)$ can be found below in Sect. 3.1. Given two positive parameters $0<\alpha <1$ and $0<\beta {<\infty }$, for any $u_h:=(u_{{\mathcal {T}}},u_{{\mathcal {F}}})\text { and }v_h:=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$, the energy scalar product reads

$$\begin{aligned} a_h(u_h,v_h):={}&(G_{RT}(u_h), G_{RT}(v_h))_{L^2(\Omega )}\nonumber \\&-\alpha \big ((1-\Pi _k)G_{RT}(u_h), (1-\Pi _k)G_{RT}(v_h)\big )_{L^2(\Omega )} \nonumber \\&+\beta (\nabla _{pw }(u_{{\mathcal {T}}}-R(u_h)),\nabla _{pw }(v_{{\mathcal {T}}}-R(v_h)))_{L^2(\Omega )}. \end{aligned}$$

(1.4)

Section 7.1.2 presents an algorithm for an effective parameter selection in the lowest-order case. The Raviart–Thomas reconstruction $G_{RT}$ of the gradient does not require a stabilization in the source problem [1, 21], but the second term on the right-hand side in (1.4) has a negative sign and another stabilization with the reconstruction R in $P_{k+1}({\mathcal {T}})$ is added. This paper investigates the a priori error analysis for discrete eigenvalues and eigenvectors and confirms optimal convergence rates. Moreover it shows that the following GLB property holds for the j-th discrete eigenvalue $\lambda _h(j)$ of (1.3) and the j-th eigenvalue $\lambda (j)$ of (1.2):

$$\begin{aligned} \sigma ^2\beta +\delta {^2}\min \{\lambda (j),\lambda _h(j)\}\le \alpha <1 \quad \text {implies}\quad \lambda _h(j)\le \lambda (j), \end{aligned}$$

(1.5)

with $\delta :=\kappa h_{\max }$ and $\sigma$, $\kappa$ related to the stability of $L^2$-projections onto piecewise polynomial spaces. (Notice that (1.5) means that each of the conditions (i) $\sigma ^2\beta +\delta ^2\lambda (j)\le \alpha <1$ (a priori) and (ii) $\sigma ^2\beta +\delta ^2\lambda _h(j)\le \alpha <1$ (a posteriori) implies the GLB property.) Numerical examples study the feasibility of the condition identified in the GLB (1.5) and the relation to (1.1) and the bounds in [20].

The remaining parts of this paper are organised as follows. After a short summary of the notation in Sect. 2, Sect. 3 introduces the new method (1.3) with all the necessary operators and the discrete bilinear forms $a_h$ and $b_h$. Theorem 4.1 in Sect. 4 establishes (1.5). Section 5 contains the a priori error analysis which hinges on the Babuška–Osborn theory [4] and is inspired by [9] for the eigenvalue approximation by means of the standard HHO method (which does not have the GLB property). Section 6 concentrates on an alternative formulation of the lowest-order version for comparison with the Crouzeix–Raviart method. The numerical experiments in the final Sect. 7 illustrate the advantage of the direct lower bounds delivered by the present HHO method in the case of non-convex domains where adaptive mesh-refinement is necessary for optimal convergence rates. These results also provide numerical evidence for the superiority of the new GLBs compared to the aforementioned methods.

2 Notation and preliminaries

2.1 Triangulations

Let ${\mathcal {T}}$ denote a shape-regular triangulation of a bounded polyhedral Lipschitz domain $\Omega \subset {\mathbb {R}}^n$ into closed n-simplices in the sense of Ciarlet [2, 6, 7, 26]. For any simplex $T\in {\mathcal {T}}$, let ${\mathcal {F}}(T)$ denote the set of its $(n+1)$ sides and let ${\mathcal {N}}(T)$ denote the set of its $(n+1)$ vertices. The intersection $T_1\cap T_2$ of two distinct, non-disjoint simplices $T_1$ and $T_2$ in ${\mathcal {T}}$ is the shared sub-simplex $conv \{{\mathcal {N}}(T_1)\cap {\mathcal {N}}(T_2)\}=\partial T_1\cap \partial T_2$ of their shared vertices. Furthermore, ${\mathcal {F}}:=\bigcup _{T\in {\mathcal {T}}}{\mathcal {F}}(T)$ (resp. ${\mathcal {F}}(\Omega )$ or ${\mathcal {F}}(\partial \Omega )$) denotes the set of all (resp. interior or boundary) sides. For any simplex or sub-simplex K, let $h_K:=diam (K)$ denote its diameter. The piecewise constant function $h_{{\mathcal {T}}}\in P_0({\mathcal {T}})$ takes the value $h_{{\mathcal {T}}}|_T=h_T$ on each simplex $T\in {\mathcal {T}}$ and $h_{\max }:=\max _{T\in {\mathcal {T}}}h_T$ denotes the maximal mesh-size. Throughout this paper, $\nu _{{\mathcal {T}}}$ is the piecewise constant function which denotes for each simplex $T\in {\mathcal {T}}$ the outer unit normal vector $\nu _{{\mathcal {T}}}|_T=\nu _{T}$.

2.2 Scalar products and differential operators

Standard notation applies to Lebesgue and Sobolev spaces, $H^1(T)$ abbreviates $H^1(int (T))$ for a compact T with interior $int (T)$. Throughout this paper, $(\bullet , \bullet )_{L^2(\omega )}$ abbreviates the $L^2$-scalar product associated with volumes $\omega \subseteq \Omega$, whereas $\langle \bullet , \bullet \rangle _{\partial \omega }$ denotes the duality brackets in $H^{1/2}(\partial \omega )\times H^{-1/2}(\partial \omega )$ that extend the scalar product in $L^2(\partial \omega )$ associated with the boundary $\partial \omega$. We also abbreviate

$$\begin{aligned} \langle \bullet , \bullet \rangle _{\partial {\mathcal {T}}}:=\sum _{T\in {\mathcal {T}}} \langle \bullet ,\bullet \rangle _{\partial T}. \end{aligned}$$

We consider the differential operators divergence ($div$), gradient ($\nabla$), and the Laplace-operator ($\Delta$), as well as their piecewise applications $div _{pw }$, $\nabla _{pw }$, and $\Delta _{pw }$. For instance, $\nabla _{pw } v$ abbreviates $(\nabla _{pw } v)|_T=\nabla (v|_T)$ for any $T\in {\mathcal {T}}$ and a piecewise function $v\in H^1({\mathcal {T}}):=\{v\in L^2(\Omega ): v|_T\in H^1(T)\text { for any }T\in {\mathcal {T}}\}$. The scalar products $a:H^1_0(\Omega )\times H^1_0(\Omega )\rightarrow {\mathbb {R}}$ and $b:L^2(\Omega )\times L^2(\Omega )\rightarrow {\mathbb {R}}$ read

$$\begin{aligned} a(u,v)&:=(\nabla u, \nabla v)_{L^2(\Omega )}\quad \!\!\text { for all } u,\,v\in H^1_0(\Omega ),\\ b(u,v)&:=(u,v)_{L^2(\Omega )}\quad \qquad \text {for all } u,\,v\in L^2(\Omega ), \end{aligned}$$

and induce the norms $\Vert \!\vert \bullet \Vert \!\vert ^2:=a(\bullet , \bullet )$ and $\Vert \bullet \Vert _{L^2(\Omega )}^2:=b(\bullet , \bullet )$. We also consider the piecewise bilinear form

$$\begin{aligned} a_{pw }(u,v)&:=(\nabla _{pw } u, \nabla _{pw } v)_{L^2(\Omega )}\quad \text { for all } u,\,v\in H^1({\mathcal {T}}), \end{aligned}$$

with induced semi-norm $\Vert \!\vert \bullet \Vert \!\vert _{pw } ^2:=a_{pw } (\bullet , \bullet )$. The same notation applies to norms of scalar- and vector-valued functions.

2.3 Discrete function spaces and $L^2$-projections

For any $M\in {\mathcal {T}}$ or $M\in {\mathcal {F}}$, $\ell \in {\mathbb {N}}_0$, $m\in {\mathbb {N}}$, let $P_\ell (M;{\mathbb {R}}^{m})$ denote the set of polynomials of total degree at most $\ell$ in each component regarded as functions in $L^\infty (M;{\mathbb {R}}^{m})$ and set

$$\begin{aligned} P_\ell ({\mathcal {T}};{\mathbb {R}}^{m})&:=\big \{q\in L^{\infty }(\Omega ;{\mathbb {R}}^{m}):\ \text {for all } T\in {\mathcal {T}}, \ q|_T \in P_\ell (T;{\mathbb {R}}^{m})\big \},\\ P_\ell ({\mathcal {F}};{\mathbb {R}}^{m})&:=\big \{ q\in L^{\infty }({\mathcal {F}};{\mathbb {R}}^{m}):\ \text {for all } F\in {\mathcal {F}}, \ q|_{F} \in P_\ell (F;{\mathbb {R}}^{m})\big \},\\ P_\ell ({\mathcal {F}}(\Omega );{\mathbb {R}}^{m})&:=\big \{ q\in P_\ell ({\mathcal {F}};{\mathbb {R}}^{m}):\ \text {for all } F\in {\mathcal {F}}(\partial \Omega ), \ q|_{F}=0\big \}, \end{aligned}$$

and we omit ${\mathbb {R}}^m$ whenever $m=1$. The piecewise Raviart–Thomas space is $RT_\ell ^pw ({\mathcal {T}}):=P_\ell ({\mathcal {T}})x+P_\ell ({\mathcal {T}};{\mathbb {R}}^n)$. The associated $L^2$-projections are denoted $\Pi _{\ell } : L^2(\Omega ) \rightarrow P_{\ell }({\mathcal {T}})$, $\Pi _{{\mathcal {F}},\ell }: L^2({\mathcal {F}})\rightarrow P_\ell ({\mathcal {F}})$, $\Pi _{{F},\ell } : L^2(F)\rightarrow P_\ell (F)$ for all $F\in {\mathcal {F}}$, and $\Pi _{RT,\ell }:L^2(\Omega ;{\mathbb {R}}^n)\rightarrow RT_\ell ^pw ({\mathcal {T}})$. These projections act componentwise, e.g., for all $f\in H^1(\Omega )$, $\Pi _\ell (f)\in P_\ell ({\mathcal {T}})$ and $\Pi _\ell (\nabla f)\in P_\ell ({\mathcal {T}};{\mathbb {R}}^n)$.

The following two properties of the $L^2$-projections are useful in the analysis below. These properties are classical (see, e.g., [7, Lemma 4.3.8], [2, Prop. 2.5.1], [22, §1.4]) and are stated without proof.

Lemma 2.1

(Commutation) $\Pi _\ell (\Pi _{RT,\ell }(f))=\Pi _\ell (f)=\Pi _{RT,\ell }(\Pi _\ell (f))$ holds for all $f\in L^2(\Omega ;{\mathbb {R}}^n)$.

Lemma 2.2

(Approximation) The following holds for all $m=1,\,\dots ,\,\ell +1$, all $T\in {\mathcal {T}}$, and all $\phi \in H^m(T)$,

$$\begin{aligned} \Vert \phi - \Pi _\ell (\phi )\Vert _{L^2(T)}+h_T^{1/2}\Vert \phi - \Pi _\ell (\phi )\Vert _{L^2(\partial T)}\le C_{apx } h_T^{m}\vert \phi \vert _{H^m(T)}, \end{aligned}$$

(2.1)

and for all $\phi \in H^m(T;{\mathbb {R}}^n)$,

$$\begin{aligned} \Vert \phi - \Pi _{RT,\ell }(\phi )\Vert _{L^2(T)}+h_T^{1/2}\Vert \phi - \Pi _{RT,\ell }(\phi )\Vert _{L^2(\partial T)}\le C_{apx } h_T^{m}\vert \phi \vert _{H^m(T)}. \end{aligned}$$

(2.2)

The constant $C_{apx }$ depends on the shape-regularity of ${\mathcal {T}}$ and on the polynomial degree $\ell$, but is independent of the cell diameter $h_T$.

The following refined stability estimates for $L^2$-projections play an important role in the devising of guaranteed lower bounds on the eigenvalues.

Theorem 2.3

(Refined stability estimates) There is $C_{st}\ge 1$ such that, for all $T\in {\mathcal {T}}$ and all $f\in H^1(T)$,

$$\begin{aligned} \Vert \nabla (1-\Pi _{\ell +1})(f)\Vert _{L^2(T)}\le C_{st}\Vert (1-\Pi _{\ell })(\nabla f)\Vert _{L^2(T)}. \end{aligned}$$

(2.3)

Moreover there is $\kappa >0$ such that for all $T\in {\mathcal {T}}$ and all $f\in H^1(T)$,

$$\begin{aligned} \Vert (1-\Pi _{\ell +1})(f)\Vert _{L^2(T)}\le \kappa h_T\Vert (1-\Pi _\ell )(\nabla f)\Vert _{L^2(T)}. \end{aligned}$$

(2.4)

The constants $C_{st}$ and $\kappa$ depend on the shape-regularity of ${\mathcal {T}}$ and on the polynomial degree $\ell$, but are independent of the cell diameter $h_T$.

Remark 2.4

(Constants $C_{st}$ and $\kappa$) The stability estimate (2.3) is established in [20] where it is shown that, for any $T\in {\mathcal {T}}$, the conditions

$$\begin{aligned} (H1) \Pi _{\ell +1}(1)=1 \quad and \quad (H2) P_\ell (T;{\mathbb {R}}^n)\cap \nabla H^1(T)\subset \nabla P_{\ell +1}(T) \end{aligned}$$

are equivalent to the existence of an $h_T$-independent constant $C_{st}(T)>0$ such that (2.3) holds on $T\in {\mathcal {T}}$, and one then sets $C_{st}:=\max \{C_{st}(T):T\in {\mathcal {T}}\}$. The estimate $C_{st}\ge 1$ readily follows from the trivial bound $\Vert \nabla (1-\Pi _{\ell +1})(f)\Vert _{L^2(T)}\ge \Vert (1-\Pi _{\ell })(\nabla f)\Vert _{L^2(T)}$ since $\nabla \Pi _{\ell +1}(f) \in P_{\ell }(T;{\mathbb {R}}^n)$. The Poincaré inequality $\Vert (1-\Pi _0)(f)\Vert _{L^2(T)} \le C_{P }h_T\Vert \nabla f\Vert _{L^2(T)}$ for all $f\in H^1(T)$ and (2.3) lead to (2.4) with $\kappa \le C_{P }C_{st}$. The Poincaré constant reads $C_{P }:=1/j_{11}$ for $n=2$ with the first root of the first Bessel function $j_{11}$ [30] and $C_{P }\le 1/\pi$ for $n\ge 3$ [3, 32]. For $\ell =0$, an upper bound on the constant $\kappa$ was first computed in [16] and improved in [15] for $n=2$. The appendix of [20] proves $\kappa ^2\le {\pi ^{-2}}+({2n(n+1)(n+2)})^{-1}$ for any space dimension n.

2.4 Vector and matrix notation

For $a,b\in {\mathbb {R}}^{m\times k}$, let $a\cdot b=a^\top b\in {\mathbb {R}}^{k\times k}$ and $a\otimes b=ab^\top \in {\mathbb {R}}^{m\times m}$. The notation $|\bullet |$ depends on the context and denotes the Euclidean length of a vector, the cardinality of a finite set, the n- or $(n-1)$-dimensional Lebesgue measure of a subset of ${\mathbb {R}}^n$. Furthermore $a \lesssim b$ abbreviates that there exists a generic constant C (independent of the mesh-size) with $a\le Cb$, whereas $a \approx b$ abbreviates $a\lesssim b\lesssim a$.

3 The modified HHO method

This section is devoted to the reconstruction and stability operators of the new method (1.3) and their properties. Moreover, the discrete bilinear forms are discussed and the abstract matrix eigenvalue problem is introduced.

3.1 Operators of interest

Set $V:=H^1_0(\Omega )$. Let $k\ge 0$ be the polynomial degree and set

$$\begin{aligned} V_h:=P_{k+1}({\mathcal {T}})\times P_k({\mathcal {F}}(\Omega )). \end{aligned}$$

(3.1)

The components of $v_h:=(v_{\mathcal {T}}, v_{\mathcal {F}})\in V_h$ are $v_{\mathcal {T}}:=(v_T)_{T\in {\mathcal {T}}}$, $v_{{\mathcal {F}}}:=(v_F)_{F\in {\mathcal {F}}}$. Note that $v_F\equiv 0$ whenever $F\in {\mathcal {F}}(\partial \Omega )$ by definition of $P_k({\mathcal {F}}(\Omega ))$. Let I denote the interpolation operator $I:V\rightarrow V_h$ such that $I(\phi )=(\Pi _{k+1}(\phi ), \Pi _{{\mathcal {F}},k}(\phi ))$ for all $\phi \in V$.

Define the reconstruction operator $R: \,V_h \rightarrow P_{k+1}({\mathcal {T}})$ such that for any $v_h:=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$, $R(v_h)\in P_{k+1}({\mathcal {T}})$ is the unique function with $\Pi _0 R(v_h)=\Pi _0 (v_{{\mathcal {T}}})$ and

$$\begin{aligned} (\nabla _{pw } R(v_h),\nabla _{pw } p)_{L^2(\Omega )}&= -(v_{{\mathcal {T}}},\Delta _{pw } p)_{L^2(\Omega )} \nonumber \\&\quad \,\,+\langle v_{{\mathcal {F}}}, \nabla _{pw } p\cdot \nu _{{\mathcal {T}}}\rangle _{\partial {\mathcal {T}}} \text { for all }p\in P_{k+1}({\mathcal {T}}). \end{aligned}$$

(3.2)

Let G denote the Galerkin projection onto $P_{k+1}({\mathcal {T}})$, i.e., for any $\phi \in H^1({\mathcal {T}})$, we have $G(\phi )\in P_{k+1}({\mathcal {T}})$ with $\Pi _0G(\phi )=\Pi _0(\phi )$ and $a_{pw }((1-G)(\phi ), p)=0\text { for all } p\in P_{k+1}({\mathcal {T}})$.

Lemma 3.1

[23, 24] $R\circ I=G$ holds in $V:=H^1_0(\Omega )$.

The Raviart–Thomas reconstruction $G_{RT}:V_h\rightarrow RT_k^{pw }({\mathcal {T}})$ defines a unique $G_{RT}(v_h)\in RT_k^{pw }({\mathcal {T}})$ for all $v_h:=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$ such that

$$\begin{aligned} (G_{RT}(v_h), q_{RT})_{L^2(\Omega )}&=- (v_{{\mathcal {T}}},div _{pw }q_{RT})_{L^2(\Omega )}\nonumber \\&\quad +\langle v_{{\mathcal {F}}}, q_{RT}\cdot \nu _{{\mathcal {T}}}\rangle _{\partial {\mathcal {T}}}\text { for all }q_{RT}\in RT_k^{pw }({\mathcal {T}}). \end{aligned}$$

(3.3)

The comparison of (3.2) with (3.3) proves that $\nabla _{pw }R(v_h)= \Pi _{\nabla P_{k+1}}G_{RT}(v_h)$ for all $v_h\in V_h$, where $\Pi _{\nabla P_{k+1}}$ denotes the $L^2$-projection onto ${\nabla _{pw }} P_{k+1}({\mathcal {T}})$ (composed of the gradients of piecewise polynomials of degree $(k+1)$). Since $\nabla _{pw } \circ G = \Pi _{\nabla P_{k+1}}\circ \nabla$, we have $(\nabla _{pw }\circ R)\circ I = \Pi _{\nabla P_{k+1}}\circ \nabla$ in $V:=H^1_0(\Omega )$.

Lemma 3.2

[1, 21] $G_{RT}\circ I=\Pi _{RT,k}\circ \nabla$ holds in $V:=H^1_0(\Omega )$.

The stabilization operator $S:V_h\rightarrow P_{k+1}({\mathcal {T}})$ is defined for any $v_h:=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$ by

$$\begin{aligned} S(v_h):=v_{{\mathcal {T}}}-R(v_h). \end{aligned}$$

(3.4)

Lemma 3.3

Given any $\phi \in V=H^1_0(\Omega )$ and any simplex $T\in {\mathcal {T}}$, the stability term fulfils

$$\begin{aligned} S(I\phi )&=\Pi _{k+1}(\phi )-G(\phi ), \end{aligned}$$

(3.5)

$$\begin{aligned} \Vert \nabla S(I\phi )\Vert _{L^2(T)}&\le \sigma \Vert (1-\Pi _k) (\nabla \phi ) \Vert _{L^2(T)}, \end{aligned}$$

(3.6)

$$\begin{aligned} \Vert \!\vert S(I\phi )\Vert \!\vert _{pw }&\le \sigma \Vert (1-\Pi _k) (\nabla \phi ) \Vert _{L^2(\Omega )} \end{aligned}$$

(3.7)

with $\sigma ^2:={C_{st}^2-1}$ and the constant $C_{st}$ from Theorem 2.3.

Proof

The definition (3.4) and Lemma 3.1 imply (3.5). Since $\nabla _{pw } (1-G)(\phi )$ is $L^2$-orthogonal to $\nabla _{pw } P_{k+1}({\mathcal {T}})$, the Pythagoras theorem proves for any $T\in {\mathcal {T}}$,

$$\begin{aligned} \Vert \nabla S(I\phi )\Vert _{L^2(T)}^2&=\Vert \nabla \Pi _{k+1}(\phi )- \nabla G(\phi )\Vert _{L^2(T)}^2 \\&=\Vert \nabla (1-\Pi _{k+1})(\phi )\Vert ^2_{L^2(T)} - \Vert \nabla (1- G)(\phi )\Vert _{L^2(T)}^2. \end{aligned}$$

The first term is estimated in (2.3) by $C_{st}^2\Vert \nabla \phi -\Pi _k(\nabla \phi )\Vert _{L^2(T)}^2$, whereas the best approximation property of $\Pi _k$ proves that

$$\begin{aligned} \Vert \nabla \phi -\Pi _k(\nabla \phi )\Vert _{L^2(T)}\le \Vert \nabla \phi -\nabla G(\phi )\Vert _{L^2(T)} = \Vert \nabla (1- G)(\phi )\Vert _{L^2(T)}. \end{aligned}$$

The combination finishes the proof of (3.6), and (3.7) follows by summation over $T\in {\mathcal {T}}$. $\square$

Remark 3.4

(Piecewise evaluation) For all $T\in {\mathcal {T}}$, the reconstructions $R(v_h)|_T$ and $G_{RT}(v_h)|_T$ and the stabilization $S(v_h)|_T$ soley depend on the local data $v_T=v_{{\mathcal {T}}}|_T$ and $v_F=v_{{\mathcal {F}}}|_F$ for all $F\in {\mathcal {F}}(T)$, so that all these quantities can be computed piecewise and in parallel.

3.2 Discrete bilinear forms

Given global constants $0<\alpha < 1$ and $0<\beta {<\infty }$, the reconstructions in (3.2)–(3.3), and the stabilization (3.4), the bilinear form $a_h: V_h\times V_h\rightarrow {\mathbb {R}}$ is defined in (1.4), and we define the $L^2$ scalar product $b_h: V_h\times V_h\rightarrow {\mathbb {R}}$ by $b_h(u_h,v_h):=(u_{{\mathcal {T}}},v_{{\mathcal {T}}})_{L^2(\Omega )}$ for all $u_h=(u_{{\mathcal {T}}},u_{{\mathcal {F}}})$ and $v_h=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$. The $L^2$-projection property of $\Pi _k$ and the definition of the piecewise bilinear form $a_{pw }$ imply that the bilinear form $a_h$ can be rewritten as follows for any $u_h,v_h\in V_h$,

$$\begin{aligned} a_h(u_h,v_h)&=(1-\alpha ) \big ((1-\Pi _k)G_{RT}(u_h), (1-\Pi _k)G_{RT}(v_h)\big )_{L^2(\Omega )} \nonumber \\&~\quad +(\Pi _kG_{RT}(u_h),\Pi _k G_{RT}(v_h))_{L^2(\Omega )}+\beta a_{pw }(S(u_h),S(v_h)). \end{aligned}$$

(3.8)

The vector space $V_h$ is equipped with the norms $\Vert \bullet \Vert _h$ [24, Eq. (28)] and $\Vert \bullet \Vert _{a,h}$, defined for any $v_h\in V_h$ by

$$\begin{aligned} \Vert v_h\Vert _h^2&:=\sum _{T\in {\mathcal {T}}}\Big ( \Vert \nabla v_T\Vert _{L^2(T)}^2 +\sum _{F\in {\mathcal {F}}(T)}h_F^{-1}\Vert v_F-v_T\Vert _{L^2(F)}^2\Big ), \\ \Vert v_h\Vert _{a,h}^2&:= a_h(v_h,v_h) \nonumber \\&=\Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}^2-\alpha \Vert (1-\Pi _k)G_{RT}(v_h)\Vert _{L^2(\Omega )}^2+\beta \Vert \!\vert S(v_h)\Vert \!\vert _{pw }^2 \nonumber \end{aligned}$$

(3.9)

$$\begin{aligned}&=(1-\alpha )\Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}^2+ \alpha \Vert \Pi _kG_{RT}(v_h)\Vert _{L^2(\Omega )}^2+\beta {\Vert \!\vert S(v_h)\Vert \!\vert _{pw }^2}. \end{aligned}$$

(3.10)

The definiteness of $\Vert \bullet \Vert _h$ is known and that of $\Vert \bullet \Vert _{a,h}$ follows from Lemma 3.5 below. This guarantees that $a_h(\bullet , \bullet )$ is a scalar product on $V_h\times V_h$ which induces a norm on $V_h$. Consequently the source problem associated with $a_h$ is well posed owing to the Lax–Milgram lemma.

Lemma 3.5

There exist constants $\underline{\gamma },\overline{\gamma }>0$, independent of the mesh-size, such that

$$\begin{aligned} \underline{\gamma }\Vert v_h\Vert _{h}^2\le a_h(v_h,v_h)\le \overline{\gamma }\Vert v_h\Vert _{h}^2\quad \text {for all }v_h\in V_h. \end{aligned}$$

Proof

The Pythagoras theorem and the best approximation property of $\Pi _{F,k}$ show for any $T\in {\mathcal {T}}$, $F\in {\mathcal {F}}(T)$, and $v_h=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$ with $v_{{\mathcal {T}}}|_T=v_T$ and $v_{{\mathcal {F}}}|_F=v_F$, that

$$\begin{aligned} \Vert v_T-v_F\Vert _{L^2(F)}^2&= \Vert (1-\Pi _{F,k}) (v_T)\Vert _{L^2(F)}^2 + \Vert \Pi _{F,k} (v_T)-v_F\Vert _{L^2(F)}^2\\&\le \Vert (1-\Pi _0) (v_T)\Vert _{L^2(F)}^2 + \Vert \Pi _{F,k}(v_T)-v_{{F}}\Vert _{L^2(F)}^2. \end{aligned}$$

The trace inequality from [8, 13] and [22, Eq. (1.42)] together with the Poincaré inequality and the shape-regularity of ${\mathcal {T}}$ lead to

$$\begin{aligned} \Vert (1-\Pi _0) (v_T)\Vert _{L^2(F)}^2&\le \frac{|F|}{|T|}\Vert (1-\Pi _0) (v_T)\Vert _{L^2(T)}\big (\Vert (1-\Pi _0) (v_T)\Vert _{L^2(T)} +2h_T/n \Vert \nabla v_T\Vert _{L^2(T)}\big ) \\&\le C_{P } \frac{h_T^2|F|}{|T|}(C_{P }+ 2/n)\Vert \nabla v_T\Vert _{L^2(T)}^2 \le C_2 h_F \Vert \nabla v_T\Vert _{L^2(T)}^2. \end{aligned}$$

It is shown in [1, 21] (see, e.g., Lemma 1 in [1]) that there is $C_1$ such that for any $T\in {\mathcal {T}}$,

$$\begin{aligned} \sum _{F\in {\mathcal {F}}(T)}h_F^{-1}\Vert \Pi _{F,k}(v_T)-v_F\Vert ^2_{L^2(T)} \le C_1 \Vert G_{RT}(v_h)\Vert ^2_{L^2(T)}. \end{aligned}$$

The combination of the preceding three displayed inequalities leads to an estimator of $h_F^{-1}\Vert v_T-v_{{F}}\Vert ^2_{L^2(F)}$. The sum over all $T\in {\mathcal {T}}$ and $F\in {\mathcal {F}}(T)$ reads

$$\begin{aligned} \sum _{T\in {\mathcal {T}}}\sum _{F\in {\mathcal {F}}(T)}h_F^{-1}\Vert v_T-v_F\Vert _{L^2(F)}^2 \le C_1\Vert G_{RT}(v_h)\Vert ^2_{L^2(\Omega )} + C_2(n+1)\Vert \!\vert v_{{\mathcal {T}}}\Vert \!\vert _{pw }^2. \end{aligned}$$

(3.11)

Since $\nabla _{pw }R= \Pi _{\nabla P_{k+1}}G_{RT}$, we infer $\Vert \!\vert R(v_h)\Vert \!\vert _{pw }= \Vert \Pi _{\nabla P_{k+1}}G_{RT}(v_h)\Vert _{L^2(\Omega )} \le \Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}$. This and the triangle inequality show that

$$\begin{aligned} \Vert \!\vert v_{{\mathcal {T}}}\Vert \!\vert _{pw }&\le \Vert \!\vert v_{{\mathcal {T}}}-R(v_h)\Vert \!\vert _{pw }+\Vert \!\vert R(v_h)\Vert \!\vert _{pw } \!=\! \Vert \!\vert S(v_h)\Vert \!\vert _{pw }+\Vert \Pi _{\nabla P_{k+1}}G_{RT}(v_h)\Vert _{L^2(\Omega )}\nonumber \\&\le \Vert \!\vert S(v_h)\Vert \!\vert _{pw }+\Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}. \end{aligned}$$

(3.12)

The combination of (3.11)–(3.12) and the last identity from (3.10) shows that

$$\begin{aligned} \Vert v_h\Vert _h^2&= \Vert \!\vert v_{{\mathcal {T}}}\Vert \!\vert _{pw }^2 +\sum _{T\in {\mathcal {T}}}\sum _{F\in {\mathcal {F}}(T)}h_F^{-1}\Vert v_T-v_F\Vert _{L^2(F)}^2\\&\le 2(1+C_2(n+1)) \Vert \!\vert S(v_h)\Vert \!\vert _{pw }^2+ (2+C_1+2C_2(n+1))\Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}^2 \\&\le \underline{\gamma }^{-1} \big ( (1-\alpha )\Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}^2+ \beta \Vert S(v_h)\Vert _{L^2(\Omega )}^2\big ) \le \underline{\gamma }^{-1} \Vert v_h\Vert _{a,h}^2, \end{aligned}$$

with the constant $\underline{\gamma }^{-1}:= \max \{2(1+C_2(n+1))/\beta , (2+C_1+2C_2(n+1))/(1-\alpha )\}$. On the other hand, for any $T\in {\mathcal {T}}$, (3.3) with $q_{RT}=G_{RT}(v_h)$, an integration by parts, and the Cauchy–Schwarz inequality lead to

$$\begin{aligned} \Vert G_{RT}(v_h)\Vert ^2_{L^2(T)}&= (\nabla v_{{\mathcal {T}}},G_{RT}(v_h))_{L^2(T)} +\langle v_{{\mathcal {F}}}-v_{{\mathcal {T}}}, G_{RT}(v_h)\cdot \nu _{{\mathcal {T}}}\rangle _{\partial T}\\&\le \Vert \nabla v_{{\mathcal {T}}}\Vert _{L^2(T)}\Vert G_{RT}(v_h)\Vert _{L^2(T)} \\&\quad +\sum _{F\in {\mathcal {F}}(T)} h_{F}^{1/2}\Vert G_{RT}(v_h)\Vert _{L^2(F)} h_{F}^{-1/2}\Vert v_F-v_T\Vert _{L^2(F)}. \end{aligned}$$

A combination of a trace and an inverse estimate for Raviart–Thomas functions shows that ${h_{T}^{1/2}\Vert G_{RT}(v_h) \Vert _{L^2(\partial T)}} \le C_3 \Vert G_{RT}(v_h)\Vert _{L^2(T)}$. Since $h_F\le h_T$ for any $F\in {\mathcal {F}}(T)$, the Cauchy–Schwarz inequality in ${\mathbb {R}}^{n+1}$ leads to

$$\begin{aligned} \Vert G_{RT}(v_h)\Vert ^2_{L^2(T)}&\le 2\Vert \nabla v_{{\mathcal {T}}}\Vert _{L^2(T)}^2+2C_3^2\sum _{F\in {\mathcal {F}}(T)} h_{F}^{-1}\Vert v_F-v_T\Vert _{L^2(F)}^2. \end{aligned}$$

The sum over all $T\in {\mathcal {T}}$ reads

$$\begin{aligned} \Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}^2&\le 2\Vert \!\vert v_{{\mathcal {T}}}\Vert \!\vert _{pw }^2 +2C_3^2 \sum _{T\in {\mathcal {T}}}\sum _{F\in {\mathcal {F}}(T)} h_F^{-1} \Vert v_F-v_T\Vert _{L^2(F)}^2 \\&\le {2\max \{1,C_3^2\}} \Vert v_h\Vert _h^2. \end{aligned}$$

The boundedness of the stability contribution follows from the triangle inequality, the estimate $\Vert \!\vert R(v_h)\Vert \!\vert _{pw }\le \Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}$ shown above and the last bound, leading to

$$\begin{aligned} \Vert \!\vert S(v_h)\Vert \!\vert _{pw } \le \Vert \!\vert v_{{\mathcal {T}}}\Vert \!\vert _{pw }+\Vert G_{RT}(v_h)\Vert _{L^2(\Omega )} \le \Big (1+\sqrt{2}\max \{1,C_3\} \Big ) \Vert v_h\Vert _h. \end{aligned}$$

The second identity in (3.10) shows that $\Vert v_h\Vert _{a,h}^2 \le \Vert G_{RT}(v_h)\Vert _{L^2(\Omega )}^2 + \beta \Vert \!\vert S(v_h)\Vert \!\vert _{pw }^2$. This concludes the proof with $\overline{\gamma }:= 2\beta +(1+2\beta )2\max \{1,C_3^2\}$. $\square$

3.3 Matrix eigenvalue problem

The algebraic realization of the eigenvalue problem (1.3) leads to a matrix eigenvalue problem with coefficient matrices and vector $(x_{{\mathcal {T}}},x_{{\mathcal {F}}})\in {\mathbb {R}}^{dim P_{k+1}({\mathcal {T}})+dim P_k({\mathcal {F}}(\Omega ))}$

$$\begin{aligned} \begin{pmatrix} A_{{\mathcal {T}}{\mathcal {T}}} &{}\quad A_{{\mathcal {T}}{\mathcal {F}}}\\ A_{{\mathcal {F}}{\mathcal {T}}} &{}\quad A_{{\mathcal {F}}{\mathcal {F}}} \end{pmatrix} \begin{pmatrix} x_{{\mathcal {T}}}\\ x_{{\mathcal {F}}} \end{pmatrix} =\lambda _h \begin{pmatrix} B_{{\mathcal {T}}{\mathcal {T}}} &{}\quad 0 \\ 0 &{}\quad 0 \end{pmatrix} \begin{pmatrix} x_{{\mathcal {T}}}\\ x_{{\mathcal {F}}} \end{pmatrix}\quad \text { and }\quad x_{{\mathcal {T}}}\cdot B_{{\mathcal {T}}{\mathcal {T}}}x_{{\mathcal {T}}}=1. \end{aligned}$$

(3.13)

The bilinear form $b_h$ solely depends on the volume components. The elimination of the face unknowns leads to the Schur complement

$$\begin{aligned} S_{{\mathcal {T}}{\mathcal {T}}}=A_{{\mathcal {T}}{\mathcal {T}}} - A_{{\mathcal {T}}{\mathcal {F}}}A_{{\mathcal {F}}{\mathcal {F}}}^{-1}A_{{\mathcal {F}}{\mathcal {T}}}, \end{aligned}$$

and the equivalent matrix eigenvalue problem

$$\begin{aligned} S_{{\mathcal {T}}{\mathcal {T}}}x_{{\mathcal {T}}}=\lambda _hB_{{\mathcal {T}}{\mathcal {T}}}x_{{\mathcal {T}}}\quad \text { and } \quad x_{{\mathcal {T}}}\cdot B_{{\mathcal {T}}{\mathcal {T}}}x_{{\mathcal {T}}}=1. \end{aligned}$$

(3.14)

The mass matrix $B_{{\mathcal {T}}{\mathcal {T}}}\in {\mathbb {R}}^{dim P_{k+1}({\mathcal {T}})\times dim P_{k+1}({\mathcal {T}})}$ is positive definite and allows the approximation of $dim P_{k+1}({\mathcal {T}})$ eigenvalues and the application of the min-max principle (e.g. [33, Chapter 6]). The alternative formulation (3.14) will be exploited in Sect. 5 below.

4 Lower eigenvalue bounds

This section proves the main theorem, namely that the modified HHO method (1.3) provides guaranteed lower bounds for the continuous eigenvalues. Recall the constants $C_{st}$ and $\kappa$ from Theorem 2.3, set $\sigma ^2:=C_{st}^2-1$, and $\delta :=\kappa h_{\max }$.

Theorem 4.1

Let $\lambda (j)$ denote the j-th continuous eigenvalue of (1.2) and $\lambda _h(j)$ the j-th discrete eigenvalue of (1.3). Then each of the conditions (i) $\sigma ^2\beta +\delta ^2\lambda (j)\le \alpha <1$ (a priori) and (ii) $\sigma ^2\beta +\delta ^2\lambda _h(j)\le \alpha <1$ (a posteriori) implies $\lambda _h(j)\le \lambda (j).$

Proof

To alleviate the notation we simply write $\lambda _h$ and $\lambda$.

• Step 1. Reduction to ${\delta ^2 \lambda <1}$. If $1\le \delta ^2\lambda$, then (i) fails and (ii) holds. Consequently, $\delta ^2\lambda _h\le \alpha < 1\le \delta ^2\lambda$ implies $\lambda _h\le \lambda$ as claimed. It remains the case $\delta ^2\lambda <1$ throughout the remainder of the proof.

• Step 2. Claim: Linear independence of ${\Pi _{k+1}(\phi _1),\dots ,\Pi _{k+1}(\phi _j)\in P_{k+1}({\mathcal {T}})}$.  For the continuous eigenvalue problem (1.2), let ${\phi _1,\dots ,\phi _j}\in H^1_0(\Omega )$ denote the first j exact eigenfunctions and $\lambda$ the j-th eigenvalue. The proof is by contraposition and concerns $\phi \in \text {span}\{\phi _1,\dots ,\phi _j\}$ with $\Vert \phi \Vert _{L^2(\Omega )}=1$ and $\Pi _{k+1}(\phi )=0$. The estimate (2.4) in Theorem 2.3 implies for $\delta = \kappa h_{\max }$ that

  $$\begin{aligned} 1=\Vert \phi \Vert _{L^2(\Omega )}=\Vert (1-\Pi _{k+1})(\phi )\Vert _{L^2(\Omega )}\le \delta \Vert (1-\Pi _{k})(\nabla \phi )\Vert _{L^2(\Omega )}. \end{aligned}$$

  The Pythagoras theorem $\Vert \nabla \phi \Vert _{L^2(\Omega )}^2=\Vert \Pi _{k}(\nabla \phi )\Vert _{L^2(\Omega )}^2+\Vert (1-\Pi _{k})(\nabla \phi )\Vert _{L^2(\Omega )}^2$ implies that

  $$\begin{aligned} \Vert (1-\Pi _{k})(\nabla \phi )\Vert _{L^2(\Omega )}^2\le \Vert \nabla \phi \Vert _{L^2(\Omega )}^2. \end{aligned}$$

  The min-max principle on the exact eigenvalues of (1.2) for $\phi$ shows that

  $$\begin{aligned} \Vert \nabla \phi \Vert _{L^2(\Omega )}^2\le \lambda =\max _{v\in span \{\phi _1,\dots , \phi _j\}}\frac{\Vert \nabla v\Vert _{L^2(\Omega )}^2}{\Vert v\Vert _{L^2(\Omega )}^2}. \end{aligned}$$

  (4.1)

  The combination of the last three displayed inequalities reads $1\le \delta ^2\lambda$.

• Step 3. Claim: ${\exists \,\phi \in { span}\{\phi _1,\dots ,\phi _j\}}$, $\Vert \phi \Vert ^2=1$, $\Vert \nabla \phi \Vert ^2 \le {\lambda }$, $\lambda _h b_h(I(\phi ), I(\phi ))\le a_h(I(\phi ), I(\phi ))$. Owing to Step 2, the subspace $U_j:=\text {span}\{I(\phi _1),\dots ,I(\phi _j)\}$ of $V_h$ has dimension j. If ${\mathcal {U}}(j)$ denotes the space of all subspaces of $V_h$ of dimension j, then the min-max principle for (1.3) (on the algebraic level) characterizes the j-th discrete eigenvalue $\lambda _h$ as

  $$\begin{aligned} \lambda _h=\min _{U_h\in {\mathcal {U}}(j)}\max _{v_h\in U_h\setminus \{0\}}\frac{a_h(v_h,v_h)}{b_h(v_h,v_h)} \le \max _{v_h\in U_j\setminus \{0\}}\frac{a_h(v_h,v_h)}{b_h(v_h,v_h)}. \end{aligned}$$

  (4.2)

  The maximum in the finite-dimensional space $U_j:=\text {span}\{I(\phi _1),\dots ,I(\phi _j)\}$ is attained for some $v_h\in U_j$. Therefore, there exists $\phi \in span \{\phi _1,\dots ,\phi _j\}$ with $\Vert \phi \Vert ^2=1$, $\Vert \nabla \phi \Vert ^2\le \lambda$ (by the above min–max principle on the continuous level cf. (4.1)), and

  $$\begin{aligned} \lambda _h b_h(I(\phi ), I(\phi ))\le a_h(I(\phi ), I(\phi )). \end{aligned}$$

• Step 4. Lower bound for ${b_h(I(\phi ), I(\phi ))}$.  Given $\phi \in span \{\phi _1,\dots ,\phi _j\}\subset H^1_0(\Omega )$ from Step 3, the estimate (2.4) and the Pythagoras theorem show that

  $$\begin{aligned} 1- \delta ^2\Vert (1- \Pi _{k})(\nabla \phi )\Vert ^2_{L^2(\Omega )}\le & {} 1-\Vert (1- \Pi _{k+1})(\phi )\Vert ^2_{L^2(\Omega )} \\= & {} \Vert \Pi _{k+1}(\phi )\Vert ^2_{L^2(\Omega )}=b_h(I(\phi ), I(\phi )). \end{aligned}$$

  Since $\delta ^2\lambda <1$ and $\Vert (1- \Pi _{k})(\nabla \phi )\Vert ^2_{L^2(\Omega )}\le \Vert \nabla \phi \Vert ^2_{L^2(\Omega )}\le \lambda$, the displayed lower bound proves $b_h(I(\phi ), I(\phi ))>0$. This also shows that $\lambda _h<\infty$.

• Step 5. Upper bound for ${a_h(I(\phi ), I(\phi ))}$.  Given $\phi \in H^1_0(\Omega )$ from Step 3, the alternative form of $a_h$ in (3.8) and Lemma 3.2 prove

  $$\begin{aligned} a_h(I(\phi ),I(\phi )) ={}&\Vert \Pi _k \Pi _{RT,k}(\nabla \phi )\Vert ^2_{L^2(\Omega )}\nonumber \\&+(1-\alpha )\Vert (1-\Pi _k)\Pi _{RT,k}(\nabla \phi )\Vert _{L^2(\Omega )}^2 +\beta \Vert \!\vert S(I\phi )\Vert \!\vert ^2_{pw }. \end{aligned}$$

  (4.3)

  The commuting property from Lemma 2.1, the Pythagoras theorem, and $\Vert \nabla \phi \Vert _{L^2(\Omega )}^2\le \lambda$ from Step 3 show that

  $$\begin{aligned} \Vert \Pi _k \Pi _{RT,k}\nabla \phi \Vert ^2_{L^2(\Omega )}&=\Vert \Pi _k \nabla \phi \Vert ^2_{L^2(\Omega )} \le \lambda -\Vert (1-\Pi _k) \nabla \phi \Vert ^2_{L^2(\Omega )}. \end{aligned}$$

  (4.4)

  Lemma 2.1 and the boundedness of $\Pi _{RT,k}$ with $\Vert \Pi _{RT,k}\Vert \le 1$ show that

  $$\begin{aligned} \Vert (1-\Pi _k)\Pi _{RT,k}(\nabla \phi )\Vert _{L^2(\Omega )}&=\Vert \Pi _{RT,k} (1-\Pi _k)(\nabla \phi )\Vert _{L^2(\Omega )}\nonumber \\&\le \Vert (1-\Pi _k)(\nabla \phi )\Vert _{L^2(\Omega )}. \end{aligned}$$

  (4.5)

  The combination of (4.3)–(4.5) with (3.7) proves (for $0<\alpha <1$) that

  $$\begin{aligned} a_h(I(\phi ),I(\phi ))&\le \lambda +(\beta \sigma ^2-\alpha )\Vert (1-\Pi _k) (\nabla \phi ) \Vert _{L^2(\Omega )}^2. \end{aligned}$$

• Step 6. Finish of the proof. The combination of Step 3–Step 5 shows that

  $$\begin{aligned} (\alpha -\beta \sigma ^2-\delta ^2\lambda _h) \Vert (1-\Pi _k) (\nabla \phi ) \Vert _{L^2(\Omega )}^2\le \lambda -\lambda _h. \end{aligned}$$

  (4.6)

  The pre-factor on the left-hand side is non-negative in the case where the assumption (ii) holds and (4.6) proves the claim $\lambda _h\le \lambda$. In the case where the assumption (i) holds, (4.6) implies that

  $$\begin{aligned} \delta ^2(\lambda -\lambda _h) \Vert (1-\Pi _k) (\nabla \phi ) \Vert _{L^2(\Omega )}^2\le \lambda -\lambda _h. \end{aligned}$$

  For contradiction assume $\lambda -\lambda _h<0$ and divide the previous inequality by this difference so that $1\le \delta ^2\Vert (1-\Pi _k) (\nabla \phi ) \Vert _{L^2(\Omega )}^2.$ This is smaller than or equal to

  $$\begin{aligned} \delta ^2 \Vert \nabla \phi \Vert _{L^2(\Omega )}^2\le \delta ^2\lambda \le \delta ^2\lambda +\sigma ^2\beta \le \alpha <1. \end{aligned}$$

  This contradiction concludes the proof.

$\square$

5 Convergence analysis

This section proves that the discrete eigenvalues converge with the expected optimal rates. The analysis hinges on the Babuška–Osborn theory for the spectral approximation of compact selfadjoint operators and adapts the arguments devised in [9] to analyze the spectral approximation using the standard HHO method.

5.1 Babuška–Osborn theory

Let H denote a Hilbert space with inner product $(\bullet ,\bullet )_H$ and let $T\in {\mathcal {L}}(H;H)$ denote a bounded, linear, compact, and selfadjoint operator. Assume that $T_n\in {\mathcal {L}}(H;H)$ is a member of a sequence of compact, selfadjoint operators that converge to T in operator norm, i.e. $\lim _{n\rightarrow \infty }\Vert T-T_n\Vert _{{\mathcal {L}}(H;H)}=0$. Let $\sigma (T)$ denote the spectrum of T and $\mu \in \sigma (T){\setminus }\{0\}$ be a non-zero eigenvalue of T with eigenspace $E_\mu =\ker (\mu I-T)$ of dimension $m=dim (E_\mu )\in {\mathbb {N}}$.

Theorem 5.1

(Convergence) For any eigenvalue $\mu \in \sigma (T){\setminus }\{0\}$ of multiplicity m, there exists m eigenvalues $\mu _{n,1},\dots , \mu _{n,m}$ of $T_n$, that converge to $\mu$ as $n\rightarrow \infty$, and

$$\begin{aligned} \max _{1\le j\le m}\vert \mu -\mu _{n,j}\vert&\le C_a\bigg (\sup _{\phi ,\psi \in E_\mu \setminus \{0\}}\frac{|((T-T_n)\phi ,\psi )_H|}{\Vert \phi \Vert _H\Vert \psi \Vert _H}+\Vert (T-T_n)|_{E_\mu }\Vert _{{\mathcal {L}}(E_\mu ;H)}^2\bigg ). \end{aligned}$$

If $w_{n,j}\in \ker (\mu _{n,j}I-T_n)$ is a unit vector in the eigenspace of $\mu _{n,j}$ for $1\le j\le m$, then there exists $u\in E_\mu =\ker (\mu I-T)$ such that for all $n\in {\mathbb {N}}$

$$\begin{aligned} \Vert u-w_{n,j}\Vert _H\le C_b\Vert (T-T_n)|_{E_\mu }\Vert _{{\mathcal {L}}(E_\mu ;H)}. \end{aligned}$$

The constants $C_a$ and $C_b$ may depend on $\mu$ but are independent of n.

Proof

These are Theorems 7.2 and 7.4 in [4] for a selfadjoint operator T, see also in [5, Section 9] or [35, Section 1.4.2]. $\square$

5.2 The source problem and relevant solution operators

Given a right-hand side $f\in L^2(\Omega )$, the weak formulation of the Poisson model problem and its solution is associated with the solution operator $T:L^2(\Omega )\rightarrow L^2(\Omega )$ with

$$\begin{aligned} a(T(f),v)=b(f,v)\quad \text {for all }v\in H^1_0(\Omega ). \end{aligned}$$

(5.1)

The source problem for the new method (1.3) seeks $u_h\in V_h$ such that

$$\begin{aligned} a_h(u_h,v_h)=b(f,v_{{\mathcal {T}}})\quad \text {for all }v_h=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h, \end{aligned}$$

(5.2)

is associated with the solution operator ${\widehat{T}}_h: L^2(\Omega )\rightarrow V_h$ with ${\widehat{T}}_h(f):=u_h$, and well-posed by Lemma 3.5. Using Lemma 3.5 and proceeding as in [9, Lemma 3.2] shows that the operator ${\widehat{T}}_h$ is bounded uniformly with respect to the mesh-size. The first component of ${\widehat{T}}_h(f)=u_h=(u_{{\mathcal {T}}},u_{{\mathcal {F}}})\in V_h$ defines the selfadjoint, positive definite operator

$$\begin{aligned} T_h:\, L^2(\Omega )\rightarrow P_{k+1}({\mathcal {T}})\subset L^2(\Omega )\quad \text {with}\quad T_h(f):=u_{{\mathcal {T}}}. \end{aligned}$$

(5.3)

This operator $T_h$ allows for the application of the Babuška–Osborn theory. If $(\lambda _h,u_h)$ with $u_h=(u_{{\mathcal {T}}},u_{{\mathcal {F}}})$ is an eigenpair of (1.3), then $(\lambda _h^{-1}, u_{{\mathcal {T}}})\in {\mathbb {R}}_+\times V_h$ is an eigenpair of $T_h$. The analysis of the solution operators ${\widehat{T}}_h$ and $T_h$, based on the discrete error estimate in Theorem 5.2 below, follows the arguments of Section 4 in [9] (reduced to the present case of a symmetric bilinear form $a_h(\bullet ,\bullet )$). Let $s>1/2$ be the index resulting from the (reduced) elliptic regularity on the polyhedral domain $\Omega$.

Theorem 5.2

(Discrete error estimate) The following holds for any $s\le m \le k+1$ and $\phi \in L^2(\Omega )$ with $T(\phi )\in H^{1+m}(\Omega )$,

$$\begin{aligned} \Vert {\widehat{T}}_h(\phi )-I(T(\phi ))\Vert _{h}\lesssim h_{\max }^m\Vert T(\phi )\Vert _{H^{1+m}(\Omega )}. \end{aligned}$$

Proof

This proof adapts the arguments of [24, Thm. 8] and [9, Lemma 3.3] to the modified HHO method. We abbreviate $u_h:={\widehat{T}}_h(\phi )\in V_h$ and $u:=T(\phi )\in H^1_0(\Omega )$. Lemma 3.5 shows that

$$\begin{aligned} {\underline{\gamma }}\Vert I(u)-u_h\Vert _{h} \le \sup _{v_h\in V_h , \Vert v_h\Vert _h=1} a_h(I (u)-u_h, v_h), \end{aligned}$$

(5.4)

where the above right-hand side represents the consistency error. The solution property $-\Delta u=\phi$ a.e. in $\Omega$, and a piecewise integration by parts show, for $v_h =(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$, that

$$\begin{aligned} a_h(u_h,v_h)&=b(\phi , v_{{\mathcal {T}}})=(-\Delta u, v_{{\mathcal {T}}})_{L^2(\Omega )} \\&=(\nabla u, \nabla _{pw } v_{{\mathcal {T}}})_{L^2(\Omega )}-\sum _{T\in {\mathcal {T}}} \sum _{F\in {\mathcal {F}}(T)}\langle v_{{\mathcal {T}}}|_T,\nabla u\cdot \nu _T\rangle _{L^2(F)}\\&=(\nabla u, \nabla _{pw } v_{{\mathcal {T}}})_{L^2(\Omega )} +\sum _{T\in {\mathcal {T}}}\sum _{F\in {\mathcal {F}}(T)}\langle v_F-v_T,\nabla u\cdot \nu _T\rangle _{L^2(F)}. \end{aligned}$$

The last equality holds since $v_{\mathcal {F}}{=(v_F)_{F\in {\mathcal {F}}}}\in P_k({\mathcal {F}}(\Omega ))$ is single-valued for $F\in {\mathcal {F}}(\Omega )$ and vanishes along $F\subset \partial \Omega$, and $v_{\mathcal {T}}=(v_T)_{T\in {\mathcal {T}}}$. The combination of the alternative form of $a_h$ from (3.8), Lemma 3.2, and Lemma 2.1 proves that

$$\begin{aligned} a_h(I(u), v_h)&= (\Pi _kG_{RT}I(u), G_{RT}(v_h))_{L^2(\Omega )}\\&~\quad +(1-\alpha ) \big ((1-\Pi _k)G_{RT}I(u), G_{RT}(v_h)\big )_{L^2(\Omega )} \\&~\quad +\beta a_{pw }( S(I u),S(v_h))\\&= \big (((1-\alpha )\Pi _{RT,k}+\alpha \Pi _{k})(\nabla u), G_{RT}(v_h)\big )_{L^2(\Omega )}\\&~\quad +\beta a_{pw }(S(Iu),S(v_h)), \end{aligned}$$

because

$$\begin{aligned} \Pi _kG_{RT}I(u)+(1-\alpha )(1-\Pi _k)G_{RT}I(u)&= (1-\alpha )G_{RT}I(u)+\alpha \Pi _kG_{RT}I(u) \\&=((1-\alpha )\Pi _{RT,k}+\alpha \Pi _k)(\nabla u). \end{aligned}$$

The abbreviation $q_{RT}:=((1-\alpha )\Pi _{RT,k}+\alpha \Pi _{k})(\nabla u)\in RT_k^{pw }({\mathcal {T}})$, the definition (3.3) of $G_{RT}(v_h)$ and an integration by parts show that

$$\begin{aligned} a_h(I(u), v_h)&=(q_{RT}, \nabla _{pw } v_{{\mathcal {T}}})_{L^2(\Omega )} \\&~\quad +\langle v_{{\mathcal {F}}}-v_{{\mathcal {T}}},q_{RT}\cdot \nu _{{\mathcal {T}}}\rangle _{\partial {\mathcal {T}}} + \beta a_{pw }(S(Iu),S(v_h)). \end{aligned}$$

The last three displayed equalities lead to

$$\begin{aligned} a_h(I (u)-u_h, v_h)&= (q_{RT}-\nabla u, \nabla _{pw } v_{{\mathcal {T}}})_{L^2(\Omega )} + \langle v_{{\mathcal {F}}}-v_{{\mathcal {T}}},(q_{RT}-\nabla u)\cdot \nu _T\rangle _{\partial {\mathcal {T}}} \\&\quad ~+ \beta a_{pw }(S(Iu),S(v_h)) =: S_1+S_2+S_3. \end{aligned}$$

For any $T\in {\mathcal {T}}$, the combination of (2.1)–(2.2) and $0<\alpha <1$ proves that

$$\begin{aligned} \Vert q_{RT}-\nabla u\Vert _{L^2(T)}&\le (1-\alpha )\Vert (1-\Pi _{RT,k})\nabla u\Vert _{L^2(T)}+ \alpha \Vert (1-\Pi _k)\nabla u\Vert _{L^2(T)}\\&\lesssim h^{m}_{T}\vert u\vert _{H^{1+m}(T)}. \end{aligned}$$

Hence, the Cauchy–Schwarz inequality shows that

$$\begin{aligned} |S_1| \le \Vert q_{RT}-\nabla u\Vert _{L^2(\Omega )} \Vert \nabla _{pw } v_{{\mathcal {T}}}\Vert _{L^2(\Omega )} \lesssim {}&h_{\max }^{m}\vert u\vert _{H^{1+m}(\Omega )} \Vert v_h \Vert _{h}. \end{aligned}$$

(5.5)

The term $S_2$ is controlled similarly, and the term $S_3$ is controlled via Lemma 3.3 and (2.1). The bounds on $S_1,S_2,S_3$ combined with the estimate (5.4) conclude the proof. $\square$

5.3 Error analysis for the eigenvalue problem

Based on Theorem 5.2, the difference $T-T_h$ in the summands in Theorem 5.1 are estimated as in [9] resulting in Theorem 5.6 below. Let us briefly outline the main steps. Recall the index $s\in (1/2,1]$ of the (reduced) elliptic regularity on the polyhedral domain $\Omega \subset {\mathbb {R}}^n$.

Lemma 5.3

$\Vert T-T_h\Vert _{{\mathcal {L}}(L^2(\Omega ))}\lesssim h_{\max }^s$ holds for some $1/2<s \le 1$.

Proof

This is [9, Lemma 4.1] for a symmetric $a_h(\bullet ,\bullet )$ in combination with Theorem 5.2. $\square$

For a spectral value $\mu \in \sigma (T){\setminus }\{0\}$, the smoothness of the functions in the eigenspaces $E_\mu$ is quantified by $t\in [s,k+1]$ (depending on $\mu$) and a constant $C_t$ such that

$$\begin{aligned} \Vert \phi \Vert _{H^{1+t}(\Omega )}+\Vert T(\phi )\Vert _{H^{1+t}(\Omega )}\le C_t\Vert \phi \Vert _{L^2(\Omega )}\quad \text { for all }\phi \in E_\mu . \end{aligned}$$

(5.6)

Since possibly $E_{\mu }\subset H^{s+\varepsilon }(\Omega )$ for some $\varepsilon >0$, we can have $t>s>1/2$.

Lemma 5.4

$\Vert (T-T_h)|_{E_\mu }\Vert _{{\mathcal {L}}(E_\mu ;L^2(\Omega ))}\lesssim h_{\max }^t$ holds for $s\le t\le k+1$ and $\mu \in \sigma (T){\setminus }\{0\}$ verifying (5.6).

Proof

The proof is analogous to [9, Lemma 4.2] utilizing Theorem 5.2. $\square$

On $E_\mu \times E_\mu$ this bound can be improved.

Lemma 5.5

For any $s\le t\le k+1$ and $\mu \in \sigma (T){\setminus }\{0\}$ verifying (5.6), any $\phi ,\,\psi \in E_\mu$ satisfy

$$\begin{aligned} {\big \vert \big ((T-T_h)(\phi ),\psi \big )_{L^2(\Omega )}\big \vert } \lesssim h_{\max }^{2t}{\Vert \phi \Vert _{L^2(\Omega )}\Vert \psi \Vert _{L^2(\Omega )}}. \end{aligned}$$

Proof

We detail the proof since it is slightly different from [9, Lemma 4.3]. For any $\phi ,\,\psi \in E_\mu$, the definition of ${\widehat{T}}_h$ and $T_h$ show that

$$\begin{aligned} \big ((T-T_h)(\phi ),\psi \big )_{L^2(\Omega )}&=(T(\phi ),\psi )_{L^2(\Omega )}-b(T_h(\phi ),\psi )\\&=(T(\phi ),\psi )_{L^2(\Omega )}-a_h({\widehat{T}}_h(\phi ),{\widehat{T}}_h(\psi )), \end{aligned}$$

where we used that ${\widehat{T}}_h$ is the solution operator in (5.2). Using the symmetry of $a_h$ and again that ${\widehat{T}}_h$ is the solution operator in (5.2), we infer that

$$\begin{aligned} \big ((T-T_h)(\phi ),\psi \big )_{L^2(\Omega )}&=(T(\phi ),\psi )_{L^2(\Omega )}-a_h(IT(\phi ),{\widehat{T}}_h(\psi )) \\&~\quad +a_h(IT(\phi )-{\widehat{T}}_h(\phi ),{\widehat{T}}_h(\psi )) \\&=\big ((1-\Pi _{k+1})T(\phi ),\psi \big )_{L^2(\Omega )}\\&~\quad +a_h(IT(\phi )-{\widehat{T}}_h(\phi ),{\widehat{T}}_h(\psi )) =:S_4+S_5. \end{aligned}$$

To exploit the additional smoothness (5.6) of $\psi \in H^{1+t}(\Omega )$ for $S_4$, the projection property is combined with the Cauchy–Schwarz inequality and (2.1) to obtain

$$\begin{aligned} S_4={}&\big ((1-\Pi _{k+1})T(\phi ),(1-\Pi _{k+1})(\psi )\big )_{L^2(\Omega )} \le C_{apx }^2C_t^2 h_{\max }^{2(1+t)}\Vert \phi \Vert _{L^2(\Omega )}\Vert \psi \Vert _{L^2(\Omega )}. \end{aligned}$$

(5.7)

The term $S_5$ needs a bit more algebraic manipulation. We first write

$$\begin{aligned} S_5=a_h(IT(\phi )-{\widehat{T}}_h(\phi ),{\widehat{T}}_h(\psi )-IT(\psi ))+a_h(IT(\phi )-{\widehat{T}}_h(\phi ),IT(\psi )). \end{aligned}$$

The Cauchy–Schwarz inequality for $a_h$, Theorem 5.2, and (5.6) prove for the first part that

$$\begin{aligned} a_h(IT(\phi )-{\widehat{T}}_h(\phi ),{\widehat{T}}_h(\psi )-IT(\psi ))\lesssim h_{\max }^{2t}C_t^2\Vert \phi \Vert _{L^2(\Omega )}\Vert \psi \Vert _{L^2(\Omega )}. \end{aligned}$$

(5.8)

With the abbreviation $S_6:= a_h(IT(\phi ),IT(\psi ))-a(T(\phi ),T(\psi ))$ the solution properties of T and ${\widehat{T}}_h$ show for the second summand of $S_5$ that

$$\begin{aligned} a_h(IT(\phi )-{\widehat{T}}_h(\phi ),IT(\psi ))-S_6&=a(T(\phi ),T(\psi ))-a_h({\widehat{T}}_h(\phi ),IT(\psi ))\nonumber \\&=(\phi , T(\psi ))_{L^2(\Omega )}-(\phi ,\Pi _{k+1}T(\psi ))_{L^2(\Omega )}\nonumber \\&=(\phi , (1-\Pi _{k+1})T(\psi ))_{L^2(\Omega )}\nonumber \\&=((1-\Pi _{k+1})(\phi ), (1-\Pi _{k+1})T(\psi ))_{L^2(\Omega )}\nonumber \\&\le C_{apx }^2C_t^2 h_{\max }^{2(1+t)}\Vert \phi \Vert _{L^2(\Omega )}\Vert \psi \Vert _{L^2(\Omega )}, \end{aligned}$$

(5.9)

where the last inequality follows as in (5.7). The alternative form of $a_h$ from (3.8), the definition of a, as well as a combination of Lemma 3.2 and Lemma 2.1 lead to

$$\begin{aligned} S_6 ={}&(\Pi _k\nabla T(\phi ), \Pi _k\nabla T(\psi ))_{L^2(\Omega )}\\&+(1-\alpha ) \big (\Pi _{RT,k}(1-\Pi _k)\nabla T(\phi ), \Pi _{RT,k}(1-\Pi _k)\nabla T(\psi )\big )_{L^2(\Omega )} \\&+\beta a_{pw }(SIT(\phi ),SIT(\psi ))-(\nabla T(\phi ), \nabla T(\psi )). \end{aligned}$$

The Cauchy–Schwarz inequality, Lemma 3.3, and (2.1)–(2.2) prove for all $\phi ,\psi \in E_\mu$ verifying (5.6) that

$$\begin{aligned} S_6&\le {} \Vert (1-\Pi _{k}) \nabla T(\phi )\Vert _{L^2(\Omega )}\Vert (1-\Pi _{k})\nabla T(\psi )\Vert _{L^2(\Omega )}\nonumber \\&\qquad +(1-\alpha ) \Vert \Pi _{RT,k}(1-\Pi _{k})\nabla T(\phi )\Vert _{L^2(\Omega )}\Vert \Pi _{RT,k}(1-\Pi _k)\nabla T(\psi )\Vert _{L^2(\Omega )}\nonumber \\&\qquad +\beta \Vert \!\vert SIT(\phi )\Vert \!\vert _{pw } \Vert \!\vert SIT(\psi )\Vert \!\vert _{pw }\nonumber \\&\le {} ~(2-\alpha )\Vert (1-\Pi _{k})\nabla T(\phi )\Vert _{L^2(\Omega )}\Vert (1-\Pi _{k})\nabla T(\psi )\Vert _{L^2(\Omega )}\nonumber \\&\qquad \!\! +\beta \sigma ^2 \Vert (1-\Pi _k) (\nabla T(\phi )) \Vert _{L^2(\Omega )}\Vert (1-\Pi _k) (\nabla T(\psi )) \Vert _{L^2(\Omega )} \nonumber \\&\le {} h_{\max }^{2t}((2-\alpha )+\beta \sigma ^2)C_t^2C_{apx }^2\Vert \phi \Vert _{L^2(T)}\Vert \psi \Vert _{L^2(T)}. \end{aligned}$$

(5.10)

The combination of (5.8)–(5.10) proves $|S_5|\lesssim h_{\max }^{2(1+t)}\Vert \phi \Vert _{L^2(\Omega )}\Vert \psi \Vert _{L^2(\Omega )}$. This and (5.7) conclude the proof. $\square$

5.4 Resulting estimates

Let $\mu \in \sigma (T){\setminus }\{0\}$ denote an eigenvalue of T of multiplicity $m\in {\mathbb {N}}$. Lemma 5.3 proves the convergence $T_h\rightarrow T$ in ${\mathcal {L}}(L^2(\Omega ))$ as $h_{\max }\rightarrow 0$. Hence there are m discrete eigenvalues $\mu _{h,1},\dots ,\mu _{h,m}$ in multiplicity which converge to $\mu$ as $h_{\max }\rightarrow 0$.

Theorem 5.6

(Error estimates) Given an eigenvalue $\mu \in \sigma (T)\setminus \{0\}$ of multiplicity m, $t\in [s,k+1]$ such that (5.6) holds, and the m eigenvalues $\mu _{h,1},\dots , \mu _{h,m}$ of $T_h$, that converge to $\mu$ as $h_{\max }\rightarrow 0$, then

$$\begin{aligned} \max _{1\le j\le m}|\mu -\mu _{h,j}|\le C_ah^{2t}. \end{aligned}$$

Moreover, given any unit vector $u_{{\mathcal {T}},j}\in \ker (\mu _{h,j}I-T_h)\subset P_{k+1}({\mathcal {T}})$, there exist an unit vector $u\in \ker (\mu I-T)=E_{\mu }$ such that

$$\begin{aligned} \Vert u-u_{{\mathcal {T}},j}\Vert _{L^2(\Omega )}\le C_bh^t. \end{aligned}$$

Given a discrete eigenfunction $u_{{\mathcal {T}}}\in \ker (\mu _{h,j}I-T_h)\subset P_{k+1}({\mathcal {T}})$, there exist an unit vector $u\in \ker (\mu I-T)=E_{\mu }$ such that $u_h:=(u_{{\mathcal {T}}}, Z_{{\mathcal {F}}}(u_{{\mathcal {T}}}))\in V_h$ satisfies

$$\begin{aligned} \Vert u_h-Iu\Vert _{a,h}^2=a_h(u_h-I u, u_h-I u)\le C_c h^{2t}. \end{aligned}$$

The constants $C_a,\, C_b,\,C_c >0$ may depend on $\mu$, the polynomial degree k, the domain $\Omega$, and the mesh regularity but are independent of the mesh-size.

Proof

The combination of Lemma 5.4–5.5 with the Babuška–Osborn theory in Theorem 5.1 provides the first two assertions. The proof for the final claim is analogue to Corollary 4.6 in [9]. In fact Lemma 5.5 provides the bound (5.10) for $\delta _u:=a_h(I u, I u)-a(u,u)=S_6$. $\square$

Remark 5.7

The eigenvalues $\lambda _h$ in (1.3) and $\lambda$ in (1.2) are associated with $\mu _h=\lambda ^{-1}_h$ and $\mu =\lambda ^{-1}$, respectively, which leads to the same estimates. If the smoothness is optimal, i.e., $t=k+1$, the proven convergence is of order $h^{2k+2}$ for the eigenvalues and $h^{k+1}$ for the eigenvectors in the $H^1$-seminorm.

6 Lowest-order case

This section is devoted to the analysis of the lowest-order case and provides a comparison to the Crouzeix–Raviart method. Throughout this section we set $k:=0$ so that $V_h:=P_1({\mathcal {T}})\times P_0({\mathcal {F}}(\Omega ))$.

Let $mid (K):=\frac{1}{m}\sum _{j=1}^mP_j\in K$ denote the barycenter of $K:=conv \{P_1,\dots , P_m\}$. The associated piecewise constant function $mid ({\mathcal {T}})\in P_0({\mathcal {T}};{\mathbb {R}}^n)$ takes on each simplex $T\in {\mathcal {T}}$ the value $mid ({{\mathcal {T}}})|_T:=mid (T)$. Let us set

$$\begin{aligned} s({\mathcal {T}})&:=1/n^2\, \Pi _0(\vert \bullet -mid ({\mathcal {T}})\vert ^2)\in P_0({\mathcal {T}}),\\ S({\mathcal {T}})&:=\Pi _0\big ((\bullet -mid ({\mathcal {T}}))\otimes (\bullet -mid ({\mathcal {T}}))\big )\in P_0({\mathcal {T}};{\mathbb {R}}^{n\times n}). \end{aligned}$$

6.1 Comparison with the Crouzeix–Raviart method

The Crouzeix–Raviart (CR) finite element space reads

$$\begin{aligned} \mathrm {CR}^1_0(\mathcal {T})&:=\{v_{CR }\in P_1({\mathcal {T}}):\ v_{CR } \text { is continuous at }mid (F)\text { for all }F\in {\mathcal {F}}(\Omega ), \\&\qquad \,\, v_{CR }(mid (F))=0\text { for all }F\in {\mathcal {F}}(\partial \Omega ) \}. \end{aligned}$$

The vector spaces $P_0({\mathcal {F}}(\Omega ))$ and $\mathrm {CR}^1_0(\mathcal {T})$ can be identified as follows. The extension operator $I_{CR }:P_0({\mathcal {F}}(\Omega ))\rightarrow \mathrm {CR}^1_0(\mathcal {T})$ maps bijectively $v_{{\mathcal {F}}}=(v_F)_{F\in {\mathcal {F}}}\in P_0({\mathcal {F}}(\Omega ))$ onto $I_{CR }(v_{{\mathcal {F}}}):=\sum _{F\in {\mathcal {F}}}v_F\psi _F$, where $\psi _F\in \mathrm {CR}^1_0(\mathcal {T})$ denotes the basis function with $\psi _F(mid (E))=\delta _{EF}$ for all $F,E \in {\mathcal {F}}$. This leads to $\Pi _{{\mathcal {F}},0}I_{CR }(v_{{\mathcal {F}}})=v_{{\mathcal {F}}}$ for any $v_{{\mathcal {F}}}\in P_0({\mathcal {F}}(\Omega ))$. Furthermore, if $I_{NC }:H^1_0(\Omega )\rightarrow \mathrm {CR}^1_0(\mathcal {T})$ denotes the nonconforming interpolation of $\phi \in H^1_0(\Omega )$, then $I_{NC }(\phi )=I_{CR }\Pi _{{\mathcal {F}},0}(\phi )$. In other words we have $I_{NC }=I_{CR }\circ \Pi _{{\mathcal {F}},0}$. Recall the operators R from (3.2), $G_{RT}$ from (3.3), and S from (3.4).

Lemma 6.1

Any $v_h:=(v_{{\mathcal {T}}}, v_{{\mathcal {F}}})\in V_h$ and $v_{CR }:=I_{CR }(v_{{\mathcal {F}}})\in \mathrm {CR}^1_0(\mathcal {T})$ satisfy

• (a) $R(v_h)=(1-\Pi _0)(v_{CR })+\Pi _0 (v_{{\mathcal {T}}})$,

• (b) $G_{RT}(v_h)=\nabla _{pw }v_{CR }+\frac{1}{n}\frac{1}{s({\mathcal {T}})}\big (\Pi _0(v_{CR }-v_{{\mathcal {T}}})\big )(\bullet -mid ({\mathcal {T}}))$,

• (c) $S(v_h)=(1-\Pi _0)(v_{{\mathcal {T}}}-v_{CR })$.

Proof

• (a) For any $p\in P_1({\mathcal {T}})$ the definition (3.2) of R and an integration by parts show that

  $$\begin{aligned} a_{pw }(R(v_h), p)&=-(v_{{\mathcal {T}}},\Delta _{pw }p)_{L^2(\Omega )}+\langle v_{{\mathcal {F}}}, \nabla _{pw } p\cdot \nu _{{\mathcal {T}}}\rangle _{\partial {\mathcal {T}}}\\&=\langle v_{CR }, \nabla _{pw } p\cdot \nu _{{\mathcal {T}}}\rangle _{\partial {\mathcal {T}}} =a_{pw }(v_{CR },p). \end{aligned}$$

  Hence, $\nabla _{pw }R(v_h)=\nabla _{pw }v_{CR }$. The condition $\Pi _0R(v_h)=\Pi _0(v_{{\mathcal {T}}})$ concludes the proof of (a).

• (b) For any $q_{RT}\in RT_0({\mathcal {T}})$, the definition (3.3) of $G_{RT}$ and an integration by parts show that

  $$\begin{aligned} (G_{RT}(v_h), q_{RT})_{L^2(\Omega )}&=- (v_{{\mathcal {T}}},div _{pw }q_{RT})_{L^2(\Omega )}+\langle v_{CR }, q_{RT}\cdot \nu _{{\mathcal {T}}}\rangle _{\partial {\mathcal {T}}}\\&=(v_{CR }-v_{{\mathcal {T}}},div _{pw }q_{RT})_{L^2(\Omega )}+(\nabla _{pw }v_{CR },q_{RT})_{L^2(\Omega )}\\&=(\Pi _0(v_{CR }-v_{{\mathcal {T}}}),div _{pw }q_{RT})_{L^2(\Omega )}\\&\quad +(\nabla _{pw }v_{CR },\Pi _0(q_{RT}))_{L^2(\Omega )}. \end{aligned}$$

  On the other hand, since any $q_{RT}\in RT_0^{pw }({\mathcal {T}})$ can be written as

  $$\begin{aligned} q_{RT}=\Pi _0q_{RT}+n^{-1} {div _{pw }q_{RT}}\,(\bullet -mid ({\mathcal {T}})), \end{aligned}$$

  the Pythagoras theorem for $\Pi _0$ and the definition of $s({\mathcal {T}})$ show that

  $$\begin{aligned} (G_{RT}(v_h),q_{RT})_{L^2(\Omega )} ={}&(\Pi _0G_{RT}(v_h),\Pi _0(q_{RT}))_{L^2(\Omega )}\\&+\big ((1-\Pi _0)G_{RT}(v_h),(1-\Pi _0)(q_{RT})\big )_{L^2(\Omega )}\\ ={}&(\Pi _0G_{RT}(v_h),\Pi _0(q_{RT}))_{L^2(\Omega )}\\&+\frac{1}{n^2}\big ({div _{pw }G_{RT}(v_h)}(\bullet -mid ({\mathcal {T}})), {div _{pw }q_{RT}}(\bullet -mid ({\mathcal {T}}))\big )_{L^2(\Omega )}\\ ={}&(\Pi _0G_{RT}(v_h),\Pi _0(q_{RT}))_{L^2(\Omega )}\\&\!\! +(s({\mathcal {T}})div _{pw }G_{RT}(v_h),div _{pw }q_{RT})_{L^2(\Omega )}. \end{aligned}$$

  The comparison of the last two displayed equalities shows that $s({\mathcal {T}})div _{pw }G_{RT}(v_h)=\Pi _0(v_{CR }-v_{{\mathcal {T}}})$ and $\Pi _0G_{RT}(v_h)=\nabla _{pw }v_{CR }$. That completes the proof of (b).

• (c) This follows directly from the definition (3.4) and (a).

$\square$

Proposition 6.2

• (a) The bilinear forms in the lowest-order case read for all $u_h:=(u_{{\mathcal {T}}},u_{{\mathcal {F}}})$ and $v_h:=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$,

  $$\begin{aligned} a_h(u_h,v_h)={}&a_{pw }(I_{CR }(u_{{\mathcal {F}}}),I_{CR }(v_{{\mathcal {F}}}))+ \beta \, a_{pw }(u_{{\mathcal {T}}}-I_{CR }(u_{{\mathcal {F}}}),v_{{\mathcal {T}}}-I_{CR }(v_{{\mathcal {F}}}))\\&+{(1-\alpha )}\big (s({\mathcal {T}})^{-1}\Pi _0(I_{CR }(u_{{\mathcal {F}}})-u_{{\mathcal {T}}}),\Pi _0(I_{CR }(v_{{\mathcal {F}}})-v_{{\mathcal {T}}})\big )_{L^2(\Omega )}, \\ b_h(u_h,v_h)={}&(u_{{\mathcal {T}}},v_{{\mathcal {T}}})_{L^2(\Omega )}. \end{aligned}$$

• (b) The discrete solution $u_h:=(u_{{\mathcal {T}}}, u_{{\mathcal {F}}})\in V_h$ of the lowest-order EVP satisfies

  $$\begin{aligned}&I_{CR }(u_{{\mathcal {F}}}) \!=\!\bigg (1-\frac{\lambda _hs({\mathcal {T}})}{1-\alpha }\bigg ) \Pi _0(u_{{\mathcal {T}}}) +\Bigg ( \bigg (1-\frac{\lambda _hS({\mathcal {T}})}{\beta }\bigg )\nabla _{pw }u_{{\mathcal {T}}}\Bigg )\cdot (\bullet -mid ({\mathcal {T}})), \end{aligned}$$

  (6.1)
  $$\begin{aligned}&a_{pw }(I_{CR }(u_{{\mathcal {F}}}),v_{CR })=\lambda _h(u_{{\mathcal {T}}},v_{CR })_{L^2(\Omega )}, \quad \text {for all }{v_{CR }}\in \mathrm {CR}^1_0(\mathcal {T}). \end{aligned}$$

  (6.2)

Proof

• (a) Using the alternative form for $a_h$ from (3.8) for the lowest-order case $k=0$, the substitution of the operators with Lemma 6.1 proves the claim.

• (b) With the bilinear forms of Proposition 6.2.a, (1.3) leads for any $v_h=(v_{{\mathcal {T}}},0)\in V_h$ with $v_{{\mathcal {T}}}\in P_1({\mathcal {T}})$ to

  $$\begin{aligned}&{(1-\alpha )}\big (s({\mathcal {T}})^{-1}\Pi _0(u_{{\mathcal {T}}}-I_{CR }(u_{{\mathcal {F}}})),v_{{\mathcal {T}}})\big )_{L^2(\Omega )}\nonumber \\&\quad +\beta \, a_{pw }(u_{{\mathcal {T}}}-I_{CR }(u_{{\mathcal {F}}}),v_{{\mathcal {T}}})=\lambda _h (u_{{\mathcal {T}}},v_{{\mathcal {T}}})_{L^2(\Omega )}. \end{aligned}$$

  (6.3)

  The choice $\Pi _0(v_{{\mathcal {T}}})\in P_0({\mathcal {T}})$ in (6.3) shows that $\frac{1-\alpha }{s({\mathcal {T}})} \Pi _0(u_{{\mathcal {T}}}-I_{CR }(u_{{\mathcal {F}}}))=\lambda _h \Pi _0 (u_{{\mathcal {T}}})$ and equivalently

  $$\begin{aligned} \Pi _0 I_{CR }(u_{{\mathcal {F}}})=\bigg (1-\frac{\lambda _hs({\mathcal {T}})}{(1-\alpha )}\bigg ) \Pi _0(u_{{\mathcal {T}}}). \end{aligned}$$

  The substitution of $(1-\Pi _0)(v_{{\mathcal {T}}})\in P_1({\mathcal {T}})$ in (6.3) proves

  $$\begin{aligned} \beta a_{pw }(u_{{\mathcal {T}}}-I_{CR }(u_{{\mathcal {F}}}), v_{{\mathcal {T}}})&=\lambda _h\big (u_{{\mathcal {T}}},(1-\Pi _0)(v_{{\mathcal {T}}})\big )_{L^2(\Omega )}. \end{aligned}$$

  Since for any $v_1\in P_1({\mathcal {T}})$, we have $v_1=\Pi _0(v_1)+\nabla _{pw }v_1\cdot (\bullet -mid ({\mathcal {T}}))$, the last displayed identity concludes the proof of (6.1) with

  $$\begin{aligned} \nabla _{pw } I_{CR }(u_{{\mathcal {F}}})=\bigg (1-\frac{\lambda _hS({\mathcal {T}})}{\beta }\bigg )\nabla _{pw }u_{{\mathcal {T}}}. \end{aligned}$$

  Since the operator $I_{CR }:P_0({\mathcal {F}}(\Omega ))\rightarrow \mathrm {CR}^1_0(\mathcal {T})$ is surjective, the choice of test functions $v_h=(I_{CR }(v_{{\mathcal {F}}}),v_{{\mathcal {F}}})\in V_h$ in (1.3) proves (6.2).

$\square$

Let $(\lambda _{CR },u_{CR })\in {\mathbb {R}}_+\times \mathrm {CR}^1_0(\mathcal {T})$ denote a Crouzeix–Raviart eigenvalue pair with

$$\begin{aligned} a_{pw }(u_{CR },v_{CR })=\lambda _{CR }b(u_{CR },v_{CR })\text { and } \Vert u_{CR }\Vert _{L^2(\Omega )}=1\quad \text { for all }v_{CR }\in \mathrm {CR}^1_0(\mathcal {T}). \nonumber \\ \end{aligned}$$

(6.4)

Corollary 6.3

(Comparison with Crouzeix–Raviart) If $\lambda _{CR }(j)$ denotes the j-th eigenvalue of (6.4) and $\lambda _h(j)$ the j-th eigenvalue of (1.3), then $\lambda _h(j)\le \lambda _{CR }(j)$.

Proof

The proof is similar to [20, Thm.6.2]. Since $I_{CR }\Pi _{{\mathcal {F}},0}(v_{CR })=v_{CR }$ for any Crouzeix–Raviart function $v_{CR }\in \mathrm {CR}^1_0(\mathcal {T})$, Proposition 6.2 shows that for $v_{CR ,h}:=(v_{CR },\Pi _{{\mathcal {F}},0}v_{CR })\in V_h$,

$$\begin{aligned} a_h(v_{CR ,h},v_{CR ,h})=a_{pw }(v_{CR },v_{CR })\quad \text { and } b_h(v_{CR ,h},v_{CR ,h})=b(v_{CR },v_{CR }). \end{aligned}$$

The discrete min-max principles for $\lambda _h(j)$ and $\lambda _{CR }(j)$ conclude the proof. $\square$

6.2 Estimate on the constant $\sigma$

Recall the a posteriori condition $\sigma ^2\beta +\delta ^2\lambda _h(j)\le \alpha <1$ in Theorem 4.1 sufficient for the j-th discrete eigenvalue $\lambda _h(j)$ of (1.3) to be a guaranteed lower bound for the j-th exact eigenvalue $\lambda (j)$ of (1.2). Thus the constants $\sigma$ and $\kappa$ (recall that $\delta :=\kappa h_{\max }$) are essential for the choice of the parameters $\alpha$ and $\beta$. The constant $\kappa$ is estimated in Remark 2.4 as $\kappa ^2\le {\pi ^{-2}}+({2n(n+1)(n+2)})^{-1}$ for any space dimension n, and for $n=2$, this bound can be improved to $\kappa \le (1/48+j_{11}^{-2})^{1/2}=0.298234942888$ [15], where $j_{11}$ denotes the first root of the first Bessel function.

The constant $\sigma$ is more difficult to estimate (recall that $\sigma :=\sqrt{C_{st}^2-1}$ but the proof of the existence of $C_{st}$ in [20, Thm 3.1] is non-constructive). Actually the constant $\sigma$ is only needed in Lemma 3.3 to bound $\Vert \!\vert S(I\phi )\Vert \!\vert _{pw }$ for all $\phi \in V:=H^1_0(\Omega )$. To bound this quantity in the lowest-order case, we can use an inverse inequality. Let us set for all $T\in {\mathcal {T}}$, $c_{inv }(T):=\sup _{{v_1\in P_1(T)}}\Vert \nabla v_1\Vert _{L^2(T)}/\Vert v_1\Vert _{L^2(T)}$. Notice that $c_{inv }(T)$ is the square root of the maximal eigenvalue of the generalized matrix eigenvalue problem with the stiffness and mass matrix of $P_1(T)$. Let us set $c_{inv }:=\max _{T\in {\mathcal {T}}}c_{inv }(T)$. Recall from Remark 2.4 the Poincaré constant $C_{P }$ such that $\Vert (1-\Pi _0)(f)\Vert _{L^2(T)} \le C_{P }h_T\Vert \nabla f\Vert _{L^2(T)}$ for all $f\in H^1(T)$.

Lemma 6.4

(Bound on $\sigma$) Let $c_{inv }$ be the constant associated with the inverse estimate in $P_1$ and let $C_{P }$ be the Poincaré constant. Then $\Vert \!\vert S(I\phi )\Vert \!\vert _{pw }\le \sigma \Vert (1-\Pi _0)(\nabla \phi )\Vert _{L^2(\Omega )}$ for all $\phi \in V:=H^1_0(\Omega )$ with $\sigma \le C_P c_{inv }.$

Proof

Any $\phi \in H^1_0(\Omega )$ satisfies

$$\begin{aligned} \Vert \!\vert S(I\phi )\Vert \!\vert _{pw }=\Vert \!\vert \Pi _1 (\phi )-I_{CR }\Pi _{{\mathcal {F}},0}(\phi )\Vert \!\vert _{pw }=\Vert \!\vert (\Pi _1-I_{NC })(\phi )\Vert \!\vert _{pw }. \end{aligned}$$

For any $T\in {\mathcal {T}}$, the projection properties of $\Pi _0$ and $\Pi _1$ and the inverse estimate for affine functions in $P_1(T)$ show that

$$\begin{aligned}&h_Tc_{inv }^{-1}\Vert \nabla (\Pi _1-I_{NC })(\phi )\Vert _{L^2(T)} =h_Tc_{inv }^{-1}\Vert \nabla (1-\Pi _0) \Pi _1(1-I_{NC })(\phi )\Vert _{L^2(T)}\\&\quad \le \Vert (1-\Pi _0) \Pi _1(1-I_{NC })(\phi )\Vert _{L^2(T)} = \Vert \Pi _1 (1-\Pi _0) (1-I_{NC })(\phi )\Vert _{L^2(T)}\\&\quad \le \Vert (1-\Pi _0) (1-I_{NC })(\phi )\Vert _{L^2(T)} \le C_{P }h_T\Vert \nabla (1-I_{NC })(\phi )\Vert _{L^2(T)}. \end{aligned}$$

This implies that $\Vert \!\vert S(I\phi )\Vert \!\vert _{pw } \le c_{inv }C_{P } \Vert \nabla (1-I_{NC })(\phi )\Vert _{L^2(T)}$ and the identity $\nabla I_{NC } = \Pi _0\nabla$ concludes the proof. $\square$

For $n=2$ the constant $c_{inv }(T)$ is computed in [18, Lemma 4.10] in terms of the minimum angle $\omega _T^0$ in $T\in {\mathcal {T}}$ as

$$\begin{aligned} c_{inv }(T)^2= 24\cot (\omega _T^0)\big (2 \cot (\omega _T^0)-\cot (2\omega _T^0) + ((2\cot (\omega _T^0)-\cot (2\omega _T^0))^2 -3)^{1/2} \big ). \end{aligned}$$

(6.5)

For a triangulation composed of right isosceles triangles, we have $c_{inv }=\sqrt{72}$. Combined with Lemma 6.4 and the estimate on $C_{P }$ from Remark 2.4 shows that $\sigma \le 2.2145$. Lemma 6.4 gives a first analytical upper bound for the constant $\sigma$ for the lowest-order method utilized in the numerical experiments below. Sharper bounds for the parameter $\sigma$ (in particular for higher polynomial degrees) may be computed by a related PDE eigenvalue problem on a reference domain; details and numerical examples shall appear elsewhere.

7 Numerical experiments

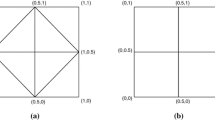
This section presents numerical experiments illustrating the superiority of the guaranteed lower bounds delivered in the framework of Theorem 4.1, compared to the guaranteed lower bounds of [16, 20] for the lowest-order variants on regular triangulations of the polygonal domains in Fig. 1 in 2D.

Fig. 1

Initial triangulation ${\mathcal {T}}_0$ of the L-shaped domain (a), the slit domain (b), and the isospectral domains (c) and (d)

7.1 Preliminaries

7.1.1 Implementation

The implementation is realized in MATLAB based on the data structure and assembling from [8, Section 7.8]. The resulting algebraic eigenvalue problem is solved with the MATLAB routine eigs exactly; the termination and round-off errors are neglected for simplicity. (An algebraic bound [31, 15.9.1] could partly circumvent the issue of inexact solve as in [16] – however, this bound solely clarifies the existence of an eigenvalue but gives no information on its numbering.)

Given a regular triangulation ${\mathcal {T}}$ of the bounded polygonal Lipschitz domain $\Omega \subset {\mathbb {R}}^2$ into triangles, the Crouzeix–Raviart eigenpairs $(\lambda _{CR }(j), u_{CR }(j))$ of (6.4) and the post-processed $GLBCR (j)$ (1.1) from [16] are computed, together with the lowest-order version of the skeletal method (SM) [20] defined in (7.1) below. All these methods deliver guaranteed lower bounds which are compared to those delivered by the present modified HHO method. The SM method features the same discrete space $V_h= P_1({\mathcal {T}})\times P_0({\mathcal {F}}(\Omega ))$ as the modified HHO method, whereas the discrete bilinear forms in the 2D case read (with $\kappa$ defined in Remark 2.4 and $I_{CR }$ from Sect. 6.1)

$$\begin{aligned} a_{SM }(u_h,v_h)&:=a_{pw }(I_{CR }(u_{{\mathcal {F}}}), I_{CR }(v_{{\mathcal {F}}}))\\&\quad +\kappa ^{-2} (h_{{\mathcal {T}}}^{-2}(u_{{\mathcal {T}}}-I_{CR }(u_{{\mathcal {F}}})),v_{{\mathcal {T}}}-I_{CR }(v_{{\mathcal {F}}}))_{L^2(\Omega )},\\ b_{SM }(u_h,v_h)&:=(u_{{\mathcal {T}}},v_{{\mathcal {T}}})_{L^2(\Omega )}=b_h(u_h,v_h) \end{aligned}$$

$\text {for any}\,u_{h}=(u_{{\mathcal {T}}},u_{{\mathcal {F}}}), v_{h}=(v_{{\mathcal {T}}},v_{{\mathcal {F}}})\in V_h$.

The discrete eigenvalue problem seeks $(\lambda _{SM }(j),u_{SM }(j))\in {\mathbb {R}}_+\times V_h$ with

$$\begin{aligned} a_{SM }(u_{SM }(j),v_h)=\lambda _{SM }(j)b_{SM }(u_{SM }(j),v_h) \text { for all }v_h\in V_h\text { and } b_{SM }(u_{SM }(j),u_{SM }(j))=1. \end{aligned}$$

(7.1)

These quantities are computed and compared with the discrete eigenvalues $\lambda _h(j)$ of the lowest-order modified HHO method (1.3) with the bilinear forms of Proposition 6.2.

7.1.2 Setting the parameters of the modified HHO method

The computable condition $\sigma ^2\beta +\delta ^2\lambda _h(j)\le \alpha <1$ shows in Theorem 4.1 that the discrete eigenvalue $\lambda _h(j)$ of the new method (1.3) is a lower bound for the exact eigenvalue $\lambda (j)$ of (1.2). This condition restricts the choice of the parameters $0<\alpha <1$ and $0<\beta <\infty$. For right-isosceles triangles Lemma 6.4 shows that $\sigma \le \sqrt{72}/j_{11}\le 2.2145$ in (3.7) and $\delta \le \kappa \, h_{\max }$ in (2.4). The numerical bound $\kappa \le 0.1893$ from [27] slightly improves the analytical bound $\kappa \le 0.2983$ from [15] in the numerical experiments below. If $\lambda _{CR }(j)$ denotes the j-th Crouzeix–Raviart eigenvalue and $\lambda _h(j)$ the j-th eigenvalue of (1.3), Corollary 6.3 proves $\lambda _h(j)\le \lambda _{CR }(j)$. This means that on a given triangulation ${\mathcal {T}}$ with known $\lambda _{CR }(j)$, the parameter choice $0<\alpha <1$ and $\beta =(\alpha -\delta ^2\lambda _{CR }(j))/\sigma ^2>0$ leads to a guaranteed lower bound $\lambda _h(j)$ of the j-th exact eigenvalue $\lambda (j)$. If the parameters are chosen beforehand, the condition $\sigma ^2\beta +\delta ^2\lambda _h(j)\le \alpha$ may not be satisfied on a coarser mesh due to the impact of $h_{\max }$. In this case the computed value $\lambda _h(j)$ is replaced by zero (which is an obvious guaranteed lower bound).

7.1.3 Adaptive mesh refinement

Adaptive mesh refinement may recover optimal convergence rates. For the related Crouzeix–Raviart adaptive finite element method (AFEM) driven by the estimator $\eta$, whose local contributions for any $T\in {\mathcal {T}}$ of area |T| read

$$\begin{aligned} \eta ^2(T):=|T|\,\Vert \lambda _{CR }u_{CR }\Vert ^2_{L^2(T)}+|T|^{1/2}\sum _{F\in {\mathcal {F}}(T)}\Vert [\partial u_{CR }/\partial s]_F\Vert _{L^2(F)}^2, \end{aligned}$$

(7.2)

[17] proves optimality for the principal eigenvalue of the CR-EVP. Since the a posteriori error analysis for the new modified HHO method and the skeletal method [20] is left open, the refinement indicator (7.2) drives adaptive mesh-refinement in the AFEM algorithm [14, Algorithm 2.2] with Dörfler marking for bulk parameter $\theta =0.5$ (and $\theta =1$ for uniform refinement) and newest-vertex bisection. This refinement preserves the interior angles in the triangulation.

7.1.4 Displayed quantities

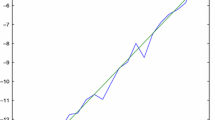
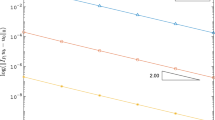
Figure 1 displays the initial triangulations ${\mathcal {T}}_0$ for the three numerical experiments below. The respective convergence history plots in Figs. 2, 4, and 6 display the difference of the exact eigenvalue and the various guaranteed lower bounds for uniform mesh refinement $\theta =1$ (solid line and filled markers) and adaptive mesh refinement $\theta =0.5$ (dashed line and striped markers) plotted against the number of triangles $|{\mathcal {T}}|$. On the uniform meshes the $GLBCR (j)$ (line color blue) and $\lambda _{SM }(j)$ (line color teal) coincide; see [20, Thm. 6.3]. The error $\lambda (j)-\lambda _h(j)$ (line color green) is replaced by $\lambda (j)$ if the condition in Theorem 4.1 is not satisfied for the chosen parameter. The number j of the eigenvalue is illustrated by different markers. Figure 8 exemplifies adaptive triangulations for the first eigenvalue on all the domains with $|{\mathcal {T}}|=1375$ triangles in (a), $|{\mathcal {T}}|=1421$ in (b), and $|{\mathcal {T}}|=1118$ in (c).

Fig. 2

L-shaped domain: comparison of the distance between $\lambda (j)$ and $\lambda _h(j)$ (computed with $\alpha =0.4$, $\beta =0.07$ (left) and $\beta =0.06$ (right)), $GLBCR (j)$ [16], and $\lambda _{SM }(j)$ [20] computed on uniform ($\theta =1$, solid) and adaptive ($\theta =0.5$, dashed) meshes with (7.2). Left: $\lambda (1)$. Right: $\lambda (103)=\lambda (104)=\lambda (105)$

Fig. 3

L-shaped domain: comparison of $GLBCR (1)$ and $\lambda _h(1)$ for parameter $\alpha$ varying in (0, 1) and $\beta =(\alpha -\delta ^2\lambda _{CR }(1))/\sigma ^2\in (0.001,0.199)$ on coarse uniform triangulations

Figures 3, 5, and 7 display a parameter study for the different domains. The figures compare the guaranteed lower bound $GLBCR (j)$ (which is on uniform triangulations the bound $\lambda _{SM }(j)$ in [20] marked by a dotted blue line) with the guaranteed lower bound $\lambda _h(j)$ (dotted green curve) computed with the new method and different choices of $\alpha$ (and $\beta =(\alpha -\delta ^2\lambda _{CR }(j))/\sigma ^2>0$ from Sect. 7.1.2). In these graphs the dot-density of the curves indicates on which triangulation ${\mathcal {T}}_{\ell }$ (the $\ell$-th uniform refinement of the initial triangulation ${\mathcal {T}}_0$) the values were computed. For comparison the eigenvalue approximation (assumed to be exact) is displayed as well (dark violet line).

Fig. 4

Slit domain: comparison of the distance between $\lambda (j)$ and $\lambda _h(j)$ (computed with $\alpha =0.4$, $\beta =0.07$), $GLBCR (j)$ [16], and $\lambda _{SM }(j)$ [20] computed on uniform ($\theta =1$, solid) and adaptive ($\theta =0.5$, dashed) meshes with (7.2). Left: $\lambda (1)$. Right: $\lambda (6)$

7.2 Experiments on the L-shaped domain

On the non-convex L-shaped domain $\Omega :=(-1,1)^2{\setminus } [0,1)\times (-1,0]$, the principal eigenvalue $\lambda (1)= 9.6397238389738806$ is computed with a $P_2$ finite element method on uniformly refined triangulations with Aitken extrapolation. The associated eigenvector is apparently in $H^1_0(\Omega )\setminus H^2(\Omega )$ resulting in the reduced convergence rate 0.8 for uniform mesh-refinement in Fig. 2a. As soon as the initial triangulation from Fig. 1a is refined three times, $\lambda _h(1)$ slightly improves the known bound $\lambda _{SM }(1)=GLBCR (1)$ on the uniform meshes. The adaptive mesh-refinement driven by the estimator (7.2) allows to recover the optimal convergence rate with the skeletal method in [20] and the modified HHO method. Remarkably, the modified HHO method with the parameter choice $\alpha =0.4$ and $\beta =0.07$ convinces with sharper bounds. In [36] the multiple eigenvalue $\lambda (103)=\lambda (104)=\lambda (105)=50\pi ^2$ and the associated eigenfunction in $C^\infty (\Omega )$ are presented. Figure 2b shows for these eigenvalues the optimal convergence rate of one with uniform mesh-refinement. The similar plots obtained with adaptive mesh-refinement are omitted for brevity. The parameter choice $\alpha =0.4$ and $\beta =0.06$ guarantees the condition $\sigma ^2\beta +\delta ^2\lambda _h(j)\le \alpha$ for $\lambda (103)=\lambda (104)=\lambda (105)$ on coarser meshes. Figure 3 illustrates that the new method improves all known guaranteed lower bounds for the principal eigenvalue on the L-shaped domain on at least three times uniform refined meshes for an appropriate parameter choice and that the parameter range that leads to improvement grows with mesh-refinement, but the improvement is more impressive on the coarser triangulation. For higher eigenvalues the parameter studies show similar results.

Fig. 5

Slit domain: comparison of $GLBCR (j)$ and $\lambda _h(j)$ for parameter $\alpha$ varying in (0, 1) and $\beta =(\alpha -\delta ^2\lambda _{CR }(j))/\sigma ^2\in (0.001,0.198)$ on coarse uniform triangulations

Fig. 6

First isospectral domain: comparison of the distance between $\lambda (j)$ and $\lambda _h(j)$ (computed with $\alpha =0.4$, $\beta =0.07$), $GLBCR (j)$, and $\lambda _{SM }(j)$. Left: $\lambda (1)$. Right: $\lambda (50)$

Fig. 7

First isospectral domain: comparison of $GLBCR (j)$ and $\lambda _h(j)$ for parameter $\alpha$ varying in (0, 1) and $\beta =(\alpha -\delta ^2\lambda _{CR }(j))/\sigma ^2\in (0.001,0.199)$

7.3 Experiments on the slit domain

On the non-convex slit domain $\Omega :=(-1,1)^2\setminus ([0,1)\times \{0\})$, the principal eigenvalue $\lambda (1)=8.371330522443726$ and the sixth $\lambda (6)=30.535991049204789$ are approximated with a $P_2$ finite element method on uniformly refined meshes and Aitken extrapolation for comparison. The first and sixth eigenfunction on the non-convex slit domain are obviously in $H^1_0(\Omega ){\setminus } H^2(\Omega )$. For uniform mesh-refinement, this leads to the reduced convergence rates 0.4 for the first in Fig. 4a and 0.6 for the sixth in Fig. 4b. The AFEM algorithm with bulk parameter $\theta =0.5$ driven by the estimator (7.2) allows to recover the optimal rates for both $\lambda _{SM }(j)$ and $\lambda _h(j)$, $j\in \{1,6\}$, in Fig. 4. The parameter choice $\alpha =0.4$ and $\beta =0.07$ allows to compute sharper bounds with the new method on finer meshes. The orange line illustrates that with the parameter choice $\alpha =0.4$ and $\beta =(\alpha -\delta ^2\lambda _{CR }(j))/\sigma ^2$, the discrete eigenvalue $\lambda _h(j)$ is a guaranteed lower bound on each triangulation. For the slit domain, Fig. 5 illustrates that the new method improves all known guaranteed lower bounds on the moderately (three resp. four times for $\lambda (1)$ and $\lambda (6)$) uniformly refined triangulation for an appropriate parameter choice with a wider range of appropriate parameters on a finer mesh.

Fig. 8

Adaptive triangulation ${\mathcal {T}}$ for $\theta =0.5$ of the L-shaped domain (a), the slit domain (b), and the first isospectral domain (c) computed for the first eigenvalue $\lambda _h(1)$ (with $\alpha =0.4$, $\beta =0.07$)

7.4 Experiments on the isospectral domains

The isospectral drums with the initial triangulation of Fig. 1c, d have the same eigenvalues. The paper [25] displays approximations for the first 25 identical eigenvalues on these domains and [36] gives the approximation $\lambda (50)=54.187936$. Figure 6 presents convergence plots for the error in the principal and the fiftieth eigenvalue. The first eigenfunction to the principal eigenvalue $\lambda (1)= 2.53794399980$ is in $H^1_0(\Omega ){\setminus } H^2(\Omega )$ and leads to the reduced convergence rate 0.8 for uniform mesh-refinement. The AFEM algorithm driven by (7.2) (after three uniform refinements to guarantee $\sigma ^2\beta +\delta ^2\lambda _h(j)\le \alpha$) recovers the optimal convergence rate for the direct lower bounds in Fig. 6a. In [36] are no remarks on the smoothness of the fiftieth eigenfunction. The numerical results displayed in Fig. 6b suggest that this eigenfunction is indeed in $H^2(\Omega )$. Uniform and adaptive mesh-refinement lead to optimal convergence rates. For brevity the adaptive results are not displayed. The parameter studies in Fig. 7 indicate that a parameter $0.1\le \alpha \le 0.5$ and an appropriate $\beta$ from Sect. 7.1.2 improve all known guaranteed lower bounds on refined meshes.

7.5 Conclusions

This subsection summarizes the empirical observations of the numerical experiments in Sects. 7.2–7.4.

• (i) All experiments confirm the a priori convergence rates of Theorem 5.1. The convergence rate depends only on the smoothness of the approximated eigenfunction. For instance in Figs. 2b and 6b, the optimal convergence rate is one for uniform refinement despite the reduced convergence rate in Figs. 2a and 6a for the principal eigenvalue in $H^1_0(\Omega ){\setminus } H^2(\Omega )$.

• (ii) Theorem 5.1 predicts a convergence provided the initial mesh is sufficiently fine. In all examples the convergence rate is visible for moderate triangulations, so this restriction does not affect the numerical examples too much.

• (iii) The parameter choice of Sect. 7.1.2 provides indeed guaranteed lower bounds in all numerical experiments and fully confirms Theorem 4.1.

• (iv) The guaranteed lower bounds computed with Theorem 4.1 do not always improve the known bounds by $\lambda _{SM }(j)$. The numerical examples suggest the conjecture that the new bounds are better for finer triangulations.

• (v) For the majority of the numerical experiments, the parameters $\alpha =0.4$ and $\beta \le \alpha /\sigma ^2-\delta ^2\lambda _h(j)/\sigma ^2$ lead to the best known guaranteed lower bounds for the eigenvalues.

• (vi) For the eigenfunctions in $H^1_0(\Omega ){\setminus } H^2(\Omega )$, the AFEM algorithm recovers the optimal convergence rates and illustrates the advantage of a direct lower bound compared to $GLBCR (j)$ in (1.1).

• (vii) This first realization of the new method concerns the lowest-order case and illustrates that the scheme can be competitive to other methodologies for the computation of guaranteed lower eigenvalue bounds. For the appropriate parameter selection, the scheme can provide the sharpest bounds in comparison to [16, 20]. Numerical benchmarks with the higher-order versions of the method suggested in the paper are even more promising provided the mesh is adapted appropriately and will be investigated in future research.