1 Introduction

Particle crushing is a key issue in the research of granular materials in civil engineering, mineral industry, and chemical industry. Large amounts of experiments have been carried out to investigate the crushing laws of granular materials since last century [1,2,3,4,5,6,7,8]. In recent decades, with the development of experimental science, some new technologies, such as X-ray technology and tomography technology, have been introduced into particle crushing studies [9,10,11]. With the aid of these technologies, the inside situation of granular specimens becomes visible in laboratory tests, while the evolution of inner flaws remains difficult to be traced clearly for the limitation of resolution ratio of X-ray and CT graphics. Besides, considering the limitation of equipment and research expenditure, some complex loading conditions are still unable to be achieved in laboratory. Hence, numerical experiments, in which the crushing process can be easily observed in multiscale views, become an important and effective supplemental means of particle crushing research.

In numerical research of granular materials, meshless methods, such as the discrete element method (DEM) [12], molecular dynamics (MD) [13, 14], as well as peridynamics (PD) [15], have been very popular. Furthermore, as the most matured method, the DEM has been widely used in particle crushing simulation for its congenital advantage in discontinuous medium modeling. In conventional DEM theory, the elementary ball is regarded as a rigid and uncrushable body. In order to model crushable particles, two methods are introduced into the DEM [16]: the agglomerate method [17,18,19,20,21] and the replacement method [22,23,24,25,26,27].

In the agglomerate method, a cluster of elementary balls are stuck together to form a macro-breakable grain. By reasonable designing of fragment size and shape, the simulation of particle crushing process can be very close to laboratory experiments [18, 28, 29]. Besides, the agglomerate method is also appropriate for the simulation of single-particle crushing. A famed agglomerate model, proposed by Potyondy [30], is known as the bonded particle method (BPM). Zhang et al. [31] proposed densely arranged BPM by introducing densely arrayed elementary balls into the BPM to simplify the calculation process and avoid the problem of inner void releasing. The replacement method was firstly put forward in MD by Tsoungui [24] and then introduced into the DEM. In this method, the crushed grains will be replaced by a group of smaller grains [24, 25, 32]. Compared with the agglomerate method, the number of particles needed in the replacement method is much smaller, which accelerates the computation speed of the replacement model [33]. It is worth noting that the grain failure criterion and replacing scheme are the most important issues in the replacement method [34, 35]. Several crushing criteria have been purposed and introduced into the replacement method [4, 22, 36]. For both agglomerate and replacement methods, the accuracy of DEM modeling is mainly based on the rationality and reliability of laws and characteristics of single-particle crushing strength and carrying capacity.

The Brazilian disc test is the most convenient and widely accepted way to investigate the crushing strength of single particles [1,2,3,4]. Plenty of Brazilian disc tests have been conducted in the past decades, and statistical data show that the distribution of grain crushing strength can be described by the Weibull distribution [1, 4, 6, 37]. Experimental results indicate that the Weibull characteristic strength of large-sized particles is lower than that of the smaller ones. The explanation for this phenomenon is that large-sized particles contain more inner defects, such as tiny flaws and weak planes, which may grow into macro-cracks under loadings [5, 38]. In order to simulate the size effect of particles, Lim et al. [39] proposed a method, in which the original flaws can be produced by deleting 0% to 25% elementary balls randomly. Wang et al. [40] and Kuang et al. [41, 42] reproduced the distribution of single-particle strength based on Lim’s method and investigated the relationship between particle strength and coordination number, while in fact, the inner porosity of most granular materials is less than 5%, and the introduction of original flaws by removing elementary balls will result in a statistical deviation of both void ratio and equivalent fragment diameter in DEM simulations. Therefore, the rationality of deleting elementary balls deserves further discussing.

Strength is an indigenous mechanical property of particles, and carrying capacity is the external expression of particle strength. Particle carrying capacity depends on both material strength and contact or loading conditions. Experimental investigations on the relationship between particle carrying capacity and its contact conditions are difficult to be conducted for the lack of specialized experimental equipment. Numerical experiments mainly focus on the effect of particle coordination number on carrying capacity. Some numerical investigations indicate that particle carrying capacity depends linearly on its coordination numbers, no matter whether the distribution of contact points is symmetric or not [40].

In this work, inhomogeneous bond stiffness and strength are introduced into the BPM, and the Weibull distribution, as well as the size effect of single-particle strength, is reproduced with this method. Several numerical experiments under complex contact conditions, including symmetric loading tests, asymmetric loading tests, and ball–ball Brazilian tests, are carried out to investigate the relationship between single-particle carrying capacity and contact conditions. The results show some interesting rules that differ from the conventional assumptions, and suggestions on the crushing criterion of particle crushing simulation with DEM are concluded at the end of this work.

2 Stress and Carrying Capacity

Granular material is a kind of non-continuum medium; hence, the stress of particles needs to be defined specially. In the DEM theory, the stress tensor of particles can be defined as Cundall and Strack [43] suggested:

$$\begin{aligned} \mathbf {\bar{{\sigma }}}_{ij} =\frac{1}{V}\sum \limits _{c=1}^{N_{\text{ c }} } {x_{i}^{(c)} F_{j}^{(c)} } \left( {i,j=1,2,3} \right) \end{aligned}$$
(1)

where \(\mathbf {\bar{{\sigma }}}_{ij} \) is the asymmetric average stress tensor of an individual ball; \(N_{\text{ c }} \) is the number of particle contact points, or the coordination number of a particle; \(x_{i}^{(c)} \) and \(F_{j}^{({c})} \) are the coordinate component and contact force component acting on the contact point, respectively; and V is the volume or area of particles.

Simplified particle stress formula is preferred in laboratory experiments, and tensile stress is assumed as the primary cause of particle crushing in the Brazilian tests. Jaeger [44] proposed a widely used formula to define the tensile strength of single particles:

$$\begin{aligned} \sigma _{\text{ f }} =\frac{F_{\text{ f }} }{d^{2}} \end{aligned}$$
(2)

where \(F_{\text{ f }} \) is the maximum reaction force acting on two loading points, and d is the diameter of a particle. It should be noted that Eq. (2) is only appropriate for the Brazilian tests, and the application of Eq. (2) under other contact conditions may result in intrinsic mistakes as particle crushing strength and criterion under complex loading conditions remain controversial. In some opinions, particle crushing is closely related to the inner tensile stress. Wang et al. [45] came up with a formula to measure the maximum tensile stress \(\sigma _{\text{ cen }} \) at the grain center:

$$\begin{aligned} \sigma _{\text{ cen }} ={\left( {\sigma _{\max } -3\sigma _{\min } } \right) } \big / 2 \end{aligned}$$
(3)

in which \(\sigma _{\max } \) and \(\sigma _{\min } \) are the maximum and minimum principal stress, respectively, while in other opinions, shear stress is regarded as the determining factor of particle crushing. McDowell [46] took the peak octahedral stress q as the stress index of particle strength:

$$\begin{aligned} q=\frac{1}{3}\left[ {\left( {\sigma _{1} -\sigma _{2} } \right) ^{2}+\left( {\sigma _{2} -\sigma _{3} } \right) ^{2}+\left( {\sigma _{3} -\sigma _{1} } \right) ^{2}} \right] ^{1 \big / 2} \end{aligned}$$
(4)

in which \(\sigma _{1} \), \(\sigma _{2} \), and \(\sigma _{3} \) are the three principal stresses. The principal stresses in Eqs. (3) and (4) can be derived from Eq. (1). It should be noticed that, in both Wang’s and McDowell’s theories, the criterion stress of a particle is assumed to be a constant even under different loading paths.

Particle carrying capacity can be measured by the maximum loading force [40,41,42]. In this work, the average loading force \(F_{\text{ ca }} \) is selected to represent particle carrying capacity:

$$\begin{aligned} F_{\text{ ca }} =\frac{1}{N_{\text{ c }} }\sum \limits _{c\subset N_{\text{ c }} } {\left\| {{{\varvec{F}}}^{c} } \right\| } \end{aligned}$$
(5)

where \(N_{\text{ c }} \) is the coordination number of a particle and \({{\varvec{F}}}^{c} \) is the contact force vector acting on a contact point.

3 Single-Particle Crushing Strength

As a kind of heterogeneous materials, an individual particle always contains several kinds of minerals, binders, and internal flaws, and these defects always induce a dispersion of mechanical properties of grains. For the purpose of describing crushing strength of particles, a particle model based on densely arrayed BPM considering the inhomogeneity of material properties is introduced in this section, and the distribution and size effect of particle crushing strength are reproduced by simulations of the Brazilian test.

3.1 DEM Modeling with Inhomogeneous Properties

As the deviation of both void ratio and fragment equivalent diameter will be introduced, it is inappropriate to simulate the inhomogeneous clump by deleting elementary balls. In this section, the inhomogeneity of materials is achieved by introducing inhomogeneous material parameters into densely arrayed BPM, with which the inherent nature of particle crushing strength can be reproduced without introducing undesirable statistical deviation. As granular material is a kind of friction materials, the cohesive force between particles and contacting objects can be ignored, and the contacting force can be described by friction coefficients and contacting stiffness. The parallel-bond model is selected as the clump bond model in this work for its advantage in the DEM simulation for geotechnical materials [20, 47]. The parallel bond can be defined by six parameters [48]: bond normal stiffness \(\bar{{k}}_{\text{ n }} \), bond shear stiffness \(\bar{{k}}_{\text{ s }} \), tensile strength \(\bar{{\sigma }}_{\text{ c }} \), cohesion c, friction angel \(\phi \), and bond radius \(\bar{{r}}\). The bond shear strength \(\bar{{\tau }}_{\text{ c }} \) can be calculated from cohesion, friction angel and normal stress. If the maximum tensile stress \(\bar{{\sigma }}_{\max } \) exceeds bond normal strength \(\bar{{\sigma }}_{\text{ c }} \), or the maximum shear stress \(\bar{{\tau }}_{\max } \) exceeds bond shear strength \(\bar{{\tau }}_{\text{ c }} \), parallel bonds will break, and the accompanying force, moment and stiffness of those bonds will vanish. The selection of parameters in this work takes both DEM theory and experimental results into consideration, and follows the suggestions of Lisjak [17] and Potyondy [20] at the same time. After a number of attempts, parameters of elementary balls and bonds are finally determined, as shown in Table 1. The inhomogeneously distributed stiffness and strength of each bond obey Gaussian distribution, with values ranging from 0.4 to 1.6 times of the average values in Table 1, as Fig. 1a shows. Bonds with low strength or low stiffness represent weak planes inside particles, and the initial structural defects can be introduced by those inhomogeneous bond parameters.

Seventy Brazilian tests are carried out to reproduce the distribution of particle crushing strength, as Fig. 1b shows. The diameters of particles range from 1.4 to 1.7 mm, and the diameter of uniformly sized elementary balls is 0.1 mm. The loading speed of top wall is 1.0 mm/min toward the particle center.

Fig. 1
figure 1

Brazilian test of single particle: a the inhomogeneous distribution of bond normal stiffness; b the agglomerate particle model

Full size image
Table 1 Parameters of single-particle Brazilian tests
Full size table

3.2 Strength Distribution and Size Effect

Numerous experimental studies indicate that single-particle crushing strength obeys the Weibull distribution law. Nakata [1] proposed a formula to describe the strength distribution of uniformly sized particles:

$$\begin{aligned} P_\mathrm{s} =\exp \left[ {-\left( {\frac{\sigma }{\sigma _{0} }} \right) ^{m}} \right] \end{aligned}$$
(6)

where \(P_\mathrm{s} \) is the survival probability of a particle under stress \(\sigma \), m is the Weibull modulus, and \(\sigma _{0} \) is the characteristic stress under which 37% of the tested particles survive.

The normalized crushing strength of seventy particles is drawn in Fig. 2, in contrast to Nakata’s experimental results [3]. The features of two curves are similar. The Weibull modulus and characteristic strength are 3.51 and 32.92 MPa in the DEM simulation and 3.04 and 30.96 MPa in Nakata’s experiment, respectively. The numerical result indicates that, in a statistical sense, particle strength distribution can be reproduced by densely arranged BPM by considering the inhomogeneity of bond parameters.

Fig. 2
figure 2

Normalized tensile strength distribution of single particles

Full size image

The characteristic strength of particles is size-dependent. In order to investigate the relationship between particle diameter and characteristic strength, more Brazilian test simulations are conducted with different-sized particles. The relationship between particle size and characteristic strength, as well as Weibull modulus are plotted in double logarithmic coordinates as Fig. 3 shows, in comparison with the quartz tests of Nakata [3]. It can be seen from Fig. 3a that particle characteristic tensile strength is exponentially dependent on particle size, and similar relationship is also reflected between Weibull modulus and particle size.

Fig. 3
figure 3

Size effect on particle tensile strength: a relationship between characteristic strength and particle size; b relationship between Weibull modulus and particle size

Full size image

Therefore, in summary, by introducing inhomogeneous bond properties to the DEM modeling, particle strength distribution and size effect can be reproduced well with the BPM. The DEM simulation results present similar characteristics and changing tendency with laboratory tests, indicating that the densely arrayed BPM considering inhomogeneous stiffness and strength properties is reliable and robust in single-particle crushing tests. Unless particularly stated, the models and material properties in the following numerical experiments are the same with those in this section.

4 Wall–Ball Loading

The amount and distribution of coordination points present significant influence on particle carrying capacity. In this section, a number of wall–ball loading tests, including symmetric loading tests and asymmetric loading tests, are conducted to investigate the relationship between particle carrying capacity and its contact conditions.

4.1 Symmetric Loading

As the simplest contact condition, symmetric contact condition is chosen to investigate the relationship between particle carrying capacity and coordination number. Five groups of spherical particles are crushed in symmetric loading path with regular polyhedron boxes, and the shapes of boxes are regular tetrahedron, hexahedron, octahedron, dodecahedron and icosahedron, respectively. In these simulations, the peak average reaction force \(F_{\text{ ca }} \), the maximum octahedral stress q, and the maximum grain center tensile stress \(\sigma _{\text{ cen }} \) are taken into statistics. Similar to particle tensile strength, particle carrying capacity can also be described by the Weibull distribution. Figure 4 records the characteristic values of \(F_{\text{ ca0 }} \) in five groups of simulations. It can be noticed that \(F_{\text{ ca0 }} \) monotonously increases with \(N_{\text{ c }} \), and particle carrying capacity and its coordination number are almost linearly related.

Fig. 4
figure 4

The relationship between particle carrying capacity and coordination number under symmetric loading

Full size image

Figure 5 exhibits the relationship between characteristic octahedral stress \(q_{0} \) and characteristic grain center tensile stress \(\sigma _{\text{ cen0 }} \) in symmetric loading tests. Two stress indexes present the same linearly changing trends with the increase of coordination number. It should be pointed out that the grain center tensile stress \(\sigma _{\text{ cen }} \) in all symmetric loading tests are negative, which indicates that no tensile stress exists in particle center when crushing occurs. Therefore, the assumption that particle crushing is caused by particle central tensile stress seems to be incorrect. Besides, the approximately linear relationship reflected in Fig. 5 indicates that stress indexes are inappropriate for particle crushing judgment. Because when particles are about to break under different loading conditions, stress indexes cannot keep constant, which runs counter to the definition and assumption of crushing criterion.

Fig. 5
figure 5

The relationship between stress index and particle coordination number: a octahedral stress; b grain center tensile stress

Full size image

A particle, generated with random seed 1031, is selected to investigate the crushing behavior of single particles. The crushing states of five particles when \(F_{\text{ ca }} \) reaches their peaks are shown in Fig. 6, in which the small disks inside clumps are discrete fracture network (DFN), and the red and black disks represent tensile and shear bond failures, respectively. Coordination number also shows influence on the category of particle crushing. The inner particle crushing can be divided into three categories [49]: fracture, attrition and abrasion. In Fig. 6, the fractures in tetrahedron, hexahedron, and octahedron mainly concentrate in certain areas near the contact points, and the main category of failure is attrition. While the distribution of fractures in dodecahedron and icosahedron is more homogeneous, and with the increase of coordination number, the type of particle crushing changes from fracture and attrition to abrasion gradually.

Fig. 6
figure 6

Particle compression tests with regular polyhedron boxes

Full size image

The peak values of \(F_{\text{ ca }} \) and the corresponding amounts of DFN are listed in Table 2. It can be noticed that the selected particle shows some features that differ from statistical laws. Unlike the characteristic reaction force \(F_{\text{ ca0 }} \), the peak reaction force shows a wavelike rising tendency with the increase of coordination number. The peak reaction forces of regular tetrahedron, hexahedron, and octahedron keep at relatively low level, as well as the number of fractures, while the peak average reaction force in dodecahedron and icosahedron tests exhibits a leapfrogging increase, and the particle carrying capacities are much higher than those in other three tests.

Table 2 Peak reaction force and bond failure events of symmetric loading tests
Full size table

To sum up, the numerical results of symmetric loading experiments indicate that coordination number has significant influences on the failure category and carrying capacity of particles. Particles with a larger coordination number are harder to be crushed integrally and can bear more cracks before losing their strengths. Particle carrying capacity, as well as stress indexes, shows a positive and almost linear relation with the coordination number in symmetric tests, which indicates that the stress indexes cannot be regarded as a particle crushing criterion. Besides, for one single particle, this monotone and positive correlation may not be correct all the time. Size can only decide the characteristic strength of particles, rather than the crushing strength and carrying capacity for one certain particle.

4.2 Asymmetric Loading

The particle crushing issues discussed above are all under absolutely symmetric contact conditions. Although the simplified crushing criterions are very popular in the replacement method, the symmetric loading condition is infrequent in actual grain crushing cases. In this part, asymmetric loading tests, including asymmetric multipoint loading tests and non-parallel Brazilian tests, are carried out to investigate the influence of loading asymmetry on particle crushing.

The asymmetric multipoint loading tests are realized by deleting one of the loading walls in symmetric multipoint tests randomly. As the tetrahedron box cannot hold a sphere clump any more after losing a plane, it is not considered in the asymmetric tests. The characteristic reaction force in asymmetric loading tests is recorded in Fig. 7, compared with symmetric loading tests. The average force \(F_{\text{ ca }} \) and particle coordination number are positively related in the asymmetric tests, similar to those in Fig. 4. The values of \(F_{\text{ ca }} \) in asymmetric tests are much lower than those in symmetric tests. This is in accordance with the common sense, but differs from the results of former research [40].

Fig. 7
figure 7

Particle carrying capacity in asymmetric loading tests: a the relationship between reaction force and coordination number; b comparison of \(F_{\text{ ca0 }} \) in symmetric and asymmetric loading tests

Full size image

Asymmetric contact conditions always induce asymmetric stress distribution. The stress indexes in asymmetric tests are recorded in Fig. 8. The characteristic octahedral stress \(q_{0} \) presents an increase with the increase of coordination number, while the grain center tensile stress \(\sigma _{\text{ cen }} \) shows totally different changing tendency. In the four series of simulations, there exists positive \(\sigma _{\text{ cen }} \) in Fig. 8b, which means that tensile stress appears in some particles. However, as the sign of \(\sigma _{\text{ cen }} \) keeps changing, it is impossible to describe \(\sigma _{\text{ cen }} \) with the Weibull distribution. Besides, the values of stress indexes are much lower than those in the symmetric tests, and also do not keep constant.

Fig. 8
figure 8

Relationship between stress index and particle coordination number in asymmetric tests: a octahedral stress; b grain center tensile stress

Full size image

DFNs of the particle with random seed 1031 under asymmetric multipoint loading conditions are imaged in Fig. 9. The reaction force, bond failure events, and stress indexes of this particle are listed in Table 3. Compared with Fig. 6 and Table 2, particles under asymmetric contact conditions lose much carrying capacity, but hold more fractures before being crushed. Similar to the symmetric tests, the category of particle crushing in asymmetric tests changes from fracture and attrition to abrasion with the increase of coordination number.

Fig. 9
figure 9

DFN distribution in asymmetric multipoint loading tests

Full size image
Table 3 Reaction force, bond failure, and stress indexes in asymmetric multipoint loading tests
Full size table

In some replacement methods, particles with the coordination number of two are assumed to obtain the same carrying capacity ignoring the symmetry of contact points. In this work, the assumption is tested by non-parallel Brazilian experiments. Several groups of spherical particles are crushed by non-parallel loading planes, and the asymmetry is characterized by the dip angle \(\alpha \) of the top plane, which ranges from \(2^{^{\circ }}\) to \(12^{^{\circ }}\), as Fig. 10 shows. DFN connects two loading points and the center of particles in non-parallel Brazilian tests. The characteristic reaction force in non-parallel Brazilian tests is recorded in Fig. 11. It can be seen that \(F_{\text{ ca0 }} \) of non-parallel Brazilian tests is lower than that of the conventional Brazilian tests and reduces monotonically with the increase of dip angle. Moreover, the angle between two planes shows remarkable influence on particle carrying capacity, and the assumption that particles with two contact points have the same carrying capacity is inconsiderable.

Fig. 10
figure 10

DFN of particles with random seed 1031 in non-parallel Brazilian tests

Full size image
Fig. 11
figure 11

The relationship between particle carrying capacity and plane dip angle

Full size image

The results of asymmetric multipoint loading tests and non-parallel Brazilian tests indicate that asymmetric contact conditions will lower the carrying capacity of particles. Stress indexes in asymmetric loading tests are also not constants, which is in accordance with the results derived from Sect. 4.1. The assumption that particles with two coordination points have constant carrying capacity is also invalid in this section. In other words, criterion stress may only be applicable for some specific occasions, but no longer appropriate for general particle crushing cases.

5 Ball–Ball Loading

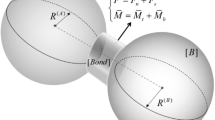
For granular materials, the proportion of wall–ball contact is relatively small, while the ball–ball contact accounts for the majority of contact. The crushing strength and carrying capacity of particles are associated with the relative size of their neighbors, and the relative size can be quantified by radius ratio \(R_{\text{ r }} \) as follows:

$$\begin{aligned} R_{\text{ r }} ={r_{\text{ n }} } \big / r \end{aligned}$$
(7)

in which r and \(r_{\text{ n }} \) are the radii of an individual particle and its neighboring particle, respectively. The ball–ball Brazilian tests are conducted as Fig. 12 shows, in which a crushable clump is clamped and crushed by two rigid balls.

Fig. 12
figure 12

Schematic diagram of ball–ball Brazilian test

Full size image

Eleven groups of particles with radius ratio ranging from 0.1 to 10 are crushed in the ball–ball Brazilian tests, and their characteristic reaction forces are recorded in Fig. 13. The characteristic values of \(F_{\text{ ca0 }} \) monotonously increase with the radius ratio \(R_{\text{ r }} \), which is consistent with the understanding that particles are more easily to be crushed by sharper objects. The relationship between \(F_{\text{ ca0 }} \) and \(R_{\text{ r }} \) is approximately linear in semi-logarithmic coordinate.

Fig. 13
figure 13

Relationship between particle carrying capacity and radius ratio

Full size image

DFNs of the particle with random seed 1031 in the ball–ball tests are imaged in Fig. 14. Most bond failures occur within a narrow columnar space, and the crushing category of particles in all ball–ball Brazilian tests is fracture absolutely. The evolution of DFN distribution indicates that radius ratio shows an impact on the occurrence and evolution of particle inner cracks.

Fig. 14
figure 14

DFN of ball–ball Brazilian tests with different radius ratios

Full size image

The position where internal fracture initiates in the Brazilian test remains controversial. Hudson [50] found that the initiation of crack always locates near the loading points in the Brazilian disc tests, and this point of view is supported by the work of Klaus [51] and Swab [52]. Another viewpoint is that the position of the first microcrack locates at the maximum shear stress point, which is about 0.2 times of particle radius away from the loading points, and this viewpoint receives theoretical and experimental support from Markides [53], Li [54], and Lin [55]. Both opinions above are manifested by the ball–ball crushing tests in this work. It can be noticed in Fig. 8 that cracks grow from both ends to the center of sphere clumps if \(R_{\text{ r }} \) is less than 2.0, while bond failures mainly concentrate in the central area of particles if \(R_{\text{ r }} \) is greater than 2.0. Moreover, the fracture region moves from two loading points to the particle center with the increase of \(R_{\text{ r }} \), which indicates that the crack growth paths are not unique, but significantly affected by contact conditions.

6 Conclusion

This paper mainly focuses on investigating the problem of single-particle crushing strength and the influence of particle contact conditions on carrying capacity. From the numerical experiments and analysis, the following conclusions can be drawn.

  1. 1.

    Densely arrayed BPM considering the inhomogeneous bond parameters shows its advantage in reproducing the Weibull distribution and size effect of single-particle crushing strength. This method does not need making flaws by deleting elementary balls or introducing extra inner voids.

  2. 2.

    Particle carrying capacity increases linearly with coordination number in both symmetric and asymmetric multi-position loading tests. The asymmetry of contact conditions reduces particle carrying capacity significantly. Both results of symmetric and asymmetric tests show that the relationship between particle carrying capacity and coordination number cannot be simply described as linear. The octahedral stress and grain center tensile stress are inaccurate as a particle crushing criterion. For a single particle, equal coordination number does not mean the same carrying capacity. The oversimplified assumptions and crushing stress criteria are proved to be inconsistent with facts.

  3. 3.

    Contact conditions present influence on particle crushing categories. For particles with lower coordination number, fracture and attrition are the main crushing categories, while with the increase of coordination number, abrasion becomes the main crushing category, and particles can bear more cracks before losing their carrying capacity in such cases.

  4. 4.

    The particle carrying capacity is exponentially related with the relative size of its neighbors. Besides, radius ratio presents obvious effect on the origin and evolution of particle inner cracks. The crack growth paths in ball–ball loading tests are not unique, and the origin position of initial cracks moves gradually from loading points to particle center with the increase of radius ratio.

The DEM numerical studies considering inhomogeneous bond parameters exhibit notable laws and features of single-particle crushing in this work. Particle crushing strength and carrying capacity are not only related to particle inherent nature, but also influenced by contact conditions. This work may help establish more reasonable particle crushing criteria, and the connections between crushing issues of single particles and granular materials still demand further study.