A stochastic SPOD-Galerkin model for broadband turbulent flows

Abstract

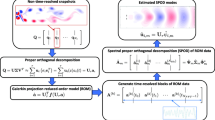
The use of spectral proper orthogonal decomposition (SPOD) to construct low-order models for broadband turbulent flows is explored. The choice of SPOD modes as basis vectors is motivated by their optimality and space-time coherence properties for statistically stationary flows. This work follows the modeling paradigm that complex nonlinear fluid dynamics can be approximated as stochastically forced linear systems. The proposed stochastic two-level SPOD-Galerkin model governs a compound state consisting of the modal expansion coefficients and forcing coefficients. In the first level, the modal expansion coefficients are advanced by the forced linearized Navier-Stokes operator under the linear time-invariant assumption. The second level governs the forcing coefficients, which compensate for the offset between the linear approximation and the true state. At this level, least squares regression is used to achieve closure by modeling nonlinear interactions between modes. The statistics of the remaining residue are used to construct a dewhitening filter that facilitates the use of white noise to drive the model. If the data residue is used as the sole input, the model accurately recovers the original flow trajectory for all times. If the residue is modeled as stochastic input, then the model generates surrogate data that accurately reproduces the second-order statistics and dynamics of the original data. The stochastic model uncertainty, predictability, and stability are quantified analytically and through Monte Carlo simulations. The model is demonstrated on large eddy simulation data of a turbulent jet at Mach number $M=0.9$ and Reynolds number $\mathrm {Re}_D\approx 10^6$.

Stochastic SPOD-Galerkin two-level model for rank 2\(\times \)129 and rank 3\(\times \)129 cases

This appendix reports the additional results for the rank $2\times 129$ and rank $3\times 129$ cases, which were omitted in Sect. 4.3 for brevity. Figure 16a–d show the comparison between the power spectra of the state coefficients $\varvec{a}_i$ and the rank $2\times 129$ expansion coefficients at different frequencies. Figure 16e–h report the corresponding results for the rank 3$\times$129 case. Good agreements between the approximations and models are observed in both cases. The corresponding SPOD eigenvalue spectra shown in Fig. 16i,j show that both models accurately reproduce the eigenvalue spectra of the LES data for a wide range of frequencies. From these observations and the favorable results obtained for the $1\times 129$ baseline model, as previously reported in Figs. 10 and 15, it concluded that subdominant SPOD modes are not required in the modal expansion.

Fig. 16

Power spectra of the state coefficients $\varvec{a}_i$ of low-rank approximations (red) and 2–level models (black) of rank 2$\times$129 (first row) and rank 3$\times$129 (second row) at four representative frequencies: a,e $St=0.2$; b,f $St=0.41$; c,g $St=0.63$; d,h $St=0.85$. Comparison of SPOD eigenvalue spectra of the LES data (black), low-rank approximations (blue) and 2–level models (red): i rank $2\times 129$; j rank $3\times 129$. Compare Figs. 10, 12 and 15