1 Introduction

Boundary lubrication (BL) is frequently observed but also a very complex matter to study. There is an interplay between contact mechanics, frictional heating, physical and chemical adsorption, chemical reactions, and wear processes. Most investigations of boundary lubrication are experimental. Due to the large number of parameters controlling the tribofilm growth and removal, it is very difficult to cover all cases experimentally. Modelling the very complex mechanisms of BL has been an almost impossible task, but during the past 10 years, the progress has been substantial. Andersson et al. [1] is one example of successful modelling attempts. In [1] and in other similar models [2, 3], it is possible to compute contact pressure, tribofilm formation and removal, and wear of surfaces. One important parameter in these models is the interface temperature because it controls tribofilm formation, mechanical properties of surfaces, and the onset of scuffing. The tribofilms can be generated at room temperatures due to the sliding contact between two surfaces, as shown by Fujita and Spikes [4]. The temperature rise due to the frictional heat at the asperity contact is short in duration but can be of very high magnitude, thus directly influencing many of the contacting surfaces mechanical and chemical properties.

Many attempts have been made to calculate the flash temperature rise theoretically. Some of the earliest reported works are those of Blok [5], Jaeger [6], and Archard [7]. These have led to numerous analytical equations that use the concept of moving heat sources to describe local asperity temperature rise in semi-infinite and insulated bodies. One important factor that plays a vital role in the development of the flash temperature is the effect of surface roughness. It has been previously shown by Ray et al. [8] that surface roughness parameters, such as the average surface roughness and mean summit curvature, can significantly affect the maximum temperature rise in sliding bodies. One of the very first attempts made on incorporating the effect of surface roughness was done by Aramaki et al. [9], Sinclair [10], and Lee [11] who investigated the effect of multiple heat sources on the maximum rise of contact temperatures.

Blok’s postulate has been used in [12] to study the maximum and average steady-state surface temperatures of moving heat sources of different geometries. In another similar framework, the steady temperatures of circular and elliptic contacts have been obtained by matching the surface temperature of both solids in [13, 14]. They utilized the work of Carslaw and Jaeger [15]. In [15], the contact spots are modelled as heat sources and the geometries of the contacting surfaces are assumed to be insulated and semi-infinite in size. These analyses, however, did not consider the influence of surface roughness on the contact temperature rise. The transient heat conduction problem is also interesting and has been studied for elliptical contacts by Bosman and Rooij [16]. Some of the most important works in the calculation of 3D transient flash temperature rise in rough surfaces have been done by Gao and Lee [17], Liu and Wang [18], and Waddad et al. [19, 20]. All of them have used equations that were derived by Carslaw and Jaeger [14]. However, because these expressions are only valid for insulated and semi-infinite bodies, their results may not prove accurate, as shown in [21]. In [21], it is shown that the Carslaw and Jaeger solutions are only valid for very short sliding times and that the heat source position plays a major role in the accuracy of the solution. For this reason, it would be preferred to instead switch to Fourier’s law of heat conduction and use the finite element method (FEM). The benefits of using finite element modelling are numerous, such as easily implementing different boundary conditions as well as the ability to work with very complex geometries. One of the earliest attempts of thermal modelling with the FEM was done by Kennedy and Ling [22], who studied the transient temperature rise in disc brakes. An attempt to use FE modelling to study the thermal effect of surface roughness was done by Ray et al. [23]. They carried out experiments and numerical analyses to find the maximum surface temperatures of different rough surfaces. Their analysis does, however, not seem to provide adequate correlation between the numerical and experimental analysis and does not give any clear information of how the temperature develops at the individual asperities. Straffelini and Velinski [24] conducted a thermal experiment of a pin-on-disc system and then used the results to validate a FEM-based numerical approach. In their analysis, however, they did not study the flash temperature development at the asperity level. A multi-scale thermal model was proposed by Lumbreras et al. [25] in which two simulations were performed separately. In their analysis, a macro simulation of a ball-on-disc system with a coarse grid was first performed with a uniform load. Later, the bulk temperature at the contact points was used as an initial condition to a second much smaller thermal model that calculated much higher flash temperatures due to the surface roughness. According to their study, using the bulk temperatures from the first large domain as an initial condition to the much smaller second domain was a way to account for the influence of the rest of the part in their bulk temperature model. Their analysis of the flash temperature model is, however, limited to very short sliding distances and thus may not be useful for studying the temperature development over longer times or until a steady state is reached.

The present work uses a contact mechanics solver developed by Sahlin et al. [26] and Almqvist et al. [27], which assumes that the contacting bodies are elasto-plastic. The solver was, thereafter, verified in [28]. This state-of-the-art model has been used in many recent investigations [29,30,31,32,33] and was further developed by Almqvist et al. in [34]. The detailed described surface topographies of the interacting bodies are among the many inputs required by the contact mechanics solver. The surface topographies are obtained with the method developed by Pérez-Ràfols and Almqvist [35] which generates random surfaces based on the given height probability distribution.

1.1 Research Questions and Objectives for the Present Work

After investigating all of the mentioned previous works, the following research questions arise:

  1. 1.

    How does the flash temperatures at the asperities (i.e. micro-scale contact) depend on the interface temperature of the macro-scale contact at all times? The maximum contact temperature at the local asperities should strongly depend on the size and shape of the whole contact. In a realistic mechanical contact between two sliding surfaces, the whole contact domain can be very large compared to the local asperities. It can be very problematic and extremely time-consuming to simulate both large mechanical systems as well as having a satisfactory fine mesh grid on the interface to capture all local asperities there as well. For this reason, this is identified as a research gap and will be one of the main topics of this paper.

  2. 2.

    How does the surface topography affect the relationship described in Research question 1.? It is still unclear how the temperature development of individual asperities changes due to certain roughness parameters. This is an important question because it guides the engineer on what type of surfaces can be considered best from the temperature point of view for mechanical applications.

  3. 3.

    Is it possible to develop a multi-scale model that can be experimentally or analytically verified? There is still no multi-scale model that can be experimentally or analytically verified.

From these research questions, the objectives for the present work are summarized in the following:

  • To develop an accurate multi-scale transient heat conduction model that can be used for accurate simulations in the contact between rough sliding surfaces. The associated numerical solution procedure should be memory inexpensive.

  • To apply the model to find a relationship that couples the temperature development of the macro scale to the temperature development of the micro-scale (asperity contact) at all times until a steady state arises.

  • To use the model to study the effect of surface roughness on the maximum flash temperature rise.

  • To validate the macro-scale contact model against experimental results.

1.2 Originality and Significance of the Present Work

The originality of the model presented in this paper lies in its ability to predict the micro- and macro-scale temperatures, for various types of complex sliding systems, quickly and efficiently. The present work proposes a method that can account for wear in a way that saves computational time and gives verifiable results in which, to the authors best knowledge, no one has done before. The thermal model can, for example, be coupled with wear simulations and compute tribofilm formation in boundary lubricated contacts. It can also be used to simulate temperature development in many thermo-mechanical events such as brakes and other sliding systems. Last but not least, it is worth mentioning that the model presented will be validated against existing theoretical [12, 13] and experimental results [24]. It should also be mentioned that the model can be further generalized by including any type of boundary conditions such as heat loss through convection and radiation.

2 Basic Theory

For a full description of the theory, the author refers to separate papers listed in the subsections below.

2.1 Contact Mechanics

The contact mechanics model is based on [26] and [27], where a mixed lubrication contact mechanics model for linear elastic and perfectly plastic rough surfaces was developed. In short, the main problem is to minimize energy, i.e.

$$\mathop {\min }\limits_{{0 \le p \le P_{L} }} \left( f \right) = \mathop {\min }\limits_{{0 \le p \le P_{L} }} \left( {\frac{1}{2}\int\limits_{\Omega } {pudS} \int\limits_{\Omega } {pgdS} } \right),$$
(1)

where u is the elastic normal deformation, p is the pressure, g is the gap between the undeformed surfaces, and PL is the hardness of the softer of the contacting bodies. In the case of a 3D contact between two elastic half-spaces the normal deformation u can be modelled as

$$u\left( {x,y} \right) = \frac{1}{{\pi E^{*} }}\mathop {\iint }\limits_{ - \infty }^{\infty } \frac{{p\left( {x^{\prime},y^{\prime}} \right)}}{{\sqrt {\left( {x - x^{\prime}} \right)^{2} + \left( {y - y^{\prime}} \right)^{2} } }}{\text{d}}x^{\prime}{\text{d}}y^{\prime},$$
(2)
$$\frac{1}{{E^{*} }} = \frac{{1 - \vartheta_{1}^{2} }}{{E_{1} }} + \frac{{1 - \vartheta_{2}^{2} }}{{E_{2} }},$$
(3)

where \({E}^{*}\) is the combined elastic modulus of the bodies with elastic modulus \({E}_{i}\) and Poisson ratio \({\vartheta }_{i}\). When discretized, Eq. (2) can be considered as a discrete convolution which can be calculated by an FFT routine to speed up the numerical solution procedure.

2.2 Interface Temperature

The temperature field in a body with density ρ, thermal conductivity k, velocity v, and specific heat capacity cp, without internal heat generation may be modelled with the conservation equation describing the balance of energy, i.e.

$$\rho c_{p} \left( {\frac{\partial T}{{\partial t}} + v\nabla T} \right) = \nabla \cdot \left( {k\nabla T} \right).$$
(4)

With specified boundary conditions such as external heat sources and heat loss through convection and radiation, Eq. (4) can be discretized and solved numerically with the finite element method. In the case of sliding, the frictional heat per unit area generated at the interface between the contacting bodies is defined as

$$q = vp\mu ,$$
(5)

where q is the total heat (i.e. thermal load) generated due to sliding velocity v, contact pressure p, and \(\mu\) is the friction coefficient. The thermal load can be applied at the contact interface between surface 1 and surface 2 according to

$$q = - k\frac{\partial T}{{\partial n}},$$
(6)

where q is the thermal load applied on the interface and k is the thermal conductivity. The thermal load can be interpreted as a boundary heat source and, depending on the contact situation and material properties, the total thermal load q will be partitioned between the two surfaces as q1 and q2 such that q1 + q2 = q. When solving Eq. (4) with the Finite Element Method, the partitioning of the total thermal load q is automatically taken into account and therefore no prior calculation of the thermal load partitioning is needed.

2.3 Wear Model

Originally developed by Archard and Holm in the 1950s [36], Archard’s law of wear has become one of the most common and fundamental models to describe wear in a sliding system. Archard’s law of wear states that the wear depth increment Δh is proportional to the sliding velocity v, time step Δt, and pressure p, i.e.

$$\Delta h = \frac{K}{{P_{L} }}pv\Delta t,$$
(7)

where K is a dimensionless coefficient of wear.

3 Methodology

The general methodology can be summarized as follows:

  1. 1.

    Define the macro-scale problem. This can be any type of contact between bodies of any size, shape, and with any kinematic condition. Surface roughness will not be included in this model.

  2. 2.

    Choose any small spot in the contact where the effect of surface roughness is most interesting and increase the number of mesh elements in that region. This region will be referred to as the “cell” containing the micro-scale contact model.

  3. 3.

    Define surface roughness according to the method developed in [35] with certain roughness parameters and solving the contact mechanic problem [26, 27] over an area equal to the cell area.

  4. 4.

    Use the contact pressure distribution from step 3 and use Eqs. (8)–(9) to apply it as input in the cell of the thermal model.

  5. 5.

    Solve the thermal model equations.

Figure 1 shows an example of a macro-scale contact problem where the upper body is stationary while the lower body has a prescribed velocity v.

Fig. 1
figure 1

An example of a macro-scale contact problem. The lower body is moving at a speed of v while the upper body is stationary. The red line indicates contact and \({q}_{M}\) is the spatially dependent thermal load generated due to frictional force

Full size image

Figure 2 shows the micro-scale contact problem, a magnified part of the contact shown in Fig. 1. It can be seen that the cell, which is shown in the middle, has a significantly finer grid size and that only a few points are in contact (contact is shown as a red line and an arrow). This is the only region where the surface roughness will be included and thus assess the flash temperatures. The rest of the contact is modelled as smooth and has a coarse grid and each element has a prescribed thermal load. The constant thermal load for each element is determined from the macro-scale problem. Notice that the thermal load does not necessarily need to be the same for each coarse element, as the pressure distribution may not be uniform (such as with the Hertzian contact in Fig. 1). In the case of a uniform contact, the average thermal load is equal everywhere in the whole contact region.

Fig. 2
figure 2

A cross-section along the contact zone parallel to the sliding direction in the macro-scale contact problem. The dashed line is the boundary of the cell and the interior defines the micro-scale contact problem. A thermal load is prescribed for each element. Outside the cell the grid is coarse and the thermal load at the element indexed (m,n) is \({q}_{M}({x}_{m},{y}_{n})\), given by Eq. (9). Inside the cell, the thermal load \({q}_{m}({x}_{i},{y}_{j})\), is given by Eq. (8), indicating that there is contact between the surfaces at index (i,j)\(({p}_{m}>0\))

Full size image

The total thermal load in the cell interface is calculated as follows:

$$q_{m} \left( {x_{i} ,y_{j} } \right) = \mu p_{m} \left( {x_{i} ,y_{j} } \right)v,$$
(8)

where \({p}_{m}\left({x}_{i},{y}_{j}\right)\) is the pressure on the element (i,j) in the micro-scale contact region. For the rest of the contact region, a thermal load \({q}_{M}\) is applied to each element grid:

$$q_{M} \left( {x_{m} ,y_{n} } \right) = \mu p_{M} \left( {x_{m} ,y_{n} } \right)v,$$
(9)

where \({p}_{M}({x}_{m},{y}_{n})\) is the pressure on the element (m,n) obtained from the macro-scale contact model.

3.1 Limitations

The following assumptions and limitations have been used throughout this work:

  • A perfectly smooth half-space surface sliding against a stationary rough elasto-plastic surface.

  • When studying the effect of surface roughness on the interface temperature, wear will not be considered in Cases 1 and 2. The effect of wear will only be considered in the model of the pin-on-disc, i.e. Case 3.

  • The contact is assumed to be perfectly dry and no boundary lubrication or tribofilm formation will be considered.

  • Only surface topographies with Weibull height distribution, generated with the method presented in [35], will be used in this study.

  • The effect of surface roughness on the flash temperature will only be considered at a single micro-scale-sized cell. The assumption is, if the rest of the macro-scale contact area around a single cell can be assumed to, approximatively, experience an averaged thermal load, this should then give approximately the correct heat fluxes in and out of that cell (due to the neighbouring thermal loads around the cell), and thus allow the cell to accumulate the correct net energy. This is a critical assumption because the cell will be the only entity to have a significantly finer mesh as compared to the rest of the contact, thus allowing to capture the effect of the asperity contacts.

  • It is assumed that the effect of surface roughness does not change the average interface temperature at any location as long as the average thermal load is kept the same. This assumption is used in order to validate the modelling approach used for the remainder of the macro-scale contact area outside the cell.

  • The temperature of the interface is considered to be equal for both interacting surfaces. This greatly simplifies the problem but is still considered sufficiently realistic for the numerical simulations performed in this work.

3.2 Generation of Surfaces

As mentioned earlier, the surface generation will be based on a method developed by Pérez-Rafols and Almqvist [35]. With this method, both the fractal characteristics of the frequency content as well as the surface height distribution can be specified. All the surfaces generated for the numerical experiments presented here were randomized from the same non-Gaussian Weibull height distribution, with fixed \({S}_{q}\) and \({S}_{sk}\), i.e. rms roughness and skewness, but with varying Hurst exponent H and high-frequency cut-off \({\omega}_{\max}\). The generated surfaces have a Weibull height probability distribution which is commonly used to model the result of wear [35]. Figure 3 shows one realization of each one of the different surfaces and the parameters used to generate them can be found in Table 1. In total, 100 surfaces were generated comprising a set consisting of 10 realizations of each of the 10 different types of surfaces, all with the same rms roughness and negative skewness values.

Fig. 3
figure 3

Examples of the surface topographies used in the simulations. The size is 1 mm × 1 mm and the corresponding roughness parameters are shown in Table 1. The arrow indicates the sliding direction

Full size image
Table 1 Parameters used for the generation of the 10 different types of surfaces with Weibull height distributions
Full size table

3.3 Contact Mechanics Solver

For each surface topography that was generated, the contact mechanics solver developed in [26, 27] was used to perform elasto-plastic simulations where the rough surface was brought into contact with a perfectly flat half-space for a given load, assuming \({P}_{L}/{E}^{*}=0.00175\). In all of the numerical experiments performed in this work, one of the bodies was considered to be moving unidirectionally with constant velocity and to be flat and perfectly smooth, while the other body was considered to be stationary and having a given topography. For simplicity, both bodies were given the same material properties as specified in Table 2. The contact mechanics simulations were performed in MATLAB, and when the pressure distribution was known, it was used as input to the thermal model.

Table 2 Material properties of the interacting half-space surfaces
Full size table

3.4 Thermal Model

The thermal model was implemented in the multi-physics software COMSOL® [37]. The inputs required by the thermal model were obtained from the contact mechanics solver in the form of the contact pressure distribution and the material properties from Table 2. Three different cases of simulations were performed, each meant to fulfil its own purpose. The different cases are described in the following sections.

3.5 Case 1: Model for Studying the Effect of Roughness Parameters

For the first set of simulations, a smaller block with dimensions 0.1 m × 0.1 m × 0.1 m was chosen to slide against a much larger block. The boundary conditions are set up such that the large block was considered infinitely long in the sliding direction. The cell, which is the small region where the flash temperatures are assessed, had a size 1 mm × 1 mm × 1 mm and was placed in the middle right between the small and the large block. That is, the upper part of the cell belongs to the small block and the lower to the large block. The cell’s interface is defined as the micro-scale contact region. Forced and natural convection to the ambient air was included in the model. The effect of radiation was not considered in this study.

Figure 4 shows the model set-up and mesh. The nominal contact pressure was set to 1 MPa and the initial temperature was set to 300 K. The large block (which includes the lower part of the cell) was given a prescribed motion of 1 m/s and the temperature at the leading edge vertical boundary of the large block was also set to 300 K. The prescribed motion of the large block meant that the coordinate system was not fixed but moving in the same direction as the large block, thus allowing the large block to be modelled as infinite in the sliding direction. The macro-scale contact region between the small and the large block was given a constant thermal load equal to the product of average pressure, sliding velocity, and coefficient of friction, as described by Eq. (9). After solving the contact mechanics problem in the micro-scale contact region defined by the cell, the heat flux, according to Eq. (8), was computed and then implemented as a boundary condition (through an interpolation function) in the thermal model. The region outside the cell was also given a heat flux boundary condition according to Eq. (9).

Fig. 4
figure 4

The computational domain and mesh for the macro-scale contact in Case 1 of the simulations, where a large block (lower body) is sliding against a stationary small block (upper body) with constant velocity v. The boundary conditions are set up such that the large body is infinite in the sliding direction. The small block has dimensions 0.1 m × 0.1 m × 0.1 m. The cell is not visible here

Full size image

The mesh used consisted of tetrahedral 3D elements everywhere except for the contact regions, that is, triangular elements for the macro-scale contact region and quadrilateral elements for the micro-scale contact region within the cell. The micro-scale contact region within the cell was discretized into a 128 × 128 grid. In total, the full 3D mesh consisted of approximately 300,000 elements out of which approximately 20,000 for the cell. As for the contact mechanics simulations, the same material was chosen for the small and large block with the material specified in Table 2. An implicit (Backward Differentiation based) time-stepping scheme was used for the time integration and the time interval simulated was set to 5 s.

The macro- and micro-scale contact regions are depicted in Fig. 5. It can be seen that the upper part of the cell belongs to the small block while the lower part of the cell belongs to the large moving block.

Fig. 5
figure 5

In a the macro-scale contact region is seen from above. The red square is the boundary of the small stationary block and the cell is located inside the blue square. In b the cell and micro-scale contact region are shown. The size of the cell is 1 mm × 1 mm × 1 mm and its micro-scale contact region is the rectangular area defined by the interface between the small- and the large block confined within the cell

Full size image

3.6 Case 2: Comparison with Analytical Expressions

To enable a comparison with the analytical expressions derived in [12] and [13], a circular heat source with radius 0.1 m and pressure of 1 MPa, moving unidirectionally with constant speed relative to a semi-infinite body, was considered as the macro-scale problem. A micro-scale cell was placed right before the trailing edge (in the sliding direction) of the circular heat source as is shown in Fig. 6. The reason for placing the cell there is that this is where the maximum temperature occurs and that it would provide a reference point for comparison with [12]. The same material properties listed in Table 2 were used also in this case.

Fig. 6
figure 6

The circular macro-scale contact zone and the cell, located inside the red square, placed right before the trailing edge

Full size image

According to [12], the maximum temperature rise for a semi-infinite body with a circular heat source moving unidirectionally with constant speed relative to another semi-infinite body is

$$\Delta T_{{{{\max}}}} = \frac{qR}{{2\pi k_{2} }}\frac{4C\sqrt \pi }{{\sqrt {1.273} + K\sqrt {1.273 + Pe} }},$$
(10)

and according to [13], the average temperature rise for the same type of situation is

$$\Delta T_{{{\text{avg}}}} = \frac{qR}{{2\pi k_{2} }}\frac{9.76C\pi }{{1.83\pi + 4C\sqrt {\pi \left( {0.6575 + Pe} \right)} }},$$
(11)
$$Pe = \frac{vR}{{2\alpha }},$$
(12)

where Pe is the Peclet number, v is the velocity, α is the thermal diffusivity, R is the heat source radius, and C is the ratio of the thermal conductivity k2 of the moving body to the thermal conductivity k1 of the stationary body and q is the thermal load.

The micro-scale contact was given a Weibull surface topography with Hurst exponent H = 0.6, high-frequency cut-off ωmax = 0.05, \({S}_{q}\) = 0.5 µm, \({S}_{sk}\) = − 2, and the main purpose was to compare the average temperature of the cell with Eq. (10) as well as compare the average temperature of the circular macro-scale contact with Eq. (11) for different sliding velocities.

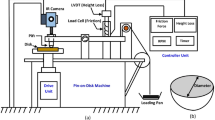
3.7 Case 3: Verification of the Model with the Pin-on-Disc System

The working conditions of the pin-on-disc system of [24] was re-created for the purpose of validating the present model. The disc was made of grey cast iron while the pin was made of a low-friction material. The disc and pin radii were 0.07 m and 0.006 m, respectively. The pin was inserted into a pin holder of radius 0.009 m. The disc was moving with 3.14 m/s and the contact pressure was 2 MPa. The average surface roughness height, \({S}_{a}\), of the disc was 2 µm and was obtained from [24]. The geometry and mesh of the model are shown in Fig. 7 together with the disc, pin, and pin holder.

Fig. 7
figure 7

The macro-scale pin-on-disc geometry and mesh as modelled in COMSOL

Full size image

In the present model, the material properties specified in Table 3 were applied. The disc was chosen to represent a rigid smooth surface and the pin’s micro-scale contact region was given a surface topography with an average roughness height of 2 µm and was allowed to deform both elastically and plastically, assuming \({P}_{L}/{E}^{*}=0.00345\). The surface topography used in the numerical simulation is shown in Figure 10. The size of the cell was chosen 0.5 mm × 0.5 mm × 1 mm and was placed directly before the trailing edge, as shown in Fig. 8. This was done to capture the highest possible asperity temperatures in the pin. The cell’s micro-scale contact region was divided into 128 × 128 grid points and the simulated time was about 640 s which corresponds to a sliding distance of roughly 1900 m.

Table 3 Material properties of the pin-on-disc machine
Full size table
Fig. 8
figure 8

The cell placement in the macro-scale contact region of the pin-on-disc model

Full size image

In order to achieve more realistic results, Archard’s wear law was used to simulate the wear of the pin during each time step in the contact mechanics simulation with the dimensionless wear coefficient K = 3 × 10–5 [24]. A time step of 5 ms was found to give representative results in terms of wear but, for 640 s of sliding, this means that 128 000 time steps would be required and this would render an unacceptably long simulation time. So to overcome this difficulty, it was decided to define and run a pretest to carefully examine the wear development and specifically answer the following questions:

  1. 1.

    How many time steps does it approximately take for the maximum asperity pressure to stabilize?

  2. 2.

    How many time steps does it approximately take for the average roughness height to reach such a small value that the effect becomes negligible?

In order to answer these questions, a pretest simulation was performed and run for 3000 timesteps. As it can be observed from Fig. 9, the maximum pressure and average roughness height tend to converge and reach an approximate steady-state value after around 2500 time steps which corresponds to 12.5 s of sliding (Fig. 10).

Fig. 9
figure 9

The maximum contact pressure evolution is shown in a and average surface height evolution is shown in b

Full size image
Fig. 10
figure 10

The surface topography used in Case 3 for the cell’s micro-scale contact region. The Hurst exponent is 0.8, the high-frequency cut-off is 0.01, the average roughness height is 2 µm, and the skewness is − 0.42. The arrow indicates the direction of motion

Full size image

The interpretation of the results shown in Fig. 9 is that the maximum contact pressure, as well as surface topography, does not significantly change after about 2500 time steps. Based on this pretest to examine the wear development, 3000 time steps, i.e. 15 s, was considered to lead to a situation in which the wear rate \(\Delta h/\Delta t\) is small enough to no longer influence the results. This suggests that the pressure distribution resulting after 15 s of the wear simulation could be used in the thermal model as an input to the thermal-load boundary condition from 15 s and onwards, without introducing significant errors. In order to correctly incorporate this in COMSOL Multiphysics® [37], it was necessary to constrain the maximum time step size to 5 ms during the time interval of 0–15 s in order to account for the rapidly changing loads from the contact mechanics solver. The total computational time for the wear and thermal simulation was approximately 2 h.

4 Results and Discussion

In this section, the results from the three cases described above will be presented and discussed. All numerical simulations have been performed on a computer with a 2.2 GHz Intel Xeon Gold 5220 2 core processor with 192 GB of memory.

4.1 Case 1

Although the surface roughness was intensively varied, as shown in Table 1, the model predicted the cell’s average contact temperature rise to be the same for all the surface topographies tested. The cell’s average contact temperature rise is depicted in Fig. 11. It can be seen that it more or less reaches a steady state after approximately 5 s.

Fig. 11
figure 11

The average contact temperature rise of the cell

Full size image

Figure 12 shows the evolution of the temperature field at the micro-scale contact region and the temperature development at the asperities, i.e. flash temperatures, can be clearly seen. The temperature field is for a Weibull surface topography with Hurst exponent 0.6, high-frequency cut-off 0.01, rms roughness 0.5 µm, and skewness − 2, i.e. type 4 in Fig. 3. As mentioned in the methodology section, ten surface topographies with roughness for each set of parameters listed in Table 1 were used to appreciate the variability.

Fig. 12
figure 12

The temperature field evolution in Kelvin of the cell’s micro-scale contact region with a Weibull surface topography for different times. The arrow indicates the direction of motion

Full size image

Figure 13 shows that the maximum flash temperature rise, \(\Delta {T}_{{\max}}\), of the micro-scale contact region decreases with increasing Hurst exponents. This is due to that the asperities on a surface topography with a small Hurst exponent has asperities with smaller summit radius (the decay of the frequency component amplitude decrease when the Hurst exponent decreases). In turn, this leads to higher local pressures (within the elastic regime) and, therefore, a higher thermal load compared with a surface topography with a higher Hurst exponent. The error bars in the figure also show the variability within the set of ten surface topographies generated for each different value of the Hurst exponents. It is hypothesized that the variability would decrease with increasing Hurst exponents. As is evident by Fig. 13, the statistical basis with 10 realizations is, however, inadequate to validate this.

Fig. 13
figure 13

The variation of the maximum flash temperature rise of the micro-scale contact region with the Hurst exponent, at the end of the simulation, i.e. t = 5 s. The high-frequency cut-off is 0.01, skewness − 2, and rms roughness 0.5 µm

Full size image

The variation of the maximum flash temperature rise with the high-frequency cut-off was considered next. Figure 14 shows the mean value as well as the variability within each set of 10 topographies generated with the same high-frequency cut-off. The result shows that the maximum temperature rise increases with increasing high cut-off frequencies. This behaviour can be explained by the fact that an increase in the high-frequency cut-off renders components with shorter wavelengths, leading to higher local contact pressures thus increasing the thermal load and therefore the maximum flash temperature rise. It can also be seen that the variability increases with increasing high-frequency cut-off. One possible explanation for this behaviour is that, with increasing high-frequency cut-off values, there is a greater local variation in the roughness height of the surface topography. The increased height variation means that there are more variable local contact pressures and therefore more variable thermal loads.

Fig. 14
figure 14

The variation of the maximum flash temperature rise of the micro-scale contact region with the high cut-off frequencies, at the end of the simulation, i.e. t = 5 s. The Hurst exponent is 0.8, skewness − 2, and rms roughness 0.5 µm

Full size image

The effect of the real area of contact on the steady-state maximum temperature rise is shown in Fig. 15. The general trend is that the maximum flash temperature increases as the real contact area decreases while keeping the nominal contact pressure constant. This is reasonable considering that the maximum pressure increases when the real contact of area decreases. There is, however, one surface category, namely type 10 with Hurst exponent 0.8, high-frequency cut-off 0.05, skewness − 2, and rms roughness 0.5 µm, which shows a higher maximum temperature rise than expected based on its relatively large real area of contact. The type 10 surface topography does, however, have the highest high-frequency cut-off of all the different types of topographies leading to high local contact pressures and thus high thermal loads.

Fig. 15
figure 15

The variation of the maximum flash temperature rise of the micro-scale contact region with the real area of contact, at the end of the simulation, i.e. t = 5 s

Full size image

To ascertain the accuracy of the maximum flash temperature rise predictions, a mesh dependence analysis was performed for the cell’s micro-scale contact region. The surface topography with the highest high-frequency cut-off, i.e. Surface type 10, was selected, as it is the topography requiring the finest mesh to be adequately resolved contact mechanically. Figure 16 shows that the maximum temperature rise at t = 5 s exhibits a convergent behaviour with an increase in the number of elements.

Fig. 16
figure 16

Maximum flash temperature rise, for Surface 10, as a function of the total number of elements, at the end of the simulation, i.e. t = 5 s. The surface has a Hurst exponent 0.8, high-frequency cut-off 0.05, skewness − 2, and rms roughness 0.5 µm

Full size image

4.2 Case 2

The results from the comparison between the present model and the models presented in [12] and [13] are shown in Fig. 17. The comparison is based on a variation of the thermal load, in terms of the varying sliding velocity. As it can be seen, there is a good agreement between the prediction by the present model and the one in [13], in terms of the macro-scale average temperature rise, and by the present model’s prediction of the micro-scale average temperature rise and the prediction by the model in [12] of the macro-scale maximum temperature. As expected, since the cell was placed near the trailing edge of the macro-scale contact region, i.e. where the maximum temperature is anticipated to occur, the average temperature rise of the micro-scale contact region should be close to the maximum temperature rise predicted by the model in [12]. As the average temperature of the micro-scale contact region should not be affected by the local (higher) flash temperatures at the asperities. This was one of the main assumptions mentioned in the limitations section, and it is thus validated here. Although the three methods give similar results, there are small deviations. One possible explanation for this is that the models presented [12] and [13] include curve-fitting errors that are not incorporated in the present approach.

Fig. 17
figure 17

Comparison between the present model's predictions and the analytical solutions presented in [12] and [13]

Full size image

As shown in Fig. 17, the temperature rise does not increase linearly with increasing thermal load but instead displays a logarithmic behaviour. One explanation for this is that increasing sliding speeds can lead to faster heat dissipation due to the moving body, which is carrying away the heat energy from the contact heat source area.

4.3 Case 3

The Archard wear evolution of the surface topography of the pin micro-scale contact region is shown in Fig. 18 at four instances. It can be seen that the surface is worn almost completely after about 10 s of sliding or about 32 m.

Fig. 18
figure 18

The Archard wear behaviour of the surface topography of the micro-scale contact region at four intermediate times

Full size image

It is important to note that not all experimental details are known, it is therefore not known if the numerical predictions of the Archard type of wear evolution, shown in Fig. 18, matches with the experimental results presented in [24]. Archard’s wear equation, i.e. Equation (7), also represents an ideal model of the realization and does not account for all types of wear that may possibly occur in the experiment. Also worth to mention is that the value of the wear coefficient may be temperature dependent, and thus may affect the thermal results when the asperities are present.

Figure 19 shows a comparison of the top view temperature distribution between the experimental findings presented in [24] and predictions calculated using the present model. A good agreement between the two temperature distributions as well as between the maximum temperatures on the disc’s wear track is observed. It can be seen that the disc’s wear track has an almost uniform temperature distribution with very little temperature variance in the circumferential direction. This is reasonable considering that the disc is rotating at 500 rpm which means that the time the disc has to cool down between two successive contacts with the pin is limited to 120 ms. Figure 20a and b shows the time-resolved disc and pin temperature as predicted by the present model and as recorded by the measurements presented in [24]. As it can be seen from both the subfigures, the present model’s predictions are in very good agreement with the temperature measurements presented in [24].

Fig. 19
figure 19

The temperature distribution, obtained from actual pin-on-disc tests, presented in [24] (a), and the temperature distribution as predicted by the present model (b). The sliding distance was approximately 1000 (318 s), and the temperature is in degrees Celsius

Full size image
Fig. 20
figure 20

Comparison between the temperature measurements presented in [24] and the present model's predictions. In a the disc surface temperature and b the temperature inside the centre of the pin, recorded at a distance of 4 mm from the tip

Full size image

To appreciate the sensitivity in the prediction of temperature on the wear evolution of the surface topography, a worst-case scenario prediction, not including wear at all, was also performed. Without wear, the initially observed high local pressures remain and this obviously results in the highest local temperature rise. The result is shown in Fig. 21. Although the negligence of wear did not affect the average interface temperature of the cell, it does significantly affect the development of the local flash temperature rise as shown in Fig. 21. This is reasonable considering how quickly the asperities wear off as shown in Fig. 18 (and 9b). As the asperities wear off, the surface becomes more and more smooth thus allowing the pressure to be more uniformly distributed over the contact region.

Fig. 21
figure 21

The maximum flash temperature development with and without the consideration of wear

Full size image

Figure 22 shows the surface topography and corresponding temperature development of the pin micro-scale contact region at eight different times and stages of wear. The effect of wear on the temperature development can be appreciated visualized from this figure where it is clear that the highest peaks of the surface (shown in bright yellow) are the ones contributing to the highest flash temperature rise (which is reasonable).

Fig. 22
figure 22

The surface topography (left) and corresponding temperature field (right) of the cell’s micro-scale contact region for eight different stages of wear of the pin. The surface height has unit µm and the temperature has units degree Celsius. The cell’s micro-scale contact area is 0.5 mm × 0.5 mm and the arrow indicates the direction of the motion of the disc

Full size image

5 Conclusions

A transient multi-scale flash temperature model has been developed and validated against existing work. The model has been applied to three different types of sliding contacts and it was used to study how the surface roughness affects the temperature development at the asperities. The model predictions were compared both to existing theoretical and experimental results and it was found that the results were in good agreement with these. The model is based on basic assumptions that greatly simplifies the problem and reduces the computational complexity, and the main advantage is that it can be easily adapted to handle many other types of contact problems, with more complex geometries than the ones considered here.

From the results, these specific conclusions can be drawn:

  • The surface roughness of the cell affects the flash temperature and thus the maximum temperature rise, but it does not affect the average interface temperature rise.

  • Increasing the high-frequency cut-off results in an increase of the maximum temperature rise.

  • A decrease in the Hurst exponent tends to give a higher maximum temperature rise.

  • Wear has a significant effect on the development of the flash temperature and should not be neglected.