Water table rise in arid urban area soils due to evaporation impedance and its mitigation by intelligently designed capillary chimney siphons

Abstract

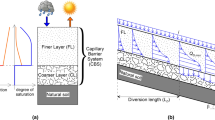
Waterlogging of urban area soil in a hyperarid climate, caused by impedance of evapotranspiration due to land cover by an impervious pavement, is studied by a multidisciplinary team of researchers (hydropedeologists, hydrogeologists, groundwater engineers, soil physicists and mathematical modelers). In this paper, a study unique for an arid/hyperarid MENA region has been conducted: from soil pedons’ data, a thin vadose zone superjacent to a shallow water table of a coastal aquifer in Oman is described with emphasis on soil profile morphology layering and determination of the van Genuchten hydraulic parameters, used in HYDRUS modeling of evaporation-driven saturated/unsaturated flows. On a large scale, for capillarity-free groundwater flow, the Dupuit–Forchheimer model is used and an analytical solution is obtained. Intensive evaporation from the water table to a bare unpaved soil surface is impeded by an impermeable surface strip (land pavement) with an ensued rise of the water table. Waterlogging is quantified by the “dry area,” S_d, under the strip. This integral is explicitly evaluated as a function of the model parameters: aquifer’s size and evaporation-normalized conductivity, the width of the strip, d, and its locus with respect to the shoreline, u₁. Nontrivial extremes of S_d(d,u₁) are found. Contrary to the surface pavement, intensification of evaporation by capillary siphons, i.e., structural heterogeneities of a porous massif, is proposed as an engineering mitigation of groundwater inundation. Composite porous media with siphons (small-size rectangular inclusions of a contrasting finer texture) are numerically tackled by MODFLOW and HYDRUS2D. A constant flux or a constant pressure head condition is imposed on the top of the flow domain. The water table is shown to drop and S_d to increase as a result of such “passive moisture pumping” from the aquifer. A potential model for 2D tension-saturated flow is used to solve a mixed boundary-value problem in a rectangular wick. Its flow rate is analytically evaluated as a function of evaporating width and the height of the “window” through which the aquifer feeds the wick. Conformal mapping of a rectangle in the physical domain onto a rectangle in the complex potential plane is realized via two reference planes and elliptic functions.

Appendix

Analytical solution for tension-saturated flow in wick

In this Appendix, we consider a simplified geometry of a rectangular wick ABCD (Fig.

Fig. 12

a Complex potential domain in the VB model; b reference plain $\varsigma$; c reference plain $\varsigma_{1}$

12) with the water table dipping towards it from a vertical constant piezometric head boundary, similarly to Sect. 3. Unlike the DF capillarity-free model of Sect. 3, here we use the Vedernikov–Bouwer potential model (Kacimov et al. 2019a) of a saturated-tension saturated flow in a vertical cross-section.

We introduce a system of Cartesian coordinates Oxy, the abscissa axis of which is counter oriented with Ox_c. The wick in Fig. 1a is a rectangular domain G_z. Along a vertical segment AD of a size h_D the siphon receives saturated water from the aquifer. First, we assume that h_D is a given constant (obtained, say, from simulations in Sect. 3). We assume that along the line AD the hydraulic head is constant, i.e., for seepage inside G_z the aquifer on the right of the siphon acts like a surface-water reservoir. This assumption is suitable if K_s1 <  < K_s and is similar to one in the problem of the conjugation of seepage in clay cores of earth dams and their coarse shoulders (Kacimov et al. 2020a).

We assume that seepage in G_z is Darcian, steady-state, and tension saturated above the phreatic line DF. We introduce a complex physical coordinate z = x + iy. The total hydraulic head, h(x,y) in G_z and the Darcian velocity, $\overrightarrow{V}\left(x,y\right)$ are related as:

$$\overrightarrow{V}=-{K}_{s1}\nabla h.$$

(6)

The complex potential is $w(x,y) = \varphi + {\text{i}}\psi$, where $\varphi = - K_{s1} h$ is the velocity potential, and $\,\psi$ is the stream function. In the Vedernikov-Bouwer (VB) model, $\varphi$ and $\psi$, as well as the pressure head $p(x,y) = - \varphi /K_{s1} - y + c_{p}$, obey the Laplace equation. We select D in Fig. 0.1a as a fiducial point where we set w = 0 and, therefore, $\varphi_{AD} = 0$ and c_p = h_D.

The segments DB and OC in G_z are impermeable, the former due to a capillary barrier between the fine wick and coarse aquifer and the latter as a lateral confining of our flow domain from the left in Fig. 1a. Therefore, $\psi_{DB} = 0$, $\psi_{AOC} = Q$ where the seepage flow rate, Q, through G_z is a part of the solution. Along BC the pressure head $p = - p_{BC}$, $0 < p_{BC} < p_{C}$ where $p_{C}$ is a given positive constant for a given soil, a parameter of the VB model, which quantifies the capillary properties of the wick. PK-77 reports $p_{C}$ from tens of cm for sandy soils up to tens of meters for clays. The value of $p_{BC}$ depends on atmospheric conditions (see a similar isobaricity condition, which we imposed in Sect. 4 along the soil surface in HYDRUS simulations). Then along BC the velocity potential $\varphi = \varphi_{B} = K_{s1} (p_{BC} + h_{D} - r)$. For water to be wicked to the atmosphere the inequality should hold $\varphi_{B} > 0$. A dashed line FD in Fig. 1a is a phreatic curve p = 0 in G_z. Thus, in the complex potential domain, we have a rectangle G_w (Fig. 12).

We map conformally G_w onto G_z using two reference planes $\varsigma = \xi + {\text{i}}\eta$ and $\varsigma_{1} = \xi_{1} + {\text{i}}\eta_{1}$ shown in Fig. 12b and c, correspondingly. By the Schwarz-Christoffel integral

$$ z(\varsigma ) = \frac{b}{2} + \frac{b}{2K(\lambda )}\int\limits_{0}^{\varsigma } {\frac{{{\text{d}}t}}{{\sqrt {(1 - t^{2} )(1 - \lambda^{2} t^{2} )} }}} = \frac{b}{2} + \frac{b}{2K(\lambda )}F(\arcsin \varsigma ,\lambda )\,. $$

(7)

The upper half-plane $\varsigma > 0$ is mapped onto the domain G_z with the correspondence of points $C \to - 1/\lambda$, $O \to - 1$,$A \to 1$,$B \to 1/\lambda$$(0 < \lambda < 1)$. Here $F(\arcsin \varsigma ,\lambda )$ and $K(\lambda )$ are incomplete and complete elliptic integrals of the first kind (see Abramowitz and Stegun, 1969, formulae 17.2.7, 17.3.1). From Eq. (7), we have $z(1/\lambda ) = b + {\text{i}}r$ and $F(\arcsin 1/\lambda ,\lambda ) = K(\lambda ) + iK^{\prime}(\lambda )$ that gives

$$ K^{\prime}(\lambda )/K(\lambda ) = 2r/b, $$

(8)

where $K^{\prime}(\lambda ) = K(\lambda^{\prime})$, $\lambda^{\prime} = \sqrt {1 - \lambda^{2} }$. In Eq. (8) we use the FindRoot routine of Mathematica and determine the modulus $\lambda$ of the elliptic integrals. An accurate asymptotic representation for $\lambda$ is

$\lambda \cong 4\exp ( - \pi r/b)$if $r > > b$.

The image of point D in the half-plane of Fig. 

Fig. 13

Seepage flow rate through the wick: as function of its width at h_B = 0.3 and h_D = 0.3, 0.5, 0.7(curves 1–3), left panel; as function of the size of the “hydraulic window”, through which groundwater infiltrates, at h_B = 0.3 and b = 0.03, 0.06, 0.09 (curves 1–3), right panel

13b is $\varsigma = \mu$. The positive parameter $\mu$ ($\varsigma < \mu < 1/\lambda$) satisfies the condition $z(\mu ) = b + {\text{i}}h_{D}$. From Eq. (8) and formula (1.2.64.1) from Prudnikov et al. (1986), we get:

$$ h_{D} = \frac{b}{2K(\lambda )}\int\limits_{1}^{\mu } {\frac{{{\text{d}} \tau }}{{\sqrt {(\tau^{2} - 1)(1 - \lambda^{2} \tau^{2} )} }}} = \frac{r}{{K^{\prime}(\lambda )}}F\left( {\arcsin \left( {\frac{{\sqrt {\mu^{2} - 1} }}{\lambda ^{\prime}\mu }} \right),\lambda^{\prime}} \right). $$

(9)

The relation (9) is an equation with respect to $\mu$, if parameters b, r, $h_{D}$ are fixed, and the corresponding modulus $\lambda$ is determined from (8). The approximate formula

$$ \mu = 0.5{\kern 1pt} \,\exp \left[ {h_{D} K^{\prime}(\lambda )} \right], $$

(10)

which solves Eq. (9), was used in our computations below.

The second reference plane is needed for mapping of the complex potential rectangle, viz. we map G_w onto the upper half-plane $\varsigma_{1} > 0$, with the correspondence of the points $C \to - 1/\lambda_{1}$, $A \to - 1$, $D \to 1$, $B \to 1/\lambda_{1}$, where $0 < \lambda_{1} < 1$. The corresponding Schwarz-Christoffel integral is:

$$ w(\varsigma_{1} ) = \frac{{{\text{i}}Q}}{2} - \frac{{{\text{i}}Q}}{{2K(\lambda_{1} )}}\int\limits_{0}^{{\varsigma_{1} }} {\frac{{{\text{d}}t}}{{\sqrt {(1 - t^{2} )(1 - \lambda_{1}^{2} t^{2} )} }}} = \frac{{{\text{i}}Q}}{2} - \frac{{{\text{i}}Q}}{{2K(\lambda_{1} )}}F(\arcsin \varsigma_{1} ,\lambda_{1} )\;. $$

(11)

As $w(1/\lambda_{1} ) = K_{s1} h_{b}$ (see Fig. 12a), then from Eq. (11) and the equality $F(\arcsin (1/\lambda_{1} ),\lambda_{1} ) = K(\lambda_{1} ) + {\text{i}}K^{\prime}(\lambda_{1} )$ follows:

$$ \frac{2K}{{K^{\prime}}} = \frac{Q}{{K_{s1} h_{b} }}, $$

(12)

where $K = K(\lambda_{1} ),\quad K^{\prime} = K(\lambda_{1}^{\prime } )$, and $\lambda_{1}^{\prime } = \sqrt {1 - \lambda_{1}^{2} }$.

Next, the $\varsigma$-half-plane (Fig. 12b) is mapped onto the $\varsigma_{1}$-half-plane (Fig. 12c). This is done by the Mobius transformation which is uniquely defined by fixing the relation of three pairs of points: $- 1/\lambda \to - 1/\lambda {}_{1}$,$1 \to - 1$,$1/\lambda \to 1/\lambda_{1}$. Then the mapping function is determined from the following relation:

$$ \frac{\varsigma + 1/\lambda }{{\varsigma - 1}}(1 - \lambda ) = \frac{{\varsigma_{1} + 1/\lambda_{1} }}{{\varsigma_{1} + 1}}(1 + \lambda_{1} ). $$

(13)

Due to the correspondence of points O and D in the two reference half-planes, we put $\varsigma = 1$ and $\varsigma = \mu$ into the left-hand side of Eq. (13), $\varsigma_{1} = - \mu_{1}$ and $\varsigma_{1} = 1$ into the right-hand side of this equation and obtain

$$ \frac{{(1 - \lambda )^{2} }}{2\lambda } = \frac{{\mu_{1} - 1/\lambda_{1} }}{{\mu_{1} - 1}}(1 + \lambda_{1} ),\quad \frac{\mu + 1/\lambda }{{\mu - 1}}(1 - \lambda ) = \frac{{(1 + \lambda_{1} )^{2} }}{{2\lambda_{1} }}. $$

(14)

The second Eq. (14) is a quadratic equation with respect to $\lambda {\kern 1pt}_{1}$ (we remind that parameters $\lambda$ and $\mu$ are determined earlier by Eqs. (8) and (10), respectively). The root of this equation, satisfying the condition $0 < \lambda {\kern 1pt}_{1} < 1$, is given by the formula:

$$ \lambda {\kern 1pt}_{1} = s - \sqrt {s^{2} - 1} ,\quad s = \frac{1/\lambda - \mu \lambda }{{\mu - 1}} > 1. $$

(15)

We introduce dimensionless quantities: ($h_{D}^{*}$,b^*, d^*, $h_{B}^{*}$, V^*, Q^*) = (h_D/r, b/r, p_B/r, V/K_s1, Q/(K_s1 r)) and drop the asterisks for dimensionless quantities. In Fig. 13, we plot the graphs of the functions Q(b) at h_B = 0.3 and $h_{D}$ = 0.3, 0.5, 0.7 (curves 1–3).

Figure 13, left panel shows the graphs Q(b) for h_B = 0.3 and h_D = 0.3, 0.5, 0.7 (curves 1–3). Obviously, in the limit $b \to 0$ the flow rate approaches zero, i.e., all three curves collapse to the origin of coordinates. However, in this limit of “thin” siphons, Mathematica stumbles with computation of elliptic integrals. Figure 13, right panel shows the graphs Q(h_D) for h_B = 0.3 and b = 0.03, 0.06, 0.09 (curves 1–3). These graphs that illustrate for the selected h_D and b if h_D is high enough (greater than about 0.7), then the flow rate increases highly nonlinearly and rapidly with h_D.