Recycled two-stage estimation in nonlinear mixed effects regression models

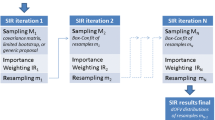
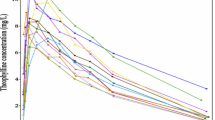
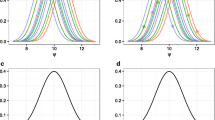
Abstract

We consider a re-sampling scheme for estimation of the population parameters in the mixed-effects nonlinear regression models of the type used, for example, in clinical pharmacokinetics. We provide a two-stage estimation procedure which resamples (or recycles), via random weightings, the various parameter's estimates to construct consistent estimates of their respective sampling distributions. In particular, we establish under rather general distribution-free assumptions, the asymptotic normality and consistency of the standard two-stage estimates and of their resampled version and demonstrate the applicability of our proposed resampling methodology in a small simulation study. A detailed example based on real clinical pharmacokinetic data is also provided.

7. Appendix

1.1 7.1. Technical details and proofs, the STS estimation case

In this section of the "Appendix" we provide the technical results needed for the proofs of Theorems 1 and 2 on the STS estimator ${\hat{\theta }}_{{STS}}$ in the hierarchical nonlinear regression model. In the sequel, we let $\phi _{1ij}(\theta ):=\phi _{ij}^{'}(\theta )$ (see (11)), and set K to denote a generic constant. Recall that (see Assumption A(1)),

$$\begin{aligned} a_{n_i}^{2}:=\sigma ^2\sum _{j=1}^{n_i}E(f^{'2}_{ij}(\theta _0+b_i))\rightarrow \infty \ \ as \ \ n_i\rightarrow \infty . \end{aligned}$$

Lemma 1

Under the conditions of Assumption A, for some $K>0$

$$\begin{aligned} a_{n_i}^{-2}\underset{|t|\le K}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b_{i1})-\frac{1}{\sigma ^2}\rightarrow 0 \ \ a.s., \end{aligned}$$

where $b_{i1}:=b_{1n_{i}}(t)$ is a sequence such that $\underset{|t|\le K}{\sup }|b_{i1}-b_i-\theta _0|\rightarrow 0,\ \ \ a.s.,$ as $n_i\rightarrow \infty$.

Proof of Lemma 1

Since $\phi _{1ij}(\theta ):=\phi _{ij}^{'}(\theta )$, we have

$$\begin{aligned} \phi _{1ij}(\theta )\equiv f^{'2}_{ij}(\theta )-\epsilon _{ij}f_{ij}^{''}(\theta )-(f_{ij}(\theta _0+b_i)-f_{ij}(\theta ))f_{ij}^{''}(\theta ). \end{aligned}$$

Accordingly, we first note that,

$$\begin{aligned} \left| a_{n_i}^{-2}\underset{|t|\le K}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b_{i1})-\frac{1}{\sigma ^2}\right|\le & \left| a_{n_i}^{-2}\underset{|t|\le K}{\sup }\sum _{j=1}^{n_i}f^{'2}_{ij}(b_{i1})-\frac{1}{\sigma ^2}\right| \\ &\quad+ a_{n_i}^{-2}\underset{|t|\le K}{\sup }\left| \sum _{j=1}^{n_i}\epsilon _{ij}f_{ij}^{''}(b_{i1})\right| \\&\quad+ a_{n_i}^{-2}\underset{|t|\le K}{\sup }\left| \sum _{j=1}^{n_i}(f_{ij}(\theta _0+b_i)-f_{ij}(b_{i1}))f_{ij}^{''}(b_{i1})\right| . \end{aligned}$$

By Assumption A (3), we have $a_{n_i}^{-2}\underset{|t|\le K}{\sup }\sum _{j=1}^{n_i}f^{'2}_{ij}(b_{i1})-\frac{1}{\sigma ^2}\rightarrow 0 \ \ a.s.,$ and by Assumption A (2) and Corollary A in Wu (1981), we also have,

$$\begin{aligned} a_{n_i}^{-2}\underset{|t|\le K}{\sup }\left| \sum _{j=1}^{n_i}\epsilon _{ij}f_{ij}^{''}(b_{i1})\right| \rightarrow 0\ \ a.s.. \end{aligned}$$

Finally, the last term converge to 0 a.s. by Assumption A, an application of Cauchy-Schwarz inequality and Corollary A in Wu (1981). Thus we have

$$\begin{aligned} a_{n_i}^{-2}\underset{|t|\le K}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b_{i1})-\frac{1}{\sigma ^2}\rightarrow 0 \ \ a.s.. \end{aligned}$$

. $\square$

Lemma 2

Let $X_i$ be a sequence of random variables bounded in probability and let $Y_i$ be a sequence of random variables which satisfies $\frac{1}{n}\sum _{i=1}^{n} |Y_i|\rightarrow 0$ in probability. Then $\frac{1}{n}\sum _{i=1}^{n} X_iY_i\overset{p}{\rightarrow }0.$

Proof of Lemma 2

Since $X_i$ is bounded in probability, for any $\epsilon >0$, there is $K_\epsilon$ such that with sufficient large i, $P(|X_i|>K_\epsilon )<\epsilon .$ Then

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }P(|\frac{1}{n}\sum _{i=1}^{n} X_iY_i|>\epsilon )= & \underset{n\rightarrow \infty }{\lim }\left[ P(|\frac{1}{n}\sum _{i=1}^{n} X_iY_i|>\epsilon , |X_i|<K_\epsilon )\right] \\+ & \underset{n\rightarrow \infty }{\lim }\left[ P(|\frac{1}{n}\sum _{i=1}^{n} X_iY_i|>\epsilon , |X_i|>K_\epsilon )\right] \\\le & \underset{n\rightarrow \infty }{\lim }P(\frac{1}{n}\sum _{i=1}^{n} |\frac{X_i}{K_\epsilon }Y_i|>\frac{\epsilon }{K_\epsilon }, |X_i|<K_\epsilon )+\epsilon \\\le & \underset{n\rightarrow \infty }{\lim }P(\frac{1}{n}\sum _{i=1}^{n} |Y_i|>\frac{\epsilon }{K_\epsilon }, |X_i|<K_\epsilon )+\epsilon =\epsilon , \end{aligned}$$

from which the desired result follows. $\square$

Lemma 3

There exists a $K>0$ such that for any $\epsilon >0$, for any i,

$$\begin{aligned} P\left[ \left| a_{n_i}^{-1}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\right| >K\right] <\frac{\epsilon }{2}. \end{aligned}$$

Proof of Lemma 3

Since $\epsilon _{ij}$ and $b_i$ are independent, for each $i=1, \dots , N$, we have that for any $j_1\ne j_2$,

$$\begin{aligned} E(\phi _{ij_1}(\theta _0+b_i)\phi _{ij_2}(\theta _0+b_i))= & E[E(\phi _{ij_1}(\theta _0+b_i)\phi _{ij_2}(\theta _0+b_i)|b_i)]\\= & E[E(\epsilon _{ij_1}\epsilon _{ij_2}f^{'}_{ij_1}(\theta _0+b_i)f^{'}_{ij_2}(\theta _0+b_i)|b_i)]\\= & E[E(\epsilon _{ij_1})E(\epsilon _{ij_2})f^{'}_{ij_1}(\theta _0+b_i)f^{'}_{ij_2}(\theta _0+b_i)]\\= & 0. \end{aligned}$$

Similarly,

$$\begin{aligned} E(\phi _{ij_1}(\theta _0+b_i))= & E[E(\epsilon _{ij_1}f^{'}_{ij_1}(\theta _0+b_i)|b_i)] = E[E(\epsilon _{ij_1})f^{'}_{ij_1}(\theta _0+b_i)]=0.\\ \end{aligned}$$

Hence, we have, $E(\phi _{ij_1}(\theta _0+b_i)\phi _{ij_2}(\theta _0+b_i))=E(\phi _{ij_1}(\theta _0+b_i))E(\phi _{ij_2}(\theta _0+b_i)).$ To conclude that,

$$\begin{aligned} Var\left( \sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\right)= & \sum _{j=1}^{n_i}Var(\phi _{ij}(\theta _0+b_i))\\= & \sum _{j=1}^{n_i}Var(\epsilon _{ij}f^{'}_{ij}(\theta _0+b_i))\\= & \sum _{j=1}^{n_i}E(\epsilon ^2_{ij})E(f^{'2}_{ij}(\theta _0+b_i))\\= & \sigma ^2\sum _{j=1}^{n_i}E(f^{'2}_{ij}(\theta _0+b_i))\equiv a_{n_i}^2. \end{aligned}$$

Accordingly, there exists a $K>0$ such that for any $\epsilon >0$, for any i,

$$\begin{aligned} P\left[ \left| a_{n_i}^{-1}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\right| >K\right] <\frac{\epsilon }{2}. \end{aligned}$$

$\square$

We are now ready to prove Theorem 1

Proof of Theorem  1

Let

$$\begin{aligned} S_{n_i}(t):= a_{n_i}^{-1}\sum _{j=1}^{n_i}\left[ \phi _{ij}(\theta _0+b_i+a_{n_i}^{-1}t)-\phi _{ij}(\theta _0+b_i)\right] -\frac{t}{\sigma ^2}. \end{aligned}$$

(16)

Next we will show for any given constant K,

$$\begin{aligned} \underset{|t|\le K}{sup}|S_{n_i}(t)|\rightarrow 0\ \ a.s. \end{aligned}$$

(17)

By a Taylor expansion, $\phi _{ij}(\theta _0+b_i+a_{n_i}^{-1}t)=\phi _{ij}(\theta _0+b_i)+\phi _{1ij}(b_{i1})a_{n_i}^{-1}t, \ \$ where $b_{i1}=\theta _0+b_i+ca_{n_i}^{-1}t$ for some $0<c<1$. Accordingly we obtain that,

$$\begin{aligned} \underset{|t|\le K}{\sup }|S_{n_i}(t)|= & \underset{|t|\le K}{\sup } \left| a_{n_i}^{-1}\sum _{j=1}^{n_i}\phi _{1ij}(b_{i1})a_{n_i}^{-1}t-\frac{t}{\sigma ^2} \right| \\= & K\left| a_{n_i}^{-2}\underset{|t|\le K}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b_{i1})-\frac{1}{\sigma ^2}\right| .\\ \end{aligned}$$

By Lemma 1, $a_{n_i}^{-2}\underset{|t|\le K}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b_{i1})-\frac{1}{\sigma ^2}\rightarrow 0\ \ a.s.$ Thus, we have proved (17). Next, by (16),

$$\begin{aligned} A_{n_i}(t):=a_{n_i}^{-1}t\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i+a_{n_i}^{-1}t)= tS_{n_i}(t)+a_{n_i}^{-1}t\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)+\frac{t^2}{\sigma ^2}. \end{aligned}$$

Thus,

$$\begin{aligned} \underset{|t|=K}{\inf }A_{n_i}(t)\ge -K\underset{|t|=K}{\sup }|S_{n_i}(t)|-Ka_{n_i}^{-1}\left| \sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\right| +\frac{K^2}{\sigma ^2}. \end{aligned}$$

By lemma 3 there exists a $K>0$ such that for any $\epsilon >0$, for any i,

$$\begin{aligned} P\left[ \left| a_{n_i}^{-1}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\right| >K\right] <\frac{\epsilon }{2}. \end{aligned}$$

(18)

So that by (18) and (17) we may choose K large enough such that for sufficiently large $n_i$,

$$\begin{aligned} P(\underset{|t|=K}{\inf }A_{n_i}(t)\ge 0)\ge & P(\underset{|t|=K}{\sup }|S_{n_i}(t)|+a_{n_i}^{-1}\left| \sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\right| \le \frac{K}{\sigma ^2})\\= & 1-P \left(\underset{|t|=K}{\sup }|S_{n_i}(t)|+a_{n_i}^{-1}\left| \sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\right|>\frac{K}{\sigma ^2}\right)\\\ge & 1-P \left(\underset{|t|=K}{\sup }|S_{n_i}(t)|>\frac{K}{4\sigma ^2})-P(a_{n_i}^{-1}\left| \sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\right| >\frac{K}{4\sigma ^2}\right)\\\ge & 1-\epsilon . \end{aligned}$$

By the continuity of $\sum _{j=1}^{n_i}\phi _{ij}(\theta )$ in $\theta$, we have, for sufficiently large $n_i$, that there exists a constant K such that the equation

$$\begin{aligned} \sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i+a_{n_i}^{-1}t)=0, \end{aligned}$$

has a root $t=T_{ni}$ in $|t|\le K$ with probability larger than $1-\epsilon$. That is, we have ${{\hat{\theta }}_{ni}}=\theta _0+b_i+a_{ni}^{-1}T_{ni},$ where $|T_{ni}|<K$ in probability. Thus, by Lemma 2,

$$\begin{aligned} {\hat{\theta }}_{{STS}}-\theta _0=\frac{1}{N}\sum _{i=1}^{N}b_i +\frac{1}{N}\sum _{i=1}^{N}a_{ni}^{-1}T_{ni}\overset{p}{\rightarrow }0. \end{aligned}$$

$\square$

For establishing the asymptotic normality result as stated in Theorem 2, we need the following Lemma.

Lemma 4

Under the conditions of Assumptions A,

$$\begin{aligned} \frac{1}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\overset{p}{\rightarrow } 0. \end{aligned}$$

Proof of Lemma 4

Let $X_{ni}:= a_{n_i}^{-1}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i),$ where, by proof of Theorem 1 we have $E(X_{ni})=0$ and $Var(X_{ni})=1$. Thus,

$$\begin{aligned} \frac{1}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)= \frac{1}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-1}X_{ni}. \end{aligned}$$

Now, for any $\epsilon >0$,

$$\begin{aligned} P(\left| \frac{1}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-1}X_{ni}\right| >\epsilon )\le \frac{\sum _{i=1}^{N}\frac{1}{a_{ni}^2}}{N\epsilon ^2}\rightarrow 0. \end{aligned}$$

Accordingly, we have $\frac{1}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\overset{p}{\rightarrow } 0,$ as required. $\square$

Proof of Theorem 2

We first note that by Lemma 1 and (16),

$$\begin{aligned} {{\hat{\theta }}_{ni}}-\theta _0-b_i=-a_{ni}^{-2}\sigma ^2\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)- a_{n_i}^{-1}\sigma ^2S_{n_i}(T_{ni}). \end{aligned}$$

Thus,

$$\begin{aligned} {\hat{\theta }}_{{STS}}-\theta _0= \frac{1}{N}\sum _{i=1}^{N}b_i -\frac{\sigma ^2}{N}\sum _{i=1}^{N}a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)-\frac{\sigma ^2}{N}\sum _{i=1}^{N}a_{n_i}^{-1}S_{n_i}(T_{ni}). \end{aligned}$$

Recall that $\sum _{i=1}^{N}b_i/N\rightarrow E(b_1)\equiv 0$. In view of (17) and since, $\underset{N,ni\rightarrow \infty }{\lim } N/a_{ni}^2<\infty$, we have

$$\begin{aligned} \frac{\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-1}S_{n_i}(T_{ni})\rightarrow 0 \ \ a.s.. \end{aligned}$$

Finally, from Lemma 4,

$$\begin{aligned} \frac{1}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi _{ij}(\theta _0+b_i)\overset{p}{\rightarrow } 0. \end{aligned}$$

Thus, it follows that $\lambda ^{-1}\sqrt{N}({\hat{\theta }}_{{STS}}-\theta _0)\Rightarrow {{\mathcal {N}}}(0,1).$ $\square$

1.2 7.2. Technical details and proofs, the recycled STS estimation case

In this section of the "Appendix" we provide the technical results needed for the proofs of Theorems 3 and 4 on the recycled STS estimator, ${\hat{\theta }}^*_{{RTS}}$, in the hierarchical nonlinear regression model. We begin with a re-statement of Lemma 2 from Boukai and Zhang (2018) which is concerned with the general random weights under Assumption W.

Lemma 5

Let $\mathbf{w}_n=(w_{1:n}, w_{1:n}, \dots , w_{n:n})^\mathbf{t}$ be random weights that satisfy the conditions of Assumption W. Then With $W_{i}=(w_{i:n}-1)/\tau _n, \ i=1\dots , n$ and ${\bar{W}}_n:=\frac{1}{n}\sum _{i=1}^{n}W_i$ we have, as $n\rightarrow \infty$, that $(i)\ \ \frac{1}{n}\sum _{i=1}^{n}W_i\overset{p^*}{\rightarrow }0$ $(ii)\ \ \frac{1}{n}\sum _{i=1}^{n}W_i^2\overset{p^*}{\rightarrow }1$ and hence $(iii)\ \ \frac{1}{n}\sum _{i=1}^{n}(W_i-\bar{W}_n)^2\overset{p^*}{\rightarrow }1$.

Lemma 6

Under the conditions of Assumption W, $\frac{1}{n}\sum _{i=1}^{n}w_{i:n}-1\overset{p^*}{\rightarrow }0 ,$ Further, let $\mathbf{u}_n=(u_1,u_2, \dots , u_n)^\mathbf{t}$ denote a vector of n i.i.d random variables that is independent of $\mathbf{w}_n$ with $E(u_i)=0$, $E(u_i^2)<\infty$. Then, conditional on the given value of the $\mathbf{u}_n$, we have $\frac{1}{n}\sum _{i=1}^{n}u_i w_{i:n} \overset{p^*}{\rightarrow }0$, as $n\rightarrow \infty$.

Proof of Lemma 6

We first note that

$$\begin{aligned} E^*(\frac{1}{n}\sum _{i=1}^{n}(w_{i:n}-1))^2= & E^*(\frac{\tau _n}{n}\sum _{i=1}^{n}W_i)^2\\= & \frac{\tau _n^2}{n^2}\sum _{i=1}^{n}E^*(W_i^2)+\frac{\tau _n^2}{n^2}\underset{i_1\ne i_2}{\sum }E^*(W_{i_1}W_{i_2})\\= & \frac{\tau _n^2}{n}+\frac{\tau _n^2}{n^2}n(n-1)O(\frac{1}{n})\rightarrow 0, \ \ \ \text {as} \ \ n\rightarrow \infty . \end{aligned}$$

To conclude that, $\frac{1}{n}\sum _{i=1}^{n}w_i-1\overset{p^*}{\rightarrow }0$, as $n\rightarrow \infty$. As for the second assertion, we note that since

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^{n}u_iw_{i:n}=\frac{\tau _n}{n}\sum _{i=1}^{n}u_iW_i+\frac{1}{n}\sum _{i=1}^{n}u_i, \end{aligned}$$

and since $\sum _{i=1}^{n}u_i/n\rightarrow 0$, as $n\rightarrow \infty$, we may only consider the first term. To that end, we note that

$$\begin{aligned} E^*(\frac{\tau _n}{n}\sum _{i=1}^{n}u_iW_i)^2= & \frac{\tau _n^2}{n^2}\sum _{i=1}^{n}E^*(u_i^2W_i^2)+\frac{\tau _n^2}{n^2}\underset{i_1\ne i_2}{\sum }E^*(W_{i_1}W_{i_2}u_{i_1}u_{i_2})\\\le & \left[ 1+(n-1)O(\frac{1}{n})\right] \frac{\tau _n^2}{n^2}\sum _{i=1}^{n}u_i^2 \rightarrow 0, \end{aligned}$$

as $n\rightarrow \infty$. We therefore conclude that $\frac{1}{n}\sum _{i=1}^{n}u_iw_{i:n}\overset{p^*}{\rightarrow }0,$ as required. $\square$

Lemma 7

Under the conditions of Assumptions Aand B, we have that $a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})\overset{p}{\rightarrow } 1,$ for all $i=1,2,\dots ,N$.

Proof of Lemma 7: Since ${{\hat{\theta }}_{ni}}\overset{p}{\rightarrow }\theta _0$, we have

$$\begin{aligned} a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})= & a_{n_i}^{-2}\sum _{j=1}^{n_i}(y_{ij}-f_{ij}({{\hat{\theta }}_{ni}}))^2f^{'2}_{ij}({{\hat{\theta }}_{ni}})\\= & a_{n_i}^{-2}\sum _{j=1}^{n_i}\epsilon _{ij}^2f_{ij}^{'2}({{\hat{\theta }}_{ni}})+a_{n_i}^{-2}\sum _{j=1}^{n_i}(f_{ij}(\theta _0+b_i)-f_{ij}({{\hat{\theta }}_{ni}}))^2f^{'2}_{ij}({{\hat{\theta }}_{ni}})\\+ & 2a_{n_i}^{-2}\sum _{j=1}^{n_i}\epsilon _{ij}(f_{ij}(\theta _0+b_i)-f_{ij}({{\hat{\theta }}_{ni}}))f^{'2}_{ij}({{\hat{\theta }}_{ni}})\\\equiv & B_1 +B_2 +B_3. \end{aligned}$$

Write,

$$\begin{aligned} B_1=a_{n_i}^{-2}\sum _{j=1}^{n_i}(\epsilon _{ij}^2-\sigma ^2)f^{'2}_{ij}({{\hat{\theta }}_{ni}})+a_{n_i}^{-2}\sigma ^2\sum _{j=1}^{n_i}f^{'2}_{ij}({{\hat{\theta }}_{ni}}). \end{aligned}$$

The first term in $B_1$ converges to 0 by Assumption A (3), and Corollary A of Wu (1981) while the second term in $B_1$ converges to 1 by Assumption A(3). Hence $B_1\overset{p}{\rightarrow } 1$. As for the second and third terms, $B_2$ and $B_3$, it follows by a direct application of the Cauchy-Schwarz inequality ogether with Assumption B (1), that $B_2\overset{p}{\rightarrow } 0$ and $B_3\overset{p}{\rightarrow } 0$. Accordingly, it follows that $a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})\overset{p}{\rightarrow } 1,$ as required. $\square$

Lemma 8

Under the conditions of Assumptions A and B, for all i,

$$\begin{aligned} E^*\big [\tau _{n_i}a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}W_{ij} \phi _{1ij}(b^*_{i1})\big ]^2\rightarrow 0 \end{aligned}$$

where $b^*_{i1}={{\hat{\theta }}_{ni}}+ca_{n_i}^{-1}t$ for some $0<c<1$, as $n_i\rightarrow \infty$.

Proof of Lemma 8

We first note that since by Theorem 1, we have ${{\hat{\theta }}_{ni}}-b_i-\theta _0\overset{p}{\rightarrow }0$, and since

$$\begin{aligned} |b^*_{i1}-b_i-\theta _0|= & |{{\hat{\theta }}_{ni}}-b_i-\theta _0+ca_{n_i}^{-1}t|\\\le & |{{\hat{\theta }}_{ni}}-b_i-\theta _0|+\frac{c\tau _{n_i}}{\sqrt{n_i}}\frac{\sqrt{n_i}}{a_{n_i}}\frac{|t|}{\tau _{n_i}}, \end{aligned}$$

it follows under Assumption B (3) that with $|t|\le K\tau _{n_i}$, we have $b^*_{i1}-b_i-\theta _0\overset{p}{\rightarrow }0.$ Thus,

$$\begin{aligned}&E^*[\tau _{n_i}a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup } \sum _{j=1}^{n_i}W_{ij} \phi _{1ij}(b^*_{i1})]^2\\\le & \tau _{n_i}^2a_{n_i}^{-4}\underset{|t|\le K\tau _{n_i}}{\sup }[\sum _{j=1}^{n_i}\phi ^2_{1ij}(b^*_{i1})+O(\frac{1}{n_i})\sum _{j_1\ne j_2}\phi _{1ij_1}(b^*_{i1})\phi _{1ij_2}(b^*_{i1})]\\\le & \tau _{n_i}^2a_{n_i}^{-4}\underset{|t|\le K\tau _{n_i}}{\sup }[\sum _{j=1}^{n_i}\phi ^2_{1ij}(b^*_{i1})+O(\frac{1}{n_i})(n_i-1)\sum _{j=1}^{n_i}\phi ^2_{1ij}(b^*_{i1})]\\= & \tau _{n_i}^2a_{n_i}^{-4}[O(\frac{1}{n_i})(n_i-1)+1]\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\phi ^2_{1ij}(b^*_{i1}). \end{aligned}$$

In light of Assumption B (2–3) , and that $\tau _{n_i}^2/n_i\rightarrow 0$, we only need to show, in order to complete the proof of Lemma 8, that

$$\begin{aligned} \underset{n_i\rightarrow \infty }{\lim } \ \ a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\phi ^2_{1ij}(b^*_{i1})<\infty . \end{aligned}$$

Toward that end, we note that,

$$\begin{aligned}&a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\phi ^2_{1ij}(b^*_{i1})\\= & a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}(f^{'2}_{ij}(b^*_{i1})-(y_{ij}-f_{ij}(b^*_{i1}))f^{''}_{ij}(b^*_{i1}))^2\\\le & a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}f^{'4}_{ij}(b^*_{i1})+a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}(y_{ij}-f_{ij}(b^*_{i1}))^2f^{''2}_{ij}(b^*_{i1})\\+ & 2a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\left| \sum _{j=1}^{n_i}f^{'2}_{ij}(b^*_{i1})(y_{ij}-f_{ij}(b^*_{i1}))f^{''}_{ij}(b^*_{i1})\right| \\\equiv & I_{1} +I_2 +I_3. \end{aligned}$$

It is straight forward to see that by Assumption B (1), $\underset{n_i\rightarrow \infty }{\lim }I_1<\infty$, and that by Cauchy-Schwarz inequality $\underset{n_i\rightarrow \infty }{\lim }I_3<\infty$. Finally we write

$$\begin{aligned} I_2= & a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}(\epsilon _{ij}^2-\sigma ^2)f^{''2}_{ij}(b^*_{i1})+a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\sigma ^2f^{''2}_{ij}(b^*_{i1})\\+ & a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}(f_{ij}(\theta _0+b_i)-f_{ij}(b^*_{i1}))^2f^{''2}_{ij}(b^*_{i1})\\+ & 2a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\left| \sum _{j=1}^{n_i}\epsilon _{ij}(f_{ij}(\theta _0+b_i)-f_{ij}(b^*_{i1}))f^{''2}_{ij}(b^*_{i1})\right| . \end{aligned}$$

The first term converges to 0 in probability by Assumption B (2) and Corollary A of Wu (1981). Then, according to Assumption A (2),

$$\begin{aligned} \underset{n_i\rightarrow \infty }{\lim } a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\sigma ^2f^{''2}_{ij}(b^*_{i1}) <\infty . \end{aligned}$$

The third term in $I_2$ converges to 0 in probability by an application of the Cauchy-Schwarz inequality combined with Assumption B (1) and (2). Finally, the fourth term in $I_2$, converges to 0 in probability again, by an application of the Cauchy-Schwarz inequality. Thus we have $\underset{n_i\rightarrow \infty }{\lim }I_2<\infty$. Accordingly, we have established that as $n_i\rightarrow \infty$,

$$\begin{aligned} E^*\left[ \tau _{n_i}a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}W_{ij} \phi _{1ij}(b^*_{i1})\right] ^2\rightarrow 0. \end{aligned}$$

$\square$

Lemma 9

Under the conditions of Assumptions A and B, there exists a $K>0$ such that for any $\epsilon >0$,

$$\begin{aligned} P^*\left[ \left| a_{n_i}^{-1}\sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\right| >K\right] <\frac{\epsilon }{2}. \end{aligned}$$

Proof of Lemma 9

By Lemma 7,

$$\begin{aligned}&V^*(a_{ni}^{-1}\sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}}))\\= & a_{ni}^{-2}\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})+a_{ni}^{-2}O(\frac{1}{n_i})\underset{j_1\ne j_2}{\sum } \phi _{ij_1}({{\hat{\theta }}_{ni}})\phi _{ij_2}({{\hat{\theta }}_{ni}})\\= & a_{ni}^{-2}\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})+a_{ni}^{-2}O(\frac{1}{n_i})(\sum _{j=1}^{n_i}\phi _{ij}({{\hat{\theta }}_{ni}}))^2 -a_{ni}^{-2}O(\frac{1}{n_i})\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})\\\le & a_{ni}^{-2}(1-O(\frac{1}{n_i}))\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})\overset{p}{\rightarrow } 1 . \end{aligned}$$

Hence we obtain,

$$\begin{aligned} P^*(\left| a_{ni}^{-1}\sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\right| >K)\le \frac{V^*(a_{ni}^{-1}\sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}}))}{K^2}\overset{p}{\rightarrow }\frac{1}{K^2}. \end{aligned}$$

Accordingly, there exists a $K>0$ such that for any $\epsilon >0$,

$$\begin{aligned} P^*\left[ \left| a_{n_i}^{-1}\sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\right| >K\right] <\frac{\epsilon }{2}. \end{aligned}$$

$\square$

Proof of Theorem 3

Let

$$\begin{aligned} S^*_{n_i}(t):= a_{n_i}^{-1}\sum _{j=1}^{n_i}w_{ij}\left[ \phi _{ij}({{\hat{\theta }}_{ni}}+a_{n_i}^{-1}t)-\phi _{ij}({{\hat{\theta }}_{ni}})\right] -\frac{t}{\sigma ^2}. \end{aligned}$$

(19)

First, we will show that for any given $K>0$,

$$\begin{aligned} E^*\left[ \tau _{n_i}^{-1}\underset{|t|\le K\tau _{n_i}}{\sup }|S^*_{n_i}(t)|\right] ^2\overset{p^*}{\rightarrow }0. \end{aligned}$$

(20)

By a Taylor expansion we have that $\phi _{ij}({{\hat{\theta }}_{ni}}+a_{n_i}^{-1}t)=\phi _{ij}({{\hat{\theta }}_{ni}})+\phi _{1ij}(b^*_{i1})a_{n_i}^{-1}t,$ where as before, $b^*_{i1}={{\hat{\theta }}_{ni}}+ca_{n_i}^{-1}t$ for some $0<c<1$. Accordingly we obtain,

$$\begin{aligned} \tau _{n_i}^{-1}\underset{|t|\le K\tau _{n_i}}{\sup }|S^*_{n_i}(t)|= & \tau _{n_i}^{-1}\underset{|t|\le K\tau _{n_i}}{\sup } \left| a_{n_i}^{-1}\sum _{j=1}^{n_i}w_{ij} \phi _{1ij}(b^*_{i1})a_{n_i}^{-1}t-\frac{t}{\sigma ^2} \right| \\= & K\left| a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}w_{ij}\phi _{1ij}(b^*_{i1})-\frac{1}{\sigma ^2}\right| \\\le & K\left| \tau _{n_i}a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}W_{ij}\phi _{1ij}(b^*_{i1})\right| + K\left| a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b^*_{i1})-\frac{1}{\sigma ^2}\right| . \end{aligned}$$

Further,

$$\begin{aligned} E^*\left[ \tau _{n_i}^{-1}\underset{|t|\le K\tau _{n_i}}{\sup }|S^*_{n_i}(t)|\right] ^2\le & K^2E^*\left| \tau _{n_i}a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}W_{ij}\phi _{1ij}(b^*_{i1})\right| ^2\\+ & K^2E^*\left| a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b^*_{i1})-\frac{1}{\sigma ^2}\right| ^2\\+ & K^2E^*\left| \tau _{n_i}a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}W_{ij}\phi _{1ij}(b^*_{i1})\right| \left| a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b^*_{i1})-\frac{1}{\sigma ^2}\right| . \end{aligned}$$

By Lemma 8 and Lemma 1, we have

$$\begin{aligned} E^*\left| \tau _{n_i}a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}W_{ij}\phi _{1ij}(b^*_{i1})\right| ^2\rightarrow 0, \end{aligned}$$

and

$$\begin{aligned} E^*\left| a_{n_i}^{-2}\underset{|t|\le K\tau _{n_i}}{\sup }\sum _{j=1}^{n_i}\phi _{1ij}(b^*_{i1})-\frac{1}{\sigma ^2}\right| ^2\rightarrow 0. \end{aligned}$$

Thus, by an application of the Cauchy-Schwarz inequality we have proved (20). Next, in light of (19) we define

$$\begin{aligned} A^*_{n_i}(t):=a_{n_i}^{-1}t\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}}+a_{n_i}^{-1}t)= tS^*_{n_i}(t)+a_{n_i}^{-1}t\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})+\frac{t^2}{\sigma ^2}. \end{aligned}$$

Accordingly,

$$\begin{aligned} \underset{|t|=K\tau _{n_i}}{\inf }A^*_{n_i}(t)\ge -K\tau _{n_i}\underset{|t|=K\tau _{n_i}}{\sup }|S^*_{n_i}(t)|-K\tau _{n_i}a_{n_i}^{-1}\left| \sum _{j=1}^{n_i}w_{ij} \phi _{ij}({{\hat{\theta }}_{ni}})\right| +\frac{K^2\tau _{n_i}^2}{\sigma ^2}. \end{aligned}$$

Recall that by Lemma 9, there exists a $K>0$ such that for any $\epsilon >0$,

$$\begin{aligned} P^*\left[ \left| a_{n_i}^{-1}\sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\right| >K\right] <\frac{\epsilon }{2}. \end{aligned}$$

(21)

Accordingly, by (21) and (20) we may choose large enough K such that for sufficiently large $n_i$,

$$\begin{aligned} P^*\left( \underset{|t|=K\tau _{n_i}}{\inf }A_{n_i}(t)\ge 0\right)\ge & P^*\left[ \underset{|t|=K\tau _{n_i}}{\sup }|S^*_{n_i}(t)|+a_{n_i}^{-1}\left| \sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\right| \le \frac{K\tau _{n_i}}{\sigma ^2}\right] \\= & P^*\left[ \underset{|t|=K\tau _{n_i}}{\sup }|S^*_{n_i}(t)|+a_{n_i}^{-1}\tau _{n_i}\left| \sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\right| \le \frac{K\tau _{n_i}}{\sigma ^2}\right] \\= & 1-P^*\left[ \underset{|t|=K\tau _{n_i}}{\sup }|S^*_{n_i}(t)|+a_{n_i}^{-1}\tau _{n_i}\left| \sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\right|> \frac{K\tau _{n_i}}{\sigma ^2}\right] \\\ge & 1-P^*\left[ \tau _{n_i}^{-1}\underset{|t|=K\tau _{n_i}}{\sup }|S^*_{n_i}(t)|>\frac{K}{4\sigma ^2}\right] -P^*\left[ a_{n_i}^{-1}\left| \sum _{j=1}^{n_i}W_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\right| >\frac{K}{4\sigma ^2}\right] \\\ge & 1-\epsilon . \end{aligned}$$

From the continuity of $\sum _{j=1}^{n_i}\phi _{ij}(\theta )$ in $\theta$, we have for sufficiently large $n_i$, that there exists a K such that the equation $\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}}+a_{n_i}^{-1}t)=0,$ has a root, $t=T^*_{ni}$ in $|t|\le K\tau _{n_i}$, with a probability larger than $1-\epsilon$. That is, we have ${\hat{\theta }}_{ni}^*={{\hat{\theta }}_{ni}}+a_{ni}^{-1}T^*_{ni},$ where $|\tau _{n_i}^{-1}T^*_{ni}|<K$ in probability. Accordingly we may rewrite ${\hat{\theta }}^*_{{RTS}}$ as,

$$\begin{aligned} {\hat{\theta }}^*_{{RTS}}= & \frac{1}{N}\sum _{i=1}^{N}u_i{{\hat{\theta }}_{ni}}+\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T^*_{ni}\\= & \frac{1}{N}\sum _{i=1}^{N}u_i(\theta _0+b_i+a_{ni}^{-1}T_{ni})+\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T^*_{ni}\\= & \frac{1}{N}\sum _{i=1}^{N}u_i\theta _0+\frac{1}{N}\sum _{i=1}^{N}u_ib_i+\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T_{ni}+\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T^*_{ni}. \end{aligned}$$

That is,

$$\begin{aligned} {\hat{\theta }}^*_{{RTS}}-\theta _0=\frac{1}{N}\sum _{i=1}^{N}(u_i-1)\theta _0+\frac{1}{N}\sum _{i=1}^{N}u_ib_i+\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T_{ni}+\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T^*_{ni}. \end{aligned}$$

Additionally, by Lemma 6, we have $\frac{1}{N}\sum _{i=1}^{N}(u_i-1)\overset{p^*}{\rightarrow }0,$ as well as, $\frac{1}{N}\sum _{i=1}^{N}u_ib_i\overset{p^*}{\rightarrow }0$. Further, we also have that

$$\begin{aligned} \frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T_{ni}= \frac{1}{N}\sum _{i=1}^{N}(u_i-1)a_{ni}^{-1}T_{ni}+\frac{1}{N}\sum _{i=1}^{N}a_{ni}^{-1}T_{ni}. \end{aligned}$$

Now by Lemma 2 and the fact $T_{ni}=O_p(1)$, we obtain, with $U_i:=(u_i-1)/\tau _N$, that

$$\begin{aligned} E^*(\frac{1}{N}\sum _{i=1}^{N}(u_i-1)a_{ni}^{-1}T_{ni})^2= & E^*(\frac{\tau _N}{N}\sum _{i=1}^{N}U_ia_{ni}^{-1}T_{ni})^2\\\le & \frac{\tau _N^2}{N^2}\sum _{i=1}^{N}a_{ni}^{-2}T^2_{ni}+(N-1)O(\frac{1}{N})\frac{\tau _N^2}{N^2}\sum _{i=1}^{N}a_{ni}^{-2}T^2_{ni} \overset{p}{\rightarrow }0, \end{aligned}$$

as well as, $\frac{1}{N}\sum _{i=1}^{N}a_{ni}^{-1}T_{ni}\overset{p}{\rightarrow } 0$. That is, we have established that, $E^*(\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T_{ni})^2\overset{p}{\rightarrow } 0$. Accordingly we conclude, $P^*(|\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T_{ni}|>\epsilon )=o_p(1)$. Similarly,

$$\begin{aligned} \frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T^*_{ni}= \frac{1}{N}\sum _{i=1}^{N}(u_i-1)a_{ni}^{-1}T^*_{ni}+\frac{1}{N}\sum _{i=1}^{N}a_{ni}^{-1}T^*_{ni}, \end{aligned}$$

where by Lemma 2, Assumption B (3) and the fact $\tau _{n_i}^{-1}T^{*}_{ni}=O_{p^*}(1)$, we obtain,

$$\begin{aligned} E^*(\frac{1}{N}\sum _{i=1}^{N}(u_i-1)a_{ni}^{-1}T^*_{ni})^2= & E^*(\frac{\tau _N}{N}\sum _{i=1}^{N}U_ia_{ni}^{-1}T^*_{ni})^2\\\le & \frac{\tau _N^2}{N^2}\sum _{i=1}^{N}a_{ni}^{-2}T^{*2}_{ni}+(N-1)O(\frac{1}{N})\frac{\tau _N^2}{N^2}\sum _{i=1}^{N}a_{ni}^{-2}T^{*2}_{ni}\\= & (1+(N-1)O(\frac{1}{N}))\frac{\tau _N^2}{N^2}\sum _{i=1}^{N}\frac{\tau ^2_{n_i}}{a_{ni}^{2}}\tau _{n_i}^{-2}T^{*2}_{ni}\overset{p}{\rightarrow }0. \end{aligned}$$

Finally, by Lemma 2,

$$\begin{aligned} \frac{1}{N}\sum _{i=1}^{N}a_{ni}^{-1}T^*_{ni}= & \frac{1}{N}\sum _{i=1}^{N}\frac{\tau _{n_i}}{a_{ni}}\tau _{n_i}^{-1}T^*_{ni}\rightarrow 0. \end{aligned}$$

Accordingly we also conclude that, $P^*(|\frac{1}{N}\sum _{i=1}^{N}u_ia_{ni}^{-1}T^*_{ni}|>\epsilon )=o_p(1)$. Hence, we have proved that $P^*(|{\hat{\theta }}^*_{{RTS}}-\theta _0|>\epsilon )=o_p(1)$. $\square$

For the related asymptotic normality results as stated in Theorem 4, we need the following two Lemmas.

Lemma 10

Suppose that the conditions of Assumptions A and B hold. If $\frac{\tau _{n_i}}{\tau _N}=o(\sqrt{n_i})$ then as $n_i\rightarrow \infty$ and $N\rightarrow \infty$,

$$\begin{aligned} \frac{\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-2}\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\overset{p^*}{\rightarrow } 0. \end{aligned}$$

Proof of Lemma 10

Let

$$\begin{aligned} X^*_{ni}:= \tau _{n_i}^{-1}a_{n_i}^{-1}\sum _{j=1}^{n_i}w_{ij} \phi _{ij}({{\hat{\theta }}_{ni}})=a_{n_i}^{-1}\sum _{j=1}^{n_i}W_{ij} \phi _{ij}({{\hat{\theta }}_{ni}}). \end{aligned}$$

Clearly $E^*(X^*_{ni})=0$, and $X^*_{n_i}$ are independent for i in $1,2,\dots , N$. Further, by Lemma 7 we have, as $n_i\rightarrow \infty$, that

$$\begin{aligned} E^*(X^{*2}_{ni})= & E^*(a_{n_i}^{-1}\sum _{j=1}^{n_i}W_{ij} \phi _{ij}({{\hat{\theta }}_{ni}}))^2\\= & a_{n_i}^{-2}\left[ \sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})+O(\frac{1}{n_i})\underset{j_1\ne j_2}{\sum }\phi _{ij_1}({{\hat{\theta }}_{ni}})\phi _{ij_2}({{\hat{\theta }}_{ni}})\right] \\= & a_{n_i}^{-2}\left[ \sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})+O(\frac{1}{n_i})\left( \sum _{j=1}^{n_i}\phi _{ij}({{\hat{\theta }}_{ni}})\right) ^2-O(\frac{1}{n_i})\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})\right] \\= & (1-O(\frac{1}{n_i}))a_{n_i}^{-2}\sum _{j=1}^{n_i}\phi ^2_{ij}({{\hat{\theta }}_{ni}})\rightarrow 1. \end{aligned}$$

Thus, with $U_i=(u_i-1)/\sqrt{\tau _N}$,

$$\begin{aligned} \frac{\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-2}\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})= & \frac{\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-1}\tau _{n_i}X^*_{ni}\\= & \frac{1}{\sqrt{N}}\sum _{i=1}^{N}U_ia_{n_i}^{-1}\tau _{n_i}X^*_{ni}+\frac{\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-1}\tau _{n_i}X^*_{ni}. \end{aligned}$$

Since $U_i$ and $X^*_{ni}$ are independent, we obtain,

$$\begin{aligned} E^*(\frac{1}{\sqrt{N}}\sum _{i=1}^{N}U_ia_{n_i}^{-1}\tau _{n_i}X^*_{ni})^2= & \frac{1}{N}\sum _{i=1}^{N}E^* (U_i^2a_{n_i}^{-2}\tau _{n_i}^2X^{*2}_{ni})\\+ & \underset{i_1\ne i_2}{\sum }E^*(U_{i_1}U_{i_2}a_{n_{i_1}}^{-1}a_{n_{i_2}}^{-1}\tau _{n_{i_1}}\tau _{n_{i_2}}X^{*}_{ni_1}X^{*}_{ni_2})\\= & \frac{1}{N}\sum _{i=1}^{N}a_{n_i}^{-2}\tau _{n_i}^2E^* (X^{*2}_{ni})\rightarrow 0. \end{aligned}$$

Finally, since $\frac{\tau _{n_i}}{\tau _N}=o(\sqrt{n_i})$, we also have,

$$\begin{aligned} E^*(\frac{\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-1}\tau _{n_i}X^*_{ni})^2= & \frac{\tau _N^{-2}}{N}\sum _{i=1}^{N}a_{n_i}^{-2}\tau _{n_i}^2E^*(X^{*2}_{ni})\\= & \frac{1}{N}\sum _{i=1}^{N}\frac{\tau _{n_i}^2}{\tau _N^{2}}a_{n_i}^{-2}E^*(X^{*2}_{ni})\rightarrow 0. \end{aligned}$$

Accordingly we obtain that,

$$\begin{aligned} \frac{\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-2}\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\overset{p^*}{\rightarrow } 0. \end{aligned}$$

$\square$

Lemma 11

Suppose that the conditions of Assumptions A and B hold. If $\frac{\tau _{n_i}}{\tau _N}=o(\sqrt{n_i})$ then as $n_i\rightarrow \infty$ and $N\rightarrow \infty$,

$$\begin{aligned} \frac{\lambda ^{-1}\tau _N^{-1}\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-1}S_{n_i}(T^*_{ni}) \overset{p^*}{\rightarrow } 0. \end{aligned}$$

Proof of Lemma 11

We first write

$$\begin{aligned} \frac{\lambda ^{-1}\tau _N^{-1}\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-1}S_{n_i}(T^*_{ni})=\frac{\lambda ^{-1}\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}U_ia_{n_i}^{-1}S_{n_i}(T^*_{ni})+\frac{\lambda ^{-1}\tau _N^{-1}\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-1}S_{n_i}(T^*_{ni}). \end{aligned}$$

By Lemma 2, Assumption B (3) and the fact $\tau _N^{-1}S_{n_i}(T^*_{ni})\overset{p^*}{\rightarrow } 0$,

$$\begin{aligned} \frac{\lambda ^{-1}\tau _N^{-1}\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}a_{n_i}^{-1}S_{n_i}(T^*_{ni})\overset{p^*}{\rightarrow } 0. \end{aligned}$$

Further, it can be seen that,

$$\begin{aligned} E^*(\frac{1}{\sqrt{N}}\sum _{i=1}^{N}U_ia_{ni}^{-1}S_{n_i}(T^*_{ni}))^2\le & \frac{1}{N}\left[ 1+(N-1)O(\frac{1}{N})\right] \sum _{i=1}^{N}a_{ni}^{-2}E^*(S^2_{n_i}(T^*_{ni}))\rightarrow 0. \end{aligned}$$

Thus we have,

$$\begin{aligned} \frac{\lambda ^{-1}\tau _N^{-1}\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-1}S_{n_i}(T^*_{ni}) \overset{p^*}{\rightarrow } 0. \end{aligned}$$

$\square$

We conclude the "Appendix" with a proof of Theorem 4.

Proof of Theorem 4

By Theorem 3 and (19) we express,

$$\begin{aligned} {\hat{\theta }}_{ni}^*-{{\hat{\theta }}_{ni}}=-a_{ni}^{-2}\sigma ^2\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})- a_{n_i}^{-1}\sigma ^2S_{n_i}(T^*_{ni}). \end{aligned}$$

Accordingly we have,

$$\begin{aligned} {\hat{\theta }}^*_{{SRS}}-{\hat{\theta }}_{{STS}}= \frac{1}{N}\sum _{i=1}^{N}(u_i-1){{\hat{\theta }}_{ni}}-\frac{\sigma ^2}{N}\sum _{i=1}^{N}u_ia_{n_i}^{-2}\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})-\frac{\sigma ^2}{N}\sum _{i=1}^{N}u_ia_{n_i}^{-1}S_{n_i}(T^*_{ni}), \end{aligned}$$

where $|T^*_{ni}|<K\tau _{n_i}$ in probability. Further,

$$\begin{aligned} \lambda ^{-1}\tau _N^{-1}\sqrt{N}({\hat{\theta }}^*_{{RTS}}-{\hat{\theta }}_{{STS}})= & \frac{\lambda ^{-1}\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}(u_i-1){{\hat{\theta }}_{ni}}\\- & \frac{\lambda ^{-1}\tau _N^{-1}\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-2}\sum _{j=1}^{n_i}w_{ij}\phi _{ij}({{\hat{\theta }}_{ni}})\\- & \frac{\lambda ^{-1}\tau _N^{-1}\sigma ^2}{\sqrt{N}}\sum _{i=1}^{N}u_ia_{n_i}^{-1}S_{n_i}(T^*_{ni})\\\equiv & I_1+I_2+I_3 . \end{aligned}$$

By Lemma 10, $I_2\overset{p^*}{\rightarrow } 0$, and by Lemma 11, $I_3\overset{p^*}{\rightarrow } 0$, and therefore it remains only to consider $I_1$. Now, observe that,

$$\begin{aligned} I_1:= \frac{\lambda ^{-1}\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}(u_i-1){{\hat{\theta }}_{ni}}=\frac{\lambda ^{-1}}{\sqrt{N}}\sum _{i=1}^{N}U_i(b_i+\theta _0)+\frac{\lambda ^{-1}}{\sqrt{N}}\sum _{i=1}^{N}U_ia_{n_i}^{-1}T_{ni}. \end{aligned}$$

By Lemma 2,

$$\begin{aligned} E^*(\frac{1}{\sqrt{N}}\sum _{i=1}^{N}U_ia_{ni}^{-1}T_{ni})^2\le & \frac{1}{N}\sum _{i=1}^{N}a_{ni}^{-2}T^2_{ni}+(N-1)O(\frac{1}{N})\frac{1}{N}\sum _{i=1}^{N}a_{ni}^{-2}T^2_{ni} \overset{p}{\rightarrow }0. \end{aligned}$$

Further by Lemma 5,

$$\begin{aligned} \bar{U}_N:=\frac{1}{N}\sum _{i=1}^{N}U_i\equiv \frac{1}{N} \sum _{i=1}^{N}\frac{u_i-1}{\tau _N}\overset{p^*}{\rightarrow } 0, \end{aligned}$$

and clearly, $\sqrt{N}(\bar{b}+\theta _0)\Rightarrow \mathcal{{N}}(\theta _0,\lambda ^2)$. Accordingly we have, $\frac{\lambda ^{-1}}{N}\sum _{i=1}^{N}(b_i-\bar{b})^2\rightarrow 1 \ \ a.s.$ as well as $\sqrt{N} \bar{U}(\bar{b}+\theta _0)\overset{p^*}{\rightarrow } 0$. Further, by Lemma 4.6 of Praestgaard and Wellner (1993), we have that

$$\begin{aligned} \frac{\lambda ^{-1}}{\sqrt{N}}\sum _{i=1}^{N}U_i(b_i+\theta _0)\Rightarrow {{\mathcal {N}}}(0,1). \end{aligned}$$

Thus we have

$$\begin{aligned} \frac{\lambda ^{-1}\tau _N^{-1}}{\sqrt{N}}\sum _{i=1}^{N}(u_i-1){{\hat{\theta }}_{ni}}\Rightarrow \mathcal{{N}}(0,1). \end{aligned}$$

Finally we conclude that as $n_i\rightarrow \infty$ and $N\rightarrow \infty$,

$$\begin{aligned} \lambda ^{-1}\tau _N^{-1}\sqrt{N}({\hat{\theta }}^*_{{RTS}}-{\hat{\theta }}_{{STS}})\Rightarrow \mathcal{{N}}(0,1). \end{aligned}$$

$\square$