Optimal components selection based on fuzzy-intra coupling density for component-based software systems under build-or-buy scheme

Abstract

Component-Based Software Engineering (CBSE) is an approach to building and developing software systems based on software components. In component-based software systems, there are various software components, including Commercial off the Shelf (COTS) and in-house components. Software developers can build their desired software component as in-house or COTS. The problem of deciding optimally between COTS and in-house components is one of the major challenges of software developers, which is known as the component selection problem. This can be resolved by evaluating the criteria for optimality in component selection and then solving the component selection problem by optimization techniques. In this paper, an attempt was made to optimize the component selection problem through the multi-objective optimization by maximizing the Fuzzy-Intra Coupling Density (Fuzzy-ICD) and functionality as objective functions, and also taking into account budget, delivery time, reliability, and Fuzzy-ICD as constraints of multi-objective problems. Fuzzy ICD is a more accurate criterion to calculate the relationship between Cohesion and Coupling of components, which is obtained through the fuzzy computing of each of them, based on the Meyers classification. Thus, after a two-criterion optimization model formulation, this optimization problem was solved by fuzzy multi objectives approach. Finally, the proposed method was evaluated by performing the case study of financial-accounting system. Comparison of the results showed that the proposed method could select optimal components with maximum functionality and Fuzzy-ICD and fewer rates of time and Budget (0.29, 0.43, 1.1 s, and 88$ were the improved rates of functionality, Fuzzy-ICD, time, and budget, respectively).

Introduction

With the progressive development of software in recent years, software development has become more complex; to overcome this complexity, a lot of cost and time is needed. An acceptable and reasonable solution is reusability of software systems. Component-Based Software Engineering (CBSE) is an approach to building and development of software systems based on existing software components [1,2,3]. These software systems, which have the maximum use of reusable materials, are called Component-Based Software Systems (CBSS) [2]. CBSSs cause the efficiency of software development in terms of demanding lower cost, reducing the time to market, improving maintainability, increasing reliability, and improving other quality parameters [2, 3].

With the development of CBSE, various software components have been presented by many software developer organizations. These components are called Commercial off the shelf (COTS). The components of COTS help software developers to select a software component from among a set of alternative software components available in the market [4,5,6]. Thus, software developers can either build their desired software components as in-house or buy them as COTS (i.e., the build-or-buy strategy) [2].

These two different strategies have advantages and disadvantages that software developers should be aware of. Components of COTS are often built by independent teams of developers in different languages, and applicable to different platforms with less complexity; then, they are available as standard components in the market. The advantages of this type of components are the existence of different versions of a COTS product, design diversity, diversity of data, and the diversity of executive environment which are available in the market by different manufacturers. On the other hand, these products have some disadvantages, including issues with security, consistency, integrity and interoperability, procurement and licensing, etc. However, the customization of the components of in-house development makes it compatible with the system, reliability, and support. Unlike the components of COTS, components of in-house prolong the time of supplying the software product to the market [2]. Thus, always there is a discussion on whether to build-or-buy software components.

To overcome this problem, software researchers evaluate in-house and COTS software components based on some criteria to finally decide what components they should build and what components they should buy. These criteria include [7]:

• Financial perspective (COTS cost, maintenance cost, upgrading cost, etc.)

• Technical perspective (reliability, safety, performance, requirements, quality, etc.)

• Business perspective (COTS vendor recognition, COTS vendor properties, Historical records, etc.)

• Legal perspective (type of contract, license agreement, escrow, etc.).

Thus, the problem of selecting the optimal component has been recognized as an optimization problem.

In addition to the above mentioned criteria, it should be noted that the efficiency of the component-based software system significantly depends on the system architecture; coupling and cohesion have a major role in reducing the complexity associated with the design and determining the quality of a software system in terms of reliability, maintainability, and accessibility [2, 8]. Cohesion as an intra modules property refers to the amount of communication that the components within a module have with each other (operating power of a module). On the other hand, coupling as an inter-modules property refers to the amount of the communication of a module with other modules (dependency between two or more modules) [9, 10]. Thus, for an optimal software component selection, the interactions of components within the modules (cohesion) need to be maximum, while the interactions between the modules (coupling) need to be minimum. Software designs with high cohesion and low coupling will create independent modules that offer some advantages, including easier development, reduced complexity, facilitated maintenance and modifications, reduced error rate, increased reusability, parallel development, and simple implementation [10, 11]. Intra Coupling Density (ICD) is a measure used to describe the relationship between coupling and cohesion of modules [2, 12, 13].

Various optimization problems have been applied by different researchers to the selection of the optimum component in a component-based software system based on the build-or-buy strategy, which will be discussed in the next section.

In this paper, the multi-objective optimization problem is addressed to carry out the optimal component selection through the build-or-buy strategy for CBSS. Fuzzy ICD and functionality are considered as two-objective functions in this problem. A multi-objective optimization problem was formulated in this study by maximizing the Fuzzy-Intra Coupling Density (Fuzzy-ICD) and functionality, and also taking into account budget, delivery time, reliability, and Fuzzy-ICD as constraints of multi objectives problems. Fuzzy ICD is a more accurate criterion for calculating the relationship between cohesion and coupling of components (which is obtained through the fuzzy computing of each of them based on the Mayers classification). Since, fuzzy approach used as an effective tool for quickly obtaining a good compromised solution in these scenario [8], after the two-objective optimization model is formulated for optimum software component selection to build or buy in CBSS, the formulated optimization problem will be solved by fuzzy multi-objective approach.

In the following, the main contributions of this paper are summarized:

• 1. Considering the application of the fuzzy measurement of coupling and cohesion to the problem of component selection: the efficiency of component-based software system depends greatly on the system architecture; coupling and cohesion have a major role in software nonfunctional requirements and reducing software complexity. Therefore, it is necessary to calculate them accurately.

• 2. Applying Fuzzy-ICD to one of the objective functions in multi-objective component selection optimization: accurate calculation of ICD as a criterion for calculating the relationship between coherence and connection of parts in the software plays a major role in developing a qualitative evaluation criterion in software.

• 3. Formulation of multi-objective optimization applicable to optimal software component selection: the multi-objective optimization problem is formulated by maximizing the Fuzzy-ICD and functionality and also taking into account the factors such as budget, delivery time, reliability, and Fuzzy-ICD as constraints. The formulated bi-objective optimization model for optimal software components selection in the build-or-buy strategy in CBSS will be solved by a fuzzy multi-objective approach.

• 4. Evaluating the proposed formulation of multi-objective component selection optimization by applying it to case study of financial-accounting system used by authors in [2].

The rest of the paper is organized as follows: in “Related Work”, first, the existing literature regarding the software component selection in CBSS is reviewed, and then existing measurement methods of coupling and cohesion are investigated. In “Fuzzy Method for Calculation of Coupling and Cohesion”, the proposed method of fuzzy computing of cohesion and coupling is described. Then, the “Selecting the Optimal Software Components with Multi-objective Optimization Approach” reports the process of optimal choice of components in the form of a series of hypotheses and problem formulation and discusses the optimization problem solution. Next, the case study used in this article is introduced in “Case Study”. In section “The Result”, the proposed method is evaluated, and finally, in seventh section, the conclusion of the article is stated.

Related work

In section “Selection methods optimized software components”, the other studies related to the optimal choice of software components are reviewed; then, in “Calculation Methods of Coupling and Cohesion”, the studies conducted in relation to measurement are discussed.

Optimization methods of software components selection

In a general classification, the methods of selecting the optimal components in component-based software systems include the methods based on the Weighted scoring method, the methods based on Analytical Hierarchical Process (AHP), the methods based on artificial intelligence, and the methods based on optimization [14, 15].

Figure 1 represents a classification of component selection methods proposed in literature by researchers working in this field.

Fig. 1

Classification of component selection methods

In these methods, the representations related to the available characteristics for the optimal selection of components are presented in the form of feature vector, XML Scheme, Requirement document templates, and Graph format.

Weighted scoring method

The Weighted scoring method (WSM) is one of the oldest methods in the selection of components and software packages. In cases where the issue of Multi-Criteria Decision Making (MCDM) exists for n number of candidate components and m criteria, manual weighting method will be applied [14]. The method proposed by Collier et al. in [16] uses weighting method to select the optimal software components.

This method, although, is simple and implementable, but if the customer needs change at the last minute, the score for each component changes according to the evaluation criteria, and it should be updated before the final calculation. As the process of weighting is manual, it is considered duplication and process is complicated [17].

Analytical hierarchical process

The Analytical hierarchical process (AHP) is a technique applicable to selection-related problems with several criteria. A lot of studies have been carried out by software developers to choose the optimal components based on AHP [4, 7, 18, 19]. Mitta et al. [19] considered reusability as an important criterion in selecting the components. They used the technique of AHP and ranked the criteria for reusability to select and evaluate the components of COTS. In another study, Garg et al. [4] applied the ranking based on fuzzy distance to the AHP technique to select COTS components on the Database Management System (DBMS). Despite the widespread application of AHP to both quantitative and qualitative parameters, its disadvantages are its lack of flexibility to changes of optimization criteria, uncertain ranking, and the lack of time optimization that is due to pairwise comparisons in the AHP method [14].

Artificial intelligence-based methods

The methods such as neural network, Decision Tree, fuzzy classifier, deductive method, and collective intelligence are a number of methods working based on artificial intelligence. In this category, a technique for training AI classifiers described to assist in the selection of software components for development projects. Researchers believe that when using AI, we are able to represent dependencies between attributes, overcoming some of the limitations of existing aggregation-based approaches to CS [1]. Maxville et al. [20] used neural networks and Decision Tree for optimal selection of components. They prepared the ideal profile data of the needed components in both training and testing categories and in the form of XML. In the neural network, they used the back propagation algorithm in the weka. The Decision Tree creates a tree by a combination of data collection and their classification. After that, the data group was pruned to create a control decision tree. In their research, they concluded that the Decision Tree (C4.5) provided better results than the neural network.

In addition, Jadhav et al. [21] offered a deductive method based on a combination of Rule Base Reasoning (RBR) and Case Base Reasoning (CBR). The RBR and CBR methods are two fundamental techniques of Knowledge Base System (KBS). In RBR, the ideal needs of the user are collected in the form of feature value, and to assess the decision-making criteria, simple if–then-else rules are used. In CBR, the ideal needs of the user are compared in the form of candidate software packages. The candidate packets are saved as "cases" in the case-based system. The collection of system results in the selection of replacement components is ranked based on similarity. This similarity identifies the software component that responds to the system ideal needs. Hybrid Knowledge Base System (HKBS), compared to the AHP and WSM methods, is more efficient because it offers the computational efficiency, ease of problem-solving, knowledge reuse, compatibility, and evaluation of the results.

The fuzzy method is used by decision makers to evaluate alternative components easily and directly using language requirements [22]. The authors in [23] used the fuzzy method to avoid ambiguity that human decision-making processes may suffer from when using AHP and WSM.

In [24], an algorithm was proposed based on the collective intelligence of ants and the left footprint of pheromone to select optimal software components. To choose the optimal software components, they considered both positive and negative feedbacks in the characteristic evaluation of the components. In their model, the positive feedback increases the amount of pheromone, whereas the negative feedback evaporates the pheromone. Finally, after enough repetition, the component with the highest pheromone is selected as the optimal component.

Optimization-based methods

The structure of the CS (Component selection) problem is more similar to the multi-part problem due to the involvement of different (and sometimes contradictory) criteria. Optimization-based methods have shown higher efficiency in solving these problems. The CS problem is transformed to an optimization problem that essentially looks for maximum/minimum values in one or more fitness functions. Optimization-based methods can be include single and multi-objective optimization, mathematical optimization and evolutionary algorithm.

Generally, optimization-based methods are divided into two categories: single-objective optimization and multi-objective optimization methods. In the former, an objective function with some constraints is formulated to choose the optimal components. This function can be one of the parameters of cost, reliability, delivery time, quality, etc. Optimization problem is finding the answer or answers from among a set of possible options (with respect the constraints of the problem) with the aim of optimizing the criterion or criteria of the problem. The multi-objective optimization problem is a branch of MCDM problem. On the other hand, the multi-objective optimization problem is originated from real-world situations where a decision maker faces a set of objectives with multiple contradictory criteria. In these types of problems, unlike the single-objective optimization, different solutions can be taken into consideration [2].

In one of the first studies related to the optimal choice of components with the use of single-objective function, Berman et al. [25] formulated the optimization problem. Their objective function was maximizing the reliability. And the constraint of their optimization was cost criterion that needed to be limited to a certain threshold value.

Cortellessa et al. [26] used the cost minimization as an objective function with reliability and delivery time constraints in the optimal choice of components in the build-or-buy frameworks in software architecture.

Kwong et al. [13] considered the maximum of relationships within the modules and minimum of relationships between modules as parameter ICD and used functionality as the objective function of the problem. Since multi-objective optimization is complex and difficult to solve, they adopted the weighting method for each of the objective functions (as expressed in Eq. (1)) to be able to convert multi-objective problem to single-objective problem and to solve it simply. Thus, with separate solution of the objective functions of functionality and ICD in minimizing and maximizing states, the values F_min, F_max, E_min, and E_max are calculated respectively. According to the obtained values and weighting of functionality and ICD, the objective function of the optimization problem is defined as below:

$$ \max w_{f} \frac{{F - F_{{\min }} }}{{F_{{\max }} - F_{{\min }} }} + w_{l} \frac{{E - E_{{\min }} }}{{E_{{\max }} - E_{{\min }} }} $$

(1)

Since the optimization is an NP-Complete problem [13], the authors in [13] used genetic algorithm to select the optimal components.

Gupta et al. [27] used the multi-objective optimization with the aim of increasing the quality, reducing the cost, increasing the reliability, and reducing the size and the time of delivery, and they discussed the constraints of time and consistency in the formulation of their proposed system. Then, they used the fuzzy approach to solve the multi-objective optimization problem, continued according to the principle of maximizing of Bellman-zadeh [28], and formulated the problem using the fuzzy membership functions suggested for solving the problem of multi-objective optimization.

Jung et al. [29] used two model of formulation in the optimal choice of components. In the first one, they built their issue with the objective function of quality and budget constraint. In the optimization process, they used the weighted value for the objective function of quality. They formulated the second model like the first one with only one difference: they added the compatibility between the components in their optimal choice to the constraints of the problem. In a similar study, Shen et al. [30] selected the optimal components by the objective function of quality weighted on budget constraint with the difference that they analyzed the budget constraint with the use of the fuzzy system.

According to Indumati et al. [8], a component-based software system uses a top-down approach. Based on this approach, at the first step, the operational needs are identified, then at the second step, the number and nature of software modules are determined. Finally, at the third step, the selection of the optimal components for each module is formulated. They considered the maximization of the ICD and reliability as the objective function, and the threshold on the ICD, reliability, cost, and time as the constraints. The authors mentioned above, despite their similar peer articles, solved the optimization problem as a nonlinear optimization problem.

Likewise, in [31], the authors examined the optimal choice of components, in a fault-tolerance modular software system. They considered simultaneously the maximization of the system reliability and minimization of the cost as an objective function. They used this method only to choose between the components of COTS. In another experiment, they considered the cost as the objective function, and reliability as the constraint. Finally, they concluded that by using multi-objective function with the aim of minimizing the cost and maximizing the reliability, and by using the technique of goal programming, favorable optimization results can be achieved.

Jha et al. [32] used the parameters of ICD, functionality, budget, and quality as the objective function to choose the optimal component in a component-based software system. Thus, they considered the objective functions of ICD, quality, and functionality as maximization and the objective function of budget as minimization in solving the optimization problem. Then, they used fuzzy multi-objective approach to solve their optimization problem. In another study [2], the optimal choice of components in modular software system with fuzzy two-criterion optimization model and under the build-or-buy scheme was formulated. This model of optimization attempts to increase the objective functions of ICD and functionality and, at the same time, takes into account the constraints of budget, reliability, and delivery time.

Also according to [50, 51], multi-objective evolutionary algorithms (MOEA) are artificial intelligence optimization problems that decompose multi-objective optimization problems into a set of simple optimization sub-problems and solve them in a common manner. This method plays a key role in tradeoffs between diversity and convergence in MOEA.

Statistical analysis result of related work

Although much research has been done on WSM, AHP, AI, and optimization-based methods, literature consists of some other methods such as semantic-based methods and cluster-based methods that are presented in the selection of components problem. The Ontology-based method proposed by Yesad and Boufaida in [33] is an example of methods based on different semantic and theories. Furthermore, in [34], Vescan et al. used fuzzy clustering algorithms.

Research shows that the use of the feature vector has been a popular approach among the researchers working in this field. The increase in the use of the feature vector is due to the greater use of feature vectors in Objective Optimization-based methods. However, it can be said that multi-objective optimization is still the best option for solving the optimal selection of components. As a result, the current paper focuses on multi-objective optimization. As can be observed in Fig. 2, the representation based on the feature vector with 69.7% has been the most used item among the papers reviewed by the authors in [1].

Fig. 2

The used representation in component selection researches

It is important to know what feature(s) of a component is the most important feature in optimizing components selection. To achieve this goal, researchers used Hundred Doller (100$) test in [35, 36]. First, they selected the most important features from a list. Then they chose their priority using the 100$ test. The results showed that cost was the most important feature for component selection.

By analyzing the results of approximately 40 criteria that could be examined in CS in [1], the statistical results of Table 1 were obtained. In these statistical results, nine types of the most popular practical criteria in CS have been evaluated.

Table 1 Statistical results for main criteria in related research

As can be seen in Table 1, from the 130 papers reviewed with 41 evaluation criteria in the field of Component selection (CS), the cost criterion with 17.70% is the most popular criterion in the optimal selection of components.

It should be noted that there is not always a consensus among researchers and large and small organizations on the optimal selection of these components.

It will be interesting to know that there is a disagreement among large and small organizations in criterion of cost. In this sense, large organizations with higher and more complete products often give priority to cost [1].

Calculation methods of coupling and cohesion

CBO, RFC, CF, OCM, CCM and DAC are Metrics for Object-Oriented Design (MOOD) coupling's metrics summarized by the authors in [37, 38, 49]. CBO (Coupling between Object Classes) shows how many classes couple together and identifies the amount of coupling. RFC (Response for Class) as a response set includes all methods in a class and other calling classes from the same class (we will consider the concept of coupling when a class is available in another class; at least some parts of this class are called by another one). CF (Coupling factor) can be calculated by Eq. (2) and it indicates the number of coupled class pairs divided by the total number of class pairs. Finally, DAC (Data abstraction coupling) equals the number of class features (methods and variables) that other classes use as their data.

$$ {\text{CF}} = \frac{{{\text{number of coupled class pairs}}}}{{{\text{total number of class pairs}}}}{\text{ }} $$

(2)

LCOM, LCOM3, RLCOM, MC, LMCC, LCC and TCC are metrics that calculate cohesion [37,38,39, 47, 48]. LCOM (Lack of cohesion in methods) indicates the number of non-similar method pairs in a class (similarity of the methods means that all methods in a class have one or more similar and common features). LCOM3 is the number of component connections in a graph, which use graph model; the vertex is the method and the edge is the link between methods. According to Eqs. (3) and (4), RLCOM and TCC (Tight class cohesion) are the number of non-similar method pairs and the number of similar method pairs, respectively, on the total number of method pairs in the class.

$$ {\text{RLCOM}} = \frac{{{\text{number of non-similar method pairs}}}}{{{\text{total number of method pairs in the class}}}}{\text{ }} $$

(3)

$$ {\text{TCC}} = \frac{{{\text{number of similar method pairs}}}}{{{\text{total number of method pairs in the class}}}}{\text{ }} $$

(4)

In [40], Felton and Melton presented a metric that uses the Myers classification (Eq. 5) to measure coupling; where N is the number of connection of x and y, and i denotes the level of the Myers model (i = 5, 4, 3, 2, 1, or 0 respectively represents content, common, control, stamp, data coupling, and no coupling).

$$ C\left( {x,y} \right) = i + n/(n + {\text{1}}) $$

(5)

Gui [41] proposed a metric in which the equation of group D is used (Eq. 6) to measure coupling.

$$ {\text{Coup}}D = \frac{{\left| {MV_{{ij}} } \right|}}{{\left| {MV_{i} } \right| + \left| {V_{i} } \right| + \left| {M_{i} } \right|}} $$

(6)

In this equation, M is the method, V signifies the variables, MV_j is the set of methods and variables called by C_j class, and MV_ij denotes the set of methods and variables in C_i class and will be called by C_j class (MV_j = UMV_ij). Since the denominator is equivalent to $\left| {MV_{i} } \right| + \left| {V_{i} } \right| + \left| {M_{i} } \right|$, the amount of coupling is calculated in range of $0 \le {\text{Coup}}D\;(i,j) \le 1$. In other words, this standardization caused Group D to be independent of class size. We also used Eq. (7) to measure coupling indirectly as follows:

$$ \begin{aligned} {\text{Coup}}T\;(i,j,p) = & \prod\nolimits_{{e_{{s,t}} \in p}} {{\text{Coup}}D\;(s,t)} \\ = & \prod\nolimits_{{e_{{s,t}} \in p}} {\frac{{\left| {MV_{{ij}} } \right|}}{{\left| {MV_{i} } \right| + \left| {V_{i} } \right| + \left| {M_{i} } \right|}}} \\ \end{aligned} $$

(7)

When a transitive relation is established between modules, indirect coupling occurs in the cases where several couplings are in indirect paths. According to Eq. (7), a path with the most coupling is used to calculate coupling (Eq. 8).

$$ {\text{Coup}}\;(i,j) = {\text{Coup}}T\;(i,j,p_{{\max }} (i,j)) $$

(8)

Thus, to calculate coupling in a system (Total coupling), Eqs. (9) and (10) were used as follow:

$$ WT_{{{\text{coup}}}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {{\text{Coup}}\;(i,j)} }}{{m^{2} - m}} $$

(9)

$$ WT_{{{\text{coup}}}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {{\text{Coup}}D\;(i,j)} }}{{m^{2} - m}} $$

(10)

where m is the number of classes in the system.

Gui in [41] also proposed a method to measure Cohesion (Jaccard measure in Eq. (11)) in which $V_{i} \cap V_{j}$ is a similar variable in i and j methods.

$$ simD(i,j) = \left| {\frac{{V_{i} \cap V_{j} }}{{V_{i} \cup V_{j} }}} \right| $$

(11)

Therefore, Gui presented Eqs. (12) and (13) to calculate cohesion indirectly as follow:

$$ \begin{aligned} simT(i,j,p) & = \mathop \prod \nolimits_{{e_{{s,t}} \in p}} simD\left( {s,t} \right) \\ & \; = \mathop \prod \nolimits_{{e_{{s,t \in p}} }} \left| {\frac{{V_{i} \cap V_{j} }}{{V_{i} \cup V_{j} }}} \right| \\ \end{aligned} $$

(12)

$$ simT(i,j) = simT(i,j,p_{{\max }} (i,j)) $$

(13)

Considering m and n, i.e., the number of methods and the number of classes, respectively, Eqs. (14) and (15) show cohesion directly and indirectly in the class, respectively, and Eqs. (16) and (17) show cohesion in the system directly and indirectly, respectively.

$$ classCohT = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {sim(i,j)} }}{{m^{2} - m}} $$

(14)

$$ classCohD = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {simD(i,j)} }}{{m^{2} - m}} $$

(15)

$$ WTCoh = \frac{{\sum\nolimits_{{j = 2}}^{n} {classCohT_{j} } }}{n} $$

(16)

$$ WICoh = \frac{{\sum\nolimits_{{j = 2}}^{n} {classCohD_{j} } }}{n} $$

(17)

In [42], a method is proposed, which calculates two matrixes to determine the amount of coupling. The first matrix uses data of elements of each component and does not consider connections among them (Table 2).

Table 2 The structure of the first matrix to calculate coupling by the method proposed in [42]

Then, the second matrix uses the first matrix and is determined by the amount of coupling between software components, which is calculated using Eq. (18) (Table 3).

$$ C_{{ij}} = \left( {\sum\nolimits_{{k = 1}}^{n} {d_{{ik}} \times d_{{jk}} \times \beta _{k} } } \right)/a_{i} $$

(18)

where $\beta _{k}$ and $a_{i}$ are determined by:

$$ a_{i} = \sum\limits_{{j = 1}}^{n} {d_{{ij}} } {\text{ and }}\beta _{k} = \sum\limits_{{j = 1}}^{m} {d_{{jk}} } $$

Table 3 The structure of the second matrix to calculate coupling by the method proposed in [42]

Fuzzy method for calculation of coupling and cohesion

Determining the amount of coupling

Coupling is computed based on communication between modules. As low coupling is required to design software with high quality and to reduce complexity, establishing this communication as a more accurate measurement is necessary.

Several couplings exist in the software system. If we consider and compute every coupling, coupling can be computed more accurately, and this means that more details are studied. In this paper, to compute coupling, the Myers classification is used. In this classification, coupling includes: Content, Common, Control, Stamp, and Data. In the following, all of them will be defined briefly [37, 39, 43].

• Content coupling: it occurs when modules can correct and change internal data directly. A module refers to another module and can be accessed without restriction.

• Common coupling: couplings communicate each other through data sharing. Modules have access only to common data or common blocks (global data can be addressed and accessed).

• Control coupling: in this method, a module sends a control variable to another module and in this way, they can communicate with each other. It is done by setting a control flag (or control variable) (a module sends a request to another module through the control flag).

• Stamp coupling: a variable type of record as a parameter is sent by the first module, and the second module uses only a subset of that record. A module sends data more than the other module's need and only some parts of that data will be used.

• Data coupling: a module sends data to another one considering its needs. All data must be homogeneous.

The methods of computing coupling in [41] are general and without considering the type of coupling they are used. The proposed method for computing coupling in this paper computes any type of coupling through changing the parameters in Eq. (19):

$$ {\text{coupling}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {{\text{coup}}(i,j)} }}{{m^{2} - m}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {\frac{{A_{{ij}} }}{{B_{i} }}} }}{{m^{2} - m}} $$

(19)

As Eq. (8) is in the range of 0–1, the proposed equation is also standard and is in the range of 0–1 (Table 4).

Table 4 Parameters used in the coupling formula

By classifying input and output parameters, total coupling is obtained by fuzzy structure (Table 5).

Table 5 Coupling is computed in the system through data fuzzification

The fuzzy inference system used in the current study is fuzzy Mamdani. It is a simple rule-based method that can be computed through If….Then…. and without complex computing.

Input data was inserted into the fuzzy system and it produced considered output through fuzzy inference (Mamdani inference). The inference is of a set of rules that is embedded in the fuzzy system. Figures 3 and 4 show the graphs of the membership function of inputs and outputs in this computing system, respectively.

Fig. 3

Membership function of input parameters

Fig. 4

Total coupling output membership function

Determining the cohesion

Since cohesion is defined based on internal communication between modules, it can be computed in many ways. According to coupling classification, the Myers method presents a different classification for cohesion. To offer a more accurate method this classification is used.

Myers classified cohesion into six types: Logical, Temporal, Procedural, Communicational, Sequential and Functional [37, 43], which are defined briefly as follow:

• Logical cohesion: elements that have the same operation are considered as the same method.

• Temporal cohesion: elements that have the same operation are placed in a method and they operate simultaneously.

• Procedural cohesion: elements from a method are connected together through some control flows.

• Communicational cohesion: it covers the elements that have procedural cohesion and work on the same data set.

• Sequential cohesion: the elements of a method that have communicational cohesion and are connected together by regular control flow have sequential cohesion.

• Functional cohesion: the elements of a method that have a sequential cohesion and also have the same work or the same goal are said to have functional cohesion.

In methods previously presented in literature, the types of cohesion have been ignored and cohesion has been computed in a system generally. Therefore, this study attempts to expand formula 14 and 16 presented in [41] and consider all types of cohesion on final cohesion according to formula 20 and 21 (similar to coupling computation) according to Table 6.

$$ class_{{coh}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {sim(i,j)} }}{{m^{2} - m}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {\frac{{A_{{ij}} }}{{B_{i} }}} }}{{m^{2} - m}} $$

(20)

$$ {\text{cohesion}} = \frac{{\sum\nolimits_{{j = 1}}^{n} {class_{{coh{\kern 1pt} j}} } }}{n} $$

(21)

where m is the method in the class, and n is the number of classes in the system.

Table 6 Cohesion parameters

By classifying input and output parameters, the total cohesion is obtained using the fuzzy structure (Table 7).

Table 7 Cohesion is computed in the software system through data fuzzification

In fuzzy computing of coupling, to compute cohesion, the Mamdani is used. The data identified in Table 4 are placed in the fuzzy system and the outputs are specified through the Mamdani inference. In Figs. 1 and 2, the graphs of membership function for cohesion inputs and an output are presented based on the coupling method.

Selecting the optimal software components with multi-objective optimization approach

In this section, after presenting the notations in Table 8, the assumptions considered for the optimization problem of components selection are addressed. Then, based on the assumptions, the optimization problem is formulated. In the formulation process, the proposed method of fuzzy computing of Cohesion and Coupling in the ICD equation is used. Then, the formulated problem is solved with the help of fuzzy multi-objective approach.

Table 8 A summary of the notations used in this paper

Table 8 summarizes the notations that are used in the rest of this article.

The assumptions of the optimization problem

In this study, a number of assumptions for component-based software system have been considered some of which are according to the assumptions presented in [2]:

• CBSS is developed using the modular approach.

• The number of modules for software system is limited.

• Each module is a logical collection of several developed independent components. And the number of the components is limited.

• It is assumed that at least one component of each module in COTS or in-house exists to choose.

• The threshold values for ICD, reliability, budget, and time of delivery are set by decision makers.

• If the component is in-house, its cost is equivalent to the cost of development. Otherwise, it is equivalent to the purchase price of a COTS component.

• The cost of an in-house component can be determined by using the basic parameters of the process.

• Different COTS components are available with different costs, reliability levels, degrees of functionality, and delivery times.

• Different in-house components are available with different functionality degrees, costs of unitary development, estimated development times, average times, and times to test a component.

• Needless repetition is not allowed for a given instance; it means that exactly one software instance is supposed to be chosen for the ith COTS component.

• Interaction data for components is exactly same for all modules, regardless of the occurred selection. Interaction associated is set by the software developers.

• The amount of interactions and relationships between the components in this article, unlike that presented in [2], has been amended; thus, the amount of interactions of C_n with C_m and the amount of interactions of C_m with C_n is not necessarily always equal. For example, in the inheritance relationship available between C_n and C_m, if C_n is parent and C_m is child, C_m has complete access to information of C_n. Thus, it has the highest degree of communication. While C_n as the parent may have no access to all the information of C_m (i.e., the amount of interactions lower than the amount of interactions of the child with father). The improved amount of interactions between the components is shown in section “Case Study” (Table 11).

Formulation of optimization problem based on fuzzy computing of ICD

The overview of the proposed method of component selection with multi-objective optimization is shown in Fig. 5. The proposed method follows a sequential process as presented below in the optimal choice of software components:

• 1. The first objective function—Fuzzy-Intra Coupling Density (Fuzzy-ICD): the stages of this calculation are as follow:

• ▪ Determining the type of coupling in the software system according to the Mayers Model (Data, Stamp, Control, Common, and Content);

• ▪ Computing the type of the Myers Model coupling using the following relation

  $$ {\text{coupling}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {coup(i,j)} }}{{m^{2} - m}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {\frac{{A_{{ji}} }}{{B_{i} }}} }}{{m^{2} - m}} $$

• ▪ Computing the total coupling based on the Fuzzy Logic;

• ▪ Determining the type of cohesion in CBSS based on the Mayers Model (Logical, Temporal, Procedural, Communicational, Sequential, Functional);

• ▪ Computing the type of the Myers Model cohesion based on the following relation:

• ▪ $class\_coh = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {sim(i,j)} }}{{m^{2} - m}} = \frac{{\sum\nolimits_{{i,j = 1}}^{m} {\frac{{A_{{ij}} }}{{B_{{ij}} }}} }}{{m^{2} - m}}$ and ${\text{cohesion}} = \frac{{\sum\nolimits_{{i = 1}}^{n} {class\_coh} }}{n}$

• ▪ Computing the total Cohesion based on the Fuzzy Logic;

• ▪ Computing ICD from the total coupling and total cohesion CBSS:

  $$ {\text{FuzzyICD}} = {\text{cohesion}}/\left( {{\text{Cohesion}} + {\text{Coupling}}} \right); $$

• 2. The second objective function—functionality

• 3. The constraints of optimization problem

• ▪ Threshold on ICD constraint

• ▪ Building decision versus buying decision

• ▪ Budget constraint

• ▪ Delivery time constraint

• ▪ The reliability of in-house components

• ▪ Threshold on the reliability constraint

• 4. Solving the optimization problem using the fuzzy multi-objective approach

Fig. 5

The overview of the proposed method of component selection with multi-objective optimization problem

In the following, each of the above cases is reviewed. For the symbols that will be used, please refer to the notations in Table 8.

Fuzzy-Intra Coupling Density (Fuzzy-ICD)

sThe Intra Coupling Density objective function, which has been provided to measure the relationship between coupling and cohesion of modules in modular software system, is calculated using the following equation [2, 12]:

$$ {\text{ICD}} = \frac{{CI_{{in}} }}{{CI_{{in}} + CI_{{out}} }} $$

(22)

where CI_in is the number of interactions of components within the module (Cohesion), and CI_out is the number of interactions between the components in distinct modules (Coupling). Thus, by using the parameters of Cohesion and Coupling in the optimization problem, the impact of software architecture on the optimal choice of components was evaluated.

Based on Eq. (22), the rate of cohesion for interactions within the jth module can be expressed as ICD_j. If each module has only one component, the amount of ICD for that module is zero. For compensating this defect, 1 is added to the fraction of Eq. (22).

$$ {\text{ICD}}_{j} = \frac{{(CI_{{in}} )_{j} + 1}}{{(CI_{{in}} )_{j} + (CI_{{out}} )_{j} }} $$

(23)

In the above equation, ICD_j is Intra Coupling Density for the j-th module, (CI_in)_j denotes the number of transactions of components within the jth module, and (CI_out)_j is the number of interactions of components between the jth module and the other modules.

Cohesion of both COTS and in-house components in the ith module can be expressed as follows:

$$ (CI_{{in}} )_{j} = \sum\limits_{{i = 1}}^{{N - 1}} {\sum\limits_{{i' = i + 1}}^{N} {r_{{ii'}} z_{{ij}} z_{{i'j}}^{{}} } } $$

(24)

The total amount of coupling and cohesion associated with the j-th module as CA_j is calculated as follows:

$$ \begin{aligned} CA_{j} = & (CI_{{in}} )_{j} + (CI_{{out}} )_{j} \\ = & \sum\limits_{{i = 1}}^{{N - 1}} {\sum\limits_{{i^{\prime} = i + 1}}^{N} {r_{{ii^{\prime}}} z_{{ij}} (\sum\limits_{{j^{\prime} = 1}}^{M} {z_{{i^{\prime}j^{\prime}}} } )} } \\ \end{aligned} $$

(25)

Additionally, the total amount of coupling and cohesion of a software system is formulated as follows:

$$ CA = \sum\limits_{{i = 1}}^{{N - 1}} {\sum\limits_{{i' = i + 1}}^{N} {r_{{ii'}} \left( {\sum\limits_{{j = 1}}^{M} {z_{{ij}} } } \right)\left( {\sum\limits_{{j' = 1}}^{M} {z_{{i'j'}} } } \right)} } $$

(26)

Thus, the total cohesion of all modules is calculated using Eq. (27):

$$ CI_{{in}} = \sum\limits_{{j = 1}}^{M} {\sum\limits_{{i = 1}}^{{N - 1}} {\sum\limits_{{i' = i + 1}}^{N} {r_{{ii'}} z_{{ij}} z_{{i'j}}^{{}} } } } $$

(27)

It is widely known that weak (low) coupling and strong (high) cohesion can lead to high maintenance capability of a software system. Therefore, the value of ICD has a great impact on maintenance capability of a CBSS to improve the quality of the system and can be expressed as follows:

$$ {\text{ICD}} = \frac{{CI_{{in}} = \sum\nolimits_{{j = 1}}^{M} {} \sum\nolimits_{{i = 1}}^{{N - 1}} {} \sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} z_{{ij}} z_{{i'j}}^{{}} } }}{{\sum\nolimits_{{i = 1}}^{{N - 1}} {} \sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} \left( {\sum\nolimits_{{j = 1}}^{M} {z_{{ij}} } } \right)} \left( {\sum\nolimits_{{j' = 1}}^{M} {z_{{i'j'}} } } \right)}}{\text{ }}0 \le {\text{ICD}} \le 1; $$

(28)

According to the above equation and the proposed method of fuzzy computing of Coupling and Cohesion, the calculation of the objective function of ICD is rewritten as follows:

$$ \begin{gathered} \max ICD = \frac{{Fuzzy\_Cohesion}}{{Fuzzy\_Cohesion + Fuzzy\_Coupling}}, \hfill \\ Fuzzy\_Cohesion = FIS_{{input\_coh}} \left(\sum\limits_{{j = 1}}^{M} {\sum\limits_{{i = 1}}^{{N - 1}} {\sum\limits_{{{i}^{\prime} = i + 1}}^{N} {r_{{ii}^{\prime}} z_{{ij}} z_{{{i}^{\prime}j}} } } } \right) \hfill \\ Fuzzy\_Coupling = FIS_{{input\_cou}} \left(\sum\limits_{{i = 1}}^{{N - 1}} {\sum\limits_{{{i}^{\prime} = i + 1}}^{N} {r_{{ii}^{\prime}} \left(\sum\limits_{{j = 1}}^{M} {z_{{ij}} } \right)\left(\sum\limits_{{{j}^{\prime} = 1}}^{M} {z_{{{i}^{\prime}{j}^{\prime}}} } \right)} } \right) \hfill \\ input\_coh = \{{\text{logical, temporal, procedural, communication , sequential, functional}}\} \hfill \\ input\_cou = \{ {\text{content, common, control, stamp, data}}\} \hfill \\ \end{gathered} $$

(29)

$FIS_{{input\_coh}} \left( {\sum\nolimits_{{j = 1}}^{M} {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i^{\prime} = i + 1}}^{N} {r_{{ii'}} z_{{ij}} z_{{i'j}}^{{}} } } } } \right)$ and $FIS_{{input\_cou}} \left( {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i^{\prime} = i + 1}}^{N} {r_{{ii'}} } \left( {\sum\nolimits_{{j = 1}}^{M} {z_{{ij}} } } \right)} \left( {\sum\nolimits_{{j^{\prime} = 1}}^{M} {z_{{i^{\prime}j^{\prime}}} } } \right)} \right)$ respectively are final cohesion and final coupling that: at the first relation, according to input_coh and input_cou and Eqs. (21) and (19), each type of cohesion and coupling are calculated (for example, logical_cohesion, content_coupling). Then, the Fuzzy system is performed to calculate final cohesion with the input {logical, temporal, procedural, communicational, sequential, functional}_cohesion and final coupling with the input {content, common, control, stamp, data}_coupling.

Functional performance

Each component in the component-based software system has a degree of functionality. COTS components functionality available in the market are different and can be prepared based on the customers or organizations’ requirements. Furthermore, the functionality of in-house components is determined by its developers. Thus, functionality is used as a criterion for evaluating a modular software system.

The purpose of functionality is to maximize overall system performance. The total functionality of all modules in the building or buying strategy is expressed as follows:

$$ \max F = \sum\limits_{{j = 1}}^{M} {\sum\limits_{{i = 1}}^{N} {\left( {f_{{ij}} y_{{ij}} + \sum\limits_{{k = 1}}^{{v_{{ij}} }} {f_{{ijk}} x_{{ijk}} } } \right)} } $$

(30)

Threshold on ICD constraint

This constraint expresses the minimum threshold H on the value of ICD for each module:

$$ \begin{gathered} \frac{{FIS_{{input\_coh}} \left( {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w_{{ii^{\prime}}} z_{{ij}} z_{{i'j}}^{{}} } } } \right) + 1}}{{FIS_{{input\_coh}} \left( {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w_{{ii^{\prime}}} z_{{ij}} z_{{i'j}}^{{}} } } } \right) + FIS_{{input\_cou}} \left( {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w_{{ii^{\prime}}} z_{{ij}} \sum\nolimits_{{j' = 1}}^{M} {z_{{i'j}}^{{}} } } } } \right)}} \ge H;{\text{ }} \hfill \\ j = 1,2,...,M;{\text{ }}j' = 1,2,...,M \hfill \\ input\_coh = \hfill \\ \{ {\text{logical, temporal, procedural, communication, sequential, functional}}\} \hfill \\ input\_cou = \{ {\text{content, common, control, stamp, data}}\} \hfill \\ \end{gathered} $$

(31)

Building decision versus buying decision

For each component, several examples of COTS and one example of in-house can be available for developers. Thus, from each component, more than one instance is available to choose.

$$ y_{{ij}} + \sum\limits_{{k = 1}}^{{v_{{ij}} }} {x_{{ij}} } = z_{{ij}} ;{\text{ }}i = 1,2,...,N;{\text{ }}j = 1,2,...,M $$

$$ \sum\limits_{{i = 1}}^{M} {z_{{ij}} } \ge 1;{\text{ }}j = 1,2,...,M $$

(32)

However, it should be noted that if the i-th component of the j-th module is bought, (for example, some x_ijk = 1), the component will not be developed in the form of in-house any more (for example y_ij = 0), and vice versa:

$$ \sum\limits_{{i = 1}}^{M} {z_{{ij}} } = 1;\,i = 1,2,...,N $$

(33)

Budget constraint

Cost constraint, as one of the most important parameters, shows the overall cost of a system. Sum of all costs in all modules in the build-or-buy strategy is calculated as follows:

$$ \sum\limits_{{j = 1}}^{M} {\sum\limits_{{i = 1}}^{N} \left(C_{{ij}} (t_{{ij}} + \tau _{{ij}} N_{{ij}}^{{tot}} ) y_{{ij}} + \sum\limits_{{k = 1}}^{{V_{{ij}} }} C_{{ij}} x_{{ijk}} \right) \le B} $$

(34)

The indices i and j represent the number of components and modules, respectively.

Delivery time constraint

The delivery time of component is the length of time a software component gets ready for delivery and use in the component-based software system, which includes the development time, the integration time, and the time to test the system. In the case of COTS components, the delivery time is given simply by d_ij, while for developed components of in-house, the time delivery of the ith component for the jth module is equal to $t_{{ij}} + \tau _{{ij}} N_{{ij}}^{{tot}}$. Therefore, the delivery time of the ith component can be expressed as follows:

$$ T_{i} = \left( {C_{{ij}} (t_{{ij}} + \tau _{{ij}} N_{{ij}}^{{tot}} )y_{{ij}} + \sum\limits_{{k = 1}}^{{V_{{ij}} }} {d_{{ijk}} x_{{ijk}} } } \right) $$

(35)

Thus, the delivery time constraint can be described as follows:

$$ \mathop {\max }\limits_{{i = 1,2,...,N}} (T_{i} ) \le T $$

(36)

where T is the threshold for the delivery time.

The reliability of in-house components

Reliability is defined as the probability of failure-free operation for a certain period of time in a particular environment [44]. The purpose of software developers is achieving maximum reliability. The reliability of COTS components for a specific module is provided by its vendors. While, the reliability of built components is estimated by the software development team.

According to the authors in [26, 32, 45], let A be the event “$N_{{ij}}^{{suc}}$ that test cases with no failure have been done” and B be the event “the alternative is failure free during a single run”. If $\rho _{{ij}}$ is the chance that the in-house developed alternative is failure free during a single run, then $N_{{ij}}^{{suc}}$ test cases have been successfully done, based on the Bayes Theorem, as expressed in Eq. (37):

$$ \rho _{{ij}} = p(B|A) = \frac{{p(A|B)p(B)}}{{p(A|B)p(B) + p(A|\bar{B})p(\bar{B})}} $$

(37)

Now, we express the test cases that are with no failure as follows:

$$ N_{{ij}}^{{suc}} = (1 - \pi _{{ij}} )N_{{ij}}^{{tot}} ;\,i = 1,2,...,N;\,j = 1,2,...,M $$

(38)

due to $p(A|B) = 1$,$p(B) = 1 - \pi _{{ij}}$, $p(A|\bar{B}) = (1 - \pi _{{ij}} )N_{{ij}}^{{suc}}$, $p(\bar{B}) = \pi _{{ij}}$, We have:

$$ \rho _{{ij}} = \frac{{(1 - \pi _{{ij}} )}}{{(1 - \pi _{{ij}} ) + \pi _{{ij}} (1 - \pi _{{ij}} )N_{{ij}}^{{suc}} }} $$

(39)

Threshold on the reliability constraint

The probability of failure on demand of the developed ith component of in-house of the jth module can be expressed as 1-$\rho _{{ij}}$. Now we can express the average number of failures of the ith component and the jth module as q_ij:

$$ q_{{ij}} = (1 - \rho _{{ij}} )y_{{ij}} + \sum\limits_{{k = 1}}^{{v_{{ij}} }} {\mu _{{ij}} x_{{ij}} } $$

(40)

The probability that the ith component of the jth module during its execution faces no failure is given by $\varphi _{{ij}} = e^{{ - q_{{ij}} }}$, which shows the probability of no failure occurs in a Poisson distribution with parameter q_ij:

$$ \prod\limits_{{i = 1}}^{N} {\varphi _{{ij}} } = \prod\limits_{{i = 1}}^{N} {e^{{ - q_{{ij}} }} \ge R_{j} ;{\,\text{ }}j = 1,2,...,M} $$

(41)

Solving the optimization problem using fuzzy multi-objective approach

In general, different optimization techniques have been introduced to solve the optimization problem in component-based software systems. These optimization problems are formulated by using the objective function and Crisp constraint. The Crisp constraint is based on judgment and decision of developers. Since human judgments are along with ambiguity and uncertainty, the use of crisp optimization is not a wise decision. This causes researchers to use the fuzzy multi-objective optimization method with fuzzy parameters [2]. The following steps are needed to be taken into action to solve the problem of fuzzy multi-objective optimization [39]:

Step 1: The construction of multi-objective optimization problem.

The formulation of multi-objective optimization on software systems expressed in “Formulation of Optimization Problem based on Fuzzy Computing of ICD” in previous subsection is as follows:

$$ \begin{gathered} \max ICD = \frac{{FIS_{{input\_coh}} \left( {\sum\nolimits_{{j = 1}}^{M} {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w{}_{{ii^{\prime}}}z_{{ij}} z_{{i'j}}^{{}} } } } } \right)}}{{FIS_{{input\_coh}} \left( {\sum\nolimits_{{j = 1}}^{M} {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w{}_{{ii^{\prime}}}z_{{ij}} z_{{i'j}}^{{}} } } } } \right) + FIS_{{input\_cou}} \left( {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w_{{ii^{\prime}}} \left( {\sum\nolimits_{{j' = 1}}^{M} {z_{{ij}} } } \right)} } \left( {\sum\nolimits_{{j' = 1}}^{M} {z_{{i'j'}} } } \right)} \right)}}, \hfill \\ input\_coh = \{ {\text{logical,}}\;{\text{temporal,}}\;{\text{procedural,}}\;{\text{communication,}}\;{\text{sequential,}}\;{\text{functional}}\} \hfill \\ input\_cou = \{ {\text{content,}}\;{\text{common,}}\;{\text{control,}}\;{\text{stamp,}}\;{\text{data}}\} \hfill \\ \end{gathered} $$

$$ \max F = \sum\limits_{{j = 1}}^{M} {\sum\limits_{{i = 1}}^{N} {\left( {f_{{ij}} y_{{ij}} + \sum\limits_{{k = 1}}^{{v_{{ij}} }} {f_{{ijk}} x_{{ijk}} } } \right)} } $$

$$ {\text{subject to }}x \in s = \left\{ {x_{{ij}} ,} \right.y_{{ij}} ,z_{{ij}} {\text{ are binary variabels}} $$

$$ \begin{gathered} \frac{{FIS_{{input\_coh}} \left( {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w_{{ii^{\prime}}} z_{{ij}} z_{{i'j}}^{{}} } } } \right) + 1}}{{FIS_{{input\_coh}} \left( {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w_{{ii^{\prime}}} z_{{ij}} z_{{i'j}}^{{}} } } } \right) + FIS_{{input\_cou}} \left( {\sum\nolimits_{{i = 1}}^{{N - 1}} {\sum\nolimits_{{i' = i + 1}}^{N} {r_{{ii'}} w_{{ii^{\prime}}} z_{{ij}} } \sum\nolimits_{{j' = 1}}^{M} {z_{{i'j'}} } } } \right)}} \ge H;{\text{ }} \hfill \\ j = 1,2,...,M;{\text{ }}j' = 1,2,...,M \hfill \\ \end{gathered} $$

$$ \sum\limits_{{j = 1}}^{M} {\sum\limits_{{i = 1}}^{N} {\left( {C_{{ij}} (t_{{ij}} + \tau _{{ij}} N_{{ij}}^{{tot}} )y_{{ij}} + \sum\limits_{{k = 1}}^{{V_{{ij}} }} {C_{{ij}} x_{{ijk}} } } \right) \le B.} } $$

$$ C_{{ij}} (t_{{ij}} + \tau _{{ij}} N_{{ij}}^{{tot}} )y_{{ij}} + \sum\limits_{{k = 1}}^{{V_{{ij}} }} {d_{{ijk}} x_{{ijk}} } \le T_{i} $$

$$ N_{{ij}}^{{suc}} = (1 - \pi _{{ij}} )N_{{ij}}^{{tot}} ;{\text{ }}i = 1,2,...,N;{\text{ }}j = 1,2,...,M $$

$$ \rho _{{ij}} = \frac{{(1 - \pi _{{ij}} )}}{{(1 - \pi _{{ij}} ) + \pi _{{ij}} (1 - \pi _{{ij}} )N_{{ij}}^{{suc}} }} $$

$$ q_{{ij}} = (1 - \rho _{{ij}} )y_{{ij}} + \sum\limits_{{k = 1}}^{{v_{{ij}} }} {\mu _{{ij}} x_{{ij}} } $$

$$ \prod\limits_{{i = 1}}^{N} {\varphi _{{ij}} } = \prod\limits_{{i = 1}}^{N} {e^{{ - q_{{ij}} }} \ge R_{j} ;{\text{ }}j = 1,2,...,M} $$

$$ y_{{ij}} + \sum\limits_{{k = 1}}^{{v_{{ij}} }} {x_{{ij}} } = z_{{ij}} ;{\text{ }}i = 1,2,...,N;{\text{ }}j = 1,2,...,M $$

$$ \sum\limits_{{i = 1}}^{M} {z_{{ij}} } = 1;{\text{ }}i = 1,2,...,N $$

$$ \sum\limits_{{i = 1}}^{N} {z_{{ij}} } \ge 1;{\text{ }}j = 1,2,...,M $$

$$ x_{{ijk}} \in \{ 0,1\} ;{\text{ }}i = 1,2,...,N;{\text{ }}j = 1,2,...,M;{\text{ }}k = 1,2,...,v_{{ij}} ; $$

$$ y_{{ij}} \in \{ 0,1\} ;{\text{ }}i = 1,2,...,N;{\text{ }}j = 1,2,...,M; $$

$$ z_{{ij}} \in \{ 0,1\} ;{\text{ }}i = 1,2,...,N;{\text{ }}j = 1,2,...,M;\} $$

Step 2: Solving multi-objective optimization problem by considering each of the objective functions separately. If both solutions (for example $X^{1} = X^{2}$$i = 1,2,...,N;$ $j = 1,2,...,M;$) are identical, one of them as the optimal compromise solution will be chosen and it ends. Otherwise, go to Step 3.

Step 3: Evaluating the objective functions of ICD and functionality separately and determining the best/worst lower limit (L), and the best/worst upper limit (U). in the other words, In this step, the two-objective functions are solved separately because the parameter of membership function (ICD_L, ICD_U, f_L and f_U are the upper limit and lower limit of ICD and functionality) for each objective function in step 4 is calculated in this step according in Table 9.

Table 9 Optimization solution set of the method for the first and second objective functions

After determining the membership functions of μ_ICD and μ_f in step 4, these membership functions are considered for constraint in the transformed optimization problem in step 5.

Step 4: Determining the membership function of any objective function of the optimization model. The membership function for ICD is calculated as follows:

$$ \mu _{{ICD}} (x) = \left\{ \begin{gathered} 1,\quad \quad \quad \quad \quad \quad \quad ICD(x) \ge ICD_{U} \hfill \\ \frac{{ICD(x) - ICD_{L} }}{{ICD_{U} - ICD_{L} }},\quad ICD_{L} \le ICD(x) \le ICD_{U} \hfill \\ 0,\quad \quad \quad \quad \quad \quad \quad ICD(x) \le ICD_{L} \hfill \\ \end{gathered} \right. $$

(42)

where ICD_L is the worst lower limit, and ICD_U is the best upper limit of the objective function of ICD. The values of x include all cases of the space of optimization problem (possible answers), which are at the constraints of optimization problem. The membership function for functionality is as follows:

$$ \mu _{f} (x) = \left\{ \begin{gathered} 1,\quad \quad \quad \quad \;f(x) \ge f_{U} \hfill \\ \frac{{f(x) - f_{L} }}{{f_{U} - f_{L} }},\quad f_{L} \le f(x) \le f_{U} \hfill \\ 0,\quad \quad \quad \quad \;f(x) \le f_{L} \hfill \\ \end{gathered} \right. $$

(43)

where f_L is the worst lower limit, and f_U is the best upper limit of the objective function of functionality.

Step 5: Fuzzy development of multi-objective optimization model.

Based on the principle of maximizing proposed by Bellman-zadeh [28] and by using the fuzzy membership functions defined above, the fuzzy multi-objective optimization model is formulated as follows:

$$ \begin{gathered} \max {\text{ }}\lambda \hfill \\ {\text{subject to }}\lambda \le \mu _{{ICD}} (x) \hfill \\ {\text{ }}\lambda \le \mu _{f} (x) \hfill \\ {\text{ 0}} \le \lambda \le 1 \hfill \\ {\text{ }}x \in S \hfill \\ \end{gathered} $$

(44)

Actually for solving the multi-objective optimization problem, the fuzzy multi-objective optimization model formulates the multi-objective problem into the principle of maximizing proposed by Bellman-Zadeh (like a single-objective problem) according to step 4 and 5, and then solves that.

Solving the above model provides a solution for decision makers; with reviewing the entire possible space arising from the objective functions of ICD and Functionality and considered constraints, they can have the best selection from COTS and in-house components.

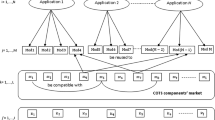
A case study of financial and accounting software [2] was performed to evaluate the proposed methodology in the optimum choice of components from the COTS components and developed components of in-house to develop CBSS. This case study is a software system with three modules: M₁, M₂, M₃. In total, twenty software components available on the market, (SC₁–SC₂₀), are available to build a set of 10 components (S₁–S₁₀). In addition, ten components can be developed as in-house (SB₁–SB₁₀). Exactly one software component in each set of alternatives will be chosen for a specific software module to meet the operational needs. For example, each one of SC₁, SC₂, SC₃, SC₄, and SB₁ can be replaced by the S₁ component. Consequently, one of the five components will be selected to meet the operational needs of S1, while SC₁, SC₂, SC₃, and SC₄ are COTS components, and SB1 is a component developed in in-house.

Case study

As mentioned earlier, a case study of financial and accounting software [2] was executed in this paper to evaluate the proposed methodology in the optimum choice of components from the components of COTS and developed components of in-house for the aim of developing CBSS. This case study is a software system with three modules: M₁, M₂, M₃. In total, twenty of the software components available in the market (SC₁–SC₂₀) are available to build a set of 10 components (S₁–S₁₀). The ten components can be developed as in-house (SB₁–SB₁₀). Exactly one software component in each set of alternatives is selected for a specific software module to meet the operational needs. As a result, one of the five components will be selected to meet the operational needs of S1, whereas SC₁, SC₂, SC₃, and SC₄ are COTS components, and SB1 is a component developed in in-house.

Table 10 shows the components of each of the three modules available in the case study along with their alternatives including in_house and COTS.

Table 10 The components of each of the three modules available in the case study along with their alternatives

Operational requirements of each component, its corresponding replacement software components, and also the rates of functionality of software components corresponding with software modules are shown in Table 11.

Table 11 Example of descriptions and functionality of in-house and COTS components in the case

The function ratings describe the degree of functional contributions of the software components toward the software modules.

The rates range of functionality is from 0 to 1, with 1 referring to very high degree of contributions, while 0 referring to very low degree of contributions.

As can be seen in Table 10, the amount of components functionality in the modules to which they belong is higher.

Table 12 shows the degree of interactions between software components. The degrees range is from 1 to 10. 1 means very low degree of interactions, while 10 refers to very high degree of interactions (Table 12).

Table 12 The modified amount of interactions of the components in the software system of the case study

Table 13 The cost and time of delivery of data collection of In-house components

In Table 13, the cost (C_ij for all i, j) in unit of 100 $ and delay time per day (d_ij for all i, j) for components of in-house are given. In addition, Table 14 shows the cost and delay time associated with COTS components.

Table 14 The cost and time of delivery of data collection of COTS components

The experimental results

This study evaluated the results of the implementation of multi-objective optimization problem of the optimal choice of components in component-based software systems based on COTS and in-house components in the form of two tests. At first, the formulation of the optimization problem with the objective functions of ICD and Functionality and constraints mentioned in the previous section is evaluated. In test No. 2, the formulation of optimization problem with the objective functions of Fuzzy-ICD and Functionality and considered constraints is evaluated. Finally, the proposed method performance is compared with that of other methods.

Simulation conditions

The model proposed in this study was implemented on the Intel system with the following processor specifications: Core 2Dou 2.53 GHz, an internal memory of 4 GB, and Windows 64-bit operating system. Furthermore, the software used to implement the model is MATLAB, version 2015 (Matlab R2015b).

Test No 1: the optimal choice of components with the objective functions of ICD and functionality

The results of each step of solving multi-objective optimization problem by using multi-objective fuzzy explained as follow:

Step 1: Construction of multi-objective optimization problem in accordance with the formulation of Step 1 of “Solving the Optimization Problem by using of Fuzzy Multi-objective Approach” in the previous section with one difference: the objective function and ICD constraint are calculated simply and without the use of the fuzzy method.

Step 2: Solving the multi-objective optimization problem by considering each of the objective functions.

According to Step 2 in Section titled “Formulation of Optimization Problem based on Fuzzy Computing of ICD” and by having two-objective functions, values of X₁ and X₂ are calculated. Each of the solutions amounts (X₁ and X₂) includes ICD values and Functionality. Notably, to solve the optimization problem, the amount of constraints has been considered based on the information presented in Table 15.

Table 15 Initial parameters and the amount of constraints in the implementation of the optimization problem of the case study

Thus, by solving the optimization problem related to the objective function of Functionality, the results of Table 16 will be achieved:

Table 16 Results of solving the optimization problem with the objective function of functionality in the case study

Additionally, by solving the optimization problem related to the objective function of ICD, the results of Table 17 will be achieved.

Table 17 Results of solving the optimization problem with the objective function of ICD in the case study

Step 3: Evaluating the first and second objective function with taking into consideration the constraints of the obtained optimization problem and determining the best/worst lower limit (L), and the best/worst upper limit (U) (see Table 18).

Table 18 Optimization solution set for the first and second objective functions

Step 4: Determining the membership of each objective function in the optimization model:

Based on optimization solving of the two mentioned objective functions, the membership function of ICD in the case study would be as follows:

$$ \mu _{{ICD}} (x) = \left\{ \begin{gathered} 1,\quad \quad \quad \quad \quad \quad \quad \;ICD(x) \ge 0.6992 \hfill \\ \frac{{ICD(x) - 0.6762}}{{0.0230}},\quad 0.6762 \le ICD(x) \le 0.6992 \hfill \\ 0,\quad \quad \quad \quad \quad \quad \quad \;ICD(x) \le 0.6762 \hfill \\ \end{gathered} \right. $$

Moreover, the membership function of f in the case study would be as follows:

$$ \mu _{f} (x) = \left\{ \begin{gathered} 1,\quad \quad \quad \quad \quad f(x) \ge 7.75 \hfill \\ \frac{{f(x) - 6.61}}{{1.14}},\quad 6.61 \le f(x) \le 7.75 \hfill \\ 0,\quad \quad \quad \quad \quad f(x) \le 6.61 \hfill \\ \end{gathered} \right. $$

Step 5: Fuzzy development of multi-objective optimization model.

According to the principle of maximizing introduced by Bellman-zadeh and by using the fuzzy membership functions defined above, the fuzzy multi-objective optimization model will be along with the results of Table 19.

Table 19 The results of fuzzy multi-objective optimization model based on Bellman-zadeh's

Test No 2 (the proposed method): the optimal choice of components with the objective functions of Fuzzy-ICD and functionality

The results of the implementation of multi-objective optimization problem by using the objective function of Fuzzy ICD are as follows.

Step1: Construction of multi-objective optimization problem (the formulation of the problem of multi-objective optimization). The formulation of the problem of multi-objective optimization in the proposed method is in accordance with the formulation of Step 1 of Section “Formulation of Optimization Problem based on Fuzzy Computing of ICD”.

Step 2: Solving the multi-objective optimization problem by considering each of the objective functions.

According to Step 2 in Section “Formulation of Optimization Problem based on Fuzzy Computing of ICD” and by having two-objective functions, values X₁ and X₂ are calculated. Each of the solutions amounts (X₁ and X₂) includes ICD values and Functionality.

Thus, by solving the optimization problem related to the objective function of Functionality, the results of Table 20 will be achieved.

Table 20 The results of the optimization of the proposed method with the objective function of functionality in the case study

In addition, by solving the optimization problem related to the objective function of ICD, the results of Table 21 will be achieved.

Table 21 The results of the optimization of the proposed method with the objective function of ICD in the case study

Step 3: Evaluating the first and second objective function with taking into consideration the constraints of the obtained optimization problem and determining the best/worst lower limit (L) and the best/worst upper limit (U) (see Table 22).

Table 22 Optimization solution set of the proposed method for the first and second objective functions

Step 4: Determining the membership of each objective function in the optimization model:

Based on the optimization solving of the two mentioned objective functions, the membership function of ICD in the case study would be as follows:

$$ \mu _{{ICD}} (x) = \left\{ \begin{gathered} 1,\quad \quad \quad \quad \quad \quad \quad \;ICD(x) \ge 0.8809 \hfill \\ \frac{{ICD(x) - 0.4940}}{{0.3869}},\quad 0.4940 \le ICD(x) \le 0.8809 \hfill \\ 0,\quad \quad \quad \quad \quad \quad \quad \;ICD(x) \le 0.4940 \hfill \\ \end{gathered} \right. $$

In addition, the membership function of f in the case study would be as follows:

$$ \mu _{f} (x) = \left\{ \begin{gathered} 1,\quad \quad \quad \quad \quad {\text{ }}f(x) \ge 7.82 \hfill \\ \frac{{f(x) - 5.40}}{{2.42}},\quad 5.40 \le f(x) \le 7.82 \hfill \\ 0,\quad \quad \quad \quad \quad {\text{ }}f(x) \le 5.40 \hfill \\ \end{gathered} \right. $$

Step 5: Fuzzy development of multi-objective optimization model.

Table 23 Results of the fuzzy multi-objective optimization model with the proposed method based on Bellman-zadeh's principle

Based on the principle of maximizing proposed by Bellman-zadeh and by using the fuzzy membership functions defined above in the proposed method, the fuzzy multi-objective optimization model will be along with the results presented as can be seen in Table 23, components SC17, SC5, SC4, SC7, SC14, SC15, SC19, SC20, SB3, SB5, and SB10 are the best components for selection with lambda = 0.7328.

Comparing the proposed method with some other methods

Table 24 shows a comprehensive comparison between the performance of the method presented in this article and that of the methods provided by some researchers working in the field of software in terms of the optimization type, objective functions, constraints, the build-or-buy strategy, and innovation of the research. As can be seen in Table 24, the optimization method presented in this paper uses the objective functions of Fuzzy-ICD and functionality and constraints of ICD, delivery time, reliability, and cost.

Table 24 A comprehensive comparison between the method presented in this paper and the methods proposed by some researchers in the area of the optimal choice of software components

To evaluate the proposed method, a comparison was made between the proposed method (Fuzzy-ICD) and the Simple-ICD method (without computing the fuzzy ICD). Table 25 presents the comparative results.

Table 25 Evaluation results between optimal component selection with Fuzzy-ICD as one of the objective functions (the proposed method) and the Simple ICD

As can be seen in a bold row in Table 25, the objective function of Intra Coupling Density in the proposed method includes more maximum values in the optimal choice of components. In addition, the optissmum component selected by using the proposed method has less budget and execution time than the Simple_ICD method in creating of software system.

Conclusion

Component-based software system design with the modular approach was shown capable of effectively reducing the level of complexity in cases where the components selection is done in the best way. The purpose of this article was to help software engineers to choose the optimal components in the process of software system development in a component-based software system. The choice in this paper was done through formulating the problem of multi-objective optimization with maximizing the objective functions of Fuzzy-ICD Fuzzy-Intra Coupling Density and functionality and taking into account the constraints of budget, delivery time, reliability, and Fuzzy-ICD. Fuzzy ICD as the method proposed in this paper is a criterion for calculating more accurately the relationship between Cohesion and Coupling of components, which is obtained through fuzzy computing of each of them based on the Mayers classification. Then, a two-criterion optimization model was formulated and it was solved with the help of the fuzzy multi-objective approach. The implementation of the proposed optimization on the case study confirmed the efficiency of the proposed method.

While fuzzy mathematical optimization has an acceptable effect on software quality parameters than evolutionary optimization, we considered optimization based on the combination of ICA and fuzzy evolution algorithms as a future solution for reducing time consumption. We are trying to evaluate the proposed objective function on other multi-objective evolution algorithms.