1 Introduction

It is well known that adhesion of hard solids is difficult to measure at macroscopic scales, and Fuller and Tabor [1] proved that even in low modulus materials (they used rubbers with \(E\sim 1\) \(\mathrm {MPa}\)), a \(\sim 1\,\mu\)m of roughness destroy adhesion almost completely, despite van der Waals adhesive forces are quite strong, giving the so-called “adhesion paradox” [2]. Adhesion of macroscopic bulk objects requires smooth surfaces, and at least one of the solids has to have a very low elastic modulus. Dahlquist [3, 4], while working at 3 M, proposed a criterion largely used in the world of adhesives, namely that the elastic Young modulus should be smaller than \(\sim 1\) \(\mathrm {MPa}\) to achieve stickiness even in the presence of roughness. This clearly is just a rough indication, but Tiwari [5] finds for example that the work of adhesion (at a given retraction speed) is reduced of a factor 700 for a rubber in contact with a rough hard sphere when the rubber modulus is \(E=2.3\) MPa (because of a certain roughness) but is actually increased for the same roughness by a factor 2 when the rubber has modulus \(E=0.02\) MPa. The threshold does not change much even if we consider nanometer scale roughness, as in the recent results of Dalvi et al. [6] for pull-off of PDMS hemispheres having four different elastic moduli against different roughened plates: Dahlquist’s criterion seems to work surprisingly well, as while there is little effect of roughness for the three cases of low modulus up to near \(E=2\) MPa, roughness has strong effect both during approach and retraction for the high modulus material (\(E=10\) MPa), where the hysteresis may be due partly to viscoelastic effectsFootnote 1. However, for the 3 low modulus materials, roughness almost systematically increases the work of adhesion rather than decreasing it as for the high modulus material, for a given retraction speed.

Roughness-induced adhesion enhancement was measured with some surprise first by Briggs and Briscoe [7] and Fuller and Roberts [8], and Persson–Tosatti’s [9] theory attributes it to the increase of surface area induced by roughnessFootnote 2. Another mechanism was put forward by Guduru et al. [10, 11]. Guduru considered a spherical contact having a concentric axisymmetric waviness and considers that the contact is complete over the contact area. The waviness gives rise to oscillations in the load-approach curve which results in up to factor 20 increase of the pull-off with respect to the standard smooth sphere case of the JKR theory [12]. Also, the curves fold on each other so that we expect jumps at some points in the equilibrium curve, which corresponds to dissipation and emission of elastic waves in the material and results in strong hysteresis. Later, Kesari and Lew [13] noticed that Guduru’s solution has an elegant “envelope” obtained by expanding asymptotically for very small wavelength of the waviness.

But most soft materials are viscoelastic, and therefore, there is a strong velocity dependence of the pull-off result. Many authors [14,15,16,17,18,19,20,21,22] have proposed that the process of peeling involves an effective work of adhesion w which is the product of the thermodynamic (Dupré) work of adhesion \(w_{0}\) and a function of velocity of peeling of the contact/crack line and temperature, as long as there is no bulk viscoelasticity involved, over a large range of crack speeds, namely of the form that has been validated also by a large amount of data including peeling tests at various peel angles:

$$\begin{aligned} w=w_{0}\left[ 1+k\left( a_{T}v_{p}\right) ^{n}\right] \end{aligned},$$
(1)

where k and n are constants of the material, with n in the range \(0.1{-}0.8\) and \(a_{T}\) is the WLF factor [23], which permits to translate results at various temperatures T from measurement at a certain standard temperature. This form of effective work of adhesion can be obtained also from theoretical models (which start from the viscoelastic constitutive equations of the material) using either Barenblatt models [24, 25] and also [19, 20, 26], or crack tip-blunting models [22], for quite wide class of materials, since the power law tends to emerge even for a single relaxation time material (standard material). But power laws emerge even for more complex rheologies: for example, [22] showed that for a frequency-dependent viscoelastic modulus \(E\left( \omega \right) \sim \omega ^{1-s}\), \(0<s<1\), in the transition region between the “rubbery region” and the “glassy region” (where the strong internal damping occurs), Eq. (1) is satisfied at intermediate velocities with \(n=\left( 1-s\right) /\left( 2-s\right)\) (so that \(0<n<1/2,\) in agreement with most of the range cited above, except for the high range \(n>0.5\)). Remark that the Gent–Schultz law tends to see viscoelasticity as an effect increasing the toughness from an “adiabatic” value at very low propagation, since the material is seen to have a finite relaxed or “equilibrium” modulus \(E_{0}>0\), whereas the well-known Barenblatt-like cohesive models of Schapery generally see viscoelasticity as an effect reducing the elastic fracture limit, where speed of propagation is wave speed in the material. There may be deviations from the simple Gent–Schultz power law for materials having more complex behaviour obtained with a general relaxation spectrum, but for the scope of the present paper, the simple form of the Gent–Schultz law permits to show exemplary results.

In applying Gent–Schultz with viscoelastic effects condensed at the crack tip, “the only hypotheses are that failure is an adhesive failure and that viscoelastic losses are limited to the crack tip; this last condition means that gross displacements must be elastic for \(\Gamma\) to be valid in kinetic phenomena” [21]. This assumption greatly simplifies the analysis and indeed is used by many authors, including in Refs. [20, 27, 28], based on the evidence that the timescales of the crack tip and the bulk deformations are very different.

The effective “toughness” w can increase of various orders of magnitude over \(w_{0}\) as the velocity increases (more precisely, of the ratio \(E\left( \infty \right) /E\left( 0\right)\), where \(E\left( \omega \right)\) is the frequency-dependent elastic modulus), and the pull-off of a sphere has also been effectively measured to increase of various orders of magnitude over an increase of peeling speed [15]. On the contrary, during crack closure, the effective work of adhesion is even smaller than \(w_{0}\), (this time it is reduced by the ratio \(E\left( 0\right) /E\left( \infty \right)\), see [20]), so in some cases, loading could become essentially an elastic model without adhesion.

Equation 1 generalizes the thermodynamic equilibrium of elastic cracks for the strain energy release G, namely, it provides a condition for crack edge velocity—when \(G>w_{0}\), the crack accelerates under the force \(G-w_{0}\) applied per unit length of crack, until a limit speed \(v_{p}\) for equilibrium is found, depending on the loading conditions. For example, \(G-w_{0}\) is a constant for classical peeling experiments, whereas it monotonically increases for flat punches and has a much richer behaviour for the smooth sphere. Therefore, for imposed tensile load smaller in absolute value than the JKR pull-off value \(P_{0}=3/2\pi wR\), the contact area simply decreases to another equilibrium value (given asymptotically by JKR theory), while for imposed load below the JKR value, it decreases with nonmonotonic velocity but without the JKR pull-off instability, so up to complete detachment. Therefore, pull-off depends on the loading condition: can be anything greater than \(P_{0}\) if load is imposed, whereas it is a precise function of the retraction rate in an experiment where the cross-head of a rigid machine keeps the remote approach velocity as constant.

Various authors [15, 20, 27] have studied the peeling of viscoelastic spheres with the above form of fracture mechanics formulation (1), and some approximate scaling results have also been given [27, 29], but a theoretical or numerical investigation about the coupled effect of viscoelasticity and roughness has not been attempted, in the best of the authors’ knowledge, not even with numerical simulations. It seems that in general, viscoelasticity can only increase the “tack”, i.e. the force or the work needed to detach two solids, whereas the role of roughness is more controversial, as we have discussed above. We are aware of the complexity of the general problem, so here, we tackle the study of a simple problem that of a sphere with a single wave of roughness, which generalizes the relatively recent work of Guduru et al. [10, 11] and following related literature, to the case of a viscoelastic substrate.

2 The Theory

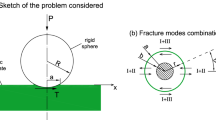
We consider the Guduru contact problem for a sphere against a flat surface, where the gap is defined as \(f\left( r\right) =\frac{r^{2}}{2R} +A\left( 1-\cos \frac{2\pi r}{\lambda }\right)\), where R is the sphere radius, \(\lambda\) is wavelength of roughness and A is its amplitude.

The Guduru problem can be solved by considering the stress intensity factor K at the contact edge (radius \(r=a\)) or equivalently the strain energy release rate G [10]

$$\begin{aligned} G\left( a,P\right) =\frac{K\left( a,P\right) ^{2}}{2E^{*}}=\frac{\left( P_{1}\left( a\right) -P\right) ^{2}}{8\pi E^{*}a^{3}} \end{aligned},$$
(2)

where \(E^{*}=E/\left( 1-\nu ^{2}\right)\) is plane strain elastic modulus (i.e. E is Young’s modulus and \(\nu\) the Poisson ratio, generally equal to 0.5 in rubbery materials, while we consider that the countersurface is generally much more rigid so we neglect its elastic properties). Notice that, according to the theory of Muller [27] for the smooth sphere, we assume that viscoelastic effects are concentrated at the contact boundary, while the bulk material remains relaxed; thus, we assume \(E^{*}=E^{*}( \omega =0)\), i.e. the relaxed modulus of the viscoelastic material.

Here, \(P_{1}\left( a\right)\) is the load required to maintain a contact radius a in the absence of adhesion, while P is the smaller load to maintain the same contact radius in the presence of adhesion. In particular, standard contact mechanics gives [10]

$$\begin{aligned} P_{1}\left( a\right) =2E^{*}\left\{ \left( \frac{2}{R}+\frac{4\pi ^{2}A}{ \lambda ^{2}}\right) \frac{a^{3}}{3}+\frac{\pi Aa}{2}H_{1}\left( \frac{2\pi a }{\lambda }\right) -\frac{\pi ^{2}Aa^{2}}{\lambda }H_{2}\left( \frac{2\pi a}{ \lambda }\right) \right\} \end{aligned},$$
(3)

where \(H_{n}\) are the Struve functions of order n.

In the adhesionless conditions, the remote approach (positive for compression) is

$$\begin{aligned} \alpha _{1}\left( a\right) =\frac{a^{2}}{R}+\pi ^{2}\frac{A}{\lambda } aH_{0}\left( \frac{2\pi a}{\lambda }\right) \end{aligned}$$
(4)

so in the adhesive condition, we have to decrease this by an amount given by a flat punch displacement giving the general result for approach:

$$\begin{aligned} \alpha \left( a,P\right) =\frac{a^{2}}{R}+\pi ^{2}\frac{A}{\lambda } aH_{0}\left( \frac{2\pi a}{\lambda }\right) -\frac{P_{1}\left( a\right) -P}{ 2E^{*}a} \end{aligned}.$$
(5)

From (5), we can obtain the general equation for the load as a function of contact radius and approach

$$\begin{aligned} P\left( a,\alpha \right) =P_{1}\left( a\right) +2E^{*}a\alpha \left( a\right) -2E^{*}\frac{a^{3}}{R}-\pi ^{2}\frac{2E^{*}A}{\lambda } a^{2}H_{0}\left( \frac{2\pi a}{\lambda }\right) \end{aligned},$$
(6)

where \(P_{1}\left( a\right)\) is given by Eq. (3) above. Imposing the condition of thermodynamic equilibrium \(G\left( a\right) =w_{0}\), using Eqs. (2) and (3), permits to write the Guduru solution explicitly as parametric equations of the contact radius a

$$\begin{aligned} P\left( a\right)&=P_{1}\left( a\right) -a^{3/2}\sqrt{8\pi w_{0}E^{*}} \end{aligned}$$
(7)
$$\begin{aligned} \alpha \left( a\right)&=\alpha _{1}\left( a\right) -a^{1/2}\sqrt{2\pi w_{0}/E^{*}} \end{aligned}$$
(8)

Using the Kesari and Lew [13] expansion, Ciavarella [30] obtained that the Guduru solution has oscillations bounded between two exact JKR [12] envelope curves for the smooth sphere, but with a corrected (enhanced or reduced, respectively, for unloading or loading) surface energy

$$P_{{{\text{env}}}} \left( a \right) = \frac{4}{{3R}}E^{*} a^{3} - a^{{3/2}} \sqrt {8\pi wE^{*} } \left( {1 \pm \frac{1}{{\sqrt \pi \alpha _{{{\text{KLJ}}}} }}} \right),$$
(9)
$$\alpha _{{{\text{env}}}} \left( a \right) = \frac{{a^{2} }}{R} - a^{{1/2}} \sqrt {\frac{{2\pi w}}{{E^{*} }}} \left( {1 \pm \frac{1}{{\sqrt \pi \alpha _{{{\text{KLJ}}}} }}} \right),$$
(10)

where

$$\alpha _{{{\text{KLJ}}}} = \sqrt {\frac{{2w_{0} \lambda }}{{\pi ^{2} E^{*} A^{2} }}}$$
(11)

is the parameter Johnson [31] introduced for the JKR adhesion of a nominally flat contact having a single-scale sinusoidal waviness of amplitude A and wavelength \(\lambda\). Thus, since Eq. (9) is JKR equation for a smooth sphere of radius R, the factor

$$\frac{{w_{{{\text{eff}}}} }}{{w_{0} }} = \left( {1 + \frac{1}{{\sqrt \pi \alpha _{{{\text{KLJ}}}} }}} \right)^{2}$$
(12)

is a roughness-induced increase that holds as long as a compact contact area can be obtained, which requires not too large roughness and/or sufficiently strong precompression. In practice, factors up to 20 have been obtained also experimentally by Guduru and Bull [11], although of course, these were achieved in geometry built for the specific goal to achieve very large enhancement. Figure 1 elucidates the behaviour of the oscillations in the Guduru solution for a representative case, which we shall later extend to the viscoelastic solution. Given these gulfs and reentrances, in the elastic solution, the real followed path will depend on the loading condition. For a soft system (close to “load control”), there will be horizontal jumps in approach while in a stiff system (close to “displacement control”), there will be vertical jumps to the next available stable position. In both cases, there will be areas “neglected” during these jumps which represent mechanical dissipated energy. Indeed, in the “envelope” solution of Kesari–Lew–Ciavarella, the combined effect of these jumps results in the different JKR loading and unloading curves that give an additional hysteresis with respect to the standard JKR case, where the only hysteresis comes as a single elastic instability in pull-in and another (different) single instability at pull-off. The dashed lines in Fig. 1 are the Kesari–Lew–Ciavarella envelopes Eqs. (9, 10) using Eq. ( 11).

Fig. 1
figure 1

The load-approach curve in the Guduru elastic problem with \(E^{*}=16500\) Pa; \(R=0.23\) m; \(w_{0}=0.008\) J/m\(^{2}\); \(\lambda /R=0.002\); \(A/\lambda =0.005\) and reference \(a_{i}\) \(=0.01\) m

Full size image

2.1 Viscoelastic Problem

For a given remote applied withdrawing of the sphere \(v=-\frac{d\alpha }{dt}\) , we can write the velocity of the contact edge as follows:

$$\begin{aligned} v_{p}=-\frac{da}{dt}=v\frac{da}{d\alpha } \end{aligned}.$$
(13)

The condition \(G\left( a\right) =w\) (which replaces the thermodynamic equilibrium \(G\left( a\right) =w_{0}\) for the elastic sphere), therefore, defines a differential equation for \(a=a\left( \alpha \right)\), obtained using Eqs. (1, 2 and 13)

$$\begin{aligned} \frac{1}{k^{1/n}a_{T}v}\left( \frac{\left( P_{1}\left( a\right) -P\right) ^{2}}{8\pi E^{*}a^{3}w_{0}}-1\right) ^{1/n}=\frac{da}{d\alpha } \end{aligned}.$$
(14)

Hence, using Eq. (6) and defining the dimensionless parameters

$$\begin{aligned} V=k^{1/n}a_{T}v\qquad ;\qquad \zeta =\left( \frac{2\pi w_{0}}{RE^{*}}\right) ^{1/3} \end{aligned},$$
(15)

we write Eq. (14) as

$$\begin{aligned} \frac{da}{d\alpha }=\frac{1}{V}\left[ \frac{\left( R/a\right) }{\zeta ^{3}} \left( \frac{\alpha }{R}-\frac{a^{2}}{R^{2}}-\pi ^{2}\frac{A}{\lambda }\frac{a }{R}H_{0}\left( \frac{2\pi a}{\lambda }\right) \right) ^{2}-1\right] ^{1/n} \end{aligned}$$
(16)

which can be solved with a numerical method. After a solution is obtained for \(a=a\left( \alpha \right)\), we substitute back into Eq. (6) to compute the load. Notice that, for a given starting point of the peeling process in terms of load P, the term under parenthesis in Eq. (14) is zero, and hence, \(\frac{da}{d\alpha }\) starts off zero giving some delay with respect to the elastic curve, which is hard to eliminate even at very low withdrawal speeds.

3 Results

3.1 Smooth Sphere

Let us first consider the detachment of a smooth sphere from a viscoelastic substrate having \(n=0.33\) and dimensionless withdrawal velocity \(V=[0.0002,0.002,0.02,0.2,2]\); the other constants, as indicated in Fig. 2 caption, are \(E^{*}=16500\) Pa; \(R=0.23\) m; \(w_{0}=0.008\) J/m\(^{2}\); for the general problem with waviness, we will use \(\lambda /R=0.002\); \(A/\lambda =0.005\). However, we solve first the problem for the smooth sphere (the equation for the smooth sphere is obviously obtained for \(A=0\) in the equations above), and the obtained results are shown in Fig. 3. As we discussed in the theory paragraph, in the initial point \(\frac{da}{d\alpha }=0\), and we find (Fig. 3c) that the velocity remains practically zero for a longer time when V is bigger. The velocity of the contact line increases monotonically from zero to infinite when pull-off occurs at zero contact area.

Fig. 2
figure 2

The geometry of the problem. A sphere of radius R with a simple axisymmetric roughness, being a single axisymmetric wave with wavelength \(\lambda\) and amplitude A. The smooth sphere case is obviously obtained for A = 0

Full size image
Fig. 3
figure 3

The load \(P/P_{0}\) (a), the contact radius \(a/a_{i}\) (b), and the velocity of contact line \(da/d\alpha =v_{p}/v\) (c) as a function of approach \(\alpha /\alpha _{i}\) for the smooth sphere. The inner black curve is the JKR classical solution, and the other five curves are obtained numerically for \(V=[0.0002,0.002,0.02,0.2,2]\) (follow the arrow). Here, \(n=0.33\), and other constants as indicated in Fig. 2 caption

Full size image

3.2 Rough Sphere

We consider here the same parameters used above, but \(A/\lambda >0\). According to Eq. (12) derived from the Guduru theory, this corresponds to an “adiabatic” elastic enhancement of the pull-off of \({{w_{{{\text{eff}}}} } \mathord{\left/ {\vphantom {{w_{{{\text{eff}}}} } {w_{0} }}} \right. \kern-\nulldelimiterspace} {w_{0} }} = 1.42\). We indicate with \(P_{0}=3/2\pi w_{0}R\) the JKR value of pull-off for the smooth sphere. The loading curve follows the elastic solution (Eqs. 7, 8), and we start withdrawing the indenter from a reference value of \(a_{i}\) \(=0.01\) m. Corresponding values of initial approach \(\alpha _{i}\) and load \(P_{i}\) can, therefore, be found from Eqs. (7, 8). Numerical solutions are found with the NDSolve algorithm in Mathematica with default options. Figure 4a shows the obtained load-approach curve in terms of \(P/P_{0}\) and \(\alpha /\alpha _{i}\) where \(P_{0}\) is JKR pull-off of the smooth sphere, and Fig. 4b shows the contact radius \(a/a_{i}\) peeling as a function of approach. The inner black wavy curves are the equilibrium Guduru solutions, and the other five curves are obtained numerically for increasing dimensionless velocities of withdrawal \(V=[0.0002,0.002,0.02,0.2,2]\). As expected, the viscoelastic peeling terminates only when contact radius is zero, and not at the JKR unstable radius. However, the minimum load is found for a contact radius which, for low velocities, is not too different from the unstable pull-off contact radius in the JKR theory.

Fig. 4
figure 4

Load \(P/P_{0}\) (a) and the contact radius \(a/a_{i}\) (b) as a function of approach \(\alpha /\alpha _{i}\). \(P_{0}\) is JKR pull-off of the smooth sphere, and \(\alpha _{i}\) the initial value of approach for unloading. The inner black wavy curve is the equilibrium Guduru solution, and the other five curves increasingly departing from it are obtained numerically for increasing dimensionless velocities of withdrawal (see the verse of the arrow) \(V=[0.0002,0.002,0.02,0.2,2]\). Here, \(n=0.33\), and other constants as indicated in Fig. 2 caption

Full size image

Figure 5a–c gives some details of the solution at the lowest dimensionless velocity of withdrawal \(V=0.0002\). In particular, Fig. 5a shows clearly that the numerical solution follows closely the prediction of the Guduru elastic solution under displacement control, as expected, with almost sharp jumps of the force at specific values of the approach. After the jump, the solution seems to return to the Guduru equilibrium solution. Obviously with the viscoelastic theory, the strict elastic solution should be obtained asymptotically at extremely low velocities, but the differential equation would then become very “stiff” corresponding to numerical difficulties following the jumps. The same behaviour is clarified in terms of the contact radius in Fig. 5b, which follows very closely the Guduru solution in some time intervals, and then extends a little before jumping almost abruptly to the following branch of the equilibrium curve. In other words, the curve does not have a “rainflow” type of behaviour over the Guduru equilibrium solution, which would be the elastic real behaviour with jump instabilities, but the contact radius “drops” over the Guduru curve only after some delays. This is further clarified in Fig. 5c, where the velocity of the contact line \(da/d\alpha =v_{p}/v\) is found to follow an oscillatory trend with “bursts” of very high (but finite) velocity where the peeling velocity is much larger than the imposed withdrawing velocity, after which the velocity drops to a low value that is where the contact area approaches the adiabatic Guduru curve since \(G\simeq w_{0}\), and which increases progressively with the decreasing approach. Slowly, the solution departs from the Guduru elastic one, because of the cumulative effects of the acceleration periods. However, from Figs. 4 and 5d, we see that there are no real “jumps”, and the solution curve is generally smoother for high velocities, with the difference between the slow regime and the fast regime being smaller. Notice that, while the velocity of peeling remains in every case equal to zero at the initial point, it remains closer to zero for a much extensive range of approach for high velocities, resulting in a curve departing away from the equilibrium Guduru curve immediately. This effect at high velocity produces curves that are generally closer to the viscoelastic curves for the smooth sphere, and therefore, closer results for pull-off and work for pull-off, as we have described in the previous paragraph.

Fig. 5
figure 5

Detail of the solution at the lowest dimensionless velocity of withdrawal a–c \(V=0.0002,\) and d \(V=2\). Here, \(n=0.33\), and other constants as indicated in Fig. 2. In particular a Load-approach b contact radius vs approach c velocity of contact line \(da/d\alpha =v_{p}/v\). d velocity of contact line \(da/d\alpha =v_{p}/v\) but for the highest dimensionless speed \(V=2\)

Full size image

3.3 Some Comparisons

Summarizing the pull-off results for \(n=0.33\) but adding some solutions also at different amplitudes of roughness A, we obtain the amplification factor for pull-off with respect to the JKR value as in Fig. 6. Notice initially that the smooth sphere results tend to a power-law scaling (linear in the log–log plot) as expected from the material law Eq. (1), after a transition from the elastic behaviour. As it is evident from Fig. 6, starting off at low velocity with increasing amplitude of roughness increases the “elastic” amplification according to the Guduru theory, but eventually the effect disappears at sufficiently large peeling speeds in the viscoelastic regime. In other words, there seems to be a “cross-over” between the two phenomena at the speed for which the two increases are the same. For example, in Fig. 6, the amplification factor \(P/P_0\) is shown for different \(A/\lambda =[0,0.005,0.015,0.045\), n = 0.33 (a) and n = 0.6 (b). Panel (a) shows that for the very “rough” sphere with \(A/\lambda =0.045\) (blue line), the Guduru enhancement factor is larger (\(\approx 7.5\)) than the viscoelastic one in this velocity range. Panel (b) (\(n=0.6\)) shows that, increasing n, the pull-off force increases faster with the dimensionless speed factor V, confirming our conclusion about the cross-over. Eventually, for large speed, the smooth sphere result is obtained. Obviously, with so many constants in the problem, it is not easy to give comprehensive results.

Fig. 6
figure 6

The pull-off amplification with respect to the JKR value, \(P/P_{0}\) as a function of dimensionless speed of withdrawal V for various amplitudes of waviness increasing as indicated by arrow: \(A/\lambda =0\) for the smooth sphere (black), \(A/\lambda =0.005\) (green)\(,A/\lambda =0.015\) (red), \(A/\lambda =0.045\) (blue). Here, all constants as indicated in Fig. 2, except a \(n=0.33\); b \(n=0.6\) (Color figure online)

Full size image

4 Discussion

Considering the experiments on our geometry done by Guduru and Bull [11], their gelatin material is indeed a viscoelastic material. Although Guduru and Bull [11] recognized this, unfortunately, they did not characterize the material in particular and tried to minimize the loading rate effects by keeping in their tensile test machine a cross-head velocity at \(v=3\) mm/min \(=50\) \(\mu\)m/s in all experiments. Even this speed is not enough to avoid viscoelastic effects, as indeed even the smooth sphere case they use for measuring the baseline work of adhesion shows significant deviations between loading and the unloading curves which are not present in the standard elastic JKR theory. The unloading has specific features similar to what we found for the smooth sphere, namely when unloading begins, the contact radius does not begin to decrease immediately. Fitting JKR curves, Guduru and Bull [11] extracted \(w_{0}=0.008\) N/m during loading and \(w_{0}^{\prime }=0.22\) N/m during unloading, a difference of a factor 27.5. They used as baseline for their comparison with the wavy surfaces the unloading value. Despite experimental results capture generally the trend of the predictions, there is a “systematic difference between the experimental observation and the theoretical prediction” as the authors say, of the order of a \(-25\%\). A possible explanation could be the effect observed in the present paper, namely that there is no multiplicative effect of roughness-induced adhesion enhancement and viscoelasticity-induced adhesion enhancement. In other words, as Guduru and Bull [11] used their elastic theory with the work of adhesion already increased by viscoelastic effects, they may have overestimated the effect of roughness-induced load amplification.

In general, there are several reasons to assume that viscoelastic effects will generally dominate over roughness-induced enhancement. Adhesion experiments with a glass ball of radius 2.19 mm on a polyurethane surface (\(n=0.6\), which incidentally is not well explained by Barenblatt models or crack tip-blunting models which start from the linear viscoelastic constitutive equations of the material [19, 20, 22]) by Barquins and Maugis [15] showed viscoelastic toughness Eq. ( 1) and pull-off increased by a factor of up to 3 orders of magnitude. That is the viscoelastic effect can be very large, and therefore, generally much larger than the geometric one studied originally by Guduru, as it has been recently shown also for other geometries, like a dimpled surface [32]. Also, Guduru effect only holds for a quite special waviness (single scale, axisymmetric), when the contact area “peels” quite uniformly around a circle and requires the initial contact area to be compact. This poses some limits to the amplitude of roughness, hence, the amplification factor that can be reached (see a more general numerical solution using Lennard-Jones force-separation law in Papangelo and Ciavarella [33]). Regarding the non-axisymmetric effect, Li et al. [34] numerical experiments for the pull-off of a sphere in contact with an elastic substrate with 2-dimensional wavy roughness, showed that the adhesion enhancement is further much reduced. For a Johnson parameter (11) \(\alpha _{KLJ}=0.37,\) they found an increase of a factor 1.7, while from Eq. (12), valid for the Guduru axisymmetric geometry, one obtains a much higher \(\frac{w_{eff}}{w_{0}}=\left( 1+\frac{1}{ \sqrt{\pi }0.37}\right) ^{2}=6.37\). Numerical experiments with random roughness suggested that this enhancement is also if not more largely reduced [34].

Returning finally to the experiments of Dalvi et al. [6], the increase of apparent work of adhesion in the smoother specimen (Polished UltraNanoCrystalline Diamond (PUNCD)) is of a factor 2, at the retraction speed of 60 nm/s. Given the large amplification factors that can be obtained due to viscoelasticity (orders of magnitude as shown by Barquins and Maugis [15]), the factor 2 increase cannot be excluded not even at the 60 nm/s speed. It remains to be clarified if the latter enhancement factor obtained in Dalvi et al. [6] experiments could be either due to area increase as from the Persson–Tosatti [9] theory, or from a reduced Guduru effect.

5 Conclusions

We have revisited the Guduru model for roughness-induced enhancement of adhesion of a sphere/flat contact, adding the effect of viscoelasticity which is expected in soft materials. The results have demonstrated that the roughness-induced amplification of pull-off in the Guduru model, which effectively can be modeled as an increased work of adhesion in the unloading curve, is reduced progressively when velocity increases with respect to the baseline smooth viscoelastic sphere. This is also in qualitative agreement with the original experiments of Guduru and Bull [11]. A significant reduction has already occurred at a “cross-over” velocity for which the two enhancements (the Guduru and the viscoelastic one) are of equal magnitude. We may be tempted, therefore, to speculate that viscoelasticity effectively damps the roughness-induced elastic instabilities, reduces roughness effects in unloading, while its effects are concentrated in the loading phase.