Portfolio optimization model with uncertain returns based on prospect theory

Abstract

When investing in new stocks, it is difficult to predict returns and risks in a general way without the support of historical data. Therefore, a portfolio optimization model with an uncertain rate of return is proposed. On this basis, prospect theory is used for reference, and then the uncertain return portfolio optimization model is established from the perspective of expected utility maximization. An improved gray wolf optimization (GWO) algorithm is designed because of the complex nonsmooth and nonconcave characteristics of the model. The results show that the GWO algorithm is superior to the traditional particle swarm optimization algorithm and genetic algorithm.

Introduction

Since 1952, the famous mean–variance model and portfolio theory proposed by Markowitz [1] have developed rapidly. Subsequent scholars have successively proposed models such as the mean-VaR (Value at Risk) and mean-CVaR (conditional value at risk) [2]. The previous portfolio optimization model mainly used probability theory to address uncertainty in investment. However, there are many uncertainties in the financial market. For example, due to the influence of national policies, emergencies, and international factors, the existing securities or historical stock data have lost their original reference value. Especially for some emerging stocks, there are no or scant data for reference; thus it is difficult for these original methods to deal with such problems. At this time, the uncertainty theory proposed by Liu et al. [3] is a powerful tool for addressing such problems. Based on uncertainty theory, Liu [4] studied a new portfolio optimization model with uncertain returns and designed a new hybrid intelligent algorithm to solve this optimization problem. Zhang, etc. [5] discussed the portfolio selection problem in an uncertain environment in which security returns cannot be well-reflected by historical data but can be evaluated by experts. Kara et al. [6] studied the robust portfolio optimization problem under parallelepiped uncertainty. Solares et al. [7] studied uncertain portfolio optimization based on confidence intervals.

The above studies all belong to the category of rational investors and modern finance based on the hypothesis of an efficient market, which believes that investors are completely rational, without individual differences, with homogeneous expectations and consistent attitudes toward risks. However, researchers have found many ‘anomalies’ that cannot be explained by modern finance in many empirical studies on financial markets, such as the stock premium, the effect of small firms, and the phenomenon of people buying insurance and lottery tickets at the same time. To explain these anomalies, some scholars began to study investors' behaviors from the perspective of investors' psychology and gradually realized that investors are not completely rational but generally exhibit irrational behaviors such as cognitive bias, overconfidence, and selection preference [8]. From psychological experiments, Kahneman and Tversky [9] found that investors often set a reference point in advance when making decisions, and their appetite for risk reverses near the reference point. Cognitive psychologists have systematically analyzed and summarized representativeness, anchoring and adjustment, framing and other heuristic strategies that commonly exist in people's decision-making process and the cognitive biases caused by them. On the basis of a series of psychological experiments, prospective theory (PT) [9] and cumulative prospective theory (CPT) [10] have been proposed successively. Under the framework of bounded rationality, the human psychology and behavior mechanism in the process of risk decision-making has been revealed and more accurately reflects the characteristics of people's decision-making under uncertain conditions [11].

In recent years, many scholars have applied prospect theory to the problem of portfolio selection [12] and have obtained fruitful research results. In fact, the S-shaped value function in prospect theory is not differentiable at the reference point, and the reference point is an inflection point; thus, the portfolio optimization model containing the S-shaped value function is nonconcave and nonsmooth, which is bound to bring great difficulties to its numerical solution [13,14,15,16]. However, the existing literature rarely mentions it. Only Forin et al. [17] noticed the difficulty of calculating the S-shaped value function and selected the linear loss aversion function in the objective function to avoid the treatment of a nonconcave objective function. Although it is easy to solve the model, the linear loss aversion function does not fit the actual situation. This article relaxes this assumption to make the research more realistic.

This paper intends to study the optimization problem of uncertain return portfolios based on prospect theory. The portfolio optimization model with an S-shaped value function is nonconcave and nonsmooth. After considering the uncertainty of return, the model is more complicated; therefore, the use of artificial intelligence optimization algorithms such as evolutionary algorithms has outstanding advantages. This paper designs an improved gray wolf optimization (GWO) algorithm to solve the built model and compares it with classical evolutionary algorithms such as particle swarm optimization (PSO) and genetic algorithms (GA). The results show that the proposed GWO has excellent performance and is suitable for processing similar nonconcave and nonsmooth complex models.

Literature review

Regarding the problem of portfolio optimization, most of the relevant research has been carried out under the following two mainstream analysis frameworks: one is the return-risk model, and the other is the expected utility maximization model [18]. Some studies have reviewed different types of investment portfolio optimization problems [18].

Return-risk model

The mean–variance model is the most classic return-risk model. In the mean–variance portfolio model, Markowitz [1] realizes the quantification of the return and risk of the asset portfolio and systematically investigates the relationship between return and risk for the first time. In this model, it is assumed that investors not only hope that their investment behavior can obtain higher returns but also hope that the risks they face are as small as possible. To meet the needs of investors for risk and return as much as possible, Markowitz uses the mean value of the return on risky assets as the expected return rate of the investment portfolio and uses the variance of the return on each risky asset as a measure of the risk of the investment portfolio. The mean–variance model can be expressed as two goals. One is to achieve the minimum risk under a certain expected rate of return constraint, and the other is to maximize the rate of return given the maximum risk that can be tolerated. This classic theory of Markowitz grasped the quantification of portfolio research for the first time, and this significant contribution laid the foundation for the development of portfolio theory and model research. Brauneis and Mestel [20] applied Markowitz’ mean–variance framework to evaluate the return risk of cryptocurrency portfolios. Dybvig and Pezzo [21]studied the mean–variance portfolio rebalancing problem of transaction costs. Pandolfo et al. [22] used the concept of a weighted Lp depth function to obtain a robust estimate of the mean and covariance matrix of asset returns, which has the advantage of not being affected by parameter assumptions. Compared with traditional technology, it is less sensitive to changes in asset return distribution. Han and Wong [23] studied the continuous-time mean–variance portfolio selection problem under the Volterra Heston model. Due to the non-Markov and non-semi-martingale properties of the model, the classic stochastic optimal control framework cannot be directly applied to related optimization problems. By constructing an auxiliary stochastic process, they obtained the optimal investment strategy dependent on the solution of the Riccati-Volterra equation. Bauder et al. [24] solved the problem of optimal portfolio selection when the parameters of asset return distribution, such as the mean vector and covariance matrix, are unknown, and historical data of asset returns need to be used for estimation. Their new method uses a Bayesian posterior prediction distribution, that is, the future realization distribution of asset returns as an observable sample. Shen et al. [25] studied the issue of asset liability management under the mean–variance criterion with institutional transformation. Among them, the dynamics of assets and liabilities are described by the non-Markov regime transition model.

With the deepening of many scholars' research on investment portfolios, the understanding and definition of investment portfolio risk are also different from each other, which results in different methods of measuring risk in risky assets. Different from using the variance of the return on assets to measure risk, some scholars believe that from the perspective of risk, investors will not pay too much attention to the excess return. Therefore, this part cannot be regarded as a risk, and only the loss faced by investors can be regarded as risk, that is, when the investor's return is lower than the expected return as the main risk factor. Therefore, Mao [26] and Estrada [27] established a mean–semivariance model, that is, removing the part whose return is higher than the expected return, and improved the mean–variance model. It is worth noting that this model is more suitable for situations where asset returns are asymmetric. If asset returns are centrally symmetrical, then the semi-variance is exactly half of the variance, which makes the model lose its optimization function. Konno [28] also proposed the method of optimizing variance to measure risk, namely, to measure portfolio risk with absolute deviation and to replace quadratic programming with linear programming. This model not only retains the advantages of mean–variance but also improves its disadvantages. In addition, Yitzhaki [29] proposed a new risk measurement method, the Gini mean difference, and on its basis, created the Gini mean portfolio model, carried out numerical analysis, and verified its feasibility. Garcia et al. [30] extended the mean–semi-variance portfolio selection model to a multiobjective trust model, which considered not only risks and returns but also the price earnings ratio to measure the performance of the portfolio. They used the NSGA-II algorithm to solve the constructed multiobjective model. Chen et al. [31] discussed the problem of multicycle portfolio selection, whose securities returns experts estimate to be timed. Taking security returns as an uncertain variable, they proposed a multiperiod mean–semi-variance portfolio optimization model considering transaction costs, cardinality and boundary constraints. The equivalent deterministic mean–semi-variance model is given on the premise that the security returns are sawtooth uncertain variables. Salah et al. [32] used the nonparametric univariate method to obtain income prediction and applied it to the mean–semi-variance model.

The mean-CVaR model is another classic return-risk model. Researchers have made corresponding improvements to the narrow hypothesis of mean variance based on the actual situation of the financial market, added more realistic factors when constructing the portfolio model, such as transaction costs, background risks, liquidity, personal preferences, and transactions, and conducted more applicable research. Xia et al. [33] studied the impact of transaction costs on the investment portfolio, studied the effective frontier of the portfolio model when the transaction costs were constant, linear and V-type functions and compared and analyzed the impact degree of different transaction cost functions on the investment portfolio model. However, it is worth noting that the introduction of transaction costs in the model will lead to a nonconvex minimization of the problem. Strub et al. [34] investigated a discrete-time mean-CVaR portfolio selection problem. Wang and Chen [35] investigated a mean-CVaR combinatorial optimization problem considering realistic constraints to maximize the mean return and minimize CVaR and proved that this was an NP-hard problem. To solve this complex problem, it is divided into asset selection and proportional distribution. Kang et al. [36] studied the data-driven robust mean-CVaR portfolio selection problem under fuzzy distribution. Liu et al. [37] studied closed-form optimal portfolios with unknown mean and variance of the closed-form optimal portfolios of the cubic mean-CVaR problem. Forsyth [38] proposed the multiperiod, time-consistent mean-CVaR (conditional risk value) asset allocation problem in the form of easy numerical calculation. Setiawan [39] studied the risk-averse mean-CVaR optimization problem and several biology-based heuristic algorithms. Kobayashi et al. [40] studied the mean-risk portfolio optimization model by taking CVaR as a risk measurement, and this model used cardinality constraints to limit the amount of invested assets. Cui et al. [41] deduced the time-consistent strategy of the multiphase mean conditional value-at-risk model and proposed the self-coordination strategy of the multiphase mean conditional value-at-risk model.

Expected utility maximization model

Based on the expected utility maximization model, some scholars have applied prospect theory to the problem of portfolio selection [42]. Kahneman and Tversky [43] showed that investment decisions are guided and influenced by psychological, emotional and behavioral factors. The behavioral framework links investment objectives with transaction behaviors. Behavioral portfolio theory emphasizes the role of behavioral preferences in portfolio selection and investor investment [44]. Grishina et al. [45] established the model of prospect theory–based portfolio optimization and designed the corresponding differential evolution algorithm and genetic algorithm. Gong et al. [46] studied the portfolio selection problem under cumulative prospect theory and gave a portfolio optimization model. Scene generation technology is combined with a genetic algorithm to solve the model. In addition, an adaptive real-coded genetic algorithm (ARCGA) is proposed to find the optimal solution of the model. The calculation results show that this method solves the portfolio selection model, and the ARCGA algorithm is effective and stable. Liu et al. [47] proposed a PBES (photovoltaic/battery energy storage/electric vehicle charging stations) portfolio optimization model based on the sustainability perspective. Kwak and Pirvu [48] studied the problem of portfolio optimization over a period when investors with multiple risky assets and one risk-free asset had accumulated prospect theory (CPT). The returns of multiple risk assets follow the multiple generalized hyperbolic t element distribution, and the results of three-fund separation of two risk portfolios and risk-free assets were obtained. Gong et al. [49], based on the coupling of a genetic algorithm and a bootstrap method, proposed a single-cycle portfolio optimization model solution method based on cumulative prospect theory. Calculation experiments show that by using this method, investors in CPT (cumulative prospect theory) display behavioral characteristics when facing a portfolio composed of risky assets. Deng et al. [50] studied the multiperiod optimal investment portfolio considering transaction costs under cumulative prospect theory and analyzed the impact of transaction costs on the choice of optimal investment portfolio. Chang and Young [51] used the additional information provided by behavioral stocks to propose a portfolio selection model to produce a profitable portfolio superior to the traditional investment benchmarks (market indexes, mutual funds and exchange-traded funds). Using the embedded holding period information of behavioral stocks, a strategy of buying and holding behavioral stocks is studied with the goal of maximizing the expected effect.

In summary, the theoretical research on stochastic uncertain portfolios has been thorough, and the research on this type of model is becoming increasingly mature. There are also some studies on portfolio optimization based on prospect theory, but research on the behavioral portfolio problem and its high-performance algorithm based on uncertain information is rare. For this reason, this paper studies the optimization problem of an uncertain return portfolio and its high-performance optimization algorithm based on prospect theory.

Problem description

This paper solves a portfolio optimization problem for newly issued stocks without historical data. The number of alternative new stocks to invest in on the market is limited, and the rate of return of stocks is uncertain. There are transaction costs associated with stock trading. In investment transactions, due to the external influence of policy, with the increase in trading amount, the unit transaction cost will gradually decrease. Therefore, the problem can be described as a portfolio optimization problem with uncertain returns and transaction costs.

Consider that real investors are not entirely rational. This paper studies the portfolio optimization problem with uncertain returns based on prospect theory. The goal of decision-making is to maximize the expected utility of investors under the constraints of risks.

Preliminaries

In this section, some essential concepts are reviewed as follows [3, 52]:

Theorem 1

If $\varepsilon$ is a linear uncertainty variable and obeys the linear uncertainty distribution $L(m,n)$, where $m,n$ are real numbers and $m < n$, the inverse distribution of $L(m,n)$ is:

$$ \phi_{{}}^{ - 1} (\zeta ) = (1 - \zeta )m + \zeta n. $$

(1)

Theorem 2

If $\varepsilon$ is a linear uncertainty variable and obeys the normal uncertainty distribution $N(\mu ,\sigma )$, where $\mu ,\sigma$ are real numbers, and $\sigma > 0$, then the inverse distribution of $N(\mu ,\sigma )$ is:

$$ \phi_{{}}^{ - 1} (\zeta ) = \mu + \frac{\sqrt 3 \sigma }{\pi }\ln \frac{\zeta }{1 - \zeta }. $$

(2)

Theorem 3

Assuming that $\varepsilon_{1} ,\varepsilon_{2} , \ldots ,\varepsilon_{n}$ are n independent uncertain variables, there are regular uncertain distributions, respectively, $\varphi_{1} ,\varphi_{2} , \ldots ,\varphi_{n}$, if the function $f(\chi_{1} ,\chi_{2} , \ldots ,\chi_{n} )$ is relative to $\chi_{1} ,\chi_{2} , \ldots ,\chi_{m}$ strictly increasing, relative to $\chi_{m + 1} ,\chi_{m + 2} , \cdots ,\chi_{n}$ strictly decreasing, then, the expectation of uncertain variables $\varepsilon = f(\varepsilon_{1} ,\varepsilon_{2} , \ldots ,\varepsilon_{n} )$ is:

$$ E(\varepsilon ) = \int_{0}^{1} {f(\phi_{1}^{ - 1} (\zeta ), \ldots ,\phi_{m}^{ - 1} (\zeta ),\phi_{m + 1}^{ - 1} (1 - \zeta ), \ldots ,\phi_{n}^{ - 1} (1 - \zeta ))d\zeta } . $$

(3)

Theorem 4

Assuming that $\varepsilon_{1} ,\varepsilon_{2} , \ldots ,\varepsilon_{n}$ are n independent uncertain variables, there are regular uncertain distributions, respectively, $\varphi_{1} ,\varphi_{2} , \ldots ,\varphi_{n}$, if the function $f(\chi_{1} ,\chi_{2} , \ldots ,\chi_{n} )$ is relative to $\chi_{1} ,\chi_{2} , \ldots ,\chi_{m}$ strictly increasing, relative to $\chi_{m + 1} ,\chi_{m + 2} , \ldots ,\chi_{n}$ strictly decreasing. If a certain loss occurs, if and only if $L(\chi_{1} ,\chi_{2} , \ldots ,\chi_{n} ) \le 0$, the risk index is $Risk = \theta$, where $\theta$ is the root of Eq. (4) [53, 54]:

$$ L(\phi _{1}^{{ - 1}} (\zeta ), \cdots ,\phi _{m}^{{ - 1}} (\zeta ),\phi _{{m + 1}}^{{ - 1}} (1 - \zeta ), \cdots ,\phi _{n}^{{ - 1}} (1 - \zeta )) = 0$$

(4)

Theorem 5

Assuming that $\varepsilon_{1} ,\varepsilon_{2} , \cdots ,\varepsilon_{n}$ are n independent uncertain variables, there are regular uncertain distributions, respectively, $\varphi_{1} ,\varphi_{2} , \ldots ,\varphi_{n}$, if the function $f({\chi }_{1},{\chi }_{2},\dots ,{\chi }_{n})$ is relative to $\chi_{1} ,\chi_{2} , \cdots ,\chi_{m}$ strictly increasing, then the uncertain variable $\varepsilon = f(\varepsilon_{1} ,\varepsilon_{2} , \ldots ,\varepsilon_{n} )$ has an inverse distribution, and the inverse distribution is:

$$\psi _{1}^{{ - 1}} (\zeta ) = f(\phi _{1}^{{ - 1}} (\zeta ), \ldots ,\phi _{m}^{{ - 1}} (\zeta ),\phi _{{m + 1}}^{{ - 1}} (1 - \zeta ), \ldots ,\phi _{n}^{{ - 1}} (1 - \zeta )).$$

(5)

Uncertain return portfolio optimization based on prospect theory

Utility function selection

In traditional expected utility theory, the utility of investors is only a function of wealth and is unrelated to changes in wealth. Prospect theory presupposes that investors preset a reference point when making decisions and measure gains and losses based on the change in final wealth relative to the reference point. People value the change in wealth rather than the final value. Near the reference point, investors’ risk appetite will be reversed, and they be risk averse in the face of gains and risk chasing in the face of losses. People have different attitudes toward losses and gains and are more sensitive to losses. The distress caused by the loss of quantity is far greater than the happiness brought by the gain, which is manifested as loss aversion. In the editing stage, the decision maker sets a reference point and edits the various possible results of the decision as gains or losses relative to a certain reference point; in the evaluation stage, decision-makers subjectively evaluate gains and losses according to the following S-shaped value function (Fig. 1):

$$ \begin{gathered} f(x,u_{0} ) = \left\{ {\begin{array}{*{20}c} {(x - u_{0} )^{\alpha } } & {x \ge u_{0} } \\ { - \lambda (u_{0} - x)^{\beta } } & {x < u_{0} } \\ \end{array} } \right. \\ { = [}(x - u_{0} )^{ + } ]^{\alpha } - \lambda [(u_{0} - x)^{ + } ]^{\beta } , \\ \end{gathered} $$

(6)

where $u_{0}$ is the reference point (it can be the wealth, income, rate of return, etc. at the end of the investment period), and $x$ is the actual value at the end of the investment period. $\alpha$ and $\beta$($0 < \alpha \le \beta \le 1$) reflect investors' attitudes toward gains and losses. $\lambda ( \ge 1)$ is the loss aversion coefficient, which means that the negative utility of unit loss to investors is λ multiplied by the positive utility of unit income. When $x \ge u_{0}$, $f(x)$ is the concave function of risk aversion; when $x < u_{0}$, $f(x)$ is the convex function of risk pursuit. $u_{0}$ is the inflection point of the value function. $(x)^{ + } = \max (x,0)$ is the plus function.

Fig. 1

Kahneman and Tversky's value function

The optimal model of uncertain return investment portfolios based on prospect theory

Suppose the investment amount of the i-th stock is $x_{i}$, $\varepsilon_{i}$ represents the return rate of the i-th stock, $\varepsilon_{i}$ is an independent uncertain variable with a regular uncertainty distribution $\phi$, and $\theta$ represents the maximum risk index that can be tolerated. Then, the loss function is expressed as:

$$ L(\varepsilon_{1} ,\varepsilon_{2} , \ldots ,\varepsilon_{n} ) = \sum\limits_{i = 1}^{n} {\varepsilon_{i} x_{i} } - \sum\limits_{i = 1}^{n} {c(} x_{i} ). $$

(7)

In investment transactions, due to external influences such as policies, as the transaction volume increases, unit transaction costs will gradually decrease. At this time, the transaction cost function is a concave function, but if it reaches a certain critical point, a short supply of stocks will lead to an increase in unit transaction fees [53]. It assumes that investors invest in a stable market; that is, transaction costs will not exceed the critical point. Therefore, assuming that the transaction cost function is $c(x_{i} ) = ax_{i}^{2} + bx_{i}$, 2…, n, where a < 0, b > 0, and the investor’s maximum risk is $\theta$, then the portfolio model with nonlinear transaction cost function is:

$$ R = \mathop {\max }\limits_{{x_{1} ,x_{2} , \cdots ,x_{n} }} E\left[ {\sum\limits_{i = 1}^{n} {\varepsilon_{i} x_{i} } - \sum\limits_{i = 1}^{n} {(ax_{i}^{2} + bx_{i} )} } \right], $$

(8)

$$ s.t.\left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {x_{i} = 1 \, } } \\ {\Pr \left\{ {\sum\limits_{i = 1}^{n} {\varepsilon_{i} x_{i} } - \sum\limits_{i = 1}^{n} {(ax_{i}^{2} + bx_{i} )} \le 0} \right\} \le \theta } \\ {x_{i} \ge 0,i = 1,2, \ldots ,n \, } \\ \end{array} } \right.. $$

(9)

According to Theorems 3 and 4, the model can be transformed into:

$$ R = \mathop {\max }\limits_{{x_{1} ,x_{2} , \cdots ,x_{n} }} \int_{0}^{1} {\left[ {\sum\limits_{i = 1}^{n} {x_{i} \phi_{i}^{ - 1} (\tau )} - \sum\limits_{i = 1}^{n} {(ax_{i}^{2} + bx_{i} )} } \right]} {\text{d}}\tau , $$

(10)

$$ s.t.\left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {x_{i} = 1 \, } } \\ {\sum\limits_{i = 1}^{n} {x_{i} \phi_{i}^{ - 1} (\theta )} \ge \sum\limits_{i = 1}^{n} {(ax_{i}^{2} + bx_{i} )} } \\ {x_{i} \ge 0,i = 1,2, \ldots ,n \, } \\ \end{array} } \right.. $$

(11)

This paper expresses the investor's utility function into two parts: one part is the traditional CRRA-type utility function at the end of the period wealth, and the other part is the S-shaped value function based on loss aversion. The utility function used in this paper is as follows:

$$ U(R,R_{0} ) = d\ln R + g\{ [(R - R_{0} )^{ + } ]^{\alpha } - \lambda [(R - R_{0} )^{ + } ]^{\beta } \} . $$

(12)

The objective function of the uncertain portfolio optimization model based on prospect theory is rewritten as:

$$ \, U(R,R_{0} ) = \mathop {\max }\limits_{{x_{1} ,x_{2} , \cdots ,x_{n} }} d\ln R + g\{ [(R - R_{0} )^{ + } ]^{\alpha } - \lambda [(R - R_{0} )^{ + } ]^{\beta } \} , $$

(13)

$$ s.t.\left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {x_{i} = 1 \, } } \\ {\sum\limits_{i = 1}^{n} {x_{i} \phi_{i}^{ - 1} (\theta )} \ge \sum\limits_{i = 1}^{n} {(ax_{i}^{2} + bx_{i} )} } \\ {x_{i} \ge 0,i = 1,2, \ldots ,n \, } \\ \end{array} } \right.. $$

(14)

Among them, $R_{0}$ is a predetermined reference point. $d,g \ge 0$ is the weight coefficient, which reflects the degree of importance investors attach to wealth and wealth change at the end of the period. When $d = 1,g = 0$, the utility function $U(R,R_{0} )$ degenerates into the traditional CRRA-type utility function at the end of the period wealth, and the relative risk aversion coefficient is 1. When $d = g = 1$, investors believe that the changes in wealth and wealth at the end of the period are equally important. When $d = 1,g > 1$, investors value the change in wealth more than wealth at the end of the period. When $d = 0,g = 1$, investors pay attention only to the change in wealth.

Constrained optimization GWO Algorithm based on real number coding

Basic GWO Algorithm

The GWO algorithm is a new type of swarm intelligence optimization algorithm proposed by Mirialili et al. [56] in 2014. It originates from the simulation of the predation behavior of gray wolves and achieves optimization through the processes of wolves tracking, encircling, hunting, and attacking prey [57].

Group predation behavior of gray wolves

Gray wolves are top carnivores and are located at the top of the food chain. Their lifestyles are mostly group-based. Usually, there are an average of 5 to 12 wolves in each group. A hierarchical pyramid of gray wolves has been constructed and has a strict hierarchical management system, as shown in Fig. 2.

Fig. 2

Schematic diagram of the gray wolf population hierarchy pyramid

The first layer of the pyramid is $\alpha$, the head wolf of the pack. $\alpha$ is the most competent individual in the pack and is mainly responsible for all decision-making matters, including predation, time and place of rest, food distribution and so on.

The second layer of the pyramid is called $\beta$. It is $\alpha$ brain trust, which assists $\alpha$ in making management decisions and handling group-organized behavior activities. When $\alpha$ appears vacant, $\beta$ will substitute for $\alpha$. $\beta$ has control over other members of the wolf pack except $\alpha$ and plays a role in coordinating feedback. It issues orders from $\alpha$ to other members of the group and supervises the implementation of feedback to $\alpha$.

The third layer of the pyramid is $\delta$, which follows the instructions of $\alpha$ and $\beta$ but commands the other lower layers, which are responsible for reconnaissance, watch-keeping, hunting, guarding and so on. The elderly individuals in $\alpha$ and $\beta$ will also be reduced to the $\delta$ level.

The bottom of the pyramid is called $\omega$, which is mainly responsible for balancing the internal relations of the population and taking care of the young.

The population level of gray wolves plays a vital role in achieving efficient group hunting of prey. The predation process is led by $\alpha$. First, the wolves search, track, and approach the prey in a team mode and then surround the prey in all directions. When the encircling circle is small and perfect, the wolves will attack by the nearest $\beta$ and $\delta$ of the prey under the command of $\alpha$. When the prey escapes, the rest of the wolves carry out replenishment and realize the transforming movement of the encirclement to continuously attack the prey in all directions and finally capture the prey.

GWO Algorithm description

In the GWO algorithm, the position of the prey is mapped to a point in the search space, the hunting behavior is performed by $\alpha$, $\beta$ and $\delta$, and $\omega$ follows the first three to track and suppress the prey and finally complete the predation task. Using the GWO algorithm to solve the continuous function optimization problem, assuming that the number of gray wolves is N, the search space is d-dimensional, and the position of the i-th gray wolf in the d-dimensional space can be expressed as $\rho_{i} { = (}\rho_{i1} {,}\rho_{i2} {,} \ldots {,}\rho_{id} {)}$, the current optimal individual in the population is denoted as $\alpha$, the second and third corresponding individuals in the fitness value are denoted as $\beta$ and $\delta$, and the remaining individuals are denoted as $\omega$. The position of the prey corresponds to the global optimal solution of the optimization problem. Three key definitions in the algorithm are given below.

(i) The distance between a gray wolf and its prey. In the predation process, the gray wolf first needs to surround the prey. Corresponding to the GWO algorithm, the distance between the individual and the prey needs to be determined:

$$ D = \left| {C \cdot X_{p} (t) - X(t)} \right|. $$

(15)

In Eq. (15), $X_{p} (t)$ is the position of the prey in the generation; $X(t)$ is the position of the gray wolf individual in the $t$ generation; the constant C is the swing factor, which is determined by formula (16):

$$ C = 2r_{1} . $$

(16)

Among them, $r_{1}$ is a random number within [0, 1].

(ii) The update of gray wolves. The updating equation can be given as (17):

$$ X(t + 1) = X_{p} (t) - A \cdot D, $$

(17)

where A is the convergence factor, which is determined by Eq. (18):

$$ A = (2r_{2} - 1)\partial . $$

(18)

In formula (18), $r_{2}$ is randomly generated in the interval [0, 1]; $\partial$ linearly decreases from 2 to 0 in the iterative process.

(iii) Location of the prey. When the gray wolf judges the location of the prey, it will be led by the head wolf α and β and δ to initiate hunting behavior. In the wolf pack, α, β, and δ are the closest to the prey, and the positions of these three can be used to determine the location of the prey. The mechanism by which individuals in the wolf pack track the position of their prey is shown in Fig. 3.

Fig. 3

Individual tracking mechanism in GWO algorithm

In the iterative process, the position of the prey is evaluated and located by α, β and δ, which is used as a standard to calculate the distance between themselves and the prey by other individuals in the population and complete the full range of approaching, encircling, attacking, etc. The three best positions obtained are averaged, and then the searched positions are updated.

The mathematical description of the individual tracking prey in a gray wolf group determines the distance between the individuals and α, β, δ in the group according to Eqs. (19) through (24) and then comprehensively judges the direction of the individuals moving to the prey via Eq. (20):

$$ D_{\alpha } = \left| {C_{1} \cdot X_{\alpha } (t) - X(t)} \right|, $$

(19)

$$ D_{\beta } = \left| {C_{2} \cdot X_{\beta } (t) - X(t)} \right|, $$

(20)

$$ D_{\delta } = \left| {C_{3} \cdot X_{\delta } (t) - X(t)} \right|, $$

(21)

$$ X_{1} = X_{\alpha } - A_{1} \cdot D_{\alpha } , $$

(22)

$$ X_{2} = X_{\beta } - A_{2} \cdot D_{\beta } , $$

(23)

$$ X_{3} = X_{\delta } - A_{3} \cdot D_{\delta } , $$

(24)

$$ X(t + 1) = \frac{{X_{1} + X_{2} + X_{3} }}{3}. $$

(25)

The optimization process of the GWO algorithm randomly generates a group of gray wolves in the search space in the process of evolution. α, β and δ are responsible for evaluating the position of the prey (global optimal solution), and the rest of the individuals in the group use this as a standard to calculate the distance between themselves and the prey, complete the full range of approaching, encircling and attacking the prey, and finally capture the prey.

Improvement strategy

The basic GWO algorithm has the characteristics of simple principles, few parameters to be adjusted, implementation ease, and strong global search capability. However, it cannot be used directly to deal with constrained portfolio optimization models. Based on Mirialili et al. [54], this paper improves the coding method and the penalty function to address the two types of constraints, making the GWO algorithm easier to solve the constrained portfolio optimization problem.

Coding improvement strategy

The real number coding strategy of the basic GWO algorithm has difficulty producing effective realistic individuals. To make the initial population meet the constraint that the sum is 1 and reduce the use of the penalty function, the initial population is normalized as follows:

pop = rand(N_SA,num);

y = sum(pop (i));

for i = 1: N_SA.

startpop(i,:) = pop (i,:)./y(i);

end.

where N_SA is the population size, num is the population dimension, and i is the individual number.

After the individual's new position is obtained, the above method is used again to normalize the new position to avoid new unrealistic individuals.

Constrained optimization strategy based on penalty function

Since the traditional GWO is a kind of unconstrained optimization technology, it is necessary to combine a suitable constraint processing technology to solve the constraint optimization problems. The penalty function method is one of the most commonly used constraint processing techniques. Its basic idea is to add a penalty term that can reflect whether the constraint is satisfied to the objective function to form an unconstrained generalized objective function and then use an optimization algorithm to determine the generalized objective function. The objective function is optimized so that the algorithm finds the optimal solution to the problem under the action of the penalty term. Based on the penalty function, construct the following fitness function value:

$$ {\text{Fitvalue = }}U(R,R_{0} ){ - }\tau {*}\left\{ {\left. {\left[ {\sum\limits_{i = 1}^{n} {(ax_{i}^{2} + bx_{i} )} - \sum\limits_{i = 1}^{n} {x_{i} \phi_{i}^{ - 1} (\theta )} } \right],0} \right\}} \right.^{ + } . $$

(26)

In the formula, $\tau$ is the penalty function factor.

The implementation steps of GWO are as follows:

Step 1. Related parameter settings. The population size is N_SA = 50, $\partial$ = 2–1 × (2/NM), and NM is the maximum number of cycles.

Step 2. Initialization of the population search body. Initialize the positions of the gray wolf individuals at random to generate a 50 × num matrix. Each row in the matrix represents a gray wolf individual.

Step 3. Calculate the fitness value of the initial population individual. By comparing the size of "Fitvalue" to determine the distribution relationship between the fitness value and demand points in the current population, the top 3 optimal individual positions $X_{\alpha }$, $X_{\beta }$, $X_{\delta }$ and the corresponding fitness values. At the same time, the fitness value and the individual are assigned to the global optimal fitness value and the optimal individual, respectively.

Step 4. GWO behavior operation. According to the distance between the individual and $X_{\alpha }$, $X_{\beta }$ and $X_{\delta }$ according to Eqs. (14)–(16), the location of each individual is updated according to Eqs. (22)–(24). Then, the parameters, $\alpha$, A and C are updated, and the new location is evaluated according to Eq. (25). At the same time, step 2 is used to normalize the new position to avoid new infeasible individuals.

Step 5. Calculate the fitness value of the new population individual and determine the optimal individual in the contemporary population and their corresponding fitness value. At the same time, the fitness value is compared with the global optimal fitness value, and if it is excellent, the original global optimal fitness value is replaced by the fitness value, and the corresponding individual is replaced at the same time. In contrast, the global optimal fitness value and the individual remain unchanged.

Step 6. Determine the termination condition. That is, determine whether the maximum number of iterations NM of the population is reached. If yes, output the global optimal fitness value and the optimal individual, that is, the location of emergency facilities and the distribution of coverage requirements from each emergency facility to each demand point; otherwise, the number of iterations is increased by 1, and Step 4 is skipped.

Numerical analysis

Parameter values and calculation results

Suppose that an investor chooses six new stocks to invest in in a certain month, xi (i = 1, 2, 3, 4) represents the investment ratio of the i-th stock. Before investing, the investor consults with stock experts and proposes six stocks. The rate of return is shown in Table 1.

Table 1 Distribution of stock returns given by experts

Based on Theorem 1, Theorem 2 and Theorem 5, the inverse distribution of the rate of return is obtained:

$$ \phi_{1}^{ - 1} (\zeta ) = 1.5\zeta - 0.4\quad \phi_{2}^{ - 1} (\zeta ) = 0.4 + \frac{\sqrt 3 }{\pi }\ln \frac{\zeta }{1 - \zeta } $$

$$ \phi_{3}^{ - 1} (\zeta ) = 0.3 + \frac{{1.2{*}\sqrt 3 }}{\pi }\ln \frac{\zeta }{1 - \zeta }\quad \phi_{4}^{ - 1} (\zeta ) = 2.4\zeta - 0.8 $$

$$ \phi_{5}^{ - 1} (\zeta ) = 1.8\zeta - 0.6\quad \phi_{6}^{ - 1} (\zeta ) = 0.4 + \frac{{1.1{*}\sqrt 3 }}{\pi }\ln \frac{\zeta }{1 - \zeta }. $$

The parameter settings of the calculation example are as follows: the nonlinear transaction cost coefficient adopts the function determined by the literature [58], a = − 0.0001, b = 0.005. Reference point interest rate $R_{0} = 0.3{\text{\% }}$; maximum risk index $\theta = 0.32$; prospect theory function parameters $\alpha = 0.88.\; \beta = 0.88$. The weight coefficients of the utility function are set as d = 0 and g = 1, indicating that investors are loss averse and pay attention to changes in wealth. The algorithm parameter settings are shown in Table 2.

Table 2 Algorithm parameter value

Using MATLAB2017b, we ran the program on a PC with an Intel(R) Core I7-8550U CPU, 16 GB memory, and 64-bit operating system. Taking the optimal value of 20 operations as the final result, the optimal target value is − 0.0269, the optimal solution is [0.2888, 0.0001, 0, 0, 0.6789, 0.0322], and the calculation time is 0.5556 s.

Algorithm performance analysis

To verify the performance of the GWO algorithm designed in this paper, we choose to compare it with two classic evolutionary algorithms, PSO and GA. According to different risk values $\theta$, three sets of calculation examples are set up. Under each set of calculation examples, each algorithm runs 20 times randomly, the calculation results are recorded, and the calculation accuracy comparison of the three algorithms (Fig. 4), the calculation time comparison (Fig. 5), and the algorithm performance data (Table 3) are obtained. The results show that in terms of calculation accuracy, GWO is better than PSO, and PSO is better than GA. Among them, the optimal solutions of GWO and PSO are consistent, but in terms of solution stability, GWO is better than PSO. However, GA is prone to fall into precocity, and it is difficult to obtain a satisfactory solution. In terms of calculation time, GWO is equivalent to GA with 0.5 s, while the calculation efficiency of PSO is poor, with an average calculation time of 2.2 s.

Fig. 4

Calculation accuracy of the three algorithms

Fig. 5

Calculation time of the three algorithms

Table 3 Algorithm performance comparison

To further test the performance of the algorithms, the data for 30 stocks were randomly generated based on the basic data of the six stocks mentioned above to conduct a large-scale example analysis. The results also show that the proposed GWO algorithm is superior to the classical PSO and GA (see Figs. 6, 7, and Table 4).

Fig. 6

Calculation accuracy of the three algorithms in large-scaled instances

Fig. 7

Calculation time of the three algorithms in large-scaled instances

Table 4 Algorithm performance comparison for large-scaled instances

Sensitivity analysis

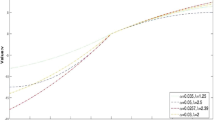
It is not difficult to see from Fig. 8 that for the same reference point return rate, the smaller the λ is, the higher the investor's expected utility level is. When λ = 0, the same reference point has the largest expected utility. At this time, investors only pay attention to the part of the ending wealth above the reference point and are indifferent to the relative loss of the part below the reference point. When λ = 1, investors believe that part of the gain above the reference point is as important as the loss of the part below the reference point. Currently, the same amount of relative gains and losses causes as much happiness as distress. With the increase in λ, the loss aversion of investors increases, and the distress caused by relative losses is much greater than the happiness caused by relative gains, so the utility of the same reference point rate of return decreases.

Fig. 8

Expected utility values at different reference points

At the same time, under the same λ, when λ > 1, with the increase of the reference point yield, the investor's expected utility increases. This is because investors prefer loss aversion and are more sensitive to losses than gains. As the rate of return on the reference point increases, investors' expectations of the rate of return increase, and the pain of loss gradually decreases. In contrast, under the same λ, when λ < 1, as the return rate of the reference point increases, the investor's expected utility decreases. The reason is that, at this time, the decision maker is a risk-preferred investor, who is more sensitive to gains than losses. With the increase in the return rate at the reference point, the utility of the investor to the return decreases continuously. In real life, most investors use the utility function for λ > 1 to protect against losses.

Figures 9 and 10 shows the optimal investment ratio for each stock with different utility functions. As seen from Figs. 9 and 10, when d = 0 and g = 1, investment is relatively dispersed. Because investors pay attention to changes in wealth, for risk-averse investors, diversification can help to reduce risks and improve utility.

Fig. 9

Optimal investment ratio under different circumstances

Fig. 10

Expected utility at different d and g

Figure 11 shows the utility values for different utility functions and different λ values. For a risk-averse investor (λ = 2.25), the utility is smaller than for a risk-averse investor because the pain of loss is more pronounced.

Fig. 11

Expected utility values at different risks

Figure 11 shows the expected utility at different risk values. As seen from Figs. 9 and 10, for the same degree of risk $\theta$, the lower λ is, the higher the expected utility of the investor, and the highest expected utility of the same reference point at λ = 0. For either a risk-tolerant decision maker (λ < 1) or a risk-averse decision maker (λ > 1), the expected utility increases with each increase over a certain range. However, when increased to a certain degree, the expected utility will remain unchanged. The reason is that the increase in acceptable risk is conducive to reducing the perceived distress of decision makers for reduced income or increased loss. When the acceptable risk degree increases to a certain level, the marginal change of the decision maker's income or loss will no longer increase. This conclusion is consistent with the decision-making psychology of different types of decision-makers in real life.

Table 5 shows the optimal investment ratios of two types of decision makers with different risk preferences under different accepted risk values. The results show that for risk-averse investors, the investment ratio is more diversified than that of risk-preference investors. The reason is that the distress caused by the loss is more significant, so the motivation to diversify investment to avoid risks is stronger. Regardless of the type of decision maker, the smaller the acceptable risk value, the more diversified the investment. When risk acceptance increases to a certain percentage, the only decision-making rule of the decision maker is to maximize profit. At this time, investment is highly concentrated.

Table 5 Optimal investment ratio at different risks (%)

Conclusion

Based on the hypothesis of rational investors, the portfolio optimization model under the framework of traditional expected utility theory believes that investors have homogeneous expectations and that the attitude toward risks is always consistent, without considering the essential characteristics and attributes of investors' decision-making behavior, and the conclusions obtained are inconsistent with reality. By means of behavioral experiments, prospect theory finds that investors have different attitudes toward wealth gain and loss in actual investment and generally show the psychological characteristics of loss aversion. In this paper, uncertain return portfolio optimization based on prospect theory is studied. First, the investor's utility function is expressed in two parts. One part is the CRRA utility function for final wealth, and the other part is the S-shaped value function for final wealth relative to the reference point. Then, expected utility maximization is taken as the decision goal to establish the portfolio optimization model. Due to the nonsmooth and nonconcave complex characteristics of the model, an improved GWO algorithm is designed. The analysis results of the calculation examples show that the performance of the proposed GWO algorithm is far superior to the traditional PSO and GA.

The issue of how to incorporate more behavioral finance research results, such as herd mentality, overconfidence, regret avoidance and other behavior characteristics, into the traditional portfolio optimization model and modify it is an area that needs to be investigated in the future.