Skip to main content
SpringerLink
Log in

Linear nearest neighbor flocks with all distinct agents

  • Regular Article - Statistical and Nonlinear Physics
  • Published:
The European Physical Journal B Aims and scope Submit manuscript

Abstract

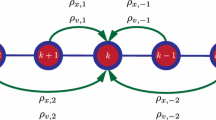
This paper analyzes the global dynamics of one-dimensional agent arrays with nearest neighbor linear couplings. The equations of motion are second-order linear ODE’s with constant coefficients. The novel part of this research is that the couplings are different for each distinct agent. We allow the forces to depend on the positions and velocity (damping terms) but the magnitudes of both the position and velocity couplings are different for each agent. We, also, do not assume that the forces are “Newtonian” (i.e. the force due to A on B equals the minus the force of B on A) as this assumption does not apply to certain situations, such as traffic modeling. For example, driver A reacting to driver B does not imply the opposite reaction in driver B. There are no known analytical means to solve these systems, even though they are linear, and so relatively little is known about them. This paper is a generalization of previous work that computed the global dynamics of one-dimensional sequences of identical agents (Cantos et al., Eur Phys J Special Topics 225:1115–1125, 2016) assuming periodic boundary conditions. In this paper, we push that method further, similar to Baldivieso and Veerman, IEEE Trans Control Network Syst (2021), and use an extended periodic boundary condition to to gain quantitative insights into the systems under consideration. We find that we can approximate the global dynamics of such a system by carefully analyzing the low-frequency behavior of the system with (generalized) periodic boundary conditions.

Graphic abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data Availability Statement

This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.]

References

  1. N.W. Ashcroft, N.D. Mermin, Solid State Physics (Saunders College, Philadelphia, 1976)

    MATH  Google Scholar 

  2. J.F. Dyson, The dynamics of a disordered linear chain. Phys. Rev. 92, 1331–1338 (1953)

    Article  ADS  MathSciNet  Google Scholar 

  3. E. Robert, Chandler, Robert Herman and Elliott W. Montroll, Traffic Dynamics: Studies in Car Following, Operations Research 6, 165–184 (1957)

    Google Scholar 

  4. B.S. Kerner, The Physics of Traffic (Springer-Verlag, Berlin, 2004)

    Book  Google Scholar 

  5. U. Mackenroth, Robust Control Systems: Theory and Case Studies (Springer-Verlag, Berlin Heidelberg, 2004)

    Book  Google Scholar 

  6. W. Ren, R. Beard, Distributed Consensus in Multi-vehicle Cooperative Control (Springer-Verlag, Berlin Heidelberg, 2008)

  7. S.E. Li, Y. Zheng, K. Li, Y. Wu, J.K. Hedrick, F. Gao, H. Zhang, Dynamical modeling and distributed control of connected and automated vehicles: challenges and opportunities. IEEE Intell. Transp. Syst. Mag. 9, 46–58 (2017)

  8. F. Lin, M. Fardad, M.R. Jovanovic, Optimal control of vehicular formations with nearest neighbor interactions. IEEE Trans. Autom. Control 9, 2203–2218 (2012)

    Article  MathSciNet  Google Scholar 

  9. R.H. Middleton, J.H. Braslavsky, String instability in classes of linear time invariant formation control with limited communication range. IEEE Trans. Autom. Control 55, 1519–1530 (2010)

    Article  MathSciNet  Google Scholar 

  10. H. Hao, P. Barooah, Stability and robustness of large platoons of vehicle with double-integrator models and nearest neighbor interaction. Int. J. Robust Nonlinear Control 23, 2097–2122 (2013)

    Article  MathSciNet  Google Scholar 

  11. C.E. Cantos, D.K. Hammond, J.J.P. Veerman, Transients in the synchronization of assymmetrically coupled oscillator arrays. Eur. Phys. J. Special Topics 225, 1115–1125 (2016)

    Article  ADS  Google Scholar 

  12. C.E. Cantos, J.J.P. Veerman, D.K. Hammond, Signal velocity in oscillator arrays. Eur. Phys. J. Special Topics 225, 1199–1210 (2016)

    Article  ADS  Google Scholar 

  13. J. Herbrych, A. Chazirakis, N. Christakis, J.J.P. Veerman, Dynamics of locally coupled oscillators with next-nearest-neighbor interaction. Diff. Equ. Dyn. Syst. 29(3), 487–509 (2021). https://doi.org/10.1007/s12591-017-0377-3

  14. P.E. Baldivieso, J.J.P. Veerman, Stability conditions for coupled autonomous vehicles formations. IEEE Trans Control Netw Syst 8(1), 513–522. https://doi.org/10.1109/TCNS.2021.3052308

Download references

Author information

Authors and Affiliations

  1. Digimarc Corporation, 9405 SW Gemini Drive, Beaverton, OR, 97008-7192, USA

    R. G. Lyons

  2. Fariborz Maseeh Department of Mathematics and Statistics, Portland State University, Portland, USA

    R. G. Lyons & J. J. P. Veerman

Authors
  1. R. G. Lyons
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. J. P. Veerman
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The basic concepts were created by both authors. The main results were anticipated by both J. J. P. Veerman and R. G. Lyons. The formal proofs and simulations were constructed by R. G. Lyons with help from J. J. P. Veerman.

Corresponding author

Correspondence to R. G. Lyons.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary material 1 (sage 6 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lyons, R.G., Veerman, J.J.P. Linear nearest neighbor flocks with all distinct agents. Eur. Phys. J. B 94, 174 (2021). https://doi.org/10.1140/epjb/s10051-021-00163-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjb/s10051-021-00163-2

Search

Navigation