Abstract
The aggregation of fuzzy information is a key process of MCDM methods used to deal with uncertainties. A class of aggregation methods for fuzzy information is fuzzy distance aggregation operators in which distance values are argument variables. This class of aggregation operators permits us to consider an ideal alternative in the aggregation process. But these operators fall in dealing with situations among which distance values cannot be aggregated directly. Therefore, we proposed some distance induced fuzzy operators in which distance values are order-inducing variables so that we can also consider an ideal alternative but take other parameters, also including distance values, as argument variables in an aggregation process. We analyzed the concepts, properties, and generalized forms of proposed distance induced fuzzy operators in this paper. Moreover, aiming at multi-criteria group decision-making (MCGDM), three frameworks of MCGDM methods with the proposed distance induced fuzzy operators are constructed for three different MCGDM situations, respectively. At the end of this paper, an example is used to explain the detailed processes of using the proposed frameworks to make a decision.
Similar content being viewed by others
1 Introduction
Information aggregation is an important problem for MCDM. At present, numerous information aggregation methods have been proposed and applied to solve lots of complex problems [1,2,3,4,5]. As a part of information aggregation methods, aggregation operators have achieved much attention [6,7,8,9,10]. With the appearance of the ordered weighted averaging (OWA) [11] and the induced ordered weighted averaging (IOWA) [12] operators, many aggregation operators for their extensions have been researched for aggregating crisp numbers [13,14,15,16,17,18]. But with the increasing complexity of problems, we cannot accurately describe a problem only through crisp numbers. Therefore, more and more different types of fuzzy numbers are proposed [19,20,21] and used to describe uncertainties. The research about combing aggregation operators with fuzzy numbers has achieved numbers of achievements [6,7,8, 22] and is applied to solve a lot of problems, such as the diagnose of COVID-19 [20]. Commonly used operators for aggregating uncertain information include the uncertain OWA (UOWA) [23], the induced uncertain linguistic OWA (IULOWA) [24], the fuzzy generalized OWA (FGOWA) [25], the fuzzy induced GOWA (FIGOWA) [26], the uncertain HOWA (UHOWA) [18], the uncertain induced HOWA (UIHOWA) [18], the fuzzy induced HOWA (FIHOWA) operators [27], and so on. These aggregation operators are all used in MCDM, especially in MCGDM.
Distance measures are effective approaches to measure similarity and difference between two elements or two vectors [28,29,30,31]. Much research has conducted aiming at how to use distance measures to deal with MCDM problems [32,33,34]. And distance aggregation operators considering distance measures in aggregation operators are studied. The first distance aggregation operator is the ordered weighted averaging distance (OWAD) operator proposed by Merigó and Gil-Lafuente [35]. Aspired by the OWAD operator, many distance aggregation operators, including the induced OWAD (IOWAD) [36], the probabilistic OWAD (POWAD) [37], the Minkowski POWAD (MPOWAD) [38], the heavy OWAD (HOWAD) [39], the induced Euclidean OWAD (IEOWAD) [40], the induced MOWAD (IMOWAD) [41], the induced Minkowski POWAD (IMPOWAD) [38], the induced HOWAD (IHOWAD) [42], the weighted IEOWAD (WIEOWAD) [43] operators, and so on, are suggested. These distance aggregation operators permit decision makers (DMs) to consider an ideal alternative in the information aggregation process.
Distance aggregation operators for aggregating fuzzy information are also proposed. Merigó and Casanovas [44] propose the linguistic OWAD (LOWAD) operator to aggregate linguistic variables. Zeng et al. [45] propose the intuitionistic fuzzy ordered weighted distance (IFOWD) operator to aggregate intuitionistic fuzzy numbers. Zeng [46] considers interval numbers in the OWAD operator and introduces the uncertain OWAD (UOWAD) operator. Zeng et al. [47] study the uncertain POWAD (UPOWAD) operator to deal with uncertain decision-making problems. Su et al. [48] consider the Euclidean distance in the UIOWAD operator to obtain the induced uncertain Euclidean OWAD (IUEOWAD) operator. The fuzzy linguistic IEOWAD (FLIEOWAD) operator considers fuzzy linguistic variables in the IEOWAD operator is studied by Xian and Sun [49]. Xian et al. [50] consider fuzzy linguistic variables and the Minkowski distance in the IOWAD operator to obtain the fuzzy linguistic IOWA Minkowski distance (FLIOWAMD) operator. Li et al. [51] propose the 2-tuple linguistic IGOWA distance (2LIGOWAD) operator obtained by considering 2-tuple linguistic variables and distance measures in the IGOWA operator. Through considering triangular fuzzy numbers in the IHOWAD operator, Zeng et al. [52] further suggest the fuzzy induced HOWA distance (FIHOWAD) operator. Some other distance aggregation operators can be seen in Ref. [53,54,55,56]. These operators are almost used to deal with MCDM problems.
Distance aggregation operators provide DMs more scenarios to select. They permit us to consider an ideal alternative in an MCDM problem, and they all regard distance values as argument variables. However, if distance measures as argument variables are not accepted in the information aggregation process, these operators cannot be used by DMs. To solve this issue, we propose some distance induced fuzzy operators. These operators are suggested for aggregating uncertain information represented by triangular fuzzy numbers. They permit us to take an ideal alternative represented by triangular fuzzy numbers into consideration in information aggregation. And in these proposed operators, the Hamming distance measures of triangular fuzzy numbers are used to induce the rank of argument variables. We analyze the concepts, properties, and general forms of these new proposed operators. To apply the distance induced fuzzy operators proposed in MCGDM, we construct three frameworks of MCGDM methods for three different decision-making situations. We find that the distance induced fuzzy operators proposed can provide more scenarios for DMs to select. We also find that it is necessary to construct different frameworks of MCGDM methods for different situations when we use the proposed distance induced fuzzy operators in MCGDM.
This paper is arranged as follows. In the Sect. 2, we review the Hamming distance, the triangular fuzzy number, and the IOWA operator. In the Sect. 3, we firstly propose the DIFOWA and WDIFOWA operators and analyze their properties, and then, we extend them through the generalized means and the quasi-arithmetic means. Three frameworks of MCGDM methods with the distance induced fuzzy operators for three different decision-making situations are constructed in the Sect. 4. The best candidate selection problem for a managerial position is presented to illustrate how to use the proposed frameworks to solve an MCGDM problem in the Sect. 5. Finally, we end this paper with some main conclusions in Sect. 6.
2 Preliminaries
We firstly review the basic concepts of the Hamming distance, the triangular fuzzy number, and the IOWA operator.
2.1 The Hamming Distance
The Hamming distance can determine the distance of both two crisp numbers or two fuzzy numbers. It is described as follows.
Definition 1
[28] Let \(A = \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right)\) and \(B = \left( {b_{1} ,b_{2} , \ldots ,b_{n} } \right)\) be two sets with \(n\) elements. A normalized Hamming distance between \(A\) and \(B\) is defined as a mapping \(f_{{NHD}} :R^{n} \times R^{n} \to R\) with the following form:
where \(a_{i}\) and \(b_{i}\) are the \(i\) th arguments of sets \(A\) and \(B\), respectively.
Definition 2
[28] Let \(A = \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right)\) and \(B = \left( {b_{1} ,b_{2} , \ldots ,b_{n} } \right)\) be two sets with \(n\) elements. A weighted Hamming distance between \(A\) and \(B\) is defined as a mapping \(f_{{WHD}} :R^{n} \times R^{n} \to R\) with an associated weighting vector \(W{\text{ = }}\left( {\omega _{{\text{1}}} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\) and \(\omega _{i} \in \left[ {0,1} \right]\) for all \(i = 1,2, \ldots ,n\), which has the following form:
where \(a_{i}\) and \(b_{i}\) are the \(i\) th arguments of sets \(A\) and \(B\), respectively.
Besides crisp numbers, we also use the Hamming distance to determine the difference of two sets or two vectors represented by fuzzy numbers, including interval numbers, triangular fuzzy numbers, and so on.
2.2 The Triangular Fuzzy Number
Triangular fuzzy numbers are commonly used to represent uncertain information. In this paper, we use triangular fuzzy numbers to research distance induced fuzzy aggregation operators. A triangular fuzzy number is described as follows.
Definition 3
[52] A triangular fuzzy number \(\tilde{q}\) is defined as a triplet \(\tilde{q} = \left[ {q^{L} ,q^{M} ,q^{U} } \right]\), \(q^{L} ,q^{M} ,q^{U} \in R\) in which \(q^{L}\), \(q^{U}\) and \(q^{M}\) represent the lower, upper and modal values, respectively. The membership function \(\mu _{{\tilde{q}}} \left( x \right)\) is defined in the following form:
where \(q^{L} \le q^{M} \le q^{U}\). When \(q^{M} - q^{L} = q^{U} - q^{M}\), \(\tilde{q}\) is a symmetrical triangular fuzzy number. When \(q^{L} = q^{M} = q^{U}\), \(\tilde{q}\) is reduced to a crisp number. Specifically, when \(q^{L} > 0\), \(\tilde{q}\) is a positive triangular fuzzy number. In this paper, all the triangular fuzzy numbers are positive triangular fuzzy numbers.
Let \(\tilde{c} = \left[ {c^{L} ,c^{M} ,c^{U} } \right]\) and \(\tilde{d} = \left[ {d^{L} ,d^{M} ,d^{U} } \right]\) be any two positive triangular fuzzy numbers, and \(\lambda > 0\). Some basic operational laws are shown as follows:
According to the extension principle of fuzzy sets, the results of five operational laws are also positive triangular fuzzy numbers.
2.3 The IOWA Operator
The IOWA operator is a basic aggregation operator. Research about extensions of the IOWA operator has achieved a lot of achievements. The IOWA operator is defined in the following form.
Definition 4
[12] A IOWA operator of dimension \(n\) is defined as a mapping \(f_{{IOWA}} :R^{n} \times R^{n} \to R\) with an associated weighting vector \(W = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\) and \(\omega _{i} \in \left[ {0,1} \right]\) for all \(i = 1,2, \ldots ,n\), we have
where \(c_{j}\) is the \(x_{i}\) value in the IOWA pair \(\left\langle {v_{i} ,x_{i} } \right\rangle\) having the \(j\) th largest \(v_{i}\), \(v_{i}\) is the order-inducing variable, and \(x_{i}\) is the argument variable.
The more general forms of the IOWA operator are the IGOWA and the quasi-IOWA operators [14] obtained by generalizing the IOWA operator with generalized means and quasi-arithmetic means, respectively.
Usually, the IOWA operator and its extensions must satisfy commutativity, monotonicity, boundedness, and idempotency.
3 Distance Induced Fuzzy Operators
3.1 The Distance Induced Fuzzy OWA operator
In this paper, we will do some research about distance induced fuzzy aggregation operators with the Hamming distance and triangular fuzzy numbers. Firstly, we will propose the distance induced fuzzy ordered weighted averaging (DIFOWA) operator with the Hamming distance in this subsection. Assume \(\tilde{X} = \left( {\tilde{x}_{1} ,\tilde{x}_{2} , \ldots ,\tilde{x}_{n} } \right)\) is an argument variable set, \(\tilde{Y} = \left( {\tilde{y}_{1} ,\tilde{y}_{2} , \ldots ,\tilde{y}_{n} } \right)\) is a reference argument variable set, \(\tilde{x}_{i} = \left[ {x_{i}^{L} ,x_{i}^{M} ,x_{i}^{U} } \right]\) and \(\tilde{y}_{i} = \left[ {y_{i}^{L} ,y_{i}^{M} ,y_{i}^{U} } \right]\) for all \(i = 1,2, \ldots ,n\) are all positive triangular numbers.
Definition 5
Let \(\Omega\) be the set of triangular fuzzy numbers, a DIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{DIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with an associated weighting vector \(W = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\) and \(\omega _{i} > 0\) for all \(i = 1,2, \ldots ,n\), such that
where \(\tilde{b}_{j}\) is the \(\tilde{x}_{i}\) value in the DIFOWA pair \(\left\langle {v_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(v_{i}\), \(v_{i}\) and \(\tilde{x}_{i}\) are the order-inducing variable and the argument variable, respectively. \(v_{i}\) is determined by Eq. (6) [52]
where \(v_{i} \in \left( {0, + \infty } \right)\).
Next, we explain the aggregation procedure of the DIFOWA operator through an example.
Example 1.
Assume the argument variable set \(\tilde{X} = \left( {\left[ {62,70,75} \right],\left[ {69,82,85} \right],\left[ {71,77,83} \right],\left[ {76,88,92} \right]} \right)\), the reference argument variable set \(\tilde{Y} = \left( {\left[ {85,90,95} \right],\left[ {88,91,95} \right],\left[ {87,93,96} \right],\left[ {88,90,92} \right]} \right)\), the associated weighting vector \(W = \left( {0.25,0.21,0.28,0.26} \right)\). According to the proposed DIFOWA operator, the detailed aggregation process is shown below.
Firstly, calculate the order-inducing variables \(v_{i}\) for \(i = 1,2,3,4\), according to Eq. (8), we have
Then, reorder the four argument variables according to the descending order of \(v_{i}\) for \(i = 1,2,3,4\), the result is
Therefore, the aggregation result is
Through the operational laws in Sect. 2.1 and example 1, we find that the result of a DIFOWA operator is a positive triangular fuzzy number.
We further obtain the weighted distance induced fuzzy ordered weighted averaging (WDIFOWA) operator using the weighted Hamming distance.
Definition 6
Let \(\Omega\) be the set of triangular fuzzy numbers, a WDIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{WDIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with two associated weighting vectors \(W_{1} = \left( {\omega _{1} ,\omega _{2} ,\ \ldots ,\omega _{n} } \right)\) and \(W_{2} = \left( {w_{1} ,w_{2} ,\ \ldots ,w_{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\), \(\sum\nolimits_{{i = 1}}^{n} {w_{i} } = 1\) and \(\omega _{i} > 0\), \(w_{i} > 0\) for all \(i = 1,2,\ \ldots ,n\), such that.
where \(\tilde{c}_{j}\) is the \(\tilde{x}_{i}\) value in the WDIFOWA pair \(\left\langle {u_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(u_{i}\), \(u_{i}\) and \(\tilde{x}_{i}\) are the order-inducing variable and the argument variable, respectively. \(u_{i}\) is determined by Eq. (8) [50]
where \(u_{i} \in \left( {0, + \infty } \right)\).
If the weighting vectors \(W_{1} = \left( {\omega _{1} ,\omega _{2} ,\ \ldots ,\omega _{n} } \right)\) and \(W_{2} = \left( {w_{1} ,w_{2} ,\ \ldots ,w_{n} } \right)\) do not such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\) and \(\sum\nolimits_{{i = 1}}^{n} {w_{i} } = 1\), the WDIFOWA operator is defined in the following.
Definition 7
Let \(\Omega\) be the set of triangular fuzzy numbers, a WDIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{WDIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with two associated weighting vectors \(W_{1} = \left( {\omega _{1} ,\omega _{2} ,\ \ldots ,\omega _{n} } \right)\) and \(W_{2} = \left( {w_{1} ,w_{2} ,\ \ldots ,w_{n} } \right)\) such that \(\omega _{i} > 0\) and \(w_{i} > 0\) for all \(i = 1,2,\ \ldots ,n\), according to the following formula
where \(\tilde{c}_{j}\) is the \(\tilde{x}_{i}\) value in the WDIFOWA pair \(\left\langle {u_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(u_{i}\), \(u_{i}\) and \(\tilde{x}_{i}\) are the order-inducing variable and the argument variable, respectively. \(u_{i}\) is determined by Eq. (10)
Next, we also use a simple example to show the aggregation procedure using the WDIFOWA operator.
Example 2.
We also use the data in example 1 and assume \(W_{2} = \left( {0.15,0.30,0.20,0.35} \right)\), the detailed aggregation process is shown below.
Firstly, calculate the order-inducing variables \(u_{i}\) for \(i = 1,2,3,4\), according to Eq. (10), we have.
\(\begin{aligned} u_{1} & = 0.15 \times \left| {\left( {62 - 85} \right) + \left( {70 - 90} \right) + \left( {75 - 95} \right)} \right| = 9.45,\quad u_{2} = 0.30 \times \left| {\left( {69 - 88} \right) + \left( {82 - 91} \right) + \left( {85 - 95} \right)} \right| = 11.43, \\ u_{3} & = 0.20 \times \left| {\left( {71 - 87} \right) + \left( {77 - 93} \right) + \left( {83 - 96} \right)} \right| = 9.00,\quad u_{4} = 0.35 \times \left| {\left( {76 - 88} \right) + \left( {88 - 90} \right) + \left( {92 - 92} \right)} \right| = 4.94. \\ \end{aligned}\),
Then, reorder the four argument variables according to the descending order of \(u_{i}\) for \(i = 1,2,3,4\), the result is
Therefore, the aggregation result is
According to the operational laws in Sect. 2.1 and example 2, the result of a WDIFOWA operator is also a positive triangular fuzzy number.
By comparing the results of examples 1 and 2, we conclude that using different calculation methods of the Hamming distance may lead to different aggregation results. The reason is that using different types of Hamming distance may lead to different reorder of order-inducing variables calculated.
In MCDM, rank multi aggregation results obtained using the DIFOWA operator or the WDIFOWA operator is unavoidable. Some methods about how to rank triangular fuzzy numbers have been proposed in the literature. We use the following method to convert a triangular fuzzy number to a crisp number. And we rank multi triangular fuzzy numbers by ranking their corresponding crisp numbers. We regard the graded mean value of a triangular fuzzy number as its corresponding crisp number [57].
Definition 8
[50] Let \(\tilde{p} = \left[ {p^{L} ,p^{M} ,p^{U} } \right]\) be a positive triangular fuzzy number, we represent the graded mean value of \(\tilde{p}\) by the following form:
where \(P\left( {\tilde{p}} \right)\) is the graded mean value of \(\tilde{p}\), i.e., we take \(P\left( {\tilde{p}} \right)\) as the corresponding crisp number of the positive triangular number \(\tilde{p}\).
Let \(\tilde{c} = \left[ {c^{L} ,c^{M} ,c^{U} } \right]\) and \(\tilde{d} = \left[ {d^{L} ,d^{M} ,d^{U} } \right]\) be two positive triangular fuzzy numbers, if \(P\left( {\tilde{c}} \right) \le P\left( {\tilde{d}} \right)\), then \(\tilde{c} \le \tilde{d}\).
The DIFOWA and WDIFOWA operators are two special cases of the IOWA operator combined with fuzzy numbers. Therefore, the DIFOWA and WDIFOWA operators also satisfy the following properties.
Theorem 1 (Commutativity)
Assume \(f\) is a DIFOWA or a WDIFOWA operator, then
where \(\left\langle {d_{1} ,\tilde{z}_{1} } \right\rangle ,\left\langle {d_{2} ,\tilde{z}_{2} } \right\rangle , \ldots ,\left\langle {d_{n} ,\tilde{z}_{n} } \right\rangle\) represents any permutation of \(\left\langle {e_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {e_{2} ,\tilde{x}_{2} } \right\rangle , \ldots ,\left\langle {e_{n} ,\tilde{x}_{n} } \right\rangle\).
Proof
Assume \(\left\langle {e_{i}^{*} ,\tilde{x}_{i}^{*} } \right\rangle\) is the \(i\) th pair according to the reordered positions \(e_{i}\) for all \(i = 1,2, \ldots ,n\) in descending order and \(\left\langle {d_{i}^{*} ,\tilde{z}_{i}^{*} } \right\rangle\) is the \(i\) th pair according to the reordered positions \(d_{i}\) for all \(i = 1,2, \ldots ,n\) in descending order, we have
since \(\left\langle {d_{1} ,\tilde{z}_{1} } \right\rangle ,\left\langle {d_{2} ,\tilde{z}_{2} } \right\rangle , \ldots ,\left\langle {d_{n} ,\tilde{z}_{n} } \right\rangle\) represents any permutation of \(\left\langle {e_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {e_{2} ,\tilde{x}_{2} } \right\rangle , \ldots ,\left\langle {e_{n} ,\tilde{x}_{n} } \right\rangle\), which implies that \(e_{i}^{*} = d_{i}^{*}\) and \(\tilde{x}_{j}^{*} = \tilde{z}_{j}^{*}\) for all \(i = 1,2, \ldots ,n\), and then,
Theorem 2 (Idempotency)
Assume \(f\) is a DIFOWA or a WDIFOWA operator, if \(\tilde{x}_{i} = \tilde{a}\) for all \(i = 1,2,\ \ldots ,n\) , then.
\(f\left( {\left\langle {e_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {e_{2} ,\tilde{x}_{2} } \right\rangle ,\ \ldots ,\left\langle {e_{n} ,\tilde{x}_{n} } \right\rangle } \right) = \tilde{a}\).
Proof
Since \(\tilde{x}_{i} = \tilde{a}\) for all \(i = 1,2,\ \ldots ,n\) and \(\sum\nolimits_{{j = 1}}^{n} {\omega _{j} = 1}\), then,
Theorem 3 (Boundness)
Assume \(f\) is a DIFOWA or a WDIFOWA operator, then
Proof
Assume \(\mathop {\min }\limits_{i} \left\{ {\tilde{x}_{i} } \right\} = \tilde{y}\) and \(\mathop {\max }\limits_{i} \left\{ {\tilde{x}_{i} } \right\} = \tilde{z}\), since \(\mathop {\min }\limits_{i} \left\{ {\tilde{x}_{i} } \right\} \le \tilde{x}_{i} \le \mathop {\max }\limits_{i} \left\{ {\tilde{x}_{i} } \right\}\) for all \(i = 1,2,\ \ldots ,n\), which implies that.
according to Theorem 2, we have
and then,
\(\mathop {\min }\limits_{i} \left\{ {\tilde{x}_{i} } \right\} \le f\left( {\left\langle {e_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {e_{2} ,\tilde{x}_{2} } \right\rangle , \ldots ,\left\langle {e_{n} ,\tilde{x}_{n} } \right\rangle } \right) \le \mathop {\max }\limits_{i} \left\{ {\tilde{x}_{i} } \right\}\).
Theorem 4 (Monotonicity)
Assume \(f\) is a DIFOWA or a WDIFOWA operator, if the reordering positions of \(e_{i}\) are the same as the ones of \(d_{i}\) and \(\tilde{x}_{i} \ge \tilde{z}_{i}\) for all \(i = 1,2, \ldots ,n\) , then
\(f\left( {\left\langle {e_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {e_{2} ,\tilde{x}_{2} } \right\rangle , \ldots ,\left\langle {e_{n} ,\tilde{x}_{n} } \right\rangle } \right) \ge f\left( {\left\langle {d_{1} ,\tilde{z}_{1} } \right\rangle ,\left\langle {d_{2} ,\tilde{z}_{2} } \right\rangle , \ldots ,\left\langle {d_{n} ,\tilde{z}_{n} } \right\rangle } \right)\).
Proof
Since the reordering positions of \(e_{i}\) are the same as the ones of \(d_{i}\), which implies that.
and since \(\tilde{x}_{i} \ge \tilde{z}_{i}\) for all \(i = 1,2, \ldots ,n\), therefore, we conclude that \(\begin{aligned} f\left( {\left\langle {e_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {e_{2} ,\tilde{x}_{2} } \right\rangle , \ldots ,\left\langle {e_{n} ,\tilde{x}_{n} } \right\rangle } \right) & \ge f\left( {\left\langle {e_{1} ,\tilde{z}_{1} } \right\rangle ,\left\langle {e_{2} ,\tilde{z}_{2} } \right\rangle , \ldots ,\left\langle {e_{n} ,\tilde{z}_{n} } \right\rangle } \right) = f\left( {\left\langle {d_{1} ,\tilde{z}_{1} } \right\rangle ,\left\langle {d_{2} ,\tilde{z}_{2} } \right\rangle , \ldots ,\left\langle {d_{n} ,\tilde{z}_{n} } \right\rangle } \right), \\ f\left( {\left\langle {e_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {e_{2} ,\tilde{x}_{2} } \right\rangle , \ldots ,\left\langle {e_{n} ,\tilde{x}_{n} } \right\rangle } \right) & = f\left( {\left\langle {d_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {d_{2} ,\tilde{x}_{2} } \right\rangle , \ldots ,\left\langle {d_{n} ,\tilde{x}_{n} } \right\rangle } \right) \ge f\left( {\left\langle {d_{1} ,\tilde{z}_{1} } \right\rangle ,\left\langle {d_{2} ,\tilde{z}_{2} } \right\rangle , \ldots ,\left\langle {d_{n} ,\tilde{z}_{n} } \right\rangle } \right), \\ \end{aligned}\), and then,
Like other aggregation operators, we can also divide the DIFOWA or WDIFOWA operator into two types, the ascending type, and the descending type, respectively. When we rank the order-inducing variables in ascending order, we obtain the ascending DIFOWA (ADIFOWA) or ascending WDIFOWA (AWDIFOWA) operator. When we rank the order-inducing variables in descending order, we obtain the descending DIFOWA (DDIFOWA) or descending WDIFOWA (DWDIFOWA) operator.
Aiming at the situation of ties of order-inducing variables, i.e., Hamming distance measures, in the DIFOWA or WDIFOWA operator, we replace the argument variables having tied order-inducing variables by their average [14]. Assume there are \(m\) DIFOWA pairs \(\left\langle {u_{1} ,\tilde{x}_{1} } \right\rangle ,\left\langle {u_{2} ,\tilde{x}_{2} } \right\rangle , \ldots ,\left\langle {u_{m} ,\tilde{x}_{m} } \right\rangle\) and \(u_{1} = u_{2} = \cdots = u_{m}\), we replace \(\tilde{x}_{1} ,\tilde{x}_{2} , \ldots ,\tilde{x}_{m}\) by their average \(\tilde{x}\) such that
3.2 The Distance Induced Generalized Fuzzy OWA operator
We further generalize the DIFOWA and the WDIFOWA operators with generalized means. So, the distance induced generalized fuzzy OWA (DIGFOWA) and the weighted distance induced generalized fuzzy OWA (WDIGFOWA) operators are obtained.
Definition 9
Let \(\Omega\) be the set of triangular fuzzy numbers, a DIGFOWA operator of dimension \(n\) is defined as a mapping \(f_{{DIGFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with an associated weighting vector \(W = \left( {\omega _{1} ,\omega _{2} , \ \ldots ,\omega _{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\) and \(\omega _{i} > 0\) for all \(i = 1,2,\ \ldots ,n\), according to Eq. (13)
where \(\tilde{b}_{j}\) is the \(\tilde{x}_{i}\) value in the DIGFOWA pair \(\left\langle {v_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(v_{i}\), \(v_{i}\) is the order-inducing variable determined by Eq. (6), \(\tilde{x}_{i}\) is the argument variable, and \(\lambda \in \left( { - \infty , + \infty } \right)\) is a parameter.
If the sum of \(W\) not equals to 1, the DIGFOWA operator is defined in the following.
Definition 10
Let \(\Omega\) be the set of triangular fuzzy numbers, a DIGFOWA operator of dimension \(n\) is defined as a mapping \(f_{{DIGFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with an associated weighting vector \(W = \left( {\omega _{1} ,\omega _{2} ,\ \ldots ,\omega _{n} } \right)\) such that \(\omega _{i} > 0\) for all \(i = 1,2,\ \ldots ,n\), we have.
where \(\tilde{b}_{j}\) is the \(\tilde{x}_{i}\) value in the DIGFOWA pair \(\left\langle {v_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(v_{i}\), \(v_{i}\) is the order-inducing variable determined by Eq. (6), \(\tilde{x}_{i}\) is the argument variable, and \(\lambda \in \left( { - \infty , + \infty } \right)\) is a parameter.
It is easy to find that the DIFOWA operator is obtained from the DIGFOWA operator when \(\lambda = 1\). Some special cases can also be obtained from the DIGFOWA operator by choosing different parameters \(\lambda\).
Remark 1
The distance induced fuzzy OWG (DIFOWG) operator is obtained if \(\lambda = 0\). The distance induced fuzzy OWQA (DIFOWQA) operator is obtained if \(\lambda = 2\). The distance induced fuzzy OWHA (DIFOWHA) operator is obtained if \(\lambda = - 1\).
The WDIFOWA operator can also be generalized in the same way using generalized means. So, the weighted distance induced generalized fuzzy OWA (WDIGFOWA) operator is obtained.
Definition 11
Let \(\Omega\) be the set of triangular fuzzy numbers, a WDIGFOWA operator of dimension \(n\) is defined as a mapping \(f_{{WDIGFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with two associated weighting vectors \(W_{1} = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) and \(W_{2} = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\), \(\sum\nolimits_{{i = 1}}^{n} {w_{i} } = 1\) and \(\omega _{i} > 0\), \(w_{i} > 0\) for all \(i = 1,2, \ldots ,n\), we have.
where \(\tilde{c}_{j}\) is the \(\tilde{x}_{i}\) value in the WDIGFOWA pair \(\left\langle {u_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(u_{i}\), \(u_{i}\) is the order-inducing variable determined by Eq. (8), \(\tilde{x}_{i}\) is the argument variable, and \(\lambda \in \left( { - \infty , + \infty } \right)\) is a parameter.
If \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } \ne 1\) and \(\sum\nolimits_{{i = 1}}^{n} {w_{i} } \ne 1\), the WDIGFOWA operator is defined as follows.
Definition 12
Let \(\Omega\) be the set of triangular fuzzy numbers, a WDIGFOWA operator of dimension \(n\) is defined as a mapping \(f_{{WDIGFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with two associated weighting vectors \(W_{1} = \left( {\omega _{1} ,\omega _{2} ,\ \ldots \,\omega _{n} } \right)\) and \(W_{2} = \left( {w_{1} ,w_{2} , \ \ldots \, w_{n} } \right)\) such that \(\omega _{i} > 0\), \(w_{i} > 0\) for all \(i = 1,2,\ \ldots \,n\), we have
where \(\tilde{c}_{j}\) is the \(\tilde{x}_{i}\) value in the WDIGFOWA pair \(\left\langle {u_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(u_{i}\), \(u_{i}\) is the order-inducing variable determined by Eq. (10), \(\tilde{x}_{i}\) is the argument variable, and \(\lambda \in \left( { - \infty , + \infty } \right)\) is a parameter.
It is easy to find that the WDIFOWA operator is obtained from the WDIGFOWA operator when \(\lambda = 1\). Some special cases can also be obtained from the WDIGFOWA operator by choosing different parameters \(\lambda\).
Remark 2
The weighted distance induced fuzzy OWG (WDIFOWG) operator is obtained if \(\lambda = 0\). The weighted distance induced fuzzy OWQA (WDIFOWQA) operator is obtained if \(\lambda = 2\). The weighted distance induced fuzzy OWHA (WDIFOWHA) operator is obtained if \(\lambda = - 1\).
It is easy to find that the DIGFOWA and the WDIGFOWA operators are the general forms of the DIFOWA and the WDIFOWA operators, respectively.
3.3 The Distance Induced Quasi Fuzzy OWA operator
We also suggest the quasi-DIFOWA and the quasi-WDIFOWA operators, respectively.
Definition 13
Let \(\Omega\) be the set of triangular fuzzy numbers, a quasi-DIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{QDIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with an associated weighting vector \(W = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\) and \(\omega _{i} > 0\) for all \(i = 1,2, \ \ldots\ ,n\), according to the following formula
where \(\tilde{b}_{j}\) is the \(\tilde{x}_{i}\) value in the QDIFOWA pair \(\left\langle {v_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(v_{i}\), \(v_{i}\) is the order-inducing variable determined by Eq. (6), \(\tilde{x}_{i}\) is the argument variable, and \(g\) is a strictly continuous monotonic function.
Similarly, if the weighting vector \(W\) does not satisfy \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\), we define the quasi-DIFOWA operator as follows.
Definition 14
Let \(\Omega\) be the set of triangular fuzzy numbers, a quasi-DIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{QDIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with an associated weighting vector \(W = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) such that \(\omega _{i} > 0\) for all \(i = 1,2, \ldots ,n\), according to the following formula.
where \(\tilde{b}_{j}\) is the \(\tilde{x}_{i}\) value in the QDIFOWA pair \(\left\langle {v_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(v_{i}\), \(v_{i}\) is the order-inducing variable determined by Eq. (6), \(\tilde{x}_{i}\) is the argument variable, and \(g\) is a strictly continuous monotonic function.
Remark 3
If \(g\left( {\tilde{x}} \right) = \tilde{x}^{\lambda }\), the DIGFOWA operator is derived.
Remark 4
If \(g\left( {\tilde{x}} \right) = \tilde{x}\), the DIFOWA operator is derived.
Definition 15
Let \(\Omega\) be the set of triangular fuzzy numbers, a quasi-WDIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{QWDIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with two associated weighting vectors \(W_{1} = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) and \(W_{2} = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\), \(\sum\nolimits_{{i = 1}}^{n} {w_{i} } = 1\) and \(\omega _{i} > 0\), \(w_{i} > 0\) for all \(i = 1,2, \ldots ,n\), according to the following formula.
where \(\tilde{c}_{j}\) is the \(\tilde{x}_{i}\) value in the QWDIFOWA pair \(\left\langle {u_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(u_{i}\), \(u_{i}\) is the order-inducing variable determined by Eq. (8), \(\tilde{x}_{i}\) is the argument variable, and \(g\) is a strictly continuous monotonic function.
Similarly, if the weighting vectors \(W_{1}\) and \(W_{2}\) do not satisfy \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\) and \(\sum\nolimits_{{i = 1}}^{n} {w_{i} } = 1\), we define the quasi-WDIFOWA operator as follows.
Definition 16
Let \(\Omega\) be the set of triangular fuzzy numbers, a quasi-WDIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{QWDIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with two associated weighting vectors \(W_{1} = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) and \(W_{2} = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)\) such that \(\omega _{i} > 0\) and \(w_{i} > 0\) for all \(i = 1,2, \ldots ,n\), according to Eq. (20)
where \(\tilde{c}_{j}\) is the \(\tilde{x}_{i}\) value in the QWDIFOWA pair \(\left\langle {u_{j} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(u_{i}\), \(u_{i}\) is the order-inducing variable determined by Eq. (10), \(\tilde{x}_{i}\) is the argument variable, and \(g\) is a strictly continuous monotonic function.
Remark 5
If \(g\left( {\tilde{x}} \right) = \tilde{x}^{\lambda }\), the WDIGFOWA operator is derived.
Remark 6
If \(g\left( {\tilde{x}} \right) = \tilde{x}\), the WDIFOWA operator is derived.
We can even define the quasi-DIOWA and the quasi-WDIOWA operators by considering another strictly continuous monotonic function \(k\) to determine the order-inducing variables \(v_{i}^{*}\) or \(u_{i}^{*}\).
Definition 17
Let \(\Omega\) be the set of triangular fuzzy numbers, a quasi-DIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{QDIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with an associated weighting vector \(W = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\) and \(\omega _{i} > 0\) for all \(i = 1,2, \ldots ,n\), according to Eq. (21)
where \(\tilde{b}_{j}\) is the \(\tilde{x}_{i}\) value in the QDIFOWA pair \(\left\langle {v_{j}^{*} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(v_{i}^{*}\), \(v_{i}^{*}\) is the order-inducing variable determined by Eq. (22), \(\tilde{x}_{i}\) is the argument variable, and \(g\) is a strictly continuous monotonic function.
here, \(v_{i}\) is determined by Eq. (8) and \(k\) is a strictly continuous monotonic function.
Definition 18
Let \(\Omega\) be the set of triangular fuzzy numbers, a quasi-WDIFOWA operator of dimension \(n\) is defined as a mapping \(f_{{QWDIFOWA}} :\Omega ^{n} \times \Omega ^{n} \to \Omega\) with two associated weighting vectors \(W_{1} = \left( {\omega _{1} ,\omega _{2} , \ldots ,\omega _{n} } \right)\) and \(W_{2} = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)\) such that \(\sum\nolimits_{{i = 1}}^{n} {\omega _{i} } = 1\), \(\sum\nolimits_{{i = 1}}^{n} {w_{i} } = 1\) and \(\omega _{i} > 0\), \(w_{i} > 0\) for all \(i = 1,2, \ldots ,n\), according to Eq. (23)
where \(\tilde{c}_{j}\) is the \(\tilde{x}_{i}\) value in the QWDIFOWA pair \(\left\langle {u_{j}^{*} ,\tilde{x}_{j} } \right\rangle\) with the \(j\) th largest value of \(u_{i}^{*}\), \(u_{i}^{*}\) is the order-inducing variable determined by Eq. (24), \(\tilde{x}_{i}\) is the argument variable, and \(g\) is a strictly continuous monotonic function.
here, \(u_{i}\) is determined by Eq. (8) and \(k\) is a strictly continuous monotonic function.
4 Three Different Frameworks of MCGDM Methods
In this section, we will research how to use the proposed distance induced fuzzy operators in MCGDM problems. Aiming at three different decision-making situations that will happen in MCGDM, we will construct three frameworks of MCGDM methods, respectively. The three decision-making situations are illustrated in the following.
Situation I. The information of every alternative is given by every DM, and every DM constructs an ideal alternative, respectively. The distance induced fuzzy operators are used to aggregating the information afforded by every DM, respectively.
Situation II. The information of every alternative is given by every DM, respectively, and a unique ideal alternative is constructed by all DMs. The distance induced fuzzy operators are used to aggregating the information afforded by every DM, respectively.
Situation III. The information of every alternative is given by every DM, respectively, and a unique ideal alternative is constructed by all DMs. The information afforded by all DMs is firstly aggregated to group information, and then, the distance induced fuzzy operators are used to aggregating the group information.
4.1 The Framework for Situation I
The detailed steps of the framework for situation I are shown as follows.
Step 1. Obtain all the individual matrices. Let \(o_{1} ,o_{2} , \ldots ,o_{p}\) represent \(p\) alternatives, \(x_{1} ,x_{2} , \ldots ,x_{n}\) represent \(n\) attributes, \(s_{1} ,s_{2} , \ldots ,s_{m}\) represent \(m\) DMs. The individual decision-making matrix of every DM is shown as Eq. (25).

where \(E_{k}\) represents the individual decision-making matrix of \(s_{k}\), \(x_{{ij}}^{k}\) represent the entries of \(E_{k}\).
Step 2. Construct all the individual ideal alternatives. Let \(o_{k}^{*} = \left\{ {x_{1}^{{k*}} ,x_{2}^{{k*}} , \ldots ,x_{n}^{{k*}} } \right\}\) be the ideal alternative given by \(s_{k}\), \(x_{j}^{{k*}}\) represents the corresponding attribute value of \(x_{j}\).
Step 3. Choose one distance induced fuzzy operator. In this step, every DM chooses one distance induced fuzzy operator based on their preference. In this step, all the operators chosen by all DMs can be the same or different.
Step 4. Calculate order-inducing variables between individual alternatives and the individual ideal alternative for every DM, respectively. According to the distance induced fuzzy operator selected by every DM, choose the associated method to calculate the Hamming distances (order-inducing variables).
Step 5. Aggregate the information of every DM with associated distance induced fuzzy operator, respectively. In this step, the aggregation result of every DM concerning every alternative can be obtained. Assume \(y_{{ik}}\) represents the aggregation result of alternative \(o_{i}\) from DM \(s_{k}\) obtained with the corresponding distance induced fuzzy operator.
Step 6. Calculate the final evaluation result of every alternative. Assume \(y_{i}\) represents the final evaluation result of \(o_{i}\), \(f\) represents an aggregation method, such as the OWA operator, and so on. \(y_{i}\) is obtained using Eq. (26).
Step 7. Rank all the alternatives and make a decision. Generally, the best alternative is the one with the maximal evaluation result or the one with the minimal evaluation result related to the aggregation method \(f\) selected.
4.2 The Framework for Situation II
The detailed steps of the framework for situation II are shown in the following.
Step 1. Obtain all the individual matrices. This step is the same as step 1 in Sect. 4.1.
Step 2. Construct a unique ideal alternative. According to the discussion of all DMs, only one ideal alternative is built. Assume \(o^{*} = \left\{ {x_{1}^{*} ,x_{2}^{*} , \ldots ,x_{n}^{*} } \right\}\) represents the ideal alternative, in which \(x_{j}^{*}\) is the corresponding value of \(x_{j}\), \(j = 1,2, \ldots ,n\).
Step 3. Choose one appropriate distance induced fuzzy operator. According to the preference and opinions, every DM only chooses one distance induced fuzzy operator. In this step, all the operators chosen by all DMs can be the same or different.
Step 4. Calculate the order-inducing variables. Based on the distance induced fuzzy operator chosen by every DM, all the order-inducing variables for the decision-making matric of every DM can be obtained by selecting the corresponding distance measure method.
Step 5. Calculate the evaluation result of every DM for every alternative. According to the order-inducing variables obtained, aggregate every individual decision matrix using corresponding distance induced fuzzy operator to get the evaluation result of every DM for every alternative.
Step 6. Aggregate individual evaluation results to final evaluation results. Aggregating the evaluation results of the same alternative of all DMs to a final evaluation result. Assume \(y_{{ik}}\) represents the evaluation result of \(o_{i}\) given by \(s_{k}\), \(y_{i}\) represents the final evaluation result of \(o_{i}\). \(y_{i}\) is determined by Eq. (27).
where \(g\) represents any aggregation function.
Step 7. Rank all the alternatives and make a decision. According to the aggregation function selected, rank all the alternatives. Generally, the best alternative is the one with either the maximal evaluation result or the minimal evaluation result.
4.3 The Framework for Situation III
The detailed steps of the framework for situation III are shown in the following.
Step 1. Obtain all the individual matrices. This step is the same as step 1 in Sect. 4.1.
Step 2. Construct a unique ideal alternative. This step is the same as step 2 in Sect. 4.2.
Step 3. Aggregate all the individual matrices into a group matrix. The group matric is shown as follows.

where \(E\) represents the group matrix, \(x_{{ij}}\) represents the collective attribute value of \(x_{j}\) for \(o_{i}\). Assume \(h\) represents any aggregation function, the value \(x_{{ij}}\) is determined by Eq. (29).
Step 4. Choose one appropriate distance induced fuzzy operator. This step is the same as step 3 in Sect. 4.2.
Step 5. Calculate all the order-inducing variables. Based on the group matrix obtained, the ideal alternative, and the distance induced fuzzy operator selected by every DM, use the corresponding distance measure function to calculate all the order-inducing variables.
Step 6. Calculate all the individual evaluation results. Aggregate the information of every alternative in the group matrix with corresponding distance induced fuzzy operator selected by every DM, respectively.
Step 7. Calculate the final evaluation results. Aggregate the evaluation results of every alternative given by all DMs to a final evaluation result. Assume \(\hat{y}_{{ik}}\) represents the evaluation result of \(o_{i}\) given by \(s_{k}\), \(\hat{y}_{i}\) represents the final evaluation result of \(o_{i}\). \(\hat{y}_{i}\) is determined by Eq. (30).
where \(l\) represents any aggregation function.
Step 8. Rank all the alternatives and make a decision. According to the aggregation function selected, rank all the alternatives. Generally, the best alternative is the one with either the maximal evaluation result or the minimal evaluation result.
5 Numerical Example
The proposed distance induced fuzzy operators in this paper can be used in numerous applications, such as multi-criteria decision-making, economic evaluation, supply chain management, and so on. In this section, we discuss an MCGDM problem using the DIFOWA operator and frameworks for situations II and III.
Suppose a company needs to employ a manager to lead the sales department according to its development status. After deep consideration, one of four candidates (\(o_{1}\), \(o_{2}\), \(o_{3}\) and \(o_{4}\)) will be considered to take this managerial position. These four candidates are evaluated from five attributes which are work experience (\(x_{1}\)), sales ability (\(x_{2}\)), leadership (\(x_{3}\)), knowledge level (\(x_{4}\)), and learning ability (\(x_{5}\)). To select the best candidate, four experts from different sales companies are invited to help to make the final decision. Assume these four experts are \(s_{1}\), \(s_{2}\), \(s_{3}\) and \(s_{4}\). The weights of these four experts are 0.20, 0.30, 0.25, 0.25, respectively. For the complexity of this decision-making problem, experts cannot express their opinion through crisp numbers, but they can give an interval and modal value regarding every attribute of every candidate so that it is suitable for experts to use triangular fuzzy numbers to express their opinions. Therefore, four experts constructed individual decision-making matrices \(E_{k}\) (\(k = 1,2,3,4\)), respectively, shown as follows. A reference alternative \(o^{*}\) also represented by triangular fuzzy numbers is built shown in Table 1 after discussion by these four experts. In this numerical example, the weights of five attributes are 0.23, 0.14, 0.18, 0.25 and 0.5, respectively. We will use the frameworks of MCGDM methods for situations II and III to make a decision, respectively.

5.1 Use the Framework for Situation II to Make a Decision
According to the framework for situation II and the known information, the detailed decision-making steps are shown as follows. Assume all the experts select the DIFOWA operator in this numerical example.
Step 1. According to Eq. (6), calculate all the order-inducing variables listed in Tables 2, 3, 4, 5 according to \(E_{1}\), \(E_{{\text{2}}}\), \(E_{{\text{3}}}\), \(E_{{\text{4}}}\) and Table 1, respectively.
Step 2. Reference the calculation process of the DIFOWA operator and the values obtained in Tables 2, 3, 4, 5, calculate the evaluation result of every candidate for every expert shown in Table 6.
Step 3. Aggregate the evaluation results of every candidate given by all experts to a final evaluation result. In this step, the following information aggregation method, i.e., Eq. (31), is used. The results are shown in Table 7.
Step 4. Convert all the final evaluation results to crisp numbers according to Eq. (11) by calculating their graded mean values. The corresponding crisp evaluation numbers for these four candidates are shown in Table 8.
Step 5. Rank these four crisp evaluation numbers in descending order, we have 82.41 > 82.21 > 82.20 > 82.03, i.e., \(o_{4} \succ o_{2} \succ o_{1} \succ o_{3}\). So, the best candidate is \(o_{4}\).
We also replace the DIFOWA operator with another six operators, respectively. And corresponding evaluation results and ranks as listed in Tables 9, 10.
5.2 Use the Framework for Situation III to Make a DECISION
According to the framework for situation III and the known information, the detailed decision-making steps are shown as follows. Same, assume the DIFOWA operator is selected by all experts in this numerical example.
Step 1. Calculate the group matrix \(E\) which is shown in the following. In this step, the following information aggregation method, i.e., Eq. (32), is used.
Step 2. According to Eq. (6), calculate the results of all the order-inducing variables shown in Table 11 according to the matrix \(E\) and the reference alternative.
Step 3. Reference the calculation process of the DIFOWA operator and the values obtained in Table 11, calculate the evaluation result of every candidate shown in Table 12.
Step 4. Convert the evaluation results shown in Table 12 to crisp evaluation numbers based on Eq. (11) by calculating their graded mean values to obtain the results shown in Table 13.
Step 5. Rank these crisp evaluation numbers in descending order, we have 82.44 > 82.24 > 82.13 > 82.10, i.e., \(o_{4} \succ o_{2} \succ o_{3} \succ o_{1}\). So, the best candidate is \(o_{4}\).
Similarly, we also replace the DIFOWA operator with another six operators, respectively. And corresponding evaluation results and ranks are shown in Tables 14, 15.
5.3 Comparison Analysis of Different MCGDM Methods
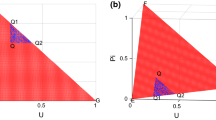
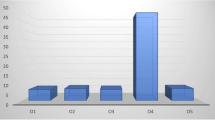
Many MCGDM methods with aggregation operators belong to one of the three proposed frameworks in which the distance induced fuzzy operators are replaced by other aggregation operators. Therefore, we replace the distance induced fuzzy operators with other aggregation operators to finish the comparison analysis of our proposed MCGDM methods with other MCGDM methods. Aiming at the frameworks for situations II and III, we consider six different MCGDM methods with Max D, Min D, FNHD, FWHD, FOWA, FOWAD operators, respectively. The corresponding comparison figures of ranks of four candidates with different MCGDM methods are shown as follows.
Aiming at the MCGDM methods according to the framework for situation II, from Table 10 and Fig. 1, we can easily find that the rank of the MCGDM method with the DIFOWA operator is only the same as the MCGDM method with the FNHD operator, totally different from the MCGDM methods with the other five operators. Aiming at the MCGDM methods according to the framework for situation III, from Table 15 and Fig. 2, we can easily find that the rank of the MCGDM method with the DIFOWA operator is different from the MCGDM methods with the other six operators. It means that the DIFOWA operator provides more selections for DMs to consider. We further conclude that the ranks of the MCGDM methods with the fuzzy aggregation operators in which distance measures are regarded as order-inducing variables are almost different from the ranks of the MCGDM methods with the fuzzy distance aggregation operators in which distance measures are taken as argument variables. Therefore, all the distance induced fuzzy operators proposed in this paper can afford more selections for DMs to select.
Noted that the rank of the MCGDM method with the DIFOWA operator in Sect. 5.1 is different from the rank of the MCGDM method with the DIFOWA operator in Sect. 5.2. It means that using the same distance induced fuzzy aggregation operator to deal with the same MCGDM problem will lead to different decisions. Therefore, aiming at the different functions of a distance induced fuzzy operator play in an MCGDM problem, it is extremely necessary to construct different frameworks of MCGDM methods for DMs to select.
In real applications, the preference, the interest, and the opinions of DMs should be considered to decide to select which distance induced operator or operators and framework of MCGDM methods to make a decision.
6 Conclusions
In this manuscript, to consider an ideal alternative in the process of fuzzy information aggregation, we combine distance measures with the induced ordered weighted averaging (IOWA) operator and triangular fuzzy numbers to propose some distance induced fuzzy aggregation operators. Compared with the existing fuzzy distance aggregation operators, the distinctive feature of our proposed operators is that the distance measures between an evaluated alternative and an ideal alternative are taken as order-inducing variables rather than argument variables. This way leads to a benefit that DMs can consider other variables as argument variables. We have proposed the DIFOWA and WDIFOWA operators and analyzed their properties. We have also extended the DIFOWA and WDIFOWA operators using generalized means and quasi arithmetic means and proposed the DIGFOWA, the WDIGFOWA, the quasi-DIFOWA, and the quasi-WDIFOWA operators, respectively.
To use the proposed distance induced fuzzy aggregation operators to solve MCGDM problems, we have constructed three different frameworks of MCGDM methods for three different decision-making situations, respectively. From the analysis of the numerical example and comparison with the MCGDM methods using some other fuzzy distance aggregation operators, we have seen that the MCGDM methods with proposed distance induced fuzzy aggregation operators afford more scenarios for DMs so that DMs have more selection to express their judgments accurately. We also found that using the proposed operators to aggregate different information in the same MCGDM problem probably lead to different decision-making conclusions. Therefore, our research about constructing different frameworks of MCGDM methods with the same distance induced fuzzy operator is extremely necessary, so that DMs will further make better decision-making.
Because an ideal alternative is needed when using the proposed distance induced fuzzy operators, how to select or construct a reasonable ideal alternative is a key issue to pay attention to. Furthermore, our proposed operators only deal with uncertain information represented by triangular fuzzy numbers so that they will fail in aggregating uncertain information represented by other kinds of fuzzy numbers. Therefore, in the future, we will explore the scientific methods to determine an ideal alternative for our proposed aggregation operators. And we will further research some other distance induced aggregation operators with different fuzzy numbers, including intuitionistic fuzzy numbers, Pythagorean fuzzy numbers, interval 2-tuple linguistic fuzzy numbers, and the like. We will also explore applying the proposed distance induced fuzzy aggregation operators with other typical decision-making methods, such as the TOPSIS method, the entropy method, and so on, to solve decision-making problems in reality.
References
Chao, X.R., Kou, G., Peng, Y., Viedma, E.H.: Large-scale group decision-making with non-cooperative behaviors and heterogeneous preferences: an application in financial inclusion. Eur. J. Oper. Res. 288, 271–293 (2021)
Wu, S.Q., Wu, M., Dong, Y.C., Liang, H.M., Zhao, S.H.: The 2-rank additive model with axiomatic design in multiple attribute decision making. Eur. J. Oper. Res. 287, 536–545 (2020)
Mohamadghasemi, A., Hadi-Vencheh, A., Lotfi, F.H.: The multiobjective stochastic CRITIC-TOPSIS approach for ssolving the shipboard crane selection problem. Int. J. Intell. Syst. 35, 1570–1598 (2020)
Aydogdu, A., Gul, S.: A novel entropy proposition for spherical fuzzy sets and its application in multiple attribute decision-making. Int. J. Intell. Syst. 35, 1354–1374 (2020)
Koksalmis, E., Kabak, O.: Sensor fusion based on Dempster-Shafer theory of evidence using a large scale group decision making approach. Int. J. Intell. Syst. 35, 1126–1162 (2020)
Zou, X.Y., Chen, S.M., Fan, K.Y.: Multiple attribute decision making using improved intuitionistic fuzzy weighted geometric operators of intuitionistic fuzzy values. Inform. Sci. 535, 242–253 (2020)
Yi, P.T., Wang, L., Li, W.W.: Density-clusters ordered weighted averaging operator based on generalized trapezoidal fuzzy numbers. Int. J. Intell. Syst. 34, 2970–2987 (2019)
Ashraf, S., Abdullah, S., Mahmood, T.: Spherical fuzzy Dombi aggregation operators and their application in group decision making problems. J. Amb. Intel. Hum. Comp. 11, 2731–2749 (2020)
Qin, Y.C., Qi, Q.F., Scott, P.J., Jiang, X.Q.: Multiple criteria decision making based on weighted Archimedean power partitioned Bonferroni aggregation operators of generalised orthopair membership grades. Soft. Comput. 24, 12329–12355 (2020)
Yang, Z.L., Ouyang, T.X., Fu, X.L., Peng, X.D.: A decision-making algorithm for online shopping using deep-learning-based opinion pairs mining and q-rung orthopair fuzzy interaction Heronian mean operators. Int. J. Intell. Syst. 35, 783–825 (2020)
Yager, R.R.: On ordered weighted averaging aggregation operators in multi-criteria decision making. IEEE. Trans. Syst. Man. Cybernet. 18, 183–190 (1988)
Yager, R.R., Filev, D.P.: Induced ordered weighted averaging operators. IEEE. Trans. Syst. Man. Cy. B. 29, 141–150 (1999)
Beliakov, G.: Learning weights in the generalized OWA operators. Fuzzy. Optim. Decis. Ma. 4, 119–130 (2009)
Merigó, J.M., Gil-Lafuente, A.M.: The induced generalized OWA operator. Inform. Sci. 179, 729–741 (2009)
Merigó, J.M.: Probabilities in the OWA operator. Expert. Syst. Appl. 39, 11456–11467 (2012)
Merigó, J.M.: Decision-making under risk and uncertainty and its application in strategic management. J. Bus. Econ. Manag. 16, 93–116 (2015)
Yager, R.R.: Heavy OWA operators. Fuzzy. Optim. Decis. Ma. 1, 379–397 (2002)
Merigó, J.M., Casanovas, M.: Induced and uncertain heavy OWA operators. Comput. Ind. Eng. 60, 106–116 (2011)
Riaz, M., Hashmi, M.R.: Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems J. . Intell. Fuzzy. Syst. 37, 5417–5439 (2019)
Hashmi, M.R., Riaz, M., Smarandache, F.: m-polar neutrosophic generalized weighted and m-polar neutrosophic generalized Einstein weighted aggregation operators to diagnose coronavirus (COVID-19). J. Intell. Fuzzy. Syst. 39, 7381–7401 (2020)
Riaz, M., Hashmi, M.R., Kalsoom, H., Pamucar, D., Chu, Y.M.: Linear Diophantine fuzzy soft rough sets for the selection of sustainable material handling equipment. Symmetry-Basel. 12, 1215 (2020)
He, W., Dutta, B., Rodriguez, R.M., Alzahrani, A.A., Martinez, L.: Induced OWA operator for group decision making dealing with extended comparative linguistic expressions with symbolic translation. Math. 9, 20 (2021)
Xu, Z.S., Da, Q.L.: The uncertain OWA operator. Int. J. Intell. Syst. 17, 569–575 (2002)
Xu, Z.S.: Induced uncertain linguistic OWA operators applied to group decision making. Inform. Fusion. 7, 231–238 (2006)
Merigó, J.M., Casanovas, M.: The fuzzy generalized OWA operator and its application in strategic decision making. Cybernet. Syst. 41, 359–370 (2010)
Merigó, J.M., Gil-Lafuente, A.M.: Fuzzy induced generalized aggregation operators and its application in multi-person decision making. Expert. Syst. Appl. 38, 9761–9772 (2011)
Merigó, J.M., Casanovas, M.: Decision making with fuzzy induced heavy ordered weighted averaging operators. Int. J. Fuzzy. Syst. 16, 277–289 (2014)
Hamming, R.W.: Error-detecting and error-correcting codes. Bell. Syst. Tech. J. 29, 147–160 (1950)
Li, C.Q., Zhao, H., Xu, Z.S.: Hesitant fuzzy psychological distance measure. Int. J. Mach. Learn. Cyb. 11, 2089–2100 (2020)
Xu, Z.S., Xia, M.M.: Distance and similarity measures for hesitant fuzzy sets. Inform. Sci. 181, 2128–2138 (2011)
Riaz, M., Naeem, K., Afzal, D.: A similarity measure under Pythagorean fuzzy soft environment with applications. Comput. Appl. Math. 39, 269 (2020)
Ozlu, S., Karaaslan, F.: Some distance measures for type 2 hesitant fuzzy sets and their applications to multi-criteria group decision-making problems. Soft. Comput. 24, 9965–9980 (2020)
Zeng, W.Y., Li, D.Q., Yin, Q.: Distance and similarity measures of Pythagorean fuzzy sets and their applications to multiple criteria group decision making. Int. J. Intell. Syst. 33, 2236–2254 (2018)
Labella, A., Liu, H., Rodríguez, R.M., Martínez, L.: A cost consensus metric for consensus reaching processes based on a comprehensive minimum cost model. Eur. J. Oper. Res. 281, 316–331 (2020)
Merigó, J.M., Gil-Lafuente, A.M.: New decision-making techniques and their application in the selection of financial products. Inform. Sci. 180, 2085–2094 (2010)
Merigó, J.M., Casanovas, M.: Decision-making with distance measures and induced aggregation operators. Comput. Ind. Eng. 60, 66–76 (2011)
Merigó, J.M., Xu, Y.J., Zeng, S.Z.: Group decision making with distance measures and probabilistic information. Knowl-Based. Syst. 40, 81–87 (2013)
Casanovas, M., Torres-Martinez, A., Merigó, J.M.: Decision making in reinsurance with induced OWA operators and Minkowski distances. Cybernet. Syst. 47, 460–477 (2016)
Merigó, J.M., Casanovas, M., Zeng, S.Z.: Distance measures with heavy aggregation operators. Appl. Math. Model. 38, 3142–3153 (2014)
Merigó, J.M., Casanovas, M.: Induced aggregation operators in the Euclidean distance and its application in financial decision making. Expert. Syst. Appl. 38, 7603–7608 (2011)
Merigó, J.M., Casanovas, M.: A new Minkowski distance based on induced aggregation operators. Int. J. Comput. Int. Sys. 4, 123–133 (2011)
Merigó, J.M., Casanovas, M.: Induced and heavy aggregation operators with distance measures. J. Syst. Eng. Electron. 21, 431–439 (2010)
Wang, J.S., Cao, C.D., Zeng, S.Z., Balezentis, T.: Weighted induced aggregation Euclidean distance operators for the decision making of robot selection. Transform. Bus. Econ. 18, 81–94 (2019)
Merigó, J.M., Casanovas, M.: Decision making with distance measures and linguistic aggregation operators. Int. J. Fuzzy. Syst. 12, 190–198 (2010)
Zeng, S.Z., Merigó, J.M., Su, W.H.: Intuitionistic fuzzy ordered weighted distance operator. Knowl-Based. Syst. 24, 1224–1232 (2011)
Zeng, S.Z.: An extension of OWAD operator and its application to uncertain multiple-attribute group decision-making. Cybernet. Syst. 47, 363–375 (2016)
Zeng, S.Z., Merigó, J.M., Su, W.H.: The uncertain probabilistic OWA distance operator and its application in group decision making. Appl. Math. Model. 37, 6266–6275 (2013)
Su, W.H., Zeng, S.Z., Ye, X.J.: Uncertain group decision-making with induced aggregation operators and Euclidean distance. Technol. Econ. Dev. Eco. 19, 431–447 (2013)
Xian, S.D., Sun, W.J.: Fuzzy linguistic induced Euclidean OWA distance operator and its application in group linguistic decision making. Int. J. Intell. Syst. 29, 478–491 (2014)
Xian, S.D., Sun, W.J., Xu, S.H., Gao, Y.Y.: Fuzzy linguistic induced OWA Minkowski distance operator and its application in group decision making. Pattern. Anal. Appl. 19, 325–335 (2016)
Li, C.G., Zeng, S.Z., Pan, T.J.: A method based on induced aggregation operators and distance measures to multiple attribute decision making under 2-tuple linguistic environment. J. Comput. Syst. Sci. 80, 1339–1349 (2014)
Zeng, S.Z., Su, W.H., Chen, J.: Fuzzy decision making with induced heavy aggregation operators and distance measures. J. Intell. Fuzzy. Syst. 26, 127–135 (2014)
Chen, J., Zeng, S.Z., Zhang, C.H.: An OWA Distance-Based, Single-valued neutrosophic linguistic TOPSIS approach for green supplier evaluation and selection in low-carbon supply chains. Int. J. Env. Res. Pub. He. 15, 1439–1453 (2018)
Su, W.H., Li, W., Zeng, S.Z., Zhang, C.H.: Atanassov’s intuitionistic linguistic ordered weighted averaging distance operator and its application to decision making. J. Intell. Fuzzy. Syst. 26, 1491–1502 (2014)
Aviles-Ochoa, E., Leon-Castro, E., Perez-Arellano, L.A., Merigó, J.M.: Government transparency measurement through prioritized distance operators. J. Intell. Fuzzy. Syst. 34, 2783–2794 (2018)
Xian, S.D., Xiao, Y., Li, L., Yu, D.X.: Trapezoidal Pythagorean fuzzy linguistic entropic combined ordered weighted Minkowski distance operator based on preference relations. Int. J. Intell. Syst. 34, 2196–2224 (2019)
Xian, S.D., Zhang, J.F., Xue, W.T.: Fuzzy linguistic induced generalized OWA operator and its application in fuzzy linguistic decision making. Int. J. Intell. Syst. 31, 749–762 (2016)
Acknowledgements
This study was supported by the National Natural Science Foundation of China (71901079, 72001151), the Heilongjiang Philosophy and Social Sciences Research Planning Project (19GLC166), the Fundamental Research Funds for the Central Universities (3072021CFW0902), the Natural Science Foundation of Liaoning Province (2020-BS-160), the Shandong Natural Science Foundation of China (ZR2019PG001) and the Scientific Research Foundation of Shandong University of Science and Technology for Recruited Talents (2017RCJJ021).
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Gong, C., Jiang, L. & Hou, L. Group Decision-Making with Distance Induced Fuzzy Operators. Int. J. Fuzzy Syst. 24, 440–456 (2022). https://doi.org/10.1007/s40815-021-01146-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-021-01146-2