Abstract
This paper is devoted to the numerical analysis of non-smooth ensemble optimal control problems governed by the Liouville (continuity) equation that have been originally proposed by R.W. Brockett with the purpose of determining an efficient and robust control strategy for dynamical systems. A numerical methodology for solving these problems is presented that is based on a non-smooth Lagrange optimization framework where the optimal controls are characterized as solutions to the related optimality systems. For this purpose, approximation and solution schemes are developed and analysed. Specifically, for the approximation of the Liouville model and its optimization adjoint, a combination of a Kurganov–Tadmor method, a Runge–Kutta scheme, and a Strang splitting method are discussed. The resulting optimality system is solved by a projected semi-smooth Krylov–Newton method. Results of numerical experiments are presented that successfully validate the proposed framework.
Similar content being viewed by others
1 Introduction
The ensemble control problems considered in this paper were proposed by Brockett [7,8,9] to design efficient and robust control strategies for steering ensembles of trajectories of dynamical systems in a desired way. For this purpose, the adequate model governing the evolution of the ensembles expressed in terms of a density is the hyperbolic Liouville (continuity) equation. In application, this ensemble may represent the probability density of trajectories of multiple trials of a dynamical system with the initial conditions specified by a distribution function, or the physical density of multiple non-interacting systems (e.g., particles). In both cases, the function that determines the dynamics of these systems appears as the drift coefficient of the Liouville equation. Therefore, the Liouville framework allows to lift the problem of controlling a single trajectory of a finite-dimensional dynamical system to the optimal control problem governed by a partial differential equation (PDE) for a continuum (ensemble) of dynamical systems subject to the same control strategy. We remark that the Liouville equation represents also the fundamental building block for continuity models as the Fokker–Planck equation for stochastic systems and the Boltzmann equation for atomistic models. In particular, it can be used to model particle streaming while neglecting collisions but allowing to consider source terms [19]. Thus, one of the purposes of this work is to present a numerical optimization framework devoted to ensemble optimal control problems that can be applied to similar problems involving continuity equations; see, e.g., [2, 13, 18, 21, 31] for different classes of these equations.
The formulation and theoretical investigation of the ensemble control problems considered in this paper are presented in [3], where existence and regularity of solutions for a class of Liouville optimal control problems is discussed in the case where the drift function corresponds to a composition of linear and bilinear (input-affine) control mechanisms for the underlying dynamical system. In this class of problems, the purpose of the controls is to steer the ensemble of trajectories along a given path and to come close to a desired target configuration at a given final time. As in [7, 8], these objectives are formulated in terms of minimizing different expectation functionals that include appropriately chosen costs of the controls. In particular, we consider \(L^2\)-, \(L^1\)- and \(H^1\)-costs of the controls, where the \(L^2\) term is a classical regularization term, the \(L^1\)-cost has the purpose to promote minimum action of the control during the time evolution by promoting sparsity [15, 37], and the \(H^1\)-cost corresponds to the minimum attention control proposed by Brockett in [9].
The challenges of the numerical investigation presented in this paper are manifold. One of these challenges is that we are a considering a nonlinear control mechanism in the Liouville model where the controls multiply the density function, and this product is subject to spatial differentiation. A further challenge posed is that the numerical approximation of the Liouville equation must guarantee non-negativity of the computed density in addition to the required properties of accuracy and stability. Moreover, turning to the functional structure of the controls’ objectives, we notice that ensemble cost functionals are a much less investigated topic, especially in combination with non-smooth costs of the controls. Furthermore, the presence of \(L^1\) costs and box constraints on the values of the controls require further numerical analysis effort due to the resulting lack of Fréchet differentiability of the resulting optimization problem.
On the other hand, our formulation covers and extends Brockett’s ensemble optimal control strategy so as to address many possible requirements in applications of this framework. For this purpose, in this work we consider all numerical analysis issues concerning the solution of our general Liouville-based ensemble optimal control problems.
As thoroughly discussed in [3] and illustrated below, the first step in solving our ensemble optimal control problems is the derivation of the corresponding first-order optimality conditions that consist of the controlled Liouville equation, its optimization adjoint (having the structure of a transport equation), and a variational inequality that we may also call (with some abuse of wording) the optimality condition equation. The numerical solution of this optimality system proceeds along two main steps that are the numerical approximation of the equations involved and their solution by a numerical optimization scheme.
For the approximation step, we present a novel formulation and analysis of discretization of the Liouville equation and its optimization adjoint model; the latter is called the adjoint Liouville equation. For the former, we consider the well-known second-order finite-volume Kurganov–Tadmor (KT) discretization scheme for the spatial flux derivatives that results in a generalized monotonic upwind scheme for conservation laws (MUSCL). For the temporal discretization, we use the second-order strong stability preserving Runge–Kutta (SSPRK2) discretization scheme. Such schemes possess several important properties (such as conservation of probability) that are inherent to the exact solutions of the Liouville equation. In addition, because the solution of the Liouville equation represents a density function, it is crucial that the numerical solution remains non-negative over all times.
We prove that our SSPRK2-KT scheme preserves positivity subject to a restriction on the time-step size. Further, we prove that our scheme is second-order convergent in the \(L^1\) norm. This result is less-known in the context of generic finite-volume schemes for linear conservation laws. For the adjoint Liouville equation, which is a transport equation with a source term, we use a second-order Strang time-splitting scheme combined with the KT spatial discretization scheme, and for the resulting approximation we prove second-order accuracy. Further, we notice that the optimality condition equation is a variational inequality involving an integral for which we use second-order accurate quadratures, and we implement a projection step in the optimization procedure. Notice that, while second-order accuracy for the above three components of the optimality system is separately guaranteed by suitable approximation, we are not able to prove this order of accuracy of the coupled system; this is an issue that remains widely open in the scientific literature, apart of the case of much simpler problems with linear control mechanisms; see, e.g., [6].
The second fundamental step in solving our ensemble optimal control problems is the design of a numerical optimization procedure. For this purpose, one recognizes that the optimality condition equation provides the semi-smooth gradient of the ensemble-cost functional along the constraint given by the Liouville model. However, because of the presence of control constraints and the combination of \(L^2\)-, \(L^1\)- and \(H^1\)-costs, the assembling of our gradient is challenging. In particular, by imposing constraints on the value of the control, we are required to implement a \(H^1\) projection of the control update. At this point, we remark that the combination of \(L^1\)- and \(H^1\)-costs and the \(H^1\) projection are less investigated in the literature.
However, this effort is very well justified by our purpose of implementing a state-of-the-art semi-smooth Krylov–Newton methodology for our new class of PDE optimal control problems. In doing this, we also rely on past experience in [14, 15], and the resulting Newton scheme is used to validate our optimal control framework.
In the next Section, we illustrate the formulation of Liouville ensemble optimal control problems, and discuss the chosen control mechanism and the constitutive terms of an ensemble cost functional. Further, in correspondence to our optimization setting, we present the optimality system and discuss the construction of the gradient.
In Sect. 3, we investigate the approximation of the Liouville equation and of adjoint Liouville equation in the optimality system. For the former, we consider a combination of a second order accurate strong stability preserving Runge–Kutta discretization in time and the Kurganov–Tadmor finite volume discretization in space. For the latter, we discuss a scheme that combines the Kurganov–Tadmor discretization and a Strang’s splitting technique. For both methods, we present a detailed analysis of stability and accuracy, and in the case of the Liouville equation we prove that our scheme is positive preserving.
Section 4 is devoted to the implementation of our semi-smooth Krylov–Newton method that requires the numerical solution of the Liouville equation and its adjoint and the implementation of the gradient together with a \(H^1\)-projection procedure for the controls.
In Sect. 5, we present results of numerical experiments with our solution methodology that validate our optimal control framework in terms of the ability of the controls to perform the given tasks. For this purpose, we consider the tracking of non-differentiable trajectories and also the case of bimodal distributions. A section of conclusion completes this work.
1.1 Notation
In this section, we present our notation that we use throughout the paper.
Given a bounded domain \(\Omega \subset {{\mathbb {R}}}^d\), the symbol \(C_c^\infty (\Omega )\) denotes the space of infinitely often differentiable functions with compact support in \(\Omega \). Given \(k\in {{\mathbb {N}}}\), we denote by \(C^k(\Omega )\) the space of all k-times continuously differentiable functions defined on \(\Omega \), and by \(C_b^k(\Omega )\) the subspace of \(C^k(\Omega )\) formed by functions which are uniformly bounded together with all their derivatives up to the order k. We equip \(C_b^k(\Omega )\) with the \(W^{k,\infty }\)-norm as follows
For \(\alpha \in \,]0,1]\), we denote with \(C^{0,\alpha }(\Omega )\) the classical Hölder space (Lipschitz space if \(\alpha =1\)), endowed with the norm
In particular, \(C^{0,1}(\Omega )\,\equiv \,W^{1,\infty }(\Omega )\).
For \(k \in \mathbb {N}\) and \(1 \le p \le +\infty \), we denote with \(W^{k,p}(\Omega )\) the usual Sobolev space of \(L^p\) functions with all the derivatives up to the order k in \(L^p\); we also set \(H^k(\Omega ):=W^{k,2}(\Omega )\). For \(1\le p < +\infty \), let \(W^{-k,p}(\Omega )\) denote the dual space of \(W^{k,p}(\Omega )\). For any \(p\in [1,+\infty ]\), the space \(L^p_{loc}(\Omega )\) is the set formed by all functions which belong to \(L^p(\Omega _0)\), for any compact subset \(\Omega _0\) of \(\Omega \).
Furthermore, we make use of the so-called Bochner spaces. Given a Banach space \((X,\left\Vert \cdot \right\Vert _X)\) and a fixed time \(T>0\), we define for \(1 \le p < \infty \), and a generic representative function \(\phi =\phi (x,t)\), the spaces
and
Given a Banach space X and a sequence \(\bigl (\Phi _n\bigr )_n\), we use the notation \(\bigl (\Phi _n\bigr )_n \subset X\) meaning that \(\Phi _n \in X\) for all \(n \in \mathbb {N}\) and that this sequence is uniformly bounded in X: there exists some constant \(M>0\) such that \(\left\Vert \Phi _n \right\Vert _X \le M~\forall n \in \mathbb {N}\).
Given two Banach spaces \((X,\left\Vert \cdot \right\Vert _X)\) and \((Y,\left\Vert \cdot \right\Vert _Y)\), the space \(X\cap Y\), endowed with the norm \(\Vert \cdot \Vert _{X\cap Y}\,:=\,\Vert \cdot \Vert _{X}+\Vert \cdot \Vert _{Y}\), is still a Banach space.
For every \(p\in [1,+\infty ]\), we use the notation \(\mathbb {L}^p_T(\mathbb {R}^d)\,:=\, L^p_T(\mathbb {R}^d) \times L^p_T(\mathbb {R}^d)\). Analogously, \(\mathbb {H}^1_T(\mathbb {R}^d)\,:=\, H^1_T(\mathbb {R}^d) \times H^1_T(\mathbb {R}^d)\). In addition, given two vectors u and v in \({{\mathbb {R}}}^d\), we write \(u\le v\) if the inequality is satisfied component by component by the two vectors: namely, \(u^i\le v^i\) for all \(1\le i\le d\).
2 Formulation of ensemble optimal control problems
Consider a particle whose position at time t is denoted with \(\xi (t) \in {{\mathbb {R}}}^d\). Suppose that this particle is subject to a velocity field a(x, t) over \({{\mathbb {R}}}^d\), where \((x,t)\in {{\mathbb {R}}}^d \times [0,T]\), for some final time \(T>0\); then the particle’s trajectory is obtained by integrating \({\dot{\xi }}(t)=\,a\bigl (\xi (t),t\bigr )\) assuming an initial condition \(\xi (0)=\xi _0\).
Now, suppose we have an infinite number of non-interacting particles subject to the same vector field and being distributed with a smooth initial density \(\rho _{|t=0}=\rho _0\); then the evolution of this material density is modelled by the following Liouville equation
with the initial condition at \(t=0\) given by \(\rho (x,0)=\rho _0(x)\). Notice that, in this model, the state variable x of the dynamical system defined by a, becomes the space variable in the Liouville equation. We call a the drift function.
We have the same model (2.1) if we consider a unique particle subject to the flow a and having the initial condition \(\xi _0\) chosen based on the probability density \(\rho _0\). In this case, the Liouville equation governs the evolution of the probability density function \(\rho \) of the position of the particle in the interval [0, T]. However, the significance of the Liouville equation above is not limited to the case where x denotes the space coordinate and a a velocity field. In fact, it applies equally well in the case where x represents the velocity of the particle and a plays the role of acceleration/force. Another possibility is to identify x with the position and velocity of a particle in the phase space, and in this case the Liouville operator corresponds to the streaming part in the transport and Boltzmann equations [10, 19].
Clearly, the interpretation of \(\rho \) as a probability or material density leads to the requirement that the initial condition for the Liouville model is non negative, \(\rho _0\ge 0\). Moreover, we can normalize the total probability or mass requiring that \(\int _{{{\mathbb {R}}}^d} \rho _0(x) \, dx=1\). With this conditions, one can show that the evolution of \(\rho \) modeled by the Liouville equation (2.1) has the following properties
The first property can be proved by the vanishing viscosity method and the maximum principle or solving along characteristics; see, e.g., [20, 22]; the second property follows from a simple application of the divergence theorem.
We remark that the Liouville equation allows to model the transport of the (material or probability) density also in the case when the drift function is non smooth [2, 18, 31], and also in the case when it includes a control mechanism.
Therefore, the representation of the ensemble of trajectories in terms of an evolving density and the fact that we can manipulate the drift with a control function to achieve some purposes of the motion of the particles leads to the formulation of the following ensemble optimal control problem
In this problem, the drift \(a(x,t;u) \in {\mathbb {R}}^d\) includes a time-dependent vector-valued control function u, and the purpose of this control is to drive \(\rho \) such that the cost functional J is minimized.
As in many application, we consider dynamical systems that are controlled by linear and bilinear control mechanisms as follows
where \(a_0\) is a given smooth vector field, which is Lipschitz in x, and \(b,\,c \in \mathbb {R}\) are constants. Moreover, the function \(u_1\) corresponds to a linear control mechanism, and \(u_2\) represents a bilinear (input-affine) control term. We assume that both functions are defined on the time interval [0, T] with values in \({{\mathbb {R}}}^d\). With \(\circ :{{\mathbb {R}}}^d \times {{\mathbb {R}}}^d \rightarrow {{\mathbb {R}}}^d\), we denote the Hadamard product of two vectors; we also use the notation \(u=(u_1,u_2)\).
Notice that, in the simple case where \(a_0=0\), \(b=c=1\), and \(\rho _0\) is a normalized Gaussian unimodal distribution, then, the Liouville dynamics can be completely described by the first- and second-moment equations that include the controls \(u_1\) and \(u_2\). To illustrate this fact, consider the following average operator applied to an integrable function g
In particular, we have the mean \(m(t)={{\mathbb {E}}}[x](t)\) and the variance \(v(t)={{\mathbb {E}}}\big [\big (x-m(\cdot )\big )^2\big ](t)\). Then, by taking the average of our controlled dynamical system (that is, using the Liouville equation), we obtain
where the control \(u_1\) appears as the main driving force of the mean value of the density, and \(u_2\) determines the evolution of the variance of the density. See [7] for more details on this construction. However, the validity of this setting is very limited by the assumptions above whereas the Liouville framework allows to accommodate a more general drift and to consider multi-modal distributions of the density function.
Next, we discuss the meaning of the different terms in our cost functional. The first term in (2.3) has the purpose to model the tracking of a desired trajectory \(\xi _D(t)\), in the sense that minimizing this term corresponds to having all trajectories of the ensemble of particles being close to \(\xi _D\). For this purpose, we choose a function \(\theta (x,t)\) that, for a fixed t, is required to monotonically increase as a function of the distance \(|x-\xi _D(t)|\). Therefore, by minimization of the first term we have that \(\rho \) is mainly concentrated on the minimum of \(\theta \) corresponding to \(\xi _D\). We refer to \(\theta \) as an attracting potential, and focus on the following choice
Similarly, the purpose of the second term in J is to model the requirement that the density \(\rho \) at final time concentrates on a final position denoted with \(\xi _T \in {{\mathbb {R}}}^d\). Therefore, we may choose
Notice that, because of (2.2), we can augment this functions by adding a constant such that J is bounded from below by zero. However, this shift would not influence the result of the optimization problem.
The last term in (2.3) represents the cost of the controls’ action. Moreover, it determines the functional space where the control is sought. In our case, the cost function \(\kappa \) is chosen based on the requirement of implementing a slowly varying control function with sparsity along the time horizon. A control that slowly changes in time can be obtained considering the following cost of the control
where \(\nu > 0\) is a positive weight, and \(|\cdot |\) denotes the Euclidean norm. In fact, as \(\nu \) is taken larger, the emerging optimal control will result in controls with small values of its time derivative, which corresponds to the “minimum attention control” in [9]. In addition, we add a \(L^2\)-cost of the control that should measure the total effort made by u as follows
where \(\gamma > 0\) is a positive weight. Clearly, if \(\nu =\gamma >0\), then these two terms together correspond to a \(H^1(0,T)\)-cost of the control.
As for inducing sparsity of the control function u, we consider the following \(L^1\)-cost of the control
where \(\delta \ge 0\). This cost promotes sparsity of the control function, in the sense that, as \(\delta \) is increased, the u resulting from the minimisation procedure will be zero on larger open intervals in (0, T); see Figure 2 of [15]. In our framework, the purpose of this control is to promote “minimum action”.
Summarizing, we specify the term \(\kappa \big (u(t)\big )\) in (2.3) as follows
where \(\gamma , \nu > 0\) and \(\delta \ge 0\). It is clear that, with this setting, the control space U corresponds to a weighted \(\mathbb {H}^1\) space given by \({\widetilde{\mathbb {H}}}^1_T \,:=\, {\widetilde{H}}^1_T \times {\widetilde{H}}^1_T\), where \({\widetilde{H}}^1_T\) corresponds to the \(H^1_T\) space, endowed with the following weighted \(H^1\)-product
The notation \('=d/dt\) stands for the weak time derivative.
In order to complete the modelling of the control space, we also require that each component of the control function u may only take values in a compact convex set of \({{\mathbb {R}}}\). Thus, we define the following set of admissible controls
where the inequalities are meant componentwise, and we choose \(u^a=\big (u^a_1,u^a_2\big )\) and \(u^b=\big (u^b_1,u^b_2\big )\) in \({{\mathbb {R}}}^{2d}\), with \(u^a < u^b\). We remark that, with \(\nu >0\), the resulting u is continuous because of the compact embedding \(H^1(0,T) \subset \subset C([0,T])\).
As discussed in detail in [3], the optimal control problem (2.3)–(2.4), with (2.5) and (2.7) and the admissible set of controls \(U_{ad}\), admits a solution. Furthermore, this solution can be characterized as the solution to the so-called first-order optimality condition. This condition can be formulated by first introducing the Liouville control-to-state map G defined by
where \(\rho \) is the unique solution to the Liouville equation with the chosen control \(u \in U_{ad}\) and the given initial data \(\rho _0 \in L^2(\mathbb {R}^d)\). Notice that, in our setting, with \(\rho _0 \in H^m(\mathbb {R}^d)\), the Liouville problem admits a unique weak solution \(\rho \in C([0,T]; H^m(\mathbb {R}^d))\); see [3] for all details.
With this map, our optimal control problem can be equivalently formulated as
where \(\widehat{J}(u) := J\big (G(u),u\big )\) represents the so-called reduced cost functional.
Now, if \(\delta =0\), then \(\widehat{J}(u)\) is Fréchet differentiable in suitable topologies [3], and a solution u to our optimal control problem necessarily satisfies the first-order optimality condition given by \((\nabla \widehat{J}(u), v-u)_U \ge 0\) for all \(v \in U_{ad}\), where \(\nabla \) represents the gradient in the control space; see [27, 40]. However, since we have \(\delta >0\), our reduced cost functional is only sub-differentiable [17, 41], and the formulation of the optimality condition becomes more involved, especially in our case where a \(\widetilde{\mathbb {H}}^1_T(\mathbb {R}^d)\) control space is involved.
In the following, we give a detailed discussion of the formulation of the optimality condition in terms of an optimality system, where the calculation of \(\nabla \widehat{J}(u)\) is achieved by introducing an auxiliary adjoint variable with its own constitutive equation. Further, we use the notion of Clarke’s subdifferential that we illustrate in detail in Sect. 4.
The derivation of the optimality system can be conveniently done in the Lagrange framework starting from following Lagrange functional
where q and \(q_0\) represents Lagrange multipliers (the adjoint variables). In this framework, the optimality system is obtained by requiring that the Fréchet derivatives of \(\mathcal {L}(\rho ,u,q)\) with respect to each of its arguments are zero. As shown in [3], Fréchet differentiability of \({\mathcal {L}}\) with respect to \(\rho \) and q involves a loss of derivatives, which is natural owing to the hyperbolic nature of the underlying PDEs and which requires more regular initial data.
Clearly, the derivatives of \(\mathcal {L}\) with respect to q and \(q_0\) give the Liouville equation and its initial conditions. On the other hand, the Fréchet derivative of \(\mathcal {L}\) with respect to \(\rho \) leads to the following adjoint Liouville equation
Notice that this is a transport problem with a given terminal condition and thus evolving backwards in time. However, with our choice of \(\theta \) and \(\varphi \) as Gaussian functions, the adjoint equation admits a solution in the same functional space of the solution of the Liouville equation [3]. We remark that the density \(\rho \) does not explicitly appear in this equation, which means that the Liouville equation and its adjoint are decoupled; however, both are driven by the same drift.
Next, we discuss the derivative of \(\mathcal {L}\) with respect to u. For this purpose, we remark that the case \(\delta , \, \gamma >0\) and \(\nu =0\) is well-known in the literature [37], whereas the case that includes the minimum attention control term (\(\nu >0\)) is novel. For this reason, to ease our discussion and make it more accessible, we first discuss the case \(\nu =0\), for which \({\widetilde{\mathbb {H}}}^1_T(\mathbb {R}^d)\) is replaced with \(\mathbb {L}^\infty _T(\mathbb {R}^d)\) in \(U_{ad}\) given by (2.8), and thereafter we also include the term with \(\nu >0\).
In the case \(\nu =0\), as proved in [3], there exists a \(\widehat{\lambda }\,\in \,\partial g(u) :=\, \delta \, \partial \big (\left\Vert u \right\Vert _{L^1}\big ) \), the Clarke’s subdifferential [16] of the \(L^1\)-cost, such that the following inequality condition must be satisfied at optimality
Notice that in this inequality condition, the argument on the left-hand side in the scalar product represents the reduced gradient in \(\mathbb {L}_T^2\).
Moreover, because of the presence of constraints for the controls, there exist \(\lambda _+\) and \(\lambda _-\), belonging to \(L^ \infty _T(\mathbb {R}^d)\), such that (2.12) is equivalent to the equations
for all \(m=1,2\) and all \(1\le r\le d\).
In (2.13), one usually refers to the first equation as the optimality condition equation; the conditions given in the second and third line are the complementarity conditions for the inequality constraints in \(U_{ad}\). Moreover, the last three lines give an equivalent expression for \(\widehat{\lambda }\,\in \,\partial g(u)\); see [37]. In our case, \(\widehat{\lambda }_m^r\) can be understood to be \(\delta \,\text {sgn}(u_m^r)\), where \(\text {sgn}{(x)}\) is the sign function.
Now, in the case \(\nu >0\), the control is sought in \(U_{ad}\) given by (2.8), which requires to construct the reduced gradient in the space \(U={\widetilde{\mathbb {H}}}^1_T(\mathbb {R}^d)\). For this purpose, let \(\mu =(\mu _1, \mu _2)\) be the \({\widetilde{\mathbb {H}}}^1\)-Riesz representative of the continuous linear functional
Then, assuming that \(u\in U_{ad}\cap H^1_0\big ([0,T];{{\mathbb {R}}}^{2d}\big )\), we compute \(\mu \) by solving the following boundary-value problem
which has to be understood in a weak sense. Notice that, in this construction, we have made the modelling choice that the control function u is zero at the beginning and at the end of the time interval. This setting corresponds to having the control switched on at \(t=0\) and off at \(t=T\).
Based on (2.12) and the definition of \(\mu \) in the \({\widetilde{\mathbb {H}}}^1\) space, we identify the reduced gradient in this space as follows
where \(m=1,2\) and \(r=1\ldots d\). Thus, the optimality condition (2.12) becomes
for all \(v\,\in \,U_{ad}\), where \(U_{ad}\) is given in (2.8), \(m=1,2\) and \(r=1\ldots d\).
The result of this section is that a solution to our ensemble optimal control problems can be characterized as the solution to the following optimality system.
Notice that, for the sake of better readability, in the following we choose \(\nu =\gamma >0\) and \(\delta >0\).
3 Approximation of the Liouville optimality system
In this section, we discuss the spatial and temporal discretization of the Liouville equation and its adjoint in the optimality system. Our aim is to develop an approximation framework that is second-order accurate and preserves the two essential properties of the continuous Liouville model given in (2.2), namely positivity and conservativeness of its solution.
For simplicity of notation, in the following we focus on a two-dimensional problem, i.e. \(d=2\). Then \(a=(a^1,a^2) \in {\mathbb {R}}^2\). In view of applications to the numerical study of our optimal control problem, we consider a large but bounded convex domain \(\Omega \subset \mathbb {R}^2\): we choose \(\Omega = (-B,B) \times (-B,B)\), for some large \(B>0\).
We also fix a smooth initial density \(\rho _0\) that is (by machine precision) compactly supported in \(\Omega \). For \(\theta \) and \(\varphi \) we take Gaussian functions having sufficiently small variance and centred sufficiently far from the boundary of \(\Omega \), so that (by machine precision) we can assume that also those functions are compactly supported in \(\Omega \). Then, we solve problems (2.17) and (2.18) in \(\Omega \times [0,T]\), supplemented with homogeneous Dirichlet boundary conditions on \(\partial \Omega \). Notice that, in this setting, it is possible to use the results of [3] to prove existence and uniqueness of smooth enough solutions to (2.17) and (2.18). For this purpose, one extends the functions \(\rho _0\), \(\theta \) and \(\varphi \) to be zero outside the domain \(\Omega \), and the drift function a to a smooth function, which is bounded on \({{\mathbb {R}}}^d\) together with all its space derivatives. We remark that this is always possible, for instance by multiplying a with a smooth compactly supported function \(\chi \) of the space variable only, such that \(\chi \equiv 1\) on a neighbourhood of \(\Omega \).
We consider our solutions on a time interval [0, T], where \(T>0\) is chosen such that the corresponding solutions \(\rho \) to (2.17) and q to (2.18) are still compactly supported in \(\Omega \), far away from its boundary \(\partial \Omega \). Observe that this property is true by finite propagation speed, since the (extended) drift is bounded on \({{\mathbb {R}}}^d\).
For \(\Omega = (-B,B) \times (-B,B)\) fixed above, we set a numerical grid that provides a partitioning of \(\Omega \) in \(N_x \times N_x\), \(N_x > 1\), equally-spaced non-overlapping square cells of side length \(h=2B/N_x\). On this partitioning, we consider a cell-centred finite-volume setting, where the nodal points at which the density and adjoint variables are defined are placed at the centres of the square volumes. These nodal points are given by
Therefore, the elementary cell is defined as
Thus, the computational domain is given by
Analogously, the time interval [0, T] is divided in \(N_t > 1\) subintervals of length \(\Delta t\) and the points \(t^k\) are given by
This defines the time mesh \(\Gamma _{\Delta t} := \{t^k~\in ~[0,T],~k = 0,\ldots ,N_t \}\). Therefore, corresponding to the space-time cylinder \(Q := \Omega \times [0,T]\) we have its discrete counterpart \(Q_{h,\Delta t} := \Omega _h \times \Gamma _{\Delta t}\).
In this setting, the cell average of the density \(\rho \) (and so of any integrable function), on the cell with centre \((x_1^i,x_2^j)\) at time \(t^k\), is given by
In particular,
Notice that, in our numerical setting, function values are identified with their cell-based average located at the cell centres. For this reason, our numerical framework aims at determining approximation of theses averages. Specifically, we discuss a discretization scheme that results in values \(\rho _{i,j}^k\) that approximate \({\bar{\rho }}_{i,j}^k\). Similarly, we denote with \(q_{i,j}^k\) the numerical approximation of \({\bar{q}}_{i,j}^k\) that is computed as in (3.1).
We also consider a piecewise constant approximation to the time-dependent control functions, where we denote with \(u^{k+1/2}\) the value of the control in the time interval \([t^k,t^{k+1})\). Further, for the projection of a continuous u to the corresponding approximation space, we set \(u^{k+1/2}=u(t^k)\). For a function f defined on \(Q_{h,\Delta t}\), we define the discrete norms \(\Vert \cdot \Vert _{1,h}\) and \(\Vert \cdot \Vert _{\infty ,h}\) as follows:
where \( f^k_{i,j} = f(x_1^i,x_2^j,t^k)\), and \((x_1^i,x_2^j,t^k)\) denotes a grid point in \(\Omega \times [0,T]\).
3.1 A Runge–Kutta Kurganov–Tadmor scheme for the Liouville equation
In this section, we discuss a suitable approximation of our controlled Liouville equation in \(\Omega \times [0,T]\). Supposing that \(\rho _0\) has compact support, and because of finite propagation speed, we can choose \(\Omega \) such that the solution \(\rho \) at the boundary \(\partial \Omega \) is zero for all times \(t\in [0,T]\).
For our purpose, we focus on the finite-volume scheme proposed by Kurganov–Tadmor (KT) in [26] that involves a generalized MUSCL flux. To describe this scheme, we denote the flux in the Liouville equation as a function of \(\rho \) with \(f(\rho ) = a\rho = a(x,t) \, \rho (x,t)\). With this definition, the KT scheme for the Liouville equation in semi-discretized form is given by
where the \(H^{x_r}_{\cdot ,\cdot }(\rho ^+,\rho ^-;t)\) are the fluxes in r-direction, \(r=1,2\). Specifically, for \(H^{x_1}_{\cdot ,\cdot }(\rho ^+,\rho ^-;t)\) we have
where \(f = (f^1,f^2) = (a^1\rho , a^2\rho )\), and similarly for \(H^{x_2}_{i,j \pm 1/2}(\rho ^+,\rho ^-;t)\). In this formula, the so-called local speeds \({\mathcal {V}}^{x_r}(t)\) are given by
since \(f(\rho )=a \, \rho \) is linear in \(\rho \).
Further in (3.3), the approximation of \(\rho \) at the cell edges is given by intermediate values that approximate the function value from above respectively from below as follows
We approximate the partial derivatives of \(\rho \) using the minmod function as follows: In direction \(x_1\), this approximation is given by
An analogous expression holds in the direction \(x_2\). The multivariable minmod function for vectors \(x\in \mathbb {R}^d\) is given by
Next, we discuss the local truncation error of the semi-discrete KT scheme (3.2)–(3.4).
Lemma 3.1
The KT scheme given in (3.2)–(3.5) is at least second-order accurate for smooth \(\rho \), except possibly at the points of extrema of \(\rho \).
Proof
The flux H, given in (3.3), is a first-order Rusanov flux [34] that is \(C^2\) with Lipschitz continuous partial derivatives with respect to \(\rho ^+,\rho ^-\), in a neighbourhood of \(\rho _{i,j}\). Further, by using a Taylor series expansion, we have the following approximation
and a similar result holds in the \(x_2\) direction, except at the points of extrema, which are characterized by \((\rho _{x_1})_{i,j}=0\) (see [30, Th. 3.2]). Using the result in [29, Lemma 2.1], we have that the semi-discrete scheme (3.2)-(3.5) is second-order accurate in space except possibly at points of extrema. \(\square \)
For the time discretization of the Liouville equation (2.4), we use a second-order strong stability preserving Runge–Kutta (SSPRK2) method [35] (also known as the Huen’s method). The combination of this scheme with the KT discretization of the flux f, given in (3.2), results in a new approximation method that we call the SSPRK2-KT-scheme. This scheme is implemented by the Algorithm 3.1 given below using the following definition
where \(H_{\cdot ,\cdot }^{x_j,k}\) denotes \(H_{\cdot ,\cdot }^{x_j}\), \(j=1,2\), given in (3.3) corresponding to the time step \(t^k\).

Now, we study the properties of the SSPRK2-KT scheme given in Algorithm 3.1.
This method has the following strong stability property [23, Lemma 2.1]
Further, we have conservativeness of the total probability (or mass) as a consequence of the finite-volume formulation:
Lemma 3.2
(Conservativeness) The SSPRK2-KT scheme is conservative, in the sense that
Proof
Fix \(k\in \lbrace 0, \ldots , N_t \rbrace \). From the first step of the SSPRK2-KT scheme, given in Algorithm 3.1, summing up over all indices \(i,j \in \lbrace 1, \ldots , N_x \rbrace \) and using the fact that the solution has zero flux on the boundary (since it has compact support in \(\Omega \)), we get
In a similar way, we have
Thus,
Iterating over k, we have
\(\square \)
Next, we show that, starting from a non-negative initial density, the solution obtained with the SSPRK2-KT scheme remains non-negative. For this purpose, we define the CFL-number
and require the conditions on the components of the drift a given in (2.5) given by
Notice that the control u belongs to the set \(U_{ad}\) defined in (2.8). Then, for \(j=1,2\), we see that
so that the aforementioned conditions on the components of the drift a are satisfied under the following CFL condition.
This CFL condition only depends on the components of the vector \(a_0\), and it does not rest on the unknowns of the problem.
With the conditions (3.9), we can prove the following lemma on the positivity of the SSPRK2-KT scheme.
Lemma 3.3
(Positivity) Under the CFL-condition (3.9), with \(u \in U_{ad}\) and \(\rho ^0_{i,j} \ge 0\), \(i,j =1,\ldots ,N_x\), the solution to the Liouville problem computed with the SSPRK2-KT scheme given in Algorithm 3.1 is non-negative, that is,
Proof
The SSPRK2-KT scheme, given in Algorithm 3.1, comprises of a two-step Euler scheme that results in the computation of \(\rho ^{(1)}\) and \(\rho ^{(2)}\) and a final averaging step. To prove positivity of the SSPRK2-KT scheme, it is enough to show that the solutions obtained in each of the two Euler steps are positive. Without loss of generality, we prove that the solution obtained in the first step of the SSPRK2-KT scheme is positive. A similar analysis holds true for the second step.
Let \(\rho _{i,j}^k \ge 0\) for fixed \(0\le k<N_t\). We will show that \(\rho _{i,j}^{k+1} \ge 0\) for all \(i,j = 1,\ldots ,N_x\). For this purpose, notice that the SSPRK2-KT scheme can be written as follows
where all discrete quantities on the right are considered at the timestep \(t^k\). We see that the first four terms on the right hand side in (3.11) are always non-negative, provided that \(\rho _{i\pm 1/2,j}^{\pm },~\rho _{i,j\pm 1/2}^{\pm } \ge 0\). The remaining terms are non-negative under the CFL-condition (3.9).
Thus, it remains to show that \(\rho _{i+1/2,j}^\pm \), \(\rho _{i,j+1/2}^\pm \ge 0\) for all \(i,j = 1,\ldots ,N_x\), where \(\rho ^\pm _{i,j}\) is given as in (3.5).
We consider each of the expressions for \((\rho _{x_1})^k_{i,j}\) in the direction of \(x_1\) given as in (3.6). First, assume that \(\left( \rho _{x_1}\right) _{i,j}^k = \frac{\rho _{i,j}^k-\rho _{i-1,j}^k}{h}\), which is one of the possible values of the minmod limiter in (3.6).
Then it follows that
This is non-negative, since \(\rho _{i,j}^k \ge 0\) for all \(i,j = 1,\ldots ,N_x\) by the inductive assumption. Further, \(\rho _{i+1/2,j}^- = \rho _{i,j}^k + \frac{h}{2}\left[ \frac{\rho _{i,j}^k-\rho _{i-1,j}^k}{h}\right] \). If \(\frac{\rho _{i,j}^k-\rho _{i-1,j}^k}{h}>0\), then it implies \(\rho _{i+1/2,j}^->0\). If \(\frac{\rho _{i,j}^k-\rho _{i-1,j}^k}{h}<0\), then by the definition of the minmod limiter, we have \(\frac{\rho _{i,j}^k-\rho _{i-1,j}^k}{h}\ge \frac{\rho _{i+1,j}^k-\rho _{i,j}^k}{h}\) and therefore
The other cases for the value of \((\rho _x)_{i,j}^k\ne 0\) follow analogously. If \((\rho _x)_{i,j}^k = 0\), then \(\rho _{i+1/2,j}^\pm = \rho _{i+1,j} \ge 0\) and \(\rho _{i,j+1/2}^\pm = \rho _{i,j+1} \ge 0\). This proves the lemma. \(\square \)
Remark 3.1
The proof of the above lemma follows similar arguments as in [25, Theorem 2.1]. However, a primary difference is that in [25], the positivity result is proved using one-sided local speeds, exploiting the structure of the hyperbolic equation, whereas in our case, the proof relies on conversion of the intermediate values \(\rho ^{\pm }\) to the cell-average values \(\rho _{i,j}^k\) and then showing that \(\rho _{i,j}^k \ge 0\) implies \(\rho _{i,j}^{k+1} \ge 0\), which seems a much simpler approach.
Remark 3.2
Under the same CFL-like condition (3.9), the proof of Lemma 3.3 can be extended to the case of a SSPRK-KT scheme with a Runge–Kutta method of pth order, \(p\in \mathbb {N}\), that is given as an average of p Euler steps.
Remark 3.3
For the case where \((\rho _{x_1})_{i,j}^k = 0\), the approximations of \(\rho \) at the cell-edges, given by (3.5), are piecewise constant in the cell \(\omega _h^{ij}\). Thus, the KT scheme given by (3.2)–(3.5), reduces to a linear upwind scheme that is locally first-order accurate, TVD and positive. This is consistent with the Godunov’s barrier theorem.
Next, we prove discrete \(L^1\) stability of the SSPRK2-KT scheme without a right-hand side.
Lemma 3.4
(Stability) The solution \(\rho ^k_{i,j}\) obtained with the SSPRK2-KT-scheme in Algorithm 3.1 is discrete \(L^1\) stable in the sense that
under the CFL condition (3.9).
Proof
Using Lemma 3.2, we have
Again, from Lemma 3.3, we have that the solution obtained with the SSPRK2-KT scheme is positive under the CFL condition (3.9). This gives us the following relation
which proves the result. \(\square \)
Next, we aim at proving the \(L^1\) convergence of the SSPRK2-KT scheme. For this purpose, we prove the following stability estimate for the discrete solution of the Liouville equation (2.4) with a right-hand side function g(x, t). We remark that in the case \(g\not \equiv 0\) the solution may not be positive.
Lemma 3.5
Let \(\rho _{i,j}^k\) be the SSPRK2-KT solution to the Liouville equation (2.4) with a Lipschitz continuous right-hand side g(x, t) and let the CFL condition (3.9) be fulfilled. Then this solution satisfies the following stability estimate
where \(g^{m}_{i,j} = g(x_1^i,x_2^j,t^m)\).
Proof
The SSPRK2-KT scheme, given in Algorithm 3.1, for the Liouville equation (2.4) with a right-hand side g(x, t) can be written as
where
with \(n=(1)\) and \(n=k\) correspond to the solution \(\rho ^{(1)}\) and \(\rho ^k\), respectively, at the time step \(t^k\) and analogously for \(\rho ^{n\pm }\). Moreover, also the drift is always considered at the time-step \(t^k\). The equations in (3.12) can be rewritten in a compact form with a suitable function \({\mathcal {H}}\) as follows
Now, the KT flux H, given in (3.3), is a combination of the monotonicity preserving Rusanov flux and the monotonicity preserving MUSCL reconstruction. This leads to the SSPRK2-KT scheme to be monotone preserving under the CFL condition [24]. Thus, \({\mathcal {H}}\) is a monotone non-decreasing function of its arguments. Then the following discrete entropy inequality holds for the specific Kruzkov entropy pair \((|\rho |,\text {sgn}(\rho ))\) (see [39, Lemma 2.4])
where \(\Psi ^{1,k}_{\cdot ,\cdot }\), \(\Psi ^{2,k}_{\cdot ,\cdot }\) are the conservative entropy fluxes defined as follows for \(i,j = 1,\ldots ,N_x\)
Therefore, we have for \(k=0,\ldots ,N_t-1\)
Summing up over all i, j and because of our assumption on \(\rho \) being zero on the boundary, we have
which iteratively gives us
\(\square \)
Next, we consider the local consistency error of our SSPRK2-KT at the point \((x_1^i,x_2^j,t^k)\) defined as
The accuracy result for the KT scheme, given by Lemma 3.1, the MUSCL reconstruction error given in Equation (60) in [28, Section 4.4] for the case when \(\kappa = 0\) (in this reference), and the accuracy result for the SSPRK2 scheme from [23, Proposition 3.1], for which we need the CFL condition, give us the following result
Lemma 3.6
Let \(\rho \in C^3\) be the exact solution of the Liouville equation (2.1). Under the CFL condition (3.9), the consistency error \(T_{i,j}^k\) satisfies the following error estimate
except possibly at the points of extrema of \(\rho \) where the consistency error can be first-order in h.
Define the error at the point \((x_1^i,x_2^j,t^k)\) as
Notice that \(\rho _{i,j}^k\) satisfies (3.12) with \(g\equiv 0\) by construction. Further, the exact solution \(\rho \) satisfies (3.12) with the consistency error \(T_{i,j}^k\) as source term. Hence, by taking the difference, the error satisfies (3.12) with the source term given by \(- T_{i,j}^k\). From Lemma 3.5, we obtain
This leads to the following result on the \(L^1\) convergence of the solution obtained using the SSPRK2-KT scheme.
Theorem 3.1
Let \(\rho \in C^3\) be the exact solution of the Liouville equation (2.1), with finite many extrema, and let \(\left\Vert \rho ^{0}_{\cdot ,\cdot } - \rho _0(\cdot ,\cdot ) \right\Vert _{1,h} = {\mathcal {O}}(h^2).\) Under the CFL condition (3.9), the solution \(\rho _{i,j}^k\) obtained with the SSPRK2-KT scheme, given by Algorithm 3.1, is second-order accurate in the discrete \(L^1\)-norm as follows
3.2 Numerical analysis of the Strang splitting scheme
In this section, we deal with the numerical solution of the adjoint equation (2.11). In this case, we have a terminal condition, and the adjoint problem requires evolution backward in time. For this reason, it is convenient to perform a change of the time variable as follows:
With this transformation, we can rewrite (2.11) in the following way
To solve this problem, we apply the Strang splitting method [38] by first rewriting (3.15) as follows
which is defined in \(\Omega \times [0,T]\). Furthermore, we assume that \(\varphi \) and \(\theta \) have (by machine precision) compact support for all times inside the interval [0, T]. See the numerical experiments section for the specific choices for \(\theta \) and \(\varphi \). Then, we solve problem (3.16), supplemented with homogeneous Dirichlet boundary conditions.
We can conveniently illustrate the Strang splitting method applied to (3.16) remaining at the continuous level within one time interval. Let us consider the solution of the adjoint equation (3.16) at time \(\tau ^k\) given by \(q^k(x)\), \(x \in \Omega \). Then, the first step of our solution scheme is to solve the following equation
For this purpose, we use the SSPRK2-KT scheme given in Algorithm 3.1. We denote the solution to this problem with \(q_1\).
In the second step, for each x fixed, we analytically solve the following linear ordinary differential equation
Let the solution obtained in this step be denoted with \(q_2\). The analytical solution of (3.18) at the discrete level is given in (3.22) below.
Notice that \(q_1(x,t)\) and \(q_2(x,t)\) denote functions of continuous variables. We define \(q_{1,i,j}^k\) and \(q_{2,i,j}^k\) as their discrete counterparts using the finite-volume approximation strategy.
The last step is to solve (3.17) with the SSPRK2-KT scheme with the initial condition \(q_2(\cdot , \tau ^{k+1/2})\) in the time interval \([\tau ^{k+1/2},\tau ^{k+1}]\). This problem is formulated as follows
In a numerical setting, the solution obtained in this step is the desired solution of the adjoint equation (3.16), and \(q^{k+1}\) denotes the adjoint variable at time \(\tau ^{k+1}\). Notice that, by our numerical approximation strategy for u, the value of u in \([\tau ^k, \tau ^{k+1})\) is constant.
The steps of the Strang splitting scheme are outlined in Algorithm 3.2 below.

Now, we discuss some properties of the Strang-splitting scheme described in Algorithm 3.2. For this purpose, we denote with \(q_{i,j}^k\) the numerical solution of (3.16) with the generic right-hand side \({\mathcal {G}}\), at the grid point \((x^1_i,x^2_j,\tau ^k)\).
We have the following discrete \(L^1\) stability estimate.
Lemma 3.7
(Stability of adjoint equation) Let q be the numerical solution of (3.16), obtained using the KTS scheme, in the interval \([\tau ^k,\tau ^{k+1}]\). Then the following estimate holds
where \(L=\Vert \mathrm{div}\,a\Vert _{L^\infty (\Omega \times [0,T])}\), \(M=\left\Vert {\mathcal {G}} \right\Vert _{L^\infty _T(L^1(\Omega ))}\).
Proof
Let \(q_{1,\cdot ,\cdot }^{k+1/2}\) be the numerical solution obtained from (3.17). Since (3.17) is solved using the SSPRK2-KT scheme, using the entropy inequality computations as in Lemma 3.5, we have
Next, denoting the numerical solution as \(q_{2,i,j}^{k+1}\) obtained as the analytical solution from (3.18), using an integrating factor approach in \([\tau ^k,\tau ^{k+1}],\) we have
where \({\mathcal {R}} = \int \mathrm{div}\,a\,d\tau \).
Notice that, because the drift and \({\mathcal {G}}\) are given explicitly, and the control u is constant in the sub-interval of integration, this equation can be solved exactly. We exemplify this calculation considering \({\mathcal {G}}\) being constant in \([\tau ^k,\tau ^{k+1})\) and equal to its value at \(\tau ^{k}\). In this case, it holds that \({\mathcal {R}}(\tau ^k) = \left( (u_2^1)^{k+1/2} + (u_2^2)^{k+1/2} \right) \tau ^k\).
In general, without any assumptions on the approximation strategy for u and \({\mathcal {G}}\), but considering the bilinear structure of our drift function (c.f. (2.5)) and the assumption on \(a_0\), we can state that there exists an \(L > 0\) such that
Thus, we have
Hence, by integration we obtain
Further, by using (3.21), we have
where \(M = \max _{\tau \in [0,T]} h^2\sum _{i,j}|{\mathcal {G}}(x^1_i,x^2_j,\tau )|\). Again, since (3.19) is solved using the SSPRK2-KT scheme, we have
which gives the desired result. \(\square \)
Next, we consider the local truncation error of our KTS scheme at the point \((x_1^i,x_2^j,\tau ^k)\) defined as [42]
where \({\mathcal {H}}\) is the SSPRK2-KT operator given in (3.13) and \(\Lambda \) is the exact integration operator for (3.18) at time \(\tau ^k\), defined in (3.22). We have the following temporal error estimate for the continuous Strang splitting scheme (for its proof see [38, Page 510], [36, Eq. (1.7)],[11, Eq. (2.13)]).
Lemma 3.8
(Time error Strang-splitting) Let \(S=S(\Delta t)\) be the exact solution operator of (3.16) in \([\tau ^k, \tau ^{k+1}]\), i.e., \(S \, q^{k} =q^{k+1}\). Denote with \(q_{SP}\) the solution of (3.16) with the Strang splitting scheme, given by (3.17)–(3.19), applied at the continuous level (no discretization of the spatial and the temporal operators) in the time interval \([\tau ^k,\tau ^{k+1}]\) and with a smooth initial condition \({\bar{q}}(\cdot , \tau ^{k})\). This solution can be written as follows
where \(S_1=S_1(\Delta t)\) denotes the exact integration of \(\partial _\tau q - \mathrm{div}\,(aq) = 0\) in time interval \([\tau ^{k},\tau ^{k+1/2}]\), and \(S_2=S_2(\Delta t)\) the same operator for \([\tau ^{k+1/2}, \tau ^{k}]\). Then the following error estimate holds
With this result and the truncation error estimate of the SSPRK2-KT scheme given in 3.6, we have the following result
Lemma 3.9
Let \(q\in C^3\) be the exact solution of the adjoint equation (3.16) Under the CFL condition (3.9), the truncation error \(Z_{i,j}^k\) satisfies the following error estimate
except possibly at the points of extrema of the exact solution q(x, t).
Define the error at the point \((x_1^i,x_2^j,\tau ^k)\) as
Then \(e_{i,j}^k\) satisfies (3.16), with the right-hand side being \( \dfrac{Z_{i,j}^k}{\Delta t}\); see the explanation after Lemma 3.6. Thus, from Lemma 3.7 we obtain
where \(M = \max _{k \in \lbrace 0,\ldots ,N_t \rbrace } h^2\sum _{i,j}|Z_{i,j}^k|\). This leads to the following result on the \(L^1\) convergence of the solution obtained using the KTS scheme
Theorem 3.2
Let \(q\in C^3\) be the exact solution of the adjoint equation (3.16), with countably many extrema, and let \(\left\Vert q^{0}_{\cdot ,\cdot } + \varphi (\cdot ,\cdot ) \right\Vert _{1,h} = {\mathcal {O}}(h^2).\) Under the CFL condition (3.9), the solution \(q_{i,j}^k\) obtained with the KTS scheme, given by Algorithm 3.2, is second-order accurate in the discrete \(L^1\)-norm as follows
Remark 3.4
We remark that results similar to Theorem 3.2 have been obtained in [11, 12]. However, in these papers the equation that has been considered is the convection diffusion equation, which is parabolic, whereas we have a hyperbolic transport (adjoint) equation with a source term. Furthermore, we employ a different analysis using an entropy inequality technique for proving the discrete stability estimate that is subsequently used for proving the convergence error estimate.
4 A projected semi-smooth Krylov–Newton method
In this section, we illustrate a semi-smooth Krylov–Newton (SSKN) method for solving the ensemble optimal control problem (2.3)–(2.4) with the drift given by (2.5) and the cost functional setting specified in Sect. 2. We remark that our SSKN scheme belongs to the class of projected semi-smooth Newton schemes discussed in [41].
In general, a Newton method is an iterative procedure aiming at finding roots of a given function. Its peculiarity is that it may generate a sequence that can converge superlinearly or even quadratically to the solution sought.
In order to explain the Newton method in simple terms, consider the problem to find a root \(\zeta ^{\star } \in {\mathbb {R}}^N\) of a map \({\mathcal {M}}:{\mathbb {R}}^N \rightarrow {\mathbb {R}}^N\), as follows
where, for the moment, we assume that \(\zeta \mapsto {\mathcal {M}}(\zeta )\) is continuously differentiable.
Now, denote with \({\mathcal {J}}(\zeta )\) the Jacobian of \({\mathcal {M}}\) at \(\zeta \). The Newton method generates a sequence \(( \zeta ^\ell )_{\ell \in {{\mathbb {N}}}}\) by means of the following two steps
The steps \(\textsc {s}_1\)–\(\textsc {s}_2\) are performed for \(\ell =0,1, 2, \ldots \), starting with a given initial guess \(\zeta ^0\).
Clearly, the Newton sequence is well defined if the Jacobian is invertible at each iterate, and we assume that this is the case in a neighbourhood \({\mathcal {N}}\) of the solution \(\zeta ^{\star }\), where also the inverse is uniformly bounded. With these assumptions and requiring that the initial guess \(\zeta ^0 \in {\mathcal {N}}\) is sufficiently close to \(\zeta ^{\star }\), one can prove that the sequence \(( \zeta ^\ell )\) converges quadratically to the root \(\zeta ^{\star }\), that is, \(\Vert \zeta ^{\ell +1}-\zeta ^{\star }\Vert _2 \le c \, \Vert \zeta ^{\ell }-\zeta ^{\star } \Vert _2^2\), for some constant \(c>0\), and \(\Vert \cdot \Vert _2\) denotes the Euclidean norm of a vector in \({{\mathbb {R}}}^N\). However, in the case where \({\mathcal {M}}\) is only differentiable and provided that the following holds
then the Newton sequence converges at least superlinearly, i.e. faster than linearly.
The same Newton procedure (4.2) can be applied to find an extremal of the minimization problem \(\min _{\zeta \in {\mathbb {R}}^N} \, f(\zeta )\), by considering \({\mathcal {M}}(\zeta ):=\nabla f(\zeta )\), where \(\nabla \) denotes the gradient in \({{\mathbb {R}}}^N\), and assuming that \(f:{\mathbb {R}}^N \rightarrow {\mathbb {R}}\) is twice differentiable. In this case, we have that \({\mathcal {J}}(\zeta ) = \nabla ^2f(\zeta )\).
Now, in the case of a constrained optimization problem \(\min _{\zeta \in K} \, f(\zeta )\), where \(K \subset {\mathbb {R}}^N\) is closed and convex, an extremal \(\zeta ^{\star }\) of this problem is characterized by the inequality \(\nabla f(\zeta ^{\star }) \cdot (\zeta - \zeta ^{\star }) \ge 0\). However, this inequality can be equivalently written as follows
where \(P_K\) is the projection of \({{\mathbb {R}}}^N\) onto K, and \(s>0\) is arbitrary but fixed. Therefore the solution of the optimality condition in the form of an inequality can be reformulated as a root problem. However, even if f is continuously differentiable, the function \({\mathcal {F}}\) is not. On the other hand, if \(\nabla f\) is locally Lipschitz, then also \({\mathcal {F}}\) is locally Lipschitz continuous.
We see that a lack of differentiability of \(\nabla f(\zeta )\) or the presence of constraints as above hinder the application of the Newton scheme to solve optimization problems. This situation has motivated a great effort towards the generalization of the notion of differentiability that makes possible to pursue the Newton approach also in non-differentiable cases; see [16, 17, 41] for details and further references.
The main assumption for this generalization is the Lipschitz continuity of the map \(\zeta \mapsto {\mathcal {F}}(\zeta )\), in which case Rademacher’s theorem [41] states that this map is almost everywhere differentiable. Based on this result, the notion of differentiability has been extended as follows; see [41] for a detailed discussion.
Definition 4.1
Assuming \({\mathcal {F}}:{\mathbb {R}}^N \rightarrow {\mathbb {R}}^N\) be locally Lipschitz continuous, we have the following generalized Jacobians of \({\mathcal {F}}\) at \(\zeta \):
-
(a)
the Bouligand subdifferential given by
$$\begin{aligned} \partial _{B}{\mathcal {F}}(\zeta ) := \bigl \{ S \in {\mathbb {R}}^{N \times N} \, : \, \exists \{ \zeta ^\ell \}_\ell \subset {\mathbb {R}}^N \setminus U_{nd} \, : \, \zeta ^\ell \rightarrow \zeta \, , \, {\mathcal {J}}(\zeta ^\ell ) \rightarrow S \bigr \} , \end{aligned}$$where \(U_{nd}\) is the set of points where \({\mathcal {F}}\) fails to be Fréchet differentiable and \({\mathcal {J}}(\zeta )\) denotes the Jacobian of \({\mathcal {F}}\) at \(\zeta \);
-
(b)
the Clarke’s subdifferential is the convex hull of \(\partial _{B}{\mathcal {F}}(\zeta )\), denoted with \(\partial {\mathcal {F}}(\zeta ) := {{\,\mathrm{co}\,}}\, \partial _{B}{\mathcal {F}}(\zeta )\).
With this construction, we can apply (4.2) by choosing a generalized Jacobian \(\widetilde{{\mathcal {J}}}^\ell \in \partial {\mathcal {F}}(\zeta ^\ell )\). However, in order to guarantee superlinear convergence of the resulting Newton sequence, the following property of semi-smoothness is required; see [32, 41].
Definition 4.2
A locally Lipschitz continuous function \({\mathcal {F}} : {\mathbb {R}}^{N} \rightarrow {\mathbb {R}}^{N}\) is said to be semi-smooth at \(\zeta \in {\mathbb {R}}^N\) if and only if \({\mathcal {F}}\) is directionally differentiable at \(\zeta \), and it satisfies the condition
Notice that the discussion above has focused on finite dimensional spaces, which is also the case of our numerical optimization problem. However, the subdifferential framework given above has been extended also to maps acting between infinite-dimensional Banach spaces [16, 17, 41]. In particular, we can apply it to our ensemble optimal control problem (2.9), that is, \(\min _{u \in U_{ad}}\widehat{J}(u) := J\big (G(u),u\big )\). One can recognize that \(\widehat{J}(u)\) is not Fréchet differentiable (see also details in [3]) due to the presence of the \(L^1\)-cost, which however is Lipschitz in u. In fact, in Sect. 2, we have used sub-differential calculus [41] to determine the gradient \({\widetilde{\nabla }} \widehat{J}(u)\), and formulated the first-order optimality condition \(({\widetilde{\nabla }} \widehat{J}(u), v-u)_U \ge 0\) for all \(v \in U_{ad}\). Therefore we can proceed as in (4.4) and consider to apply the Newton scheme with generalized Jacobian to the equation
However, although this procedure is standard with control problems with \(L^2\)–\(L^1\) costs [14, 15, 41], it becomes very cumbersome in our case with \(H^1\) costs. For this reason, we consider a projected semi-smooth Newton (pSSN) scheme with the following steps
with \(\ell =0,1, 2, \ldots \), and starting with a given initial guess \(u^0 \in U_{ad}\). In the following, we discuss the step \(\textsc {s}_1\) and thereafter \(\textsc {s}_2\).
Concerning the step \(\textsc {s}_1\), we see that the main computational effort in the procedure (4.6) would be the assembly and inversion of the Jacobian \(\widetilde{{\mathcal {J}}}(u^\ell )\), but this is not possible because of the size of the problem. In fact, in PDE optimization, one implements the action of the Jacobian (reduced Hessian) on a vector and uses a Krylov approach. Thus, we replace the step \(\textsc {s}_1\) in this procedure with the step: Solve
by a Krylov method (e.g. minres) to a given tolerance. In this way, we have a projected SSKN scheme.
Next, we illustrate how the action of the Jacobian on the increment \(\Delta u^\ell \) is constructed. For this purpose, we determine the second-order directional derivative of our Lagrange functional (2.10) with respect to u, and this requires to consider the linearizations of the forward and adjoint equations with respect to u. We have the following
where \(L(\rho ,u):=\partial _t\rho +\mathrm{div}\,(a(u) \,\rho )\) represents the Liouville operator, and \(*\) means adjoint. In (4.7), the function \({\hat{\rho }}\) is the solution of the following linearized Liouville problem
where \({\hat{a}}= \frac{\partial a}{\partial u} \, \Delta u\).
Equation (4.8) is obtained in the following way. First, define a small variation \({\hat{\rho }}\) of \(\rho \) such that \((\rho + {\hat{\rho }}) \in C_T(L^2(\mathbb {R}^d))\) and \(({\hat{\rho }})_{|t=0}=0\). Then, insert \(\rho +{\hat{\rho }}\) for \(\rho \) in equation (2.4), use the linearity of (2.1) with respect to \(\rho \) and take into account that \(\rho \) itself solves (2.1).
To complete the discussion of (4.7), we explain how to compute \({\hat{q}}\). It is obtained solving the following linearized adjoint problem, resulting from a linearization procedure similar to that for \({\hat{\rho }}\). We have
We solve (4.8) and (4.9) with our KTS scheme. For further details on the implementation of the action of the Jacobian on a vector, we refer to, e.g., [5], Chapter 6.3.5.
Specifically, for our case one can verify that (4.7) is explicitly given component-wise by
where the components of \(\Phi \) are solutions to the following boundary-value problem
We approximate this problem by finite differences for the time derivative, which results in a tridiagonal linear system, and solve it with the Thomas algorithm. Compare this boundary-value problem with (2.14).
Notice that, in general in optimal control problems, the reduced Hessian has a favourable spectral structure, in the sense that it is spectrally equivalent to a second-kind Fredholm integral operator, and in this case Krylov solvers can converge in a mesh-independent number of iterations [1]. We remark that our numerical experience is consistent with this statement. Moreover, it is supported by our estimate of the condition number of the Jacobian. For this purpose, we use the power method to estimate the largest eigenvalue of \(\mathcal {\widetilde{J}}(u)\), and the inverse power method to estimate its smallest eigenvalue, and obtain an approximation to the spectral condition number of the Jacobian. (Notice that these methods also do not require the assembly of \(\mathcal {\widetilde{J}}(u)\).) We compute this condition number in correspondence to different mesh sizes and report these values in Table 1. A plot of these values for different mesh sizes is shown in Fig. 1, where we see that the condition number has similar values for different mesh sizes.
Next, we discuss step \(\textsc {s}_2\) of (4.6). This step is required to ensure that any control update results in a control function in \(U_{ad}\). To implement the \(H^1\) projection, \(P_{U_{ad}} \), we solve the following optimization problem
Since \(\widetilde{\mathbb {H}}^1_T\) is a Hilbert space and \(U_{ad}\) is non-empty, closed and convex, we know that there exists a unique projection (see [33], Theorem 4.11). This problem can equivalently be written as follows
Notice that, corresponding to this optimization problem, we have the following Lagrange functional with Lagrange multipliers \(q_a, \, q_b\),
To solve this optimization problem to implement the projection \(P_{U_{ad}}\), we use a gradient descent scheme; see, e.g., [4], Section 2.8.
Next, we summarize the Newton procedure to solve our Liouville ensemble optimal control problem in the following algorithm that determines the reduced gradient at a given u.

Notice that \(\delta \) enters in step 3 of Algorithm 4.1 through \({\hat{\lambda }}\). With Algorithm 4.1, we can define our projected semi-smooth Krylov–Newton algorithm as follows.

In this algorithm, we use the difference between consecutive iterations of the control as termination criterion, specifically to stop the algorithm, if the difference is less then a threshold \(tol>0\). Moreover, we define a maximum number of iterations \(\ell _{\max } \in {\mathbb {N}}\).
5 Numerical experiments
In this section, we present results of numerical experiments to validate the accuracy of our numerical framework and to demonstrate the ability of the ensemble optimal control in driving the density in order to perform a achieve given objectives.
We have proved second-order accuracy of our SSPRK2-KT scheme for the Liouville equation in Theorem 3.1. In order to validate this estimate, we define a setting that admits an exact solution. Thus, we choose the following control function
which results in the following drift
Further, we take the initial condition
where \(v_0=\frac{1}{4}\).
With this setting, the Liouville problem
admits the solution
where the mean \(m(t)=(m_1(t),m_2(t))\) and the variance \(v=(v_1(t),v_2(t))\) are the solutions to (2.6) with the initial conditions \(m(0) = (0,0)\) and \(v(0)=(1,1)\). Now, we use this setting to determine the solution error of our algorithm. For this purpose, we solve the corresponding Liouville problem and report the values of the discrete \(L^1\) norm of the solution error given by
In Table 2, the values of \(e_{KT}\) corresponding to different grids are presented, and in Fig. 2, we compare the rate of change of these values with that of first- and second-order accuracies. We see that the obtained numerical accuracy lies between these reference rates, becoming closer to second-order by refining the mesh size.
Next, we validate our estimate for the KTS scheme in solving a transport problem with source term (the adjoint problem) as given in Theorem 3.2. We proceed in a similar way as for the Liouville problem. In fact, since (5.3) solves the Liouville problem with the drift (5.1) and the initial condition (5.2), it is easy to verify that this solution satisfies the problem
where \({\tilde{a}}(x,t)=-a(x,t)\), \(\theta = {\bar{\rho }} \nabla a\) and \(-\varphi = \rho _0\). Thus, we have the solution \({\bar{q}}={\bar{\rho }}\).
However, notice that the KTS scheme uses the Strang splitting in order to accommodate the source term \( - \theta \). Therefore, the solution \({\bar{q}}={\bar{\rho }}\) is appropriate to independently test the KTS scheme. Thus, we define
Hence, we perform a second series of experiments where we compute the values of this norm in correspondence to solutions obtained on different grids. These values are reported in Table 3, and in Fig. 3, we compare the rate of change of \(e_{KTS}\) with that of first- and second-order accuracies. Also in this case, we see that the resulting rate of convergence is approximately of second-order.
Next, we validate the ability of our optimization framework to construct controls that steer the ensemble density in order to follow a desired path. For this purpose, we start considering the tracking of a piecewise smooth trajectory with an initial density given by an unimodal distribution. Thereafter we demonstrate that our approach allows to construct control functions that are able to drive the evolution of the density with a bimodal structure.
In our first experiment on tracking, we choose \(\Omega = [-1,1] \times [-1,1]\), and the initial density on this domain is given by
This \(\rho _0 \in C^\infty (\Omega )\) represents a unimodal Gaussian distribution centred in \({\xi _0}=(-0.5,0.5)\), with variance \(\sigma =\frac{1}{4}\), and we take \(C_0 = \frac{1}{10}\). Notice that, by this choice, the value of \(\rho _0\) at the boundary of \(\Omega \) is of the order of machine precision.
In this experiment, the purpose of the control is to drive the ensemble of trajectories along the following piecewise smooth desired trajectory
A plot of this trajectory in \(\Omega \) is given in Fig. 4a. Correspondingly, our potentials in the objective functional are chosen as follows
where \(x \in \Omega \) and \(t \in [0,T]\), and the values of \(C_\theta ,\,C_\varphi , \, \sigma _\theta \) and \(\sigma _\varphi \) are given in Table 4.
Now, we specify a setting that facilitates a comparison of our results of ensemble control with a simple dynamics for the trajectory. Specifically, suppose that our desired trajectory is the result of the following dynamics
Then we can immediately compute the control \(u_1\) in this equation such that the solution to (5.5) is given by (5.4). This control is plotted in Fig. 5b, and we refer to it as the single-trajectory control, specifically taken \(u_2 \equiv 0\), which corresponds to no change in the variance. Notice that this control is not in our control space \(U_{ad}\) (recall its definition (2.8) above), since it is not continuous. Moreover, in its construction, we do not require to satisfy the conditions of its value being zero at initial and final times.
In our drift (2.5), we choose \(a_0=0\), \(b=1\) and \(c=0\), and with this setting we solve our Liouville control problem, taking the numerical values given in Table 4. The resulting control function is depicted in Fig. 5a, which appears similar to the single-trajectory control in Fig. 5b. We see that the former is in \(\mathbb {H}^1_T\) and is zero at \(t=0\) and \(t=T\) as required, we refer to it as the Liouville control.
Corresponding to the Liouville control, we obtain an evolution of the density with which we compute the function \({{\mathbb {E}}}[x](t)=\int x \, \rho (x,t) \, dx\). This function is shown in Fig. 4b. Notice that it closely resembles the desired trajectory.
In our second experiment, we consider the setting \(a_0=0\), \(b=1\) and \(c=1\), an we take a smooth initial \(\rho _0\) that is given by a bimodal Gaussian distribution as follows
where
The values of the other parameters are specified in Table 5.
In this case, we choose the following desired trajectory
We have that \({\xi _D(0)}\) corresponds to the midpoint between the centres of the two Gaussians defining the initial density; see Fig. 6a, where we plot circles around the centres of the two Gaussians with radius of their standard deviation.
With this setting, we solve our Liouville optimal control problem and obtain the controls shown in Fig. 6b. The values of \(C_\theta ,\,C_\varphi , \, \sigma _\theta \) and \(\sigma _\varphi \) together with the values of the numerical parameters are given in Table 5.
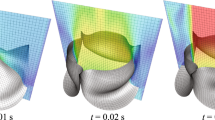
Corresponding to these controls, we obtain the evolution of the density depicted in Fig. 7a. Specifically, we plot the shape of the density \(\rho \) at all times. One can see that the bimodal density is driven towards the desired trajectory becoming unimodal. The same result is visualized in Fig. 7b from a different perspective.
We would like to conclude this section considering a setting that generalizes our framework. Our purpose is to demonstrate that our control framework is also able to drive a smooth bimodal distribution to follow two trajectories. In this case, we choose a potential \(\theta \) that resembles a double well, so that it provides two basins of attraction corresponding to the two trajectories.
In this experiment, we consider the initial bimodal \(\rho _0\) given in (5.6), and consider the following two desired trajectories
In correspondence to these trajectories, we define \(\theta \) as follows
Similarly, we define \(\varphi (x)=\theta (x,T)\).
We solve the resulting ensemble control problem with Algorithm 4.2 and obtain the controls depicted in Fig. 8. In correspondence to these controls, we obtain the evolution of the initial bimodal density shown in Fig. 9b. We see that the two initial Gaussians are driven along the desired trajectories \({\xi _{D1}}\) and \({\xi _{D2}}\) shown in Fig. 9a and merge at the final time.
6 Conclusion
A numerical optimization framework to solve non-smooth ensemble optimal control problems governed by the Liouville equation was presented. In these problems, the cost functional has the structure of an expected value function for the ensemble of trajectories and includes \(L^2\), \(L^1\) and \(H^1\) costs of the controls.
The solutions to these Liouville control problems were characterized as solutions to first-order optimality systems consisting of the Liouville equation, its optimization adjoint, and a variational inequality in \(H^1\). In order to numerically solve the Liouville problem, a strong stability-preserving Runge–Kutta method (SSPRK2) in time and a Kurganov–Tadmor (KT) scheme in space were discussed, proving that the combined SSPRK2-KT scheme provides a second-order accurate solution. Moreover, positivity and conservativeness of the SSPRK2-KT scheme were also shown under a CFL condition. To solve the adjoint Liouville equation, a Strang splitting technique combined with the SSPRK2-KT scheme and exact integration were proposed. The resulting Kurganov–Tadmor–Strang scheme was shown to be second order accurate.
The above approximation schemes were used to implement a \(H^1\)-projected semi-smooth Krylov Newton method to solve the Liouville optimal control problems. Results of numerical experiments were presented that successfully validated the proposed computational framework and the ability of the resulting control functions to drive the ensemble of trajectories in the case of both unimodal and bimodal initial distributions.
References
Akçelik, V., Biros, G., Ghattas, O., Hill, J., Keyes, D.B.: In: Heroux, M.A., Raghavan, P., Simon, H.D. (eds.) van Bloemen Waanders, Parallel algorithms for PDE-constrained optimization. In: Parallel Processing for Scientific Computing, vol. 16, pp. 291–322. Society for Industrial and Applied Mathematics (2006)
Ambrosio, L., Crippa, G.: Continuity equations and ODE flows with non-smooth velocity. Proc. R. Soc. Edinb. Sect. A 144, 1191–1244 (2014)
Bartsch, J., Borzì, A., Fanelli, F., Roy, S.: A theoretical investigation of Brockett’s ensemble optimal control problems. Calc. Var. Partial Differ. Equ. 58, 34 (2019)
Bertsekas, D.P.: Constrained optimization and Lagrange multiplier methods. In: Jovanovich, H.B. (ed.) Computer Science and Applied Mathematics. Academic Press, New York (1982)
Borzì, A., Ciaramella, G., Sprengel, M.: Formulation and Numerical Solution of Quantum Control Problems. Computational Science & Engineering, vol. 16. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2017)
Borzì, A., Kunisch, K., Kwak, D.Y.: Accuracy and convergence properties of the finite difference multigrid solution of an optimal control optimality system. SIAM J. Control Optim. 41, 1477–1497 (2002)
Brockett, R.: Notes on the control of the Liouville equation. In: Control of Partial Differential Equations of Lecture Notes in Mathematics, vol. 2048, pp. 101–129. Springer, Heidelberg (2012)
Brockett, R.W.: Optimal control of the Liouville equation. In: Proceedings of the International Conference on Complex Geometry and Related Fields, Volume 39 of AMS/IP Stud. Adv. Math., Amer. Math. Soc., Providence, pp. 23–35 (2007)
Brockett, W.: Minimum attention control. In: Proceedings of the 36th IEEE Conference on Decision and Control, vol. 3, pp. 2628–2632. IEEE (1997)
Cercignani, C.: The Boltzmann Equation and Its Applications. Applied Mathematical Sciences, vol. 67. Springer, New York (1988)
Chertock, A., Kurganov, A.: On splitting-based numerical methods for convection-diffusion equations. Numer. Methods Balance Laws 24, 303–343 (2010)
Chertock, A., Kurganov, A., Petrova, G.: Fast explicit operator splitting method for convection-diffusion equations. Int. J. Numer. Methods Fluids 59, 309–332 (2009)
Cho, H., Venturi, D., Karniadakis, G.E.: Numerical methods for high-dimensional probability density function equations. J. Comput. Phys. 305, 817–837 (2016)
Ciaramella, G., Borzì, A.: A LONE code for the sparse control of quantum systems. Comput. Phys. Commun. 200, 312–323 (2016)
Ciaramella, G., Borzì, A.: Quantum optimal control problems with a sparsity cost functional. Numer. Funct. Anal. Optim. 37, 938–965 (2016)
Clarke, F.: Optimization and Nonsmooth Analysis, Canadian Mathematical Society Series of Monographs and Advanced Texts. Wiley, New York (1983)
Clarke, F.: Functional Analysis, Calculus of Variations and Optimal Control, vol. 264 of Graduate Texts in Mathematics. Springer, New York (2013)
DiPerna, R.J., Lions, P.-L.: Ordinary differential equations, transport theory and Sobolev spaces. Invent. Math. 98, 511–547 (1989)
Duderstadt, J.J., Martin, W.R.: Transport Theory. A Wiley-Interscience Publication. Wiley, New York (1979)
Feireisl, E., Novotný, A.: Singular Limits in Thermodynamics of Viscous Fluids, Advances in Mathematical Fluid Mechanics. Birkhäuser Verlag, Basel (2009)
Gerya, T.: Numerical solutions of the momentum and continuity equations. In: Introduction to Numerical Geodynamic Modelling, pp. 82–104. Cambridge University Press (2019)
Godlewski, E., Raviart, P.-A.: Hyperbolic Systems of Conservation Laws, vol. 3/4 of Mathématiques & Applications (Paris). Ellipses, Paris (1991)
Gottlieb, S., Shu, C.-W.: Total variation diminishing Runge–Kutta schemes. Math. Comput. 67, 73–85 (1998)
Kraposhin, M., Bovtrikova, A., Strijhak, S.: Adaptation of Kurganov–Tadmor numerical scheme for applying in combination with the PISO method in numerical simulation of flows in a wide range of Mach numbers. Procedia Comput. Sci. 66, 43–52 (2015)
Kurganov, A., Petrova, G.: A second-order well-balanced positivity preserving central-upwind scheme for the Saint–Venant system. Commun. Math. Sci. 5, 133–160 (2007)
Kurganov, A., Tadmor, E.: New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equations. J. Comput. Phys. 160, 241–282 (2000)
Lions, J.-L.: Optimal Control of Systems Governed by Partial Differential Equations. Springer, New York (1971)
Nishikawa, H.: A truncation error analysis of third-order MUSCL scheme for nonlinear conservation laws. Int. J. Numer. Methods Fluids (2020)
Osher, S.: Convergence of generalized MUSCL schemes. SIAM J. Numer. Anal. 22, 947–961 (1985)
Osher, S., Chakravarthy, S.: High resolution schemes and the entropy condition. SIAM J. Numer. Anal. 21, 955–984 (1984)
Pogodaev, N.: Optimal control of continuity equations. Nonlinear Differ. Equ. Appl. 23, pp. Art. 21, 24 (2016)
Qi, L., Sun, D.: A nonsmooth version of Newton’s methods. Math. Programm. 58, 353–367 (1993)
Rudin, W.: Real and Complex Analysis, 3rd edn. McGraw-Hill, New York (1987)
Rusanov, V.: Calculation of intersection of non-steady shock waves with obstacles. J. Comput. Math. Phys. USSR 1, 267–279 (1961)
Shu, C.-W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77, 439–471 (1988)
Speth, R.L., Green, W.H., MacNamara, S., Strang, G.: Balanced splitting and rebalanced splitting. SIAM J. Numer. Anal. 51, 3084–3105 (2013)
Stadler, G.: Elliptic optimal control problems with \(L^1\)-control cost and applications for the placement of control devices. Comput. Optim. Appl. 44, 159–181 (2009)
Strang, G.: On the construction and comparison of difference schemes. SIAM J. Numer. Anal. 5, 506–517 (1968)
Tang, T., Teng, Z.: Monotone Difference Schemes for Two Dimensional Nonhomogeneous Conservation Laws. Pitman Research Notes in Mathematics Series, pp. 229–243 (1998)
Tröltzsch, F.: Optimal Control of Partial Differential Equations. Graduate Studies in Mathematics, vol. 112. American Mathematical Society, Providence (2010)
Ulbrich, M.: Semismooth Newton Methods for Variational Inequalities and Constrained Optimization Problems in Function Spaces. MOS-SIAM Series on Optimization, vol. 11. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2011)
Urabe, M.: Theory of errors in numerical integration of ordinary differential equations. J. Sci. Hiroshima Univ. Ser. A-I (Math.) 25, 3–62 (1961)
Acknowledgements
The first author acknowledges partial support by SPARC Industries sarl, Luxemburg. The third author has been partially supported by the LABEX MILYON (ANR-10-LABX-0070) of Université de Lyon, within the program “Investissement d’Avenir” (ANR-11-IDEX-0007), and by the projects BORDS (ANR-16-CE40-0027-01) and SingFlows (ANR-18-CE40-0027), all operated by the French National Research Agency (ANR).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bartsch, J., Borzì, A., Fanelli, F. et al. A numerical investigation of Brockett’s ensemble optimal control problems. Numer. Math. 149, 1–42 (2021). https://doi.org/10.1007/s00211-021-01223-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01223-6