Abstract
As an enhanced version of probabilistic hesitant fuzzy sets and dual hesitant fuzzy sets, probabilistic dual hesitant fuzzy sets (PDHFSs) combine probabilistic information with the membership degree and non-membership degree, which can describe decision making information more reasonably and comprehensively. Based on PDHFSs, this paper investigates the approach to group decision making (GDM) based on incomplete probabilistic dual hesitant fuzzy preference relations (PDHFPRs). First, the definitions of order consistency and multiplicative consistency of PDHFPRs are given. Then, for the problem that decision makers (DMs) cannot provide the reasonable associated probabilities of probabilistic dual hesitant fuzzy elements (PDHFEs), the calculation method of the associated probability is given by using an optimal programming model. Furthermore, the consistency level for PDHFPRs is tested according to the weighted consistency index defined by the risk attitude of DMs. In addition, a convergent iterative algorithm is proposed to enhance the unacceptable consistent PDHFPRs’ consistency level. Finally, a GDM approach with incomplete PDHFPRs is established to obtain the ranking of the alternatives. The availability and rationality of the proposed decision making approach are demonstrated by analyzing the impact factors of haze weather.
Similar content being viewed by others
Introduction
Group decision making (GDM) determines the most ideal alternative according to evaluation information expressed by a group of decision makers (DMs) [1]. Due to the advantages of overcoming the limitations of empirical knowledge and the cognitive abilities of individual DMs, it has been widely used [2]. The uncertainty and fuzziness of the decision making environment make more suitable for DMs to express evaluation information with fuzzy information than with clear numbers. Fuzzy sets (FSs) [3] have become useful tools for expressing uncertainty information in GDM problems [4,5,6], and they have been applied in semiconductor inter-bay handling systems [7], green supply chain management [8, 9], disease diagnosis [10,11,12], and many other fields [13, 14]. Thus far, different extensions of FSs have been proposed. Zhu et al. proposed dual hesitant FSs (DHFSs) in [15]. Using DHFSs, DMs can provide hesitant evaluation information from the perspective of membership degrees (MDs) and non-membership degrees (NMDs). Zhu established probabilistic hesitant FSs (PHFSs) in [16], where different MDs in PHFSs have different occurrence possibilities. However, the occurrence possibilities of membership and non-membership values are not considered in DHFSs, and NMDs and their corresponding importance are not considered in PHFSs. Therefore, DHFSs and PHFSs cannot fully express the evaluation information. Hao et al. [17] established probabilistic DHFSs (PDHFSs), which can comprehensively consider MDs, NMDs and their occurrence possibilities.
However, in GDM problems, it may be more intuitive for DMs to provide evaluation information by using preference relation (PR). PR is a judgment matrix obtained by comparing the paired alternatives. With the development of FS theory, fuzzy PR [18] has developed into other extended forms, e.g., probabilistic hesitant fuzzy PR [19], intuitionistic fuzzy PR (IFPR) [20], and hesitant fuzzy PR [21]. Based on PDHFSs, probabilistic dual hesitant fuzzy PRs (PDHFPRs) is a valuable extension of fuzzy PR. In GDM problem, some DMs think that the possible values of \(x_{i}\) prior to \(x_{j}\) are 0.4 and 0.5, while the possible values of \(x_{i}\) inferior to \(x_{j}\) are 0.2 and 0.3, and the importance of these values is different. However, due to time constraints and limited knowledge of DMs, the importance of these degrees is sometimes difficult to obtain. Therefore, there is an urgent need to study probability calculation method of incomplete PDHFPRs.
The purpose of GDM is to choose the most ideal decision from a group of alternatives. One of the most common methods is to build a model based on the consistency of PRs. Moreover, the consistency of PR is used to measure the degree of agreement among the preference values provided by the individual DMs. The lack of consistency of PR may lead to unreasonable results. To date, the research on the consistency of PR has been fruitful [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. However, only Shao and Zhang [37] have focused on the consistency of PDHFPRs. In addition, Shao and Zhang’s method [37] has certain limitations, which is manifested in that the consistency index does not consider the risk attitude of DMs, and the weight of DMs is given subjectively. Thus, it is urgent to study the consensus of PDHFPRs and use it to solve the GDM problem.
The above analysis motivate us to further study some issues related to PDHFPRs, such as how to obtain the probability information of incomplete PDHFPRs, how to measure the consistency level of PDHFPRs, and how to use consistency to solve the GDM problem with PDHFPRs.
The rest of the sections are listed as follows: In “Related work”, the related work is briefly reviewed. In “Preliminaries”, some basic concepts are briefly reviewed. “Probability calculation method based on the multiplicative consistency of PDHFPRs” defines multiplicative consistency of PDHFPRs and proposes a probability calculation method based on the multiplicative consistency of PDHFPRs. In “A GDM approach with incomplete PDHFPRs”, a convergent algorithm to adjust the consistency level for individual PDHFPRs is built, and a GDM approach with incomplete PDHFPRs is constructed. In “Illustrative example”, the proposed approach is used to analyze the impact factors of haze weather. “Conclusion and future work” provides some conclusions.
Related work
In this section, we introduce the GDM method based on PR and review the existing research on probabilistic dual hesitant fuzzy environment that are most related to our work.
As an effective technique in decision making field, GDM based on various types of PR is widely concerned, which are summarized in Table 1. From Table 1, to date, it is rare to discuss the consistency of PDHFPRs [37].
Furthermore, probabilistic dual hesitant fuzzy environment has been widely used in GDM, which are listed in Table 2. Table 2 shows that most of the existing researches concentrated on GDM based on PDHFSs, and only Shao and Zhang [37] discussed GDM based on PDHFPRs.
Based on the above discussion, it is meaningful to study GDM problems based on PDHFPRs. The main contributions of this paper are summarized as follows:
-
1.
An optimization model based on multiplicative consistency is established to obtain the reasonable associated probabilities of PDHFEs.
-
2.
For an unacceptable consistent PDHFPR, based on a linear optimization model, a convergent algorithm is investigated to improve the consistency level.
-
3.
A GDM approach with incomplete PDHFPRs is constructed, and the effectiveness and applicability of the proposed decision making approach are verified by analyzing the impact factors of haze weather.
Preliminaries
This section reviews some basic concepts of DHFS, PHFS, PDHFS, and PDHFPRs:
Definition 1
[15] A DHFS F on a set of alternatives X is defined by
\(h_{F}(x)\) indicates the possible degrees to the set X of x, \(m_{F}(x)\) indicates the possible NMDs to the set X of x. In addition,
for \(i=1,2,\ldots , \# h_{F}(x)\), \(j=1,2,\ldots ,\# m_{F}(x)\), where \(\alpha _{i}\in h_{F}(x)\), \(h_{F}(x)=(\alpha _{1},\alpha _{2}, \ldots , \alpha _{\# h_{F}(x)})\), \(\alpha ^{+}=\bigcup _{\alpha _{i}\in h_{F}(x)}\max \{\alpha _{i}\}\), \(\beta _{j}\in m_{F}(x)\), \(m_{F}(x)=(\beta _{1},\beta _{2}\), \(\ldots , \beta _{\# m_{F}(x)})\), and \(\beta ^{+}=\bigcup _{\beta _{i}\in m_{F}(x)}\max \{\beta _{j}\}\). \(\# h_{F}(x)\), \(\# m_{F}(x)\) are the cardinal numbers of \(h_{F}(x)\) and \(m_{F}(x)\), respectively.
Definition 2
[16] A PHFS H on a set of alternatives X is defined by
where \(h_{x}\in [0,1]\) indicates the possible values to the set X of x, \(p_{x}\in [0,1]\) is the associated probabilities of \(h_{x}\). In addition, \(h_{x}(p_{x})\) is called a probabilistic hesitant fuzzy element and simplified to be expressed by
where \(\gamma _{i}\in h_{x}\), \(p_{i}\in p_{x}\) is the associated probability of \(\gamma _{i}\) and \(\sum _{i=1}^{\# h_x} p_i=1\). \(\#h_x\) is the cardinal number of \(h_{x}(p_{x})\).
Definition 3
[17] A PDHFS B on a set of alternatives X is defined by
h(x) |p(x) and m(x) |q(x) denote some possible elements, where h(x) indicates the possible degrees to the set X of x, p(x) is the associated probabilities of h(x), m(x) indicates the possible NMDs to the set X of x, and q(x) denotes the associated probabilities of m(x). In addition,
where \(\varepsilon \in h(x)\), \(\varepsilon ^{+}\in h^{+}(x)=\bigcup _{\varepsilon \in h(x)}\max \{\varepsilon \}\), \(\delta \in m(x)\), \(\delta ^+\in m^{+}(x)=\bigcup _{\delta \in m(x)}\max \{\delta \}\), \(p_i\in p(x)\) and \(q_i\in q(x)\). \(\# h\) and \(\# m\) are the cardinal numbers of h(x) |p(x) and m(x) |q(x), respectively.
Remark 1
Hao et al. [17] define \(b=(h(x) | p(x),m(x) | q(x))\) as a PDHFE. For convenience, \(b=(h(x) | p(x),m(x) | q(x))\) is simplified to \(b=(h | p,m | q)\).
Remark 2
Particularly, if \(p=q\) , then a PDHFS is simplified to a DHFS. Similarly, if \(h\ne \phi \), \(m=\phi (q=\phi )\), then a PDHFS reduces to a PHFS.
Definition 4
[37] A PDHFPR D on a set of alternatives \(X=\{x_1,x_2,\ldots ,x_n\}\) is characterized by \(D=(d_{ij})_{n\times n}\), where \(d_{ij}=(h_{ij}|p_{ij},m_{ij}|q_{ij})\) is a PDHFE. \(h_{ij}\) and \(m_{ij}\) are the possible degrees to which \(x_i\) is preferred and non-preferred to \(x_j\), \(p_{ij}\) is the associated probabilities of \(h_{ij}\), and \(q_{ij}\) is the associated probabilities of \(m_{ij}\), \(d_{ij}\) should satisfy the following requirements:
-
1.
For \(i=1,2,\ldots ,n\), \(d_{ij}=(\{0.5|1\},\{0.5|1\})\).
-
2.
For \(i\ne j\), \(i,j=1,2,\ldots ,n\),
-
(a)
If \(h_{ij}\ne \phi \), \(m_{ij}\ne \phi \), then
$$\begin{aligned} \left\{ \begin{array}{l} {h_{ij,r}=m_{ji,r},m_{ij,e}=h_{ji,e},}\\ {p_{ij,r}=q_{ji,r},q_{ij,e}=p_{ji,e},} \end{array}\right. \end{aligned}$$(8)for all \(r=1,2,\ldots ,\# h_{ij}-1\), \(e=1,2,\ldots ,\# m_{ij}-1\), where \(h_{ij,r}\in h_{ij}\) indicates the rth element in \(h_{ij}\), \(p_{ij,r}\) is the associated probability of \(h_{ij,r}\) and \(\sum _{r=1}^{\# h_{ij}}p_{ij,r}=1\), \(m_{ij,e}\in m_{ij}\) indicates the eth element in \(m_{ij}\), \(q_{ij,e}\) is the associated probability of \(m_{ij,e}\) and \(\sum _{e=1}^{\# m_{ij}}q_{ij,e}=1\), \(h_{ij,r}<h_{ij,r+1}\) and \(m_{ij,e}<m_{ij,e+1}\).
-
(b)
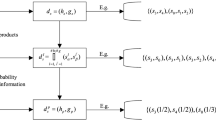
If
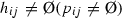 ,
, 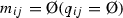 , then $$\begin{aligned}&h_{ij,r}+h_{ji,(\# h_{ij-r+1})}=1, \nonumber \\&p_{ij,r}=p_{ji,(\# h_{ij-r+1})}, \# h_{ij}=\# h_{ji}, \end{aligned}$$(9)
, then $$\begin{aligned}&h_{ij,r}+h_{ji,(\# h_{ij-r+1})}=1, \nonumber \\&p_{ij,r}=p_{ji,(\# h_{ij-r+1})}, \# h_{ij}=\# h_{ji}, \end{aligned}$$(9)for all \(r=1,2,\ldots ,\# h_{ij}-1,\), where \(h_{ij,r}\in h_{ij}\) indicates the rth element in \(h_{ij}\), \(p_{ij,r}\) is the associated probability of \(h_{ij,r}\) and \(\sum _{r=1}^{\# h_{ij}}p_{ij,r}=1\), and \(h_{ij,r}<h_{ij,r+1}\).
-
(c)
If
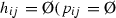 ,
,  , then $$\begin{aligned}&m_{ij,e}+m_{ji,(\# g_{ij-e+1})}\nonumber \\&\quad =1, q_{ij,e}=q_{ji,(\# g_{ij-e+1})}, \# m_{ij}=\# m_{ji}, \end{aligned}$$(10)
, then $$\begin{aligned}&m_{ij,e}+m_{ji,(\# g_{ij-e+1})}\nonumber \\&\quad =1, q_{ij,e}=q_{ji,(\# g_{ij-e+1})}, \# m_{ij}=\# m_{ji}, \end{aligned}$$(10)for all \(e=1,2,\ldots ,\# m_{ij}-1\), where \(m_{ij,e}\in m_{ij}\) indicates the eth element in \(m_{ij}\), \(q_{ij,e}\) is the associated probability of \(m_{ij,e}\) and \(\sum _{e=1}^{\# m_{ij}}q_{ij,e}=1\), and \(m_{ij,e}<m_{ij,e+1}\).
-
(a)
Example 1
The decision information of alternatives \(\{x_1,x_2,x_3\}\) is provided by the DM as follows:
For \(i\ne j\) and \(i,j=1,2,3\), there are \(0\le p_{ij,r},q_{ij,r}\le 1\), \(\sum _{r=1}^2p_{ij,r}=1\) and \(\sum _{r=1}^2q_{ij,r}=1\).
From Definition 4, D is a PDHFPR.
Probability calculation method based on the multiplicative consistency of PDHFPRs
The limited knowledge of DMs makes it hard for DMs to provide accurate associated probabilities of PDHFEs through subjective evaluation. This section proposes probability calculation method based on the multiplicative consistency of PDHFPRs.
Multiplicative consistency of PDHFPRs
Definition 5
[20] An IFPR on the set \(X=\{x_1,x_2,\ldots ,x_n\}\) is defined by \(A=(a_{ij})_{n\times n}\), where \(a_{ij}=\langle u_{ij},v_{ij}\rangle \) is an intuitionistic fuzzy value (IFV), \(u_{ij}\) indicates the degree that \(x_i\) is prior to \(x_j\), \(v_{ij}\) indicates the degree that \(x_i\) is not prior to \(x_{j}\) and for \(i,j=1,2,\ldots ,n\),
Definition 6
[20] Let \(a_{ij}=\langle u_{ij}, v_{ij}\rangle \) be an IFV. The score function of the IFV is defined by
Definition 7
[27] An IFPR on the set \(X=\{x_1,x_2,\ldots ,x_n\}\) is defined by \(A=(a_{ij})_{n\times n}\), if there is a normalized intuitionistic fuzzy weight vector \(\phi =(\phi _1,\phi _2,\ldots ,\phi _n)^T\) such that
then, A is a multiplicatively consistent IFPR, where \(\phi _{i}=\langle \phi _{i\mu }, \phi _{i\nu }\rangle \), \(\phi _{i\mu },\phi _{i\nu }\in (0,1]\), \(\phi _{i\mu }+\phi _{i\nu }\le 1\), \(\sum _{j\ne i}\phi _{j\mu }\le \phi _{i\nu }\), and \(\sum _{j\ne i}\phi _{j\nu }\le \phi _{i\mu }+n-2\), \(i,j=1,2,\ldots ,n\).
The following introduces the order consistency and multiplicative consistency of PDHFPRs. For complete PDHFPRs, order consistency provides a quick and effective way to obtain the order of alternatives.
Definition 8
A PDHFPR \(D=(d_{ij})_{n\times n}\) on the set \(X=\{x_1,x_2,\ldots ,x_n\}\) is an order consistent PDHFPR, if \(d_{sj}\ge d_{tj}\) for all \(j=1,2,\ldots ,n\), where \(s,t=1,2,\ldots ,n\).
Definition 9
A PDHFPR on the set \(X=\{x_1,x_2,\ldots ,x_n\}\) is represented by \(D=(d_{ij})_{n\times n},\) where \(d_{ij}=(h_{ij}|p_{ij},m_{ij}|q_{ij})\). \(U_{d_{ij}}\) and \(V_{d_{ij}}\) are denoted by
where \(h_{ij,r}\in h_{ij}\) indicates the rth element in \(h_{ij}\), \(p_{ij,r}\) is the associated probability of \(h_{ij,r}\) and \(\sum _{r=1}^{\# h_{ij}}p_{ij,r}=1\), \(m_{ij,e}\in m_{ij}\) indicates the eth element in \(m_{ij}\), \(q_{ij,e}\) is the associated probability of \(m_{ij,e}\) and \(\sum _{e=1}^{\# m_{ij}}q_{ij,e}=1\).
Based on Definition 4, for \(\forall i,j=1,2,\ldots ,n\), then \(\# h_{ij}=\# m_{ji}\), \(\# m_{ij}=\# h_{ji}\) and \(U_{d_{ii}}=V_{d_{ii}}=0.5\). Furthermore,
Since \(h_{ij,r},m_{ij,e},p_{ij,e},q_{ij,e}\in [0,1]\), then
Thus, \(E_D=\langle U_{d_{ij}},V_{d_{ij}}\rangle \) is an IFPR.
Definition 10
A PDHFPR on the set \(X=\{x_1,x_2,\ldots ,x_n\}\) is denoted as \(D=(d_{ij})n\times n,\) where \(d_{ij}=(h_{ij}|p_{ij},m_{ij}|q_{ij})\). If a normalized weight vector \(W=(w_1,w_2,\ldots ,w_n)^T\) exists such that
then PDHFPR D is multiplicative consistent, where \(w_i=\langle w_{i\mu },w_{i\nu }\rangle \) satisfies \(w_{i\mu },w_{i\nu }\in (0,1]\), \(w_{i\mu }+w_{i\nu }\le 1\), \(\sum _{j\ne i}w_{j\mu }\le w_{i\nu }\), and \(\sum _{j\ne i}w_{j\nu }\le w_{i\mu }+n-2\), \(i,j=1,2,\ldots ,n\).
Probability calculation method
Due to the complexity and uncertainty of the decision problem, the DMs cannot provide the accurate associated probabilities of PDHFEs, and it is challenging to give PDHFPRs with multiplicative consistency. At this time, the decision making result is not rational. When a PDHFPR does not satisfy multiplicative consistency, Eq. (15) does not hold, which implies that
The non-negative deviation variables \(\tau _{ij}\) and \(\rho _{ij}\) are defined as follows:
The smaller the value of the non-negative deviation variables \(\tau _{ij}\) and \(\rho _{ij}\) , the higher the level of multiplicative consistency of PDHFPR D.
From \(\sum _{r=1}^{\# h_{ij}}h_{ij,r}\cdot p_{ij,r}=\sum _{r=1}^{\# m_{ji}}m_{ji,r}\cdot q_{ji,r}\) and \(\sum _{e=1}^{\# m_{ij}}m_{ij,e}\cdot q_{ij,r}=\sum _{e=1}^{\# h_{ji}}h_{ji,e}\cdot p_{ji,e}\), we can obtain \(\tau _{ij}=|\sum _{r=1}^{\# h_{ij}}h_{ij,r}\cdot p_{ij,r}-\sqrt{w_{i\mu }\cdot w_{j\nu }}|=|\sum _{e=1}^{\# m_{ij}}m_{ji,e}\cdot q_{ji,e}-\sqrt{w_{i\nu }\cdot w_{j\mu }}|=\rho _{ji}\) and \(\tau _{ij}=\rho _{ji}\) Thus, we only need to consider the upper triangular elements of PDHFPR and can simplify the optimization model as follows:
(M-1)
Then, there exist four non-negative deviation variables \(o_{ij}^-,o_{ij}^+,\varsigma _{ij}^-,\varsigma _{ij}^+\) satisfying the following conditions \(o_{ij}^-\cdot o_{ij}^+=0\) and \(\varsigma _{ij}^-\cdot \varsigma _{ij}^+=0\) such that model (M-1) can be expressed as follows:
(M-2)
Here, \(g_{ij}^-\), \(g_{ij}^+\) , \(n_{ij}^-\) and \(n_{ij}^+\) are the weights of non-negative deviation variables. In this paper, the weights of these deviation variables were chosen to be equal, namely, \(g_{ij}^-=g_{ij}^+=n_{ij}^-=n_{ij}^+=1\). Furthermore, a simplified model is as follows:
(M-3)
From the above discussion, solving model (M-3) can obtain the accurate associated probabilities \(p_{ij,r}\) and \(q_{ij,e} (i,j=1,2,\ldots ,n, r=1,2,\ldots ,\#h_{ij}, e=1,2,\ldots ,\# m_{ij})\) of the PDHFE; the optimal variables \(\widetilde{o_{ij}^+}\), \(\widetilde{o_{ij}^-}\), \(\widetilde{\varsigma _{ij}^+}\), \(\widetilde{\varsigma _{ij}^-}\) and the optimal normalized weight vector \(w^{*}\).
If \(\widetilde{J}=0\), since \(\widetilde{o_{ij}^+}, \widetilde{o_{ij}^-}, \widetilde{\varsigma _{ij}^+}, \widetilde{\varsigma _{ij}^-}\ge 0\) and using the constraints of model (M-3), we can get
Thus, \(D=(d_{ij})_{n\times n}\) is a multiplicative consistent PDHFPR.
The rationality of the proposed method is proven by Example 1. First, based on model (M-3), the corresponding model can be obtained. Using the MATLAB Optimization Toolbox to solve the corresponding model, the following expression is obtained:
Therefore, the complete PDHFPR D in Example 1 is as follows:
In addition, \(\triangle (\widetilde{w_{1}})=0.0174\), \(\triangle (\widetilde{w_{2}})=-0.336\), \(\triangle (\widetilde{w_{3}})=-0.6816\) are obtained, and the ranking of the alternatives is \(x_1\succ x_2\succ x_3\).
According to Definition 8, the complete PDHFPR D satisfies \(d_1\succ d_2\succ d_3\), for all \(j=1,2,3\). Then, the ranking is \(x_1\succ x_2\succ x_3\). Therefore, the feasibility of the probability calculation approach based on the consistency of PDHFPRs is verified.
A GDM approach with incomplete PDHFPRs
A convergent method to improve the consistency of individual PDHFPRs
In the decision making process, PDHFPRs are difficult to achieve full consistency. Considering the risk attitude of DMs, the consistency level for PDHFPRs is tested by a weighted consistency index.
Definition 11
If \(D=(d_{ij})_{n\times n}\) is a PDHFPR, \(\gamma _0\ge 0\) is the given consistency index threshold. A weighted consistency index can be denoted by
\(\mathrm{{OCI}}(D)=\frac{2}{n\cdot (n-1)} \sum _{i=1}^{n-1} \sum _{j=i+1}^n(o_{ij}^-+o_{ij}^++\varsigma _{ij}^++\varsigma _{ij}^-)\) is the DM’s optimistic consistency index, denoting that attitude of the DM is optimistic; \(\mathrm{{PCI}}(D)=\max \{o_{ij}^-+o_{ij}^+ +\varsigma _{ij}^+ +\varsigma _{ij}^-\}\) is the DM’s pessimistic consistency index, denoting that the DM’s attitude is pessimistic; and \(0\le \lambda \le 1\) s the weight coefficient of \(\mathrm{{OCI}}(D)\), which represents the risk attitude of the DM.
If \(\mathrm{{WCD}}(D)\le \gamma _0\), the consistency of PDHFPR \(D=(d_{ij})_{n\cdot n}\) is acceptable. For an unacceptable consistent PDHFPR, the decision result obtained from it is usually unreliable. Next, a convergent automatic iterative algorithm is used for adjusting the consistency level, and the corresponding ranking weight vector is calculated to make a decision.
Algorithm 1
Input: The initial PDHFPR \(D=(d_{ij})_{n\times n}\), the given consistency index threshold \(\gamma _0\), the weight coefficient \(\lambda \), the adjusted coefficient \(\theta \), and the maximum number of iterations \(t_{max}\). Note that \(d_{ij}=(h_{ij}|p_{ij},m_{ij}|q_{ij})\) is a PDHFE, \(h_{ij,r}\in h_{ij}\) indicates the rth element in \(h_{ij}\), \(p_{ij,r}\) is the associated probability of \(h_{ij,r}\) satisfying \(\sum \limits _{r=1}^{\# h_{ij}}p_{ij,r}=1\), \(m_{ij,e}\in m_{ij}\) indicates the eth element in \(m_{ij}\), and \(q_{ij,e}\) is the associated probability of \(m_{ij,e}\) satisfying \(\sum \limits _{e=1}^{\# m_{ij}}q_{ij,e}=1\). Moreover, the associated probabilities \(p_{ij,r}\) and \(q_{ij,e}\) of PDHFEs are unknown.
Output: The acceptable consistent PDHFPR \(D^{*}=(d_{ij}^{*})_{n\times n}\), the optimal normalized weight vector \(w^{*}\) , and the weighted consistency index \(\mathrm{{WCI}}(D^{*})\).
Step 1: Let \(D^{(t)}=(d_{ij}^{(t)})_{n\times n}\), where \(d_{ij}^{(t)}=(h_{ij}^{(t)}|p_{ij},m_{ij}^{(t)}|q_{ij})\) is a PDHFE, and when \(t=0\), \(D^{(0)}=D\).
Step 2: Model (M-3) is used to obtain the accurate associated probabilities \(p_{ij,r}\) and \(q_{ij,e}\), \((i,j=1,2,\ldots ,n, r=1,2,\ldots ,\# h_{ij}, e=1,2,\ldots ,\# m_{ij})\) of PDHFEs, the optimal variables \(\widetilde{o_{ij}^{(t)+}}, \widetilde{o_{ij}^{(t)-}},\widetilde{\varsigma _{ij}^{(t)+}}, \widetilde{\varsigma _{ij}^{(t)-}}\) and the optimal normalized weight vector \(\widetilde{w^{(t)}}=(\widetilde{w_1^{(t)}},\widetilde{w_2^{(t)}}, \ldots ,\widetilde{w_n^{(t)}})\).
Step 3: The weighted consistency index \(\mathrm{{WCI}}(D^{(t)})\) is calculated according to the risk attitude of DMs:
Step 4: If \(\mathrm{{WCI}}(D^{(t)})\le \gamma _0\) or \(t\ge t_{max}\) , turn to Step 6; or else, proceed to the next step.
Step 5: Use Eq. (23) to determine where DMs need to modify preference values.
where \(\widetilde{h_{zc,r}^{(t)}}=h_{zc,r}^{(t)} +\widetilde{o_{zc}^{(t)-}}-\widetilde{o_{zc}^{(t)+}}\) and \(\widetilde{m_{zc,e}^{(t)}}=m_{zc,e}^{(t)} +\widetilde{\varsigma _{zc}^{(t)-}}-\widetilde{\varsigma _{zc}^{(t)+}}\).
Furthermore, by Definition 4, the lower triangular elements of PDHFPR \(D^{(t+1)}\) can be obtained, and then the improved PDHFPR \(D^{(t+1)}=(d_{ij}^{(t+1)})_{n\times n}\) can be obtained. Let \(t=t+1\) , and return to Step 2.
Step 6: Let \(D^{*}=D^{(t)}\) and \(w^{*}=\widetilde{w^{(t)}}\), and get the ranking of the alternatives according to \(w^{*}\).
Next, Theorem 1 is used to prove that Algorithm 1 is convergent.
Theorem 1
If \(D=(d_{ij})_{n\times n}\) is a PDHFPR, where \(d_{ij}=(h_{ij}|p_{ij},m_{ij}|q_{ij})\), \(\{D^{(t)}\}\) are PDHFPR sequences in Algorithm 1, \( \mathrm{{WCI}}(D^{(t)})\) is the weighted index of \(D^{(t)}\). Then, for each iteration t,
Proof
According to the Eqs. (23) and (24), we have \(i\ne z,j\ne c, \widetilde{o_{ij}^{(t+1)+}}=\widetilde{o_{ij}^{(t)+}}, \widetilde{o_{ij}^{(t+1)-}}=\widetilde{o_{ij}^{(t)-}}, \widetilde{\varsigma _{ij}^{(t+1)+}}=\widetilde{\varsigma _{ij}^{(t)+}}\), and \(\widetilde{\varsigma _{ij}^{(t+1)-}}=\widetilde{\varsigma _{ij}^{(t)-}}\).
If \(\widetilde{o_{ij}^{(t)-}}>0, \widetilde{\varsigma _{ij}^{(t)-}} >0\), then \(\widetilde{o_{ij}^{(t)+}}=0\) and \(\widetilde{\varsigma _{ij}^{(t)+}}=0\). There are two possible conditions as follows:
-
(a)
If \(h_{zc,r}^{(t+1)}=\theta \cdot \widetilde{h_{zc,r}^{(t)}} +(1-\theta )\cdot h_{zc,r}^{(t)}\) and \(m_{zc,e}^{(t+1)}=\theta \cdot \widetilde{m_{zc,e}^{(t)}}+(1-\theta )\cdot m_{zc,e}^{(t)}\), then \(h_{zc,r}^{(t+1)}>h_{zc,r}^{(t)}\) and \(m_{zc,e}^{(t+1)}>m_{zc,e}^{(t)}\). Thus, \((\widetilde{o_{zc}^{(t+1)+}} +\widetilde{o_{zc}^{(t+1)-}}+\widetilde{\varsigma _{zc}^{(t+1)+}} +\widetilde{\varsigma _{zc}^{(t+1)-}})< (\widetilde{o_{zc}^{(t)+}} +\widetilde{o_{zc}^{(t)-}}+\widetilde{\varsigma _{zc}^{(t)+}} +\widetilde{\varsigma _{zc}^{(t)-}})\).
-
(b)
If \(h_{zc,r}^{(t+1)}=1-\max _{m_{zc,e}^{(t+1)} \in m_{zc}^{(t+1)}}\{m_{zc,e}^{(t+1)}\}\) or
$$\begin{aligned} m_{zc,e}^{(t+1)} =1-\max _{h_{zc,r}^{(t+1)}\in h_{zc}^{(t+1)}}\{h_{zc,r}^{(t+1)}\}, \end{aligned}$$then \(h_{zc,r}^{(t+1)}\ge h_{zc,r}^{(t)}\) and \(m_{zc,e}^{(t+1)} \ge m_{zc,e}^{(t)}\) and
$$\begin{aligned}&(\widetilde{o_{zc}^{(t+1)+}}+\widetilde{o_{zc}^{(t+1)-}} +\widetilde{\varsigma _{zc}^{(t+1)+}}+\widetilde{\varsigma _{zc}^{(t+1)-}})\\&\quad \le \widetilde{(}{o_{zc}^{(t)+}}+\widetilde{o_{zc}^{(t)-}} +\widetilde{\varsigma _{zc}^{(t)+}}+\widetilde{\varsigma _{zc}^{(t)-}}). \end{aligned}$$
In other cases, the same can be proved. Therefore,
We have \(\mathrm{{OCI}}(D^{(t+1)})\le \mathrm{{OCI}}(D^{(t)})\), \(\mathrm{{PCI}}(D^{(t+1)})\le \mathrm{{PCI}}(D^{(t)})\) and
\(\square \)
A GDM approach with incomplete PDHFPRs
Faced with complicated decision making problems, the decision results obtained based on individual PDHFPRs may not be accurate due to the limitations of the expertise and experience of a DM, and a group of DMs need to make decisions at the same time. Because different DMs have various professional knowledge and experience, it is more reasonable for different DMs to give different weights. In other words, the weights of DMs should be proportional to the consistency level for the corresponding PDHFPR.
Suppose that \(X=\{x_1,x_2,\ldots ,x_n\}\) is an alternative set, \(P=\{p_1,p_2,\ldots ,p_m\}\) represents the set of DMs, and \(\psi =\{\psi _1,\psi _2,\ldots ,\psi _m\}\) is the weight vector of DMs. The detailed steps of the GDM approach based on the consistency of PDHFPRs are as follows:
Algorithm 2
Input: A list of PDHFPRs \(D_1,D_2,\ldots ,D_m\), where the associated probabilities of the corresponding PDHFEs are unknown, the given consistency index threshold \(\gamma _0\), the weight coefficient \(\lambda \), the adjusted coefficient \(\theta \) and the maximum number of iterations \(t_\mathrm{{max}}\).
Output: Improved complete PDHFPRs \(D_l^{*}(l=1,2,\ldots ,m)\), the ranking of \(x_i(i=1,2,\ldots ,n)\) and the overall priority weights of alternatives \(\varpi _i\).
Step 1: Construct PDHFPR series \(D_{l}=(d_{ij}^{l})_{n\times n}(1\le l\le m)\) on the condition of the decision information provided by the DMs, where \(d_{ij}^{l}=(h_{ij}^{l}|p_{ij}^l,m_{ij}^{l}|q_{ij}^l)\) is a PDHFE and the associated probabilities of the PDHFEs are unknown.
Step 2: For \(l=1,2,\ldots ,m\), Algorithm 1 is used to obtain the accurate associated probabilities of the PDHFEs and check the consistency of PDHFPRs \(D_{l}=(d_{ij}^{l})_{n\times n}\) . When \(\mathrm{{WCI}}(D_l)>\gamma _0\), the individual consistency can be improved using Algorithm 1. Thus, the improved PDHFPRs \(D_{l}^{*}(1\le l\le m)\) can be constructed, and the associated probabilities \(p_{ij,r}^l,q_{ij,k}^l\), the optimal variables \(\widetilde{o_{ij}^{l+}},\widetilde{o_{ij}^{l-}}, \widetilde{\varsigma _{ij}^{l+}},\widetilde{\varsigma _{ij}^{l-}}\) and the individual priority weights of alternatives \(\widetilde{w^{l}}=(\widetilde{w_1^{l}}, \widetilde{w_2^{l}},\ldots ,\widetilde{w_n^{l}})^T\) can be obtained, where \(\widetilde{w_i^l}=(\widetilde{w_{i\mu }^l}, \widetilde{w_{i\nu }^l})\).
Step 3: The following formula is used to calculate the weights \(\psi _l(l=1,2,\ldots ,m)\) of DMs:
Thus, \(0\le \psi _l\le 1\) and \( \sum _{l=1}^m\psi _l=1\).
Step 4: Calculate the overall priority weights: \(\varpi _i=\sum _{k=1}^m\psi _k\cdot \bigtriangleup (\widetilde{w_i^k})\), where \(\bigtriangleup (\widetilde{w_i^k})=\widetilde{w_{i\mu }^k} -\widetilde{w_{i\nu }^k}\).
Step 5: Obtain the ranking of \(x_i(i=1,2,\ldots ,n)\) using the value of \(\varpi _i\).
Assuming that the number of alternatives is n, the number of DMs participating in GDM is m, the maximum number of iterations is \(t_\mathrm{{max}}\), and the number of preference values given by the kth decision expert in the ith row and jth column of the decision-making matrix is \(\#d_{ij}^l\). The time complexity of Algorithm 2 is as follows:
-
1.
The time complexity for the initialization process of the decision-making matrix is \(O(m\times n^2)\);
-
2.
the time complexity for the calculation process of the associated probabilities of the PDHFEs is \(O(m\times n^2)\);
-
3.
the time complexity for the testing process of the consistency is \(O(m\times n^2)\);
-
4.
the time complexity for the improving process of the consistency level in the worst case is \(O(t_\mathrm{{max}}\times m\times n^2)\);
-
5.
the time complexity for the calculation process of the weights of DMs is O(m);
-
6.
the time complexity for the calculation process of the overall priority weights of alternatives is O(n);
Thus, the total time complexity of of Algorithm 2 is \(O(t_\mathrm{{max}}\times m\times n^2)\).
The space complexity of Algorithm 2 is as follows:
The space required to store the basic parameters of Algorithm 2 is constant, the space required to store the initial preference values given by DMs is \((\sum _{l=1}^{m}\sum _{i}^n\sum _{j}^n(\#d_{ij}^l))+2n\), the space required to store the calculated probabilities is \((\sum _{l=1}^{m}\sum _{i}^n\sum _{j}^n(\#d_{ij}^l))-2n\), the space required to store the optimal variables is \(m\times n^2\), the space required to store the optimal normalized weight vector is 2n, the space required to store the improved preference values is \(2\times \sum _{l=1}^{m}\sum _{i}^n\sum _{j}^n(\#d_{ij}^l)\), the space required to store the weights of DMs is m.
To sum up, the total space complexity of Algorithm 2 is \(O(m\times n^2+\sum _{l=1}^{m}\sum _{i}^n\sum _{j}^n(\#d_{ij}^l))\).
Illustrative example
Application to analyze the impact factors of haze
Haze is produced from the interaction of human activities and specific climatic conditions. In recent years, severe haze weather has occurred in many regions of China. A large number of fine particles will inevitably be discharged because of the social and economic activities of high-density populations. When the emission of fine particulate pollutants is increasing and exceeds than the atmospheric circulation and carrying capacity, its concentration in the air will continue to increase, resulting in haze. The frequent occurrence of haze not only seriously affects air quality but is also the main cause of asthma and other diseases, which seriously affect people’s health and economic development. Therefore, it is of practical significance to study the causes of haze weather.
Shanghai has been harmed by haze weather for a long time. Three related experts \(P=\{p_1,p_2,p_3\}\) use PDHFPRs to express their preference for four evaluation factors of haze weather. The four evaluation factors of haze weather are PM2.5 (\(x_1\)), relative humidity (\(x_2\)),\(NO_2(x_3)\), and PM10 (\(x_4\)). Let the given consistency index threshold \(\gamma _0=0.2\), the weight coefficient \(\lambda =0.2\), and the adjusted coefficient \(\theta =0.5\). We use Algorithm 2 to explore the four evaluation factors of haze weather and analyze the leading causes of haze weather.
Step 1: Based on professional knowledge and experience, PDHFPRs \(D_l=(d_{ij}^l)_{4\times 4}=(h_{ij}^l|p_{ij}^l,m_{ij}^l| q_{ij}^l)_{4\times 4}(l=1,2,3)\) are given by experts and are shown in Tables 3, 4 and 5.
Step 2: Using the PDHFPR \(D_1\) given by expert \(P_1\), the following optimization model is established according to model (M-3):
By using the MATLAB Toolbox, we obtain
Therefore, \(\mathrm{{WCI}}(D_1)=0.0490<\gamma _0\) , which implies that \(D_1\) is an acceptable consistent PDHFPR. Similarly, using PDHFPR \(D_2\) given by expert \(p_2\), an optimization model is built in line with model (M-3), and the solution is as follows:
Therefore, \(\mathrm{{WCI}}(D_2)=0.0905<\gamma _0\) , which implies that \(D_2\) is an acceptable consistent PDHFPR. Similarly, using PDHFPR \(D_3\) given by expert \(p_3\), an optimization model is built and we can obtain \(\mathrm{{WCI}}(D_3)=0.3623>\gamma _0\), which implies that \(D_3\) is an unacceptable consistent PDHFPR. For this case, Algorithm 1 can be applied to improve the consistency of \(D_3\).
Using Eq. (23) to determine where expert \(e_3\) needs to modify preference values, we can obtain \((u,m)=(2,3)\). The improved PDHFE \(d_{23}^{3*}=\{\{0.46|p_{23,1}^3,0.56|p_{23,2}^3\}, \{0.27|1\}\}\) is obtained according to Eq. (24). Thus, an improved PDHFPR \(D_3^{*}\) can be constructed by introducing \(d_{23}^{3*}\) to \(D_3\). Furthermore, according to model (M-3), the results are obtained as follows:
We can obtain \(\mathrm{{WCI}}(D_3^{*})=0.1909<\gamma _0\), which implies that \(D_3^{*}\) is an acceptable consistent PDHFPR.
Step 3: The individual weights of DMs can be calculated as follows: \(\psi _1=0.3562,\psi _2=0.3407,\psi _3=0.3031.\)
Step 4: Compute overall priority weights: \(\varpi _1=-0.1677\), \(\varpi _2=-0.7631\), \(\varpi _3=-0.3588\), \(\varpi _4=-0.6843\).
Step 5: As \(\varpi _1\succ \varpi _3\succ \varpi _4\succ \varpi _2\), the four evaluation factors of haze weather are ranked as
Therefore, PM2.5 is the most critical cause of haze in Shanghai. This result agrees with the calculation results of this method.
Sensitivity analysis of \(\lambda \) and \(\theta \)
For \(0\le \lambda \le 1(\theta =0.5)\), we take 0.1 as the interval and conduct 11 experiments in total. The influence of \(0\le \lambda \le 1(\theta =0.5)\) on DMs’ weights and ranking results of four evaluation factors are shown in Table 6. Figure 1 shows the influence of \(0\le \lambda \le 1(\theta =0.5)\) on the overall priority weights of alternatives \(\varpi _i=(i=1,2,3,4)\).
Table 6 shows that DMs weights change with \(0\le \lambda \le 1(\theta =0.5)\). Furthermore, when \(0\le \lambda \le 1\) takes different values, the ranking of haze impact factors changes. When \(\lambda \le 0.1\), the ranking result is \(x_1\succ x_3\succ x_2\succ x_4\). When \(0.1<\lambda \le 1\), the ranking is \(x_1\succ x_3\succ x_4\succ x_2\). Therefore, the weight coefficient of \(\mathrm{{OCI}}(D)\) affects the ranking results, which proves the flexibility of the decision approach in this paper. However, regardless of how \(\lambda \) changes, the most important factor affecting haze is still PM 2.5. Therefore, our proposed approach exhibits good stability.
Moreover, we study the ranking of haze impact factors when \(0\le \theta \le 1(\lambda =0.2)\) changes from 0.1 to 1. The specific ranking results are shown in Table 6, and the values of overall priority weights \(\varpi _i(i=1,2,3,4)\) are shown in Fig 2. The ranking results do not change with \(\theta \) because \(\theta \) is the consistency adjusted coefficient, which only affects the speed of \(D_3\) reaching the consistency threshold. Specifically, the larger the adjusted coefficient \(\theta \) is, the faster \(D_3\) reaches the consistency threshold.
Comparative analysis
To prove the superiority of our approach, we will use the same illustrative example to compare our method with the methods proposed in Hao et al. [17], Garg and Kaur [40, 42] and Zhao et al. [43]. Under PDHFS environment, the method in Hao et al. [17] and Garg and Kaur [40, 42] requires all PDHFEs to be complete. When applying the methods in [17, 40] to address the illustrative example, the missing associated probabilities of PDHFEs are derived from the associated probability calculation method in this paper.
(1) Hao et al. [17] defined basic operators for PDHFSs and then proposed a visualization GDM method with PDHFSs based on the operator. For the sake of comparison, the individual weights of DMs is set as the calculation result of the method in this paper, that is, \(\psi _1=0.3562,\psi _2=0.3407,\psi _3=0.3031\) Now, we use the method in Hao et al. [17] to analyze the influencing factors of haze weather.
First, the comprehensive PDHFPR matrix \(D^{*}=(d_{ij}^{*})_{n\times n}\) is obtained using the probabilistic dual hesitant fuzzy weighted average (PDHFWA) operator (Eq. (19) in [17]), where the following elements of the comprehensive matrix are shown:
Second, the preference values \(d_{ij}^{*}\) are aggregated to obtain the aggregated probabilistic dual hesitant fuzzy preference values \(d_{i}^{*}\) of the factor affecting haze \(x_i\). Due to the length limitation of this paper, only some elements of \(d_{i}^{*}\) are shown as follows:
Next, the score function of \(d_i^{*}\) is calculated as follows:
Finally, the ranking of the factors affecting haze is as follows:
(2) Garg and Kaur [40] defined the correlation coefficients on PDHFSs and proposed the multi-criteria decision-making (MCDM) method based on the correlation coefficients for PDHFSs. Now, we use the method in Garg and Kaur [40] to handle the above problem, and the main steps are as follows:
First, by using Algorithm 1 in Garg and Kaur [40], the aggregated decision matrix \(D^{*}=(d_{ij}^{*})_{n\times n}\) is obtained. The MDs and NMDs and their corresponding probabilities are listed as follows:
Second, the ideal alternative \(d^{*}\) is determined by Eq. (15) in [40]as follows:
Then, the correlation coefficient index \(K_1,K_2,K_3,K_4\), (Eq. (10), (11), (12), (13)) in [40]) is used to obtain the measurement between \(d_i^{*}(i=1,2,3,4)\) and \(d^{*}\), and we getthe following:
The selection of \(\omega \) in [40] is subjective. When \(\omega =(0.25,0.25,0.25,0.25)^T.\) we get the following:
Finally, the ranking of four evaluation factors is \(x_1\succ x_4\succ x_2\succ x_3\) when the correlation coefficient index \(K_1\) and \(K_3\) are used and is \(x_1\succ x_2\succ x_4\succ x_3\) when the correlation coefficient index \(K_2,K_4\) are used.
(3) Garg and Kaur [42] studied some distance measures between PDHFSs and distance measure-based maximum deviation method were set to calculate the weights of criteria. Then, a new MCDM method with unknown attribute weights was proposed. By using the method in Garg and Kaur [42], the following steps are involved:
First, a comprehensive matrix is obtained by aggregating the individual PDHFPRs using Algorithm 1 in Garg and Kaur [42], and the elements of the comprehensive matrix are the same as Garg and Kaur’s [40] method.
Second, because the number of elements in MDs and NMDs of each PDHFE is different, the distance measure \(d_2\) (Eq. (10) in [42]) is used to obtain the following weights:
Then, the probabilistic dual hesitant fuzzy weighted Einstein average
(PDHFWEA) operator (Eq. (31) in [42]) is used to obtain the aggregate values of each alternative. Due to the length limitation of this paper, only some elements of the PDHFPR matrix are shown as follows:
Similarly, the probabilistic dual hesitant fuzzy ordered weighted Einstein average (PDHFOWEA) operator (Eq. (32) in [42]), probabilistic dual hesitant fuzzy weighted Einstein geometric (PDHFWEG) operator (Eq. (33) in [42]), and probabilistic dual hesitant fuzzy ordered weighted Einstein geometric (PDHFOWEG) operator (Eq. (34) in [42]) operators are used to calculate the aggregated values for each alternative, and the score function values and ranking results using the four types of operators are given in Table 7.
Table 7 shows that the most crucial indicator affecting the generation of haze in Shanghai is PM 2.5, which matches the result of this paper.
(4) When the probability values of the MDs and the NMDs are equal, the PDHFPRs degenerates into the dual hesitant fuzzy PRs. With respect to the GDM problem with dual hesitant fuzzy PRs, Zhao et al. [43] developed new GDM methods to obtain the best alternative, which includes a consensus reaching process. The method 1 in Zhao et al. [43] is utilized as the comparison algorithm.
The dual hesitant fuzzy PRs corresponding to PDHFPRs \(D_l=(d_{ij}^l)_{4\times 4}=(h_{ij}^l|p_{ij}^l, m_{ij}^l|q_{ij}^l)_{4\times 4}(l=1,2,3)\) are recorded as \(c_l=(h_{ij}^l,m_{ij}^l)_{4\times 4}\), and the calculation process is as follows:
First, the compatibility degrees \(C_{kl}=CO_1(C_k,C_l),k,l=1,2,3\) between \(C_k\) and \(C_l\) are computed by \(CO_1\) (Eq. (5) in [43]), which are given as follows:
Therefore, the weights of experts are determined by Eq. (9) in [43]:\(\psi _1^1=0.3295,\psi _2^1=3416,\psi _3^1=0.3289\).
Second, for all \(l=1,2,3\), let \(C_l^0=C_l\). Then, using the symmetric dual hesitant fuzzy weighted averaging operator (Eq. (10) in [43]), all dual hesitant fuzzy preference relations \(C_1^0\) are fused into \(C^0=(c_{ij0})_{4\star 4}\), where \(c_{ij0}=(h_{ij0},g_{ij0}),(i,j=1,2,3,4)\) . Due to the length limitation of this paper, some elements in \(C^0\) are shown as follows:
Then, the compatibility degrees \(CO_1(C^0,C_l^0)\) between \(C_l^0, (l=1,2,3)\) and \(C^0\) are calculated using Eq. (5) in [43] as follows:
Thus, the group reaches the given threshold.
Using the symmetric dual hesitant fuzzy averaging operator (Eq. (13) in [43]), we integrate the dual hesitant fuzzy preference values of each alternative \(x_i(i=1,2,3,4)\) into the collective dual hesitant fuzzy preferences \(d_i(i=1,2,3,4)\). Then, using Definition 3 in Zhao et al. [43], the score values are as follows:
Thus, the ranking of the four evaluation factors is as follows:
In the above process, if we measure the agreement of preferences by compatibility measure (Eq. (6) in [43]) instead of (Eq. (5) in [43]), the ranking of the factors affecting haze is \(x_1\succ x_3\succ x_2\succ x_4\).
Based on the same example of analyzing the impact factors of haze weather, the calculation results of the above four methods are shown in Table 8.
Table 9 visually demonstrates the comparison of different methods, and the following detailed comparative analysis shows the superiority of the proposed GDM method:
-
1.
By comparing the decision results in Table 8, it is shown that the most crucial factor affecting haze in Shanghai is PM 2.5, which proves the reasonable effectiveness of our method.
-
2.
Our method combines the DMs’ risk attitude when calculating the consistency level for PDHFPR. When the weight coefficient \(\lambda \le 0.1\), the ranking result is \(x_1\succ x_3\succ x_2\succ x_4\), which is the same as the ranking result by Hao et al. [17], Garg and Kaur [42] and Zhao et al. [43]. And when \(0.1<\lambda \le 1\), the ranking result is \(x_1\succ x_3\succ x_4\succ x_2\). Therefore, the DMs’ risk attitude affects the ranking results, which proves the flexibility of our method.
-
3.
Comparison with the methods in Hao et al. [17] and Garg and Kaur [42], all the methods solve GDM problem with probabilistic dual hesitation fuzzy environment. However, Hao et al. [17] and Garg and Kaur [42] used PDHFSs to directly evaluate alternatives, while the PDHFPRs proposed in this paper only require the DMs to give evaluation information through pairwise comparison, so PDHFPRs are more appropriate for the fuzzy decision of DMs in complicated environments. In addition, Hao et al.s [17] and Garg and Kaurs [42] method can only handle GDM problems with known probability information of PDHFEs. In contrast, our method comprehensively considers the situation of incomplete decision making information and unknown weights of DMs, which is more suitable for the increasingly complicated decision environment.
-
4.
From Table 8, although Garg and Kaurs [42] method selects the same most crucial factor affecting haze with our method, there is a different ranking between the four factors affecting haze in the method of Garg and Kaur [42] and our method. This is mainly because Garg and Kaurs [42] method used the correlation coefficients for PDHFSs to get the ranking result while our method uses the optimization model of PDHFPRs to directly obtain the ranking of alternatives and needs to calculate the overall priority weights of the four evaluation factors by improving the consistency level for the individual PDHFPRs. Therefore, our method can obtain more credible decision results.
-
5.
The comparison with the method in Zhao et al. [43] is as follows: First, Zhao et al.’s [43] method neglects the associated probabilities of MDs and NMDs, which may lose and distort the original information. Our method uses the original PDHFPR information for calculation, which can better retain the original information. Second, our method requires higher consistency than Zhao et al. [43]. In our method, the original PDHFPR of decision expert \(p_3\) is unacceptable consistent while the consistency level of decision expert \(p_3\) is not required to be improved in Zhao et al. [43]. Finally, our approach only adjusts one preference value each time, so the adjusted PDHFPR matrix is closer to the original PDHFPRs, which can better retain the wishes of DMs and greatly improve the accuracy of decision-making results.
Based on the above discussion and Table 9, our method compensates for the deficiencies of the existing methods and offer good application value.
Conclusion and future work
In this paper, the concept of PDHFPRs has been first given, and the multiplicative consistency, order consistency and acceptable consistency of PDHFPRs have been proposed. Considering that decision making experts cannot give accurate probabilities of the elements in PDHFPRs, based on multiplicative consistency, an optimization model that minimizes the deviation variable as the objective function has been constructed. Then, the probability calculation method has been given. According to the risk attitude of DMs, the consistency level for PDHFPRs has been tested using the weighted consistency index. For unacceptable consistency PDHFPRs, the obtained optimal deviations have been used to improve the PDHFE with the largest deviation one by one to adjust the consistency level for the original PDHFPRs. Based on the improved acceptable preference relation, the GDM method of PDHFPRs has been set, and the overall priority weights have been obtained. Finally, by analyzing the impact factors of haze weather, the validity of our method has been illustrated.
Although the method proposed in this paper has many advantages, it also has certain disadvantages. On the one hand, this paper presents the weight calculation methods for DMs, but they are not accurate enough, On the other hand, the given consistency threshold in this paper is determined by the DMs, which has a certain degree of subjectivity. Future research could focus on how to give a reasonable calculation method of accurate weights for DMs as well as an objective and appropriate consistency threshold. In addition, due to the different knowledge and experience of DMs, DMs may use heterogeneity preference relations to express their decision information. Therefore, it is interesting to further study the GDM approach with heterogeneity PDHFPRs.
Code availability
All authors declare that all software applications or custom codes comply with field standards.
References
Hochbaum DS, Levin A (2006) Methodologies and algorithms for group-rankings decision. Manag Sci 52(9):521–530
Chuan Y (2019) A normalized projection-based group decision-making method with heterogeneous decision information and application to software development effort assessment. Appl Intell 49(10):3587–3605
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Cao Q, Liu XD, Wang ZW, Zhang S, Wu J (2020) Recommendation decision-making algorithm for sharing accommodation using probabilistic hesitant fuzzy sets and bipartite network projection. Complex Intell Syst 6(2):431–445
Mardani A, Hooker RE, Ozkul S, Sun YF, Nilashi M, Sabzi HZ, Fei GC (2019) Application of decision making and fuzzy sets theory to evaluate the healthcare and medical problems: a review of three decades of research with recent developments. Expert Syst Appl 137:202–231
Liu CF, Luo YS (2019) Power aggregation operators of simplified neutrosophic sets and their use in multi-attribute group decision making. IEEE-CAA J Autom 6(2):242–250
Su TS, Hsiao HH (2020) Developing a fuzzy-set-based shortcut layout approach for a semiconductor inter-bay handling system. Int J Adv Manuf Technol. https://doi.org/10.1007/s00170-020-06150-8
Stekelorum R, Laguir I, Gupta S, Kumar S (2021) Green supply chain management practices and third-party logistics providers’ performances: a fuzzy-set approach. Int J Prod 235:108093. https://doi.org/10.1016/j.ijpe
Wu Q, Zhou LG, Chen Y, Chen HY (2019) An integrated approach to green supplier selection based on the interval type-2 fuzzy best-worst and extended VIKOR methods. Inf Sci 502:394–417
Reddy GT, Reddy M, Lakshmanna K, Rajput DS, Kaluri R, Srivastava G (2020) Hybrid genetic algorithm and a fuzzy logic classifier for heart disease diagnosis. Evol Intell 13:185–196
Lin MW, Huang C, Chen RQ, Fujita M, Wang X (2021) Directional correlation coefficient measures for Pythagorean fuzzy sets: their applications to medical diagnosis and cluster analysis. Complex Intell Syst. https://doi.org/10.1007/s40747-020-00261-1
Gadekallu TR, Gao XZ (2021) An efficient attribute reduction and fuzzy logic classifier for heart disease and diabetes prediction. Recent Adv Comput Sci Commun 14(1):158–165
Asghar MZ, Subhan F, Ahmad H, Khan WZ, Hakak S, Gadekallu TR, Alazab M (2021) Senti-eSystem: a sentiment-based eSystem-using hybridized fuzzy and deep neural network for measuring customer satisfaction. Softw Pract Exp 51:571–594
Broumi S, Talea M, Bakali A, Smarandache F, Nagarajan D, Lathamaheswari M, Parimala M (2019) Shortest path problem in fuzzy, intuitionistic fuzzy and neutrosophic environment: an overview. Complex Intell Syst 5:371–378
Zhu B, Xu ZS, Xia MM (2012) Dual hesitant fuzzy sets. J Appl Math 22:1–13
Zhu B (2014) Decision method for research and application based on preference relation. Southeast University, Nanjing
Hao ZN, Xu ZS, Zhao H, Su Z (2017) Probabilistic dual hesitant fuzzy set and its application in risk evaluation. Knowl Based Syst 127:16–28
Tanino T (1984) Fuzzy preference orderings in group decision making. Fuzzy Set Syst 12:117–131
Li J, Wang ZX (2018) A programming model for consistency and consensus in group decision making with probabilistic hesitant fuzzy preference relations. Int J Fuzzy Syst 20(8):2399–2414
Xu ZS (2007) Intuitionistic preference relations and their application in group decision making. Inf Sci 177:2363–2379
Liao HC, Xu ZS, Xia MM (2014) Multiplicative consistency of hesitant fuzzy preference relation and its application in group decision making. Int J Inf Technol Decis 13(1):47–76
Liang P, Hu JH, Li B, Liu YM, Chen XH (2020) A group decision making with probability linguistic preference relations based on nonlinear optimization model and fuzzy cooperative games. Fuzzy Optim Decis Mak 19:499–528
Jin FF, Ni ZW, Pei LD, Chen HY, Tao ZF, Zhu XH, Ni LP (2017) Approaches to group decision making with linguistic preference relations based on multiplicative consistency. Comput Ind Eng 114:69–79
Li J, Wang ZX (2018) Consensus building for probabilistic hesitant fuzzy preference relations with expected additive consistency. Int J Fuzzy Syst 20(5):1495–1510
Meng FY, Tang J, An QX, Chen XH (2019) Decision making with intuitionistic linguistic preference relations. Int Trans Oper Res 26:2004–2031
Wu J, Chiclana F, Liao HC (2018) Isomorphic multiplicative transitivity for intuitionistic and interval-valued fuzzy preference relations and its application in deriving their priority vectors. IEEE Trans Fuzzy Syst 26:193–202
Jin FF, Ni ZW, Chen HY, Li YP (2016) Approaches to group decision making with intuitionistic fuzzy preference relations based on multiplicative consistency. Knowl Based Syst 97:48–59
Wu P, Zhu J, Zhou L, Chen H, Chen Y (2019) On consistency and priority weights for uncertain 2-tuple linguistic preference relations. Int J Comput Int Syst 12(2):1339–1352
Jin FF, Garg H, Pei LD, Liu JP, Chen HY (2020) Multiplicative consistency adjustment model and data envelopment analysis-driven decision-making process with probabilistic hesitant fuzzy preference relations. Int J Fuzzy Syst 22(7):2319–2332
Chen HP, Xu GQ (2019) Group decision making with incomplete intuitionistic fuzzy preference relations based on additive consistency. Comput Ind Eng 135:560–567
Zhang ZM, Chen SM, Wang C (2020) Group decision making with incomplete intuitionistic multiplicative preference relations. Inf Sci 516:560–571
Song YM, Li GX (2019) Handling group decision-making model with incomplete hesitant fuzzy preference relations and its application in medical decision. Soft Comput 23:6657–6666
Zhou W, Xu ZS (2018) Probability calculation and element optimization of probabilistic hesitant fuzzy preference relations based on expected consistency. IEEE Trans Fuzzy Syst 26(3):1367–1378
Tang XA, Zhang Q, Peng ZL, Yang SL, Pedrycz W (2019) Derivation of personalized numerical scales from distribution linguistic preference relations: an expected consistency-based goal programming approach. Neural Comput Appl 31(12):8769–8786
Gao J, Xu ZS, Liang ZL, Liao HC (2019) Expected consistency-based emergency decision making with incomplete probabilistic linguistic preference relations. Knowl Based Syst 176:15–28
Ren ZL, Xu ZS, Wang H (2019) The strategy selection problem on artificial intelligence with an integrated VIKOR and AHP method under probabilistic dual hesitant fuzzy information. IEEE Access 7:103979–103999
Shao ST, Zhang XH (2021) Multiobjective programming approaches to obtain the priority vectors under uncertain probabilistic dual hesitant fuzzy preference environment. Int J Comput Intell Syst 14(1):1189–1207
Garg H, Kaur G (2021) Algorithms for screening travelers during COVID-10 outbreak using probabilistic dual hesitant values based on bipartite graph theory. Appl Comput Math 20:22–48
Zhao Q, Ju YB, Pedrycz W (2020) A method based on bivariate almost stochastic dominance for multiple criteria group decision making with probabilistic dual hesitant fuzzy information. IEEE Access 8:203769–203786
Garg H, Kaur G (2020) A robust correlation coefficient for probabilistic dual hesitant fuzzy sets and its applications. Neural Comput Appl 32:8847–8866
Garg H, Kaur G (2020) Quantifying gesture information in brain hemorrhage patients using probabilistic dual hesitant fuzzy sets with unknown probability information. Comput Ind Eng 140:1–16
Garg H, Kaur G (2018) Algorithm for probabilistic dual hesitant fuzzy multi-criteria decision-making based on aggregation operators with new distance measures. Mathematics 6:280–309
Zhao N, Xu ZS, Liu F (2016) Group decision making with dual hesitant fuzzy preference relations. Cogn Comput 8:1119–1143
Acknowledgements
The work was supported by the National Natural Science Foundation of China (No. 71901001), the Foundation for Innovative Research Groups of the National Natural Science Foundation of China (No. 71521001), Natural Science Foundation of Anhui Province (No. 2008085QG333), Key Research Project of Humanities and Social Sciences in Colleges and Universities of Anhui Province (No. SK2020A0038), and the Training Program of the Major Research Plan of National Science Foundation of China (No. 91546108).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Song, J., Ni, Z., Jin, F. et al. A new group decision making approach based on incomplete probabilistic dual hesitant fuzzy preference relations. Complex Intell. Syst. 7, 3033–3049 (2021). https://doi.org/10.1007/s40747-021-00497-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-021-00497-5



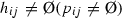 ,
, 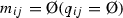 , then
, then 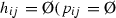 ,
,  , then
, then 
