Stability of High Entropy Alloys to Spinodal Decomposition

Abstract

When a high entropy alloy (HEA) system contains a single binary miscibility gap, the gap spreads across the entire composition space of the system. Beneath the miscibility gap is a spinodal hypersurface above which HEAs are stable to a continuous change of phase via spinodal decomposition. When there are additional binary miscibility gaps, the stability limits appear separately at high temperature but combine on cooling to form a continuous surface that may contain a cone point, an important feature for the design of age hardening alloys. In this work, an understanding of how spinodal surfaces form, combine, and develop critical features is obtained by investigating several ternary systems each with three binary miscibility gaps. Because their topology is the same, bisection isopleths and isothermal sections of ternary phase diagrams given in this work will help interpret calculated bisection isopleths and isotherms of 5- and 6-dimensional HEA phase diagrams.

1 Introduction

In the past decade there have been occasional reports of spinodal decomposition in high entropy alloys (HEAs). Spinodal decomposition is important when designing age hardening alloys but must be avoided when designing stable, single-phase HEAs. Most reports involve seeing spinodal-like microstructures in quenched alloys but don’t confirm the presence of miscibility gaps in the solid phase, a necessary, but not sufficient condition for spinodal decomposition to occur. Munitz et al.[1] found a spinodal microstructure in an AlCrFeNiMo0.3 alloy and did calculate a miscibility gap, but it was for the liquid phase. Li et al.[2] found spinodal microstructures in several AlNiCoFeCr alloys. The authors confirmed that spinodal decomposition occurred by using a phase field model that predicted spinodal decomposition. These alloys must have been unstable in a single phase for their model descriptions.

The condition for stability to spinodal decomposition on a phase diagram was given by J. W. Cahn in his seminal 1961 paper.[3] The condition is that an alloy is stable at temperatures above the coherent spinodal and unstable below it. In his 1968 review paper on spinodal decomposition,[4] Cahn cites and reproduces binary phase diagrams for Al-Zn[5] and Au-Ni,[6] on which both the equilibrium miscibility gap and coherent spinodal are plotted. After Cahn’s work there have been few reports about the coherent spinodal on ternary phase diagrams. The one, and possibly only, exception is a ternary phase diagram with a coherent spinodal by Y-Y. Chuang, R. Schmid, and Y. A. Chang for the Fe-Cu-Ni system.[7] Nothing was found in a literature survey on HEAs, the topic herein.

The current work begins with a brief review of the relationship between chemical and coherent spinodals. Although these spinodals are not the same, they are similar except for distortions caused by non-uniform mechanical and density properties and predicted by a spinodal theory.[3,4] Therefore, it is a premise of this work that what is known about the shape of the chemical spinodal will likely apply to the coherent spinodal.

Although HEA phase diagrams are multi-dimensional, they can be readily viewed on 2-D sections. The best sections to search for HEAs are core composition diagrams. With these, as few as five sections can survey the entire temperature versus composition range of a 5-component system. Also, it is shown below that HEA systems containing only 2-phase miscibility gaps will look much like a binary spinodal, which is itself a 2-D section. Although 3-phase miscibility gaps have not been reported in the past, there are reasons to believe that they will be found for the first time in HEA systems.[8]

The current work deals extensively with 3-phase miscibility gaps. Mechanisms by which they form were the topic of a recent paper by the current authors.[9] The focus of that work was phase equilibria while that of the current work is phase stability. The objective is to give readers a broad background on how coherent spinodals may appear on calculated phase diagrams and be applied to alloy and heat treatment design. The basic thermodynamics on phase stability can be found in the books by Hillert[10] and de Fontaine.[11]

2 Miscibility Gaps and the Spinodal

The relationship between a miscibility gap and its chemical spinodal is well known. The two are tangent at a critical point and their outlines are similar. That is true for both binary and HEA systems. The coherent spinodal is always inside the chemical spinodal on a phase diagram and is a suppressed version of the chemical spinodal.

2.1 Binary Systems

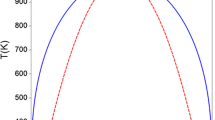
Figure 1 is a calculated binary phase diagram for the binary Au-Ni system using the description from Liu et al.[12] and the coherent spinodal using an approach like Chen et al.[13] It shows the relationship between the curves for the binodal (i.e., the equilibrium phase boundary), the chemical spinodal, and coherent spinodal. The individual diagrams show how the difference between the chemical spinodal and coherent spinodal depends on the elastic modulus, E, and the variation of lattice parameter with Au concentration, η. In Fig. 1(a) with constant E and η, the coherent spinodal occurs at a lower temperature and the location of its peak concentration has not changed much. In Fig. 1(b) with constant η and varying modulus, the peak shifts toward the Au-rich side where the modulus is lower. In Fig. 1(c), the peak shifts further toward the Au-rich side where $\left|\eta \right|$ is larger. In addition, it shows that the calculated coherent spinodal can occur at negative values of the temperature, which has no physical significance other than to indicate stability there. The critical temperature of the coherent spinodal is higher than that in Ref.[6] since no attempt was made to fit this temperature.

Fig. 1

Binodal (blue lines) and spinodal (solid red lines) for the Au-Ni system illustrating how the coherent spinodal (dashed red line) varies with composition (a) with constant η and E, (b) with constant η and varying E, and (c) same as (b) but with a linear variation of η with composition.

2.2 Ternary, Quaternary and HEA Systems

In binary phase diagrams, there is a single chemical and coherent spinodal line. However, in 2-D sections of ternary, quaternary, or HEA systems, there are multiple spinodal lines.[14] The uppermost coherent spinodal line with respect to temperature is the stability limit for spinodal decomposition, while the lowermost line is the instability limit. Above the stability limit, an alloy is stable to all composition fluctuations, while below the instability limit, an alloy is unstable to all composition fluctuations. Between the uppermost and lowermost spinodal lines the alloy is unstable to a specific range of fluctuations.[14]

The appearance of a coherent spinodal depends on the binary miscibility gaps within an HEA system. This dependance was suggested by Meijering,[15] who used a thermodynamic model to predict the shape of spinodal surfaces in ternary regular solutions. He found that ternary systems could be placed into eight categories depending on the sign and magnitude of its binary interaction parameters. Shapes of spinodal surface from the eight categories were later illustrated as contour diagrams[16] in which each contour line has the shape of the spinodal line at a given temperature.

Example contour diagrams from Ref. [16] are illustrated in Fig. 2. As can be seen in these figures, the spinodal surface covers the entire composition space between the binaries. When there are no binary positive interaction parameters, i.e. no binary miscibility gaps, a ternary spinodal surface is possible if the difference between the binary interaction parameters is sufficiently large.[15] Figure 2(a) and (b) show that the isothermal spinodal line can look like an isolated loop when the spinodal surface has a peak. This occurs when there are no binary miscibility gaps, Fig. 2(a), and in certain other systems when there are one or two binary miscibility gaps, Fig. 2(b). In the only paper on a coherent spinodal in a real ternary alloy system, Fe-Cu-Ni, by Chuang et al.[7] the coherent spinodal is calculated and plotted as an isolated loop. Per the referenced work by Meijering,[15] this indicates that the coherent spinodal surface must contain a peak. According to the premise of the current work, the chemical spinodal surface must contain a peak as well. That possibility is suggested by the shape of the calculated chemical spinodal which is nearly a loop, except where it connects to the Cu-Ni binary.

Fig. 2

Ternary regular solution spinodal surfaces[15, 16] with numerical value of T/T_c for each isothermal contour curve; (a) with a peak but no binary miscibility gaps; (b) with a peak for certain systems with one or two binary miscibility gaps; (c) with no peak in certain systems containing one, two, or three binary miscibility gaps; and (d) with a cone point in certain systems with three binary miscibility gaps.

Figure 2(a)–(c) occur inside 2-phase miscibility gaps, while the central portion of Fig. 2(d) only occurs inside a 3-phase miscibility gap. It contains a cone point in the spinodal surface,[15,16,17] which can have a significant influence on how HEAs are designed, and heat treated to optimize properties. The contour lines outside the central triangle in Fig. 2(d) have the same shape as a binary spinodal, while inside the triangle they are a loop.

In Fig. 2(d), all the 2-phase miscibility gaps are attached to the edges of the diagram where they meet binary 2-phase miscibility gaps. These produce a miscibility gap with the rose geometry[17,18,19] which can yield more complex 2-D phase diagram sections.

3 Phase Diagrams for HEA

A two-component binary system is a 2-D diagram of temperature versus one independent concentration variable. It follows that a five-component HEA phase diagram is a 5-D diagram of temperature versus four independent concentration variables. A 5-D diagram cannot be visualized globally, but a 2-D section can be readily calculated and interpreted. Calculated diagrams can predict all equilibrium or metastable phases, but only a diagram with one crystal structure is needed to determine the stability of a phase. Single-crystal-structure phase diagrams are less complex and contain only miscibility gaps and spinodal lines.

3.1 The Core Composition

An unlimited number of 2-D sections can be calculated for an HEA phase diagram. However, sections that pass through the core composition of an alloy system are particularly effective for HEA analysis. The core composition is the central (a.k.a. equi-atomic) composition of an alloy system. For a binary A-B system, the core composition is the middle point of an A-B composition line. The core composition is the center of an A-B-C composition triangle for a ternary system, and the center of an A-B-C-D composition tetrahedron for a quaternary system. The core composition for five- or six-component HEA systems are the center of 4-D and 5-D polyhedrons, respectively. These systems can be efficiently surveyed with isopleths of temperature and composition.

3.2 Bisecting Isopleths

As its name implies, a bisecting isopleth cuts the global temperature versus composition phase diagram in half. For an HEA system, it passes through a pure element corner of the polyhedron and the core composition of the system. There are only five such bisecting isopleths for a 5-component system, each one passing through a different pure element corner of the composition polyhedron. As shown in Table 1, this is the type of 2-D section that can survey the entire diagram with the least number of sections.

Table 1. Special 2-D sections of HEA and n-component phase diagrams

The composition axis of a bisecting isopleths through the A corner of a 5-component alloy is A_xBCDE in which x is the number of moles of A while the number of moles for each of other elements is equal to one. These were the axes used in the pioneering work on HEA phase diagrams by Liang and Schmid-Fetzer.[20]

The composition coordinate of a bisecting isopleth passes through two core compositions. For the ABCDE system above, one is when $x=0$, where is the core composition of the quaternary BCDE system. The other is when $x=1$, where is the core composition of the 5-component ABCDE system. To generalize, a bisecting isopleth of an n-component system passes through two core compositions, one is of the n-component system and the other is of the surrounding (n−1)-component system.

3.3 Constant Core Component (CCC) Isotherms

Isotherms for ternary systems are 2-D because they involve only two independent variables. However, isotherms for n-component systems are (n-1)-D. For example, a four-component isotherm is a 3-D tetrahedron and needs to be sectioned. Relevant sections for these can be named constant-core-component diagrams. In these diagrams, the concentrations of enough components are held constant to reduce the (n-1)-D composition space to a 2-D space, i.e., a space with only 2 independent variables. These diagrams could be plotted on a triangle-like ternary isotherm to show the variation of the variables as well as the two independent variables. The number of ways that an n-component system can have two independent variables is given by the combinatorial equation in Table 1 along with computed values for HEAs.

Although the number of bisecting and CCC isotherms is limited as shown in Table 1, CCC isopleths at several temperatures are often necessary to characterize the system versus temperature isotherms. Each CCC isotherm has two independent composition variables and other composition variables are held constant. Therefore, each CCC isotherm can have two CCC isopleths, and the total number of CCC isopleths diagrams needed is twice the number of CCC isotherms for a given system.

3.4 Polythermal Projection Diagrams

Polythermal Projections like Fig. 2 or Fig. 21 in later section for HEAs can be drawn with a series of CCC isotherms at different temperatures. Therefore, the total number of isotherms needed must be multiplied by ${N}_{T}$, the number of temperatures on the diagram. Characteristic lines can be drawn on each polythermal projection as well.

The following begins with a brief history of work on the stability of alloys. It begins in the 19^thcentury when important discoveries were made on spinodal surfaces in ternary systems. Then more recent work is described on 3-phase miscibility gaps, Gibbs energy surfaces, curvature, and the Gibbs energy Hessian.

4 Gibbs and Korteweg Contributions

An alloy phase is thermodynamically unstable when its free energy curvature is negative, a concept established by Gibbs.[21] Gibbs gave an equation for the stability limit, i.e., the spinodal, in terms of the free energy, a concept he discovered and is now referred to as the Gibbs energy. Since his equation was for an n-component system, it readily applies to HEAs. A detailed analysis of n-component equation is given in the appendix.

Professor J.D. van der Waals at the University of Amsterdam quickly understood Gibbs’ work,[22] and the concept of free energy became known to others at the University of Amsterdam, notably D.J. Korteweg, H.W.B. Rooseboom, and F.A.H. Schreinemakers. Korteweg had been a graduate student of van der Waals and in 1879 as a Professor of Mathematics, he wrote “La théorie générale des plis”.[23] Plis, a.k.a. plaits, means folds in English (e.g. like folds in a blanket) and refers to undulations in a 2-dimensional Gibbs energy surface. The undulations create common tangent points for planes and critical points where two tangent points merge. By a geometric analysis of the surface, Korteweg predicted spinodal lines, both stable and unstable critical points, cone points, and mechanisms by which 3-phase miscibility gaps could form. Later, Schreinemakers[24] sketched phase diagrams illustrating two of these mechanisms by making use of Korteweg’s theory and drawings. In the 1950s Meijering, another renowned Dutch scientist, wrote about the differential geometry of Gibbs energy surfaces and stability limits in ternary and quaternary systems.[15] He found a third mechanism by which a 3-phase miscibility gap could form that was also anticipated by Korteweg. Also, Meijering found a cone point in the ternary spinodal surface. The cone point occurred at the equi-atomic composition in a regular solution model that had equal binary interaction terms.

It appears that Korteweg’s contributions are not well known although his theory of plaits is discussed by Meijering.[15] He studied in detail[23] how spinodal lines form, combine, and cross binodal lines when the formation of 3-phase miscibility gaps is involved. However, Korteweg’s detailed diagrams cannot be found in the English literature except in the comprehensive history and technical review by Sengers.[25] Korteweg also contributed to naming mechanisms of 3-phase miscibility gap formation. He showed that the mechanisms could involve single, double, or triple critical points and wrote that a mechanism was homogeneous if it formed in a stable region and heterogeneous if it formed in a metastable region. In the current work the mechanisms listed below will be referred to as types 1, 2, and 3:

Type 1: the homogeneous critical-end-point mechanism

Type 2: the heterogeneous double-critical-point mechanism

Type 3: the homogeneous triple-critical-point mechanism

In the previous work,[9] the mechanisms by which 3-phase miscibility gaps could form were studied using Pandat computer simulations[26] with regular and sub-regular solution models. The publication validated the phase diagram sketches by Schreinemakers and expanded on the hand calculated diagrams given by Meijering. Although spinodal lines were included on these diagrams, they were not discussed in detail as in this work. Similar diagrams are given below, although with additional features.

5 Three Mechanisms of 3-Phase Miscibility Gap Formation

The type 1 critical-end-point mechanism can be seen in Fig. 3. The mechanism involves the intersection of two miscibility gaps. As the bottom miscibility gap enters the upper miscibility gap, a stable 3-phase tie-triangle forms, while part of the 2-phase miscibility gap becomes metastable inside the tie-triangle. The name of the mechanism is derived from the critical point touching the end of a tie-line which expands into a tie-triangle on cooling. An unexpected feature not mentioned by Schreinemakers is the small circular spinodal loop at the center of Fig. 3(d). It is related to a cone point.

Fig. 3

Type 1 critical-end-point mechanism. Red lines are the spinodal, red dots are critical points and dashed lines indicate a metastable 2-phase miscibility gap. (a) Two miscibility gaps approach each other as the temperature is lowered. (b) The bottom miscibility gap enters the upper one to form a 3-phase miscibility gap in the shape of a tie-triangle. (c) Same as (b), but at a lower temperature. (d) At a lower temperature after spinodal lines have merged.

The type 2 double-critical-point mechanism can be seen in Fig. 4. Here a double critical point forms at 460K and then divides into two separate critical points. One critical point is associated with a metastable 2-phase miscibility gap that forms spontaneously within the stable 2-phase region while the other critical point is unstable. As the temperature is lowered, the metastable miscibility gap moves across the stable binodal line to form a 3-phase miscibility gap, i.e., a tie-triangle, in its wake. The formation of stable and unstable critical points was described by Korteweg in La théorie générale des plis,[23] a reference that includes a sketch of Fig. 4(d).

Fig. 4

Type 2 heterogeneous double-critical-point mechanism. (a) A 2-phase miscibility gap at 460K where a double critical point form. On further cooling the double critical point divides into two critical points. (b) At 424.1K one critical point has moved to the 2-phase region binodal. (c) At 410K the critical point ϒ and its accompanying miscibility gap has crossed the original 2-phase binodal and is now stable. (d) Details at 410K of binodals associated with the two critical points.

The third mechanism is illustrated in Fig. 5 and is a homogeneous triple-critical-point mechanism. It occurs when the critical points in Fig. 5(a) spontaneously form triple critical points at 777.78 K. In Fig. 5(b) each triple point divides on cooling and forms a 3-phase miscibility gap and two additional miscibility gaps. All miscibility gaps continue to grow as the temperature is lowered. In Fig. 5(c) the critical points of two adjacent 2-phase miscibility gaps merged and the spinodal curves became straight lines. Korteweg predicted that when two spinodal lines merge, it could only occur at a saddle point in the Gibbs energy surface where two critical points merged, however he did not anticipate this mechanism of forming 3-phase miscibility gaps. Meijering reported that the straight lines occur because the regular solution equation for the spinodal becomes a product of linear equations at 750K. His hand calculated diagrams have been verified several times using modern phase diagram prediction software.[16, 17, 27]

Fig. 5

Type 3 homogeneous triple-critical-point mechanism. (a) At 777.78K three triple critical points form spontaneously (b) At 755K each triple critical point has divided into three critical points associated with a 3-phase tie-triangle and additional two 2-phase miscibility gaps. (c) At 750K critical points of adjacent 2-phase miscibility gaps merge and spinodal lines become straight.

6 The Gibbs Energy Surface

The Gibbs energy versus composition diagram is a continuous undulating surface that was calculated in Ref. [9] with the equation:

$$G={x}_{1}{G}_{1}^{^\circ }+{x}_{2}{G}_{2}^{^\circ }+{x}_{3}{G}_{3}^{^\circ }+RT\left({x}_{1}ln{x}_{1}+{x}_{2}ln{x}_{2}+{x}_{3}ln{x}_{3}\right)+{L}_{12}{x}_{1}{x}_{2}+{L}_{13}{x}_{1}{x}_{3}+{L}_{23}{x}_{2}{x}_{3}+{x}_{1}{{x}_{2}x}_{3}{(L}_{1}{x}_{1}{{+{L}_{2}x}_{2}+{L}_{3}x}_{3})$$

(1)

which gives the Gibbs energy as a function of elemental values, ${G}_{i}^{^\circ }$, molar fractions, ${x}_{i}$, temperature, T, and various interaction parameters. The classic regular solution equation, with only binary interaction parameters, ${L}_{12}, {L}_{13},$ and ${L}_{23}$, was used to model the type 2 and type 3 mechanisms, while the sub-regular solution equation with the additional ${L}_{1}$ term was used to model the type 1 mechanism. The sub-regular solution term was needed to stabilize the upper miscibility gap in Fig. 3(a).

Figure 6(a) illustrates a contour diagram of the Gibbs energy surface for the phase diagram in Fig. 3(c). Figure 6(b) is part of the surface with ${x}_{A}$ less than 0.4 to focus on the surface for the lower miscibility gap. Here there are two valleys where a rolling tangent plane under the surface generates tie-lines on the isotherm at 820K. Figure 6(c) is a 2-D section of the Gibbs energy on a normal plane that passes through the surface along the dashed line in Fig. 6(b) at ${x}_{A}$=0.18. The two valleys and location of where a tangent line could be drawn are apparent.

Fig. 6

(a) Contour map of the Gibbs energy surface for the system in Fig. 3(c). (b) An expanded view of (a) for ${x}_{A}$ ≤ 0.4. (c) A plot of Gibbs energy on the plane passing through the Gibbs energy surface and the line ${x}_{A}$ = 0.18.

6.1 Review of Surface Curvature

A review of terminology is given in Fig. 7. The plane in Fig. 6(c) is a normal plane. A normal plane is a plane that passes through a vector that is normal to another plane. Figure 7 is a sketch of a normal plane for the current application. The plane passes through a vector that is normal to the composition plane. The normal curve on the plane is the intersection between the normal plane and the Gibbs energy surface.

Fig. 7

Illustration of the composition plane for a ternary isotherm, a vector normal to the composition plane, a normal plane passing through the vector, a normal curve obtained by intersecting a surface, the composition direction of the normal plane, and distance s in the composition direction.

Curvature along the normal curve is determined using the standard equation for a curve on a 2-D plane:

$$k= \frac{\frac{{\partial }^{2}G}{\partial {s}^{2}}}{{\left(1+{\left(\frac{\partial G}{\partial s}\right)}^{2}\right)}^{3/2}}$$

(2)

in which s is the distance along the normal plane. It can be seen in Eq. 2 that the curvature is zero when the second derivative of Gibbs energy is zero. In what follows, it will be assumed that the second derivative alone is the curvature, which is true when the curvature is zero, but approximate when the second derivative is not zero.

The curvature at any composition is a function of the composition direction of the plane. If the composition plane is rotated around a normal vector at a specific composition, the curvature will vary continuously and have a maximum and a minimum. The maximum and minimum are principal curvatures, and they occur at principal composition directions, which are always perpendicular.

6.2 Curvature and the Gibbs Energy Hessian

It is clear from equations presented by Gibbs that he had a deep understanding of how the Gibbs energy curvature was related to the matrix of second derivatives of the Gibbs energy with respect to mole fractions, $\left[{G}_{ij}\right]$. As explained in the appendix, he used his understanding to give equations for the limit of stability (i.e., the spinodal) and critical points in terms of $U$ equal to the $det\left|{G}_{ij}\right|$ and $V$ equal to the same determinant except with a row replaced with coefficients of $\frac{\partial U}{\partial {x}_{i}}$. The limit of stability then was $U=0$ and critical points when both $U=0$ and $V=0$.

The $\left[{G}_{ij}\right]$ matrix, the Gibbs energy Hessian, is a well-known matrix for determining the curvature of functions having multiple variables. In the pioneering work by de Fontaine,[14] multiple spinodal surfaces were interpreted, and it was shown that the coherent spinodal can be predicted by modifying the Gibbs energy function to include the effect of internal coherency stress. Therefore, one can apply the equations and observations given here to both liquid and solid solutions.

The Hessian is a symmetric matrix with real eigenvalues. Its eigenvalues and eigenvectors are the principal curvatures and their composition directions at a point on the Gibbs energy surface. For a ternary system, the eigenvalues/principal curvatures are:

$${\lambda }_{1}=\frac{\begin{array}{c}\left({G}_{11}+ {G}_{22}\right)-\sqrt{{\left({G}_{11}+ {G}_{22}\right)}^{2}-4 det\left|{G}_{ij}\right| }\\ \end{array}}{2}$$

(3)

$${\lambda }_{2}=\frac{\begin{array}{c}\left({G}_{11}+ {G}_{22}\right)+\sqrt{{\left({G}_{11}+ {G}_{22}\right)}^{2}-4 det\left|{G}_{ij}\right| }\\ \end{array}}{2}$$

(4)

Equation 3 and 4 shows that ${\lambda }_{1}<{\lambda }_{2}$ in all cases regardless of the thermodynamic model or parameters involved. This is an important consideration when interpreting phase diagrams. The corresponding eigenvectors/principal composition directions are:

$${\overrightarrow{v}}_{1}=\left[{\lambda }_{1}-{G}_{22}, { G}_{12}\right]$$

(5)

$${\overrightarrow{v}}_{2}=\left[{\lambda }_{2}-{G}_{22}, {G}_{12}\right]$$

(6)

The eigenvectors are perpendicular, which can be verified by showing that their scalar product is zero.

Other properties of a symmetric matrix with real eigenvalues are that its determinant is equal to the product of its eigenvalues:

$$det\left|{G}_{ij}\right|={\lambda }_{1}{\lambda }_{2}$$

(7)

and its trace is equal to the sum of its eigenvalues:

$$Tr\left[{G}_{ij}\right]={\lambda }_{1}+{\lambda }_{2}$$

(8)

Equation 7 and 8 are Gaussian and mean curvatures, respectively, and Eq. 7 is what Gibbs defined as $U$.

The normal curvature along the line in Fig. 6(c), $\frac{{\partial }^{2}G}{\partial {s}^{2}}$, is plotted in Fig. 8(a) as a blue line. For comparison, the principal curvatures ${\lambda }_{1}$ and ${\lambda }_{2}$ of the surface at each point along the normal curve are plotted as green lines. It can be seen in Fig. 8(a) that the normal curvature is always between the principal curvatures because the principal curvatures are the maximum and minimum curvatures. Also, the ${\lambda }_{1}$ line is always below the ${\lambda }_{2}$ line, as required by Eq. 3 and 4.

Fig. 8

(a) Plots of curvature versus s along the normal plane in Fig. 6(c). The blue line is the normal curvature, while the green lines are the principal curvatures ${\lambda }_{1}$ and ${\lambda }_{2}$. The blue line is calculated for $v=s$ while the green lines are calculated along the distance in the eigenvector direction, ${\overrightarrow{v}}_{i}$, of the eigenvalue ${\lambda }_{i}$. (b) The angle of each eigenvector with respect to the normal plane direction. Note that angles of 0° and -180° are equivalent.

The normal curvature and principal curvature must overlap in Fig. 8(a) when eigenvectors are parallel to the normal plane. Figure 8(b) gives the eigenvector angle from the normal plane as a function of distance. For this reason, when in Fig. 8(b) the angle of ${\overrightarrow{v}}_{1}$ is zero degree and when ${\overrightarrow{v}}_{2}$ is −180 degree the normal curvature and principal curvature are the same.

6.3 Gauge Invariance

Use of the equation ${x}_{1}+{x}_{2}+{x}_{3}=1$ in the current calculations allows for three different pairs of independent variables, ${(x}_{1},{x}_{2}), {(x}_{2},{x}_{3})$ and ${(x}_{3},{x}_{1})$. For most properties on a ternary phase diagram (e.g., binodal lines, tie-lines and tie-triangles, spinodal lines, and critical points), calculations with any pair give the same result. These properties are gauge invariant because they are not affected by which coordinate pair is involved in the calculations. However, other properties may not be gauge invariant. An example is the eigenvalue illustrated in Fig. 9.

Fig. 9

Comparison of three contour diagrams of the ${\lambda }_{1}$ curvature field for the system in Fig. 5(a). Each diagram was calculated using a different coordinate pair as the independent variables. The spinodal ${\lambda }_{1}=0$ lines and critical points are the same in all diagrams indicating that they are gauge invariant, while the rest of the curvature field is not.

Figure 9 gives three isotherms calculated for the system in Fig. 5(a). Each diagram contains only plots of spinodal lines, critical points, and the contour field of eigenvalue ${\lambda }_{1}$. Each diagram was calculated with a different pair of independent variables. The gauge invariant properties, spinodal lines and critical points, are the same on all three diagrams, while in general the eigenvalue fields are not the same. It is only the line where ${\lambda }_{1}$= 0, the spinodal, where the field is gauge invariant. At other compositions, the calculated curvature depends on the independent variables.

In Fig. 6 and in what follows there are contour field diagrams of both the Gibbs energy and the determinant of the Hessian. These fields are gauge invariant. Therefore, in Fig. 6 the Gibbs energy profile is gauge invariant while the eigenvalue lines for curvature in Fig. 9 are not gauge invariant, except where they are a spinodal.

7 Stability Limits and Characteristic Directions in Ternary Systems

In a 3-dimensional diagram of temperature vs ternary composition, the eigenvalues ${\lambda }_{1}=0$ (now ${\lambda }_{1}^{^\circ }$) and ${\lambda }_{2}=0$ (now ${\lambda }_{2}^{^\circ }$) are spinodal surfaces related to the limits of stability. The upper surface with respect to temperature, ${\lambda }_{1}^{^\circ }$, is “the stability limit.” Above the surface the phase is stable, while below the surface it is conditionally unstable, meaning that it is unstable to composition fluctuations in a limited range of composition directions.[14] The lower surface,${\lambda }_{2}^{^\circ }$, is the “unstable stability limit.” Above that spinodal surface, the phase is conditionally unstable, while below the surface it is unstable to fluctuations in all composition directions.

In Fig. 3, 4, 5 and 9 isotherms, all spinodal lines are sections of the ${\lambda }_{1}=0$ spinodal surface. Spinodal lines from the ${\lambda }_{2}=0$ surface occur in isotherms at lower temperatures. Figure 10 gives additional isotherms for the type 3 mechanism in Fig. 5 with temperatures low enough for both ${\lambda }_{1}$ and ${\lambda }_{2}$ spinodal lines to appear. The isotherm in Fig. 10(a) is 1K below Fig. 5(c) and shows that the 2-phase regions near the center of the diagram have merged and that a ${\lambda }_{2}$ spinodal line has appeared in the center of the diagram. Figure 10(b) is at the eutectic/eutectoid temperature of 721.35K where the three tie-triangles merge into one tie-triangle. Figure 10(c) is at a much lower temperature where the merged tie-triangle has enlarged to cover nearly the entire diagram space.

Fig. 10

Like Fig. 5 for the type 3 mechanism, except at lower temperatures (a) At 749K the 2-phase regions and spinodal lines have merged. (b) At 721.35K, the eutectic/eutectoid temperature, where the three tie-triangles merge into one. (c) At 500K the merged tie-triangle is much larger.

Spinodal lines divide the Gibbs triangle into various regions, with the adjoining regions having different stability. Figure 11(a) shows how to interpret the different regions in Fig. 10(c). In the corner regions both ${\lambda }_{1}$ and ${\lambda }_{2}$ are positive (+ +). Therefore, the phase in that region is stable. The boundaries of those regions are ${\lambda }_{1}=0$ spinodal lines. On the other side of the spinodal lines, ${\lambda }_{1}$ is negative while ${\lambda }_{2}$ remains positive. In this (− +) region, the phase is conditionally unstable to a range of composition directions. The range of composition directions for a specific composition varies between two extremes where the curvature is zero. The directions of these extremes are given by:

Fig. 11

(a) The isotherm in Fig. 10(c) with just spinodal lines. The stability of each region is indicated by the sign, plus or minus, of the first and second eigenvalues. (b) The percentage of composition directions that are unstable along the line from the ${B}_{0.5}{C}_{0.5}$ composition to pure A.

$$\frac{d{x}_{1}}{d{x}_{2}}=\frac{{-G}_{12} \pm \sqrt{- det\left|{G}_{ij}\right| }}{{G}_{11}}$$

(9)

Equation 9 is the same as Eq. 43 in Ref. [14], except for several apparent typographical errors. Note for example, the square root must contain a minus sign because $det\left|{G}_{ij}\right|$ is negative in the conditionally unstable region where Eq. 9 applies. Figure 11(b) is a plot of how the percentage of unstable composition directions change with distance along the line between the ${B}_{0.5}{C}_{0.5}$ composition to pure A.

8 Cone Points

In ternary solutions it is possible for spinodal surfaces to develop a double cone in the central region of the phase diagram.[16, 17] Meijering found them in his hand-calculated regular solution model[15] of the type 3 mechanism. Calculations of his model were repeated in more detail later using phase diagram prediction software.[9] In the current work, double cones were found in both type 1 and 3 mechanisms systems.

Figure 12(a) gives an illustration of a normal double cone. It can be compared with isothermal sections of the double cone for the type 1 mechanism. As indicated on the figure, the upper cone is a ${\lambda }_{1}=0$ surface while the lower cone is a ${\lambda }_{2}=0$ surface. Inside the upper cone the solution is stable and inside the lower cone the solution is unstable. Between the upper and lower cones, the solution is conditionally unstable. Inside the upper cone, the first composition direction to become unstable depends on a vector radiating along the cone from the cone point. This was shown in Ref. [16, 17] on a cone that was mapped onto thermodynamic axes.

Fig. 12

A normal double cone compared to variations in isothermal sections of the spinodal surface versus temperature in the vicinity of a cone point. The equi-atomic composition is given by a small blue circle at the center of the diagram. Sections above 814.8K are of the upper cone and below 814.8K are of the lower cone.

Sections through the cones for the type 1 mechanism can be seen in Fig. 12. Figure 12(b) and (c) are sections through the upper cone while Fig. 12(e) and (f) are through the lower cone. Figure 12(d) exactly passes through the cone point at 814.8K. Both the type 1 and type 3 cones are similar in that they have the same cone point composition, although their cone point temperatures differ. The double cones are readily identified by how the size of their cross-sectional areas decrease on cooling down to the cone point and then increase on further cooling. However, the shape of the cones differ and the center line of the cone in Fig. 12(b)–(f) is tilted with respect to the temperature axis, while the one in Fig.10 is not. The tilt is apparent from the variation of the equi-atomic composition with respect to the cone surface with temperature.

Two isopleth sections of the phase diagram in Fig. 3 are given in Fig. 13. One is at a constant concentration of ${x}_{A}=0.33333$ and the other passes through the pure A and the ${B}_{0.5}{C}_{0.5}$ composition. Both pass through the cone point which is at 814.8K and ${x}_{C}=0.33333$. Blue lines are binodals while f symbols indicate the number of phases in each region.

Fig. 13

Isopleth sections of the type 1 mechanism phase diagram in which the blue lines are binodals and red lines are spinodals. (a) Section parallel to the B-C axis at ${x}_{A}=$ 0.33333 and (b) section along the line from pure A to the ${B}_{0.5}{C}_{0.5}$ composition. Both sections pass through the cone point which is at 814.8K and ${x}_{C}=0.33333$.

There appear to be two spinodal lines in each diagram that cross. However, crossing is impossible, because, according to Eq. 3 and 4, ${\lambda }_{1}<{\lambda }_{2}$. That means that on cooling the ${\lambda }_{2}=0$ line will always be at a lower temperature than the ${\lambda }_{1}=0$ line.

Figure 14 shows the spinodal lines of Fig. 13(b) after the isopleth is moved away from the section of A–B_0.5C_0.5 with two spinodal crossing-points to the isoplethal sections of (a) A–B_0.51C_0.49, (b) A–B_0.52C_0.48 and (c) A–B_0.55C_0.45. It illustrates that the apparent crossing point at 814.8K is just where two spinodal curves meet at a point. Also, it shows that the upper cone bounds the stable region, that the lower cone bounds the unstable region, and that the surrounding region is conditionally unstable. It follows that double cone found on random 2-D sections will look more like the conic sections in Fig. 14(c) than the double cone in Fig. 14(a). Figure 14 illustrates, as well, that not all crossing points are cone points as indicated by the crossing point near 440K.

Fig. 14

(a) Isopleth from Fig. 13(b) showing just the spinodal lines. Lines at the cone point and another point appear to cross. (b) and (c) show similar isopleths that are rotated away from the cone point. Note that ${\lambda }_{1}$ is always above ${\lambda }_{2}$ and that near the cone point one obtains a conic section.

9 Critical Points

Critical points on phase diagrams occur in miscibility gaps where the length of tie-lines reduces to zero, i.e., where two phases become indistinguishable. In binary phase diagrams there are only stable critical points, but Korteweg[23] determined that both stable and unstable critical points can occur on a ternary free energy surface when 3-phase miscibility gaps form. Meijering discussed both types of critical points but only included stable critical points on his diagrams. In the following, a graphical method is used to show how the two types of critical points form and how to distinguish between them.

9.1 Calculation of Critical Points

The condition for a binary critical point is $\frac{{\partial }^{2}G}{\partial {x}^{2}}=0$ and $\frac{{\partial }^{3}G}{\partial {x}^{3}}=0$. For a general treatment of the critical point the concentration is replaced by a concentration vector $\overrightarrow{v}$. In a binary system, concentration vector $\overrightarrow{v}$ has only one direction along the composition axis, either in the direction of ${x}_{1}$ or ${x}_{2}$. The criteria for critical points in a binary system are then that $\frac{{\partial }^{2}G}{\partial {v}^{2}}=0$ and $\frac{{\partial }^{3}G}{\partial {v}^{3}}=0$ at a given temperature, pressure, and mole fraction, $v$. Gibbs recognized that these criteria apply to multicomponent systems when the concentration v is along a principal curvature direction and the determinant of the Gibbs energy Hessian U = 0. Mathematically, it can be shown that critical points occur on a spinodal line where the corresponding eigenvector is tangent to the spinodal line. This is the basis for Gibbs’ solution given in section 6.2 and derived in the Appendix.

9.2 Stable and Unstable Critical Points

Multiple stable and unstable critical points were found in the current systems. Calculated examples of the two types of critical point and their miscibility gaps are given in Fig. 15. The first two figures are the same as Fig. 4(d) except that tie-lines have been added to identify the two miscibility gaps in the figure. The third figure is the miscibility gap near the B-C side in Fig. 5(b). Additional tie-lines have been added to that diagram as well to identify the three miscibility gaps in that figure.

Fig. 15

Miscibility gaps containing stable (solid red dot) and unstable (open red circle) critical points. Tie-lines are drawn between binodals of individual miscibility gaps. (a) Details of the stable miscibility gap in Fig. 4(d) with its stable critical point, $\gamma$. (b) Details of the unstable miscibility gap in Fig. 4(d) with its unstable critical point, $\beta$. (c) Details of miscibility gaps from Fig. 5(b) with an unstable critical point in the middle and stable critical points on either side.

In Fig. 15, the first two figures have two binodal lines meeting at a cusp on either end. This unique shape was predicted by Korteweg[23] in his study of the geometry of a 2-D free energy surface in a 3-D space. He found that when a spinodal line crosses a binodal line, two binodal lines must meet in a cusp. Since the spinodal line crosses two binodal lines, two cusps occur. Figure 15(c) was predicted by Korteweg, as well. Here the spinodal line crosses a binodal on each side of the diagram and, accordingly, there are cusps on each side.

The difference between stable and unstable critical points can be seen in Fig. 15. It depends on the stability of the binodal lines in the miscibility gap. In Fig. 15(a) the stable binodal ${d}_{1}-{c}_{1}-\gamma -{c}_{2}$ is on the stable side of the spinodal line, while Fig. 15(b) the binodal ${d}_{1}-\beta -{d}_{2}-{c}_{2}$ is on the conditionally unstable side of the spinodal line. As shown in Fig. 4, the stable critical point with its miscibility gap grows outside the 2-phase region to where it is stable, while the unstable critical point remains inactive inside the conditionally unstable 2-phase region. In Fig. 15(c) the location of the middle miscibility gap shows that it is in a conditionally unstable region, too, while the other two miscibility gaps are stable.

9.3 Graphical Methods of Determining Critical Points

Figure 16(a) and (b) contain the ${\lambda }_{1}=0$ spinodal line from the miscibility gap along the B-C side of Fig. 5(b). Eigenvector directions are plotted around the spinodal line and critical points occur where the eigenvectors rotate and become tangent to the spinodal line, confirming Gibbs’ solution. However, in the current work, critical points were determined graphically by calculating lines where the third directional derivative of the Gibbs energy was zero. The lines were calculated in the eigenvector direction, ${\overrightarrow{v}}_{1}$, of the local ${\lambda }_{1}$.

Fig. 16

(a) Illustration of how the eigenvector ${\overrightarrow{v}}_{1}$ rotates along a spinodal line and is tangent to the spinodal line at the critical point. Pink lines are where the third derivative of the Gibbs energy is zero when calculated in the eigenvector direction of the local ${\lambda }_{1}$. In this calculation ${x}_{A}$ and ${x}_{C}$ are used as the independent variables. (b) Same as (a) except extra lines are added where the third derivative of the Gibbs energy is zero when calculated in the eigenvector direction of the local ${\lambda }_{1}$ using ${x}_{A}$ and ${x}_{B}$ as the independent variables.

The constant $\frac{{\partial }^{3}G}{\partial {{v}_{1}}^{3}}=0$ lines are plotted in Fig. 16(a) and intersect the spinodal at both the stable and unstable critical points. In Fig. 16(a) the third directional derivative lines were calculated using ${x}_{A}$ and ${x}_{C}$ as the independent variables, while in Fig. 16(b) third directional derivative lines have been added using ${x}_{A}$ and ${x}_{B}$ as the independent variables. The third directional derivative lines differ because they are not gauge invariant, but they both predict the same correct critical points. Other critical points in figures in this work are also determined from the intersection between spinodal lines and $\frac{{\partial }^{3}G}{\partial {{v}_{1}}^{3}}=0$ lines.

9.4 Double and Triple Critical Points

The conditions when double and triple critical points form are illustrated in Fig. 17 and 18. They show how the third derivative lines migrate with temperature to first form the multiple critical points and then cause the multiple critical points to separate and become associated with individual stable and unstable miscibility gaps.

Fig. 17

Illustration of how a double critical point forms as a function of temperature. (a) A constant third derivative line approaches the spinodal on cooling. (b) A double critical point forms at 460K when the two lines are tangent. (c) As the third derivative line crosses the spinodal the double critical point separates into single stable and unstable critical points. (d) Critical lines formed by the critical points on cooling have been projected onto a temperature versus A-C plane.

Fig. 18

Formation of a triple critical point in the type 3 mechanism. (a)(800K) third derivative lines indicate one critical point on each spinodal. (b) (777.78K) a triple critical point form on each spinodal. (c-e) (777-755K) Each triple critical point separates into two stable and one unstable critical point. (f) (745K) Three unstable critical points can be seen on the upper spinodal cone.

Figure 17 is an example from the type 2 mechanism of how a double critical point forms. At high temperatures such as 480K in Fig. 17(a) the spinodal line and the third derivative line are separate. As shown in Fig. 17(b) a double critical point forms when the third derivative line is tangent to the ${\lambda }_{1}^{^\circ }$ line. Then in Fig. 17(c) the critical points have separated as the third derivative line migrates into the conditionally unstable side of the spinodal line.

A projection of the critical point trajectories onto the temperature versus A-C plane is given in Fig. 17(d). The double critical point is at the summit of the graph. The stable critical point moves to the A-C binary at ${x}_{A}$=0.5, while the unstable critical point remains in the 2-phase region of the phase diagram.

Figure 18 is an example from the type 3 mechanism of how a triple critical point form. Here the third derivative lines are given for a range of temperatures, and it is apparent that triple critical points occur at 777.78 K. Around 777.78 K there are two third-derivative lines. At 800K, one third-derivative line intersects with A–B binary side spinodal, the other intersects with the spinodal lines on A–C and B–C binary sides. At 777.78 K the second third-derivative line becomes tangent to the A–B side spinodal to form a triple critical point with the first third-derivative line intersecting the spinodal. For the A–C and B–C side spinodals, the second third-derivative line begins to intersect both spinodal lines three times just below 777.78 K, which implies that a triple critical point form on each of these spinodals at 777.78 K as well. On cooling below 777.78 K the unstable critical point remains stationary while the two stable critical points move apart as indicated in Fig. 15(c). It can be found from Fig. 18 that the third-derivative lines interact with each other below 776K to form two different third-derivative lines as seen at 755K. Although the third-derivative line is not gauge invariant, their intersection points with spinodal lines, the critical points, are gauge invariant.

10 Saddle Points and Merging Spinodal Line

Critical points can happen where the Gibbs energy has various types of curvatures. Figure 19 shows three Gibbs energy contour diagrams of the type 3 mechanism in which Gibbs energy values are relative to the tangent plane at the critical point. In Fig. 19(a) the Gibbs energy surface has a positive curvature at the critical point. In Fig. 19(b) the Gibbs energy surface has a value of zero for both principal curvatures but is a true saddle point at the middle critical point. Spinodal lines do become straight as they approach the saddle point as shown in Fig. 19(b). Figure 19(c) is calculated at the cone point temperature and the Gibbs energy surface has six-fold symmetry and is a “monkey” saddle point at the critical point in the center.

Fig. 19

Gibbs energy contour diagrams near a critical point for the type 3 mechanism (a) positive curvature at the critical point (b) a special saddle point with zero principal curvatures (c) a monkey saddle point at the spinodal cone point where three critical points merge.

When two spinodal lines merge they must either have critical points already or form them spontaneously before merging. An example from Fig. 3 is given in more detail in Fig. 20. In Fig. 3(c) two spinodal lines approach each other at 820K, but only one line has a critical point, while in Fig. 3(d) the spinodal lines have merged. Lines at the corners of the diagram are without critical points, while a small nearly circular spinodal feature, that is a section near the cone point, has critical points, but the feature was too small to be included.

Fig. 20

How spinodal lines merge in Fig.3. At 818.84K the critical point becomes a triple critical point. At 817.66K two double critical points form. At 817.6K the double critical points have separated. At 817.55K two double critical points form from four critical points as two spinodal lines approach each other and the stable critical points merge. At 817.5K the merging is complete.

Figure 20 shows what happens in Fig. 3 during cooling from 819 to 817.5 K. At 819 K in Fig. 20(a), only the lower spinodal line has one critical point. When temperature decreases to 818.84K, this critical point becomes a triple critical point and will split into three critical points as seen in Fig. 20(c) and (d). When temperature reaches 817.66 K as in Fig. 20(c), the upper spinodal line starts to form two double critical points and both will split into two critical point with decreasing temperature. Figure 20(d) shows the four critical points that originate from the two double critical points on the upper spinodal line and the three critical point that originate from the one triple critical point on the lower spinodal line. When the temperature continues to drop, the two spinodal lines will touch and merge at 817.55 K, as shown in Fig. 20(e), and the two critical points merge to form a double critical point that disappears on further cooling. The only remaining critical points at lower temperature are three unstable critical points along the upper spinodal cone, as seen in Fig. 20(f). On cooling down to the cone point, the trace of the critical points are three critical lines that meet at a triple critical point at the cone point.

11 Polythermal Projections and Characteristic Lines

Polythermal projections of the upper spinodal surface, i.e., the stability limit, for the three types of critical point mechanisms are shown in Fig. 21. Spinodal lines are red, while characteristic lines along the spinodal surface are green. Characteristic lines indicate the composition direction of unstable fluctuations on crossing the stability limit[17].

Fig. 21

Polythermal projections of stability limits for the three mechanisms of forming 3-phase miscibility gaps. (a) The type 1 mechanism, (b) details in (a) with ${x}_{A}\ge 0.8$, (c) the type 2 mechanism, and (d) the type 3 mechanism. Isotherms of the spinodal are given in red. Characteristic lines of constant instability direction are given in green. The unstable direction of each line is given as an angle with respect to the B-C axis.

In Meijering’s comprehensive investigation of miscibility gaps in ternary regular solutions, systems were classified into nine categories. Figure 21(c) and (d) are in two of the categories, his IV(a) and IV(b). Figure 21(a) is not included in this classification because it was calculated with a sub-regular solution model.

Examples of stability limits for eight of Meijering’s categories along with their characteristic lines can be found in the literature.[15, 16] The current regular solution diagrams confirm the previous work, having a cone point in Fig. 21(d), but not in Fig. 21(c). However, Fig. 20(a) contains two cone points and the appearance of two isolated miscibility gaps that form above 1000K.

The high temperature miscibility gaps are a result of the sub-regular solution term in Eq. 1, ${x}_{1}^{2}{x}_{2}{x}_{3}{L}_{1}$. It has been established before[17] that the term ${x}_{1}{x}_{2}{x}_{3}{L}_{1}$ produces three isolated miscibility gaps on cooling. Apparently by squaring ${x}_{1}$ in the current model, one of the three miscibility gaps is suppressed. The remaining two miscibility gaps serve to maintain the 2-phase miscibility gap that stretches between the A-B and A-C sides of the diagram before it is intersected by the miscibility gap coming from the B-C side.

Figure 21(d) with its equal interaction parameters and single cone point is identical to the diagram of the spinodal surface by Meijering. Characteristic lines were added later, along with calculated polythermal spinodal surfaces for eight of Meijering’s categories. The categories differed by the number of binary miscibility gaps in the system and the ratio of their interaction parameters.

12 Discussion

A HEA system contains five or more components with near equi-atomic composition. It is common that one or more binary subsystems have miscibility gaps in the solid phase, such as bcc in Nb-Cr, Fe-Cr, and Nb-Zr binary systems. Since a single binary miscibility gap will spread across the entire multi-composition space of the system, such an alloy will have the tendency to undergo spinodal decomposition on cooling.

If an alloy system is unstable with respect to spinodal decomposition, a miscibility gap as well as chemical spinodal and coherent spinodal lines will appear in the isopleths. If that were the case, then the uppermost coherent spinodal line ${\lambda }_{1}$ would be the stability limit below which alloys would become unstable. To avoid spinodal decomposition, alloys would have to remain at higher temperatures when in service.

On age hardening below the ${\lambda }_{1}$ stability limit, alloys are in a region of conditional instability until the ${\lambda }_{n-1}$ unstable stability limit line is crossed, where instability is possible in all composition directions. For example, in the Fig. 9 isotherm for ternaries, the range of unstable directions increases from one direction to all directions between the ${\lambda }_{1}$ and ${\lambda }_{2}$ lines. The same would happen in a 5-component system when varying either the composition or temperature between the ${\lambda }_{1}$ line and ${\lambda }_{4}$ line. ${\lambda }_{2}$ and ${\lambda }_{3}$ lines are the limits of conditional instability, and they track how the range of instability changes with temperature. Each of the four lines is an eigenvalue associated with an eigenvector of Gibbs energy function. Below these conditionally unstable stability limits there would be a driving force for a wider range of composition fluctuations versus temperature. In a sense these spinodal lines are similar to the characteristic lines plotted on polythermal projections. This means that age hardening could be sensitive to the aging temperature in unexpected ways.

Gauge invariance is an important concept for studying the stability of alloys from Gibbs energy functions. Since the molar fractions are normalized to satisfy $\sum {x}_{i}=1$, many derived properties from the derivatives of the Gibbs energy functions are not gauge invariant and dependent on the selection of independent molar fractions. For example, the eigenvalue of Hessian is not gauge invariant but the eigenvalue equal to zero, i.e., the spinodal line, is gauge invariant.

In principle, a critical point can be calculated from the Gibbs equations: $U=0$ and $V=0$, as mentioned in section 6.2 as well as the appendix. The two methods presented in this work, eigenvector and $\frac{{\partial }^{3}G}{\partial {{v}_{1}}^{3}}=0$, are visually more effective. Most of the critical points in the current 2-D section diagrams are determined by locating the intersections between spinodal and $\frac{{\partial }^{3}G}{\partial {{v}_{1}}^{3}}=0$ line.

Many different types of diagrams have been calculated and most of them were calculated directly using Pandat software.[26] For the calculation of diagrams with spinodal, eigenvalues, eigenvectors, and the third derivative of Gibbs energy, these properties must first be defined as thermodynamic properties of phases. The diagrams were calculated using the contour property diagram utility of Pandat. However, the characteristic lines in Fig. 21 were calculated using a standalone code.

13 Summary

A high entropy alloy has near equi-atomic composition, which makes the alloy having the tendency to undergo spinodal decomposition if any of its constituent binary systems has a solid miscibility gap. This work discussed in detail the mechanisms of 3-phase miscibility gap formation and stability related concepts using ternary regular solution model, which would help us understand the stability of an HEA if spinodal decomposition happens during age hardening of the alloy.

An example of Au-Ni binary system was used to review the relationships among binodal, chemical spinodal and coherent spinodal. Different types of 2-D diagrams, 2-D bisection, constant core component (CCC) isothermal section, and polythermal projection, are summarized for presenting the HEA phase relationships.

This work focuses on the phase stability analysis and gives readers a broad background on how chemical and coherent spinodals may appear in calculated phase diagrams and they can be applied to HEA and heat treatment design. The concepts discussed include Gibbs energy surface curvature, Hessian, eigenvalue, eigenvector, gauge invariance, stability limit, characteristic directions, saddle points of the Gibbs energy, stable and unstable critical points, and cone points, which are all important to study alloy stability. In addition, it also covers how to determine critical points and how the critical points and spinodal lines merge and split.

Historical contributions on phase separation (miscibility gap) from Gibbs, Korteweg, Schreinemakers, and Meijering were briefly introduced as well. A detailed analysis of Gibbs stability condition in an n-component system is presented in the appendix.

Appendix: Analysis of Gibbs’ Conditions for the Critical Point

Gibbs was a talented mathematician, which enabled him to make numerous contributions to the fields of physics, chemistry, and mathematics. Near the end of his career, he was awarded the Copley Medal by the Royal Society of London for his work on mathematical physics. However, his work often was not well understood by colleagues because of its depth and lack of explanations. An example is his solution for the critical point on a spinodal surface.

The following are conditions given by Gibbs for the critical point. The conditions were then explained in terms of basic matrix and vector analysis methods. It is significant that one of Gibbs’s accomplishments was developing and promoting the use of modern vector calculus. That might suggest why Gibbs could conclude that critical points occur when $U=0$ and $V=0,$ in which $U$ is the determinant of the Gibbs energy Hessian for an n-component system:

$$U=\left|\begin{array}{cccc}\frac{{\partial }^{2}G}{\partial {x}_{1}^{2}}& \frac{{\partial }^{2}G}{\partial {x}_{1}\partial {x}_{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{1}\partial {x}_{n-1}}\\ \frac{{\partial }^{2}G}{\partial {x}_{2}\partial {x}_{1}}& \frac{{\partial }^{2}G}{\partial {x}_{2}^{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{2}\partial {x}_{n-1}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{{\partial }^{2}G}{\partial {x}_{n-1}\partial {x}_{1}}& \frac{{\partial }^{2}G}{\partial {x}_{n-1}\partial {x}_{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{n-1,n-1}^{2}}\end{array}\right|$$

(1A)

and $V$ is the determinant formed by substituting any row in $U$ with the row vector:

$$\left(\frac{\partial U}{\partial {x}_{1}}, \frac{\partial U}{\partial {x}_{2}},\cdots ,\frac{\partial U}{\partial {x}_{n-1}}\right)$$

(2A)

Explanation: An elementary equation in matrix algebra that diagonalizes a matrix $\left[G\right]$ like the Hessian is:

$${\left[v\right]}^{-1}\left[G\right]\left[v\right]=\left[\lambda \right]$$

(3A)

in which $\left[G\right]$ is the original matrix in Eq. 1A, $\left[v\right]$ is a matrix of eigenvectors, and $\left[\lambda \right]$ is a diagonal matrix of eigenvalues. Multiplying Eq.3A by $\left[v\right]$ yields Eq.4A, which is written in full for the Gibbs energy Hessian:

$$\left(\begin{array}{cccc}\frac{{\partial }^{2}G}{\partial {x}_{1}^{2}}& \frac{{\partial }^{2}G}{\partial {x}_{1}\partial {x}_{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{1}\partial {x}_{n-1}}\\ \frac{{\partial }^{2}G}{\partial {x}_{2}\partial {x}_{1}}& \frac{{\partial }^{2}G}{\partial {x}_{2}^{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{2}\partial {x}_{n-1}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{{\partial }^{2}G}{\partial {x}_{n-1}\partial {x}_{1}}& \frac{{\partial }^{2}G}{\partial {x}_{n-1}\partial {x}_{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{n-1,n-1}^{2}}\end{array}\right)\left(\begin{array}{cccc}{v}_{11}& {v}_{12}& \cdots & {v}_{1,n-1}\\ {v}_{21}& {v}_{22}& \cdots & {v}_{2,n-1}\\ \vdots & \vdots & \ddots & \vdots \\ {v}_{n-\mathrm{1,1}}& {v}_{n-\mathrm{1,2}}& \cdots & {v}_{n-1,n-1}\end{array}\right)$$

$$=\left(\begin{array}{cccc}{v}_{11}& {v}_{12}& \cdots & {v}_{1,n-1}\\ {v}_{21}& {v}_{22}& \cdots & {v}_{2,n-1}\\ \vdots & \vdots & \ddots & \vdots \\ {v}_{n-\mathrm{1,1}}& {v}_{n-\mathrm{1,2}}& \cdots & {v}_{n-1,n-1}\end{array}\right)\left(\begin{array}{cccc}{\lambda }_{1}& 0& \cdots & 0\\ 0& {\lambda }_{2}& \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0& 0& \cdots & {\lambda }_{n-1}\end{array}\right)$$

(4A)

Equation 4A shows the relationship between the Gibbs Hessian, its ${\lambda }_{i}$ eigenvalues and the corresponding ${\overrightarrow{v}}_{j}$ column eigenvectors.

Since the Gibbs Hessian has the eigenvalues ${\lambda }_{i}$ , another elementary equation of matrix algebra gives the determinant of the Hessian matrix as:

$$U=\left|\begin{array}{cccc}\frac{{\partial }^{2}G}{\partial {x}_{1}^{2}}& \frac{{\partial }^{2}G}{\partial {x}_{1}\partial {x}_{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{1}\partial {x}_{n-1}}\\ \frac{{\partial }^{2}G}{\partial {x}_{2}\partial {x}_{1}}& \frac{{\partial }^{2}G}{\partial {x}_{2}^{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{2}\partial {x}_{n-1}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{{\partial }^{2}G}{\partial {x}_{n-1}\partial {x}_{1}}& \frac{{\partial }^{2}G}{\partial {x}_{n-1}\partial {x}_{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{n-1,n-1}^{2}}\end{array}\right|={\lambda }_{1}{\lambda }_{2}\cdots {\lambda }_{n-1}$$

(5A)

When $U$ is equal to zero, the smallest eigenvalue ${\lambda }_{z}$ becomes zero, which indicates the system is at a temperature, pressure, and composition of a stability limit (spinodal). Therefore, Gibbs’ condition that $U=0$ assures that a critical point will be on the spinodal.

The condition that $V=0$ is more complicated, but can be solved in several ways. Fundamentally, it is when the third derivative of the Gibbs energy with respect to composition along the eigenvector direction is zero on the spinodal. The Gibbs solution infers that a critical point occurs when the eigenvector ${\overrightarrow{v}}_{z}$ of the smallest eigenvalue is in the plane tangent to the spinodal surface.

Calculating the condition when the eigenvector direction is in the tangent plane to the spinodal surface begins by multiplying the eigenvalue and eigenvector matrices in Eq. 4A and equating terms multiplied by the zth eigenvector:

$$\left(\begin{array}{cccc}\frac{{\partial }^{2}G}{\partial {x}_{1}^{2}}& \frac{{\partial }^{2}G}{\partial {x}_{1}\partial {x}_{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{1}\partial {x}_{n-1}}\\ \frac{{\partial }^{2}G}{\partial {x}_{2}\partial {x}_{1}}& \frac{{\partial }^{2}G}{\partial {x}_{2}^{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{2}\partial {x}_{n-1}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{{\partial }^{2}G}{\partial {x}_{n-1}\partial {x}_{1}}& \frac{{\partial }^{2}G}{\partial {x}_{n-1}\partial {x}_{2}}& \cdots & \frac{{\partial }^{2}G}{\partial {x}_{n-1,n-1}^{2}}\end{array}\right)\left(\begin{array}{c}{v}_{1z}\\ {v}_{2z}\\ \vdots \\ {v}_{n-1,z}\end{array}\right) =\left(\begin{array}{c}{v}_{1k}{\lambda }_{z}\\ {v}_{2k}{\lambda }_{z}\\ \vdots \\ {v}_{n-1,k} {\lambda }_{z}\end{array}\right)=0$$

(6A)

Equation 6A shows that along the spinodal all matrix elements on the right of the equal sign are zero. That means that for any row vector in the Hessian, ${\overrightarrow{G}}_{i}$, we have

$${\overrightarrow{G}}_{i} {\overrightarrow{v}}_{z}=0$$

(7A)

This equality is illustrated in Fig. 22 for a quaternary system. The three row vectors ${\overrightarrow{G}}_{1}, {\overrightarrow{G}}_{2}, {\overrightarrow{G}}_{3}$ that are perpendicular to the eigenvector ${\overrightarrow{v}}_{z}$ are depicted. Also, there is a spinodal surface with a tangent plane and normal vector $\overrightarrow{n}$ at a point c on the surface. If this is a critical point, the three row vectors would have to be in the normal plane containing the normal vector. The eigenvector must lie in the tangent plane as well. However, this is only true if the normal and eigenvector are perpendicular.

Fig. 22

Spinodal surface (shaded) with a normal vector $\overrightarrow{n}$ and tangent plane at a critical point c on the surface. In addition, there are three row vectors of the Gibbs energy Hessian ${\overrightarrow{G}}_{1}, {\overrightarrow{G}}_{2}, {\overrightarrow{G}}_{3}$ that are perpendicular to the eigenvector ${\overrightarrow{v}}_{z}$ associated with the smallest eigenvalue. Eigenvector ${\overrightarrow{v}}_{z}$ is in the tangent plane to the spinodal surface at the critical point c.

Since the function $U({x}_{1}, {x}_{2}, \dots {,x}_{n-1})=0$ is the equation of the (n-2)-dimensional spinodal surface, the normal vector to the spinodal surface is:

$$\overrightarrow{n}=\left(\frac{\partial U}{\partial {x}_{1}}, \frac{\partial U}{\partial {x}_{2}},\cdots ,\frac{\partial U}{\partial {x}_{n-1}}\right)$$

(8A)

And a critical point, the eigenvector ${\overrightarrow{v}}_{z}$ is in the tangent plane to the spinodal surface. Then, the normal vector $\overrightarrow{n}$ at the critical point c must be perpendicular to ${\overrightarrow{v}}_{z}$,

$$\overrightarrow{n} {\overrightarrow{v}}_{z}=0$$

(9A)

The Gibbs solution is to replace a row of the Hessian matrix in Eq. 6A with Eq. 8A. When the determinant of that new matrix is zero, i.e., when $V=0$, there is a critical point.