Learning and planning with logical automata

Abstract

We introduce a method to learn policies from expert demonstrations that are interpretable and manipulable. We achieve interpretability by modeling the interactions between high-level actions as an automaton with connections to formal logic. We achieve manipulability by integrating this automaton into planning via Logical Value Iteration, so that changes to the automaton have predictable effects on the learned behavior. These qualities allow a human user to first understand what the model has learned, and then either correct the learned behavior or zero-shot generalize to new, similar tasks. Our inference method requires only low-level trajectories and a description of the environment in order to learn high-level rules. We achieve this by using a deep Bayesian nonparametric hierarchical model. We test our model on several domains of interest and also show results for a real-world implementation on a mobile robotic arm platform for lunchbox-packing and cabinet-opening tasks.

1 Introduction

In the imitation learning (IL) problem, desired behaviors are learned by imitating expert demonstrations (Abbeel and Ng 2004; Daumé III et al. 2009; Ross et al. 2011). IL has had success in tackling tasks as diverse as camera control, speech imitation, and self-driving for cars (Taylor et al. 2017; Codevilla et al. 2018; Ho and Ermon 2016; Yue and Le 2018). However, an IL model trained to imitate a specific task must be re-trained on new expert data to learn a new task. Additionally, in order for a robot to correctly learn a task, the expert demonstrations must be of high quality: most imitation learning methods assume that experts do not make mistakes. Therefore, we ask

• 1. How can expert demonstrations for a single task generalize to much larger classes of tasks?

• 2. What if the experts are unreliable and err?

This paper provides answers to these questions by applying elements of formal logic to the learning setting. We require our policies to be derived from learned Markov Decision Processes (MDPs), a standard model for sequential decision making and planning (Bertsekas and Tsitsiklis 1996; Sutton and Barto 1998). We assume these MDPs can be factored into a “low-level” MDP that describes the motion of the robot in the physical environment and a small finite state automaton (FSA) that corresponds to the rules the agent follows. After learning the transition and reward functions of the MDP and FSA, it is possible to manually change the FSA transitions to make the agent perform new tasks and to correct expert errors. Additionally, the FSA provides a symbolic representation of the policy that is often compact.

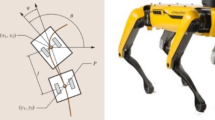
For example, imagine the robotic arm in Fig. 1 packing first a sandwich and then a banana into a lunchbox. The physical environment and the motions of the robotic arm can be described by a low-level MDP. The rules the robot follows are described using FSAs. In the FSA, transitions are dependent on logical truth statements called propositions. In this environment there are three propositions—“robot has grasped sandwich”, “robot has grasped banana”, and “robot has dropped whatever it is holding into the lunchbox”. The truth values of these propositions control transitions between the FSA states, which we also refer to as logic states. For example, when “robot has grasped sandwich” is true, the FSA transitions from being in an initial state to being in a state in which “the robot has grasped the sandwich.” When it is in this new state and “robot has dropped whatever it is holding into the lunchbox” is true, it transitions to the next state, “the robot has placed the sandwich into the lunchbox.” We assume that the propositions correspond to locations in 2D space (i.e., we assume that the manipulator has a pre-programmed behavior to grasp a banana when it is in the vicinity of the banana and “robot has grasped banana” becomes true). This assumption enables us to factor the product MDP into a high-level FSA and a low-level MDP. A simpler example of a product MDP is illustrated in Fig. 2.

Fig. 1

The Jaco mobile arm platform opening a cabinet and packing a lunchbox following rules learned from demonstrations

The agent infers the FSA and rewards associated with this product MDP and generates a policy by running a planning algorithm on the product MDP. This approach has two benefits: (1) the learned policy is interpretable in that the relations between high-level actions are defined by an FSA, and (2) the behavior of the agent is manipulable because the rules that the agent follows can be changed in a predictable way by modifying the FSA transitions. These benefits address the questions posed before: performing new tasks without re-learning, and correcting faulty behaviour.

Fig. 2

An illustration of how an MDP and an FSA create a product MDP. The MDP is a 2D gridworld with propositions a, b, and o. The FSA describes the rule “go to a, then b, and avoid o. The resulting product MDP represents how these rules interface with the 2D gridworld

In Araki et al. (2019), we introduce “Logical Value Iteration Networks” (LVIN), a deep learning technique that uses Logical Value Iteration to find policies over the product of a low-level MDP and an FSA. However, the limitation of LVIN is that it requires not just low-level trajectories as data but also high-level FSA state labels. In order to label the trajectories with FSA state labels, a significant amount of information about the FSA must be known before learning occurs. In Araki et al. (2020), we introduce a Bayesian inference model that uses only the low-level trajectories as data; no knowledge of the FSA is required at all. We accomplish this by modeling the learning problem as a partially observable Markov decision process (POMDP), where the hidden states and transitions correspond to an unknown FSA. We compose the POMDP with a planning policy to create a hidden Markov model (HMM) in which the hidden states are FSA state labels. The HMM has high-level latent parameters describing the reward function and the structure of the FSA. We fit the HMM with stochastic variational inference (SVI) on expert demonstrations, so that we simultaneously learn the unknown FSA and the policy over the resulting MDP. This learning problem is very challenging, so we also introduce a spectral prior for the transition function of the FSA to help the algorithm converge to a good solution.

We test our learning algorithm on a number of domains, including two robotic manipulation tasks with real-world experiments. Our algorithm significantly outperforms the baseline in all experiments; furthermore, the learned models have the properties of interpretability and manipulability, so we can zero-shot generalize to new tasks and fix mistakes in unsafe models without additional data.

1.1 Contributions

• 1. We solve logic-structured POMDPs by learning a planning policy from task demonstrations alone.

• 2. We introduce a variation on value iteration called Logical Value Iteration (LVI), which integrates a high-level FSA into planning.

• 3. We use spectral techniques applied to a matrix representation of a finite automaton to design a novel prior for hierarchical nonparametric Bayesian models.

• 4. Our model learns the FSA transition matrix, allowing us to interpret the rules that the model has learned.

• 5. We explain how to modify the learned transition matrix to manipulate the behavior of the agent in a simulated driving scenario and on a real-world robotic platform in the contexts of packing a lunchbox and opening a locked cabinet.

• 6. We expand on the experiments in Araki et al. (2020), adding four more experimental domains, a safety experiment, and more details on the manipulation experiments and the implementation of our real-world experiments.

This work is a union of Araki et al. (2019) and Araki et al. (2020). The list above summarizes the contributions of the previous two papers; the unique contribution of this work is Contribution 6.

2 Related work

The model presented in this paper extends Araki et al. (2019), which introduces Logical Value Iteration as a planning algorithm over the product of a low-level MDP with a logical specification defined by an FSA. In the previous work, the input trajectories had to be labelled with FSA states, which required significant prior knowledge of the structure of the FSA. The model in this paper infers the FSA state labels and the structure of the FSA from only low-level trajectories. There are a number of other works that incorporate logical structure in the imitation and reinforcement learning settings. Paxton et al. (2017) use LTL to define constraints on a Monte Carlo Tree Search. Li et al. (2017, 2019), Hasanbeig et al. (2018), and Icarte et al. (2018a) use the product of an LTL-derived FSA with an MDP to define a reward function that guides the agent through a task during training. Icarte et al. (2018b) use LTL to design a sub-task extraction procedure as part of a more standard deep reinforcement learning setup. However, these methods assume that the logic specification is already known, and they do not allow for a model that is interpretable and manipulable. Our algorithm requires only the low-level trajectory as input, and it learns a model that is both interpretable and manipulable by integrating the learned FSA into planning.

There are also a number of learning algorithms that infer some sort of high-level plan from data. Burke et al. (2019) infer a program from robot trajectories, but their programs can only be constructed using three simple templates that are less expressive than LTL or FSAs. Icarte et al. (2019) learn the structure of “reward machines” via a discrete optimization problem. Shah et al. (2018) and Shah et al. (2019) take the approach of learning a logic specification from proposition traces using probabilistic programming and then planning over the resulting distribution of specifications. Shah et al. (2018) give methods for learning a posterior over logic specifications from demonstrations. Their approach differs from ours in that the input is the proposition traces of the demonstrations; they do not take the low-level trajectories and the layout of the environment into account. Our method uses both proposition traces and the low-level trajectories as input; this additional information is useful in learning rules that involve avoiding propositions. For example, the obstacle proposition will never appear in an expert proposition trace, but it is evident from the low-level trajectories that the agent will take a longer path to avoid an obstacle. Our algorithm can infer from this information that the obstacle proposition is associated with the low-reward trap state. Shah et al. (2019) introduce objectives for planning over a distribution of planning problems defined by logic specifications which reduces to the problem of solving MDPs. Our work directly considers the problem as a POMDP and introduces data-driven prior assumptions on the distribution of the FSA to mitigate the hardness of the problem. We also never have to enumerate an exponentially sized MDP.

Logical Value Iteration is an extension of Value Iteration Networks (VIN) (Tamar et al. 2016) to a hierarchical logical setting. Karkus et al. (2017) is a similar extension of VIN to partially observable settings. Their model is a POMDP planning algorithm embedded into a neural network that is trained over distributions of task demonstrations. Our work differs from theirs since we focus on factoring the transition dynamics hierarchically into an interpretable and manipulable FSA. We also therefore prefer a structured Bayesian approach rather than a deep learning approach for learning the unknown FSA.

Our Bayesian model draws inspiration from many similar methods in the Bayesian machine learning literature. There are a number of other works that have studied hierarchical dynamical models in the nonparameteric Bayesian inference setting and have developed specialized techniques for inference (Fox et al. 2011a, b; Chen et al. 2016; Johnson et al. 2016; Linderman et al. 2017; Mena et al. 2017; Buchanan et al. 2017). These models typically focus on fitting hierarchical linear dynamical systems and do not use ideas from logical automata. Zhang et al. (2019) apply some of these ideas specifically to solving POMDPs by locally approximating more complicated continuous trajectories as linear dynamical systems. Our primary contribution to this literature is the way we incorporate the logical automaton into planning so that our model is both interpretable and manipulable.

Rhinehart et al. (2018) also introduce a deep Bayesian model for solving POMDPs, and they achieve a degree of manipulability in that it is possible to modify their objective function to specify new goals and rules. However, changes to the objective function require the policy to be re-optimized, and the objective function is also less interpretable than an FSA as a way of understanding and modifying the behavior of an agent.

There are a few other domains that our work fits into. Multi-task learning and meta-learning are also methods that solve classes of tasks assuming a distribution over tasks (Caruana 1995; Andreas et al. 2016; Duan et al. 2016; Finn et al. 2017; Huang et al. 2018). The problem of multi-task reinforcement learning has also been studied from the lens of hierarchical Bayesian inference (Wilson et al. 2007). However, these methods require samples from many different tasks in order to adapt to new tasks from the task distribution, and they are not manipulable without additional data. Few-shot learning approaches are another solution concept to the manipulability problem, but suffer from lack of interpretability (James et al. 2018; Tanwani et al. 2018). There are also notions of interpretable policy classes from machine learning which make no use of finite automata, but which are not easily manipulable (Rodriguez et al. 2019; Koul et al. 2018). Other approaches attempt to use machine learning techniques to distill models into interpretable forms (possibly using automata), but are also difficult to manipulate (Michalenko et al. 2019; Bastani and Solar-lezama 2018).

Other works tackle the problem of unreliable experts in imitation learning. MacGlashan and Littman (2015) interpolate between imitation and intention learning with an approach based on inverse reinforcement learning. Gao et al. (2018) use reinforcement learning with expert demonstrations to correct faulty policies, whereas with our approach, fixes to the policy can be made by directly modifying the learned automaton.

There is also extensive work in automaton identification and learning theory (Gold 1967, 1978; Angluin 1987) that provides theoretical bounds on the decidability and complexity of learning automata. These works differ in scope from ours in that they often consider how many expert queries are necessary to learn an automaton and whether it is possible to identify the automaton producing a set of sentences. Our work, by contrast, is grounded in the imitation learning problem setting and aims to learn a distribution over automata that describes a fixed set of expert demonstrations. Our algorithm minimizes a nonlinear objective function using gradient descent. Thus, due to the differences between the considered problems and approaches, the decidability and complexity guarantees from (Gold 1967, 1978; Angluin 1987) are not immediately applicable to our work.

Finally, we can also view our problem setup through the lens of hierarchical reinforcement learning (HRL): the FSA is a high-level description of the task that the agent must accomplish. The first instance of HRL was introduced by Parr and Russell (1998). Related is the options framework of Sutton et al. (1998), in which a meta-policy is learned over high-level actions called options. Andreas et al. (2016) apply the options framework and introduce policy sketches, sequential strings of sub-policies from a sub-policy alphabet, to build an overall policy. Our work differs from the options framework in that the options framework only has hierarchical actions, whereas our method also has a hierarchical state space defined by the low-level MDP states and the high-level FSA states. Le et al. (2018) combine high-level imitation policies with low-level reinforcement learning policies to train more quickly. Keramati et al. (2018) build a hierarchy of planning by learning models for objects rather than only considering low-level states. Both approaches lack an interpretable high-level model that can be easily modified to change policy behavior.

3 Problem formulation

Our key objective is to infer rules and policies from task demonstrations. The rules are represented as a probabilistic automaton $\mathcal {W} = (\mathcal {F}, \mathcal {P}, TM, \mathtt {I}, \mathtt {F})$. $\mathcal {F}$ is the set of states of the automaton; $\mathcal {P}$ is the set of propositions; $TM : \mathcal {F} \times \mathcal {P} \times \mathcal {F} \rightarrow [0, 1]$ defines the transition probabilities between states; $\mathtt {I}$ is a vector of initial state probabilities; and $\mathtt {F}$ is the final state vector. The number of FSA states is $F = \vert \mathcal {F} \vert$, and the number of propositions is $P = \vert \mathcal {P} \vert$. We assume that $\mathtt {I}$ and $\mathtt {F}$ are deterministic—the initial state is always state 0, and the final state is always state $(F-1)$.

Fig. 3

Each data point is an expert trajectory including low-level state and proposition information. Each trajectory is associated with a proposition map that relates every position in the domain to a proposition. We use spectral learning to create a prior for the FSA transition function. The Bayesian model learns variational parameters that define distributions over the reward function and FSA

We formulate the overall problem as a POMDP. The state space is $\mathcal {C} = \mathcal {S} \times \mathcal {P} \times \mathcal {F}$, where $\mathcal {S} = \mathcal {X} \times \mathcal {Y}$ is a 2D grid (examples are shown in Fig. 6); $\mathcal {F}$ is the set of states of the automaton; and $\mathcal {P}$ is the set of propositions (Fig. 2 is an illustration of this joint state space). The agent can travel to any neighboring cell, so the action space is $\mathcal {A} = \{N, E, S, W, NE, NW, SE, SW\}$. In addition to the automaton transition function TM, there is also a low-level transition function $T: \mathcal {S} \times \mathcal {A} \times \mathcal {S} \rightarrow [0, 1]$ and a “proposition map” $M : \mathcal {S} \times \mathcal {P} \times t \rightarrow \{0, 1\}$. We assume that every low-level state is associated with a single proposition that is true at that state; the proposition map defines this association. We allow M to vary with time, so that propositions can change location over time; however, we consider only one domain, a driving scenario, in which proposition values change with time. Note that we overload all the transition functions so that given their inputs, they return the next state instead of a probability. The most general form of the reward function is $\mathcal {R} : \mathcal {C} \times \mathcal {A} \rightarrow \mathbb {R}$; however, we assume that the reward function does not vary with $\mathcal {P}$, $\mathcal {S}$, or $\mathcal {A}$, so it is a function of only the FSA state, $\mathcal {R} : \mathcal {F} \rightarrow \mathbb {R}$. This reward function can work by rewarding the agent for reaching the goal state and penalizing the agent for ending up in a trap state. The observation space is $\varOmega = \mathcal {S} \times \mathcal {P}$, and the observation probability function is $\mathcal {O} : \mathcal {C} \times \mathcal {A} \times \varOmega \rightarrow [0, 1]$. Therefore we have a POMDP described by the tuple $(\mathcal {C}, \mathcal {A}, T \times M \times TM, \mathcal {R}, \varOmega , \mathcal {O}, \gamma _d)$.

We formulate the POMDP learning problem as follows. There are N data points, and each data point i is a trajectory of state-action tuples over $T_i$ time steps, so that dataset $\mathcal {D} = \langle d_0, \dots , d_N \rangle$, where $d_i = \langle (s_0^i, a_0^i), \dots , (s_{T_i}^i, a_{T_i}^i) \rangle$. Expanding the POMDP tuple gives $(\mathcal {S} \times \mathcal {P} \times \underline{\mathcal {F}}, \mathcal {A}, T \times M \times \underline{TM}, \underline{\mathcal {R}}, \mathcal {S} \times \mathcal {P}, \mathcal {O}, \gamma _d)$. Unknown elements have been underlined to emphasize the objective of learning the set of FSA states $\mathcal {F}$, the FSA transition function TM, and the reward function $\mathcal {R}$. We assume that the actions $\mathcal {A}$, the low-level transitions T, the proposition map M, the observation probabilities $\mathcal {O}$, and the discount factor $\gamma _d$ are known. We also assume that $\mathcal {O}$ is deterministic—in other words, that the agent has sensors that can perfectly sense its state in the environment. The goal of solving a POMDP is to find a policy that maximizes reward—in this case, a policy that mimics the expert demonstrations.

4 Method

We formulate the POMDP composed with the policy as a Hidden Markov Model (HMM) with recurrent transitions and autoregressive emissions. The hidden states and transitions of the POMDP are latent variable parameters (shown in Fig. 4a). The unobserved logic state at every time step is the hidden state of the HMM, and TM, $\mathcal {R}$, and F are high-level latent variables.

Fig. 4

In the two models above, white circles are latent variables; grey circles are observed variables; black dots are priors. M is an input to the models because every instance of the environment has a unique proposition map. The plates around the HMM indicate that those variables are repeated for N trajectories

A sketch of the learning algorithm is shown in Alg. 1, and Fig. 3 illustrates the inputs and outputs. The data consist of a proposition map and a set of expert trajectories over a domain. The domain in this example is a $3\times 3$ gridworld where the agent must first go to a (orange proposition), then to b (green proposition), while avoiding obstacles o (black proposition). e is the “empty” proposition (light grey proposition). The figure also illustrates the proposition map M, which maps every location to a proposition. Each layer of the map is associated with a single proposition, and the locations where a proposition is true are highlighted with the associated color. Note that only one proposition is true at any given location, and that each instance of an environment is defined by its proposition map M.

The algorithm approximates the posterior of a Bayesian model and returns the modes of the latent variable approximations (Sect. 4.1). One notable feature of the algorithm is that it uses Logical Value Iteration (LVI), a hierarchical version of value iteration, to calculate policies (see Sect. 4.2) in order to evaluate the likelihoods of proposed FSAs and reward functions. One issue with learning complex Bayesian models is that they are prone to converging to local minima, particularly in the case of discrete distributions such as the high-level transition function TM. We use spectral learning to obtain a good prior (see Sect. 4.3).

Posterior inference finds distributions over the number of automaton states F, the reward function $\mathcal {R}$, and the transition function TM. In Fig. 3, TM is represented as a collection of matrices—each matrix is associated with the “current FSA state”; columns correspond to propositions and rows correspond to the next FSA state. The entry in each grid is the probability of transitioning, $TM(f' \vert f, p)$. Black indicates 1 and white indicates 0. Therefore in the initial state S0, a causes a transition to S1, whereas o causes a transition to the trap state T. The outputs of the algorithm are valuable for two reasons: (1) TM is relatively easy to interpret, giving insight into the rules that have been learned; and (2) $\mathcal {R}$ and TM can be used for planning, so modifications to TM result in predictable changes in the agent’s behavior.

4.1 Bayesian model

We now give an overview of the Bayesian model. For a more detailed discussion, please refer to Araki et al. (2020). The graphical model is shown in Fig. 4a. The main challenge in this model is to infer the number of FSA states F, the reward function $\mathcal {R}^F$, and the transition function $TM^F$. We use the graphical model to specify a likelihood function $p(\overline{\mathcal {R}}, \overline{TM}, \theta \vert \mathcal {D}, \alpha , \overline{\beta }, \overline{\gamma })$, and we also define a model for a variational approximation $q(\overline{\mathcal {R}}, \overline{TM}, \theta \vert \mathcal {D}, \hat{\alpha }, \hat{\overline{\beta }}, \hat{\overline{\gamma }})$, shown in Fig. 4b. A bar over a variable indicates that it is a list over values of F.

Fig. 5

We create a spectral learning prior from the data in a three-step process. In the first step, the expert trajectories are converted into proposition traces. The frequency of each trace is used to populate an empirical Hankel matrix (only a portion of the matrix is shown). We then find the rank decomposition of the matrix and use the resulting weighted automaton as a prior for the Bayesian model

The objective of the variational inference problem is to minimize the KL divergence between the true posterior and the variational distribution:

$$\begin{aligned}&\mathcal {L} = \text {KL} ( q(\overline{\mathcal {R}}, \overline{TM}, \theta \vert \mathcal {D}, \widehat{\alpha }, \widehat{\overline{\beta }}, \widehat{\overline{\gamma }}) \vert \vert p(\overline{\mathcal {R}}, \overline{TM}, \theta \vert \mathcal {D}, \alpha , \overline{\beta }, \overline{\gamma }) )\\&\widehat{\alpha }^*, \widehat{\overline{\beta }}^*, \widehat{\overline{\gamma }}^* = {{\,\mathrm{arg\,min}\,}}_{(\widehat{\alpha }, \widehat{\overline{\beta }}, \widehat{\overline{\gamma }})} \mathcal {L} \end{aligned}$$

$\widehat{\alpha }^*$, $\widehat{\overline{\beta }}^*$, and $\widehat{\overline{\gamma }}^*$ serve as approximations of $\alpha$, $\overline{\beta }$, and $\overline{\gamma }$, and therefore define distributions over F, $\overline{TM}$, and $\overline{\mathcal {R}}$. Letting $F^* = {{\,\mathrm{arg\,max}\,}}_{F} \widehat{\alpha }^*$, we get priors for $TM^{F^*}$ ($\widehat{\beta }^{F^*}$) and $\mathcal {R}^{F^*}$ ($\widehat{\gamma }^{F^*}$) which can be used for planning.

One of the benefits of the Bayesian approach is that it is straightforward to incorporate known features of the environment into the model as priors. Many of these priors rely on the assumption that every automaton we consider has one initial state, one goal state, and one trap state. Our assumptions about the rules of the environment are built into each $\beta ^F$, which are the priors for the transition function $TM^F$. We incorporate the following priors into our model:

• 1. $\bar{\beta }$ is populated with the value 0.5 before adding other values, since for Dirichlet priors, values below 1 encourage peaked/discrete distributions. In other words, this prior biases the TM towards deterministic automata.

• 2. We add a prior to the trap state that favors self-transitions. This is because the trap state is a “dead-end” state.

• 3. We add an obstacle prior to bias the model in favor of automata where obstacles lead to the trap state.

• 4. We add a goal state prior, so that the model favors self-transitions for the goal state.

• 5. We add an empty state prior, so that for the empty state proposition, the model favors transitions leading back to the current state.

• 6. We use spectral learning (see Sect. 4.3) to find a prior for $\alpha$ and for the other transitions.

• 7. We also give priors to the reward function so that the goal state has a positive reward and the trap state has a negative reward.

The variational problem was implemented using Pyro (Bingham et al. 2019) and Pytorch. Pyro uses stochastic variational inference to approximate the variational parameters.

4.2 Logical value iteration (LVI)

The autoregressive emissions of the model draw an action from a policy at every time step. In this work, the policy is found using “Logical Value Iteration” (LVI) on the learned MDP. LVI integrates the high-level FSA transitions TM into value iteration (Araki et al. 2019). The LVI equations are shown below. The first two equations are identicial to normal value iteration—in the first step, the Q-function Q is updated using reward function R, low-level transitions T, and value function V. Next, the value function is updated. LVI adds a third step, where the values are propagated between logic states using TM. Note that we use M(s) as an input to TM rather than p; the two are equivalent, since M(s) deterministically relates a state s to a proposition p.

$$\begin{aligned} Q^{t+1}(s,f,a)&\leftarrow R(s,f,a) + \gamma _d \sum _{s' \in \mathbb {S}}T(s' \vert s, a)V^t(s',f) \\ \widehat{V}^{t+1}(s,f)&\leftarrow \max _a Q^{t+1}(s,f,a)\\ V^{t+1}(s,f)&\leftarrow \sum _{f' \in \mathbb {F}} TM(f' \vert f, M(s)) \widehat{V}^t(s, f') \end{aligned}$$

4.3 Spectral learning for weighted automata

One of the main issues of using variational inference on complex Bayesian models is its tendency to converge to undesirable local minima. Our choice of modeling the distribution of FSAs as a continuous distribution over transition weights is particularly prone to converging to local minima. To avoid this, we use the output of spectral learning for weighted automata as a prior for the transition function TM.

Spectral learning uses tensor decomposition to efficiently learn latent variables. We summarize here our discussion of the topic in Araki et al. (2020). Spectral learning can be used to learn automaton transition weights by decomposing a Hankel matrix representation of the automaton (Arrivault et al. 2017). A Hankel matrix is a bi-infinite matrix whose rows correspond to prefixes and whose columns correspond to suffixes of all possible input strings of an automaton. The value of a cell is the probability of the corresponding string.

We construct an empirical Hankel matrix from the proposition strings in the dataset, as shown in Fig. 5. We then find a rank factorization of the matrix. We use the open-source Sp2Learn toolbox (Arrivault et al. 2017) to process the data and generate the Hankel matrices. We use Tensorflow to perform the rank factorization. We can then obtain transition weights for the automaton.

Fig. 6

Example instances of seven domains

Spectral learning outputs a weighted automaton that is better suited as a prior rather than as the primary means of determining TM. This is because the transition weights of the learned automaton are not constrained to add to one—they are weights, not probabilities. In addition, the learned automaton will not include propositions that are not present in the proposition traces. Therefore spectral learning is incapable of learning that the agent seeks to avoid certain propositions, such as obstacles, because these propositions never occur in the expert data set.

In order to create a prior for the size of the FSA, we learn automata with number of states ranging from 4 to 2P. We have observed that for every domain tested, the optimization loss drops by one or two orders of magnitude when the number of states reaches the true number. We therefore use the optimization losses to create a prior on the number of states (defined as $\alpha$ in Sect. 4.1). If the optimization loss for a certain number of states F is $c_F$, then the prior for F states is $\text {log}(c_F / c_{F-1})$. We also use the transition weights as prior values for $\overline{\beta }$ in the Bayesian model.

5 Experiments and results

5.1 Generating expert data

Linear temporal logic We use linear temporal logic (LTL) to formally specify tasks (Clarke et al. 2001). In our experiments, the LTL formulae were used to define expert behavior but were not used by the learning algorithm. Formulae $\phi$ have the syntax grammar

$$\begin{aligned} \qquad \qquad \phi := p \;|\; \lnot \phi \;|\; \phi _1 \vee \phi _2 \;|\; \bigcirc \phi \;|\; \phi _1 {{\,\mathrm{\mathcal {U}}\,}}\phi _2 \end{aligned}$$

where p is a proposition (a boolean-valued truth statement that can correspond to objects or goals in the world), $\lnot$ is negation, $\vee$ is disjunction, $\bigcirc$ is “next”, and ${{\,\mathrm{\mathcal {U}}\,}}$ is “until”. The derived rules are conjunction $(\wedge )$, implication ($\implies$), equivalence $(\leftrightarrow )$, “eventually” ($\diamondsuit \phi \equiv \texttt {True} {{\,\mathrm{\mathcal {U}}\,}}\phi$) and “always” ($\Box \phi \equiv \lnot \diamondsuit \lnot \phi$) (Baier and Katoen 2008). $\phi _1 {{\,\mathrm{\mathcal {U}}\,}}\phi _2$ means that $\phi _1$ is true until $\phi _2$ is true, $\diamondsuit \phi$ means that there is a time where $\phi$ is true and $\Box \phi$ means that $\phi$ is always true.

Generating data In our test environments, we define desired behavior using LTL, and we then use SPOT (Duret-Lutz et al. 2016) and Lomap (Ulusoy et al. 2013) to convert the LTL formulae into FSAs. Every FSA that we consider has a goal state G, which is the desired final state of the agent, and a trap state T, which is an undesired terminal state. We generate a set of environments in which obstacles and other propositions are randomly placed. Given the FSA and an environment, we run Dijkstra’s shortest path algorithm on the product MDP to create expert trajectories that we use as data for imitation learning.

LSTM baseline: We compare the performance of LVI to an LSTM network, which is a generic method for dealing with time-series data. The cell state of the LSTM serves as a kind of memory for the network, preserving state from time step to time step. This is similar to the FSA state of our model; the FSA state at a given time step represents the agent’s progress through the FSA and is a sort of memory. The cell state therefore loosely corresponds to an unstructured FSA state. We believe that LSTMs are a good baseline for our model because of their widespread use and because they represent an unstructured, model-free alternative to our method. The first layer of the LSTM network is a 3D CNN with 1024 channels. The second layer is an LSTM with 1024 hidden units.

5.2 Environments

Gridworld domains The gridworld domains are simple $8\times 8$ gridworlds with sequential goals. Gridworld1 has goals a and b (shown in Fig. 6a); Gridworld2 (Fig. 6b) adds goal c, and Gridworld3 (Fig. 6c) adds goal d. The specification of Gridworld1 is $\diamondsuit ( a \wedge \diamondsuit b ) \wedge \Box \lnot o$. Gridworld2’s specification is $\diamondsuit ( a \wedge \diamondsuit ( b \wedge \diamondsuit c ) ) \wedge \Box \lnot o$ and Gridworld3’s is $\diamondsuit ( a \wedge \diamondsuit ( b \wedge \diamondsuit ( c \wedge \diamondsuit d ) ) ) \wedge \Box \lnot o$.

Lunchbox domain The lunchbox domain (Fig. 6d) is an $18\times 7$ gridworld where the agent must first pick up either a sandwich a or a burger b and put it in a lunchbox d, and then pick up a banana c and put it in the lunchbox d. The specification is $\diamondsuit ((a \vee b) \wedge \diamondsuit (d \wedge \diamondsuit (c \wedge \diamondsuit d))) \wedge \Box \lnot o$.

Cabinet domain The cabinet domain is a $10\times 10$ gridworld where the agent must open a cabinet. First it must check if the cabinet is locked (cc). If the cabinet is locked (lo), the agent must get the key (gk), unlock the cabinet (uc), and open it (op). If the cabinet is unlocked (uo), then the agent can open it (op). The specification is $\diamondsuit (cc \wedge \diamondsuit ( ( uo \wedge \diamondsuit op ) \vee ( lo \wedge ( \diamondsuit (gk \wedge \diamondsuit ( uc \wedge \diamondsuit op ) ) ) ) ) ) \wedge \Box \lnot o$. Because many of the propositions lie in nearly the same point in space (e.g. checking the cabinet, observing that it is unlocked, and opening the cabinet), we define a “well” (as shown in Fig. 6e) that contains the relevant propositions in separate grid spaces but represents a single point in space in the real world.

Dungeon domain The dungeon domain is a $12\times 9$ gridworld and shows our model’s ability to learn complex sequential specifications. In this environment (Fig. 6f) there are 10 propositions: keys ka, kb, kc, kd that unlock doors da, db, dc,  and dd, respectively; and g for the goal and o for obstacles. To progress to the goal, the agent must follow the specification $\diamondsuit g \wedge \Box \lnot o \wedge (\lnot da \; {{\,\mathrm{\mathcal {U}}\,}}\; ka) \wedge (\lnot db \; {{\,\mathrm{\mathcal {U}}\,}}\; kb) \wedge (\lnot dc \; {{\,\mathrm{\mathcal {U}}\,}}\; kc) \wedge (\lnot dd \; {{\,\mathrm{\mathcal {U}}\,}}\; kd)$—it must first pick up Key A, then go get Key D, then Key B, then Key C, before it can access the room in which the goal is located.

Driving domain The driving domain (Fig. 6g) is a $14\times 14$ gridworld where the agent must obey three “rules of the road”—prefer the right lane over the left lane (l): $\Box \diamondsuit \lnot l$; stop at red lights (r) until they turn green (h): $\Box (r \Rightarrow (r \; {{\,\mathrm{\mathcal {U}}\,}}\; h))$; and reach the goal (g) while avoiding obstacles (o): $\diamondsuit g \wedge \Box \lnot o$. Unlike the other domains, this domain has a time-varying element (the red lights turn green); it also has an extra action—“do not move”—since the car must sometimes wait at the red light.

Performance Our experiments were run on an Intel i9 processor and an Nvidia 1080Ti GPU. The simplest environment, Gridworld1, takes $\sim 1.4$ hours to train; the most complicated, the Dungeon domain, takes $\sim 7.5$ days to train. The KL divergence for all environments shows a typical training pattern in which the divergence rapidly decreases before flattening out.

Table 1 Training and test performance of LVI versus LSTM

Performance of LVI (shorthand for our model) versus the LSTM network is shown in Table 1. We measure “success rate” as the proportion of trajectories where the agent satisfies the environment’s specification. LVI achieves virtually perfect performance on every domain with relatively little data. The results for Gridworld1 in Table 1 show that LVI achieves almost perfect performance on the domain; the LSTM achieves a success rate of 88.8% on the training data, which decreases to 64% on the test data. Similar results hold for Gridworld2 and 3; however, the LSTM performs much better on these domains. This is likely because these two domains have fewer obstacles than the Gridworld1 domain (the LSTM seems to struggle to avoid randomly placed obstacles). The LSTM network achieves fairly high performance on the lunchbox and cabinet domains, but has poor performance in the time-varying driving domain. Lastly, the LSTM is completely incapable of learning to imitate the long and complicated trajectory of the dungeon domain. On top of achieving better performance than the LSTM network, the LVI model also has an interpretable output that can be modified to change the learned policy.

The LVI model requires much less data than the LSTM network for two reasons. One is that the LVI model can take advantage of the spectral learning prior to reduce the amount of data needed to converge to a solution, whereas the LSTM network cannot use the prior. The second is that since the LVI model is model-based, once it learns an accurate model of the rules it can generalize to unseen permutations of the environment better than the LSTM network, which is only capable of interpolating between data points.

5.3 Interpretability

Our method learns an interpretable model of the rules of an environment in the form of a transition function TM. Learned versus true TMs are shown in Figs. 7 and 8 (we leave out the goal and trap states of the TMs, since they are trivial). The plots show values of the learned variational parameter $\widehat{\beta }^{F^*}$. Therefore the plots do not show the values of the actual TM but rather the values of the prior of the TM, giving an idea of how “certain” the model is of each transition.

Figure 7a shows the TM of Gridworld1. Each matrix corresponds to the transitions associated with a given automaton state. Columns correspond to propositions (e is the empty proposition) and rows correspond to the probability that, given current state f and proposition p, the next state is $f'$. Inspecting the learned TM of Gridworld1, we see that in the initial state S0, a leads to the next state S1, whereas b leads back to S0. In S1, going to b leads to the goal state G. In both states, going on an obstacle o leads to the trap state T. Therefore simply by inspection we can understand the specification that the agent is following. Gridworld2 and Gridworld3 follow analogous patterns.

Figure 8a shows the TM of the lunchbox domain. Inspection of the learned TM shows that in the initial state S0, picking up the sandwich or burger (a or b) leads to state S1. In S1, putting the sandwich/burger into the lunchbox (d) leads to S2. In S2, picking up the banana c leads to S3, and in S3, putting the banana in the lunchbox d leads to the goal state G.

Fig. 7

Learned vs. true $TM\hbox {s}$ for the gridworld domains

Fig. 8

Learned vs. true $TM\hbox {s}$ for three domains

The cabinet domain can be interpreted similarly. However, the dungeon and driving domains require closer inspection. In the dungeon domain, instead of learning the intended general rules (“Door A is off limits until Key A is picked up”), the model learns domain-specific rules (“pick up Key A; then go to Door A; then pick up Key B; etc”) (see Fig. 9). Crucially, however, this learned TM is still easy to interpret. In the initial state S0, most of the columns are blank because the model is uncertain as to what the transitions are. The only transition it has learned (besides the obstacle and empty state transitions) is for Key A (ka), showing a transition to the next state. In S1, the only transition occurs at Door A (da). Then Key D (kd), Door D (dd), Key B (kb), Door B (db), Key C (kc), Door C (dc), and finally the goal state g. So we can see by inspecting the learned TM that the model has learned to go to those propositions in sequence. Although this differs from what we were expecting, it is still a valid set of rules that is also easy to interpret.

The driving domain (Fig. 8c) also requires closer inspection. In the expected TM, there is a left lane rule so that initial state S0 transitions to a lower-reward state S1 when the car enters the left lane, because the left lane is allowed but unideal; S0 transitions to S2 when the car is at a red light, and then back to S0 when the green light h turns on. Our model learns a different TM, but due to the interpretability of these models, it can still be parsed. Unlike in the “true” TM, in the learned TM, the green light acts as a switch—the agent cannot reach the goal state unless it has gone to the green light. This is an artifact of the domain, since the agent always passes a green light before reaching the goal, so the learning algorithm mistakes the green light as a goal that must be reached before the actual goal. The red light causes a transition from S0 to S1, which is a lower-reward duplicate of S0. The agent will wait for the red light to turn green because it thinks it must encounter a green light before it can reach the goal. Regarding the left lane, the TM places significant weight on a transition to low-reward S1 when in S0, which discourages the agent from entering the left lane. Therefore although not as tidy as the true TM, the learned TM is still interpretable.

Fig. 9

Learned vs. true $TM\hbox {s}$ for the dungeon domain

5.4 Manipulability experiments on Jaco Arm

Our method allows the learned policy to be manipulated to produce reliable new behaviors. We demonstrate this ability on a real-word platform, a Jaco arm. The Jaco arm is a 6-DOF arm with a 3-fingered hand and a mobile base. An Optitrack motion capture system was used to track the hand and manipulated objects. The system was implemented using ROS (Quigley et al. 2009). The Open Motion Planning Library (Şucan et al. 2012) was used for motion planning. The motion capture system was used to translate the positions of the hand and objects into a 2D grid, and an LVI model trained on simulated data was used to generate a path satisfying the specifications.

We modified the learned $TM\hbox {s}$ of the lunchbox and cabinet domains. We call the original lunchbox specification $\phi _{l1}$. We tested three modified specifications—pick up the sandwich first, then the banana ($\phi _{l2}$, Fig. 10a); pick up the burger first, then the banana ($\phi _{l3}$, Fig. 10b); and pick up the banana, then either the sandwich or the burger ($\phi _{l4}$, Fig. 10c). These experiments are analogous to the ones in Araki et al. (2019) and are meant to show that though significantly less information is given to our model in the learning process, it can still perform just as well.

Fig. 10

Modifications to the learned TM of the lunchbox domain so that the agent follows the new specifications. Deleted values are marked in red, and added values in green (Color figure online)

Fig. 11

Cabinet TM modifications, $\phi _{c1} \rightarrow \phi _{c2}$. Red indicates that a transition has been deleted; green that one has been added (Color figure online)

Table 2 Performance of Jaco robot in executing learned lunchbox and cabinet tasks

In these modified lunchbox experiments, a indicates that the sandwich has been picked up, b that the burger has been picked up, and c that the banana has been picked up. d indicates that the robot has dropped whatever it was holding into the lunchbox. Fig. 10a shows the modifications made to the lunchbox TM to cause it to pick up only the sandwich, and not the burger, first. In order to achieve this, in S0 we set b (the burger proposition) to transition back to S0 rather than to S1, indicating to the agent that picking up the burger does not accomplish anything. With this change, the agent will only pick up the sandwich (a). Fig. 10b shows the analogous changes to make the agent pick up only the burger first. Fig. 10c shows how to make the agent pick up the banana first, and then either the sandwich or burger. In order to do this, we first modify S0 so that picking up the banana (c) leads to the next state, whereas picking up the sandwich or burger (a or b) leads back to S0. This change makes the agent pick up the banana first. S1 does not need to be modified; the agent should still put whatever it is holding into the lunchbox. We then modify S2 so that this time, picking up the banana leads back to S2, whereas picking up the sandwich or burger leads to the next state, S3. With these changes, the agent will not pick up the banana but will instead pick up either the sandwich or burger.

We also modified the learned cabinet TM ($\phi _{c1}$), so that if the agent knows that the cabinet is locked, it will pick up the key first before checking the cabinet ($\phi _{c2}$). The modifications to the TM are shown in Fig. 11. The TM is modified so that the agent will get the key (gk) before checking the cabinet (cc). Therefore, in the initial state S0, cc is set to go to the trap state so that the agent will avoid it; gk is set to transition to S2, indicating to the agent that it should get the key first. In S2, we modify the TM so that cc is the goal instead of gk, so that the agent will then head to the cabinet and check it. Finally, in S4, once the agent has checked the cabinet, it must unlock the cabinet and it does not need to get the key, so we set gk to the trap state so the agent will be certain to unlock the cabinet and not try to get the key. These modifications change the behavior of the agent to always get the key before checking the cabinet.

We tested each specification 20 times on our experimental platform; as shown in Table 2 there were only a few failures, and these were all due to mechanical failures of the Jaco arm, such as the manipulator dropping an object or losing its grasp on the cabinet key.

5.5 Fixing expert errors

Our interpretable and manipulable model can also be used to fix the mistakes of faulty experts. Suppose the real-world driving data contains bad behavior from drivers breaking the rules. We model this scenario in Table 3, where the Unsafe TM shows a scenario in which the model has learned to run a red light 10% of the time. This result can be observed directly from the TM, since the probability of entering the initial state given that the agent is on a red light is 10%, meaning it will ignore the red light, while the probability of recognizing that it is in a “red light” state is 90%. We correct the TM by setting the initial state entry to 0 and the red light state entry to 1. We perform 1000 rollouts using each of these TMs. The Unsafe TM results in the agent running $9.88\%$ of red lights while the Safe TM prevents the agent from running any red lights.

Table 3 In this scenario, LVIN has learned a transition function TM for the driveworld domain in which in 10% of cases, the car will ignore a red light. The unsafe TM can be modified by deleting the 0.1 entry in the “Initial State”’ row of TM and adding it to the “Red Light” row, so that the agent will never ignore a red light. Over 1000 rollouts of the policy for the unsafe and safe TMs, the unsafe TM indeed causes the agent to run 9.88% of red lights, while the modified safe TM prevents the agent from ever running a red light

6 Conclusion

Interpretability and manipulability are desirable properties of learned policies that many imitation learning approaches struggle to achieve. This work introduces a method to learn interpretable and manipulable policies by factoring the environment into a low-level environment MDP and a high-level automaton. The unknown automaton and reward function are learned using a nonparametric Bayesian model that observes only the low-level trajectories and propositions. We demonstrate the effectiveness of our technique on several domains, showing how the learned transition matrices can be interpreted and manipulated to produce predictable new behaviors. We believe that the general idea behind our approach—factoring the MDP into a low-level environment MDP and a high-level rules-based FSA, and using a dynamic programming-based method to find a policy—is interesting because it allows the learned policy to be both interpretable and manipulable. We believe that this idea can be extended further to make learning algorithms that are applicable to continuous state spaces and that are even easier to interpret and compose.