Abstract
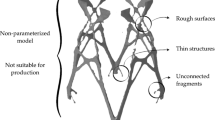
The topology optimization methodology is widely applied in industrial engineering to design lightweight and efficient components. Despite that, many techniques based on structural optimization return a digital model that is far from being directly manufactured, mainly because of surface noise given by spikes and peaks on the component. For this reason, mesh post-processing is needed. Surface smoothing is one of the numerical procedures that can be applied to a triangulated mesh file to return a more appealing geometry. In literature, there are many smoothing algorithms available, but especially those based on the modification of vertex position suffer from high mesh shrinkage and loss of important geometry features like holes and surface planarity. For these reasons, an improved vertex-based algorithm based on Vollmer’s surface smoothing has been developed and introduced in this work along with two case studies included to evaluate its performances compared with existent algorithms. The innovative approach herein developed contains some sub-routines to mitigate the issues of common algorithms, and confirms to be efficient and useful in a real-life industrial context. Thanks to the developed functions able to recognize the geometry feature to be frozen during the smoothing process, the user’s intervention is not required to guide the procedure to get proper results.
Similar content being viewed by others
1 Introduction
Topology optimization (TO) is a numerical design technique that allows designing efficient and lightweight components (Bendsøe and Sigmund 2011). This design methodology is used especially in the automotive and aerospace industries. In these applications, the light-weighting research is taken to extremes and reflects on better performances, reduction of manufacturing and maintenance costs and emissions. On the one hand, due to the resulting complex and intricated solution coming from TO analyses, the 3D models can’t be directly manufactured by traditional processes based on chip removal. On the other hand, the complexity of the structure well matches with additive manufacturing (AM) techniques which are based on adding material layer by layer (Gao et al. 2015). AM is known for the high freedom of shaping, time reduction in the design-to-manufacturing cycle, the capability of building complex biomimetic shapes with a high strength to weight ratio, called lattice structures (Savio et al. 2019), and reduction of parts thus avoiding bolted connections or welding. The design workflow belonging to AM is well summarized by the expression: "What You See Is What You Build" (Gibson etal. 2015).
Due to the aforementioned benefits, the AM and TO coupling is becoming a recurring theme in the research community, especially in the last few years when there has been a positive trend to bring AM to the small industry and even to the single consumer (Bacciaglia et al. 2020). Several contributions combining TO and AM are already available in the literature (Gaynor et al. 2014; Rezaie et al. 2013), but the overall design workflow is still not user-friendly and far from being direct. (Zegard and Paulino 2016) try to fill the gap by proposing a simple methodology to streamline the last step of making manufacturable the 3D models coming from structural optimization, especially for voxel-based models. They describe the importance of intermediate steps before the manufacturing process, even if AM shows outstanding properties for the production of TO models. For this reason, they developed a tool called TOPslicer useful to analyze and improve optimized models based on voxels. Voxelization is a representation method that uses hexahedral elements to discretize a control volume in which the 3D model is contained (Jense 1989) and has many applications in the AM field (Bacciaglia et al., 2019).
However, there is still a gap in the design-to-manufacturing workflow for topologically optimized structures discretized by tetrahedral mesh elements. As stated before, the Standard Triangulation Language (STL) file of the 3D models coming from TO needs post-processing routines before the production phase to analyze and repair non-manifold edges, cracks and peaks which may originate from the optimization. The external surface smoothing is inspired by the image denoising techniques aiming at removing the noise that affects the pixels in an image and uniformly deters their information (Buades et al. 2005), (Ming Zhang and Gunturk 2008). The same basic concept is applied to surface smoothing which is a numerical method useful to detect and remove noise and spikes from the surface model, returning a more appealing geometry by evolving the surface iteratively (Desbrun et al. 1999).
Literature has several approaches for surface fairing based on the modification of mesh using the position of vertices (Sorkine 2005), using local curvature of neighbour faces (Belyaev and Ohtake 2003), filters based on patch normal (Wei et al. 2019) or by filtering the surface with a frequency-based approach (Taubin 1995). Each approach shows advantages and disadvantages, depending on the specific application, but the methodologies based on vertex position are known to be easy to implement, fast and with reasonable performances. However, some issues as volume shrinkage need to be considered and solved. Despite all these efforts, there is a lack of user-friendly methodology to post-process tetrahedral 3D models using smoothing algorithms based on mesh modification of the position of vertices. In particular, a good smoothing framework fitting the AM and TO requirements should carry out efficiently the following tasks:
-
improve the external shape of the model both in the case of voxel and surface mesh.
-
limit the volume shrinkage during the smoothing iterations.
-
reduce or completely avoid the loss of features of TO models during the numerical process (e.g. holes or flat surfaces), so that they do not need to be post-processed (these regions will be referred to as "no-smoothing-space").
Some researches aim at preserving mesh features in denoising processes as done in (Lee and Wang 2005). However, the approach therein described does not mention in a detailed way the consistency of the 3D model volume and does not offer a strong edge and corner preserving capability. To fill this technological gap, the work herein described aims at developing a smoothing methodology for triangulated mesh based on vertex position for 3D models coming from TO analysis whose external surface is discretized with tetrahedral elements. The developed methodology is easy to use, maintains important features of the no-smoothing space and addresses all the known problems which affect the vertex-based smoothing methods as volume shrinkage and vertex drifting. The new algorithm has been implemented in Matlab, and applied to different 3D models, characterized by complex shapes and containing no-smoothing spaces. These models come from a topology optimization code embedded in FreeCAD, an open-source Computer-Aided Design (CAD) software that allows the development of new workbenches. The innovative algorithm has been compared to well established vertex-based methodologies available in literature to evaluate its performances during the smoothing process and to demonstrate its advantages.
The manuscript is organized as follows. Section 2 briefly describes the structural optimization methodologies available in literature and describes an analysis where our methodology can be applied along with a list of available smoothing algorithms. Section 3 embeds a detailed description of the innovative post-processing methodology where several sub-routines are used to get the optimal result. Examples and applications for the developed methodology are shown in Sect. 4 along with a discussion of the results. Finally, the work is summarized in Sect. 5 and provides conclusions and possible future developments of the established research topic.
2 Design and surface smoothing for unconventional structures
Topology optimization, ground structure method and generative design are the main approaches for structure optimization used in industrial applications as aerospace (Wong et al. 2018), automotive (Mantovani et al. 2020) and biomedicine (Machado and Trabucho 2004).
TO minimizes a fitness function that in most cases is represented by the overall structural compliance, maximizing the global stiffness. To solve the problem it is mandatory to have information about the boundary conditions, the load case applied to a predefined working volume, the presence of passive elements (e.g. holes) and the maximum material volume fraction needed to avoid a fully dense solution (Sigmund 1997). The ground structure method approximates a truss-like structure with a finite number of beam elements removing unnecessary elements from a connected truss structure while freezing the nodal positions (Ohsaki 2011). Generative design is an iterative process that, knowing the boundary conditions, will generate a certain number of possible solutions that meet the initial constraints; thanks to the designer intervention, the best solution will be chosen (Krish 2011).
Whatever it is the optimization approach chosen by the designer, the common optimization methods are related to the quality of the component mesh of the finite element model. In this case, the optimal solution can be far from the manufacturable status, because of the presence of peaks, cracks or non-manifold edges in the mesh that discretizes the 3D shape. At this point there are two possibilities of the design process: (a) use post-processing approaches applied directly on the optimal solution or (b) re-design the component sketching it from scratch taking inspiration from the optimal result of the previous step. The research community is pushing towards the first solution to accelerate the design-to-manufacturing cycle, decrease the cost and increase the design workflow efficiency, especially in industrial contests. For example, there are some recent contributions that couple the TO method with the Non-Uniform Rational Basis Spline (NURBS) hyper-surfaces framework (Costa et al. 2018). This combination provides CAD-compatible descriptors of the topology of the structure, that are not related to the mesh quality of the finite element model; moreover, the boundaries’ reconstruction becomes a straightforward task thanks to the NURBS implementation (Costa et al. 2021). However, this approach highly depends on the designer’s experience when NURBS discrete parameters should be set: after the optimization process, the overall structure external smoothing highly depends on the NURBS weights. Lastly, a higher amount of NURBS control point reflects not only on improved performances but also on long computational time.
To overcome the aforementioned issues, this work tries to contribute in the same direction to propose a general-purpose post-processing approach for surface smoothing. Indeed, the developed approach aims at covering a wider number of circumstances compared to the TO-NURBS approach, since it can smooth the external surface of meshes coming from different sources such as topology optimization or reverse-engineering from points clouds obtained through 3D scanners and photogrammetry. In this specific research, the developed methodology is applied to finite element based optimized structures without the need of redesigning them within a CAD system. Aim of this work, only 3D models coming from TO analyses will be considered in the following, and the same process can be applied for any kind of optimization methodology or engineering design approach as long as the 3D model can be exported as an STL surface mesh.
2.1 Topology optimization
TO is a numerical design methodology that can guarantee the best material distribution, by assigning material or void to all the elements of the discretized volume without forcing the algorithm to pre-designed shapes. This design freedom gives the possibility to obtain innovative and high-performance shapes reducing the material and the structure weight but maintaining the same degree of functionality. In literature, there are different TO numerical techniques, a non-inclusive list includes:
-
SIMP (Solid Isotropic Material with Penalization) this method is mainly used for the minimum compliance problem. It’s a gradient-based approach that updates the 3D model at each iteration after the structural analysis using a continuous distribution of material density (Bendsøe 1989).
-
ESO (Evolutionary Structural Optimization method) this approach uses a fully dense control volume and at each iteration subtracts unneeded material until reaching an optimal structure (Xie and Steven 1996).
-
BESO (Bi-directional ESO) this numerical method is based on the ESO approach but has also the capability of adding material if it is necessary to reach the optimum (Li et al. 2001).
In the following, we will refer only to the SIMP approach in which the design variable (\({\rho }_{e}\)) is the density of the material of a discrete element e. Its name comes from the dependency of the single e-th element stiffness tensor (\({{\varvec{E}}}_{e}\)) from the material density by the power-law (Eq. 1):
where \({{\varvec{E}}}_{\mathbf{o}}\) is the assigned isotropic material stiffness tensor and \(p\) is the penalization factor (usually higher than 3). \({\rho }_{\mathrm{min}}\) the minimum allowable relative density value for empty elements that are greater than zero. This density value ensures the numerical stability of the FEM (Finite Element Method) analyses. The TO problem is known to be not well-posed because the solution is mesh-dependent. To reduce this dependency, the TO problem needs to be restricted using some methods such as the density filter (Bourdin 2001) or the sensitivity one (Sigmund 1997). For a more detailed description of the TO methodology, please refer to (Bendsøe and Sigmund 2011).
The case studies that will be shown in the following to test the smoothing algorithm are obtained by an own TO framework, called ToOp, embedded in FreeCAD and based on Python macros. It is based on a SIMP approach using a sensitivity filter to make the problem well-posed. Differently from other TO open-source codes available in literature, our framework is capable of returning an optimized structure after a TO analysis using a user-friendly GUI (Graphic User Interface) and an easy workflow from the design of the control volume, the simulation settings through the meshing and FEM analysis directly to the post-processing of the 3D model using the same software.
Often the TO solutions show an external surface that is far from being smooth and ready to be manufactured. This comes directly from the TO process that assigns material or void to the tetrahedral elements which compose the discretized control volume according to the sensitivity analysis to make the resulting structure more efficient. For this reason, the solution is characterized by an external surface made of spikes and peaks which are undesired in the final 3D model. Noisy 3D optimized models come from the ToOp own-built framework as will be seen in the case studies included in this research.
This is the reason why a post-processing algorithm for external surface smoothing is essential to make the TO framework useful in a design context where the optimized solution should be directly ready to be manufactured through AM processes due to the high complexity of the resulting shapes. To comply with this request, a smoothing process based on vertices position modification is developed in Matlab, but before describing in detail the new algorithm, it is worth understanding which are the available smoothing approaches in literature.
2.2 Surface smoothing
Nowadays, lots of methods useful to optimize the external surface of mesh files based on the manipulation of different data of the STL files are available. STL file contains the coordinates of the vertices composing the mesh, the IDs of the vertices that compose a triangular facet and the components of the normal vector for each facet. These are the information that a smoothing approach can manipulate taking as input the STL file format, whatever is the AM process and the material selected to manufacture the object.
In the following, the attention will be directed to vertex-based approaches available in literature: they are the simplest and the easiest to be implemented even if they suffer from critical problems as high volume reduction during the iterations. As the name says, these approaches use neighbourhood information in terms of spatial position to update the mesh. The largest part of the vertex-based approaches takes inspiration from the Laplacian smoothing (Sorkine 2005) whose operation can be modelled as a diffusion problem. This mathematical problem shows two desirable properties: the mesh connectivity is maintained and only the position of the vertices changes; each vertex is moved using only the information about its neighbours. The above-mentioned diffusion equation can be expressed as (Sorkine 2005):
where \({\varvec{X}}\) is a tensor that embodies the vertices of the mesh that will change during the iterative process, L is the Laplacian function, λ is a weight factor between 0 and 1 representing the diffusion speed and \(\partial t\) embodies the variation of the surface mesh during the iterative process. Assuming a Laplacian’s operator linearization, an explicit or implicit solution scheme can be used to find the evolving surface mesh during the iterations. To reduce complexity, in the following, only an explicit solving scheme will be used. Given Eq. 2, the available algorithms mainly vary among them by a different expression of the Laplacian operator that in the linearized form is represented by Eq. 3. \({N}_{1}(i)\) represents the 1-ring-neighbourhood vertex set which consists of all vertices that are connected to the i-th vertex by one edge, while \({{\varvec{x}}}_{{\varvec{i}}}\) is the vector of coordinates of the spatial position of the i-th vertex.
The standard Laplacian smoothing replaces a mesh vertex with the average position of its neighbours \({w}_{ij}=\frac{1}{n}\) where n is the number of the one-ring neighbours. This smoothing method shows the advantage of being very simple and computationally fast. However, it is affected by a strong vertex drifting (vertex movement not along the surface normal direction) and mesh shrinkage (mesh volume reduction) as the number of iterations grows.
An improvement of the previously cited approach is the Scale-Dependent Laplacian smoothing in which the Laplacian operator uses weights, called Scale-Dependent Umbrella (SDU) or Fujiwara weights, which are proportional to the relative distance between the vertices \({w}_{ij}=\frac{1}{\left|{e}_{ij}\right|}\) (Desbrun et al. 1999). This feature preserves the size of the triangles and decreases the vertex drifting. However, mesh shrinkage is still a critical issue. Besides, SDU weights introduce the Laplacian operator’s dependency on the solution of the previous iteration, because \({e}_{ij}\) must be updated at each mesh change. However, (Desbrun et al. 1999) shows that keeping constant the Fujiwara weights produces a negligible error.
Another vertex-based approach taken under consideration is the Improved Laplacian smoothing, also called HC-algorithm (HC stands for Humphrey’s Classes) (Vollmer et al. 1999). This methodology aims at improving the Laplacian approach and decreases volume shrinkage. This is obtained by adding to a first step (called push-forward and consists of the application of the classic Laplacian operator), a second step (push-back) to partially push towards the old position the vertices by a value that is the average of its own and its neighbours’ difference position vectors weighted by a factor β. Moreover, combined with the above-mentioned strategy to decrease the volume shrinkage, the new position of a vertex is evaluated considering not only the neighbour vertices but also the central vertex position. Indeed, the original vertex position is weighted by a factor α and included to help the algorithm to converge easily. The variables \(\alpha \) and \(\beta \) should be set by the user to obtain \(\alpha >0\) and \(\beta >0.5\). Thanks to all these improvements, the HC algorithm preserves better the mesh features and size during the iterations, even if a bit of shrinkage is still present. To examine in depth the mathematical background of this approach, the readers are referred to (Vollmer et al. 1999).
Taubin’s algorithm is one of the best smoothing algorithms present in literature. This approach is similar to the HC one because of the implementation of a two-step smoothing (forward and backwards) to correct the shrinkage. However, Taubin allows fine-tuning of both the steps by setting two scalar values (λ and μ) so that they balance each other (Taubin 1995). These two values should be chosen to satisfy the following mathematical expression: \(0.01<\frac{1}{\lambda }+\frac{1}{\mu }<0.1\).
Though, the available algorithms are still non-optimized for complex shapes coming from TO analyses where the designer wants to freeze important features such as holes or surfaces that should be kept planar in the ready-to-be-manufactured digital model. To fill this technological gap, the authors developed the Optimized Humphrey’s Classes—Scale-Dependent Umbrella algorithm (in the following Optimized HC-SDU algorithm) that combines the SDU and a modified version of the HC-algorithms to exploit their advantages, also including several sub-routines to solve the problems addressed before.
3 Optimized Humphrey’s Classes—Scale-Dependent Umbrella algorithm
This section contains a description of the innovative vertex-based smoothing algorithm developed. The scope of this methodology is to satisfy the necessity to post-process 3D models coming from TO analysis with the scope of maintaining important features without suffering from volume shrinkage. The flowchart containing the overall methodology is shown in Fig. 1.
The innovative approach takes as an input an STL mesh file usually coming from a TO analysis. The file is analyzed and the topology information pieces (vertices V, facets F and normal components N) are saved in matrices.
In the following, the algorithm asks the user to insert a numerical value for the four parameters needed for the smoothing, which are: \(\alpha \) and \(\beta \) coming from the HC-algorithm, \(\lambda \) that controls the diffusion speed of the process and \({iter}_{\mathrm{max}}\) which controls the maximum number of iterations the algorithm can do before stopping if the convergence is not reached (the difference between two consecutive solutions should be < 0.01). Pre-set values are suggested: \(\alpha \)=0.27, β = 0.51, λ = 0.6307 and \({iter}_{\mathrm{max}}\)=150.
The following steps involve the introduction of two own programmed sub-routines which are used to recognize features of the 3D model, the so-called no-smoothing-space. Following the flowchart shown in Fig. 1, a Matlab function called detect_flat_surface is used to find the vertices belonging to a flat surface by studying the components of the normal vector of the selected facet and the neighbour’s ones with a more detailed description in Sect. 3.1. The second subroutine is used to find holes that may be present in the digital model, independently from the shape of the cavity and will be described in detail in Sect. 3.2. To fulfil this capability, a function called detect_holes_edges searches for closed-loop sharp edges which belong to the summit of holes, taking inspiration from the methodology presented in (Qu and Stucker 2005) for different purposes. Both the cited sub-routines return the IDs of the vertices that belong to a flat surface or an edge of a hole. By the union of these two ID lists, the algorithm obtains an array containing the vertices belonging to the no-smoothing space that is passed to the core function of the algorithm.
The core of the process is made by the smoothing algorithm itself based on the HC methodology with a small change in the forward step where an SDU weight scheme is adopted instead of the classic Laplacian one to reduce the vertex drifting. Another change occurs in the inclusion of the original mesh: the original version of the HC algorithm uses a weighted original vertex position to evaluate the relative position vector. However, in the Optimized HC-SDU algorithm, the mean position between the original and the current mesh will be used to compute the difference vector. This is done to delete the background noise of smoothed models by the original HC algorithm, which is a behaviour that affects the latter smoothing method. Moreover, at the end of each iteration, the volume of the smoothed mesh is compared to the initial volume and rescaled according to a modified version of (Desbrun et al. 1999) formulation. Volume rescaling is necessary to avoid high mesh shrinkage due to the diffusion process that models the surface smoothing for vertex-based approaches. More details will be given in Sects. 3.3 and 3.4.
3.1 Flat surface detection
Following the flowchart shown in Fig. 1, the first sub-routine implements a function that recognizes flat surfaces of the 3D model (pseudo-code is available in the following, where the symbol stands for’is a function of’). The function inputs are the matrices containing the facet topologies (F), the normal vector components for each triangular face (N) and a scalar value (L) that will be explained later on. The function scrolls each facet of matrix F and compares its components of the normal vector with the neighbour triangles (IDs saved in vector q). The sub-routine is capable of counting the number of neighbour facets with the same normal (saved in the scalar variable z). Assuming that the i-th facet has x neighbours, if the number of the facets with the same normal to the i-th facet is higher than x−L, then the i-th facet belongs to a planar surface and the three vertices are saved in an array (\({{\varvec{a}}}_{1}\)). A threshold value (L) is imposed on the function to capture facets that belong to a planar surface that are near a sharp edge of the component. Indeed, assuming L = 0, many facets belonging to planar surfaces are lost during the process in the transition regions where the surface curvature suddenly changes (sharp edges). After several trials, a threshold value of L = 2 is chosen for the case studies that will be presented in Sect. 4. In fact, by choosing L > 2, the function starts to select triangles that do not belong to the planar surface anymore. Figure 2 shows the capability of recognizing planar surfaces (in yellow colour) from an STL model.

3.2 Holes detection
The second add-on included in the smoothing process is a function, called detect_holes_edges, whose aim is to recognize the presence of holes and cavities in the digital model. The procedure follows a technique similar to the algorithm developed in (Qu and Stucker 2005) where circular holes are detected for path-planning in CNC (Computerized Numerical Control) machine context. A pseudo-code explaining the methodology behind this function is available in the following (where the ← symbol stands for ‘is a function of’)

Firstly, all the sharp edges (S_E) are selected by the function being available the matrices of mesh faces F, mesh normal N, mesh edges E and face adjacencies saved in matrix ADJ. An edge is defined as sharp when it is in common between two adjacent facets (common_edge), which have an angle θ between the two normal vectors, that is between 85 and 95°. Up to now, only holes perpendicular to an external surface can be captured by the developed methodology, but in further studies, this limitation will be mitigated. Then the add-on investigates each edge of the mesh: if the i-th edge is sharp (check_edge = 0) then it’s saved as the first element of a loop, otherwise, the following edges are investigated. If the edge is sharp, the endpoint is saved as the initial starting point in the variable SPinitial. Next, that endpoint is used as a new starting point (SP) and all the edges linked to SP are investigated (link_edge). The function counts the number of sharp edges connected to SP. Usually, holes are determined by a simple closed loop of sharp edges meaning that no intersections are present. For this reason, on the one hand, if more than one sharp edge is found to be linked with SP, the function clears the k-th loop, clears the variable SPinitial and investigates the following edge of the mesh. On the other hand, if only a new sharp edge is connected with the previous one, the new edge is saved in the k-th closed-loop, SP is updated with the new endpoint and compared SPinitial. If SP and SPinitial. are equivalent, then the loop is closed, and the next edge is investigated to look for other loops. If SP is not equal to SPinitial, then the chain continues including more sharp edges in the k-th loop until the first edge is found to close the actual loop. In the end, the function returns the number of closed loops made of sharp edges found in the model and an array containing the IDs of the vertices touched by the selected sharp edges (a). Fig. 3 shows the flowchart of the methodology to understand if a sharp edge belongs to the summit of a hole.
Figure 4 shows the performance of holes detection of the described functionality in a model with several through-holes of different shapes.
3.3 Volume rescaling
As mentioned before, volume shrinkage is the main issue in all the smoothing processes based on the modification of the vertex position of the surface mesh. This is a critical issue that drove the research community to find alternative approaches to smooth the external surface. However, (Desbrun et al. 1999) shows that it is possible to rescale at each smoothing iteration the matrix describing the position of the vertices by a scalar value \(\gamma \) which is given by the comparison of the STL original mesh volume \({\mathrm{Vol}}_{0}\) with the volume of the i-th iteration \({\mathrm{Vol}}_{i}\) by the Eq. 4:
Each vertex position is then multiplied by the \(\gamma \) factor at the end of each iteration if the two volumes are different. In this way, the initial volume value is constant and the shrinkage is avoided. However, it is important to note that this scheme where V is just multiplied by a scalar value will not preserve the location of geometric constraints such as the size of the bounding box or the prescribed location of supports. To overcome this issue, the volume rescaling is applied by multiplying the matrix of the vertices by B defined as an identity matrix multiplied by the factor \(\gamma \) of Eq. 4. However, in the main diagonal, there are some identity elements, i.e. \(\mathbf{B}\left(i,i\right)=1\), if the index \(i\) is a member of vector a (array that contains the IDs of all the nodes belonging to holes or flat surfaces that do not need a smoothing process) (Eq. 5). In this way, the i-th node will not undergo the volume rescaling process, guarantying the preservation of constraining positions.
3.4 Core of the algorithm
After the description of all the sub-routines implemented to fulfil the research goal, in this section, the core of the developed approach is described. As the name of the algorithm introduces, the developed smoothing methodology is based on the coupling of the SDU weight functions with the HC algorithm. For the sake of clarity, the former is a Laplacian smoothing approach where the relative weight functions of mesh vertices are defined to be proportional to the relative distance between the vertices \({w}_{ij}=\frac{1}{\left|{e}_{ij}\right|}\). This feature maintains the size of the triangles and decreases the vertex drifting. The latter is a smoothing approach with a first classic Laplacian step and a second step to moderately push towards the old position of the node by a value that depends on the relative difference position vectors of all the neighbours. In addition, in the original HC approach, the new position of a vertex depends also on the original central vertex position. This dependency is modified in the developed algorithm compared to the original HC. In the latter, the relative position vector (diffi) is a function of the original mesh by a scalar weight. In the former, the relative position vector depends on the mean position between the original and the current mesh, weighted by the same scalar value α. This is done to alleviate the main disadvantage of the HC algorithm, which is the mitigation of the biggest mesh peaks and surface noise, while light background noise is still present on the smoothed model.
In the following, this nomenclature will be respected: the positioning vector of the i-th vertex in the original noisy mesh will be denoted as \({{\varvec{o}}}_{{\varvec{i}}}\), the positioning vector of the vertex that is still not modified by the current iteration of the smoothing algorithm is called \({{\varvec{c}}}_{{\varvec{i}}}\). Lastly, the vertex belonging to the smoothed mesh will be defined with \({{\varvec{s}}}_{i}\). As prescribed in the HC algorithm, two steps are used to smooth the mesh. Though, a major difference involves the push-forward step which is characterized by the implementation of the SDU weights to decrease the vertex drifting instead of the classic Laplacian. From a mathematical perspective, the forward step is characterized by the evaluation of the temporary smoothed position of the i-th vertex; along with \({{\varvec{s}}}_{i}\), in this step, the vector containing the relative distance positioning vector to the original position by the \(\alpha \) weight is estimated:
Then a push-back step is characterized by the same approach developed for the HC algorithm to calculate the final smoothed position of the i-th vertex:
The overall algorithm is repeated until a satisfactory result is obtained (‘smooth enough’) with a while cycle. This verbatim collects the mathematical condition for which the difference in terms of distance between two consecutive solutions should be < 0.01.
By introducing the sub-routines described before, the overall smoothing algorithm can be described thanks to the following pseudo-code (where the ← symbol stands for ‘is a function of’):

4 Case studies
This section describes two case studies that have been used to evaluate the performances of the developed algorithm and compare it with algorithms available in literature. The performances are compared by the evaluation of the mesh volume variation during the iterations and the Total Change of the STL model. The change of the model is defined as the Euclidian distance between the original vertex position and the smoothed one. The Total Change is defined as the sum of all the changes for the overall surface (Gostler 2015). For benchmarking proposes, the Optimized HC-SDU algorithm is compared with the classic Laplacian smoothing, the Laplacian smoothing using SDU weights, the HC-algorithm and Taubin approach (μ will be set to − 0.53 for the following simulations, as literature suggests).
In the following case studies, \(\alpha \) and \(\beta \) (scalar variables affecting the HC and Optimized HC-SDU algorithms) have been set after a sensitivity analysis to find the optimal values. The best condition is defined as the one for which the algorithm converges, meaning that the distance between two consecutive meshes is lower than 0.01 without reaching the maximum number of iterations \({iter}_{\mathrm{max}}\), and the total change is maximized. \(\alpha \) and \(\beta \) are ranged following literature suggestions: Vollmer states that the HC-algorithm converges if 0 < α < 1 and 0.5 < β < 1 (Vollmer et al. 1999). Several simulations are performed to study how the developed algorithm performs: α is changed using a 0.09 step from 0.18 to 0.72 because extreme values badly perform, while β is changed using a 0.07 step from 0.51 to 1. The diffusion speed value \(\lambda \) is chosen from literature (\(\lambda \)= 0.6307) because it represents a good trade-off value useful to better preserve the mesh volume using a limited number of iterations (Desbrun et al. 1999). Finally, \({iter}_{\mathrm{max}}\) is chosen to be a compromise between a good-quality solution and low computational effort for the smoothing process and is arbitrary fixed to be 150 as the first attempt. All the simulations are performed by running the Matlab programmed codes on a workstation with 32 GB RAM and an Intel Zeon CPU @ 3.50 GHz.
4.1 Cantilevered beam with passive elements
A 100 × 30 × 10 mm cantilever beam with a shear load of 100 N applied on the free-end is optimized by the ToOp environment and an STL model, made of 11,369 vertices and 22,798 facets, is used as an input file to test the developed smoothing algorithm. For the sake of clarity, in the TO analysis, a volume fraction of 0.4, a penalization factor of 3, a volume mesh size of 1 mm and the AlMg3 material are set. The peculiarity of this geometry is the presence of two passive element regions (two 10 mm diameter circular through-holes) that were not optimized by the TO algorithm and that should be maintained even after the surface post-processing, as it may happen in a real-life context in industrial engineering where cables and other structural elements may cross a structure.
The chosen input values for the variables involved in the process are \(\alpha \)=0.8, \(\beta \). (=0.51, \(\lambda \)=0.6307 and \({iter}_{\mathrm{max}}\)=150. A 3 × 3 sensitivity matrix is obtained by varying α and β around the optimum value by a step forward and backwards (Table 1) procedure. The optimum value is defined as the input configuration where the total change is maximized while the distance between two consecutive meshes is lower than 0.01 (convergence criteria). The other parameters such as λ and \({iter}_{\mathrm{max}}\) are chosen conveniently: the diffusion speed matches literature benchmarks, while the maximum number of iteration is set to limit the computational time and cost. The best input configuration is highlighted in bold in the sensitivity matrices.
Following the methodology shown in Fig. 1, the two functions detect_flat_surfaces and detect_holes_edges are run to detect automatically the no-smoothing space. The results are shown in Fig. 5.
After the surface fairing, the 3D models are also visually compared (Fig. 6). Moreover, a quantitative performance evaluation is done studying the behaviour of the mesh Total Volume and Total Change during the iterative process (Fig. 7). Table 2 collects the computational time needed to run the smoothing process, the required iterations to reach the convergence and quantitative comparison of the dimensions of the features of the model. Indeed, thanks to the modification of the volume rescaling proposed by Desbrun by a matrix multiplication, the position of geometric constraints is guaranteed, as it can be seen in Fig. 8 where the absolute nodal displacement from the original to the smoothed model is plotted.
4.2 General Electric bracket
The same approach has been applied to the model of a jet engine bracket (‘General Electric Jet Engine Bracket Challenge’) used in a real-life industrial application. The model is firstly optimized within the ToOp environment: the four holes in the base of the component have been constrained and a shear load of 4525 N has been applied on the two upper wings at 45° to the basement; a volume fraction of 50%, an initial volume mesh size of 2 mm and the Ti6Al4V material are chosen, while the penalization factor is set to 3. The resulting geometry is shown in Fig. 9. After the optimization, an STL model made of 7358 vertices and 14,738 facets is used as an input file to the smoothing algorithms. For this case study, the chosen values for the variables of the smoothing process are \(\alpha \)=0.27, \(\beta \)=0.51, \(\lambda \)=0.6307 and \({iter}_{max}\)=150. Even in this case, a 3 × 3 sensitivity matrix is built to demonstrate that this setup is the best one, as done for the previous case study where the best input configuration is highlighted in bold (Table 3).
Figure 9 shows also the no-smoothing spaces which are automatically detected by the developed functions.
As done for the previous component, the quantitative (Fig. 10) and qualitative (Fig. 11) results of the smoothing process are shown. Table 4 collects the computational time needed to run all the smoothing algorithms, the required iterations to reach the convergence, and a comparison with the model’s dimensions.
4.3 Discussion of the results
From the results shown in the previous section, it can be said that the Laplacian smoothing with classic weights and with SDU weights reaches poor results in quality for both case studies. As it can be seen in Figs. 6 and 11, they both suffer from high volume shrinkage (average reduction of 76% and 49%, respectively) even if high values of total changes are reached for both geometries. Moreover, they both do not reach convergence after 150 iterations, meaning that the distance between two consecutive solutions is higher than 0.01; this reflects on the highest values of computational time.
During the smoothing process, the no-smoothing spaces of the digital models are highly modified, making them completely unrecognizable. Just to provide some numerical values, the classic Laplacian reduces the hole by 38% on average, while the SDU of more than 50%. For all the mentioned reasons, these 2 smoothing approaches are considered not applicable in a real-life context to post-process complex geometries which come from TO analyses before manufacturing them.
Classic Laplacian and SDU approaches poorly post-process the 3D models, while Taubin’s algorithm has a mid-field behaviour. On the one hand, it performs well in the cantilever beam example, but on the other hand, it shows worse behaviour in the bracket case study. In general, this smoothing approach, highly appreciated in literature contributions, is fast, reaches convergence criteria but suffers from a sensitive amount of volume shrinkage (25% mean reduction between the two case studies) and the features are not preserved.
A different discussion involves the HC algorithm which always converges very rapidly but with small changes and no significant improvements on the final mesh geometry. For this reason, the volume shrinkage level and the feature degradations can be considered negligible.
Lastly, Optimized HC-SDU algorithms decisively perform better. Looking at the choice of the input parameters addressed with the sensitivity matrices (Tables 1 and 3), it has been found that fixing β = 0.51 (near the lower boundary of β suggested by Vollmer) reflects satisfactory results, with maximization of total change and matching of convergence criteria. However, the choice of α is not straightforward as the previous parameter, because two different values have been set for the case studies presented in this work. It has been found that α depends on the number of vertices belonging to the no-smoothing-space: on the one hand, the beam example has almost 50% of vertices of the overall STL file belonging to flat surfaces or holes edges and a higher α value is needed to give more importance on the original mesh topology. On the other hand, the bracket mesh model has only 30% of nodes that belongs to the no-smoothing space, reflecting on a lower α input value to satisfy convergence criteria but reaching at the same time high levels of total change.
Focusing the attention on the smoothed results of the developed methodology, it can be said that it reaches convergence, reflecting on a faster smoothing process on the same order of magnitude of Taubin’s approach. For this reason, it is arguable that the developed functions of feature detection and volume rescaling that force the algorithm during the iterations do not affect the computational cost. Looking at the values of the mesh volumes (Tables 2 and 4), the Optimized HC-SDU algorithm, thanks to the volume rescaling sub-routine, perfectly maintains the initial volume value. The developed algorithm behaves better than Taubin when the task to maintain model features is addressed: the dimensions of the hole match perfectly between the original and the optimized model while Taubin’s algorithm shows a reduction in holes size (4% diameter reduction on the beam model, 24% on the bracket) which is an undesired effect in a real-life application. The connections between many components in a complex real-life assembly could be a straightforward example: if some holes used to connect components are modified in shape or reduced in diameter, the assembly can’t be completed and the object has to be discarded and re-designed. In other applications, holes may require further machining to respect GD&T (Geometrical Dimensioning and Tolerances) prescription where errors in diameter and more dramatically in the position may lead to discard the component.
From the previous results and comparison, it can be said that Taubin and Optimized HC-SDU algorithms can be considered the two best approaches considered in this research. Looking closely at a particular region of the GE bracket smoothed model (Fig. 12), it can be said that both algorithms perform roughly similarly, with the biggest mesh peaks and surface noise that is mitigated compared to the original mesh (Fig. 12a). However, as previously said, Taubin’s approach does not preserve the no-smoothing space as the flat surfaces and the dimensions of the holes (Fig. 12b). Referring to the developed methodology, the reader’s concern may be that it is difficult to assess if the main improvement is due to the application of the detect_flat_surface and detect_holes_edges functions before the surface smoothing or the actual Optimized HC-SDU algorithm itself in its completeness. However, this doubt can be easily solved because, as can be seen in Fig. 12c, Taubin’s algorithm coupled with the two developed functions to isolate the no-smoothing space, does not produce satisfactory results. Moreover, thanks to additional simulations that are not included here for the sake of brevity, it was noticed that the modified version of Taubin is slower and does not reach the levels of Total Change reached by the Optimized HC-SDU approach. Due to brevity, only Taubin’s approach coupled with the developed functions to detect the no-smoothing-space is shown, but similar discussions could be applied to the other methodologies compared in this research. The final geometry is distorted and much worse than the overall developed methodology (Fig. 12d). Thanks to these sets of results it can be noticed that the Optimized HC-SDU approach is the best one compared to the methods taken under consideration in this work where both high frequency and background noises are smoothed.
A parameter that helps to summarize the results is the total change behaviour represented in Figs. 7 and 10. Its amount needs to be a trade-off between two diverging demands: a good-looking model (highly smoothed), and a model which does not collapse on itself (high shrinkage). Therefore, the ranking of the suitability of the algorithms for the smoothing of TO analysed components have been set by looking at the same time to the total change and the total volume plots: the best performances are characterized by the coupling of high total change (good smoothing) and low or null total volume decrease. Using this evaluation scale, the Optimized HC-SDU algorithm shows better performances compared to the other ones with Taubin’s algorithm that is not far away, even if small model degradation occurs. The developed algorithm maintains the initial mesh volume and preserves the features the designer would like to maintain still showing a high total change value. The Scale-Dependent Laplacian and the classic Laplacian obtain high values of total change and a smoothed external surface, but as evident from Figs. 6 and 11, the models collapsed on themselves and the shrinkage effect is dramatic. The automatic detection procedure for holes proved to be reliable and useful to detect features to keep unsmoothed without human intervention.
As mentioned in this section, the performances of the innovative methodology seem satisfactory from the denoising point of view. However, a detailed discussion should focus on how the smoothing process impacts the structure performances in loading conditions, such as the final structure compliance and how the smoothing post-processing could be optimized to limit the impact on structure performance changes. This point will be analysed in detail in further researches. To provide the reader with some numerical data, the compliance of the smoothed structure of the GE bracket has been computed and compared to the compliance value of the corresponding noisy model. Let c be the compliance of the structure, U the nodal generalized displacement, K the global stiffness matrix and F is the matrix of the nodal generalized external forces, \({\rho }_{e}\) the element density and \({\mathbf{K}}_{\mathbf{e}}\) the element stiffness matrix, following the approach described in (Costa et al. 2018), c can be computed with:
Combining both Eq. 8, it can be seen that the compliance depends on the displacement field and the nodal external forces. Assuming a mesh with \(n\) nodes, both U and F have dimensions [\(nx3\)]; this implies that c has dimensions [3 × 3]. However, just to have a scalar and comparable value, the same approach used in the Top3D software, developed by (Liu and Tovar 2014) is used, where the 9 elements are summed up.
Therefore, it is possible to estimate the overall structure compliance values which are reported in Table 5: the displacement values available from the topology optimization analysis have been used, together with the load conditions already described for the GE bracket. In the following, the structure compliance of the noisy mesh is assumed as the benchmarking value, since it comes directly from the topology optimization analysis. Indeed, structure compliance is the fitness function which the SIMP TO process minimizes during the optimization runs. After these computations, it is possible to compare the structural performance of the smoothed structure to the noisy 3D model: from Table 5, it can be seen that the overall compliance increases, going in the opposite direction compared to the aim of the topology optimization. However, the increment is limited to 2%, which is very close to the value of the unsmoothed part. On the one hand, the structure compliance slightly increases, but on the other hand, the smoothing approach returns a 3D model based on the results of the TO which is ready to be manufactured without the need to model from scratch in CAD software the optimized component. This accelerates the design-to-manufacturing cycle and reduces the designer’s workload, even if a small approximation in terms of compliance should be accepted (Table 5).
To sum up, the methodology does not require complex mathematical operations and could be easily integrated into commercial Topology Optimization software to improve the final results. The Optimized HC-SDU algorithm requires the setting of four parameters, but average values could be used as a default: in this way, the algorithm shows encouraging results and the end-user is not required to do a lot of tests to set the values.
5 Conclusions
Mesh post-processing techniques are crucial in the design-to-manufacturing cycle especially in those contexts where TO design methodologies are employed. Indeed, the resulting geometry is far from being manufacturable as it is and for this reason, smoothing algorithms need to be applied to return a more appealing external surface. Several procedures are already available in literature, however, a large part of them show important weaknesses as volume shrinkage and loss of model features when applied, especially for vertex-based approaches. To bridge the gap, the authors developed a smoothing methodology based on the HC-Laplacian one. At first, the Scale-Dependent-Umbrella weights are used instead of the classic Laplacian ones to decrease the vertex drifting. Moreover, a volume rescaling formula is used to resize the mesh at each iteration to maintain the initial volume of the digital volume; this is done to avoid the shrinkage effect which affects the majority of available algorithms. Besides, two functions are developed to automatically recognize features like holes and planar surfaces which should be maintained during the smoothing process to be present either in the final digital model. Two case studies included in the work show the efficiency of the developed methodology compared to existent ones. The results suggest that the main goals that pushed the algorithm design have been addressed properly. Specifically, volume shrinkage is completely deleted during the process with a satisfactory total change value and computational time compared to the other approaches. Moreover, features that should be frozen during the process are perfectly recognized and maintained in the final 3D models.
In the future, the methodology will be improved to detect every type of orientation of the holes: up to now only holes perpendicular to the body surface can be recognized. For the preliminary study, the input parameters are set after a trial and error approach and sensitivity matrices are built to show the optimum input setup in terms of scalar coefficients for the HC algorithm. The diffusion speed and the maximum number of iterations are chosen following literature suggestions and a good trade-off between computational cost and accuracy of the smoothed model. In further studies, the convergence parameters as well as the mesh distance and the maximum number of iterations will be changed to study how these parameters may affect the final result. Moreover, performance studies will be carried out to compare the structure compliance between the optimized noisy model and the smoothed version. Additionally, it’s straightforward to note that the proposed rescaling scheme may not preserve orientation near blocked nodes even if this has not been an issue in the case studies shown in this research; further studies with different geometries must better address this issue. Supplementary studies should be carried out involving both the developed algorithm, the Laplace–Beltrami operator, the methodologies which consider local curvatures and the iso-surface approaches to investigate the results and compare the efficiency of the algorithms.
To sum up, thanks to the proposed results, it is possible to say that the Optimized HC-SDU method is suitable for implementation in commercial software and could help in obtaining structures ready for Additive Manufacturing just as the output of the Topology Optimization process. In this way, the painstakingly CAD sketching from scratch of the optimized component where the output of TO is imitated is avoided, with a strong gain in time to market, reduction of operator efforts, and increase in precision.
References
Bacciaglia A, Ceruti A, Liverani A (2019) A systematic review of voxelization method in additive manufacturing. Mech Ind 20(6):630. https://doi.org/10.1051/meca/2019058
Bacciaglia A, Ceruti A, Liveran A (2020) Additive Manufacturing Challenges and Future Developments in the Next Ten Years. In: Rizzi C, Oreste Andrisano A, Leali F, Gherardini F, Pini F, Vergnano A (eds) Design tools and methods in industrial engineering, In: Caterina Rizzi, Angelo Oreste Andrisano. Lecture Notes in Mechanical Engineering. . Springer International Publishing, Cham, pp 891–902
Belyaev A, Ohtake Y (2003) A comparison of mesh smoothing methods. In:Israel-Korea Bi-national conference on geometric modeling and computer graphics, pp 83–87. Tel Aviv University, Tel Aviv
Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1(4):193–202. https://doi.org/10.1007/BF01650949
Bendsøe MP, Sigmund O (2011) Topology optimization: theory, methods, and applications. 2nd edn, Corrected printing. Engineering Online Library. Springer, Berlin
Bourdin B (2001) Filters in topology optimization. Int J Numer Meth Eng 50(9):2143–2158. https://doi.org/10.1002/nme.116
Buades A, Coll B, Morel JM (2005) A review of image denoising algorithms, with a new one. Multisc Model Simul 4(2):490–530. https://doi.org/10.1137/040616024
Costa G, Montemurro M, Pailhès J (2018) A 2D topology optimisation algorithm in NURBS framework with geometric constraints. Int J Mech Mater Des 14(4):669–696. https://doi.org/10.1007/s10999-017-9396-z
Costa G, Montemurro M, Pailhès J (2021) NURBS hyper-surfaces for 3D topology optimization problems. Mech Adv Mater Struct 28(7):665–684. https://doi.org/10.1080/15376494.2019.1582826
Desbrun, Mathieu, Mark Meyer, Peter Schröder, and Alan H. Barr. 1999. Implicit fairing of irregular meshes using diffusion and curvature flow. In: Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques - SIGGRAPH ’99, pp 317–24. ACM Press, Not Known
Gao W, Zhang Y, Ramanujan D, Ramani K, Chen Y, Williams CB, Wang CCL, Shin YC, Zhang S, Zavattieri PD (2015) The status, challenges, and future of additive manufacturing in engineering. Comput Aided Des 69(12):65–89. https://doi.org/10.1016/j.cad.2015.04.001
Gaynor AT, Meisel NA, Williams CB, Guest JK (2014) Multiple-material topology optimization of compliant mechanisms created via polyjet three-dimensional printing. J Manuf Sci Eng 136(6):061015. https://doi.org/10.1115/1.4028439
‘GE Jet Engine Bracket Challenge’. n.d. Accessed 23 April 2020. https://grabcad.com/challenges/ge-jet-engine-bracket-challenge.
Gibson I, Rosen D, Stucker B (2015) Additive manufacturing technologies. Springer, New York
Gostler A (2015) Denoising medical surface meshes for 3D-printing. Bachelor Thesis, TU Wien-Faculty of Informatics, Institute of Visual Computing & Human-Centered Technology. https://www.cg.tuwien.ac.at/research/publications/2015/gostler-2015-3dp/gostler-2015-3dp-Thesis.pdf
Jense GJ (1989) Voxel-based methods for CAD. Comput Aided Des 21(8):528–533. https://doi.org/10.1016/0010-4485(89)90061-4
Lee KW, Wang WP (2005) Feature-preserving mesh denoising via bilateral normal filtering. In: Ninth international conference on computer aided design and computer graphics (CAD-CG’05). pp 275–80 IEEE, Hong Kong
Krish S (2011) A practical generative design method. Comput Aided Des 43(1):88–100. https://doi.org/10.1016/j.cad.2010.09.009
Li Q, Steven GP, Xie YM (2001) A simple checkerboard suppression algorithm for evolutionary structural optimization. Struct Multidiscip Optim 22(3):230–239. https://doi.org/10.1007/s001580100140
Liu K, Tovar A (2014) An efficient 3D topology optimization code written in matlab. Struct Multidiscip Optim 50(6):1175–1196. https://doi.org/10.1007/s00158-014-1107-x
Machado G, Trabucho L (2004) Some results in topology optimization applied to biomechanics. Comput Struct 82(17–19):1389–1397. https://doi.org/10.1016/j.compstruc.2004.03.034
Mantovani S, Barbieri S, Giacopini M, Croce A, Sola A, Bassoli E (2020) Synergy between Topology optimization and additive manufacturing in the automotive field. Proc Inst Mech Eng Part B. https://doi.org/10.1177/0954405420949209
Zhang M, Gunturk BK (2008) Multiresolution bilateral filtering for image denoising. IEEE Trans Image Process 17(12):2324–2333. https://doi.org/10.1109/TIP.2008.2006658
Ohsaki M (2011) Optimization of finite dimensional structures. CRC Press/Taylor & Francis, Boca Raton
Qu X, Stucker B (2005) Circular hole recognition for STL-based toolpath generation. Rapid Prototyp J 11(3):132–139. https://doi.org/10.1108/13552540510601255
Rezaie R, Badrossamay M, Ghaie A, Moosavi H (2013) Topology optimization for fused deposition modeling process. Procedia CIRP 6:521–526. https://doi.org/10.1016/j.procir.2013.03.098
Savio G, Meneghello R, Concheri G (2019) Design of variable thickness triply periodic surfaces for additive manufacturing. Progress Addit Manuf 4(3):281–290. https://doi.org/10.1007/s40964-019-00073-x
Sigmund O (1997) On the design of compliant mechanisms using topology optimization*. Mech Struct Mach 25(4):493–524. https://doi.org/10.1080/08905459708945415
Sorkine O (2005) Laplacian mesh processing. Eurographics 2005-state of the art reports, 18 p. https://doi.org/10.2312/EGST.20051044.
Taubin G (1995) a signal processing approach to fair surface design. In: Proceedings of the 22nd annual conference on computer graphics and interactive techniques - SIGGRAPH ’95. pp 351–58. ACM Press
Vollmer J, Mencl R, Muller H (1999) Improved laplacian smoothing of noisy surface meshes. Comput Graph Forum 18(3):131–138. https://doi.org/10.1111/1467-8659.00334s
Wei M, Huang J, Xie X, Liu L, Wang J, Qin J (2019) Mesh denoising guided by patch normal co-filtering via kernel low-rank recovery. IEEE Trans Visual Comput Graph 25(10):2910–2926. https://doi.org/10.1109/TVCG.2018.2865363
Wong J, Ryan L, Kim IY (2018) Design optimization of aircraft landing gear assembly under dynamic loading. Struct Multidiscip Optim 57(3):1357–1375. https://doi.org/10.1007/s00158-017-1817-y
Xie YM, Steven GP (1996) Evolutionary structural optimization for dynamic problems. Comput Struct 58(6):1067–1073. https://doi.org/10.1016/0045-7949(95)00235-9
Zegard T, Paulino GH (2016) Bridging topology optimization and additive manufacturing. Struct Multidiscip Optim 53(1):175–192. https://doi.org/10.1007/s00158-015-1274-4
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. Open access funding provided by Alma Mater Studiorum - Università di Bologna within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Replication of results
All the information required to replicate the results found in Sects. 3–4 is fully disclosed in this paper. The same results will be obtained by implementing the equations and process presented here. The algorithms discussed in this paper are implemented in Matlab and Python by the authors, which cannot be shared due to further researches.
Additional information
Responsible Editor: Gengdong Cheng
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bacciaglia, A., Ceruti, A. & Liverani, A. Surface smoothing for topological optimized 3D models. Struct Multidisc Optim 64, 3453–3472 (2021). https://doi.org/10.1007/s00158-021-03027-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-021-03027-6