1 Introduction

Primary cosmic rays, which are charged particles, reach the Earth with energies at relativistic levels. After entering the Earth’s atmosphere, galactic cosmic rays (GCRs) interact with its particles and atomic nuclei, suffering energy losses through hadronic and electromagnetic processes (e.g. Dorman, 2004). Since the 1950s, secondary cosmic rays have been measured on the Earth using neutron monitors (NMs) (e.g. Simpson, 2000; Moraal, Belov, and Clem, 2000) and by muon telescopes (e.g. Munakata et al., 2014; Maghrabi et al., 2021) and in situ by space probes (e.g. Mckibben et al., 1995; Stone et al., 1998).

The average solar diurnal GCR variation is shaped due to the modulation of the GCR flux by the solar wind. This has been explained, based on the diffusion–convection theory of the GCR heliospheric propagation (Ahluwalia and Dessler, 1962; Krymsky, 1964; Parker, 1964), as a consequence of an equilibrium established between the radial convection of GCR particles by the solar wind and the radial component of the inward diffusion of the GCR particles, owing to the existence of a radial gradient, along the heliospheric magnetic field. This picture has later been developed to include the effects of particle drifts in the large-scale magnetic field (Jokipii, Levy, and Hubbard, 1977; Kóta and Jokipii, 1983). Anisotropy for the part of the time interval studied here, i.e. 2001 – 2014, was discussed by Tezari and Mavromichalaki (2016) for two neutron monitors having various cut-off rigidities located at the same longitude and different latitudes: Athens and Oulu. They have shown that the GCR diurnal anisotropy behaves in a different way during the opposite phases of the solar cycle, depending on the solar magnetic-field polarity, confirming previous results (e.g. Munakata et al., 2014). Thomas et al. (2017) underlined that the differences between solar cycles turned out to be greater when the solar transients visible in GCR were removed. The dependence of anisotropy on the heliospheric magnetic polarity was analyzed by Alania, Bochorishvili, and Iskra (2003), who have shown that within positive sectors anisotropy is greater during the 1976 solar minimum. Kudo and Mori (1990) established that the time intervals with greater values of anisotropy amplitudes from muon telescopes in the declining phase of Solar Cycle (SC) 21 appeared two years before that observed by neutron monitors. Tiwari, Singh, and Agrawal (2012) investigating Solar Cycles 20 – 23 showed clear dependencies on the level of the solar-activity cycle, revealing that annual-average anisotropy reaches maximal values during the declining phases for all solar cycles, while during the minimum epochs, anisotropy took the lowest values. Moreover, they presented evidence of substantial differences between the descending epochs of the odd (21 and 23) and even (20 and 22) solar cycles. The GCR anisotropy amplitudes for the even SCs are smaller than for the descending epochs of the odd SCs, while for the ascending epochs there are no significant dissimilarities. Studies of the GCR diurnal anisotropy prove its utility in the recognition of other aspects of heliospheric changes, for instance analyzes of Forbush-decrease features (Gololobov et al., 2017), or a recurrence of the GCR anisotropy as a unique proxy of the level of solar activity, as well as solar-wind states (Mavromichalaki, Papageorgiou, and Gerontidou, 2016; Modzelewska and Alania, 2018).

In this article, we continue research on the temporary changes of GCR diurnal variation alongside the solar-cycle variations. Previously, we showed the usage of diurnal variation for determining the modulation parameters characterizing the heliospheric transport of cosmic rays using NM data (Ahluwalia et al., 2015), muon-telescope observations (Ahluwalia and Modzelewska, 2020), and Forbush ion-chamber data (Ahluwalia and Modzelewska, 2021), earlier discussed also by, e.g., Bieber and Chen (1991), Chen and Bieber (1993), and Munakata et al. (2014).

We studied (Modzelewska et al., 2019) in detail the behavior of the GCR diurnal variation over Solar Cycle 24 and the solar minima between Solar Cycles 23/24 and 24/25 (the interval 2007 – 2018) and we estimated the contribution of drift effect to GCR modulation for the solar minima between Solar Cycles 23/24 and 24/25. We examined the polarity and rigidity dependence of the recurrent GCR intensity and anisotropy by Advanced Composition Explorer (ACE)/Cosmic Ray Isotope Spectrometer (CRIS), Solar Terrestrial Relations Observatory (STEREO), Solar and Heliospheric Observatory (SOHO)/Electron Proton Helium Instrument (EPHIN) and NMs (Modzelewska and Gil, 2021). The above-mentioned results concern the different average regular patterns of the GCR diurnal variation on different time scales, e.g. the annual or three-year averaging of the GCR diurnal variation used for the calculation of heliospheric-modulation parameters or analysis of its periodic character connected with solar cycle, solar magnetic cycle, and solar rotation. However, the GCR diurnal variation besides the regular character (on time scales of solar rotation, one year, or longer, etc.) has also a highly fluctuating term at short temporal scales (from a few to dozens of days). Moreover, recent studies carried out by Christodoulakis et al. (2019) and devoted to GCR intensity observed by selected NMs underlined the importance of considering smaller scales also. Therefore, the aim of this article is to analyze the scaling properties of the fluctuations of the GCR diurnal variation, focusing on relatively short temporal scales up to \(\approx100\) days compared to the \(\approx11\text{-year}\) solar-activity cycle.

In particular, we compute the quantitative parameter called the Hurst exponent, which allows us to consider the state of randomness of the GCR diurnal-variation fluctuations through the SC 24 and the solar minima between Solar Cycles 23/24 and 24/25. In the analysis, data from four NM stations are used, and two independent methods for the determination of Hurst exponent are applied: structure-function scaling and detrended-fluctuation analysis. It is worth stressing that the Hurst exponent has been widely used in various aspects of space-weather studies (e.g. Takalo and Timonen, 1998; Wanliss, 2004; Panchev and Tsekov, 2007; De Michelis et al., 2021; Alberti, Consolini, and De Michelis, 2021), solar activity (Ruzmaikin, Feynman, and Robinson, 1994), or GCR intensity (Christodoulakis et al., 2019), but this is the first time that this parameter is applied for the description for the GCR diurnal variation.

This article is organized as follows: Section 1 is an introduction. In Section 2 the data used in this investigation are briefly presented. In Section 3 we describe the structure-function and detrended-fluctuation-analysis methods. Section 4 shows the main results of the article. The last section discusses the implications of our findings and summarizes the results.

2 Data

In our calculations we use the GCR count rates with one-hour time resolution from four neutron monitors with various cut-off rigidities, from \(\approx0.8~\text{GV}\) up to almost 7 GV, located in the Southern and Northern Hemispheres. Details of the stations, such as their location or cut-off rigidities, are gathered in Table 1.

Table 1 Neutron monitors used in the computations (details from cidas.isee.nagoya-u.ac.jp/WDCCR/station_list.php).
Full size table

We analyze the daily amplitude and phase of the diurnal (24-hour) variation of the GCR intensity, calculated by means of normalized and detrended (excluding 25-hour trend) hourly data of the GCR intensity using the harmonic-analysis method (e.g. Gubbins, 2004). In our computations of the GCR diurnal variation in 2007 – 2019, we follow the procedure described by Modzelewska and Alania (2018) and Modzelewska et al. (2019). We exclude from consideration the diurnal amplitudes \(>0.7\%\) as irregular events related to transient disturbances in the heliosphere, generally connected with coronal mass ejections (CMEs) and solar flares. Various methods can be used for padding gaps in the observations (e.g. Munteanu et al., 2016). Here we fill data gaps with random values from empirical distributions of GCR diurnal-variation amplitude and phase.

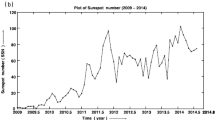
The daily values of the GCR diurnal-variation amplitude and phase for Newark NM (as an example) in SC 24 and the solar minima between Solar Cycles 23/24 and 24/25 (for 2007 – 2019) are presented in the second and third panel of Figure 1. Moreover, as an indicator of the 11-year solar-activity cycle, the upper panels of Figure 1 presents the daily values of the sunspot number (SSN).

Figure 1
figure 1

Daily data of the sunspot number (SSN, upper panel), GCR diurnal amplitude (middle panel), and phase (bottom panel) for the Newark NM for SC 24 and the solar minima between Solar Cycles 23/24 and 24/25 for 2007 – 2019; the shaded area indicates the time around solar maximum 2012 – 2014; \(\text{A} > 0\) and \(\text{A} < 0\) indicate positive and negative magnetic polarity.

Full size image

Figure 1 shows the temporal evolution of parameters of diurnal variation of cosmic rays for the Newark NM at the resolution of one day for SC 24 and solar minima 23/24 and 24/25 in 2007 – 2019. Although the dispersion of the data is very high, one could recognize the regular behavior of the parameters of GCR diurnal variation through the solar cycle with an average amplitude \(\approx0.3\%\). Namely, there is observed a tendency for the 11-year variability of GCR diurnal amplitude to be in phase with the solar-activity cycle (Figure 1, middle panel); the phase oscillates around \(\approx18\) hour (Figure 1, lower panel) and shows the trend of shifting towards the earlier hours near the solar minimum between Solar Cycles 24/25, with positive magnetic polarity (\(\text{A}>0\)) in 2017 – 2019, (e.g. Modzelewska et al., 2019), confirming the drift effect in GCR anisotropy over the 22-year solar magnetic cycle (Hale-cycle dependence). Recently, Dubey, Kumar, and Dubey (2018) confirmed the same for the GCRs diurnal phase during 1986 – 2017. Park et al. (2018) examined the diurnal variation comparing the results of calculations by the pile-up method and harmonic-analysis method. Oh, Yi, and Bieber (2010) established that the higher energy NMs contribute more to the 11-year variation of GCR anisotropy due to the diffusion process.

Since the nature of the GCR diurnal variation is highly scattered with relatively small amplitudes (\(<0.7\%\)) compared to the solar-cycle effect of modulation of GCR intensity being, e.g. \(\approx10\%\) for Newark NM, we study here the scaling properties of the time series assessing the Hurst exponent, which can be used as an indicator of the randomness of the GCR diurnal-variation fluctuations.

3 Methodology

We study here the scaling properties of the time series assessing the Hurst exponent [\(H\)]: the parameter used as an indicator of the randomness state of a time series (e.g. Fuss, Weizman, and Tan, 2021). The Hurst exponent, a classical self-similarity parameter, measures three types of behavior in a time series: persistence, randomness, and anti-persistence. More precisely, when the process has a long-range dependency (i.e. correlated) structure, then the Hurst exponent is in the interval 0.5 – 1. This situation is typical for processes observed to have more slowly evolving variations (i.e. more persistent), e.g. in monofractal and multifractal time series (e.g. Ihlen, 2012). When the time series has an independent or uncorrelated structure, such as in Brownian motion, then the Hurst exponent is close to 0.5. For time series with anticorrelated structure (anti-persistent), the Hurst exponent is in the interval 0 – 0.5.

The concept of the Hurst exponent has its origins in hydrology (Hurst, 1951), and from that time it has been increasingly used in other disciplines: in finance (e.g. Di Matteo, 2007), in biomedical time series (e.g. Ihlen, 2012), or space-weather studies (e.g. Takalo and Timonen, 1998; Wanliss, 2004; De Michelis et al., 2016, 2020, 2021; Alberti, Consolini, and De Michelis, 2021), as well as in solar-activity predictions (e.g. Singh and Bhargawa, 2017). Moreover, using the Hurst exponent (Ruzmaikin, Feynman, and Robinson, 1994; Oliver and Ballester, 1996) revealed the stochastic character of the solar-activity temporal profile. The Hurst-exponent properties were used in the analysis of compound-diffusion properties, i.e. when the particles are closely connected to the magnetic-field lines and the perpendicular transport origins in the random walk (Kóta and Jokipii, 2000). Recently, Christodoulakis et al. (2019) investigated the scaling features of the GCR intensity for 2000 – 2017 using NM data. They found that \(H\)-values were \(\approx1\) for the whole period and consequently GCR intensity time series exhibit positive long-range correlations. Moreover, multifractal behavior was detected at all NMs with a great degree of multifractality only for smaller time scales (\(\leq100~\text{days}\)).

There are several techniques for the determination of the \(H\)-exponent from experimental data (Esposti, Ferrario, and Signorini, 2008). In this article, we use two approaches for establishing the Hurst exponent: the structure-function and detrended-fluctuation-analysis methods.

3.1 Structure Function Scaling

The first technique that we adopt to evaluate the Hurst exponent uses the scaling properties of the structure function (SF). This method is based on the investigation of the scaling properties of a time series directly via the computation of SF being the \(q\)-order moments of the distribution of the increments over the time \(\tau \) (e.g. Takalo and Timonen, 1998; Di Matteo, Aste, and Dacorogna, 2005; De Michelis et al., 2020):

$$ S ( q,\tau ) =\bigl\langle \bigl\vert X ( t+\tau ) -X ( t ) \bigr\vert ^{q} \bigr\rangle . $$
(1)

The \(q\)-order moments of the distribution of the increments are a good quantity to characterize the statistical evolution of a stochastic variable \(X ( t )\). Hurst analysis examines whether some statistical properties of time series \(X ( t )\) scale with the time resolution and the observation period [\(T\)]. The Hurst exponent [\(h(q)\)] can be defined from the scaling behavior of \(S ( q,\tau )\) as

$$ S ( q,\tau ) \propto \tau ^{qh(q)}. $$
(2)

For \(q=1\), \(h(1)\) describes the scaling behavior of the absolute values of the increments.

We are interested in the temporal profile of the Hurst exponent of GCR diurnal variation in Solar Cycle 24 and the solar minima between Solar Cycles 23/24 and 24/25 for 2007 – 2019 with resolution of one month. Thus, we consider a moving-scale window of 360 days with the displacement of 30 days. The analyzed data are detrended by removing the linear trend. The scale with \(T = 360\) days is more than ten times larger than the resolution that we want to investigate: 30 days. Here we consider the case for \(q=1\) (hereafter in this article we designate \(h ( 1 ) =H\)) and the scale from 1 to 36 days. This choice permits us to have a reliable estimation of the statistics of the monthly variability of the Hurst exponent [\(H\)] of GCR diurnal variation. The Hurst exponent [\(H\)] is computed through a linear least-squares fitting of Equation 2.

3.2 Detrended Fluctuation Analysis

In the next part of the analysis, to determine Hurst exponent for the daily values of the GCR diurnal-variation parameters, we apply the detrended-fluctuation-analysis (DFA) methodology (Peng et al., 1994, 1995; Kantelhardt et al., 2001; Ihlen, 2012). DFA was first proposed by Peng et al. (1994), and from that time the algorithm has found widespread application (e.g. Chen et al., 2002 and the references therein). Moreover, DFA methodology, whose predecessors were the rescaled Hurst interval analysis (Hurst, 1951) and fluctuation analysis (FA) (Peng et al., 1992), has been modified and generalized in subsequent years (e.g. Kantelhardt et al., 2001, 2002; Ihlen, 2012).

In the framework of the basic DFA methodology, the four following steps are executed (Peng et al., 1994; Kantelhardt et al., 2001; Ihlen, 2012). In the first step, the considered time series \(X\) of size \(N\) (in our case \(N =360\)) is integrated by computing the accumulated departure from the mean of the whole series:

$$ Y ( k ) = \sum_{i =1}^{k} \bigl[X_{i}- \langle X \rangle\bigr] $$
(3)

where \(k =1,\dots , N \) and \(\langle X \rangle = \frac{1}{N} \sum_{j =1}^{N} X ( j )\).

In the second step, the integrated series \(Y\) is divided into \(N_{s} = \frac{N}{s}\) non-overlapping segments \(v\) (subseries) of length \(s\). Note that \(s\) corresponds to \(\tau \) mentioned in the context of SF technique (Section 3.1). In the third step, the series \(Y\) is locally detrended. More precisely, for a given segment \(v =1,\dots , N_{s}\) of size \(s\), the characteristic size of fluctuation \(F\) for integrated and detrended series is calculated by

$$ F^{2} ( v, s ) = \frac{1}{s} \sum _{j =1}^{s} \bigl[ Y \bigl( ( v -1 ) s + j \bigr) - Y_{v}^{m} ( j ) \bigr]^{2} $$
(4)

where \(Y_{v}^{m} ( j )\) denotes an \(m\)th-order polynomial fitted to the \(Y\) in segment \(v\). It is worth stressing that various degree polynomial functions can be used (Kantelhardt et al., 2001; Hu et al., 2001). In the analysis presented here, similarly to SF methodology, the first-order (\(m =1\)) polynomial has been applied.

The computation expressed by Equation 4 is repeated over various segment sizes \(s\) to provide a relationship between \(F\) and \(s\):

$$ F ( s ) = \sqrt{\frac{1}{N_{s}} \sum_{v =1}^{N_{s}} \bigl[ F^{2} ( v, s ) \bigr]}. $$
(5)

Finally, a power law is expressed as

$$ F ( s ) \propto s^{H} $$
(6)

where the scaling exponent [\(H\)] is the Hurst exponent and is expressed as the slope of a double-logarithmic plot of \(F ( s )\) as a function of \(s\). One of the important aspects of the procedure matching the exponent \(H\) (Equation 6) is the appropriate consideration of the minimal and maximal segment size \(s\). Selected studies considered the maximum box size equal to one-tenth of the signal length (\(N/10\)) (Hu et al., 2001) or \(s>N/ 4\) (e.g. Ma, Yang, and Cai, 2005). The limitation of large scale is related to the fact that for very large-scale sizes the function calculated in Equation 4 ceases to be statistically significant as the number of segments \(N_{s}\) decreases. Next, for too small scales, systematic variations of the scaling factors may also occur. As many studies showed, the minimum value of the scale parameter should not be less than 10 and generally larger than the order \(m\) of DFA (e.g. Phothisonothai and Nakagawa, 2007). In our study, the Hurst-exponent determination based on Equation 6 was performed in a scaling range from 10 to 90 days (\(\leq N/4\)). Also, to perform analysis of the diurnal variation of cosmic rays in the years 2007 – 2019, the numerical calculations, similarly to SF analysis, were carried out in a 360-day moving window with the displacement of 30 days.

It is worth noting that each step of the SF (Takalo and Timonen, 1998; Di Matteo, Aste, and Dacorogna, 2005; De Michelis et al., 2020) and DFA (Peng et al., 1994, 1995; Kantelhardt et al., 2001) procedures presented above has been implemented in MatLab software and checked on data with known Hurst exponents.

4 Results

Figures 2 and 3 present the values of Hurst exponent [\(H\)] determined for GCR diurnal amplitude (Figure 2) and phase (Figure 3) by using two SF (blue) and DFA (red) methods. The panels correspond to data from Oulu (case a), Newark (case b), Hermanus (case c), and Potchefstroom (case d) NMs measured during Solar Cycle 24 and the solar minima between Solar Cycles 23/24 and 24/25, for the period 2007 – 2019. Although the SF and DFA methods represent different approaches to the calculation procedure, Figures 2 and 3 show a relatively good agreement between the temporal profiles of \(H\) obtained by using SF and DFA methods. This can be considered as confirmation of the reliability of the scaling properties of the analyzed data. Of course, one cannot expect one-to-one correspondence between SF and DFA methods, but still they converge, being good tools to study the self-similarity problem of the time series.

Figure 2
figure 2

Temporal profile of the Hurst exponents [\(H\)] of the GCR diurnal amplitude for SC 24 and the solar minima between Solar Cycles 23/24 and 24/25 for the period of 2007 – 2019 for Oulu (a), Newark (b), Hermanus (c), and Potchefstroom (d) NMs using SF (blue) and DFA (red) methods; the shaded area indicates the time around the solar maximum 2012 – 2014.

Full size image
Figure 3
figure 3

Temporal profile of the Hurst exponents [\(H\)] of the GCR diurnal phase for SC 24 and the solar minima between Solar Cycles 23/24 and 24/25 for the period of 2007 – 2019 for Oulu (a), Newark (b), Hermanus (c), and Potchefstroom (d) NMs using SF (blue) and DFA (red) methods; the shaded area indicates the time around the solar maximum 2012 – 2014.

Full size image

Detailed analysis of Figure 2 reveals that the Hurst exponents [\(H\)] for GCR diurnal amplitude vary in the range from \(\approx0.3\) to \(\approx0.8\) for all NMs. One can see that the Hurst exponent is evolving with the 11-year solar-activity cycle with significant variability for different solar-cycle phases. Particularly, for the period 2007 – 2009, representing the solar minimum 23/24 with negative magnetic polarity (\(\text{A}<0\)), \(H\) is visibly larger than 0.5 with the average value \(\approx0.65\) for all considered NMs. Next, we can see the rapid decrease of \(H \) around 2012 for all NMs. This drop of \(H\) to \(\approx0.5\) is relatively shorter for NMs with low cut-off rigidity, Oulu and Newark, but significantly longer in duration for NMs with high cut-off rigidity, Hermanus and Potchefstroom, lasting up to 2016. Considering the period near the solar minimum between Solar Cycles 24/25 in 2017 – 2019, when \(\text{A}>0\), we can observe the tendency of rising \(H\) for Newark and Hermanus NMs in 2017 – 2018.

Figure 3 shows that the Hurst exponents [\(H\)] for GCR diurnal phase vary in the range from \(\approx0.4\) to \(\approx0.9\) for all NMs. For almost all of the NMs, the parameter \(H\) is higher for the solar minimum between Solar Cycles 23/24 in 2007 – 2009; next, one can see the rapid decrease for almost all of the stations in 2012, except for Hermanus NM, where the decrease is rather gradual for the DFA method.

For better visualization of how the Hurst exponent [\(H\)] changes with the phase of the solar cycle, we plot as an indicator of the 11-year solar cycle the monthly SSN in the top panels of both Figures 4 and 5. The average \(H\) for all NMs for the SF and DFA methods is presented in Figure 4 for GCR diurnal amplitude and Figure 5 for the diurnal phase. Additionally, for the estimation of a long-term trend, we plot the 37-month-smoothed \(H\) and SSN in the bottom panels of both Figures 4 and 5.

Figure 4
figure 4

Temporal profile of the monthly sunspot number (SSN) for SC 24 and the solar minima between Solar Cycles 23/24 and 24/25 (upper panel); the Hurst exponents [\(H\)] averaged for all NMs of the GCR diurnal amplitude for the period of 2007 – 2019 using SF (blue) and DFA (red) methods (middle panel); 37 month-smoothed \(H\) and SSN (bottom panel); shaded area designates the time of solar maximum 2012 – 2014.

Full size image
Figure 5
figure 5

Temporal profile of the monthly sunspot number (SSN) for SC 24 and the solar minima between Solar Cycles 23/24 and 24/25 (upper panel); the Hurst exponents [\(H\)] averaged for all NMs of the GCR diurnal phase for the period of 2007 – 2019 using SF (blue) and DFA (red) methods (middle panel); 37-month-smoothed \(H\) and SSN (bottom panel); shaded area designates the time of solar maximum 2012 – 2014.

Full size image

Figure 4 (middle panel) shows that the average \(H\) for GCR diurnal amplitude is visibly larger than 0.5 for the solar minimum between Solar Cycles 23/24 in 2007 – 2009; next we can see a rather rapid decrease in 2012 with further recovery during 2012 – 2014 (shaded area). During the period 2015 – 2019, \(H\) fluctuates near a value of 0.5 with some increase around 2017 – 2018. The average \(H\) of the GCR diurnal amplitude for SF and DFA methods, respectively, are as follows:

  1. i)

    for solar minimum 23/24, 2007 – 2009, \(H = 0.62\pm 0.04\) and \(H = 0.63\pm 0.05\)

  2. ii)

    for solar maximum of SC 24, 2012 – 2014, \(H = 0.51\pm 0.05\) and \(H = 0.52\pm 0.05\)

  3. iii)

    for solar minimum 24/25, 2017 – 2019, \(H = 0.52\pm 0.04\) and \(H = 0.52\pm 0.02\)

Figure 5 (middle panel) shows that the average \(H\) for GCR diurnal phase has a value larger than 0.5 for almost the whole considered period 2007 – 2019. Similar to the evolution of \(H\) for GCR diurnal amplitude, here one can see also the rather rapid decrease in 2012. During the period 2015 – 2019, \(H\)-values significantly differ for the SF and DFA methods, with larger values for the SF method. The average \(H\) of the GCR diurnal phase for SF and DFA methods, respectively, are as follows:

  1. i)

    for solar minimum 23/24, 2007 – 2009, \(H=0.58\pm 0.02\) and \(H=0.59\pm 0.05\)

  2. ii)

    for solar maximum of SC 24, 2012 – 2014, \(H=0.54\pm 0.05\) and \(H=0.55\pm 0.04\)

  3. iii)

    for solar minimum 24/25, 2017 – 2019, \(H=0.61\pm 0.03\) and \(H=0.54\pm 0.03\)

Additionally, considering the 37-month smoothing (Figures 4 and 5, bottom panels) for long-term trends, one can see that the level of \(H\) is a bit higher for the diurnal phase than for the diurnal amplitude with a tendency for \(H\) to be systematically above 0.5 for both. Moreover, one can see the anticorrelation of the Hurst-exponent timelines of both GCR diurnal amplitude and phase with solar activity for 2007 – 2014.

5 Discussion and Conclusions

In this article, we analyzed the scaling properties of fluctuations in the diurnal variation of cosmic rays for Solar Cycle 24 and the solar minima between Solar Cycles 23/24 and 24/25. We applied two methods, structure-function and detrended-fluctuation analysis, to consider the variation of the Hurst exponent as the randomness indicator in GCR diurnal amplitude and phase. The results obtained show that the Hurst exponents [\(H\)] for the GCR diurnal variation parameters vary in the range from \(\approx 0.3\) to \(\approx 0.9\) through Solar Cycle 24 and the solar minima between Solar Cycles 23/24 and 24/25. Moreover, the Hurst exponent is evolving with the 11-year solar-activity cycle with significant variability for different GCR diurnal variation parameters. The level of \(H\) is a bit higher for the diurnal phase than for the diurnal amplitude, with a tendency for \(H\) to be systematically above 0.5 for both. It suggests that the GCR diurnal variation has a more persistent structure than Brownian motion. However, the time series of the GCR diurnal amplitude and phase evolve from a more persistent structure in and near the solar minimum between Solar Cycles 23/24 in 2007 – 2009 to a more random character in and near the solar maximum 2012 – 2014. Particularly, the results show (Figures 4 and 5, third panels) a transition from a weakly correlated structure (\(H \approx 0.63\) for the amplitude and \(\approx0.60\) for the phase) near the solar minimum between Solar Cycles 23/24 to uncorrelated (\(H \approx 0.50\) and 0.55 for the amplitude and phase, respectively) near the solar maximum of Solar Cycle 24 of heliospheric dynamics represented by GCR diurnal variation. It is in agreement with the general configuration of the heliosphere, being more regularly structured near solar minimum with the established heliospheric magnetic field and more turbulent near solar maximum. Nevertheless, the temporal profiles of \(H\) for GCR diurnal amplitude and phase around the solar minimum between Solar Cycles 24/25 in 2017 – 2019 differ in comparison with 2007 – 2009, suggesting dependence on solar magnetic polarity. Moreover, during the period 2015 – 2019, \(H\)-values for GCR diurnal phase differ significantly for SF and DFA methods, with phase causing a different scaling character of the diurnal phase by SF and DFA methods. The above-mentioned scaling features of GCR diurnal variation evolve over 11-year solar-activity cycle, and thus these results could be important for the understanding of the GCR modulation over the solar cycle.

This article is the first attempt to study the scaling features of the GCR diurnal variation. Our work is still ongoing, and future studies will focus on the analysis of the larger dataset, e.g. for the whole solar magnetic cycle, also considering high energy GCRs, especially the from Princess Sirindhorn Neutron Monitor, with vertical cut-off rigidity 16.8 GV (e.g. Deeprom and Nutaro, 2017) and muon telescopes from the Global Muon Detector Network (Kihara et al., 2021). We will continue to test the structure-function and detrended-fluctuation-analysis methods, focusing on the influence of different trend-removal techniques (Kantelhardt et al., 2001). This will allow us to perform a more systematic and detailed identification of trends in data, and perhaps in this way we may reveal further differences between the considered solar minima, as well as the magnetic polarity. Finally, in the next phase of our work, we plan to perform analysis of GCR diurnal variation using a multifractal-based approach (Kantelhardt et al., 2002; Ihlen, 2012; Christodoulakis et al., 2019). This may support a fuller description of the complexity of the data considered and shed more light on the GCR particle transport in the turbulent heliosphere.