Abstract
The Teukolsky master equation describes the dynamics of massless fields with spin on a Kerr black hole. Under separation of variables, spin-reversal for this equation is accomplished through the so-called Teukolsky–Starobinsky identities. These identities are associated to the so-called Teukolsky–Starobinsky constants, which are spin-dependent. We collect some properties of the Teukolsky–Starobinsky constants and dispel some myths present in the literature. We show that, contrary to popular belief, these constants can be negative for spin larger than 2. Such fields thus exhibit a novel form of energy amplification which occurs for non-superradiant frequencies.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Since as early as the 1950s [RW57], the study of perturbations of stationary black holes has been a central theme of research in classical general relativity. In 4 spacetime dimensions and in vacuum, the paradigmatic and, conjecturally, only examples of stationary black hole solutions are the rotating black holes in the Kerr family [Ker63], parameterized by mass M > 0 and specific angular momentum |a| ⩽ M.
While studying stability of Kerr, Teukolsky [Teu73] introduced what became to be known as the Teukolsky master equations. In Boyer–Lindquist coordinates 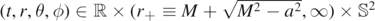 and with Kinnersley's choice of spin frame, these are given by
and with Kinnersley's choice of spin frame, these are given by
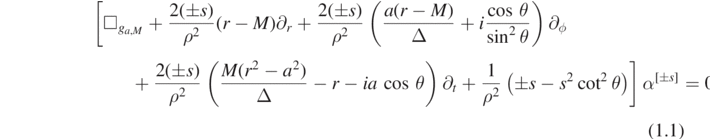
where Δ = r2 − 2Mr + a2, ρ2 = r2 + a2 cos2
θ and 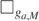 the covariant scalar wave operator on the Kerr background. Here, ±s denotes a spin parameter, making α[±s] a spin-weighted function; this notion, and hence (1.1), is well-defined for any
the covariant scalar wave operator on the Kerr background. Here, ±s denotes a spin parameter, making α[±s] a spin-weighted function; this notion, and hence (1.1), is well-defined for any  , see [PR84]. The Teukolsky master equations (1.1) play a crucial role in characterizing perturbations of Kerr black holes. For s = 0, they reduce to the scalar wave equation on Kerr. For s = 1 and 2, they describe the dynamics of gauge-invariant electromagnetic and curvature quantities under the linearized Maxwell and Einstein equations, respectively, in the Newman–Penrose formalism [NP62]. Some half-integer spin cases can also be interpreted physically: s = 1/2 corresponds to the Dirac equation for (massless) neutrinos; the case s = 3/2 is known as the Rarita–Schwinger equation. The case s > 2 of the Teukolsky master equations (1.1), although less often considered, is of mathematical interest in its own right and might play a role in higher-spin theories [Vas96].
, see [PR84]. The Teukolsky master equations (1.1) play a crucial role in characterizing perturbations of Kerr black holes. For s = 0, they reduce to the scalar wave equation on Kerr. For s = 1 and 2, they describe the dynamics of gauge-invariant electromagnetic and curvature quantities under the linearized Maxwell and Einstein equations, respectively, in the Newman–Penrose formalism [NP62]. Some half-integer spin cases can also be interpreted physically: s = 1/2 corresponds to the Dirac equation for (massless) neutrinos; the case s = 3/2 is known as the Rarita–Schwinger equation. The case s > 2 of the Teukolsky master equations (1.1), although less often considered, is of mathematical interest in its own right and might play a role in higher-spin theories [Vas96].
In this paper, we focus on separable solutions of (1.1) (see [Car68, Teu73]): for  ,
, 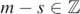 and
and  , these take the form
, these take the form
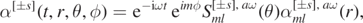
where ![${S}_{ml}^{[{\pm}s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn7.gif) and
and ![${\alpha }_{ml}^{[{\pm}s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn8.gif) satisfy ODEs, respectively referred to as the angular ODE, given below as (2.1), and the radial ODE, given below as (3.1).
satisfy ODEs, respectively referred to as the angular ODE, given below as (2.1), and the radial ODE, given below as (3.1).
As discovered by Starobinsky [SC74] and Teukolsky [TP74] for s = 1, 2 and later generalized to all  [KMW89], the angular and radial Teukolsky ODEs of spin ±s exhibit a curious property: on applying a certain first order differential operator s times to a solution to the ODE with spin +s, one obtains a solution to the ODE with spin −s, and vice-versa. Though seldom remarked in the classical literature, each of the radial Teukolsky–Starobinsky operators of spin ±s acts differently on the ingoing and outgoing components of the radial solutions, and a similar statement is true in the angular setting, see propositions 2.5 and 3.1 below. Nevertheless, by applying these operators in succession to a solution of the angular or radial ODE, one can check that, at least for |s| ⩽ 3, the exact same solution is recovered up to a constant: respectively, the angular Teukolsky–Starobinsky constant, denoted by
[KMW89], the angular and radial Teukolsky ODEs of spin ±s exhibit a curious property: on applying a certain first order differential operator s times to a solution to the ODE with spin +s, one obtains a solution to the ODE with spin −s, and vice-versa. Though seldom remarked in the classical literature, each of the radial Teukolsky–Starobinsky operators of spin ±s acts differently on the ingoing and outgoing components of the radial solutions, and a similar statement is true in the angular setting, see propositions 2.5 and 3.1 below. Nevertheless, by applying these operators in succession to a solution of the angular or radial ODE, one can check that, at least for |s| ⩽ 3, the exact same solution is recovered up to a constant: respectively, the angular Teukolsky–Starobinsky constant, denoted by  , and the radial Teukolsky–Starobinsky constant, denoted by
, and the radial Teukolsky–Starobinsky constant, denoted by
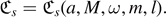
It is on the radial Teukolsky–Starobinsky constant, 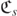 , that we focus on for the rest of this introduction.
, that we focus on for the rest of this introduction.
In the classical literature, see e.g. [Cha90, KMW89, KMW92],  is frequently denoted as the square of the modulus of a complex number. Taking this claim literally, we would conclude
is frequently denoted as the square of the modulus of a complex number. Taking this claim literally, we would conclude
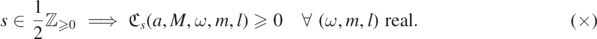
To justify (×), some authors point to the fact that α[−s] and Δs α[+s] satisfy complex conjugate equations. Unfortunately, this argument is incorrect: (×) does not follow from the fact that these radial ODEs are complex conjugates of each other. In fact, we show that (×) is manifestly false for general spin s:
Fact 1 (TS constant sign I). The radial Teukolsky–Starobinsky constant can be negative: for any |a| ∈ (0, M],
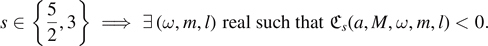
The proof of fact 1 is short and elementary: we require only the high frequency expansions for spin-weighted spheroidal angular eigenvalues, on which  depends (see lemma 3.3), which were obtained
4
in recent work of the first author and collaborators [CO05, COW19]. We note here the importance of the assumption a ≠ 0: it is well-known that
depends (see lemma 3.3), which were obtained
4
in recent work of the first author and collaborators [CO05, COW19]. We note here the importance of the assumption a ≠ 0: it is well-known that 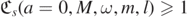 , at least if |s| ⩽ 3.
, at least if |s| ⩽ 3.
The implications of fact 1 are quite surprising. To explain these, recall that the Teukolsky–Starobinsky identities serve to define an energy identity for α[±s], which will thus depend on the constants 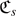 ; this observation goes back to [TP74] but the reader may find a rigorous statement below in lemma 4.1. In the case s = 0, corresponding to the scalar wave equation, where
; this observation goes back to [TP74] but the reader may find a rigorous statement below in lemma 4.1. In the case s = 0, corresponding to the scalar wave equation, where  plays no role in the energy, it is well-known that energy amplification occurs if and only if the frequency parameters (ω, m, l) are superradiant, i.e. such that
plays no role in the energy, it is well-known that energy amplification occurs if and only if the frequency parameters (ω, m, l) are superradiant, i.e. such that
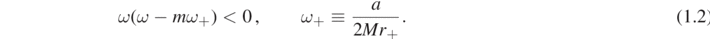
Condition (1.2) is intimately tied to the Kerr geometry, as ω+ is uniquely specified by the Kerr parameters and the amplification effect generated can be linked to the presence of an ergoregion in Kerr. For higher s, the superradiant condition is

as the half-integer spin particles do not interact with the ergoregion. If one could show  unconditionally, then superradiance (1.3) would be the only source of energy amplification, with half-integer spins experiencing none. Such claims are often made in the classical literature. However, in view of fact 1, we see that this is another fiction: in general, energy amplification may occur for half-integer spins and, in general, it may occur for integer spins and (ω, m, l) not in (1.3):
unconditionally, then superradiance (1.3) would be the only source of energy amplification, with half-integer spins experiencing none. Such claims are often made in the classical literature. However, in view of fact 1, we see that this is another fiction: in general, energy amplification may occur for half-integer spins and, in general, it may occur for integer spins and (ω, m, l) not in (1.3):
Fact 2 (Non-superradiant amplification). If s = 5/2 and |a| ∈ (0, M], there are real (ω, m, l) for which there is energy amplification. If s = 3 and |a| ∈ (0, M], there are real (ω, m, l) such that the superradiant condition does not hold, i.e. ω(ω − mω+) > 0, but for which there is energy amplification.
Some numerical evidence of this novel non-superradiant amplification effect is given below in section 4.
Remark 1.1. It is important to note that the novel amplification effect uncovered in fact 2 in no way invalidates the mode stability theorems for (1.1) obtained in [And+17, Shl15, TdC20, Whi89]. To explain why this is, we briefly review the strategy of these works.
For spin −s, mode stability is shown in these works by application of the transformations introduced in [TdC20, Whi89]. These transformations map solutions of (1.1) to solutions of a scalar wave equation on a new, ergoregionless, spacetime. The energy identity for this new scalar wave equation with real potential, as one expects for scalar fields, does not depend on any Teukolsky–Starobinsky-type constant.
Now consider spin +s. If the frequency triple (ω, m, l) is such that the Teukolsky–Starobinsky  constant vanishes, then one may easily deduce that there is no mode solution associated to (ω, m, l), i.e. no separable solution to (1.1) which is outgoing at the spacetime's future null infinity and ingoing at the black hole's future event horizon, see [TdC20, lemma 2.19]. Otherwise, if (ω, m, l) is such that
constant vanishes, then one may easily deduce that there is no mode solution associated to (ω, m, l), i.e. no separable solution to (1.1) which is outgoing at the spacetime's future null infinity and ingoing at the black hole's future event horizon, see [TdC20, lemma 2.19]. Otherwise, if (ω, m, l) is such that  , the Teukolsky–Starobinsky identities are applied to show that mode stability for spin −s implies mode stability for spin +s.
, the Teukolsky–Starobinsky identities are applied to show that mode stability for spin −s implies mode stability for spin +s.
Remarkably, even though the classical argument commonly used to justify this is incorrect, non-negativity of  does hold for the physical spins s ⩽ 2:
does hold for the physical spins s ⩽ 2:
Fact 3 (TS constant sign II). If s ⩽ 2, the radial Teukolsky–Starobinsky constant is never negative: for any |a| ∈ [0, M],
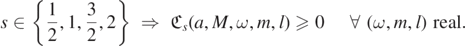
Hence, for s ∈ {1/2, 3/2}, there is no energy amplification, and for s ∈ {1, 2}, energy amplification occurs if and only if (1.2) holds.
Fact 3 follows not from any property of the radial ODE alone, but from a comparison between the two Teukolsky–Starobinsky constants  and
and  , as the latter can be easily shown to have definite sign. To the best of our knowledge, it was Teukolsky and Press [TP74] who first noted this in the s = 1 case.
, as the latter can be easily shown to have definite sign. To the best of our knowledge, it was Teukolsky and Press [TP74] who first noted this in the s = 1 case.
Remark 1.2. Fact 3 implies that, as claimed in the literature,  can sometimes—whenever s ⩽ 2, to be precise—be denoted as the square of a complex number. Most literature available, such as the classical reference [Cha83], focuses precisely on such cases. However, fact 1 highlights the importance of stressing the caveat in bold.
can sometimes—whenever s ⩽ 2, to be precise—be denoted as the square of a complex number. Most literature available, such as the classical reference [Cha83], focuses precisely on such cases. However, fact 1 highlights the importance of stressing the caveat in bold.
In light of the results present here for the sign of  , it is natural to try to understand whether
, it is natural to try to understand whether  for some real (ω, m, l). Such frequencies are known as real algebraically special [Cha84, Wal73] Since
for some real (ω, m, l). Such frequencies are known as real algebraically special [Cha84, Wal73] Since  , at least for s ⩽ 3, it follows from fact 1 that
, at least for s ⩽ 3, it follows from fact 1 that
Fact 4 (AS frequencies I). There are real algebraically special frequencies for s > 2: for any |a| ∈ (0, M],
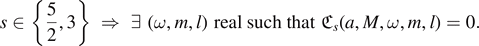
In the case s ⩽ 2, fact 3 gives one hope of ruling out algebraically special frequencies. We show that these hopes are well-founded, thus answering a question raised in [Wal73]:
Fact 5 (AS frequencies II). There do not exist real algebraically special frequencies for s ⩽ 2: for any |a| ∈ [0, M],
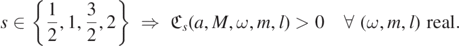
To the best of our knowledge, prior to this work, this result had only been noted in the s = 2 case, in work of the second author and collaborators, in [SRTdC20, TdC20].
We contrast fact 5 with the following result
Fact 6 (TS lower bound). For any a ∈ (0, M], as |ω| → ∞, we have
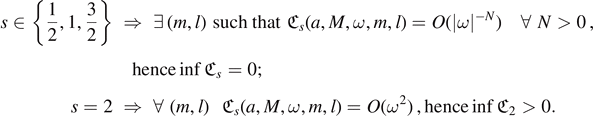
Indeed, for fixed a ≠ 0, we show that the limit when |ω| → ∞ is algebraically special for some (l, m) if s ⩽ 3/2. In the case s = 2, no such limit can be algebraically special: the comparison with the angular Teukolsky–Starobinsky constant gives  and it is the latter term which ensures that
and it is the latter term which ensures that  has a positive lower bound.
has a positive lower bound.
To conclude this introduction, we remark that we fully expect that our facts 1, 2 and 4 can be generalized to higher 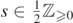 . Furthermore, we expect facts 3, 5 and 6 to also hold for the Kerr–(anti-)de Sitter black hole spacetimes, for which there is a generalization of the Teukolsky–Starobinsky identities and constants [Tor88] (see also the more recent [DS13]).
. Furthermore, we expect facts 3, 5 and 6 to also hold for the Kerr–(anti-)de Sitter black hole spacetimes, for which there is a generalization of the Teukolsky–Starobinsky identities and constants [Tor88] (see also the more recent [DS13]).
2. The angular Teukolsky–Starobinsky constants
In this section, we introduce the angular ODE corresponding to the Teukolsky equation (1.1). We then define the angular Teukolsky–Starobinsky constants and characterize their sign.
2.1. The angular ODE
Consider the angular ODE
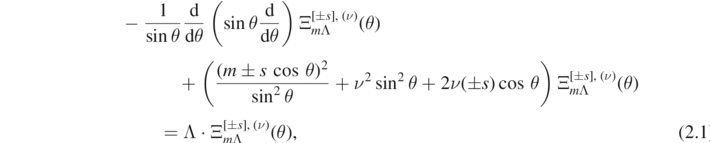
where θ ∈ (0, π),  ,
,  ,
,  and
and  . An asymptotic analysis leads us to conclude that for a solution to (2.1) there is a unique set of real numbers
. An asymptotic analysis leads us to conclude that for a solution to (2.1) there is a unique set of real numbers ![${a}_{i}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn34.gif) , i = 1, ..., 4, such that
, i = 1, ..., 4, such that
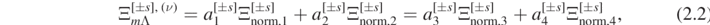
where ![${{\Xi}}_{\mathrm{norm},i}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn35.gif) , for i = 1, ..., 4, encode the two linearly independent behaviors that solutions may take at the regular singular points θ = 0, π [Olv73, chapter 5]:
, for i = 1, ..., 4, encode the two linearly independent behaviors that solutions may take at the regular singular points θ = 0, π [Olv73, chapter 5]:
- If |m| ≠ s, take
![${{\Xi}}_{\mathrm{norm},1}^{[{\pm}s]}{(1-\mathrm{cos}\enspace \theta )}^{-\frac{m{\pm}s}{2}}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) and
and ![${{\Xi}}_{\mathrm{norm},2}^{[{\pm}s]}{(1-\mathrm{cos}\enspace \theta )}^{\frac{m{\pm}s}{2}}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) to be smooth as θ → 0 and normalized at the θ = 0 end;
to be smooth as θ → 0 and normalized at the θ = 0 end; - If |m| ≠ s, take
![${{\Xi}}_{\mathrm{norm},3}^{[{\pm}s]}{(1+\mathrm{cos}\enspace \theta )}^{-\frac{m\mp s}{2}}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) and
and ![${{\Xi}}_{\mathrm{norm},4}^{[{\pm}s]}{(1-\mathrm{cos}\enspace \theta )}^{\frac{m\mp s}{2}}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) to be smooth as θ → π and normalized at the θ = π end;
to be smooth as θ → π and normalized at the θ = π end; - If |m| = s, take
![${{\Xi}}_{\mathrm{norm},4}^{[+s]}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) ,
, ![${{\Xi}}_{\mathrm{norm},1}^{[+s]}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) ,
, ![${{\Xi}}_{\mathrm{norm},3}^{[-s]}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) and
and ![${{\Xi}}_{\mathrm{norm},2}^{[-s]}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) exactly as above; the definition of the remaining functions requires a logarithmic correction which we need not specify here.
exactly as above; the definition of the remaining functions requires a logarithmic correction which we need not specify here.
We say that ![${{\Xi}}_{m{\Lambda}}^{[{\pm}s],\enspace (\nu )}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn44.gif) is a smooth (±s)-spin-weighted function if
is a smooth (±s)-spin-weighted function if ![${a}_{4}^{[{\pm}s]}={a}_{2}^{[{\pm}s]}=0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn45.gif) when m > s, if
when m > s, if ![${a}_{3}^{[{\pm}s]}={a}_{1}^{[{\pm}s]}=0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn46.gif) when m < −s and if
when m < −s and if ![${a}_{3}^{[+s]}={a}_{2}^{[+s]}=0={a}_{4}^{[-s]}={a}_{1}^{[-s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn47.gif) when |m| ⩽ s. These conditions ensure that
when |m| ⩽ s. These conditions ensure that ![${\mathrm{e}}^{im\phi }{{\Xi}}_{m{\Lambda}}^{[{\pm}s],\enspace (\nu )}(\theta )$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn48.gif) are smooth sections of the Hopf bundle over
are smooth sections of the Hopf bundle over  which transform in a particular way (according to the value of ±s) under rotation of the orthonormal frame in the tangent space of
which transform in a particular way (according to the value of ±s) under rotation of the orthonormal frame in the tangent space of  , see for instance [2019, section 2.2.1] and [Bey+14, CL78]. The space of such solutions is somewhat small, as the following proposition indicates:
, see for instance [2019, section 2.2.1] and [Bey+14, CL78]. The space of such solutions is somewhat small, as the following proposition indicates:
Proposition 2.1 (Smooth spin-weighted spheroidal harmonics). Fix  , let
, let  , and assume
, and assume  . Consider the angular ODE (2.1) with the boundary condition that
. Consider the angular ODE (2.1) with the boundary condition that ![${\mathrm{e}}^{im\phi }{S}_{m,\boldsymbol{\lambda }}^{[{\pm}s],\enspace (\nu )}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn54.gif) is a non-trivial, normalized, smooth (±s)-spin-weighted function. There are countably many such solutions to this eigenvalue problem. Using l as an index, we write such solutions, also called (±s)-spin-weighted spheroidal harmonics with spheroidal parameter ν, as
is a non-trivial, normalized, smooth (±s)-spin-weighted function. There are countably many such solutions to this eigenvalue problem. Using l as an index, we write such solutions, also called (±s)-spin-weighted spheroidal harmonics with spheroidal parameter ν, as ![${\mathrm{e}}^{im\phi }{S}_{ml}^{[{\pm}s],\enspace (\nu )}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn55.gif) and denote the corresponding eigenvalues, which are real and independent of the sign chosen for s, by
and denote the corresponding eigenvalues, which are real and independent of the sign chosen for s, by  . The parameter l is chosen so that
. The parameter l is chosen so that  , l ⩾ max{|m|, s} and
, l ⩾ max{|m|, s} and  . The following alternative notation will also be used:
. The following alternative notation will also be used:

Proof. We refer the reader to the careful treatment of the Sturm–Liouville theory for (2.1) for general  in [HW74, Ste75], and [MS54] for the s = 0 case. □
in [HW74, Ste75], and [MS54] for the s = 0 case. □
Remark 2.2. In what follows, we often lighten the notation, replacing the spin-weighted spheroidal eigenvalues  by Λ and similarly for Ł. However, non-bold characters Λ and Ł ≡ Λ − 2mν + s are not the same: they denote real parameters which are not constrained to be the eigenvalues identified in proposition 2.3 for some (m, l).
by Λ and similarly for Ł. However, non-bold characters Λ and Ł ≡ Λ − 2mν + s are not the same: they denote real parameters which are not constrained to be the eigenvalues identified in proposition 2.3 for some (m, l).
Given that (2.1) is analytic in the coefficient ν, the spin-weighted spheroidal eigenvalue  admits an expansion in powers of ν as |ν| → ∞. Such expansions for s ≠ 0 go back to [BRW77], but they were completed and corrected by the work of the first author and collaborators:
admits an expansion in powers of ν as |ν| → ∞. Such expansions for s ≠ 0 go back to [BRW77], but they were completed and corrected by the work of the first author and collaborators:
Proposition 2.3 ([CO05, COW19]). Fix  , a number m such that
, a number m such that  , a number l such that
, a number l such that 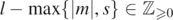 , and
, and  . Let
. Let  be as in proposition 2.1. Then, as ν → ∞, for any N > 0, we can find real constants Ak
= Ak
(s, l, m, ν), k ⩽ N, such that
be as in proposition 2.1. Then, as ν → ∞, for any N > 0, we can find real constants Ak
= Ak
(s, l, m, ν), k ⩽ N, such that
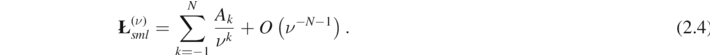
The first two coefficients are
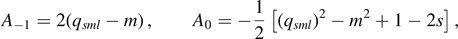
where, denoting by odd(⋅) a function on  which is one if the argument is odd and zero otherwise, we may express qsml
as
which is one if the argument is odd and zero otherwise, we may express qsml
as
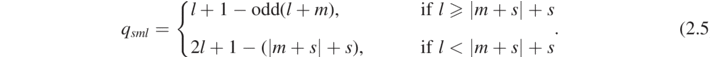
The following coefficients may be computed as follows. Let
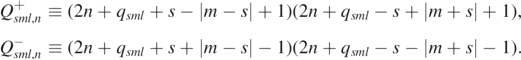
Then, for k ⩾ 1, we have
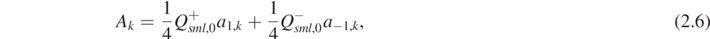
where a1,k and a−1,k are computed from the following recursive relations for n ≠ 0:
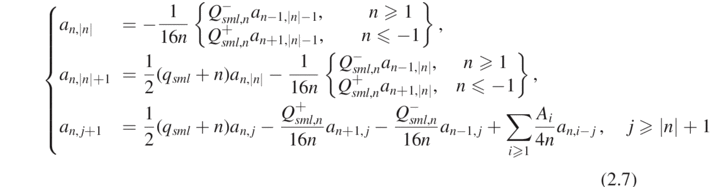
initialized by the choice a0,0 = 1 and a0,j = 0 if j ≠ 0. In particular, for k ⩽ 7, Ak are explicitly determined in [COW19, equations (3.15)–(3.21)].
Remark 2.4. Due to the symmetries of the angular ODE (2.1), the high frequency limit ν → −∞ follows from proposition 2.3 by replacing m → −m.
2.2. The angular Teukolsky–Starobinsky identities and constants
In this section, we will require the notation
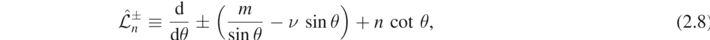
where θ ∈ (0, π),  ,
,  .
.
Proposition 2.5 (Angular TS identities). Fix  , m such that
, m such that  ,
,  and
and  . Then, if
. Then, if ![${{\Xi}}_{m{\Lambda}}^{[{\pm}s],\enspace (\nu )}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn74.gif) solve (2.1) and admit the decomposition (2.2),
solve (2.1) and admit the decomposition (2.2),
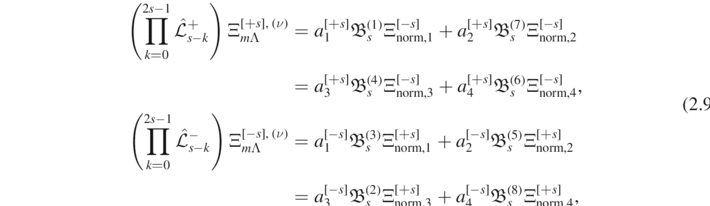
where the products on the left-hand side are replaced by the identity if s = 0 and, if s ≠ 0, have index k increasing from right to left. Here,  for i = 1, ..., 8. Indeed, if s = 0,
for i = 1, ..., 8. Indeed, if s = 0,  for i = 1, ..., 8. For s ≠ 0, we easily obtain
for i = 1, ..., 8. For s ≠ 0, we easily obtain
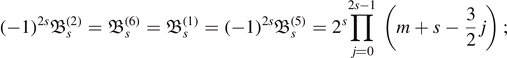
the other  can be computed explicitly in terms of the first s coefficients of the asymptotic expansions of
can be computed explicitly in terms of the first s coefficients of the asymptotic expansions of ![${{\Xi}}_{\mathrm{norm},1}^{[+s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn78.gif) ,
, ![${{\Xi}}_{\mathrm{norm},3}^{[+s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn79.gif) ,
, ![${{\Xi}}_{\mathrm{norm},2}^{[-s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn80.gif) and
and ![${{\Xi}}_{\mathrm{norm},4}^{[-s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn81.gif) , which in turn can be explicitly computed in terms of (ν, m, Λ).
, which in turn can be explicitly computed in terms of (ν, m, Λ).
Proof. The result follows from differentiating the asymptotic formulas for ![${{\Xi}}_{\mathrm{norm},i}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn82.gif) , i = 1, ..., 4. In doing so, it can be useful to note that
, i = 1, ..., 4. In doing so, it can be useful to note that
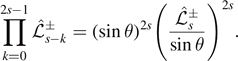
For further details, we refer the reader to an analogous proof, in the setting of the radial Teukolsky–Starobinsky identities, in [TdC20, proposition 2.14]. □
We are ready to define the angular Teukolsky–Starobinsky constants:
Definition 2.1 (Angular TS constants). Fix  , m such that
, m such that  ,
,  , and
, and  . Consider the operator
. Consider the operator
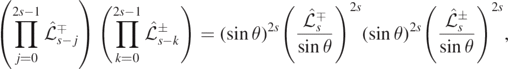
with indices j, k increasing from right to left on the product, and the latter being replaced by the identity if s = 0. If solutions of the angular ODE (2.1) with spin ±s are eigenfunctions of the above operator corresponding to the same eigenvalue, the eigenvalue is denoted by  and it is called the angular Teukolsky–Starobinsky constant.
and it is called the angular Teukolsky–Starobinsky constant.
Remark 2.6. Note that, in definition 2.1, we do not constrain Λ to be a spin-weighted spheroidal eigenvalue, as defined in proposition 2.1. In what follows, if we do take  and
and  for some l, then we write
for some l, then we write 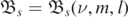 .
.
2.3. Examples of angular Teukolsky–Starobinsky constants
By direct computation, we can check that an angular Teukolsky–Starobinsky constant exists at least for low values of Teukolsky spin:
Lemma 2.7. For any  , there exists an angular Teukolsky–Starobinsky constant. Moreover, it is given by:
, there exists an angular Teukolsky–Starobinsky constant. Moreover, it is given by:
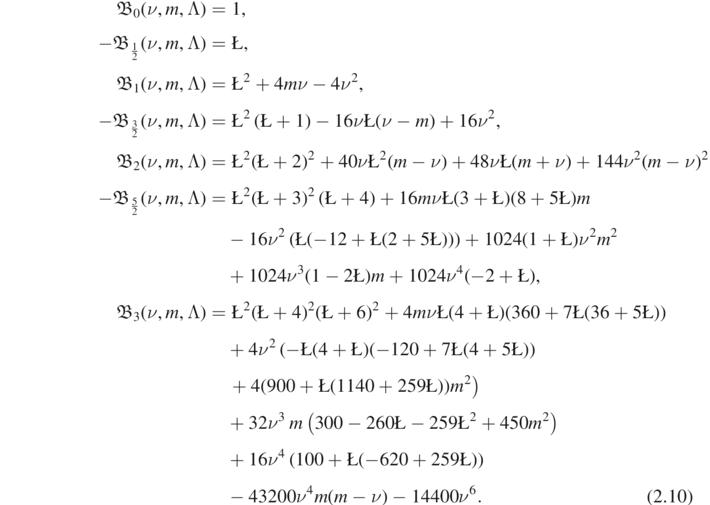
In all the above examples, if ν = 0 and  corresponds to a spin-weighted spheroidal eigenvalue with spheroidal parameter ν = 0 for some l, then
corresponds to a spin-weighted spheroidal eigenvalue with spheroidal parameter ν = 0 for some l, then  .
.
Proof. The proof of existence is similar to the case of the radial constants, in lemma 3.3 to come, so we do not present it here, though see the attached Mathematica notebook for the computations (https://stacks.iop.org/CQG/38/165016/mmedia). For the final statement, it is easy to see that, if ν = 0, only the first term of each expression in (2.10) remains. The least value is attained by  . □
. □
Remark 2.8. We expect that the angular Teukolsky–Starobinsky constant can be defined for all 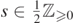 . However, no proof has been given in the literature.
. However, no proof has been given in the literature.
2.4. Properties of the angular Teukolsky–Starobinsky constants
If they exist,  are non-negative (integer s) or non-positive (half-integer s):
are non-negative (integer s) or non-positive (half-integer s):
Lemma 2.9 (Sign of angular TS constants). If an angular Teukolsky–Starobinsky constant exists for a certain (ν, m, Λ) satisfying the constraints in definition 2.1, then  .
.
Proof. To show that one has  , recall the integration by parts identity of [Cha83, section 68, lemma 4] (earlier in [TP74]): for f and h sufficiently regular functions of θ,
, recall the integration by parts identity of [Cha83, section 68, lemma 4] (earlier in [TP74]): for f and h sufficiently regular functions of θ,
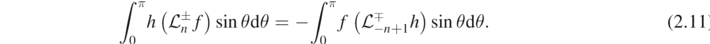
Without loss of generality, let Ξ[±s] be real solutions to (2.1) normalized to have unit L2 norm. Then, by (2.11), assuming existence of the constant,
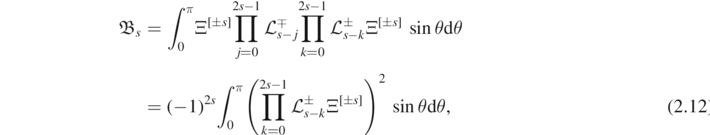
where the integral on the right-hand side is non-negative. □
Remark 2.10. We note that the non-negativity of  provides nontrivial constraints on the values that Λ can take in terms of m and ν; see also lemma 3.3 for concrete examples.
provides nontrivial constraints on the values that Λ can take in terms of m and ν; see also lemma 3.3 for concrete examples.
We may go further when we let  be a spin-weighted spheroidal eigenvalue for some l:
be a spin-weighted spheroidal eigenvalue for some l:
Lemma 2.11 (Zeros of angular TS constants). Fix  , a number m such that
, a number m such that  , a number l such that
, a number l such that  , and
, and  . If an angular Teukolsky–Starobinsky constant exists for such (ν, m, l), then
. If an angular Teukolsky–Starobinsky constant exists for such (ν, m, l), then  .
.
Proof. If the angular Teukolsky–Starobinsky constant exists, then in proposition 2.5, we must have
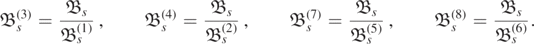
We deal first with the case |m| > s, where we follow the strategy of the proof of [TdC20, lemma 2.19], an analogous result for the radial ODE. Suppose m < −s and  ; for a spin-weighted spheroidal harmonics, we have
; for a spin-weighted spheroidal harmonics, we have ![${a}_{3}^{[{\pm}s]}={a}_{1}^{[{\pm}s]}=0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn107.gif) , but by (2.9),
, but by (2.9), ![${a}_{2}^{[-s]},{a}_{4}^{[+s]}=0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn108.gif) too, which would force
too, which would force ![${S}_{ml}^{[{\pm}s],\enspace (\nu )}\equiv 0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn109.gif) . Now suppose m > s and
. Now suppose m > s and  ; for a spin-weighted spheroidal harmonics, we have
; for a spin-weighted spheroidal harmonics, we have ![${a}_{4}^{[{\pm}s]}={a}_{2}^{[{\pm}s]}=0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn111.gif) , but by (2.9), this implies
, but by (2.9), this implies ![${a}_{1}^{[+s]},{a}_{3}^{[-s]}=0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn112.gif) too, which leads to another contradiction.
too, which leads to another contradiction.
Finally, suppose −s ⩽ m ⩽ s, so that a spin-weighted spheroidal harmonic has ![${a}_{3}^{[+s]}={a}_{2}^{[+s]}=0={a}_{4}^{[-s]}={a}_{1}^{[-s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn113.gif) . On the other hand, from the formula (2.12), we find that
. On the other hand, from the formula (2.12), we find that 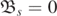 if and only if (2.9) vanish, in which case one must also have
if and only if (2.9) vanish, in which case one must also have ![${a}_{1}^{[+s]}={a}_{4}^{[+s]}=0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn115.gif) , given that
, given that  , and that
, and that ![${a}_{2}^{[-s]}={a}_{3}^{[-s]}=0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn117.gif) , given that
, given that  . We conclude
. We conclude ![${S}_{ml}^{[{\pm}s],\enspace (\nu )}\equiv 0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn119.gif) , which is a contradiction.
, which is a contradiction.
Hence,  . By lemma 2.9, the conclusion follows. □
. By lemma 2.9, the conclusion follows. □
In spite of the angular Teukolsky–Starobinsky constants' positivity, they approach arbitrarily small values, at least in the cases considered in lemma 2.7.
Lemma 2.12. Fix 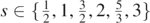 . Then, there are some pairs (l, m), where
. Then, there are some pairs (l, m), where  and
and  , for which we have, as ν → ∞,
, for which we have, as ν → ∞,
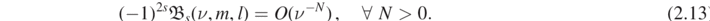
Proof. For s = 1/2, the leading order term vanishes if and only if
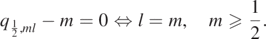
For s = 1,  , where the leading order term vanishes if and only if any one of the following holds
, where the leading order term vanishes if and only if any one of the following holds
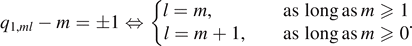
For s = 3/2, the leading order term of  vanishes if and only if any one of the following holds
vanishes if and only if any one of the following holds
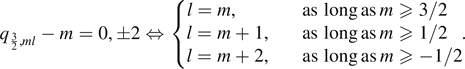
For s = 2,  , and the leading order term vanishes if and only if any one of the following holds
, and the leading order term vanishes if and only if any one of the following holds
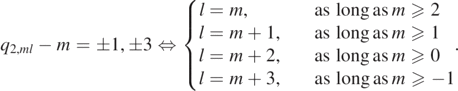
For s = 5/2, the leading order term of  vanishes if and only if any one of the following holds
vanishes if and only if any one of the following holds
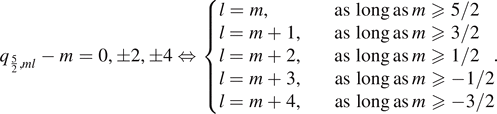
For s = 3, the leading order term of  vanishes if and only if any one of the following holds
vanishes if and only if any one of the following holds
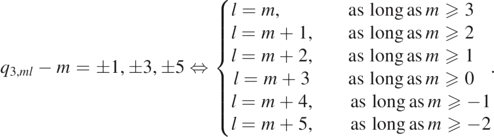
To obtain (2.13) for some N > 0, we need to compute the coefficients Ak of the asymptotic expansion (2.4) up to k = N − 1 + 2s. The formulas in [COW19, equation (3.15)–(3.21)] for Ak up to k = 7, for instance, yield that (2.13) holds for N ⩾ 7 + 1 − 2s for all (s, l, m) identified in the preceding paragraph.
In the cases
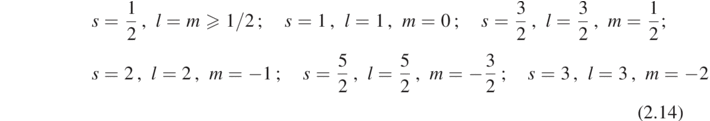
the formulas [COW19, equations (3.15)–(3.21)] in fact imply that A−1 = ±2 and that Ak = 0 for k = 0, ..., 7. By the recursive formulas (2.6) and (2.7), we must have that Ak = 0 for all k ⩾ 1. Hence, for such (s, m, l), (2.13) holds for all N > 0, as stated. □
Remark 2.13. Computer-based symbolic computations suggest that, in fact, all of the triples (s, m, l) identified in the first paragraph of the proof of lemma 2.12 verify the conclusion of the lemma, rather than just the smaller set in (2.14). This is confirmed by numerical analysis, see figure 1. However, to establish such a result would require a much more detailed analysis of the recursive relations (2.6) and (2.7) than we pursue here.
Figure 1. Logarithmic plot of  as a function of ν for m = 1 (blue) and m = 0 (red), obtained by numerically computing
as a function of ν for m = 1 (blue) and m = 0 (red), obtained by numerically computing  via [BHP]. The linear relation in the logarithmic plot suggests exponential decay of
via [BHP]. The linear relation in the logarithmic plot suggests exponential decay of  as ν → ∞ for these modes.
as ν → ∞ for these modes.
Download figure:
Standard image High-resolution imageIn the case s = 1, numerical computations suggest that the superpolynomial decay with ν identified in lemma 2.12 for some (l, m) is actually exponential, see figure 1.
3. The radial Teukolsky–Starobinsky constants
In this section, we introduce the radial ODE corresponding to the Teukolsky equation (2.1) and define the radial Teukolsky–Starobinsky constants. The last subsection contains the proof of facts 1–6.
3.1. The radial ODE
We consider the radial ODEs
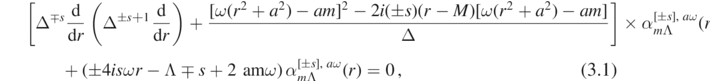
where M > 0, |a| ⩽ M, r ∈ (r+, ∞), 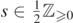 , m such that
, m such that  ,
,  , and
, and  . An asymptotic analysis of (3.1) shows that a solution to (3.1) admits a unique set of complex numbers
. An asymptotic analysis of (3.1) shows that a solution to (3.1) admits a unique set of complex numbers ![${a}_{{\mathcal{H}}^{+}}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn136.gif) ,
, ![${a}_{{\mathcal{H}}^{-}}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn137.gif) ,
, ![${a}_{{\mathcal{I}}^{+}}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn138.gif) and
and ![${a}_{{\mathcal{I}}^{-}}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn139.gif) such that
such that
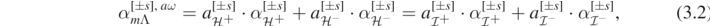
where ![${\alpha }_{{\mathcal{I}}^{+}}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn140.gif) and
and ![${\alpha }_{{\mathcal{I}}^{-}}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn141.gif) are solutions of (3.1) with outgoing and ingoing, respectively, boundary conditions as r → ∞ which are normalized at r = ∞, and where
are solutions of (3.1) with outgoing and ingoing, respectively, boundary conditions as r → ∞ which are normalized at r = ∞, and where ![${\alpha }_{{\mathcal{H}}^{+}}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn142.gif) and
and ![${\alpha }_{{\mathcal{H}}^{-}}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn143.gif) are solutions of (3.1) with ingoing and outgoing, respectively, boundary conditions as r → r+ which are normalized at r = r+. Concretely,
are solutions of (3.1) with ingoing and outgoing, respectively, boundary conditions as r → r+ which are normalized at r = r+. Concretely,
-
![${\alpha }_{{\mathcal{I}}^{+}}^{[{\pm}s]}{\text{e}}^{-\text{i}\omega r}{r}^{-2iM\omega +1{\pm}2s}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) and
and ![${\alpha }_{{\mathcal{I}}^{-}}^{[{\pm}s]}{\text{e}}^{\text{i}\omega r}{r}^{2iM\omega +1}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) are smooth functions of 1/r as r → ∞ which are normalized at r = ∞;
are smooth functions of 1/r as r → ∞ which are normalized at r = ∞; - If |a| < M,
![${\alpha }_{{\mathcal{H}}^{+}}^{[{\pm}s]}{(r-{r}_{+})}^{i\frac{2M{r}_{+}}{{r}_{+}-{r}_{-}}(\omega -m{\omega }_{+}){\pm}s}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) and
and ![${\alpha }_{{\mathcal{H}}^{-}}^{[{\pm}s]}{(r-{r}_{+})}^{-i\frac{2M{r}_{+}}{{r}_{+}-{r}_{-}}(\omega -m{\omega }_{+})}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) are smooth as r → r+ and normalized at r = r+;
are smooth as r → r+ and normalized at r = r+; - If |a| = M,
![${\alpha }_{{\mathcal{H}}^{+}}^{[{\pm}s]}{(r-M)}^{2iM\omega {\pm}2s}{\text{e}}^{-\text{i}\frac{2{M}^{2}}{r-M}(\omega -m{\omega }_{+})}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) and
and ![${\alpha }_{{\mathcal{H}}^{-}}^{[{\pm}s]}{(r-M)}^{-2iM\omega }{\text{e}}^{\text{i}\frac{2{M}^{2}}{r-M}(\omega -m{\omega }_{+})}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) are smooth in 1/(r − M) as r → M and normalized at r = M.
are smooth in 1/(r − M) as r → M and normalized at r = M.
3.2. The radial Teukolsky–Starobinsky identities and constants
In this section, we will require the notation
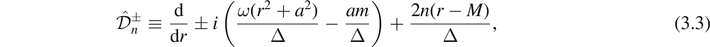
where M > 0, |a| ⩽ M, r ∈ (r+, ∞),  and
and  .
.
We quote from [TdC20, proposition 2.14] the following:
Proposition 3.1 (Radial TS identities). Fix M > 0, |a| ⩽ M and  , m such that
, m such that  ,
,  . Then, if α[±s] solve (3.1) and admit the decomposition (3.2),
. Then, if α[±s] solve (3.1) and admit the decomposition (3.2),
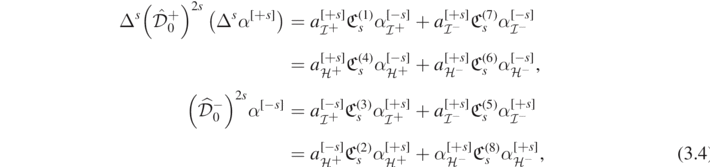
where the products on the left-hand side are replaced by the identity if s = 0 and, if s ≠ 0, have indices increasing from left to right. Here,  for i = 1, ..., 8. Indeed, if s = 0,
for i = 1, ..., 8. Indeed, if s = 0,  for i = 1, ..., 8. For s ≠ 0, we easily obtain
for i = 1, ..., 8. For s ≠ 0, we easily obtain
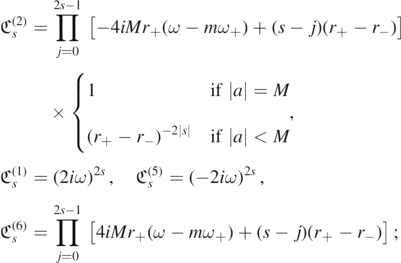
the remaining  can be computed explicitly in terms of the first s coefficients in the asymptotic expansions of
can be computed explicitly in terms of the first s coefficients in the asymptotic expansions of ![${\alpha }_{{\mathcal{I}}^{\mp }}^{[{\pm}s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn158.gif) and
and ![${\alpha }_{{\mathcal{H}}^{\mp }}^{[\mp s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn159.gif) , which in turn can be explicitly computed in terms of (a, M) and (ω, m, Λ).
, which in turn can be explicitly computed in terms of (a, M) and (ω, m, Λ).
We are now ready to define the radial Teukolsky–Starobinsky constants:
Definition 3.1 (Radial TS constants). Fix  , m such that
, m such that  ,
,  , M > 0, |a| ⩽ M and
, M > 0, |a| ⩽ M and 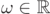 . Consider the operator
. Consider the operator
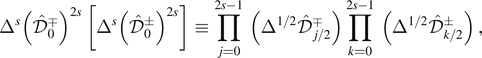
with indices j, k increasing from right to left on the product, and the latter being replaced by the identity if s = 0. If ![${{\Delta}}^{\frac{s}{2}(1{\pm}1)}{\alpha }_{m{\Lambda}}^{[{\pm}s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn164.gif) , where
, where ![${\alpha }_{m{\Lambda}}^{[{\pm}s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn165.gif) solve the radial ODE (3.1) of spin ±s, are eigenfunctions of the above operator corresponding to the same eigenvalue, the eigenvalue is denoted by
solve the radial ODE (3.1) of spin ±s, are eigenfunctions of the above operator corresponding to the same eigenvalue, the eigenvalue is denoted by 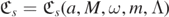 and it is called the radial Teukolsky–Starobinsky constant.
and it is called the radial Teukolsky–Starobinsky constant.
Remark 3.2. Note that, in definition 3.1 and lemma 3.3 below, we once again do not constrain Λ to be an eigenvalue of the angular ODE (2.1) with spheroidal parameter ν = aω. In what follows, if we do take  and
and  for some l, then we write
for some l, then we write  .
.
3.3. Examples of radial Teukolsky–Starobinsky constants
By direct computation, we can check that a radial Teukolsky–Starobinsky constant exists at least for low values of Teukolsky spin:
Lemma 3.3. For any  , there exists a radial Teukolsky–Starobinsky constant. Furthermore, it can be computed explicitly, for instance:
, there exists a radial Teukolsky–Starobinsky constant. Furthermore, it can be computed explicitly, for instance:
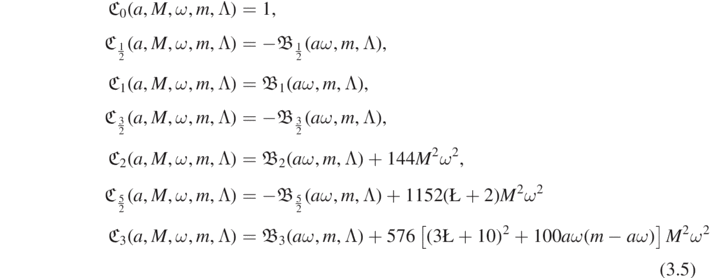
where  may be read off from (2.10). In the above, if aω = 0, and
may be read off from (2.10). In the above, if aω = 0, and  corresponds to a spin-weighted spheroidal eigenvalue with spheroidal parameter ν = aω for some l, then
corresponds to a spin-weighted spheroidal eigenvalue with spheroidal parameter ν = aω for some l, then  .
.
Proof. There are several ways of showing existence of the radial Teukolsky–Starobinsky constants. One option is to use definition 3.1, i.e. to apply the operators in the products above to radial functions one by one and using the radial ODE (3.1) to trade second order derivatives of those functions by first and zeroth order terms (see for instance [Cha83, sections 70 and 81] for s = 1, 2). With the aid of a standard laptop, this naive approach allows one to verify existence of the constant beyond the upper bound s = 3 of the statement; indeed, the reader can check this with the Mathematica notebook attached.
Alternatively, in light of the radial Teukolsky–Starobinsky identities of proposition 3.1, if the radial Teukolsky–Starobinsky constant exists, we must have
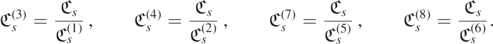
Hence, one may compute  from one of
from one of  . As the latter are computable from the recursive formulas which yield the first s coefficients of certain asymptotic series for solutions of (3.1), this method is less computationally demanding than the previous one and has been suggested earlier in [Fiz09] (see also the companion paper [Fiz10]).
. As the latter are computable from the recursive formulas which yield the first s coefficients of certain asymptotic series for solutions of (3.1), this method is less computationally demanding than the previous one and has been suggested earlier in [Fiz09] (see also the companion paper [Fiz10]).
To conclude, we note that, for ω = 0, a glance at the formulas gives 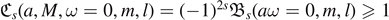 , from lemma 2.7. □
, from lemma 2.7. □
We remark that the formulas for  given here in lemma 3.3 match those obtained before in [Cha90] and [KMW89], although in the latter papers they appear under the somewhat misleading notation |Cs
|2.
given here in lemma 3.3 match those obtained before in [Cha90] and [KMW89], although in the latter papers they appear under the somewhat misleading notation |Cs
|2.
3.4. Properties of the radial Teukolsky–Starobinsky constants
3.4.1. Why the complex-conjugation argument for non-negativity is false
This section examines the argument in [KMW89, KMW92], subsequently picked up by other authors, purportedly showing non-negativity of the Teukolsky–Starobinky constant for general  . These authors claim that non-negativity of
. These authors claim that non-negativity of  may be viewed as a consequence of
may be viewed as a consequence of ![${{\Delta}}^{\frac{s}{2}(1{\pm}1)}{\alpha }_{m{\Lambda}}^{[{\pm}s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn180.gif) satisfying complex conjugate equations and the radial Teukolsky–Starobinsky identities being generated by complex conjugate operators somehow imply non-negativity of the Teukolsky–Starobinky constant.
satisfying complex conjugate equations and the radial Teukolsky–Starobinsky identities being generated by complex conjugate operators somehow imply non-negativity of the Teukolsky–Starobinky constant.
No justification is given for why the authors believe this implication should be true. One potential argument would be to try draw an analogy with the angular setting, where the relation between 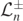 and
and  in the ODE (2.1) and in the identities (2.11) leads to the conclusion of lemma 2.9. However, (2.11) establishes an adjointness relation between the angular operators
in the ODE (2.1) and in the identities (2.11) leads to the conclusion of lemma 2.9. However, (2.11) establishes an adjointness relation between the angular operators  and
and  in the space of (real-valued) smooth spin-weighted functions. In contrast, the relation between
in the space of (real-valued) smooth spin-weighted functions. In contrast, the relation between 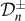 and
and  is one of complex-conjugation.
is one of complex-conjugation.
It is a fact of life that, in a space of complex-valued functions, as solutions to the radial ODE (3.1) are bound to lie in, the complex conjugate and the adjoint of an operator are not necessarily the same 5 . Indeed, for some weight w(r): (r+, ∞) → [0, ∞), and for f and h sufficiently regular complex-valued functions of r that the boundary terms in the following vanish, we have
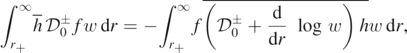
so the adjoint of  will be
will be  . This makes the notation used in classical references such as [Cha83] (see also the more recent [Teu15]), where
. This makes the notation used in classical references such as [Cha83] (see also the more recent [Teu15]), where  is written as
is written as  thus suggesting an adjointness relation, rather unfortunate.
thus suggesting an adjointness relation, rather unfortunate.
The upshot is that there is, in fact, no hope of establishing an analogue of lemma 2.9 by a similar method to the one used there. Indeed, let us try to run the argument backward to see where it goes wrong. Copying the proof of lemma 2.9, we would like to show that there is some weight w(r): (r+, ∞) → [0, ∞) such that for any α[±s] is chosen with unit  norm,
norm,
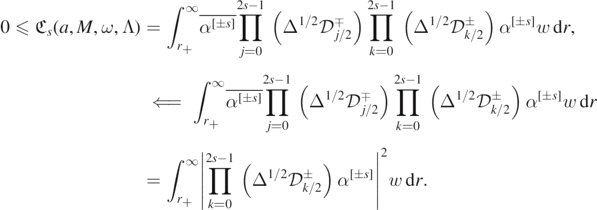
The latter equality would hold only if we could prove
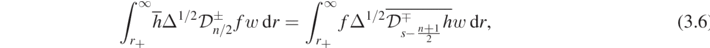
for suitably regular f and h; but there is no choice of w ⩾ 0 which would make (3.6) hold. It follows that, if  is indeed non-negative for some s, a different proof strategy should be sought.
is indeed non-negative for some s, a different proof strategy should be sought.
3.4.2. Saving and improving non-negativity for s ⩽ 2
As we have noted that the angular Teukolsky–Starobinsky constants have a definite sign (lemma 2.9), it is natural to try to compare the explicit expressions for such constants with those of the radial ones, i.e. lemmas 2.7 and 3.3 in the case where the spheroidal parameter in the angular ODE is ν = aω. As is clear from our (3.5) (see also [KMW92]),
Lemma 3.4. Fix  , m such that
, m such that  ,
,  , M > 0, |a| ⩽ M and
, M > 0, |a| ⩽ M and  . Then, there is a real
. Then, there is a real  such that
such that
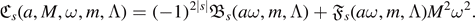
Indeed, one has  for
for  and
and
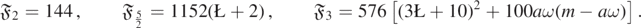
Lemma 3.4 indeed yields, in the restricted case s ⩽ 2, non-negativity of the Teukolsky–Starobinsky constant, as correctly noted in Teukolsky's original paper on the identities [TP74]. Indeed, by lemma 2.11, it even yields positivity:
Lemma 3.5 (Positivity of radial TS constant for  ). Fix
). Fix  , m such that
, m such that  ,
,  , M > 0, |a| ⩽ M and
, M > 0, |a| ⩽ M and  . Then,
. Then, 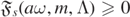 hence
hence  .
.
Furthermore, if 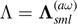 is a spin-weighted spheroidal eigenvalue for some
is a spin-weighted spheroidal eigenvalue for some  , then
, then  . In particular, there are no real algebraically special frequencies (ω, m, l) for any Kerr parameters (a, M).
. In particular, there are no real algebraically special frequencies (ω, m, l) for any Kerr parameters (a, M).
Remark 3.6. For s > 2,  depends nontrivially on Λ. Without more constraints on Λ in terms of the black hole parameters (a, M) and frequencies ω and m, one cannot hope to investigate the validity of lemma 3.5 for s > 2.
depends nontrivially on Λ. Without more constraints on Λ in terms of the black hole parameters (a, M) and frequencies ω and m, one cannot hope to investigate the validity of lemma 3.5 for s > 2.
In fact, for s ⩽ 2, we can use lemma 3.4 and the last statement in lemma 3.3 to obtain a more precise statement when Λ = Λ is a spin-weighted spheroidal eigenvalue:
Lemma 3.7 (Lower bound for radial TS constant for  ). Fix s = 2,
). Fix s = 2,  ,
, 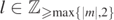 , M > 0, |a| ⩽ M and
, M > 0, |a| ⩽ M and  . The radial Teukolsky–Starobinsky constant
. The radial Teukolsky–Starobinsky constant  admits a positive lower bound, i.e. there is a b > 0 such that
admits a positive lower bound, i.e. there is a b > 0 such that
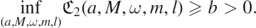
Numerically, using [BHP], we find b ≈ 150 is enough.
Proof. First note that, once a and (s, m, l) are fixed, ![${\mathbf{\unicode{321}{}}}_{ml}^{[s],\enspace (a\omega )}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn216.gif) is continuous in ω (see, for instance, [MS54] or [HW74]), hence
is continuous in ω (see, for instance, [MS54] or [HW74]), hence  is also continuous in ω.
is also continuous in ω.
At ω = 0, 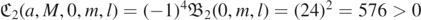 . Hence, by continuity in ω, there is a δ > 0 such that
. Hence, by continuity in ω, there is a δ > 0 such that  for |Mω| ⩽ δ. On the other hand, if |Mω| > δ, by the non-negativity of
for |Mω| ⩽ δ. On the other hand, if |Mω| > δ, by the non-negativity of  (lemma 2.9)
(lemma 2.9)  . This concludes the proof. □
. This concludes the proof. □
However, lemma 3.7 does not extend to s < 2. Though always positive, it follows from lemma 2.12 that the radial Teukolsky–Starobinksy constants for those spins asymptotically approach 0 as ω → ∞ if a ≠ 0 is fixed and suitable (l, m) are chosen:
Lemma 3.8. Fix M > 0, 0 < |a| ⩽ M and  . Then, there are some pairs (l, m), where
. Then, there are some pairs (l, m), where  and
and 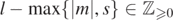 , for which we have, as ω → ∞,
, for which we have, as ω → ∞,
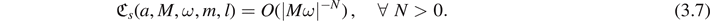
3.4.3. A myth debunked: negative values for 
Not only is the pervasive argument outlined in section 3.4.1 or in [Cha90, KMW89, KMW92] purportedly asserting non-negativity of  for all s incorrect, but its conclusion is also false. Lemma 2.12 is our starting point to debunk this myth; we now consider the contribution of
for all s incorrect, but its conclusion is also false. Lemma 2.12 is our starting point to debunk this myth; we now consider the contribution of  :
:
Lemma 3.9 (Negativity for  ). Fix M > 0, 0 < |a| ⩽ M and
). Fix M > 0, 0 < |a| ⩽ M and  . Then, there are some pairs (l, m), where
. Then, there are some pairs (l, m), where 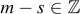 and
and 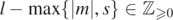 , for which there is an A > 0 such that, as ω → ∞,
, for which there is an A > 0 such that, as ω → ∞,
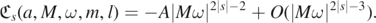
Proof. We use proposition 2.3 once more, appealing to the proof of lemma 2.12. Indeed, if s = 5/2,  , and we note that
, and we note that
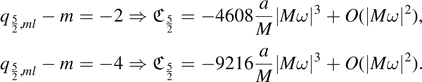
For s = 3, ![${\mathfrak{F}}_{3}=576\left[36{({q}_{3,ml}-m)}^{2}-100\right]{(a\omega )}^{2}+O(\vert M\omega \vert )$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn233.gif) , and we note that
, and we note that
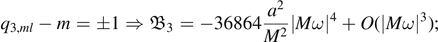
see also figure 2. As shown in the proof of lemma 2.12, the above conditions may be realized for pairs (l, m) satisfying the constraints of the present lemma. □
Figure 2. Plot of 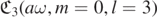 as a function of ν = aω for a = 0.8M, and obtained through numerical computation of the
as a function of ν = aω for a = 0.8M, and obtained through numerical computation of the ![${{\Lambda}}_{ml}^{[s],(\nu )}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn235.gif) .
.
Download figure:
Standard image High-resolution imageWhile for  may take negative values for some (ω, m, l), they can also take positive values, for instance if ω = 0 (see lemma 3.3). Appealing once more to continuity in ω (see proof of lemma 3.7), we thus conclude
may take negative values for some (ω, m, l), they can also take positive values, for instance if ω = 0 (see lemma 3.3). Appealing once more to continuity in ω (see proof of lemma 3.7), we thus conclude
Lemma 3.10. Fix M > 0, 0 < |a| ⩽ M and 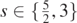 . There exist real algebraically special frequencies, i.e. real (ω, m, l), such that
. There exist real algebraically special frequencies, i.e. real (ω, m, l), such that 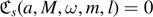 .
.
4. On non-superradiant amplification for s > 2 fields
In this section, we consider the implications of the properties of the radial Teukolsky–Starobinsky constants on the energy associated to the Teukolsky radial ODE (3.1).
4.1. Energy for the Teukolsky equation
We begin by discussing a notion of energy compatible with (1.1) for any  with the stationary Kerr Killing field fails to produce a conservation law unless s = 0. However, as
with the stationary Kerr Killing field fails to produce a conservation law unless s = 0. However, as ![${({r}^{2}+{a}^{2})}^{\frac{1}{2}}{{\Delta}}^{{\pm}\frac{s}{2}}{\alpha }_{m{\Lambda}}^{[{\pm}s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn240.gif) satisfy complex conjugate ODEs, see (3.1), the Wronskian
satisfy complex conjugate ODEs, see (3.1), the Wronskian
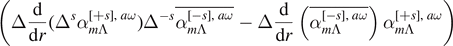
is independent of r, and hence is conserved. From the Teukolsky–Starobinsky identities, given a solution ![${\alpha }_{m{\Lambda}}^{[+s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn241.gif) to (3.1) with spin +s, we may generate a
to (3.1) with spin +s, we may generate a ![${\alpha }_{m{\Lambda}}^{[-s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn242.gif) which solves (3.1) with spin −s, and vice-versa, to plug into this conservation law. Multiplying through by ω makes each of the terms of the conservation law into an energy, see already remark 4.2 and [SRTdC20, section 5.3]. Thus, we obtain:
which solves (3.1) with spin −s, and vice-versa, to plug into this conservation law. Multiplying through by ω makes each of the terms of the conservation law into an energy, see already remark 4.2 and [SRTdC20, section 5.3]. Thus, we obtain:
Lemma 4.1 (TS energy identity). Fix M > 0, |a| ⩽ M,  ,
,  and
and  . Suppose there exists a radial Teukolsky–Starobinsky constant
. Suppose there exists a radial Teukolsky–Starobinsky constant 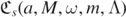 as given in definition 3.1.
as given in definition 3.1.
Let ![${\alpha }_{m{\Lambda}}^{[{\pm}s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn247.gif) be a solution to (3.1), and let its decomposition (3.2) be characterized by
be a solution to (3.1), and let its decomposition (3.2) be characterized by
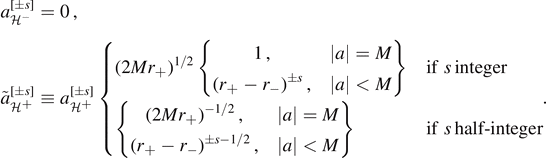
Then, it satisfies the energy identity
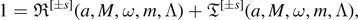
where ![${\mathfrak{R}}^{[{\pm}s]}(a,M,\omega ,m,{\Lambda})$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn248.gif) and
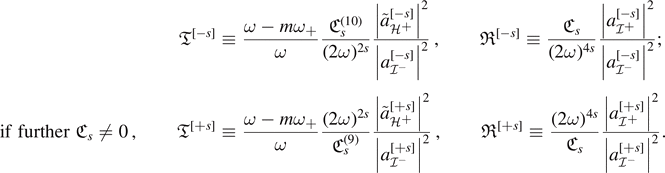
and ![${\mathfrak{T}}^{[{\pm}s]}(a,M,\omega ,m,{\Lambda})$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn249.gif) are called the reflection and transmission coefficients, respectively, and are given as follows. If s is an integer,
are called the reflection and transmission coefficients, respectively, and are given as follows. If s is an integer,
If s is half-integer,

Here, we take  when s = 0,
when s = 0,  and
and ![${\mathfrak{C}}_{s}^{(10)}={\left[4M{r}_{+}(\omega -m{\omega }_{+})\right]}^{2}+{({r}_{+}-{r}_{-})}^{2}/4$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn252.gif) if s = ±1/2, and otherwise, using the shorthand notation
if s = ±1/2, and otherwise, using the shorthand notation ![${\mathfrak{C}}_{s,j}{:=}{\left[4M{r}_{+}(\omega -m{\omega }_{+})\right]}^{2}+{(s-j)}^{2}{({r}_{+}-{r}_{-})}^{2}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn253.gif) ,
,
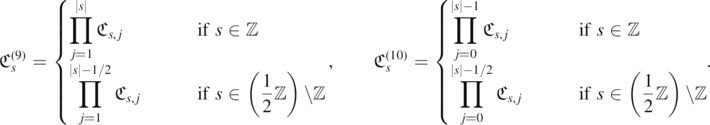
Proof. The proof is sketched in the paragraph above, but we encourage the reader to see [And+17, section 2.2] and [SRTdC20] for details. □
Remark 4.2. The notion of energy put forth in lemma 4.1 is consistent with previous literature: it matches that introduced in [TP74] for s = 1, 2, [Unr73] for s = 1/2 and [TS90] for s = 3/2.
If ![${\mathfrak{T}}^{[{\pm}s]}{< }0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn254.gif) and
and ![${\mathfrak{R}}^{[{\pm}s]}{ >}0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn255.gif) , there is amplication in the energy reflected to future null infinity. As
, there is amplication in the energy reflected to future null infinity. As
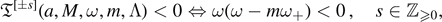
we refer to this as superradiant amplification. On the other hand, if ![${\mathfrak{T}}^{[{\pm}s]}{ >}0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn256.gif) and
and ![${\mathfrak{R}}^{[{\pm}s]}{< }0$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn257.gif) , there is amplication in the energy transmitted into the future event horizon. As
, there is amplication in the energy transmitted into the future event horizon. As
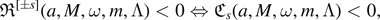
we refer to this as non-superradiant amplification. By lemmas 3.5 and 3.9, if we constrain Λ to be a spin-weighted spheroidal eigenvalue,  for some l, we see that non-superradiant amplification occurs for some (ω, m, l) when s > 2, see figure 3.
for some l, we see that non-superradiant amplification occurs for some (ω, m, l) when s > 2, see figure 3.
Figure 3. Plot showing the behavior of ![${\mathfrak{T}}^{[-3]}(a,M,\omega ,m,l)$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn259.gif) and
and ![${\mathfrak{R}}^{[-3]}(a,M,\omega ,m,l)$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn260.gif) for a = 8M/10, m = 1 and l = 3, as functions of Mω. Plot (a) captures superradiant amplification, with the solid red line corresponding to
for a = 8M/10, m = 1 and l = 3, as functions of Mω. Plot (a) captures superradiant amplification, with the solid red line corresponding to ![${\mathfrak{T}}^{[-3]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn261.gif) , and the dashed blue line denoting
, and the dashed blue line denoting ![${\mathfrak{R}}^{[-3]}-1$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn262.gif) . Plot (b) captures non-superradiant amplification, with the solid blue line corresponding to
. Plot (b) captures non-superradiant amplification, with the solid blue line corresponding to ![${\mathfrak{R}}^{[-3]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn263.gif) , and the dashed red line denoting
, and the dashed red line denoting ![${\mathfrak{T}}^{[-3]}-1$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn264.gif) .
.
Download figure:
Standard image High-resolution image4.2. Energy for the system of linearized Maxwell or Einstein equations
In the previous section, we considered a scattering problem under the evolution equation (1.1) alone. Consequently, the notion of energy in lemma 4.1 involves a single spin sign. If, for s = 1, 2, one considers a scattering problem under the entire system of linearized Maxwell or Einstein equations, respectively, then the natural notion of energy involves both spin signs. We extend this reasoning to other spins:
Lemma 4.3 (TS energy identity under TS correspondence). Fix M > 0, |a| ⩽ M, 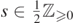 ,
, 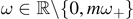 and
and  . Suppose there exists a radial Teukolsky–Starobinsky constant
. Suppose there exists a radial Teukolsky–Starobinsky constant  as given in definition 3.1. Further assume that the frequencies are such that
as given in definition 3.1. Further assume that the frequencies are such that  .
.
Let ![${\alpha }_{m{\Lambda}}^{[{\pm}s],\enspace a\omega }$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn270.gif) be solutions to (3.1) which are related to each other by the radial Teukolsky–Starobinsky identities of proposition 3.1. Assume their decompositions (3.2) to be characterized by
be solutions to (3.1) which are related to each other by the radial Teukolsky–Starobinsky identities of proposition 3.1. Assume their decompositions (3.2) to be characterized by
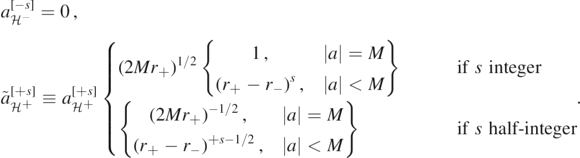
Then, one has the energy identity
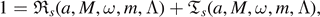
where the reflection and transmission coefficients,  and
and  respectively, are given as follows:
respectively, are given as follows:
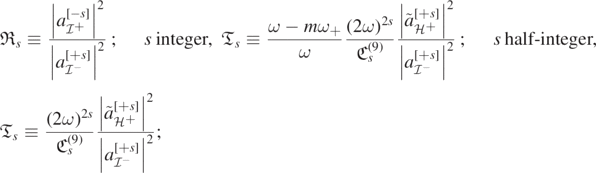
where we take  to be the same as in lemma 4.1.
to be the same as in lemma 4.1.
Remark 4.4. The notion of energy considered in lemma 4.3 matches that of the recent [Mas20, section 1.3.4] on scattering under the linearized Einstein vacuum equations around a = 0 in Kerr. Indeed, when considering this system, the two gauge-invariant curvature quantities satisfy the Teukolsky master equation (1.1) with spin ±2 together with a physical space version of the radial Teukolsky–Starobinsky identities of proposition 3.1, see [Mas20, equations (1.5) and (1.6)]. A similar situation arises when one considers the linearized Maxwell equations, as one may readily deduce from [Pas19, equations (3.11)–(3.16)].
We note that it is only under the notion of energy in lemma 4.3 that amplification does not occur for non-superradiant frequencies for fields of any spin.
Acknowledgments
MC acknowledges partial financial support by CNPq (Brazil), process number 310200/2017-2. RTdC acknowledges support from EPSRC (United Kingdom), Grant EP/L016516/1, and thanks Simon Becker for helpful suggestions concerning the analysis of the angular ODE in this paper and Yakov Shlapentokh-Rothman for numerous discussions. This work makes use of the Black Hole Perturbation Toolkit for the Numerics aides indicated along the text.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Footnotes
- 4
Earlier work on these limits [BRW77] suffered from flaws which were corrected in the references given.
- 5
This is true already for matrices: the adjoint of a complex-valued matrix is obtained by complex-conjugation followed by transposition. Performing only one of these operations on the matrix will not, in general, produce its adjoint.

![${{\Xi}}_{\mathrm{norm},1}^{[{\pm}s]}{(1-\mathrm{cos}\enspace \theta )}^{-\frac{m{\pm}s}{2}}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn36.gif)
![${{\Xi}}_{\mathrm{norm},2}^{[{\pm}s]}{(1-\mathrm{cos}\enspace \theta )}^{\frac{m{\pm}s}{2}}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn37.gif)
![${{\Xi}}_{\mathrm{norm},3}^{[{\pm}s]}{(1+\mathrm{cos}\enspace \theta )}^{-\frac{m\mp s}{2}}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn38.gif)
![${{\Xi}}_{\mathrm{norm},4}^{[{\pm}s]}{(1-\mathrm{cos}\enspace \theta )}^{\frac{m\mp s}{2}}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn39.gif)
![${{\Xi}}_{\mathrm{norm},4}^{[+s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn40.gif)
![${{\Xi}}_{\mathrm{norm},1}^{[+s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn41.gif)
![${{\Xi}}_{\mathrm{norm},3}^{[-s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn42.gif)
![${{\Xi}}_{\mathrm{norm},2}^{[-s]}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn43.gif)

![${\alpha }_{{\mathcal{I}}^{+}}^{[{\pm}s]}{\text{e}}^{-\text{i}\omega r}{r}^{-2iM\omega +1{\pm}2s}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn144.gif)
![${\alpha }_{{\mathcal{I}}^{-}}^{[{\pm}s]}{\text{e}}^{\text{i}\omega r}{r}^{2iM\omega +1}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn145.gif)
![${\alpha }_{{\mathcal{H}}^{+}}^{[{\pm}s]}{(r-{r}_{+})}^{i\frac{2M{r}_{+}}{{r}_{+}-{r}_{-}}(\omega -m{\omega }_{+}){\pm}s}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn146.gif)
![${\alpha }_{{\mathcal{H}}^{-}}^{[{\pm}s]}{(r-{r}_{+})}^{-i\frac{2M{r}_{+}}{{r}_{+}-{r}_{-}}(\omega -m{\omega }_{+})}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn147.gif)
![${\alpha }_{{\mathcal{H}}^{+}}^{[{\pm}s]}{(r-M)}^{2iM\omega {\pm}2s}{\text{e}}^{-\text{i}\frac{2{M}^{2}}{r-M}(\omega -m{\omega }_{+})}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn148.gif)
![${\alpha }_{{\mathcal{H}}^{-}}^{[{\pm}s]}{(r-M)}^{-2iM\omega }{\text{e}}^{\text{i}\frac{2{M}^{2}}{r-M}(\omega -m{\omega }_{+})}$](https://content.cld.iop.org/journals/0264-9381/38/16/165016/revision4/cqgac11a8ieqn149.gif)


