Abstract
Inspired by Shulman's question 'where do teachers' explanations come from?', this study explores two issues: the extent to which student teachers (STs) of physics can detect consequential gaps in a given explanation (RQ1), and the extent to which they will sacrifice simplicity for completeness when designing an explanation for a given audience (RQ2). The chosen topic was the rainbow; focussing on the case of the primary rainbow, a very limited explanation based on the interaction of a raindrop with a ray of sunlight was discussed with 33 STs, using two successive questionnaires. The results suggest that the STs were often largely unaware that the explanation was deeply incomplete (RQ1). This was accompanied by the lack of a 'functional approach' questioning how a changed variable might affect the phenomenon in question, even where this involves accepting a patently incoherent explanation. In relation to RQ2, the results suggest that the simplicity-coherence issue often remained unresolved for STs even after a critique of the explanation's incompleteness. The final part of the paper centres on teacher preparation and the need to more explicitly address the simplicity-coherence dilemma in order to help STs to develop their critical awareness and responsible choice of explanations.
Export citation and abstract BibTeX RIS
1. Introduction
In helping students to develop an understanding of a given body of knowledge, teaching in the first place involves choosing what is to be taught, and which explanations to adopt in pursuit of teaching goals. The explanations used in teaching necessarily differ to some extent from the consensus views expressed by experts in that field; as Ogborn et al [1] asserted, 'scientific knowledge, as stabilized in the scientific community, must be radically transformed before its form is adapted to a given teaching act' (p 59). This transformation, known in the French tradition as didactic transposition [2], involves deliberate decisions on the part of teachers or policy makers. The question of how these decisions are made was originally raised by Shulman [3] in the context of pedagogical content knowledge: 'where do teachers' explanations come from? How do teachers decide what to teach, how to represent it?' (p 8).
It seems reasonable that a thorough analysis of the proposed content and a critical analysis of typical explanations should precede any such decision. To articulate the strengths and weaknesses of an explanatory text, it has recently been proposed [4–6] to use grids based on criteria such as internal consistency, completeness, violation of a law, narrative structure and confusion between the realistic and symbolic status of an image. The present study focuses on the criterion of completeness and two other criteria that may seem a priori incompatible (simplicity) or congruent (coherence). Indeed, among the multiple criteria that might be used to characterise an explanatory text, completeness, simplicity and coherence seem especially relevant in determining student teachers (STs)' teaching choices. This is confirmed by previous research with the same population [4–7], which shows that this population values completeness and coherence, while seeking also simplicity for the sake of adaptation to context. Focussing on these three criteria, the study investigates the extent to which STs detect consequential gaps in a given explanation, and how this influences their decision-making process. The chosen topic (the rainbow) was confined to the case of the primary rainbow to avoid dispersion of STs' concerns while addressing the main questions raised by this phenomenon.
Following a brief discussion of previous research, rationale and research questions (section 2), the paper includes a content analysis of the primary rainbow (section 3) and a description of the experimental design (section 4). The results are presented and discussed in sections 5 and 6, and the paper concludes with some remarks regarding teacher preparation (section 7).
2. Previous research, rationale, and research questions
How STs make decisions about explanations that they will use in teaching a given audience in a given context can be understood as a two-step process: a critical analysis of explanations commonly applied to the topic in question—possibly supported by the use of analytical grids [4]—and a decision based on the perceived benefits and risks of each candidate explanation, often involving some form of compromise [5, 6]. With regard to the first step, a series of surveys across several topic areas [7] confirmed that STs find it difficult to make critical comments on physics explanations, however incoherent or incomplete. It is important to note that defining incompleteness and incoherence is far from straightforward in this context; for instance, an explanation is never complete because the list of prerequisites would be infinite. As Ogborn [3] put it, 'explanations are like the tip of an iceberg, with a large amount of supporting knowledge lurking below the surface' (p 65). With regard to incompleteness, previous investigations [4–8] and the present study focussed on cases of a missing logical link within a line of reasoning—in other words, logical incompleteness. Additionally, there is no obvious limit defining the end point of an explanation; in the present case, for instance, the discussion was confined to the primary rainbow. Finally, in the present context, incoherence refers to cases of logical invalidity or contradiction of a consensually accepted law.
Beyond the issue of habit, which pleads for the unexamined perpetuation of how things have always been done [9], two opposing processes seem to discourage critique. STs who are less familiar with a subject commonly refrain from expressing any criticism of an explanation even when no specialized knowledge of the field is required, often citing feelings of incompetence to account for this attitude. At the other end of the competence spectrum, STs who are expert in the field often exhibit expert anaesthesia, refraining from criticising a faulty text as if they had inadvertently corrected or completed the defective explanation. If an ST is made aware of evaluative criteria such as coherence or logical completeness, their decision to take these into account is not at all straightforward. For example, even after deeming an explanation incoherent, some STs continue to prioritise it for teaching purposes because, for example, 'it is the most simple' [5]. On the other hand, an ST may have a change of mind, abandoning a flawed common explanation following a thorough critical analysis. In short, it is common to observe a conflict between completeness (which favours coherence) and simplicity (which can be spoiled by completeness).
This conflict echoes a long-standing debate around learning progression. Pedagogical authorities have always had to negotiate any conceptual progression proposed to students for the obvious reason that, as teachers often comment, you cannot say everything at the same time. The spiral progression approach [10] derived from Bruner's spiral curriculum model [11] has been proposed as a means of resolving this difficulty. More recently, it has been argued that the key requirement is to help students to develop the drive for coherence rather than providing them with a supposedly coherent succession of conceptual inputs [12]. On the grounds that the same objective should inform the preparation of physics teachers, it seems important to document STs' willingness or otherwise to seek coherence, even at the expense of simplicity.
In the present study, the participating STs were introduced to critical analysis as the detection of gaps in an extremely limited explanation (a method also adopted in [8]). Particular attention was devoted to one of these gaps because (as explained in the content analysis section below) it renders the explanation logically invalid. The study addresses two research questions.
RQ1: To what extent do STs recognise the gaps in an incomplete explanation of a given topic (in this case, the primary rainbow)? In particular, do they realise that one of these gaps renders the explanation incoherent?
RQ2: In discussing the consequences of an explanatory gap, do participants consider it necessary to provide an explanation that is more coherent and less simple—in this case, for first-year university students—and why?
3. Content analysis
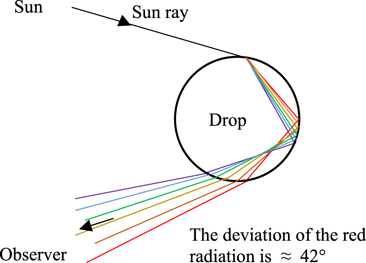
To understand how a rainbow is formed, the first step is to consider the geometry of a spherical drop and the Snell–Descartes relationship between the angles of incidence and refraction (i and r) at the interface between media of different indices (n1 and n2); that is, n1 sin i = n2 sin r. It is also important to understand that, in cases where (n1 sin i)/n2 is greater than 1, the beam would be reflected at the interface, where the angle of reflection r is equal to −i. For someone who has mastered these ideas, it should not be difficult to understand the path of a ray interacting with a drop (as in figure 1). An elementary calculation specifies the deviation D of the incident ray as a function of its incidence id on the drop (box 2). A crucial element of the explanation is that all of the mentioned variables (other than first incidence id and the air index) depend on the frequency of the wave associated with the incident ray.
Figure 1. This type of figure is used on various web sites (e.g. [13–15]) to illustrate a common explanation of the primary rainbow as a single internal reflection.
Download figure:
Standard image High-resolution imageThat said, it must also be understood that a drop receives parallel rays on half of its air/water interface, (i.e. at different angles of incidence id with respect to this interface). Figure 1 therefore represents the continuation (for each wavelength) of an incident direction of maximum reflected intensity, which undergoes a similar deviation for the neighbouring impacts of solar rays on a drop, or for which dD/did is equal to zero, where D is the deviation and id is the angle of incidence on the drop. This makes it possible to determine the incidence (and hence the deviation Dm ) that is most efficient in terms of reflected intensity (box 2). In the absence of such an explanation, the diagram in figure 1 seems completely arbitrary, as another solar ray impacting on the drop results in a completely different light path in and out of the drop - including a straight line without reflection in the case of a diametrical ray. A Geogebra simulation that visualises the concentration of light near this deviation (Dm ) can be found in [15].
An explanation confined to the elements in figure 1 raises a number of difficulties. One of these relates to a missing link in deducing the apparently circular shape of a rainbow seen by an observer from the deviation shown in figure 1. The required explanation must take into account the fact that a ray crossing from behind the observer's eye (i.e. from the Sun to the 'anti-solar' point: dotted line in figure 2) is an axis of symmetry for the phenomenon if we consider the system 'Sun/observer/drops distributed in space'. Additionally, the order of the colours seen by the observer (starting from the centre of the rainbow) is not self-evident from figure 1. This point is addressed in many illustrations such as figure 2 which point out that the drops that contribute to the red arc and the blue arc at any given time are not the same.
Figure 2. The drops that contribute to the red arc and the blue arc at a given time are not the same. (The size of the drops and the difference in deviation of red and blue light rays are exaggerated here.)
Download figure:
Standard image High-resolution imageIncidentally, Descartes 'cheated' in his famous drawing by representing a unique drop of exaggerated size (figure 3).
Figure 3. Descartes' explanation of the rainbow. The same drop is represented as contributing to the primary and the secondary rainbow, thanks to its exaggerated size. Reproduced from [17]. Image stated to be in the public domain.
Download figure:
Standard image High-resolution imageAnother potential difficulty relates to a common line of reasoning; when we see something, we tend to infer the presence of a material object such as a table or a mountain, which would be visible to other people in the same place in the landscape. This idea that a rainbow is seen in the same place in the landscape by different observers looking at it at a given time, makes it tempting to ask where is it? In fact, this question is irrelevant because a rainbow is not an object seen at the same place at any time by all observers. Contrary to what is suggested on various websites, a rainbow is not a material object or still less a flat object [13, 14, 16, 18], as any drop located on a cone of given anti-solar axis and apex can contribute to a rainbow, regardless of its distance from the observer located at the apex of this cone (figure 4). On this account, an illustration like figure 2 may be misleading (without being strictly wrong) because it suggests that all the drops contributing to the rainbow lie in a vertical plane.
Figure 4. Any drop located on a cone of given anti-solar axis and apex, and of appropriate apex angle, can contribute to a rainbow, regardless of its distance from the observer located at the apex of this cone (the size of the drops is exaggerated).
Download figure:
Standard image High-resolution imageIn the same way, it is uncommon (and has never been observed in any of the sources consulted by the author (e.g. [13–18]) to explain that a rainbow moves in time for a stationary observer. Indeed, as a rainbow's vertical plane of symmetry contains the Sun, the observer and their shadow, this plane may differ for any two observers at a given moment and moves in time for a stationary observer (figure 5) like their own shadow.
Figure 5. A composite photo combining two photos taken from the same place with a lapse of 1 min. Reproduced with permission from Ken Sekimoto.
Download figure:
Standard image High-resolution imageThis content analysis confirms that the rainbow is a conceptually rich topic encompassing geometric and physical ideas (e.g. about light). Thus, it seems reasonable then to assume that all of these elements contribute to the understanding of the rainbow and to the definition of a minimum conceptual goal for explaining this topic to a given audience. This question was asked of participants indirectly, focussing on whether they detected the logical incompleteness of the explanation related to the non-justification of the particular impact selected in figure 1 and what decisions they would make regarding the teaching of rainbow to first-year university students.
4. Experimental design
The participants were STs (N = 33) completing the fifth and final year of a Master's degree at two different universities (n = 17, n = 16) offering the same programme ('teaching, education and formation, physical sciences'). All had volunteered to complete the study questionnaire. As they were preparing for a career as secondary school physics–chemistry teachers, all had majored in physics/chemistry. They were good or medium students, and a few held a PhD degree in physics-related subjects. During this master's programme, they completed complementary courses in physics and chemistry, as well as courses and workshops in physics/chemistry education and the high school curriculum. They also had autonomous teaching experience (9 h per week) and were required to prepare a research report on their teaching. As physics/chemistry majors, they had studied Snell–Descartes' laws, prisms and optical imaging. They also knew how geometrical optics is taught in secondary schools, but the topic of rainbows was not necessarily covered in great detail.
For methodological reasons, the present study could not simultaneously explore what explanations STs had in mind before responding to the questionnaire and their intellectual path when discussing the very limited explanation they were presented with. For that reason, another independent study would be needed to establish precisely what they understood about rainbows beforehand—all the more so because, to the author's knowledge, no physics education study to date has documented students' ideas on this topic. For the purposes of this investigation, it was assumed that the STs had all the requisite knowledge to understand how the path of a ray through a drop of water can be analysed. As our results indicate, this hypothesis was not invalidated by the participants' responses.
Two questionnaires were distributed to each of the 33 STs. For practical reasons linked to the COVID-19 pandemic, participants completed these questionnaires from home and were allowed as much time as they needed (within a period of a few days).
The first questionnaire (quest. 1, box 3) explored what additional explanations they thought first-year university students would need beyond those in figure 1.
It is worth noting that the questionnaires focus on what the participants felt should be further explained rather than on what they knew or did not know about the rainbow. It was anticipated that their responses would reflect their need for coherence and their possible frustration in this regard; in other words, they were expected to focus on what was unclear in a given explanation rather than on what they supposedly already knew. In the particular case of the rainbow, it is one thing to realise that the choice of a particular angle of incidence should be justified and another to be able to justify this choice. Knowing why the proposed explanation chose to refer to a particular angle of incidence of a ray on a drop was not a logically necessary condition for realising the incompleteness of this explanation. As all of the participants knew that diametrical incidence of a ray on a drop results in no deviation at all, they could all identify this explanatory gap. That said, it seems likely that knowing the explanation for this choice of incidence (linked to a maximum reflected intensity) makes it easier to detect the incompleteness. Although it was not possible to question the STs directly about their knowledge of the complete explanation, it seems very likely that most did not know it, as confirmed by some explicit comments on the second questionnaire (e.g. 'I have learned something').
Participants' responses were compared to a list of additional explanations (see table 1, results section) based on the content analysis above. The first three items (1–3) relate to basic elements that are clearly indispensable for understanding how a rainbow is formed: the processes of refraction and internal reflection described in the Snell–Descartes formulae (even though the questionnaire stated that they were supposed to be known); how light is decomposed given how light deviation depends on wavelength; and how the geometry of the situation explains the rainbow's position and shape and the order of colours as seen by a given observer. Table 1 includes another logically indispensable addendum (4): the justification of the particular incidence id on the drop for calculation of the deviation (box 2) and/or the role of intensity (5). The two subsequent items (6 and 7) relate to the differences between rainbows seen by a number of observers situated at different places on Earth at a given moment and change over time in a rainbow seen by a motionless observer. These last four items concern the impact on the rainbow of a change in one variable; asking questions about how such a change affects the phenomenon under study is referred to below as a functional approach.
Table 1. Additional explanations requested as a priority and total number of occurrences across the sample of 33 STs
| Additional explanations requested | Npriority | N | |
|---|---|---|---|
| 1 | Calculation details to evaluate the deviation of a ray (for a given | 4 | 6 |
| wavelength) of given incidence on a drop, after two refractions | |||
| and an internal reflection | |||
| 2 | Knowledge about light, white light and colours, number of colours, prism | 11 | 13 |
| 3 | Overall geometry of what a person sees when observing a rainbow? | 12 | 22 |
| Where is the observer with respect to the drop and the angular | |||
| direction of the sun? | |||
| 4 | Justification of the particular incidence id on the drop taken into account | 1 | 4 |
| for the calculation of the deviation. Link between deviation and intensity | |||
| 5 | Role of intensity (without further details) | 2 | 2 |
| 6 | Differences between the rainbows seen by several observers situated | 0 | 0 |
| at different places on Earth at a given time | |||
| 7 | Change in time of the rainbow seen by a motionless observer | 0 | 0 |
| 8 | Other | 1 | 7 |
| 9 | No need for any additional explanation | 2 | 2 |
Box 1. Calculation of the incidence and deviation corresponding to maximum emergent intensity for a given wavelength (see also [16])
 |
Box 2. Questionnaire (quest. 1) submitted to 33 STs at the end of their preparation to become physics teachers
| The image opposite (figure 1) aims to explain 'a minima' the primary rainbow by describing the path |
| of a ray of white light from the Sun during (one refraction, one total reflection, one refraction) and |
| after its interaction with a drop of water. Snell–Descartes' formulas for refraction and total reflection |
| are assumed to be known, as well as the principle of the dependence of the water index on the |
| frequency of the wave. |
| To understand the primary rainbow, what additional explanations do you think are necessary for |
| someone who already knows the formulas for refraction and total reflection and the principle of the |
| dependence of the water index on the wavelength? Please list (without expanding on them, i.e. by |
| asking questions without solving them) these desirable additional explanations, in descending order |
| of priority, for a first-year university student, regardless of whether you know the answer or not. |
| For each suggested additional information, any comments are welcome. |
Box 3. Questionnaire 2.
| Do you think this information - the idea of a deviation extremum - is very important | |
| for a first year university student to understand the rainbow? | |
| Yes, without this complement the reduced explanation presented in the | |
| image seems arbitrary | □ |
| No, it's quite complicated and I don't think it's very important | □ |
| Other | □ |
| Have you changed your mind from your first answers (quest.1). How and why? | Any comments |
| are welcome | |
| Thank you for your participation |
After the first questionnaires were returned, a second questionnaire (quest. 2) was sent to the STs; because of a technical problem, only 20/33 answers were collected. Quest. 2 begins by explaining why only a specific impact on the drop was considered in figure 1 (see items 4 and 5, table 1) based on the conceptual elements presented in box 1. Participants were then asked what value they assigned to the explanation of this point (box 3) in ensuring a good understanding of the rainbow among first-year university students. STs' comments in response to quest. 2 were grouped on the basis of a thematic analysis.
5. Main results
STs' responses to quest. 1 are summarised in table 1. In the absence of a clear difference between the two universities, all the responses were grouped in a unique sample. Two numbers are provided for each item: the number of STs who made a particular request at the first rank (Npriority), and total occurrence of requests of this type across all participants whatever the ascribed priority (N).
Table 1 indicates a concentration of ST priority requests in relation to items 2 and 3. This is unsurprising, as without this information, it would not be possible to gain even a minimal understanding of how we see a rainbow. Note that in fact point 1 was not relevant because the questionnaire states that basic knowledge in geometrical optics is supposed to be known.
The rarity of priority requests in relation to items 4, 5, 6 and 7 warrants further attention. These items ask what happens when the so-called 'functional approach' is adopted to vary certain elements of the explanation: the point of impact of a sunray on a drop, the location of the observer or the time of observation. Note that requests regarding 'the role of intensity' (item 5) may refer to the role of the ray's incidence on a drop (item 4), although this interpretation is somewhat speculative. In any case, the number of priority requests that relate directly (item 4) or indirectly (possibly item 5) to the effect of first incidence on deviation value is very low (three at most, and only one explicitly). This clearly indicates that the issue of logical incompleteness is scarcely detected in this group even though it invalidates the explanation. The lack of requests of types 6 and 7 also indicates acceptance of a very limited explanation, but this is not linked to a logical flaw; rather, the explanation is accepted despite being less rich that it might have been.
Looking at total occurrence of requests rather than priority requests alone leads to the same conclusions while also indicating that an explanation of the overall geometry of what a person sees when observing a rainbow (item 3) was the most frequent request as both a priority and non-priority choice. More specifically, the maximum number of requests per participant (5) was observed with a strong contribution of this item, while 20 participants requested only one or no additional explanation (N = 18 and N = 2, respectively).
When asked whether they would use the proposed additional explanation at first-year university level (why only one incidence on the drop was taken into account), 17 STs chose the answer yes, without this complement the reduced explanation presented in the image seems arbitrary, 0 chose no, it is quite complicated and I do not think it is very important and 3 responded other. Among those who responded positively to this question (17/20), most of the comments insisted that this explanation is needed to fully understand the rainbow.
Participants often expressed surprise:
A few students have distanced themselves a little from these majority positions. One of those who answered other referred to a particular difficulty in understanding the explanation:
Two others suggested a different pedagogical use of the explanation:
Finally, one ST made a somewhat enigmatic response, a yes accompanied with this comment:
6. Recapitulation and discussion of the results
This study was inspired by Shulman's question [1] 'where do teachers' explanations come from?' The study focuses on one of the criteria that may influence their choice—an explanation's (in)completeness—and its possible impact on two other qualities: coherence and simplicity. More specifically, the research investigates the extent to which STs realize the limitations of a logically incomplete explanation (in the present case, of the primary rainbow), and whether, on becoming aware of this incompleteness, they would resolve this issue when teaching the topic at first-year university level.
In relation to the first question, the STs were asked which additional explanations they would recommend for teaching the topic at this level. Their responses were sorted according to a list of addendum types (see items in table 1). Their answers are concentrated on items 2 and 3, which is unsurprising, as it is impossible without these explanatory elements to understand how light is decomposed (point 2), and how the geometry of the situation shapes the rainbow (point 3). In contrast, very few responses relate to items 4, 5, 6 and 7, which asked what happens when certain elements of the explanation are varied using a 'functional approach'—specifically, the point of impact of a Sun ray on a drop (4, 5), the location of the observer or the time of observation (6, 7). In this regard, we note that a learner is more often than not invited to process certain data to determine the state of a system or the value of other quantities; using this static approach, the relationship between variables makes it possible to calculate one by knowing the others. However, pedagogical activity more rarely addresses how the result depends (or does not depend) on a change in one or other variable. In the present case, for example, does a ray's deviation depend on its impact on the drop, and therefore on the angle of incidence? Does the apparent position of the rainbow in the landscape at a given time depend on the position of the observer? Does this relative position depend on the time for a given position of the observer? As all of these questions contribute to our comprehension of the phenomenon, it is worth questioning the decision not to teach them for a given audience. That said, the consequences of not considering these questions differ for each. Understanding how the rainbow's geometry depends on the position of the observer or the time of observation is conceptually enriching but not strictly indispensable for primary comprehension. In contrast, considering the particular incidence of a ray on a drop (id) without justifying this decision ruins the coherence of the explanation. The fact that very few STs drew attention to this choice (item 4) or to the issue of light energy (item 5) indicates a kind of critical abstention that cannot be explained solely in terms of defective knowledge of the subject. Indeed, anyone might notice that a ray hitting a drop diametrically would pass through it without any deviation. It is also worth noting that realising there is an explanatory gap may prompt various pedagogical decisions that take account of the complexity of a complete explanation. For example, the teacher might decide not to teach the rainbow at all, or might decide to teach the topic while acknowledging that no justification was provided for the chosen ray's angle of incidence. Alternatively, they might decide to add that while the justification for that particular value was not provided, it was based on the search for a maximum deflected intensity; or again, they might decide to provide a more complete explanation of the point. Adapting an explanation for a given audience does not necessarily mean sacrificing coherence. In any case, this is an opportunity for teachers to clarify the approach he or she intends to take, and to indicate what capacity he or she will try to develop in the students. This kind of awareness was explicitly cited by some STs as a potential benefit of the approach proposed here.
In relation to this question (what one would decide to do once warned of a logical gap), the results are very surprizing. Almost all of the participants declared that they would provide their students with a more complete explanation regarding id; only one denied the relevance of this approach, declaring that the diagram in figure 1 was 'correct' without noting that it was incoherent in the absence of an argument about the choice of id. While he did finally say that he would also explain this choice, he pointed out the 'simplicity' of not doing so. One ST was uneasy about this latter approach ('It's Chinese!'), and two others proposed an active teaching style to introduce this additional explanation. These were the only others to diverge (slightly) from the majority view that the explanatory gap should be filled, and that the proposed additional explanation was both very informative and surprizing.
When compared to similar investigations of other physics topics [6], an unexpected finding of this kind must be viewed with caution, as this quasi-unanimity relates to new awareness, involving both surprise and conceptual interest. To determine what these STs might really decide when preparing their lesson for the following day, it would be probably necessary to insert a delay between the two episodes—first clarification, then questioning—which for practical reasons occurred in close succession here (quest. 2). That said, some STs in previous investigations [6] declared after becoming aware of an explanatory flaw that they would use it anyway because it was 'simpler', even when others claimed that this apparent simplicity was misleading. In the present study, only one ST exhibited the kind of intellectual tension that might accompany the coherence-simplicity dilemma. Briefly, beyond verifying the recurring presence of this dilemma, we are still unable to predict what proportion of a given group of STs would favour explanatory simplicity or coherence when teaching a given topic to a given audience. On the other hand, the fact that a good number of teachers expressed surprise and interest at the end of this experiment is a noteworthy finding.
7. Concluding remarks
Several interesting points emerged from this investigation. First, when seeking further explanation or considering what might be lacking, many STs do not seem to question what might change if one aspect of the explained situation were to change. This is a crucial aspect of scientific thinking in general, and it can be argued that the failure to engage in this functional analysis risks an almost complete lack of understanding. Clearly, then, it is important to develop STs' awareness of this fundamental element of science education, as advocated for example by Etkina and Planinsic [19].
More specifically, this investigation confirms that many STs exhibit a low level of critical vigilance and should be helped to improve in this regard [4]—but how can this be achieved in practice? The study uses a very analytical approach, applying a set of validity criteria for explanatory texts in physics. One important aspect of this analytical approach is that, whatever their choice of explanation, STs learn to make more conscious decisions by becoming more aware of its strengths and weaknesses.
To perform this kind of analysis, STs must understand the nuances of these criteria. For example, it is uncontroversial to link coherence to logical validity and consensually accepted laws. On the other hand, as emphasised above, incompleteness may take several forms. It may refer to the lack of reminder of the prerequisites; in this sense, any explanation is incomplete. It can also refer to a weak exploitation of the first conclusions of the explanation, even if it is necessary to stop somewhere. Finally, it may indicate a lack of logical connection at the heart of the argument, which invalidates it on logical grounds. It is important to help STs to distinguish between these different forms of incompleteness.
The same applies to simplicity. Indeed, simplifying an argument may involve neglecting one aspect of the situation in relation to another—for instance, neglecting Archimedes' up-thrust on a nail in relation to the action of the hammer. Even where it is preferable to make such simplifications clear, ignoring them is not necessarily a disqualifying factor. In contrast, simplification can destroy the very logic of the explanation it claims to serve, as for instance when a particular incidence on a drop is arbitrarily chosen to explain the rainbow, or when the pressure is said to be the same everywhere inside and outside a hot air balloon [9]. Learning to detect unacceptable forms of 'simplification' is a relevant goal for teacher preparation. Frequent practice with multi-criteria critical diagnoses and explicit consideration of the interrelated issues of simplicity, consistency and completeness would enrich STs' 'habits of mind' [20, 21], enabling them, in Sikorski and Hammer's terms [12], to 'seek coherence for themselves' and to construct autonomous and well-informed pedagogical decisions. Further research is needed to optimise teacher preparation in this regard, taking due account of the conceptual and the critical as two inseparable facets of intellectual development.
This work was carried out in accordance with the principles outlined in the journal's ethical policy and informed consent to publish was obtained from all participants.