Abstract
A new method to calculate the electric field inside a spherical shell with surface charge σ = σo cos θ in terms of solid angle is presented. The integral can be readily carried out without invoking special functions typically used for this classical problem. For a flat surface of uniform charge density, the electric field normal to the surface is shown to be proportional to the solid angle subtended by the surface only.
Export citation and abstract BibTeX RIS
1. Introduction
The electric field inside a uniformly charged spherical shell is a standard example discussed in the introductory university physics. The field inside is zero and on the outside it behaves like a point charge at the center. This can be traced back the original Newton's shell theorem for gravitational force [1] and it is usually proven with the use of Gauss's law and spherical symmetry of the electric field [2, 3]. In fact, students are usually very surprised to find out the contributions from the small dome close to a point is cancelled out exactly by the larger dome farther away if one separates the spherical shell into two parts by a plane containing the point and perpendicular to the line connecting the point and the center of sphere.
Solid angle is a key concept to the proof of Gauss's law. The notation is often introduced in calculus based college physics textbooks and but usually not much more beyond the definition. It can be used to easily prove the exact cancellation of electric fields from opposing spherical segments [1, 2].
Field calculations for more complicated charge distributions, such as a charged ring or a disk are usually limited to points on the symmetry axis. General solutions are typically reserved as boundary value problems in more advanced courses [4–6]. However, new formulations or treatments are still of current interest [7–14].
One classical E&M problem is the field inside a spherical shell with a charge density varying as σ = σo cos θ. It describes of charge distribution of several systems such as the bound surface charge density of a uniformly polarized sphere or the induced surface charge density of a spherical conductor inside a uniform electric field. In the case of uniformly polarized sphere σo = p, p is the dipole moment per unit volume. The calculation of the field is a standard example of boundary value problem, easily found in any intermediate electromagnetism books [4]. It should also be noted for this charge density there exists another clever method to show the field is uniform by superposing two oppositely charged spheres of charge Q separated by vanishingly small distance d but with a finite diploe moment of Qd.
2. Results
Here we demonstrate that field inside a sphere with surface charge density σ = σo cos θ is constant by a simple integration with the use of solid angle concept.
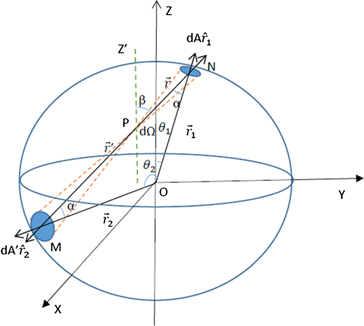
Consider an arbitrary point P inside a sphere as shown in figure 1, where the vertical axis corresponds to z-axis or θ = 0. From point P construct two intersecting infinitesimal cones with P at the vortex. The two infinitesimal cones of same solid angle dΩ intersect with the sphere with an infinitesimal area of dA, and dA' at points N, and M, respectively. dA is defined at spherical angle θ1 with  as its normal direction so
as its normal direction so 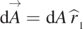 . Similarly, dA' is at θ2 and
. Similarly, dA' is at θ2 and 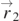 . It should be noted that because the line MPN and its associated cone are arbitrary, the plane defined by OMN in general does not contain the z-axis. The implication of this is that θ1 and θ2 are not co-planar in general. Nevertheless, it can be defined and discussed in vector notations without confusions. For example, the displacement vector from M to N can be defined as
. It should be noted that because the line MPN and its associated cone are arbitrary, the plane defined by OMN in general does not contain the z-axis. The implication of this is that θ1 and θ2 are not co-planar in general. Nevertheless, it can be defined and discussed in vector notations without confusions. For example, the displacement vector from M to N can be defined as 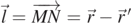 ,
, 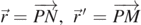 and the angle α between line PN and ON or PM and OM with
and the angle α between line PN and ON or PM and OM with 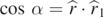 . OMN is an isosceles triangle, because r1 = r2 = R, R is the radius of the sphere with origin at O.
. OMN is an isosceles triangle, because r1 = r2 = R, R is the radius of the sphere with origin at O.
Figure 1. Electric field due to two intersecting infinitesimal cones on a spherical surface.
Download figure:
Standard image High-resolution imageThe solid angle dΩ is related to the area dA by 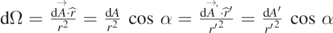 , where
, where 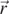 and
and 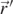 are the displacement vectors from P to N and M, respectively.
are the displacement vectors from P to N and M, respectively.
The electric fields from dA and dA' are 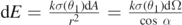 and
and 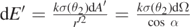 . If the charge density is the same, the two contributions balance out completely, thus zero net field anywhere inside a uniformly charged spherical shell, also known as shell theorem.
. If the charge density is the same, the two contributions balance out completely, thus zero net field anywhere inside a uniformly charged spherical shell, also known as shell theorem.
In the case when σ = σ0 cos θ, the net electric field contribution
![$\mathrm{d}{E}_{n}=\mathrm{d}E-\mathrm{d}{E}^{\prime }=\frac{k\enspace \mathrm{d}{\Omega}}{\mathrm{cos}\enspace \alpha }\left[\sigma \left({\theta }_{1}\right)-\sigma \left({\theta }_{2}\right)\right]=\frac{k{\sigma }_{o}\enspace \mathrm{d}{\Omega}}{\mathrm{cos}\enspace \alpha }\left[\mathrm{cos}\enspace {\theta }_{1}-\mathrm{cos}\enspace {\theta }_{2}\right]$](https://content.cld.iop.org/journals/0143-0807/42/5/055202/revision2/ejpac0e1dieqn12.gif) along the
along the  direction (
direction (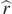 is from P to N).
is from P to N).
Now consider  ,
, 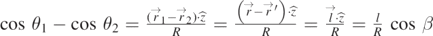 .
.
Thus, 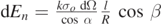 , since
, since 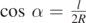 , it simplifies to dEn
= 2kσo
cos β dΩ.
, it simplifies to dEn
= 2kσo
cos β dΩ.
The result is surprisingly simple, dependent only the polar angle β between  and the vertical direction, independent of the azimuth angle. This leads to cancellation of field in the horizontal plane and leaves only the vertical component when dΩ rotates about vertical axis at a fixed β.
and the vertical direction, independent of the azimuth angle. This leads to cancellation of field in the horizontal plane and leaves only the vertical component when dΩ rotates about vertical axis at a fixed β.
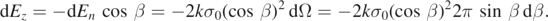
The total electric field is then given by

Note the range of β is from 0 to  instead of 0 to π to avoid double counting. The integral does not require special functions such as the Legendre polynomials, except the notation for solid angle in spherical coordinates.
instead of 0 to π to avoid double counting. The integral does not require special functions such as the Legendre polynomials, except the notation for solid angle in spherical coordinates.
In principle, one can express the infinitesimal field contribution from any infinitesimal charge on the surface and integrate over to get the same result, but in reality, the expression is usually too complicated to contemplate.
Another interesting geometry where solid angle can be used directly to calculate the electric field is that of a flat surface of uniform charge density. Assuming a uniform charge density σ is on the xy plane, as in figure 2(a), the electric field component in the z-axis direction anywhere due to an infinitesimal charge dq = σ dA is given by
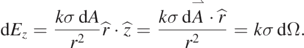
Figure 2. (a) dE from an infinitesimal surface charge; (b) E at the tip of a truncated cone; (c) E on the plane bisecting the plates.
Download figure:
Standard image High-resolution imageThe total field in the z-axis direction is thus Ez = kσΩ if the charge density is constant, here Ω is the solid angle subtended by the surface from the point. The result is interesting that it only depends on the solid angle, independent of the distance from the plane. For example, the surface bounded by dashed line in figure 2(a) would contribute exactly the same field in the z-axis direction.
The result is especially useful if the point is on the symmetry axis, such that the axial component is the total field. A familiar example is that the field due to a uniformly charged circular dish, given by
E = kσΩ = kσ2π(1 − cos θ). A trivial example is when Ω = 2π for an infinitely large sheet with E = 2πkσ.
A fun example is that of the electric field at the tip of a uniformed charged cone or truncated cone. Here the contribution from each layer of thickness dz contributing exactly the same dE = kρ dzΩ, and the total field E = khρΩ = khρ2π(1 − cos θ), where ρ is the uniform volume charge density and h is the height of the truncated or full cone, as in figure 2(b).
The result can also be used to calculate the axial field for a parallel plate capacitor [14]. For example, the electric field on the plane bisecting the plates separated by a distance d is simply given by E = 2kσΩ, assuming σ is constant. For far away points, 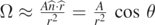 , the result gives the well known dipole electric field
, the result gives the well known dipole electric field
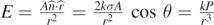 , with P = σAd, as shown in figure 2(c).
, with P = σAd, as shown in figure 2(c).
3. Conclusion
In summary, we have presented a new way with the aid of solid angle concept to calculate the electric field inside a spherical shell of charge density σo cos θ. To our knowledge, this is a new method to solve this problem and the present approach is not available or published in the literature. The approach is vigorous with elementary calculus only without the use of special functions to this classical EM problem.
For a uniformly charged flat surface, the electric field at a given point in the direction perpendicular to the surface is only dependent on the solid angle subtended by the area to the point. The result is surprisingly simple and appealing.
Acknowledgments
The author wants to thank many colleagues in the physics department for useful discussions.