Efficient design parameter selection for nonlinear bearings to achieve multi-objective optimization of seismic performance of girder bridges by utilizing the stochastic structural response of equivalent linear systems

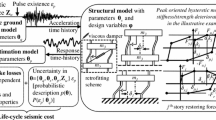
Abstract

In the process of performance-based design of bridges with aseismic bearings, there exist intrinsic trade-off between minimization of the bearing displacement and pier displacement during strong earthquake events. However, difficulty in selecting the optimal parameters of the bearings that satisfy the two objectives arises, in conjunction with considerable computational resource requirements for nonlinear time-history analysis (NTHA). A computationally efficient approach to determine the optimal bearing design parameters by utilizing the stochastic structural response of equivalent linear systems is proposed in this paper. The key idea is to use the assumed optimal parameters obtained from a stochastic model as the approximation of the exact optimal parameters found from a deterministic model. The stochastic model allows rapid exploration of optimal parameter candidates. A computationally intensive deterministic model is used to determine the performance-based optimal design by performing NTHA only for the design parameter candidates obtained by exploiting the stochastic model. Compared with the exhaustive search approach, the required number of NTHA cases in this method can be significantly reduced. As a numerical example, the proposed method is applied to optimal parameter selection of two slide type bearings in a girder bridge, namely the uplifting slide shoe and the functionally discrete bearings. The seismic performance indices of the bridge with the design parameters determined by the proposed procedure are shown to be almost equivalent to the optimal values found by the exhaustive search approach. An extended parameter search algorithm is incorporated with the proposed procedure for refinement of the assessment at the slightly increased cost of computation.

Appendices

Appendix 1: Normal force of UPSS in the stochastic and deterministic models

1.1 Normal force of UPSS in the deterministic model

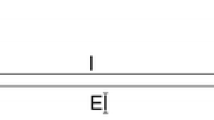
The normal force generated on the slope interface of UPSS is obtained by the dynamic equilibrium of the forces acting on the slider. Let us assume that the slider perfectly slides on the inclined sliding surface at the positive side without take-off behavior, as shown in Fig. 18, where the ground motion $z$ and the motion of the pier top $u_{1}$ are given. The dynamic equilibrium conditions for the slider can be expressed as:

$$ \left\{ {\begin{array}{*{20}l} {x: } & {m_{2} \left( {\ddot{u}_{1} + \ddot{u}_{b,x} + \ddot{z}} \right) = - \mu f_{N} \cos \theta - f_{N} \sin \theta } \\ {y: } & {m_{2} \ddot{u}_{b,y} = f_{N} \cos \theta - m_{2} g - \mu f_{N} \sin \theta } \\ {x - y:} & {\tan \theta = \ddot{u}_{b,y} /\ddot{u}_{b,x} } \\ \end{array} } \right. $$

(19)

where $f_{N}$ is the normal force of the sliding surface; $u_{b,x}$ and $u_{b,y}$ indicate the bearing displacement relative to the pier top in the $x$ and $y$ directions, respectively; $g$ is the gravitational acceleration.

Fig. 18

Dynamic equilibrium condition of UPSS in the bridge system

Hence, the expression of the normal force can be solved as:

$$ \begin{array}{*{20}c} {f_{N} = m_{2} g\cos \theta - m_{2} \left( {\ddot{z} + \ddot{u}_{1} } \right)\sin \theta } \\ \end{array} $$

(20)

where $\ddot{z}$ and $\ddot{u}_{1}$ are updated at each step of the nonlinear time-history analysis.

1.2 Normal force of UPSS in the stochastic model

The normal force is formulated as an explicit expression. For this purpose, the dynamic equilibrium condition and the energy conservation condition are combined to solve the normal force. Firstly, the slider represented by the point mass is assumed to stay in contact with the inclined surfaces at which a constant horizontal acceleration $\ddot{z}$ takes place, as shown in Fig. 19a. Based on the dynamic equilibrium condition, the normal force can be expressed as:

$$ \begin{array}{*{20}c} {f_{N} = m_{2} g\cos \theta + m_{2} \ddot{z}\sin \theta } \\ \end{array} $$

(21)

where the horizontal acceleration $\ddot{z}$ term is equivalent to the $\left( {\ddot{z} + \ddot{u}_{1} } \right)$ term in the Eq. (20).

Fig. 19

UPSS is sliding on the inclined surface

Then, the slider is assumed to undergo an infinitesimally small increment ${\Delta }u$ in the horizontal direction without considering the change of kinetic energy, as shown in Fig. 19b. The energy conservation condition of this process can be expressed as:

$$ \begin{array}{*{20}c} {m_{2} \ddot{z}\Delta u = m_{2} g\Delta u\tan \theta + \mu f_{N} \frac{{{\Delta }u}}{\cos \theta }.} \\ \end{array} $$

(22)

Substituting Eq. (22) into Eq. (21), the normal force can be solved as:

$$ \begin{array}{*{20}c} {f_{N} = \frac{{m_{2} g}}{{\left( {\cos \theta - \mu \sin \theta } \right)}}.} \\ \end{array} $$

(23)

Appendix 2: Sensitivity of optimal parameter selection in various single-objective function spaces

The stochastic model allows rapid exploration of some design characteristics, such as solution robustness, local minima, and parameter sensitivities, within a practical time frame. In this appendix, sensitivities of the bearing’s parameter in various single-objective optimization problems are explored. Define a single-objective optimization problem as:

$$ \begin{array}{*{20}c} {\mathop {\min }\limits_{{\varvec{x}}} J\left( {\varphi_{s} } \right) \;\;subject to: x_{j,lb} < \phi_{sj} < x_{j,ub} \left( {j = 1,2, \ldots ,k} \right)} \\ \end{array} $$

(24)

where $x_{j,lb}$ and $x_{j,ub}$ are the lower and upper bound of $j$ th design variable for the bearings in practice, as given in Table 1.

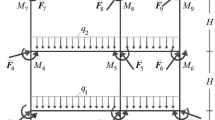
The performance objective indices are selected to minimize the second-order moment of displacement responses of the example bridge, as:

$$ \begin{array}{*{20}c} {J_{I} = \sigma_{{u_{1} }} , \;J_{II} = \sigma_{{u_{2} }} , \;J_{III} = \sigma_{{u_{b} }} = \sqrt {\sigma_{{u_{1} }}^{2} + \sigma_{{u_{2} }}^{2} - 2\sigma_{{u_{1,2} }}^{2} } } \\ \end{array} $$

(25)

where $\sigma_{{u_{1} }}$, $\sigma_{{u_{2} }}$, and $\sigma_{{u_{b} }}$ correspond to the standard deviation of the pier, girder, and bearing response displacements, respectively.

In addition, the portion of energy dissipated by bearings is considered as a global performance index to improve the robustness of design compared with other performance indices (Basili and De Angelis 2007; De Angelis et al. 2019; Reggio and De Angelis 2013, 2015). The energy balance equation of the system can be expressed as:

$$ \begin{array}{*{20}c} {E_{{i,{ }total}} = E_{{i,{ }1}} + E_{{i,{ }b}} = E_{{k,{ }1}} + E_{{k,{ }b}} + E_{{d,{ }1}} + E_{{d,{ }b}} + E_{{e,{ }1}} + E_{{e,{ }b}} } \\ \end{array} $$

(26)

where $E_{i, total}$ is the total input energy, the subscript ‘$1$’ denotes the bridge pier, ‘b’ denotes the bearings, and ‘k’ denotes the kinetic energy, ‘d’ denotes the damping, and ‘e’ associates with the elastic potential energy.

Considering the conservation of mechanical energy, the following relation holds: $E_{k, 1} + E_{e, 1} = 0$ and $E_{k, b} + E_{e, b} = 0$. Therefore, the total input energy can be simplified as:

$$ \begin{array}{*{20}c} {E_{{i,{ }total}} = E_{{d,{ }1}} + E_{{d,{ }b}} .} \\ \end{array} $$

(27)

Since the excitation is assumed to be a stationary random process, the rate of total input energy can be evaluated by applying the expectation operator $E\left[ \cdot \right]$ at unit time increment ${\Delta }t$, so that it yields:

$$ \begin{array}{*{20}c} {E\left[ {e_{{i,{ }total}} } \right] = E\left[ {e_{{d,{ }1}} } \right] + E\left[ {e_{{d,{ }b}} } \right]} \\ \end{array} $$

(28)

where the following relationship is satisfied: $E_{{i,{ }total}} = \sum e_{{i,{ }total}} {\Delta }t$, $E_{{d,{ }1}} = \sum e_{{d,{ }1}} {\Delta }t$, and $E_{{d,{ }b}} = \sum e_{{d,{ }b}} {\Delta }t$.

Based on the formula of the energy dissipation by the damping ratio, namely $E_{d} = \sum c\dot{u}^{2} {\Delta }t = \sum 2m\omega_{0} h\dot{u}^{2} {\Delta }t$, the mean energy dissipated by the pier and the bearing per unit time increment can be expressed as:

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {E\left[ {e_{{d,{ }1}} } \right] = 2m_{1} \omega_{1} h_{1} E\left[ {\dot{u}_{1}^{2} } \right] = 2m_{1} \omega_{1} h_{1} \sigma_{{\dot{u}_{1} }}^{2} { }} \\ {E\left[ {e_{{d,{ }b}} } \right] = 2m_{2} \omega_{b} h_{b} E\left[ {\dot{u}_{b}^{2} } \right] = 2m_{2} \omega_{b} h_{b} \sigma_{{\dot{u}_{b} }}^{2} } \\ \end{array} } \\ \end{array} $$

(29)

where

$$ \begin{array}{*{20}c} {\sigma_{{\dot{u}_{b} }} = \sqrt {\sigma_{{\dot{u}_{1} }}^{2} + \sigma_{{\dot{u}_{2} }}^{2} - 2\sigma_{{\dot{u}_{1,2} }}^{2} } .} \\ \end{array} $$

(30)

Therefore, the energy-based performance index to maximize the energy dissipated by the bearing is given as:

$$ \begin{array}{*{20}c} {J_{IV} = 1 - \frac{{E\left[ {e_{{d,{ }b}} } \right]}}{{E\left[ {e_{{d,{ }1}} } \right] + E\left[ {e_{{d,{ }b}} } \right]}} = 1 - \frac{{m_{1} \omega_{b} h_{b} \sigma_{{\dot{u}_{b} }}^{2} }}{{m_{1} \omega_{1} h_{1} \sigma_{{\dot{u}_{1} }}^{2} + m_{2} \omega_{b} h_{b} \sigma_{{\dot{u}_{b} }}^{2} }}} \\ \end{array} $$

(31)

The optimal parameter selection of the bearings considering various intensities of ground motions and soil conditions is examined. The intensity of ground motions is varying from 0.1 g to 1.0 g, and three soil conditions (Kiureghian and Neuenhofer 1992) representing different ground characteristics are shown in Table 5. The corresponding response matrices are presented in Table 6.

Table 5 Parameters for K-T model with various soil types

Table 6 Optimization objectives

The optimal parameter selection for UPSS in the example bridge is shown in Fig. 20. With the increase of intensity, minimizing $J_{II} , J_{III} , J_{IV}$ (bearing related objectives) tends to require a greater friction coefficient and an inclined angle of the sliding surfaces, while minimizing $J_{I}$ (pier response) results in a larger friction coefficient but a smaller inclined angle. It is interesting to see that minimizing the energy index $J_{IV}$ will cause a greater inclined angle as the intensity increases, since a greater inclined angle of UPSS implies a larger stiffness, and a shorter natural period, although elongation of the natural period is regarded as an effective approach to improve the performance of an isolation bearing under strong earthquakes.

Fig. 20

Comparison of optimal parameters for different ground motions (UPSS)

Similar results for FDB are shown in Fig. 21. As the intensity of ground motion increases, minimizing $J_{I} , J_{II} ,J_{III} ,{\text{ or}} J_{IV}$ tends to require a greater friction coefficient. Minimizing $J_{II} ,J_{III}$ (bearing related displacements) always results in a short natural period of the elastomeric bearing, while minimizing $J_{I} ,J_{IV}$ requires a longer natural period of the elastomeric bearing.

Fig. 21

Comparison of optimal parameters for different ground motions (FDB)

Note that the optimal parameter selection that minimizes $J_{II} ,J_{III}$ is not necessarily unique. The corresponding results are excluded when the intensity of ground motion is at a low level, since the bearing response displacement becomes zero in different parameter selections. In the computation of the nonlinear stochastic response of the example bridge with the two slide bearings, for a ground motion of low intensity, the bearing displacement response ($\sigma_{b}$) becomes small, leading to a large value of equivalent stiffness of the bearings as a result of evaluation based on the relationship that the equivalent stiffness is inversely proportional to the displacement. In the next iterative step, the large equivalent stiffness results in a yet smaller bearing displacement. With the repetition of this process, the iterative evaluation procedure can be terminated with zero bearing displacement.

In a practical application, the variation of bearing properties will cause mistuned problems due to the installation error or deterioration over service life. The sensitivity of the optimal parameter selection of the two types of bearings is examined for a ground motion of 0.5 g PGA at medium soil condition. As shown in Fig. 22, the minimum values of the objective functions $J_{I}$ through $J_{IV}$ for the two types of bearings fall onto a relatively broad range of parameter values. It implies that the optimal values of the bearing parameters can vary depending on the objective function to be minimized, hence the bearing parameter mistuning is not critical when solved as a single-objective function problem.

Fig. 22

Optimal parameters selection in the single-objective function space