Feedback control method to suppress stick-slip in drill-strings featuring delay and actuation constraints

Abstract

In this work, performance of a modified-integral resonant controller with integral tracking is investigated numerically under the effects of actuator delay and actuation constraints. Actuation delay and constraints naturally limit controller performance, so much so that it can cause instabilities. A 2-DOF drill-string m with nonlinear bit–rock interactions is analysed. The aforementioned control scheme is implemented on this system and analysed under the effects of actuation delay and constraints and it is found to be highly effective at coping with these limitations. The scheme is then compared to sliding-mode control and shows to be superior in many regimes of operation. Lastly, the scheme is analysed in detail by varying its gains as well as varying system parameters, most notably that of actuation delay.

1 Introduction

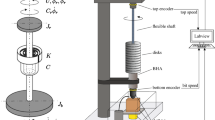
In the Oil and Gas industry, drill-strings are critical engineering systems and structures for exploration and production drilling. Over the years there has been a significant interest in understanding the dynamics of drill-strings, namely real-time data gathering via MWD [1] (Measurement While Drilling) and the use of FE models [2, 3]. Due to the complex dynamics inherent within drill-strings and their frictional interactions with the borehole, they are highly susceptible to unwanted oscillatory effects, which come in three primary forms, namely torsional [4,5,6,7], lateral [7, 8] and axial [7, 9] vibrations. These problems occur in all types of well configurations (vertical [10, 11], directional [11] and horizontal [11,12,13]) and their accompanying drilling methodologies (rotational [14] and percussive [14]) (Fig. 1).

These unwanted oscillations present challenges with the drilling procedure and can and will continue to produce downtime, and incur significant financial losses, on rigs due to the damage they cause entire drill assemblies [15]. This paper focuses on a class of torsional vibrations known as stick-slip oscillations [16]. Stick-slip is one of the most commonly encountered vibration phenomenon in any type of well and is the most common reason for down-hole tool and tool joint failure [10]. Thus, stick-slip has garnered great interest in its cause as well as its necessary prevention. Stick-slip studies began with the majority of its studies focusing on simplifying and isolating the stick-slip phenomenon to low DOF drill-string models [17, 18] based on the torsional pendulum. The friction model developed for lumped-mass modelling, is a discontinuous switch case one by Navarro-Lopez [19]. This friction model elegantly captures the stick-slip dynamics while preserving essential bifurcation behaviour caused by changes in Weight-on-Bit (WOB) and top-torque. By focusing solely on stick-slip, low-degree of freedom models have allowed for a greater understanding of this phenomenon without involving the other aforementioned axial and lateral vibrations. while simultaneously allowing for the development of friction models.

Fig. 1

A diagram of the simplified 2-DOF representation of the vertical drill-string modelled as a connected series of rotating pendulum featuring a highly nonlinear opposing bit–rock interaction $T_b$. The accompanying Table 1 presents the model parameters, their meanings and corresponding values adopted for this paper (from [37])

A drill-string, in general, can be modelled by an ‘infinite’ number of rotational spring-mass-dampers connected in series. Due to the overall complexity of drill-strings, FEA modelling of them was of the utmost importance to understand the overall behaviour of drill-strings [20] including their cutting ends [21]. This type of modelling is too complex to design control signals for and as a result, lumped-parameter models [17, 18] became popular, as they isolate specific dynamics and allow for controllers to be designed for these problems. In recent years, 2-DOF models are still used for producing and benchmarking novel control methods for stick-slip [22, 23] as well being used for researching dynamics involving complex blade patterns on rock cutting [24]. In this paper, a 2-DOF vertical drill-string model is adopted and derived from first principles as the system of choice. The choice to use a 2-DOF model allows for a sufficiently complex system that demonstrates multiple rich dynamics of stick (no drilling), stick-slip and constant drilling to exist for a range of WOB and top-torque values and is still relevant in the benchmarking of novel control schemes.

A number of strategies aimed at mitigating stick-slip oscillations have been reported in the literature. The company Tomax patented their unique AST (Anti-Stall Tool) [25, 26] which tackles the stick-slip problem from that of a mechanical design perspective. The control input to the drill-string itself, whether it be top-torque, WOB or top-drive rpm, acts as other potential control parameters for the prevention of stick-slip. In recent times, the $\mu$-synthesis control method [27, 28] has been proposed as a way with which to overcome stick-slip oscillations, however this methodology relies on linearisation methods which only possess expected performance in a very small range around the equilibria of interest. There has also been the suggestion that a linear quadratic regulator-based controller to suppress stick-slip using a discretised model of axial and torsional dynamics [29]. Another source suggested using WOB as a control parameter [30], but this requires knowing the exact WOB being applied at any given instant to a drill-string, which is a very challenging precondition. Consequently, this method lacks robustness in the face of uncertain values of WOB. PID and PD control has been proposed by [31,32,33,34] as a way with which to avoid stick-slip. Soft-Torque control (patented by Shell in [35]) and Z-torque control [36] are effectively PI controllers and have great sensitivity to actuator delays and measurement delays which also belong to the PID family. None of these control methods are particularly robust to system parameters or bit–rock changes. In order to mitigate the very real problem of system parameter changes while making sure constant drilling occurs, Sliding-mode Control (SMC) has been thoroughly investigated [37, 38]. Due to its robustness to parameter uncertainties, the SMC has emerged as a benchmark against which all other stick-slip mitigating control schemes are compared. That being said, SMC has one sizeable downside, its inherent complexity in its design procedure.

The control of systems with delay is always a challenging area of research. Drill-strings are subject to three main types of delay, namely regenerative state-based cutting delay terms [23, 24, 39] due to PDC heads, actuation delays [40] and measurement delays [41]. Actuation delays even exist in experimental setups such as the in-house experiment [37]. There is a lack of detailed work with actuation delay as well as measurement delay. Some work in recent times has factored in studying the effects of state-based delay on PID performance on a lumped-mass model [42]. In addition to stick-slip and actuation delay, there is also a lack of literature on actuation constraints affecting the ability to reach a desired control outcome. In this paper, a combined control approach to tackling stick-slip featuring both actuation delay and constraints is considered by utilising the ‘Modified Integral Resonant Control’ (MIRC) with Integral Tracking [43]. This aforementioned scheme is a modified version of the IRC damping scheme first developed to mitigate linear system resonances [44], and is capable of imparting significant damping to nonlinear resonances as well [45]. This combined control scheme is a simple, combination of two first-order controllers that work by adding two extra state equations to the system in question and requires no complicated design as required by the SMC. It then includes the use of integral tracking to meet the desired criterion of constant drilling. Incidentally, the scheme only requires a selection of the control gain/s—easily achievable via a limited numerical search. Moreover, as it is of a similar complexity to PID control, this allows for easy implementation. It should also be noted that this controller does not rely on the linearisation of the drill-string model unlike the $\mu$-synthesis control, thus allowing for more realistic global performance.

The rest of the paper is structured as follows: Sect. 2 presents the open-loop model for the drill-string and classifies all the different parameters and demonstrates its well known open-loop behaviour; Sect. 3 introduces the controller structure and demonstrates how it is added to the drill-string model presented in Sect. 3 with a subsection devoted to demonstrating its results. Section 4 introduces the Sliding-Mode Control with its parameters and construction. Section 5 compares said scheme with the SMC directly via more simulations. Section 6 delves into the detail of the scheme’s behaviour in terms of its gains and also further investigates the effects of varying actuation delay on the drill-string system response. Finally, Sect. 7 concludes the paper.

2 Experimental model with open-loop behaviour

In this section, the open-loop model for a 2-DOF underactuated drill-string is presented along with a table of parameters. The model is numerically simulated and its dynamical behaviour is explored via bifurcation diagrams, phase portraits and time histories.

To derive the system equations, the Euler–Lagrange equation can be used:

$$\begin{aligned} \dfrac{\partial }{\partial t}\left( \dfrac{\partial L}{\partial {\dot{q}}_k}\right) -\dfrac{\partial L}{\partial q_k}+\dfrac{\partial D}{\partial {\dot{q}}_k} = {\mathcal {Q}}_k, \end{aligned}$$

(1)

where the generalised coordinates can be defined as $q_k = \left[ \phi _t,\quad \phi _b\right] ^T\in {\mathbb {R}}^{2\times 1}$, time is $\{t\in {\mathbb {R}}:t\ge 0\}$, the Langrangian is ${\mathcal {L}}: {\mathbb {R}}^{2\times 1}\rightarrow {\mathbb {R}}$ such that ${\mathcal {L}}={\mathcal {T}}-{\mathcal {U}}$ (where ${\mathcal {T}}: {\mathbb {R}}^{2\times 1}\rightarrow {\mathbb {R}}$ and ${\mathcal {U}}: {\mathbb {R}}^{2\times 1}\rightarrow {\mathbb {R}}$), Rayleigh’s Dissipation Function is ${\mathcal {D}}: {\mathbb {R}}^{4\times 1}\rightarrow {\mathbb {R}}$ and the generalised force vector ${\mathcal {Q}}_k: {\mathbb {R}}^{2\times 1}\rightarrow {\mathbb {R}}^{2\times 1}$. Assuming that; $\phi _t>\phi _b$ (as choosing a consistent convention for Lagrangian Mechanics is essential), the total kinetic energy ${\mathcal {T}}$ can be defined as follows:

$$\begin{aligned} {\mathcal {T}}=\dfrac{1}{2}J_t{\dot{\phi }}_t^2+\dfrac{1}{2}J_b{\dot{\phi }}_b^2. \end{aligned}$$

(2)

The total potential energy ${\mathcal {U}}$ can be defined as follows:

$$\begin{aligned} {\mathcal {U}}= \dfrac{1}{2}k_s(\phi _t-\phi _b)^2. \end{aligned}$$

(3)

Consequently, Rayleigh’s Dissipation Function ${\mathcal {D}}$ can be defined as follows:

$$\begin{aligned} {\mathcal {D}}= \dfrac{1}{2}c_{r}{\dot{\phi }}_t^2+\dfrac{1}{2}c_s({\dot{\phi }}_t-{\dot{\phi }}_b)^2. \end{aligned}$$

(4)

Lastly, the generalised force vector ${\mathcal {Q}}_k$ can be defined as follows:

$$\begin{aligned} {\mathcal {Q}}_k= \begin{bmatrix} u,&-T_b \end{bmatrix}^T. \end{aligned}$$

(5)

where u and $T_b$ are the input top- and friction torques, respectively. By substituting Eqs. (2, 3, 4 and 5) into (1) and evaluating for each coordinate $q_k$, the set of differential equations which describe the model are

$$\begin{aligned}&J_t \ddot{\phi }_t + \left( c_s+c_{r}\right) {\dot{\phi }}_t +k_s\phi _t - c_s{\dot{\phi }}_b- k_s\phi _b = u, \end{aligned}$$

(6)

$$\begin{aligned}&J_b \ddot{\phi }_b + c_s{\dot{\phi }}_b + k_s \phi _b -c_s {\dot{\phi }}_t - k_s\phi _t = -T_b. \end{aligned}$$

(7)

The friction model for $T_b$ used is defined as follows [17]:

$$\begin{aligned} T_b = {\left\{ \begin{array}{ll} \tau _r, &{} \text {if} \quad \Vert {\dot{\phi }}_b\Vert<\zeta \quad \text {and} \quad \Vert \tau _r\Vert \le \tau _s \\ \tau _s\,\text {sgn}\left( \tau _r\right) , &{} \text {if} \quad \Vert {\dot{\phi }}_b\Vert <\zeta \quad \text {and} \quad \Vert \tau _r\Vert > \tau _s \\ \mu _b R_b WOB\,\text {sgn}\left( {\dot{\phi }}_b\right) , &{} \text {if} \quad \Vert {\dot{\phi }}_b\Vert \ge \zeta . \end{array}\right. }\nonumber \\ \end{aligned}$$

(8)

The adopted friction model operates the drill-string in one of the three key phases. Phase 1 is the sticking phase in which the bit is not moving (${\dot{\phi }}_b < \zeta$) due to the static friction torque $\tau _s$ being equal to or more than the absolute value of the reaction torque $\tau _r$: $\Vert \tau _r\Vert \le \tau _s$. Phase 2 is the stick-to-slip shase in which the bit just about to move (${\dot{\phi }}_b < \zeta$) as the static friction torque $\tau _s$ is less than the absolute value of the reaction torque $\tau _r$: $\Vert \tau _r\Vert > \tau _s$. Phase 3 is the slip phase in which the bit begins to move (${\dot{\phi }}_b \ge \zeta$) and cuts into the rock. Table 2 presents the relevant mathematical expressions/ranges for all the system parameters.

Table 1 Model parameters, values and units

Table 2 Description of model parameters

For simulation purposes, Eqs. (6, 7) and the friction model (8), can be seen as producing three separate state-space models that the system can discontinuously switch between, based on initial conditions, WOB and u. To numerically simulate Eqs. (6 and 7), the following state-variables are defined:

$$\begin{aligned} X&= \begin{bmatrix} {\dot{\phi }}_t ,&\phi _t-\phi _b ,&{\dot{\phi }}_b \end{bmatrix}^T = \begin{bmatrix} x_1,&x_2,&x_3 \end{bmatrix}^T. \end{aligned}$$

(9)

Equations (6 and 7) can be rearranged as a system of first-order differential equations as follows:

$$\begin{aligned} \begin{aligned} {\dot{x}}_1&=\dfrac{1}{J_t}\left[ u - \left( c_s+c_{r}\right) x_1+ c_s x_3 - k_s x_2 \right] \\ {\dot{x}}_2&= x_1-x_3 , \\ {\dot{x}}_3&=\dfrac{1}{J_b}\left[ c_s x_1 -c_s x_3 + k_s x_2 -T_b \right] . \end{aligned} \end{aligned}$$

(10)

To classify the precise behaviour of the drill-string, details about the equilibria of the uncontrolled system need to be extracted. Let $\Gamma$ be a manifold where the bit velocity equals zero:

$$\begin{aligned} \Gamma {:}{=} \{ q_k\in {\mathbb {R}}^{2\times 1}:{\dot{\phi }}_b=0 \}. \end{aligned}$$

(11)

Similarly, let $\Sigma$ be a manifold where the bit velocity equals some constant angular velocity $\Omega _c$:

$$\begin{aligned} \Sigma {:}{=} \{ q_k\in {\mathbb {R}}^{2\times 1}:{\dot{\phi }}_b=\Omega _c \}. \end{aligned}$$

(12)

There exists a subset of $\Gamma$ that represent a unique attractive region depending upon the WOB, u and the initial conditions of the system. Let ${\hat{\Gamma }}_{s}\subseteq \Gamma$ which relates to the Stick-phase, i.e. ${\dot{\phi }}_b=0$:

$$\begin{aligned} {\hat{\Gamma }}_s {:}{=} \{ q_k\in \Gamma : | c_s{\dot{\phi }}_t+k_s\left( \phi _t-\phi _b\right) | < \mu _{sb}R_bWOB\}.\nonumber \\ \end{aligned}$$

(13)

Let ${\hat{\Sigma }}_{c}\subseteq \Sigma$ which concerns the case of steady drilling, namely $[{\dot{\phi }}_t,{\dot{\phi }}_b]=\Omega _c$, where $\Omega _c$ represents a constant angular velocity:

$$\begin{aligned} {\hat{\Sigma }}_c {:}{=} \{ q_k\in \Sigma : |k_s\left( \phi _t-\phi _b\right) |>\mu _{sb} R_b WOB\}. \end{aligned}$$

(14)

The creation of these subsets is caused by the friction model defined by Eq. (8) and can lead to three different behaviours. The bit remains stuck in the borehole: $\forall t > t_{tr},q_k\in {\hat{\Gamma }}_s$. Thus, after a finite transient time $t_{tr}$, the system reaches the attractive region ${\hat{\Gamma }}_s$ and remains there indefinitely. The bit goes into steady drilling mode and enters the attractive region ${\hat{\Gamma }}_c$: $\forall t > t_{tr},q_k\in {\hat{\Gamma }}_c$. Thus, after a finite transient time $t_{tr}$, the system reaches the attractive region ${\hat{\Gamma }}_c$ and remains there indefinitely. The system enters and leaves the subset ${\hat{\Gamma }}_s$ in the form of stick-slip oscillations. In this case, the system can never permanently stay in the attractive region of permanent sticking nor can it reach constant-drilling region.

To infer some important information about the drill-string model, the equilibria of the system should be considered. There exists two distinct equilibria, namely the constant drilling and the stick equilibria, respectively. Consider the case of stick in which the top-drive and bit-head velocities are zero, respectively, (${x}_1={x}_3 = 0$) and the state variable derivative is also zero (${\dot{X}} = 0$ and) in Eq. (10). Then, the equilibrium for $x_{e2}$ is

$$\begin{aligned} x_{e2}= \dfrac{u}{k_s}. \end{aligned}$$

(15)

This translates to an overall equilibrium vector ${\bar{x}}_s$ as follows:

$$\begin{aligned} {\bar{x}}_s=\left[ 0,\dfrac{u}{k_s},0\right] ^T. \end{aligned}$$

(16)

Now, consider the case of constant drilling in which the top-drive and bit-head velocities are some positive constant $\Omega _c$, respectively, (${x}_1={x}_3 = \Omega _c$) and the state variable derivative is also zero (${\dot{X}} = 0$ and ${x}_1={x}_3 = \Omega _c$) in Eq. (10). Then, the equilibrium $x_{e2}$ can be shown to be

$$\begin{aligned} x_{e2} =\dfrac{u - c_{r}\Omega _c}{k_s}. \end{aligned}$$

(17)

This translates to an overall equilibrium vector ${\bar{x}}_c$ as follows:

$$\begin{aligned} {\bar{x}}_c=\left[ \Omega _c,\dfrac{L}{k_s},\Omega _c\right] ^T. \end{aligned}$$

(18)

With these system equilibria demonstrated, the behaviour of Eq. (10) and the aforementioned bit–rock model (8) is shown overleaf in the form of a labelled centre figure (see Fig. 2).

Fig. 2

Red triangles, blue circles and black squares represent the states of stick-slip, constant drilling and stick, respectively. a–c represent combined time histories with phase portraits for the top-torques of; $u=3,15,60$, respectively. d is the central top-torque bifurcation diagram from which (a–c), (e) and (f) are generated from. e represents a co-existing basins plot at $u=45$. f shows the Weight-On-Bit bifurcation perspective of (d). g shows the two co-existing responses of stick-slip and constant drilling together on the same phase-plane for $u=45$

Bifurcation diagrams (d) and (f) show that the WOB and top-torque both play an equally pivotal role for producing co-existing attractors. The region of $u=[8,20]\,\hbox {N m}$ in (d) possesses an unstable constant-drilling branch not accessible practically (or via traditional numerical integration) except with the method of numerical continuation or via some stabilising control method. As can be seen in Fig. 2d, stick-slip and constant-drilling attractors coexist within the region bound by $u=[21,56]\,\hbox {N m}$ while $u=[57,60]\,\hbox {N m}$ denotes region where the drill-string only operates in the constant-drilling mode. Another important point to note is that as shown in the basins of attraction plotted in Fig. 2e, the parameter-space defined by the range of initial conditions analysed herewith is dominated by stick-slip. With the adopted drill-string and bit–rock models validated via the simulation results shown in Fig. 2, this work proceeds to design and implement the Modified Integral Resonant Control with Integral Tracking aimed at eliminating the unwanted stick-slip oscillations featuring actuation constraints and actuation delay.

3 Modified integral resonant control-based damping with integral tracking featuring delay and constraints

The main control objective for any effective drill-string control strategy is to minimise (ideally eliminate) the damaging stick-slip oscillations and guide the system into a state of constant drilling where possible [46, 47]. The MIRC-based damping scheme with Tracking Control is a combination of four gains with a desired reference variable viz: the Output gain $\lambda$, the Feed-Through gain $\kappa$ and the Integrator gain $\eta$, which are all connected to an Integrator belonging to the MIRC; as depicted in Fig. 3f, [43] and then a single integrator gain $k_i$ with desired reference $\Omega _c$. These gains are easily selected via a simple numerical search over a range of parameter-space. Two new controller states $\psi$ and $\nu$ are defined and then embedded into Eqs. (6 and 7) by producing extra state differential equations. Consider the following closed-loop Lagrangian, with an adapted set of generalised coordinates $q_k^{cl} = [\phi _t,\quad \phi _b, \quad \psi , \quad \nu ]\in {\mathbb {R}}^{4\times 1}$ accompanied by a new generalised forcing vector ${\mathcal {Q}}_k^{cl}$:

$$\begin{aligned} {\mathcal {L}}_{cl}={\mathcal {L}}+\dfrac{1}{2}\int {\dot{\psi }}^2dt -\dfrac{\kappa \eta }{2}\psi ^2 + \dfrac{1}{2}\int {\dot{\nu }}^2dt. \end{aligned}$$

(19)

The updated generalised force vector ${\mathcal {Q}}_k$ is then redefined as

$$\begin{aligned} {\mathcal {Q}}_{k}^{cl}= \begin{bmatrix} u+\eta \psi ,&-T_b,&-\lambda \left( {\dot{\phi }}_b-{\dot{\phi }}_t\right) ,&\Omega _c - {\dot{\phi }}_t \end{bmatrix}^T.\qquad \end{aligned}$$

(20)

Thus, by applying the Euler–Lagrange equation to ${\mathcal {L}}_{cl}$ the controller differential equation can be written as

$$\begin{aligned} {\dot{\psi }} + \kappa \eta \psi +\lambda \left( {\dot{\phi }}_b-{\dot{\phi }}_t\right) = 0. \end{aligned}$$

(21)

Consequently, the system dynamics can be described by

$$\begin{aligned}&J_t \ddot{\phi }_t + \left( c_s+c_{r}\right) {\dot{\phi }}_t +k_s\phi _t - c_s{\dot{\phi }}_b- k_s\phi _b = \overbrace{u + \eta \psi + k_i \nu }^{\text {New Input}} \nonumber ,\\&J_b \ddot{\phi }_b + c_s{\dot{\phi }}_b + k_s \phi _b -c_s {\dot{\phi }}_t - k_s\phi _t = -T_b\nonumber ,\\&{\dot{\psi }} +\eta \kappa \psi + \lambda \left[ {\dot{\phi }}_b-{\dot{\phi }}_t\right] = 0,\nonumber \\&{\dot{\nu }} - \left[ \Omega _c - x_1\right] = 0. \end{aligned}$$

(22)

To aid in simulation, a state-vector ${\bar{X}}$ includes the controller variable:

$$\begin{aligned} {\bar{X}} = \begin{bmatrix} {\dot{\phi }}_t ,&\phi _t-\phi _1 ,&\dot{\phi _1},&\psi ,&\nu \end{bmatrix}^T= \begin{bmatrix} x_1,&x_2,&x_3,&x_4,&x_5 \end{bmatrix}^T. \end{aligned}$$

(23)

This redefinition allows the aforementioned equations (22) to be re-written as a system of first-order differential equations given by

$$\begin{aligned} {\dot{x}}_1&=\dfrac{1}{J_t}\left[ u + \eta x_4 + k_i x_5 - \left( c_s+c_{r}\right) x_1+ c_s x_3 - k_s x_2 \right] \nonumber ,\\ {\dot{x}}_2&= x_1-x_3 , \nonumber \\ {\dot{x}}_3&=\dfrac{1}{J_b}\left[ c_s x_1 -c_s x_3 + k_s x_2 -T_b \right] ,\\ {\dot{x}}_4&= -\kappa \eta x_4 - \lambda \left[ x_3-x_1\right] .\nonumber \\ {\dot{x}}_5&= \Omega _c-x_1.\nonumber \end{aligned}$$

(24)

A full discussion on the closed-loop stability as well as closed-loop equilibria is shown in the appendix. Both experimental and real-life drill-string structures are subject to system-induced delay and in the case of many experiments, actuator constraints as well. Equations (24) are modified to include control actuation delay and actuation according to Table 1:

$$\begin{aligned} {\dot{x}}_1&=\dfrac{1}{J_t}\left[ u + \eta x_4(t-\tau _d) + k_i x_5(t-\tau _d) - \left( c_s+c_{r}\right) x_1\nonumber \right. \\&\left. \quad + c_s x_3 - k_s x_2 \right] ,\nonumber \\ {\dot{x}}_2&= x_1-x_3 \nonumber , \\ {\dot{x}}_3&=\dfrac{1}{J_b}\left[ c_s x_1 -c_s x_3 + k_s x_2 -T_b \right] ,\nonumber \\ {\dot{x}}_4&= -\kappa \eta x_4 - \lambda \left[ x_3-x_1\right] \nonumber ,\\ {\dot{x}}_5&= \Omega _d - x_1. \end{aligned}$$

(25)

The following table details the exact scheme gains used for the following simulations seen in Fig. 3.

Fig. 3

a–c Represent the time-history, 2D and 3D phase-plane, respectively, for the case in which $u=40$. The natural system response is given by (.- red) and scheme altered response (- blue), respectively. d is the central top-torque bifurcation diagram from which the results of (a–c), (e) and (g) are derived and is marked to show the stick-slip to constant-drilling transition. e shows the control input for this case. (f) shows the scheme’s structure. g shows the scheme controlled basins of attraction

Table 3 Controller parameters and value(s)

To verify the effectiveness of the scheme, the notion of ‘Vibration Reduction Factor’ (VRF) must be introduced. VRF is a relative means of comparing the amplitude of stick-slip oscillations in open-loop with the amplitude of the closed-loop response. There exists four possible controller outcomes with which VRF can assist with classifying effectiveness, namely Case 1 ($\ge 95\%$VRF) which is constant drilling, Case 2 ($\le 95\%$VRF) and no bit-sticking which is torsional vibration, Case 3 ($+ve\%$VRF) with bit-sticking (reduced stick-slip amplitude) and lastly, Case 4 ($-ve\%$VRF) with bit-sticking (in which the stick-slip is made worse). Successful results lie in Cases 1 and 2, respectively, wherein the drill-string is no longer undergoing stick-slip. The formula used to classify VRF is as follows:

$$\begin{aligned} VRF\% = 100\cdot \dfrac{{\bar{a}}_{ol} - {\bar{a}}_{cl}}{{\bar{a}}_{ol}}, \end{aligned}$$

(26)

where ${\bar{a}}_{ol}$ is the average open-loop stick-slip amplitude of vibration and ${\bar{a}}_{cl}$ is the average closed-loop vibration amplitude. It should be noted that this formula does not indicate if a system is under stick-slip or not in cases 3 and 4. In these cases, extra care is required to label and classify the response along with the VRF result. The following simulation shows preliminary results of the MIRC with tracking control under the effects of delay and constraints.

Figure 3d shows the detailed bifurcation diagram. In this diagram, the top-torque is varied from $u\in [0,60]\,\hbox {N m}$. In the experimental setup, as discussed in Table 1, there are minimum and maximum torque constraints. To reflect this, the unstable constant-drilling solutions that are not reachable are represented by grey pentagons. When within these control input limits, the scheme is capable of finding the blue circle constant-drilling attractors and eliminating the stick-slip found within this region. Figure 3a, b and c shows the natural system response of stick-slip being driven to that of the other natural system response of constant drilling thanks to the scheme’s resonance suppression and tracking effects. The system is first settled into a stick-slip regime up to $t=30\,\hbox {s}$ and then the scheme is activated therewith. Under both actuation constraints and actuation delay, tracking a constant velocity of $\Omega _d = 2.992\hbox {rad s}^{-1}$ and suppressing stick-slip is observed. Figure 3e depics the control input graph and demonstrates a brief saturation of the upper and low control input limits and settles once constant drilling is achieved. Figure 3g demonstrates that with the scheme enabled, the initial conditions do not affect the final response of the system thereby demonstrating invariance. The following simulations demonstrate the scheme’s ability to track from different scenarios.

Fig. 4

Open-loop (.- red) and scheme controlled (- blue). a–c show three cases in the scheme aims to $\Omega _d=2.11\,\hbox {rad s}^{-1}$, $\Omega _d=2.99\,\hbox {rad s}^{-1}$ and $\Omega _d=3.87\,\hbox {rad s}^{-1}$ from stick-slip, respectively. e–g show three more cases in which the scheme tracks $\Omega _d=2.99\,\hbox {rad s}^{-1}$ starting in stick, attempts to track $\Omega _d=1.28\,\hbox {rad s}^{-1}$ starting in stick-slip and tracks $\Omega _d=5.19\,\hbox {rad s}^{-1}$ from constant drilling

In these simulations, six test scenarios are chosen. (a), (b) and (c) are all started in stick-slip at $u_{st}=40$ and then lower, middle and higher desired velocities are chosen. Each case is successful as none of these desired velocities rely on a final $u<u_l$. The next three cases consider the situations of starting from stick, attempting to track from stick-slip to the natural constant-drilling attractor and starting from constant drilling and going to a high desired velocity. The scheme is successful for cases Fig. 4e and g as the desired velocity requires a final u that is within the constraints given. Figure 4f is naturally unsuccessful as the scheme is attempting to track a velocity that requires a lower u than the minimum constraint. To examine the controller’s robustness, a multi part bifurcation diagram which examines how the change in the drill-string stiffness $k_s$ changes affects the controller’s ability to suppress stick-slip and track a desired velocity is examined overleaf.

Fig. 5

c is the central bifurcation diagram in which the bifurcation parameter is spring coefficient $k_s$. Bifurcation diagrams (a) and (e) use the desired velocity $\Omega _d$ as the bifurcation parameter and are derived from (c). b, d and f show three examples of successful, unsuccessful and partially successful responses from the bifurcation diagrams

The centre Fig. 5c acts as the primary bifurcation diagram for all other plots around it. In (d) the bifurcation variable is the torsional spring coefficient $k_s$ and for each $k_s$, the controlled system is made to track $\Omega _d = 2.552\,\hbox {rad s}^{-1}$. Figure 5a and e is sub-bifurcation diagrams derived from Fig. 5d at $k_s=10\,\hbox {N m rad}$ and $k_s=20\,\hbox {N m rad}$, respectively, in which the bifurcation parameter is the desired velocity $\Omega _d$. Overall the scheme has great success up to $k_s=15$ upon which it fails to suppress stick-slip and guide the system to the desired velocity ($100\%\, VRF$) which is confirmed by Fig. 5a. In addition to this, Fig. 5a shows that when $k_s\le 15$, any desired velocity that requires a final u within the constraints mentioned, it is successful. Overall, there exists some excellent robustness to the main changing system parameter $k_s$ and the scheme, when not working optimally for $k_s>15$, does not cause system instabilities as seen in Fig. 5e, but overall the scheme can not stabilise the majority of velocities for this $k_s$ range. In the following section, the SMC is defined and compared directly to the scheme in question (Tables 3, 4).

4 Sliding-mode control

In this section, the SMC is defined mathematically, investigated and compared directly to the scheme in question. Bifurcation plots and basins of attraction like plots are used to make these comparisons. The SMC adopted as a candidate for comparison starts by defining a sliding surface given by [37]

$$\begin{aligned} s = \left( x_1 - \Omega _d\right) + \Gamma \int _{0}^{t}\left( x_1 - \Omega _d\right) d\tau + \Gamma \int _{0}^{t}\left( x_1 - x_3\right) d\tau , \end{aligned}$$

(27)

where $\Gamma$ is a user chosen control variable and $\Omega _d$ is the desired angular speed. The key benefit of this SMC is its capability of utilising estimated system parameters. But this is easily matched by the proposed MIRC-based damping+tracking scheme by its excellent robustness to parameter uncertainty. The estimated parameters are denoted as: $\hat{c}_r$, $\hat{c}_s$, $\hat{k}_s$ and $\hat{J}_t$. The ideal controller equation can be derived by differentiating (27) and substituting it into equations (10) and rearranging for u. Upon doing this, by replacing all original variables with their estimated ones, the estimated controller equation is shown to be:

$$\begin{aligned} u_{est}= & {} \left( \hat{c}_r+\hat{c}_s\right) x_1 - \hat{c}_sx_3 + \hat{k}_sx_2 - \hat{J}_t \Gamma \left( x_1 -\Omega _d\right) \nonumber \\&- \hat{J}_t \Gamma \left( x_1 -x_3\right) . \end{aligned}$$

(28)

In addition, the upper bounds of the estimated model are given as

$$\begin{aligned} \Vert \hat{c}_r - c_r\Vert&\le M_{cr}, \quad \Vert \hat{c}_s - c_s \Vert \le M_{cs}, \quad \nonumber \\ \Vert \hat{k}_s - k_s \Vert&\le M_{ks}, \quad \Vert \hat{J}_t - J_t\Vert \le M_{jt}. \end{aligned}$$

(29)

Fig. 6

b is the central bifurcation diagram in which the bifurcation parameter is spring coefficient $k_s$. Bifurcation diagrams (a) and (d) use the desired velocity $\Omega _d$ as the bifurcation parameter and are derived from (b). c and e show a basins of attraction style plot in which the $k_s$ and $\Omega _d$ are varied on a grid to infer regions of desired responses for both the SMC and the scheme in question

From this, the asymptotically convergent switching law is defined as

$$\begin{aligned} u_{sw}&= -\dfrac{M_{cr}\Vert x_1-x_3\Vert s}{\Vert s\Vert + \delta _1 \exp \left( -\delta _2\int \Vert x_1-x_3\Vert d\tau \right) }\nonumber \\&\quad -\dfrac{M_{cs}\Vert x_1\Vert s}{\Vert s\Vert + \delta _1 \exp \left( -\delta _2\int \Vert x_1\Vert d\tau \right) } +\cdots \nonumber \\&\quad -\dfrac{M_{ks}\Vert x_2\Vert s}{\Vert s\Vert + \delta _1 \exp \left( -\delta _2\int \Vert x_2\Vert d\tau \right) }\nonumber \\&\quad -\dfrac{M_{jt}\Gamma \Vert x_1-\Omega _d\Vert s}{\Vert s\Vert + \delta _1 \exp \left( -\delta _2\int \Gamma \Vert x_1-\Omega _d\Vert d\tau \right) }+\cdots \nonumber \\&\quad -\dfrac{M_{jt}\Gamma \Vert x_1-x_3\Vert s}{\Vert s\Vert + \delta _1 \exp \left( -\delta _2\int \Gamma \Vert x_1-x_3\Vert d\tau \right) } - \rho s, \end{aligned}$$

(30)

where $\delta _1$ and $\delta _2$ are small controller parameters that are user chosen and are much smaller than 1 and $\rho$ is another user chosen control parameter. The final SMC control input is defined as

$$\begin{aligned} u = u_{est} + u_{sw}. \end{aligned}$$

(31)

The SMC parameter table can be found in the appendix. To compare the SMC to the scheme in question, Fig. 5a, c, and e is repeated for the SMC. In addition to this, a basins of attraction like analysis for $k_s$ and $\Omega _d$ is carried out for the SMC and scheme, respectively, to compare their regions of success. For the simulations overleaf, the scheme control gains are set to $\kappa =1$, $\eta = 70$, $\lambda = -10$ and $k_i=3$.

Table 4 Weighted percentage results

5 Scheme vs sliding-mode control comparison

To compare the scheme in question with the SMC, similar analyses seen in Fig. 5 are carried out. To fully compare the two methodologies, additional basins of attraction like simulations are also carried out between the two to fully compare the regions of operation.

Fig. 7

a–c show the effects of varying each respective controller gain when tracking the same desired velocity. d–f show the effects of varying each respective gain while also varying the desired velocity target

When comparing Fig. 6b to Fig. 5c, it is clear that the SMC performs much more poorly than the scheme highlighted in this work. There exists only a single $100\%\,VRF$ result whereas the scheme had constant $100\%\,VRF$ results up to and including $k_s=15$. Comparing Fig. 6a to Fig. 5a reinforces the success of the scheme over the SMC as the SMC is incapable of generating any $100\%\,VRF$ results for a range of desired velocities. Comparing Fig. 6e to Fig. 5d, a similar performance is observed between the two methodologies with the SMC coming out on top slightly by providing more partial successes (torsional vibration responses) for $k_s=20$. Figure 6c and e perfectly summarises the performance difference between the two methodologies. The scheme in question has a large range of constant-drilling responses whereas the SMC only has a large range of torsional vibration responses with a few constant-drilling ones. It is clear that the scheme has superior performance to the SMC. In the following result table, a constant-drilling response scores 2/2, torsional vibration response 1/2 and stick-slip response 0/2 and any positive result is scaled and added together appropriately.

Fig. 8

a–c show the effects of the row 1 gains chosen in Table 7 for the cases of $k_s=1,10,20$ and demonstrates clear regions of success and failure in each case. d–f show the effects of the row 2 gains chosen in Table 7 for the cases of $k_s=1,10,20$. For these cases, the change in $\lambda$ creates a greater desired regime for $\Omega _d\ge 3$ for $\tau _d\in [0,2.4]$. This comes at the price of losing access to lower desired velocities across most delays

6 Detailed scheme analysis

To understand the effects that the scheme’s gains have on the system response, a gain study for; $\lambda$, $\eta$ and $\kappa$ is performed. In the following simulations top row of simulations, the desired outcome is to suppress stick-slip and reach the desired velocity of $\Omega _d = 2.552\,\hbox {rad s}^{-1}$. In the second row of simulations, the desired velocity $\Omega _d$ is varied along with the gain of interest. When investigating a single gain, others are kept constant. Table 6 used for this simulation can be found in the Appendix and details each simulation’s parameters.

The $\lambda$ and $\kappa$ gains are the two main gains, as seen in Fig. 7b and c, and e and f, that produce resonance suppressive effects or can even induce torsional vibrations in the drill-string as evidenced by the small regions of torsional vibrations in the basins-like plots. The $\eta$ gain serves to engage the scheme and has only a small part to play in producing the ideal response of constant drilling. Conclusively, there exists very defined regions of optimal operation for each gain which aids in the robustness of the scheme to variations in system response as well the desired velocity. Further to this, a detailed analysis is carried out with three test cases of $k_s=1,10,20$ under the effects of varying actuator delay $\tau _d$ and desired velocity $\Omega _d$. Table 7, seen in the appendix, details the simulation parameters for investigating varying delay and changing the $\lambda$ gain.

In the first row of simulations, there are clear regions in which the scheme successfully produces the ideal response under varying delay and even under changing $k_s$. In general, the higher the $k_s$, the harder it becomes to drive in the presence of increasing delay. In these simulations, it is shown that under the effects of varying delay and the same actuation constraints, extra robustness to delay can be produced by altering the $\lambda$ gain, but this comes at the cost of the ability to track smaller target velocities even within the actuation constraints. The overall robustness to the incredibly detrimental effect of actuator delay is an impressive feature of this scheme especially when aggressive control is not possible due to the actuation limits thereby proving its worth over the SMC (Fig. 8).

7 Closing remarks

In this work, a modified integral resonant controller with integral tracking is investigated on a 2-DOF drill-string featuring actuator delays as well as actuation constraints. The combination of these systematic limitations, which are based directly on an in-house experiment, make for a unique investigative opportunity to test the aforementioned controller. First, the 2-DOF model with nonlinear bit–rock interaction is verified numerically in the form of torque and weight-on-bit bifurcation diagrams. Time histories, combined with 2D and 3D phase portraits are shown to demonstrate the three main drilling responses available to the aforementioned model, namely stick (no drilling), stick-slip (a limit cycle response) and constant drilling. Further to this, the bifurcation diagrams also reveal the co-existence of system solutions for a given torque and weight-on-bit, i.e. the co-existence of constant drilling and stick-slip. The ideal case of constant drilling is the desired response and is the main control focus in this work.

The scheme in question is subsequently introduced and it is able to successfully track to steady drilling when the drill-string is started in stick-slip. Due to the control input constraints caused by the motor’s characteristics as well as actuation delay, saturation of the control input is observed, but despite this saturation and delay it does not affect the chosen case with the stabilisation of constant drilling. Subsequent to this, numerous cases from different starting points on the torque bifurcation diagram in to determine if the scheme runs into stick-slip on the way to any of the solutions. It is found that tracking is possible from almost any starting torque or initial condition except when it comes to trying to reach an unstable constant-drilling solution due to the lower control input constraint imposed. When verifying the scheme’s robustness, it is tested under the most commonly varying drill-string model parameter, namely the torsional spring coefficient and is the primary bifurcation variable of choice. Change in stiffness of this variable has the potential to greatly affect the ability for it to work properly especially while contesting with constrained inputs and actuation delay. It is found that stabilisation of the ideal constant-drilling response is possible for a large range spring coefficients is possible, but failure occurs for larger spring values when the gains are not changed. Two sub-bifurcation diagrams, which utilise the desired velocity as the bifurcation parameter, also confirm its success and failure in extreme cases. Using these bifurcation diagrams as the framework for control performance, the Sliding-Mode Controller is subsequently introduced as the previous state-of-the-art for comparing the scheme to. It is found that the SMC has much worse performance over the successful range that the scheme in question has and at best, produces a torsional vibration response only with many stick-slip responses. The scheme is found to have a very clear and defined region of constant drilling whereas the SMC has only a clear torsional vibration response with a small region of constant drilling for low spring values. These simulations confirmed that the scheme is superior in overall performance as well as for consistency in operation when compared to the SMC.

A detailed gain analysis on the MIRC portion of it is carried out as it is responsible for the majority of the stick-slip suppression. It is found that there is connection between reaching the desired response of constant drilling and each gain. In particular, the output feedback gain $\lambda$ has the greatest effect on reaching the desired response as it has the greatest affect on resonant dynamics present within a system. The feedforward gain $\kappa$ is also found to have an impact on the resonant dynamics of the system response but to a lesser degree. Lastly, the scheme is also investigated under varying actuator delay while still under the same actuation constraints. It is found that there exists small regions of successful constant drilling when its gains are not tuned to the system. When tuning the output feedback gain $\lambda$, it is found that greater consistent ranges of constant drilling can be produced as the cost of losing the ability to track lower desired velocities for smaller actuator delay values.

Conclusively, the scheme has promising robustness to varying system parameters, varying actuator delay and actuation constraints and proves itself to be superior to that of the previous state-of-the-art SMC. Further work would include an experimental verification of the controller with extensive gain testing to confirm the simulations in this work.

Appendix

See Tables 5, 6, 7.

Table 5 Values of SMC parameters

Table 6 Gain simulations parameters

Table 7 Delay simulations parameters