Flavour observables and composite dynamics: leptons

Abstract

We review lepton flavor physics and corresponding observables in the composite Higgs framework with partial compositeness, considering ‘UV complete’ setups as well as effective and holographic approaches. This includes anarchic flavor setups, scenarios with flavor symmetries, and minimal incarnations of the see-saw mechanism that naturally predict non-negligible lepton compositeness. We focus on lepton flavor violating processes, dipole moments, and on probes of lepton flavor universality, all providing stringent tests of partial compositeness. We discuss the expected size of effects in the different approaches to lepton flavor, which will be useful to understand how a composite lepton sector could look like, given up-to-date experimental constraints.

1 Introduction

Within the composite Higgs (CH) framework, partial compositeness (PC) offers an attractive means to address the hierarchies present in the flavor sector, while simultaneously suppressing dangerous flavor-chaning neutral currents (FCNCs) via a ’geometric’ GIM-like mechanism [1,2,3,4,5]. While the basic properties of quarks and leptons share some similarities, such as the large hierarchies in the masses of the charged states, reading

$$\begin{aligned} m_e=0.51\, \mathrm{MeV} \ \ll \ m_\mu =106\, \mathrm{MeV} \ \ll \ m_\tau =1.78\, \mathrm{GeV} \end{aligned}$$

(1)

in the lepton sector, they also feature striking differences: the leptonic mixing angles are rather sizable [6], all leptons are significantly lighter than the weak scale, and neutrinos are even many orders of magnitude lighter than any other Standard Model (SM) particle, $m_{\nu _i}\lesssim 1$ eV.

Following the paradigm of PC, the lepton masses quoted in Eq. (1) could lead to the expectation that leptons are largely elementary and that the known leptons should behave basically SM-like and for example have a negligible impact on the one-loop Higgs potential or on not extremely well-constrained lepton observables. However, as we will see below, explicit models addressing the structure of charged and neutral lepton masses and mixings can lead to different conclusions and predict a moderate lepton compositeness. Beyond that, even in the case of mostly elementary leptons, the stringent limits from lepton flavor physics can lead to non-trivial bounds on the parameter space.

PC for leptons has been considered in [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], mostly from a low-energy point of view and via holographic methods. More recently, UV complete realizations of partially composite leptons have been envisaged, considering the fundamental degrees of freedom and the dynamics that leads to the bound states that mix linearly with the elementary fermions, which adds structure and potentially correlations to the setups [34,35,36,37,38,39,40]. Some promising scenarios, which are dubbed “fundamental partial compositeness” (FPC) [38,39,40] and will be very briefly reviewed below, assume the fermionic bound states to be composed of an elementary fermion ${\mathcal F}$ and a scalar ${\mathcal S}$, each. The inclusion of scalars has the advantage that the scaling dimension of the corresponding composite operator ${\mathcal O}_F$ is expected to vary moderately around the canonical value of $[{\mathcal O}_F]_0 =[{\mathcal F}]+[{\mathcal S}]=5/2$, which would allow to reproduce a viable spectrum of fermion masses via modest anomalous dimensions. While the presence of elementary scalars could reintroduce a hierarchy problem, purely fermionic constructions of PC [34,35,36,37] face strong challenges since they require extremely large anomalous dimensions of the composite operators such as to bring their scaling dimension towards $[{\mathcal O}_F] \approx 5/2$, starting from a canonical dimension of $3 \times 3/2=9/2 \gg 5/2$. Such large anomalous dimensions seem disfavoured [41,42,43], which leads in general to too suppressed fermion masses. On the other hand, the approach invoking scalars could be seen as a promising intermediate step to a full UV theory and it would, in fact, be very interesting to construct (potentially more involved) viable models without scalar constituents in the UV, realizing the techni-baryons with purely fermionic content and building on the pioneering work of [34,35,36,37], see also [44].¹

2 UV realization of partial compositeness for leptons

Assuming that the composite operators consist of a fermion and a scalar state, ${\mathcal O}_F = \langle {\mathcal F S} \rangle$, several models have been studied in the literature, considering the confining technicolor (TC)-like group $G_\mathrm{TC}$ to be SU($N_\mathrm{TC}$), SO($N_\mathrm{TC}$), or Sp($N_\mathrm{TC}$) [38, 39, 47]. In the following, we will focus on $G_\mathrm{TC}=$ Sp($N_\mathrm{TC}$) with four Weyl fermions ${\mathcal F}^a, a=1,..,4$, per techni-color, resulting in the global symmetry breaking (SB) pattern SU(4)$_{\mathcal F}$ $\rightarrow$ Sp(4)$_{\mathcal F}$ after formation of the fermionic condensate [39, 47]

$$\begin{aligned} \langle {\mathcal F}^a \epsilon _\mathrm{TC}\, {\mathcal F}^b \rangle = \Lambda _c f^2 \Sigma _\theta ^{ab} \,. \end{aligned}$$

(2)

Here $a,b\in$ SU(4)$_{\mathcal F}$,² which contains the SM electroweak (EW) group, $\Lambda _c \sim 4\pi f$ denotes the TC condensation scale (with f the pNGB decay constant), $\epsilon _\mathrm{TC}$ is the antisymmetric tensor of $G_\mathrm{TC}$, and $\Sigma _\theta$ an (antisymmetric) matrix parametrizing the alignment of the vacuum with the Sp(4)$_{\mathcal F}$ group. The techni-fermions are accordingly assumed to form a weak doublet ${\mathcal F}_{1,2}$ with vanishing hypercharge as well as two $SU(2)_L$ singlets ${\mathcal F}_{3,4}$ with hypercharges $Y=\mp 1/2$, respectively [39, 47].

The vacuum matrix can be written as

$$\begin{aligned} \Sigma _\theta = \cos \theta \left( \begin{array}{l@{\quad }l} i \sigma _2 &{} 0 \\ 0 &{} -i \sigma _2 \end{array}\right) + \sin \theta \left( \begin{array}{l@{\quad }l} 0 &{} \mathbf {1}_2\\ -\mathbf {1}_2 &{} 0 \end{array}\right) \,, \end{aligned}$$

(3)

with the EW vacuum expectation value (vev) $v=\sin \theta f$, such that $\sin \theta \!=\!0$ $(\sin \theta \!=\!1)$ corresponds to unbroken (fully broken) EW symmetry. Finally, the pNGBs of the SU(4)$_{\mathcal F}/$Sp(4)$_{\mathcal F}$ coset are parameterized as fluctuations around this vacuum via the Goldstone matrix

$$\begin{aligned} \Sigma (x)= \exp \left[ i \frac{2 \sqrt{2}}{f}\Pi _{\hat{a}}(x) T_\theta ^{\hat{a}}\right] \Sigma _\theta \,, \end{aligned}$$

(4)

where $T_\theta ^{\hat{a}}$ are the broken generators of SU(4)$_{\mathcal F}/$Sp(4)$_{\mathcal F}$, $\Pi _{1,2,3}$ are the EW Goldstone modes, $\Pi _4$ is the Higgs boson, and $\Pi _5$ an additional EW singlet.

Beyond this, 12 complex scalar degrees of freedom are introduced to realize FPC with $[{\mathcal O}_F] \approx 5/2$, residing in 3 generations of color triplets ${\mathcal S}_q$ with hypercharge $Y=-1/6$, and corresponding color singlets ${\mathcal S}_l$ with $Y=1/2$. Defining ${\mathcal S}=({\mathcal S}_q,{\mathcal S}_l)^T$, the full kinetic and mass terms of the TC sector are thus given by

$$\begin{aligned} {\mathcal L}_\mathrm{kin}= & {} -\frac{1}{4} {\mathcal G}_{\mu \nu }^a {\mathcal G}^{a\,\mu \nu } \!+ i {\mathcal F}^\dagger \bar{\sigma }^\mu D_\mu {\mathcal F} -\!\left( \!{\mathcal F}^T \frac{m_{\mathcal F}}{2} \epsilon _\mathrm{TC} {\mathcal F} \!+\!\mathrm{h.c.}\!\right) \nonumber \\&+(D_\mu {\mathcal S})^\dagger (D^\mu {\mathcal S}) -{\mathcal S}^\dagger m_{\mathcal S}^2 {\mathcal S}, \end{aligned}$$

(5)

describing the TC gauge, fermion, and scalar sectors. Note that, arranging the techni-scalars as $\Phi =({\mathcal S},-\epsilon _{TC} {\mathcal S}^*)^T$, in the absence of the mass matrix $m_{\mathcal S}$ a global Sp(24)$_{\mathcal S}$ symmetry becomes manifest in the scalar sector, under which $\Phi$ transforms as the fundamental representation. The setup described here is called “minimal fundamental partial compositeness” (MFPC), since it corresponds to the minimal viable amount of techni-matter that leads to a pNGB Higgs and fermionic resonances mixing linearly with the SM fields [38, 39, 47].

Uplifting the SM-like fermions to spurions, i.e. assigning them transformation properties under the full global symmetry, ${\psi ^i}_a \equiv {(\Psi y)^i}_a \in 24_{\mathcal S}\otimes \bar{4}_{\mathcal F}$, with i (a) an Sp(24)$_{\mathcal S}$ (SU(4)$_{\mathcal F}$) index and y being Yukawa matrices, the Yukawa Lagrangian connecting the TC sector with the SM can be written in compact form as [39, 47]

$$\begin{aligned} -{\mathcal L}_\mathrm{yuk}= {\psi ^i}_a \epsilon _{ij}\, \Phi ^j \epsilon _\mathrm{TC} {\mathcal F}^a\, + \mathrm{h.c.}\,, \end{aligned}$$

(6)

with $\epsilon _{ij}$ the antisymmetric Sp(24)$_{\mathcal S}$ tensor and the elementary fields being embedded in $\psi$. In particular, Eq. (6) contains the UV realization of PC for leptons, reading

$$\begin{aligned}&{\mathcal L}_\mathrm{yuk} \supset L_\alpha \, y_L\, {\mathcal S}_l \epsilon _\mathrm{TC} F^\alpha -\bar{\nu }\, y_{\bar{\nu }}\, {\mathcal S}^*_l \bar{\mathcal F}^4 + \bar{e}\, y_{\bar{e}} \, {\mathcal S}^*_l \bar{\mathcal F}^3 \nonumber \\&\quad - \bar{\nu }\, \tilde{y}_{\bar{\nu }} \, {\mathcal S}_l \bar{\mathcal F}^3 + \mathrm{h.c.}\,, \end{aligned}$$

(7)

with the weak doublet $F^\alpha =({\mathcal F}^1,{\mathcal F}^2)^T$.³ Such an explicit UV construction of a CH with PC fermions will leave its imprint in flavor and precision observables at low energies, as we will discuss below.

On the other hand, to capture a broader range of potential UV completions for the phenomenological study and in particular to make contact with a large set of previous works on lepton flavor – which were performed in an effective/holographic approach, many of them employing the SO(5)/SO(4) coset—we will consider an effective description of PC in the following. We will thus, in most cases, not specify the microscopic interactions that lead to the linear interactions between elementary fields and composite states. Still, we will comment on specific predictions of the MFPC framework. We also note that even though no fundamental (4D) UV completion for the CH with elementary fermions exists for the SO(5)/SO(4) coset [48], it can be considered as a minimal benchmark model to study the generic features of the CH setup, where many characteristics are expected to still hold for modified cosets. Moreover, the mentioned holographic 5D duals [5] can be seen as a completion of the setup, even though, being higher dimensional, ultimately they require their own completion, like string theory [48,49,50,51,52,53], and the low cutoff on the IR brane leads to only moderately suppressed uncalculable effects.

3 Effective description: different embeddings of the lepton sector

At an effective level, below the scale $\Lambda _\mathrm{UV}$ where the elementary/composite-sector interactions are generated (Eq. (7) for MFPC), PC for leptons can be described via linear mixings of the SM-like elementary fields with composite operators ${\mathcal O}^l_{L,R}$ of the confining sector

$$\begin{aligned} {\mathcal L}_\mathrm{mix} = \frac{\lambda _L^\ell }{\Lambda _\mathrm{UV}^{\gamma ^\ell _L}}\, \bar{l}^\ell _L {\mathcal O}^\ell _L + \frac{\lambda _R^\ell }{\Lambda _\mathrm{UV}^{\gamma ^\ell _R}}\, \bar{l}^\ell _R {\mathcal O}^\ell _R + \frac{\lambda _R^{\nu _\ell }}{\Lambda _\mathrm{UV}^{\gamma ^{\nu _\ell }_R}}\, \bar{\nu }^\ell _R {\mathcal O}^{\nu _\ell }_R \, \, +\mathrm{h.c.}, \end{aligned}$$

(8)

responsible for their masses. Here, $\ell =e,\mu ,\tau$ (with an obvious analogue for quarks), $\lambda _{L,R}^l$ are ${\mathcal O}(1)$ couplings and $\gamma ^l_{L,R} = [{\mathcal O}^l_{L,R}]-5/2$ are the anomalous dimensions of the composite-sector operators. Moreover, $l^\ell _L$, $l^\ell _R$, and $\nu _R^\ell$ correspond to the embeddings of the SM-like elementary fields into irreducible representations of the global symmetry of the composite sector, such as SO(5) in the Minimal Composite Higgs Model (MCHM) [5], according to the representation of the operators they mix with. Treating them as spurions of the full global symmetry, their ’background values’ correspond to the SM-like multiplets and the spurious symmetry can be used to estimate their contribution to the Higgs potential via explicit global SB (see, e.g., [53] and below).

For the further analysis, we define the ’degree of compositeness’

$$\begin{aligned} \epsilon ^l_{L,R}\sim \frac{\lambda _{L,R}^{l}}{g_*}(\mu /\Lambda _\mathrm{UV})^{\gamma _{L,R}^{l}}, \end{aligned}$$

(9)

of a chiral SM-like field, with $g_*$ the coupling of the resonances in the strong sector and $\mu \!\sim \!\Lambda _c\!\sim \!\mathcal {O}(\mathrm {TeV})$ the IR scale where the composite sector condenses. Note that in explicit models a SM-like fermion might mix with more than a single type of composite operator. This is for example required for the fundamental representation of SO(5) [17, 54], see also [53], leading to more terms in Eq. (8) (for the fundamental of SO(5), i.e. the MCHM$_5$, one needs for example ${\mathcal O}_L^\ell , {\mathcal O}_L^{\ell ^\prime }, {\mathcal O}_R^\ell , {\mathcal O}_R^{\nu _\ell }$).⁴ Modest differences in the anomalous dimensions $\gamma ^l_{L,R}$ will automatically lead to a hierarchical spectrum of fermion masses from an anarchic flavor structure in the UV, after integrating out the heavy resonances excited by the operators ${\mathcal O}^l_{L,R}$, leading to $m_\ell \sim g_*v/\sqrt{2}\epsilon _L^\ell \epsilon _R^\ell$.⁵ Also the hierarchical pattern of the CKM matrix in the quark sector follows directly due to a Froggatt-Nielsen-like structure in the mass matrices [9, 55, 56]. Finally, the leptonic mixing matrix with its ${\mathcal O}(1)$ entries, can be obtained, too—with certain assumptions on the model structure, also depending on how neutrino masses are realized [7,8,9,10,11,12,13,14,15,16,17,18, 21,22,23,24,25,26,27,28,29,30,31,32,33, 57,58,59], as we will discuss now.

3.1 Basic anarchic setup

Similar to the quark sector, the lepton sector in CH models can be realized by assuming anarchic values for the dimensionless input parameters, generating the hierarchies in charged-lepton masses after condensation in the composite sector by the UV-scale suppression, $\Lambda _{UV} \gg \mu$ , in Eq. (8). The leptonic mixing matrix as well as the neutrino masses, on the other hand, could be kept non-hierarchical by appropriate assumptions on the PC structure. Such scenarios have been envisaged in Refs [11, 14, 15, 19, 23, 33]. In general however, even though there is some suppression of FCNCs from PC, it remains a challenge to evade the very stringent flavor constraints, as we will see below, pushing f above the TeV scale.

3.2 Models with flavor symmetries

Table 1 Popular choices for flavor symmetry $G_f$ in the lepton sector, where below $X \in \{A_5, \Delta (96),\Delta (384)\}$

There exist several frameworks that refine the fully anarchic approach by invoking flavor symmetries to generate the sought particular form of the leptonic mixing matrix and of neutrino masses together with hierarchical charged-lepton masses and a protection from flavor constraints, going beyond the geometric GIM. Popular flavor groups $G_f$ that have been envisaged in the composite Higgs framework are summarized in Table 1. While early constructions focused on $A_4,S_4$, or the double tetrahedral $T^\prime$, the discovery of a non-zero $\theta _{13}$ mixing angle [60,61,62,63] lead to a broadening to other (product) groups or to considering spontaneous breaking of such symmetries, which can incorporate this finding. It would be worthwhile to explore such symmetries in a fundamental theory of partial compositeness.

Interestingly, such models with flavor symmetries often feature a suppression of the Yukawa couplings in the composite sector (inducing lepton masses after linear mixing), since those control the magnitude of the breaking of $G_f$ (see, e.g., [17]). Moreover, there is a suppression of the left-handed (LH) lepton compositeness, which is bound to be small due to the absence of custodial protection of the $Z \bar{\ell }_L \ell _L$ couplings. In turn, the $\tau _R$ needs to mix quite significantly with the composite sector to generate the moderately large $m_\tau$. This can lead to new LHC signatures [20] and interesting effects in Higgs physics [29, 64, 65], while EW precision tests (EWPT) can be met due to the custodial protection of right-handed (RH) $\tau$ couplings. On the other hand, non-negligible compositeness in the charged lepton sector can also emerge beyond such models of flavor symmetries, simply from the scale of neutrino masses—namely in minimal realizations of a seesaw in the CH framework as we will discuss now.

3.3 Minimal seesaw model and composite leptons

In the composite Goldstone-Higgs framework, a very minimal realization of the lepton sector is possible that allows to explain the tiny neutrino masses, by envisaging a type-III seesaw mechanism with heavy fermionic SU(2)$_L$ triplets, which provides at the same time an efficient flavor protection. In fact, if in the MCHM setup neutrino masses are realized via such triplets, a unification of the RH lepton sector is possible and a single, symmetric, representation of SO(5) can host both the charged RH leptonic SU(2)$_L$ singlet as well as the RH seesaw triplet [29, 31, 32]. This leads to a more minimal model for leptons than conventional analogues to the quark sector [17] and the Type-III seesaw construction could also be interesting in the context of leptogenesis, see, e.g., [66, 67].

In consequence, the PC Lagrangian in Eq. (8) can be written with only two terms (instead of the usual four) and becomes simply

$$\begin{aligned} {\mathcal L}_\mathrm{mix} = \frac{\lambda _L^\ell }{\Lambda _\mathrm{UV}^{\gamma ^\ell _L}}\, {\bar{L}}^\ell _L {\mathcal O}^\ell _L + \frac{\lambda _R^\ell }{\Lambda _\mathrm{UV}^{\gamma ^\ell _R}}\, {\bar{L}}^\ell _R {\mathcal O}^\ell _R \, +\mathrm{h.c.}\,, \end{aligned}$$

(10)

where $L^\ell _L \sim \mathbf{5}$ and $L^\ell _R \sim \mathbf{14}$, with less degrees of freedom than in minimal leptonic versions of the MCHM envisaged before [17]. In the holographic 5D-dual picture, $L_L^\ell$ and $L_R^\ell$ would correspond to bulk fermions reading [29, 31, 32]

$$\begin{aligned} \zeta _{1}^{\ell }= & {} \ell ^{\prime }_{1}[-,+]\oplus \left( \begin{array}{r}\nu _{1}^{\ell }[+,+]~ ~\tilde{\ell }_1[-,+]\\ \ell _{1}[+,+]~ \tilde{Y}_1^{\ell }[-,+]\end{array}\right) \text { and}\nonumber \\ \zeta _{2}^{\ell }= & {} \ell ^{\prime }_{2}[-,-]\oplus \left( \begin{array}{r} \nu _{2}^{\ell }[+,-]~~ \tilde{\ell }_2[+,-]\\ \ell _{2}[+,-]~ \tilde{Y}_2^{\ell }[+,-]\end{array}\right) \nonumber \\&\oplus \left( \begin{array}{r} \hat{\lambda }^{\ell }_2[-,-]~~\nu _{2}^{\ell \prime \prime }[+,-]~ ~~\ell _2^{\prime \prime \prime }[+,-]\\ \hat{\nu }_2^{\ell }[-,-]~~~\ell _{2}^{\prime \prime }[+,-]~Y_2^{\ell \prime \prime \prime }[+,-]\\ \hat{\ell }_2[-,-]~Y_2^{\ell \prime \prime }[+,-]~\Theta _2^{\ell \prime \prime \prime }[+,-] \end{array}\right) , \end{aligned}$$

(11)

where we have explicitly shown the decomposition under SO(4)$\cong$ SU(2)$_L \times$ SU(2)$_R$: the $\mathbf{5}$ of SO(5) decomposes as a singlet and a bi-doublet, the latter represented by a $2\times 2$ matrix on which the SU(2)$_L$ (SU(2)$_R$) transformation acts vertically (horizontally). The $\mathbf{14}$ accordingly decomposes as a singlet, bi-doublet, and bi-triplet and both representations feature a charge of $Q_X\!=\!-1$ under the abelian U(1)$_X$ factor [31].⁶ The boundary conditions at the two ends of the compactified $AdS_5$ space—the UV brane, localized at $z\!=\!R\sim M_\mathrm{Pl}^{-1}$, and the IR brane, localized at $z\!=\!R^{\prime }\sim \mathrm{TeV}^{-1}$, with z the coordinate of the additional spatial dimension $R\le z\le R^{\prime }$—are specified in square brackets. A Dirichlet boundary condition for the RH (LH) chirality is denoted by $[+]$ ($[-]$).

Now, the SM-like fields correspond to chiral zero modes of these 5D Dirac fermions, where LH (RH) zero modes are present for components with $[+,+] ([-,-])$ boundary conditions. We can thus identify the SU(2)$_L$ doublet leptons with the zero mode of the left $T_R^3=+1/2$ column in the first bi-doublet, $l_L^\ell \subset ({\nu _1^\ell }_L,{\ell _1}_L)^T$, and the RH charged SM-like leptons as $\ell _R \subset {\ell _2^\prime }_R$. In addition, the see-saw triplet resides in the $T_R^3=+1$ component of the bi-triplet, $\Sigma _{\ell R} \subset ({{\hat{\lambda }}_{2R}^\ell }, {{\hat{\nu }}_{2R}^\ell },{{\hat{\ell }}_{2R}})^T$, see [31, 32] for more details. These zero modes will be localized along the extra dimension according to the value of the 5D Dirac-mass $M_i$ of the multiplets, parametrized in terms of the dimensionless $c_i \equiv M_i R$, which correspond to the anomalous dimensions in Eq. (10) as [68] $\gamma ^\ell _{L,R} = |c_{1,2}\mp 1/2|-1$. UV localization, i.e. $c_i<-1/2$ $(c_i>1/2)$ for LH (RH) zero modes [1, 57, 68], is identified with elementary fermions in the dual picture, with a suppressed mixing with the composite sector, whereas the more the modes are localized towards the IR brane, the bigger their compositeness.

A (Majorana) mass term is added in the elementary sector, reading

$$\begin{aligned} \mathcal {L}_\mathrm{el} = -\frac{1}{2}\left[ M_{\Sigma }^{\ell \ell ^{\prime }}\mathrm {Tr}\left( \bar{\Sigma }_{\ell R}^{c}\Sigma _{\ell ^{\prime }R} \right) +\mathrm {h.c.} \right] \end{aligned}$$

(12)

with

$$\begin{aligned} \Sigma _{\ell }=\left( \begin{array}{ll} \hat{\nu }^\ell /\sqrt{2}&{}\hat{\lambda }^\ell \\ \hat{\ell }&{} -\hat{\nu }^\ell /\sqrt{2}\end{array}\right) , \qquad \ell =e,\mu ,\tau \,. \end{aligned}$$

(13)

This explains the tiny neutrino masses with ${\mathcal O}(1)$ Yukawa couplings via a large $M_\Sigma ^{\ell \ell \prime } \gg v$, realizing the (type-III) seesaw mechanism. In the 5D theory, the elementary Majorana mass term corresponds to a brane localized mass for the 5D version of the multiplet $\Sigma _\ell \ (\subset \xi _2^\ell )$, simply adding the Lagrangian of Eq. (12) on the UV brane at $z=R$ (where SO(4) is broken). If now $\Sigma _\ell$ would be fully elementary, i.e. the zero modes of $\xi _2^\ell$ would be localized on the UV brane, it would receive an effective Majorana mass of ${\mathcal O}(M_\mathrm{Pl})$, which is the fundamental scale of the theory (and the warp factor on the UV brane being $a\!\equiv \! R/z\!=\!1$). However, this would lead to a significantly too strong suppression of neutrino masses. This calls for a non-negligible compositeness of the $\Sigma _\ell$ multiplets, corresponding to a reduced overlap of the $\xi _2^\ell$ zero modes with the UV brane, such as to warp down the effective 4D Majorana mass significantly below $M_\mathrm{Pl}$.

The resulting increased IR localization (i.e., smaller anomalous dimension) of the light modes in $\xi _2^\ell$, including RH charged leptons with a sizable degree of compositeness, will lead to interesting phenomenological consequences, as discussed further below. Custodial symmetry will still guarantee the agreement of the $Z \bar{\ell }_R \ell _R$ couplings with measurements [20, 64]. On top of that, the picture lined out above allows for a very strong flavor protection, as we will see now.

To avoid dangerous FCNCs, a U(3)$_1 \times$ U(3)$_2$ flavor symmetry in the composite sector is envisaged [31, 32], corresponding to rotations in flavor space of the $\mathbf{5}$ and the $\mathbf{14}$ of SO(5). This is broken by the vev of a spurion ${\mathcal Y}$ in the strong sector, while the purely elementary sector, represented by the Majorana mass term, does not respect the symmetry to start with. The breaking via ${\mathcal Y}$ is necessary in order to induce a massive chiral low-energy spectrum after integrating out the heavy resonances. In the 5D picture, this corresponds to a breaking of a gauge flavor symmetry SU(3)$_1 \times$ SU(3)$_2$ via an IR-brane coupling between the Dirac spinors $\sim \xi _1^\ell {\mathcal Y}\xi _2^\ell$ [31], linking the LH and RH SM-like fermions, where

$$\begin{aligned} \xi _1^\ell \sim (\mathbf{3},\mathbf{1})\,, \ \ \xi _2^\ell \sim (\mathbf{1},\mathbf{3})\,,\quad {\mathcal Y} \sim (\mathbf{3},\mathbf{\bar{3}})\,. \end{aligned}$$

(14)

In terms of this source of flavor breaking, the bulk masses (or PC coefficients) can now be expanded as

$$\begin{aligned} c_1=\eta _1 \mathbf{1}+\rho _1 {\mathcal Y} {\mathcal Y}^{\dagger },\qquad c_2=\eta _2 \mathbf{1}+\rho _2 {\mathcal Y}^{\dagger } {\mathcal Y}, \end{aligned}$$

(15)

with $\eta _{1,2},\rho _{1,2}\in \mathbb {R}$. This is an appealing picture, since the elementary sector can generate a non-trivial flavor structure, reproducing the leptonic mixing matrix, while the fact that a single spurion breaks the flavor symmetry allows to fully diagonalize the strong sector via a simple unitary rotation. In consequence, no leptonic FCNCs are generated—up to very small effects suppressed by the large Majorana masses.

Fig. 1

Left: mass of the lightest top partner versus $m_h$ as a function of the tuning $\Delta _\mathrm{BG}$ in the minimal seesaw model with $f=1\,$TeV (colored points) and corresponding prediction in the MCHM$_5$ (gray points). Right: coefficient of 4e contact operator $c_{ee}$ versus f, where the blue (yellow) line shows a fit to the prediction (the upper 95% C.L. limit)

Regarding the resulting hierarchy of lepton compositeness, it is interesting that actually the electron will feature the largest compositeness, which can be understood from inspecting the scaling of the lepton masses. In fact, the physical charged lepton masses now, in the presence of significant RH compositeness, scale like $\mathcal {M}_{e}\sim \delta _{\ell \ell ^{\prime }} v g_*\epsilon ^\ell _{L}$ (see Eqs. (9) and (10)), which can be understood from the fact that for $\gamma _{R}^{\ell }<0$ a large correction to the $L^\ell _R$ kinetic term emerges at $\mu =\mathcal {O}(\mathrm {TeV})$, where the conformal sector becomes strongly coupled, such that after canonically normalizing the kinetics, $\epsilon ^\ell _{R}$ drops out of $\mathcal {M}_{e}$. From the 5D perspective, this becomes clear realizing that the corresponding wave functions are in a regime where the overlap with the IR brane is no longer exponentially sensitive to the bulk mass. Along the same lines, the neutrino mass matrix reads $\mathcal {M}_{\nu }\sim v^2 g_*^2 \epsilon ^\ell _{L}\epsilon ^\ell _{R}(M_{\Sigma }^{\ell \ell ^{\prime }})^{-1} \epsilon ^{\ell ^{\prime }}_{L}\epsilon ^{\ell ^{\prime }}_{R}$, where the suppression by the elementary Majorana mass $M_{\Sigma }$, expected to reside at the Planck scale, is lifted by the appreciable RH lepton compositeness $\epsilon ^\ell _{R}$, see also [21]. Since the Dirac masses are suppressed similarly to charged lepton masses, quantitatively this requires entries in the resulting effective Majorana mass matrix even much smaller than $M_\mathrm{GUT}$. It now follows directly that realizing hierarchical charged lepton masses and a non-hierarchical neutrino mass matrix requires $\epsilon ^e_{L}\ll \epsilon ^\mu _{L}\ll \epsilon ^\tau _{L}\ll 1$ and $\epsilon ^\ell _{L} \epsilon ^\ell _{R}\sim \mathrm {constant}$, and thus $0 \ll \epsilon ^\tau _{R}\ll \epsilon ^\mu _{R}\ll \epsilon ^e_{R}$. This will lead to interesting signatures, like a non-negligible violation of lepton flavor universality (LFU) within the first generations, as we will discuss below.

The appreciable compositeness of leptons in this minimal see-saw model will also have important consequences on the radiatively generated Higgs potential [29]. In fact, since the quantum numbers of the symmetric representation $\mathbf{14}$ of SO(5) allow for the lepton contribution to the Higgs mass to appear at leading order in the degree of compositeness $\epsilon ^\ell _R$, contrary to the general case, large effects are expected even for moderately composite leptons, being actually comparable to the top-quark contribution to $m_h$ in the MCHM$_5$, as can be seen in a spurion analysis and also in explicit calculations [29]. By interfering destructively with the top contribution in a sizable region of parameter space, this allows for a larger top-quark breaking of the global symmetry, while still reproducing the light Higgs mass. In turn, the ultra-light top partners that are present in conventional minimal composite Higgs scenarios to reduce the SO(5) breaking for a fixed $m_t$ can be lifted, which will be shown numerically below, see Fig. 1. In this context, note that the additional contribution to the Higgs potential also allows for a viable EWSB in previously excluded most minimal holographic setups for the quark sector (see [29]), where the contribution of the top alone would not be sufficient. This is the case for a fully composite $t_R$ singlet, with the LH doublet being embedded in a $\mathbf {5}$, which we will employ in the following, corresponding to $\xi _{U}^{i}\sim \mathbf {5}_{2/3},\, \xi _{u}^i\sim \mathbf {1}_{2/3},\, \xi _{D}^{i}\sim \mathbf {5}_{-1/3},\, \xi _{d}^i\sim \mathbf {1}_{-1/3}$, $i=1,2,3$, with the subscript denoting $Q_X$.

The numerical confirmation of the discussion above has been presented in [29, 31]. Performing a scan with ${\mathcal O}(1)$ input parameters, fitting the leptonic and quark spectra, the mass of the lightest top partner versus the Higgs mass was evaluated at the compositeness scale, assumed to be $f\!=\!1\,$TeV, after accounting for correct EWSB with $v\approx 246$ GeV. The results are reported as colored points in Fig. 1, with the yellow band being a conservative estimate of the Higgs mass at this scale [29]. We can see from the figure that, in contrast to the conventional MCHM$_5$ (displayed by gray points for comparison), top-partners can be raised significantly above f, reaching up to $5\,$TeV without blowing up the tuning, measured by the Barbieri-Giudice (BG) prescription [69]. The model thus allows to maintain a small $f \approx 0.8$ TeV (as suggested by naturalness arguments, taking into account EWPT), without running into conflict with LHC top partner searches—which are pushing $m_{t^\prime } \gtrsim 1.3$ TeV [70,71,72]—and brings us basically back to the tuning already required pre-LHC, see [73].⁷ On the other hand, the top partner bound corresponds already to f surpassing a TeV in the MCHM$_5$ [29, 74,75,76], driving the tuning in this model.

While a dedicated survey of bounds on lepton compositeness from flavor and precision physics will be carried out in the next section, a straightforward test of the setup at hand is given by searches for four-lepton contact interactions

$$\begin{aligned} \mathcal {O}_{XY}^{\ell ^1\!\ell ^2\!\ell ^3\!\ell ^4} = (\bar{\ell }^1_X\gamma _{\mu } \ell ^2_X)(\bar{\ell }^3_Y\gamma ^{\mu } \ell ^4_Y)\,, \end{aligned}$$

(16)

with coefficients scaling as $C_{XY}^{\ell ^1\!\ell ^2\!\ell ^3\!\ell ^4} \!\sim \frac{g_*^2}{m_*^2}\epsilon _X^{\ell ^1}\epsilon _X^{\ell ^2}\epsilon _Y^{\ell ^3}\epsilon _Y^{\ell ^4}$, where $m_*$ is the mass scale of the composite resonances. With the hierarchies quoted before, the largest coefficient is $c_{ee} \equiv C_{RR}^{eeee}$, which is constrained as $|c_{ee}|\!<\!4 G_F/\sqrt{2}\!\times \!0.003$ at 95% C.L. [77]. The prediction of the minimal seesaw model is shown in the right panel of Fig. 1 in dependence on f, where the blue curve corresponds to the best fit to the parameter points and the experimental bound is given by a yellow line. We find that $f\!=\!m_*/ g_*\gtrsim \,0.9\,$TeV allows in principle for an agreement with the data in the composite electron scenario.

4 Predictions and constraints

In this final section, we will discuss important lepton flavor observables and corresponding predictions in the scenarios introduced above. The focus will be on lepton flavor violating (LFV) processes, leptonic dipole moments, as well as LFU violating interactions.

4.1 Lepton flavor violation and dipole moments

Fig. 2

Left: prediction for $\mathrm{BR}(\mu \rightarrow e \gamma )$ in the MCHM$_5$-like setup with $A_4$ flavor symmetry versus the $A_4$ breaking vev (over the cutoff) $v/\Lambda$ in the elemenatry sector, scanning the parameter space with $m_*\sim 3\,$TeV, $g_*\sim 4$ (from [17]). The solid (dashed) line shows the old MEGA (projected MEG) limit. Right: histogram of predictions for the ratio $R_{e\mu }$ after a parameter space scan in the MFPC scenario (adapted from [47]), see text for details

A stringent test for every model of lepton compositeness is provided by the strong experimental bounds on the decay $\mu \rightarrow e \gamma$, which does not conserve lepton flavor. In composite models, this decay is induced from one-loop penguin diagrams involving heavy resonances [11, 19], generating the dipole operators

$$\begin{aligned} {\mathcal O}_{\ell \ell ^\prime }^\gamma \equiv e v \, F_{\mu \nu } \bar{\ell }_{L} \sigma ^{\mu \nu } \ell ^\prime _{R}, \end{aligned}$$

(17)

with here $\ell \!=\!\mu ,\ell ^\prime \!=\!e$. The latest experimental limit on the branching ratio (BR) reads $\mathrm{BR}(\mu \rightarrow e \gamma ) < 4.2 \times 10^{-13}$ at 90$\%$ CL [78], which is significantly stronger than those on the equivalent processes involving the tau lepton, which are $\mathrm{BR}(\tau \rightarrow e \gamma ) < 3.3 \times 10^{-8}$ and $\mathrm{BR}(\tau \rightarrow \mu \gamma ) < 4.4 \times 10^{-8}$ [6].

In the anarchic scenario of Sect. 3.1, the BR scales as (see also [19, 23, 79, 80])

$$\begin{aligned} \begin{aligned} \mathrm{BR}(\mu \rightarrow e \gamma ) = 96 \pi ^2 e^2 \frac{v^6}{m_\mu ^2}\left( \left| C^\gamma _{\mu e}\right| ^2 + \left| C^\gamma _{e \mu }\right| ^2 \right) \,, \qquad \\ C^\gamma _{\mu e} \sim \frac{1}{16 \pi ^2} \frac{g_*^3}{\sqrt{2} m_*^2} \epsilon ^\mu _L \epsilon ^e_R\,,\quad C^\gamma _{e \mu } \sim \frac{\sqrt{1}}{16 \pi ^2} \frac{g_*^3}{\sqrt{2}m_*^2} \epsilon ^e_L \epsilon ^\mu _R\,. \end{aligned}\, \end{aligned}$$

(18)

The experimental constraint quoted before then leads to the bound

$$\begin{aligned} \frac{g_*^3}{m_*^2} \sqrt{|\epsilon _L^\mu \epsilon _R^e|^2+|\epsilon _L^e \epsilon _R^\mu |^2} \lesssim \frac{10^{-7}}{\mathrm{TeV}^2}\,. \end{aligned}$$

(19)

Employing $m_\ell \sim g_*v/\sqrt{2}\epsilon _L^\ell \epsilon _R^\ell$, we can derive a stringent conservative limit on the resonance scale by setting $\epsilon _R^\ell =\epsilon _L^\ell$, which becomes

$$\begin{aligned} \frac{m_*}{g_*} \gtrsim 20\, \mathrm{TeV}\quad (\mathrm{BR}(\mu \rightarrow e \gamma ))\,, \end{aligned}$$

(20)

agreeing with the results given in [33, 79] to good accuracy. It is evident that the fully anarchic scenario is pushed to rather large mass scales due to this bound—even for modest $g_*\sim 4$ the resonances would be expected to reside well beyond the reach of current or near-future colliders. The constraints from flavor-changing tau decays on the resonance scale can be obtained straightforwardly from the above expressions, but are a factor of $\gtrsim 10$ weaker.

If new CP violation is present due to the strong sector, another powerful bound arises from the electric dipole moment (EDM) $d_e$ of the electron, which is proportional to the imaginary part of the diagonal (1,1) component of the dipole coefficient, see Eq. (17), and scales as [33, 79]

$$\begin{aligned} d_e \sim \mathrm{Im}(c_e) \frac{e}{16 \pi ^2 } \frac{g_*^3}{m_*^2} \epsilon ^e_{L} \epsilon ^e_{R} \frac{v}{\sqrt{2}}\,, \end{aligned}$$

(21)

with $c_e$ containing the (assumed ${\mathcal O}(1)$) phase of the anarchic setup. The recent stringent limit of the ACME collaboration of $d_e < 1.1 \times 10^{-29} e\,\mathrm{cm}$ [81] thus constrains (again for $\epsilon _R^\ell =\epsilon _L^\ell$)

$$\begin{aligned} \frac{m_*}{g_*} \gtrsim 75\, \mathrm{TeV}\quad (\mathrm{eEDM},\ \mathrm{Im}(c_e)\!\sim \!1)\,, \end{aligned}$$

(22)

which agrees well with the limits presented in [33, 79], after updating the bounds used there to the latest ACMEII limit. The corresponding dipole moments for the muon or the tau do not lead to meaningful current constraints. Moreover, the limit above depends crucially on the amount of CP violation in the new sector.

Finally, bounds from $\mu -e$ conversion in Gold constrain the flavor-changing couplings to the Z boson, which are sensitive to the combinations $\epsilon ^\mu _{L} \epsilon ^e_{L}$ and $\epsilon ^\mu _{R} \epsilon ^e_{R}$. Setting once more $\epsilon _R^\ell =\epsilon _L^\ell$, the SINDRUMII $90\%$ CL limit of $\mathrm{\Gamma }(\mu Au \rightarrow e Au)/\mathrm{\Gamma }_\mathrm{capture}(\mu Au) < 7 \times 10^{-13}$ [82] puts a bound on the resonance scale of (see [33, 79])

$$\begin{aligned} \frac{m_*}{\sqrt{g_*}} \gtrsim 3\, \mathrm{TeV}\quad (\mu Au \rightarrow e Au)\,. \end{aligned}$$

(23)

This is significantly weaker than the exclusions above and the bound from $\mu \rightarrow eee$ transitions, probing the same operator, is another factor $\sim 3$ less constraining. Similar decays involving the $\tau$ lepton are even less constraining, and the same holds true for the anomalous magnetic moment of the muon, see [33] for a recent overview.

In composite scenarios with a protection due to flavor symmetries, discussed in Sect. 3.2, the bounds from LFV quoted above are typically very much weaker, and vary over the different models considered in Tab. 1. For example, in models with an $A_4$ symmetry the limits can be reduced to the 1 TeV scale. In such setups, the non-trivial transformation properties of LH doublets and RH neutrinos under $A_4$ in flavor space [13, 17] lead to flavor-universal PC mixing parameters for the corresponding multiplets. On the other hand, the sector of charged RH leptons is diagonal, with the different flavors living in different singlet representations of $A_4$, but non-universal. In turn, after spontaneous breaking of $A_4$ in the elementary and confining sectors, to leading order this allows to rotate to a basis where the full flavor structure is diagonal, up to Majorana masses in the elementary sector. This induces a powerful suppression of LFV such that resonances around $m_*\approx 3$ TeV are in agreement with limits from LFV for a typical strongly coupled sector with $g_*\approx 4$ [17] (see also [25]). This is shown more quantitatively in the left panel of Fig. 2, where for small $A_4$ breaking, parametrized by the breaking vev over the cutoff $v/\Lambda$, most of the points are in agreement with a bound of $\mathrm{BR}(\mu \rightarrow e \gamma ) < 5 \times 10^{-13}$. Similar statements hold true for the minimal seesaw model of Sect. 3.3, where LFV does not impose stringent constraints after invoking a similar flavor protection, as discussed in detail in Sect. 3.3.

Turning to minimal 4D UV completions of PC, considering the MFPC scenario as introduced in Sect. 2, it is interesting to see whether additional predictions emerge just from the UV setup, leading to (8) at low energies. First of all, in the MFPC construction no custodial protection for $Z\bar{f}f$ couplings is present [38], which (depending on further structure) limits the size of potentially observable effects in flavor physics due to stringent constraints from Z-pole measurements at LEP, pushing the compositeness scale. Still, interesting effects are possible, as we will see below. Moreover, with additional ingredients such a protection could be achieved [38] and a further investigation of this issue, in particular in the context of lepton compositeness and flavor observables discussed here, would be interesting.

Besides, now the flavor structure in the effective theory is induced by the corresponding properties of the fundamental constituents. If for example the scalar mass matrix in Eq. (5) has a flavor-trivial form, $m_{\mathcal S}^2 \sim \mathbf{1}$, as can in fact emerge if the TC scalars acquire their mass solely from strong TC interactions (and the TC-scalar potenital conserves flavor) [38], important consequences arise. The coefficient of the dipole operator in Eq. (17) will be proportional to the corresponding SM-fermion Yukawa matrix, $C^\gamma _{\ell \ell ^\prime } \propto y^\mathrm{SM}_{\ell \ell ^\prime }$, to leading approximation, and thus diagonal and real in the same basis. This allows to push both the $\mathrm{BR}(\mu \rightarrow e \gamma )$ and the electron dipole moment $d_e$ below the experimental limit, even for TC scales below a TeV and $g_*\sim 4 \pi$ [38], i.e.,

$$ \begin{aligned} \left( \frac{m_*}{g_*}\right) _\mathrm{\! \!MFPC} \!\!\!\gtrsim 100\, \mathrm{GeV}\quad (\mathrm{BR}(\mu \rightarrow e \gamma )\, \& \ \mathrm{eEDM})\,. \end{aligned}$$

(24)

4.2 Lepton flavor universality violation

Fig. 3

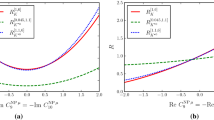
Left: prediction in the $R_K - R_{K^*}$ plane in the MFPC scenario, varying 1 TeV$<f<$3 TeV (from [47]), see text for details. Right: corresponding viable points in the minimal seesaw model [83] with $f=1.2\,$TeV, where the color code displays deviations in the $B_s$ mass difference from the SM prediction

We now turn to processes that are diagonal in lepton flavor, but might be flavor non-universal. In particular, we will focus mostly on tests of LFU between the first and second generation in neutral-current B decays, parametrized by the ratios

$$\begin{aligned} R_K\equiv & {} \frac{\mathrm{BR}(B^+ \rightarrow K^+ \mu ^+\mu ^-)}{\mathrm{BR}(B^+ \rightarrow K^+ e^+e^-)}\,,\nonumber \\ R_{K^*}\equiv & {} \frac{\mathrm{BR}(B^0 \rightarrow K^*\mu ^+\mu ^-)}{\mathrm{BR}(B^0 \rightarrow K^*e^+e^-)} \end{aligned}$$

(25)

and explored extensively from the experimental side at LHCb [84,85,86] and Belle [87, 88]. Due to the PC mechanism of mass generation, a certain level of LFU violation is in fact a generic prediction of models with PC leptons, even in the absence of LFV, with potentially measurable effects being well motivated in some setups. The current experimental results and (dominant) statistical uncertainties for the dilepton invariant mass squared within $1.1\!<\!q^2/\mathrm{GeV}^2 \!<\!6$ read $R_K=0.846^{+0.060}_{-0.054}$ and $R_{K^*}=0.69^{+0.11}_{-0.07}$ [85, 86], and strongly disfavor $R_{K,K^*}>1$, where in the SM $R_K=R_{K^*}=1$, up to $1\%$ effects due to $m_e \ne m_\mu$.⁸

In the CH framework, crucial operators in this context are four-fermion contact terms, induced from exchange of heavy EW resonances, reading (c.f. Eq. (16))

$$\begin{aligned} \mathcal {O}_{XY}^{q^1\!q^2 \ell ^1\!\ell ^1} = (\bar{q}^1_X\gamma _{\mu } q^2_X)(\bar{\ell }^1_Y\gamma ^{\mu } \ell ^2_Y)\,, \end{aligned}$$

(26)

with coefficients scaling as $C_{XY}^{q^1\!q^2 \ell ^1\!\ell ^2}\!\!\sim \frac{g_*^2}{m_*^2}\epsilon _X^{q^1}\epsilon _X^{q^2}\epsilon _Y^{\ell ^1}\epsilon _Y^{\ell ^2}$ and becoming important for sizable compositeness [31, 33, 47, 83, 89,90,91]. Whether these can lead to a good agreement with the measurements above sensitively depends on the compositeness of the various fermion chiralities. In fact, taken together, the LHCb results already significantly constrain a potential sizable compositeness of RH muons in general (if some $b\!-\!s$ current talks non-negligibly to the strong sector, i.e. $\epsilon _X^{s}\epsilon _X^{b} > 0$) and of LH muons or electrons in combination with a somewhat composite RH $b\!-\!s$ current [83]. From general arguments, moving into the quadrant of $R_{K,K^*}<1$ requires either LH muon or electron compositeness and basically LH $b\!-\!s$ compositeness or RH electron compositeness, irrespectively of the $b\!-\!s$ chirality [83] (see also [89, 92]). For example, focusing on LH muons or RH electrons, we find that the single-coefficient best fit solutions [92,93,94] could be achieved with

$$\begin{aligned} \frac{g_*^2}{m_*^2}\epsilon _L^{s}\epsilon _L^{b}\epsilon _L^{\mu }\epsilon _L^{\mu } \sim \frac{10^{-3}}{\mathrm{TeV}^2}\ \quad \mathrm{or}\ \quad \frac{g_*^2}{m_*^2}\epsilon _X^{s}\epsilon _X^{b}\epsilon _R^{e}\epsilon _R^{e} \sim 4 \cdot \frac{10^{-3}}{\mathrm{TeV}^2}\,, \end{aligned}$$

(27)

where $X\!=\!L,R$. Trying to realize one of these patterns led to some efforts in the CH community, envisaging for example enhanced muon compositeness [33, 47, 89,90,91].

In MFPC, this would correspond to sizable fundamental Yukawa couplings in the LH muon sector, i.e. large $(y_L)_{22}$ in Eq. (7) (sticking to a lepton-flavor diagonal structure to leading order, similarly to as discussed in Sect. 4.1), while in turn $(y_{\bar{e}})_{22}$ would be tiny in order not to make the muon to heavy. Further important constraints on scenarios with sizable LH compositeness are given by strong bounds on deviations in charged current semi-leptonic kaon and pion decays, which are known to better than percent level, like the ratio $R_{e\mu }(K^+ \rightarrow \ell ^+ \nu )\equiv \mathrm{BR}(K^+ \rightarrow e^+ \nu )/\mathrm{BR}(K^+ \rightarrow \mu ^+ \nu )$. Moreover, stringent constraints on the partial width of the Z boson are particularly relevant for the MFPC scenario, lacking custodial protection.⁹ The right panel of Fig. 2 shows a histogram of a scan in the MFPC setup [47], after imposing bounds from meson-antimeson mixing. The yellow and green points are excluded from Z-boson partial width and flavor constraints (semi-leptonic charged current decays), respectively, while the red points violate both, see [47] for more details. Keeping only viable points, finally the left panel of Fig. 3 displays the prediction in the $R_K - R_{K^*}$ plane after a full scan of the MFPC model [47]. We can see that the best fit values can be reached by a set of viable points, and similar conclusions were drawn in the holographic [90, 91] and 4D effective [89] incarnations of PC.

Finally, while it is appealing that CH models are flexible enough to account for the found tendency, it would also be interesting to find a motivated setup that makes a clearer prediction on the form of LFU violation, increasing the opportunities to probe it. In fact, the minimal seesaw model of Sect. 3.3 furnishes such a setup since due to its minimal and unifying character, as explained there, it unambiguously predicts a RH electron compositeness as the dominating effect, leading straightforwardly to $R_{K,K^*}<1$. Ending up in any other quadrant in this plane would exclude the model, as can be seen from the scan provided in the right panel of Fig. 3. On the other hand a good fit of $R_{K,K^*}\sim 0.8$ is easily obtained while keeping the deviation in the $B_s$ mass difference $\Delta M_{B_s}$—which is generated due to $\epsilon _X^{s}\epsilon _X^{b} >0$ and indicated by the shades of blue—at an acceptable $\lesssim 20\,\%$ level. In addition, the parameter space is not significantly restricted from measurements of charged current decays like $R_{e\mu }(K^+ \rightarrow \ell ^+ \nu )$ or $\mathrm{BR}(\pi \rightarrow e \nu )$, since the LH leptons in the minimal seesaw model are very elementary. In light of the custodial protection of RH Z couplings and the discussed flavor protecion, the most stringent bound is in fact expected from the 4e contact interactions, which is fulfilled for the given scan with $f=1.2\,$TeV (see Sect. 3.3). Moreover, it is interesting to note that the updated constraint on $\Delta M_{B_s}$ from Ref. [95] poses a strong challenge to significantly reducing $R_{K^{(*)}}$ via LH muon compositeness. A similar reduction due to RH electron compositeness remains viable, since it is consistent with effects both in LH and RH quark currents, as discussed before, which can cancel to some extent in $\Delta M_{B_s}$. We conclude noting that, as becomes clear form the discussions above, also in the case that with more statistics the fit might move towards $R_{K,K^*}\!\approx \!1$, tests of LFU violation remain a crucial part of the program to probe PC in general.

5 Conclusions

We have reviewed lepton flavor physics in composite Higgs models with partial compositeness, both from a fundamental and an effective point of view. After discussing the particularities of different approaches to lepton flavor, including anarchic setups, scenarios with flavor symmetries, and unified see-saw models, motivating non-negligible lepton compositeness, we reviewed their phenomenology and confronted them with various measurements. Our discussion included observables sensitive to lepton flavor violation, to CP violation, and to lepton flavor universality violation, pointing out crucial differences between the models, including varying limits on the compositeness scale. In fact, different patterns of predictions for these observables, combined with results from searches for (potentially light) resonances, offer a promising means to get a handle on the nature of leptons, after a potential establishment of deviations from SM predictions, or further increased limits.