Quantum-enhanced analysis of discrete stochastic processes

Abstract

Discrete stochastic processes (DSP) are instrumental for modeling the dynamics of probabilistic systems and have a wide spectrum of applications in science and engineering. DSPs are usually analyzed via Monte-Carlo methods since the number of realizations increases exponentially with the number of time steps, and importance sampling is often required to reduce the variance. We propose a quantum algorithm for calculating the characteristic function of a DSP, which completely defines its probability distribution, using the number of quantum circuit elements that grows only linearly with the number of time steps. The quantum algorithm reduces the Monte-Carlo sampling to a Bernoulli trial while taking all stochastic trajectories into account. This approach guarantees the optimal variance without the need for importance sampling. The algorithm can be further furnished with the quantum amplitude estimation algorithm to provide quadratic speed-up in sampling. The Fourier approximation can be used to estimate an expectation value of any integrable function of the random variable. Applications in finance and correlated random walks are presented. Proof-of-principle experiments are performed using the IBM quantum cloud platform.

Introduction

Simulation of physical processes on quantum computers^1,2 has many facets, with recent developments improving the usage of this technology^{3,4,5,6,7,8,9,10,11,12,13,14}. While one obvious task for a quantum computer is to simulate quantum mechanical behaviors of nature¹, quantum simulation of probability distributions and stochastic processes has gained attention recently^{15,16,17,18,19,20}. Since quantum mechanics can be viewed as a mathematical generalization of probability theory, where nonnegative real-valued probabilities are replaced by complex-valued probability amplitudes, quantum computing appears to be a natural tool for simulating classical probabilistic processes. Intuitively, some quantum advantage is expected since the probability amplitudes can interfere, unlike in classical probabilistic computing. Indeed, a quadratic quantum speed-up has been reported for solving financial problems when compared to Monte-Carlo simulations^16,21.

Classically, Monte-Carlo methods are essential for estimating expected values of random variables in DSPs, since the number of realizations increases exponentially with the time steps. When the Monte Carlo sampling is repeated N times, the expectation value to be found converges with ${{{\mathcal{O}}}}(1/\sqrt{N})$ regardless of the number of realizations. The central limit theorem ensures this, but it is important to note that this convergence is only attained in the limit of N → ∞. When this limit is not nearly attained, it is often crucial to have sampling strategies to reduce the variance of the estimate. The reason for this is that less likely events can, on the other hand, be of high impact. This can create a bias in the computation as the estimation can be dominated by more probable, but less important values. To correctly sample with a given N that is not near the limit of the large number, it is beneficial to modify the probability of the process in a way that balances the importance of the events. This is called importance sampling^{22,23,24,25,26,27,28}. This makes apparent two problems with Monte-Carlo algorithms. First, it may be difficult to calculate the probability of a particular realization of a random variable. Second, the importance sampling strategy relies on a sophisticated understanding of the probability distribution.

In this manuscript, we show that the characteristic function of a DSP can be efficiently calculated on a quantum computer, and in so doing we introduce an effect called quantum brute force. The random variables of the DSP of interest do not need to be identically and independently distributed, and non-Markovian processes can also be studied. The quantum-state space that grows exponentially with the number of qubits is used to move along all paths of the discrete stochastic process simultaneously in a quantum superposition, and hence the term quantum brute force is adequate.

The method proposed in this work maps the expectation value of interest into a probability of measuring a particular computational basis state of a qubit. This probability can essentially be thought of as the success parameter of a Bernoulli trial, i.e., a coin toss, whose statistics are well-known. As a consequence, the variance is optimal in the sense that it behaves according to the central limit theorem for all sample sizes, not only for large numbers. This leads to a crucial result that no sampling strategies are necessary.

Moreover, we connect quantum amplitude estimation (AE)²⁹, which can be utilized to overcome the classical limit on the sampling convergence of Monte-Carlo methods^15,16,30,31, to our method. In brief, the single-qubit measurement scheme can be replaced by an application of AE to the full system. With this modification, our algorithm uses resources that scale linearly instead of quadratically, and thus achieves a quantum speed-up. The methods developed here point therefore to an exciting and promising use of quantum computers: less variance and faster convergence for Monte-Carlo sampling. Equivalently, it is possible to reduce the sample size without losing precision.

Applications of our method span extensively across many fields in science and engineering; any physical behavior that can be mathematically modeled as a DSP can be studied in principle. In particular, we show how the found simulation procedure can be applied to option pricing theory and to correlated random walks which leads to various applications in biology, ecology, and finance. For each example, we experimentally demonstrate the proof-of-principle using the IBM quantum cloud platform.

Although the main focus of this work is to achieve quantum sampling advantage for discrete stochastic processes, we note that quantum memory advantages have been shown for stochastic processes with causal structures^18,19,20,32 and in rare-events sampling³³. An interesting connection concerning our result to this line of research comes from the work by Binder et al.³² which presented the construction of a unitary quantum simulator for generating all possible realizations of a hidden Markov model (HMM) that requires less memory than any classical counterparts throughout the simulation. The focus of this body of work has been sampling from a distribution, but with respect to the results discussed here, it can also be used to estimate expectation values, in particular characteristic functions.

Results

A discrete stochastic process can be described with n discrete random variables ${X}_{l}:{{{\Omega }}}_{l}\to {\mathbb{R}}$, l = 1, …, n for some $n\in {{\mathbb{N}}}_{+}$, each having at most k nonzero realizations, i.e., given a sample space Ω_l, there exist at most k elements ${x}_{l,0},\ldots ,{x}_{l,k-1}\in {\mathbb{R}}$ with X_l(Ω_l) = {x_l,0, …, x_l,k−1}. In plain words, a discrete stochastic process consists of n steps, and in each step, one of k possible events occurs at random with a certain probability. Hereinafter, we use the following notations. Each realization of the stochastic process is identified with an index vector ${{{\bf{j}}}}={({j}_{1},\ldots ,{j}_{n})}^{\top }\in {K}^{n}$ with K = {0, …, k − 1} and is denoted by ${{{\bf{x}}}}({{{\bf{j}}}})={({x}_{1,{j}_{1}},\ldots ,{x}_{n,{j}_{n}})}^{\top }$. Moreover, we define ${{{\rm{sum}}}}\left\{{{{\bf{x}}}}({{{\bf{j}}}})\right\}:=\mathop{\sum }\nolimits_{l = 1}^{n}{x}_{l,{j}_{l}}$ and ${{{{\bf{x}}}}}^{(m)}({{{\bf{j}}}})={({x}_{1,{j}_{1}},\ldots ,{x}_{m,{j}_{m}})}^{\top }$ with m ≤ n. The first and the second subscripts of the random variables and probabilities label the time step and the event, respectively. A quantity of interest for such processes is the expectation value of an integrable function $f:{\mathbb{R}}\to {\mathbb{R}}$ of the random variable ${S}_{n}=\mathop{\sum }\nolimits_{l = 1}^{n}{X}_{l}$

$${\mathbb{E}}\left[f({S}_{n})\right]=\mathop{\sum}\limits_{{{{\bf{j}}}}\in {K}^{n}}f({{{\rm{sum}}}}\left\{{{{\bf{x}}}}({{{\bf{j}}}})\right\}){\mathbb{P}}\left[{{{\bf{X}}}}={{{\bf{x}}}}({{{\bf{j}}}})\right].$$

(1)

The summation is over all possible realizations, each indexed by j, and X is the random variable representing the sequence of events that can occur in a particular realization. The number of terms in the summation (i.e., the number of realizations) is kⁿ.

Now, we explain how to encode the described stochastic process in a quantum state, and evaluate Eq. (1) by making a measurement on the quantum state. The quantum state consists of an index system and a data system defined in a Hilbert space ${{{{\mathcal{H}}}}}_{{{{\mathcal{I}}}}}\otimes {{{{\mathcal{H}}}}}_{{{{\mathcal{D}}}}}={{\mathbb{C}}}^{{k}^{n}}\otimes {{\mathbb{C}}}^{2}$, where ${{{\mathcal{I}}}}$ (${{{\mathcal{D}}}}$) indicates the index (data) system. Each realization of the stochastic process is represented as a unitary operator $U(\cdot ):{{\mathbb{R}}}^{n}\,\longrightarrow \,B({{{{\mathcal{H}}}}}_{{{{\mathcal{I}}}}}\otimes {{{{\mathcal{H}}}}}_{{{{\mathcal{D}}}}})$ parametrized by some n-dimensional vector ($B({{{\mathcal{H}}}})$ is the space of linear operators on a Hilbert space ${{{\mathcal{H}}}}$). Then a DSP can be represented as

$$\left|{\Psi }_{f}\right\rangle =\mathop{\sum}\limits_{{{{\bf{j}}}}\in {K}^{n}}p({{{\bf{j}}}})\left|{{{\bf{j}}}}\right\rangle \otimes U({{{\bf{j}}}})\left|\psi \right\rangle .$$

(2)

The factor of each part of the sum is denoted by p(j) with ∑_jp²(j) = 1 and the state of the index system is denoted by $\left|{{{\bf{j}}}}\right\rangle =\left|{j}_{n}\cdots {j}_{1}\right\rangle =\left|{j}_{n}\right\rangle \otimes \cdots \otimes \left|{j}_{1}\right\rangle$, where $\left|{j}_{l}\right\rangle$ for j_l = 0, …, k − 1 is the orthogonal basis. Measuring an expectation value of an observable M on the data system of the final state in Eq. (2) yields the convex sum of independent expectation values measured from all kⁿ trajectories³⁴ as

$$\begin{array}{lll}\langle M\rangle \,=\,\left\langle {{{\Psi }}}_{f}\right|{I}_{{{{\mathcal{I}}}}}\otimes M\left|{{{\Psi }}}_{f}\right\rangle \\ \qquad\,=\,\mathop{\sum}\limits_{{{{\bf{j}}}}\in {K}^{n}}{p}^{2}({{{\bf{j}}}})\left\langle \psi \right|{U}^{{\dagger} }({{{\bf{j}}}})MU({{{\bf{j}}}})\left|\psi \right\rangle \\ \qquad\,=\,\mathop{\sum}\limits_{{{{\bf{j}}}}\in {K}^{n}}{p}^{2}({{{\bf{j}}}}){\langle M({{{\bf{j}}}})\rangle }_{\psi },\end{array}$$

(3)

where M(j) = U^†(j)MU(j). The coefficient p²(j) can be identified with the joint probability and the expectation value with the evaluation of f, i.e.,

$${p}^{2}({{{\bf{j}}}})\equiv {\mathbb{P}}\left[{X}_{1}={x}_{1,{j}_{1}},\ldots ,{X}_{n}={x}_{n,{j}_{n}}\right]$$

(4)

$$\langle M({{{\bf{j}}}})\rangle \equiv f({x}_{1,{j}_{1}}+\cdots +{x}_{n,{j}_{n}})$$

(5)

for a function $f:{\mathbb{R}}\to {\mathbb{R}}$ that we will specify below.

In the worst case, evaluation of Eq. (3) requires two expensive procedures as follows. First, kⁿ probabilities need to be encoded as the amplitudes of kⁿ computational basis given by n qudits of dimension k. This can be done with various quantum state preparation techniques with a substantial amount of computational overhead^35,36. Next, kⁿ unitary operators, conditioned on all possible index states, need to be applied to an input state $\left|\psi \right\rangle$. Such operators can be expressed as

$${{\mbox{c-}}}U({{{\bf{j}}}})=\left|{{{\bf{j}}}}\right\rangle \left\langle {{{\bf{j}}}}\right|\otimes \left(V({x}_{n,{j}_{n}})\cdots V({x}_{1,{j}_{1}})\right)+\left|{{{\bf{j}}}}\right\rangle \left\langle {{{\bf{j}}}}\right|_{\perp }\otimes {I}_{{{{\mathcal{D}}}}}$$

with $V:{\mathbb{R}}\to {{{{\mathcal{H}}}}}_{{{{\mathcal{D}}}}}$. On the other hand, for many interesting DSPs, the number of necessary unitary operators can be reduced to ${{{\mathcal{O}}}}(nk)$.

Before explaining such exponential reduction in detail, we introduce two results in the next two propositions (with proofs provided in Supplementary Information) to establish the grounds for the measurement scheme.

Proposition 1 (Pauli X and Y Measurement). Let $V(x)={R}_{z}(2x)=\left|0\right\rangle \left\langle 0\right|+{e}^{ix}\left|1\right\rangle \left\langle 1\right|$ with $x\in {\mathbb{R}}$, then by setting M = σ_x or M = σ_y and $\left|\psi \right\rangle =(\left|0\right\rangle +\left|1\right\rangle )/\sqrt{2}$, we find

$${\langle {I}_{{{{\mathcal{I}}}}}\otimes {\sigma }_{x}\rangle }_{{{{\Psi }}}_{f}}={\mathbb{E}}\left[\cos ({S}_{n})\right],$$

(6)

$${\langle {I}_{{{{\mathcal{I}}}}}\otimes {\sigma }_{y}\rangle }_{{{{\Psi }}}_{f}}={\mathbb{E}}\left[\sin ({S}_{n})\right].$$

(7)

As the true value of ${\mathbb{E}}\left[\cos ({S}_{n})\right]$ and ${\mathbb{E}}\left[\sin ({S}_{n})\right]$ must be estimated, in general, the convergence behaves according to the central limit theorem, which guarantees that the measurement statistics approaches to a normal distribution around a mean that corresponds to ${\mathbb{E}}\left[f({S}_{n})\right]$ as the number of experiments N_S → ∞. The speed of convergence is moreover given by ${{{\mathcal{O}}}}(1/\sqrt{{N}_{S}})$. Taking into account that the Pauli measurements have two eigenvalues, the task is essentially estimating a probability of a Bernoulli trial, which specifies how the central limit theorem is realized. Given confidence of 1 − α, the number of experiments to be within a margin of error ϵ > 0 is ${N}_{S}=\lceil {z}_{\alpha }^{2}/(4{\epsilon }^{2})\rceil$ with z_α = z (1 − α/2) being the quantile function. In contrast, with classical Monte-Carlo sampling, the convergence rate by the central limit theorem is achieved with the caveat that the Monte-Carlo simulation samples from a usually unknown stochastic process and concise estimates on the number of experiments given a margin of error are in general not easily accessible. As we see, the property that Eq. (2) encompasses all possible paths with the correct probability with a quantum measurement leads to the seemingly small advantage of knowing the convergence beforehand, irrespective of the distribution of the underlying DSP. Contemplation on this fact reveals that this is no small feat: the quantum advantage lies in the fact that no sampling strategies are necessary.

The quantum amplitude estimation algorithm²⁹ can provide further speed-up compared to the convergence rate of the classical Monte-Carlo method given by the central limit theorem^15,16,30,31. The algorithm uses m ancilla qubits in addition to data and index qubits and ${{{\mathcal{O}}}}({{{\rm{poly}}}}(m))$ number of Grover-like iterators followed by ${{{\mathcal{O}}}}({m}^{2})$ Hadamard and controlled phase-shift gates for quantum Fourier transform (QFT)³⁷ to estimate an amplitude with an error of ${{{\mathcal{O}}}}(1/{2}^{m})$. The number of repeated measurements needed to reach confidence that the estimation succeeded is independent of m. The quantum AE algorithm can be adapted to our method to construct an even more powerful strategy by formulating an AE problem as follows. Given the final state in Eq. (2) written as a linear combination $\left|{{{\Psi }}}_{f}\right\rangle =\left|{{{\Psi }}}_{0}\right\rangle +\left|{{{\Psi }}}_{1}\right\rangle$ by separating the full Hilbert space into two orthogonal subspaces, we estimate the amplitude defined as a = 〈Ψ₁∣Ψ₁〉. Then, the following proposition connects AE with the DSP simulation.

Proposition 2 (Amplitude Estimation). Let $V(x)={R}_{y}(x)=\cos (x/2)I-i\sin (x/2){\sigma }_{y}$, $x\in {\mathbb{R}}$, $\left|\psi \right\rangle =\left|0\right\rangle$, then the final state is

$$\left|{{{\Psi }}}_{f}\right\rangle =\left|{{{\Psi }}}_{0}\right\rangle +\left|{{{\Psi }}}_{1}\right\rangle$$

(8)

with

$$\left|{{{\Psi }}}_{0}\right\rangle =\mathop{\sum}\limits_{{{{\bf{j}}}}\in {K}^{n}}\qquad p({{{\bf{j}}}})\cos \left(\frac{1}{2}{{{\rm{sum}}}}\left\{{{{\bf{x}}}}({{{\bf{j}}}})\right\}\right)\left|{{{\bf{j}}}}\right\rangle \left|0\right\rangle$$

(9)

$$\left|{{{\Psi }}}_{1}\right\rangle =\mathop{\sum}\limits_{{{{\bf{j}}}}\in {K}^{n}}\qquad p({{{\bf{j}}}})\sin \left(\frac{1}{2}{{{\rm{sum}}}}\left\{{{{\bf{x}}}}({{{\bf{j}}}})\right\}\right)\left|{{{\bf{j}}}}\right\rangle \left|1\right\rangle.$$

(10)

With AE the value $\tilde{a}$ will be estimated, hence ${\mathbb{E}}\left[\cos ({S}_{n})\right]=1-2\tilde{a}$. Conversely, if V(x) = R_y (−x), $\left|\psi \right\rangle ={R}_{y}(\pi /2)\left|0\right\rangle$, then there exists a similar decomposition $\left|{{{\Psi }}}_{f}^{\prime}\right\rangle =\left|{{{\Psi }}}_{0}^{\prime}\right\rangle +\left|{{{\Psi }}}_{1}^{\prime}\right\rangle$ so that with ${a}^{\prime}=\langle {{{\Psi }}}_{1}^{\prime}| {{{\Psi }}}_{1}^{\prime}\rangle$ we therefore find ${\mathbb{E}}\left[\sin ({S}_{n})\right]=1-2\tilde{a}^{\prime}$.

The above result opens up an exciting avenue towards a fast Monte-Carlo alternative without the need of sampling strategies. These propositions in conjunction with Theorem 1 which is stated in the following section show that a quantum computer can simulate the quantities ${\mathbb{E}}\left[\cos ({S}_{n})\right]$ and ${\mathbb{E}}\left[\sin ({S}_{n})\right]$ efficiently. As a result, one can calculate a random variable’s characteristic function ${\varphi }_{X}(v)={\mathbb{E}}\left[{e}^{ivX}\right]={\mathbb{E}}\left[\cos (vX)\right]+i{\mathbb{E}}\left[\sin (vX)\right]$ with two sets of experiments per $v\in {\mathbb{R}}$.

In order to extend the above ideas to estimate expectation values of a range of integrable functions $f:{\mathbb{R}}\to {\mathbb{R}}$, a Fourier series is used. If f is P-periodic, then

$${f}_{L}(x)=\mathop{\sum }\limits_{l=-L}^{L}{c}_{l}{e}^{i\frac{2\pi l}{P}x}$$

(11)

is the Fourier approximation of order L for f(x). By linearity of the expectation value, this approximation carries over to

$${\mathbb{E}}\left[{f}_{L}({S}_{n})\right]=\mathop{\sum }\limits_{l=-L}^{L}{c}_{l}{\varphi }_{{S}_{n}}\left(\frac{2\pi l}{P}\right).$$

(12)

As a consequence, it is possible to approximate any such expectation value in ${{{\mathcal{O}}}}(LN)$ experiments, where N is the number of shots per experiment. Convergence on Fourier series is a rich and mature field^38,39,40, which establishes basic results about convergence and the rate of convergence of each coefficient for given properties of the function f.

The underlying idea of simulating DSPs on a quantum computer has been laid out. Now we show that the simulation can be performed efficiently with a quantum circuit.

Independent increments

To deliver the underlying idea with a simple example, we start by presenting the case for DSPs with independent increments. To this end, the strategy taken is as follows. We first construct the state ${\sum }_{{{{\bf{j}}}}\in {K}^{n}}p({{{\bf{j}}}})\left|{{{\bf{j}}}}\right\rangle \in {{{{\mathcal{H}}}}}_{{{{\mathcal{I}}}}}$, and systematically entangle the data system ${{{\mathcal{D}}}}$ with the index system. When each of the increments are independent of each other, i.e., ${\mathbb{P}}\left[{X}_{i}=x,{X}_{j}=y\right]={\mathbb{P}}\left[{X}_{i}=x\right]{\mathbb{P}}\left[{X}_{j}=y\right]$ for pairwise different i ≠ j, Eq. (1) can be written as

$${\mathbb{E}}\left[f({S}_{n})\right]=\mathop{\sum}\limits_{{{{\bf{j}}}}\in {K}^{n}}f({{{\rm{sum}}}}\left\{{{{\bf{x}}}}({{{\bf{j}}}})\right\})\mathop{\prod }\limits_{l=1}^{n}{\mathbb{P}}\left[{X}_{l}={x}_{l,{j}_{l}}\right],$$

(13)

and ${p}_{l,{j}_{l}}^{2}={\mathbb{P}}\left[{X}_{l}={x}_{l,{j}_{l}}\right]$. This structure allows to partition ${{{\mathcal{I}}}}$ into subsystems, so-called level-index (sub)systems: ${{{{\mathcal{H}}}}}_{{{{\mathcal{I}}}}}{ = \bigotimes }_{l = 1}^{n}{{{{\mathcal{H}}}}}_{{{{{\mathcal{I}}}}}_{l}}$, where each ${{{{\mathcal{H}}}}}_{{{{{\mathcal{I}}}}}_{l}}={{\mathbb{C}}}^{k}$ represents a qudit Hilbert space. Let $\left|\alpha (n)\right\rangle \in {{{{\mathcal{H}}}}}_{{{{\mathcal{I}}}}}$ be the index-state. Then it can be described as a product state

$$\left|\alpha (n)\right\rangle =\mathop{\sum}\limits_{{{{\bf{j}}}}}p({{{\bf{j}}}})\left|{{{\bf{j}}}}\right\rangle = \mathop{\bigotimes}\limits_{l = 1}^{n}\left(\mathop{\sum }\limits_{{j}_{l}=0}^{k-1}{p}_{l,{j}_{l}}\left|{j}_{l}\right\rangle \right).$$

(14)

Each evolution from $\left|\alpha (l)\right\rangle \to \left|\alpha (l+1)\right\rangle$ is done by an unitary operator ${A}_{l+1}\in B({{{{\mathcal{H}}}}}_{{{{{\mathcal{I}}}}}_{l}})$ as given by ${A}_{l+1}\left|0\right\rangle =\mathop{\sum }\nolimits_{j = 0}^{k-1}{p}_{l+1,j}\left|j\right\rangle$. After n levels, i.e., the application of A = A_n ⋯ A₁, the final state $A{\left|0\right\rangle }_{n}=\left|\alpha (n)\right\rangle$ shown in Eq. (14) is created. Since each of the operators A_l only acts on a separate subspace ${{{{\mathcal{H}}}}}_{{{{{\mathcal{I}}}}}_{l}}$, they commute and can be applied in parallel. This is a consequence of the independence of the increments X_l. For example, an n-step DSP with k = 2 possible paths at each time step can be realized with n index qubits each prepared by a single-qubit unitary operation ${A}_{l}\left|0\right\rangle ={R}_{y}({\theta }_{l})\left|0\right\rangle =\cos ({\theta }_{l}/2)\left|0\right\rangle +\sin ({\theta }_{l}/2)\left|1\right\rangle$, where θ_l is chosen to satisfy ${\cos }({\theta }_{l}/2)={p}_{l,0}$ and ${\sin }({\theta }_{l}/2)={p}_{l,1}$.

Now, for each step of the DSP, k unitary operators applied to the data system controlled by an index qudit split the data space into k spaces, each attached to an orthogonal subspace of the index system. In other words, in each time step, the data system undergoes k independent trajectories. Thus n steps of k controlled unitary operations allow for the encoding of kⁿ independent realizations of a DSP to the index-data quantum state. To this end, we identify to each realization ${x}_{l,{j}_{l}}$ of the random variable X_l to the application of the operator $V({x}_{l,{j}_{l}})\in B({{{{\mathcal{H}}}}}_{{{{\mathcal{D}}}}})$ to the data system. In fact, the operator will be defined in such a way that the lth index-level state’s branches ${\left|{j}_{l}\right\rangle }_{l}$ with the amplitudes ${p}_{l,{j}_{l}}$ (for j_l ∈ K) control the operator, thereby identifying the probability ${p}_{l,{j}_{l}}^{2}={\mathbb{P}}\left[{X}_{l}={x}_{l,{j}_{l}}\right]$ with the occurrence of $V({x}_{l,{j}_{l}})$. We denote a projection to the lth index subsystem ${{{{\mathcal{I}}}}}_{l}$ as

$${{{\Pi }}}_{lj}=\left|j\right\rangle \left\langle j\right|_{l}\,\widehat{=}\ {I}_{k}^{\otimes l-1}\otimes \left|j\right\rangle \left\langle j\right|\otimes {I}_{k}^{\otimes n-l},$$

(15)

where I_k is the k-by-k unit matrix and its perpendicular pendant as ${{{\Pi }}}_{lj}^{\perp }$. Then the following theorem establishes the desired result (see Supplementary Information for the proof).

Theorem 1 Let $x\in {\mathbb{R}}$ and j ∈ K. Define operators

$$\,{{\mbox{c-}}}\,{V}_{l{j}_{l}}(x):= {{{\Pi }}}_{l{j}_{l}}\otimes V(x)+{{{\Pi }}}_{l{j}_{l}}^{\perp }\otimes I$$

(16)

with $\,{{\mbox{c-}}}\,{V}_{l{j}_{l}}(x)\in B({{{{\mathcal{H}}}}}_{{{{{\mathcal{I}}}}}_{l}}\otimes {{{{\mathcal{H}}}}}_{{{{\mathcal{D}}}}})$. Furthermore, for l = 1, …, n and ${{{\bf{x}}}}\in {{\mathbb{R}}}^{k}$, define the operator

$${U}_{l}({{{\bf{x}}}})=\mathop{\prod }\limits_{j=0}^{k-1}\,{{\mbox{c-}}}\,{V}_{l{j}_{l}}({x}_{j})\in B({{{{\mathcal{H}}}}}_{{{{\mathcal{I}}}}}\otimes {{{{\mathcal{H}}}}}_{{{{\mathcal{D}}}}}).$$

(17)

Then U(j) = U_n(x_n) ⋯ U₁(x₁) for ${{{{\bf{x}}}}}_{l}\in {{\mathbb{R}}}^{k},\ l=1,\ldots ,n$. The application of nk controlled operations $\,{{\mbox{c-}}}\,{V}_{l{j}_{l}}({x}_{l,{j}_{l}})$ is thus necessary. See Fig. 1for a depiction of Eqs. (16) and (17).

Fig. 1: Circuit design of DSPs with independent increments.

a A quantum circuit including preparation of the index system (operators in blue denoted by A_l) and the realization of c − U(j) (operators in green denoted by U_l(x) with a verticle line connected to black squares). A black square is placed on a control register, and the green box denoted by U_l(x) is placed on a target register. Unlike the conventional symbol for a controlled-NOT gate between qubits, the black square indicates that one of the k different unitary transformations is performed conditioned on the state of the control register of dimension k. b Schematic circuit representation of the applications of $c-{U}_{l}\in B({{{{\mathcal{H}}}}}_{{{{{\mathcal{I}}}}}_{l}}\otimes {{{{\mathcal{H}}}}}_{{{{\mathcal{D}}}}})$ for l = 1, …, n as used in (a). We use the notation V_lj = V(x_l,j). The open circle with a number j means that the unitary operator V_lj is applied if the control register state is $\left|j\right\rangle$.

Propositions 1, 2 and Theorem 1 establish that for V(x) = R_z(2x) or V(x) = R_y(x), $x\in {\mathbb{R}}$, we can compute given expectation values of Eqs. (6) and (7), respectively, with ${{{\mathcal{O}}}}(nk)$ controlled gates. The above algorithm can be visualized quite intuitively. Consider a set of unitary operators ${{{\mathcal{V}}}}=\{{V}_{l{j}_{l}}=V({x}_{l,{j}_{l}}):l=1,\ldots ,n,\ {j}_{l}\in K\}$ as above. These operators span an ordered tree of height n and a maximal degree of k. The label of the nodes themselves are of secondary importance, but each edge is labeled by one of the operators of the family ${{{\mathcal{V}}}}$ in such a way that, given the level l (l = 1 is the root), each node of the lth level has k edges, each of them are labeled by ${V}_{l{j}_{l}},\,{j}_{l}\in K$. A path between any two nodes, i.e., $({V}_{l{j}_{l}},\ldots ,{V}_{(l+i){j}_{l+i}})$, can be interpreted as a concatenation of operators, i.e., $V({j}_{l},\ldots ,{j}_{l+i})={V}_{(l+i){j}_{l+i}}\circ \cdots \circ {V}_{l{j}_{l}}$. After l level operations, paths from the root to every nodes at (l + 1)th level in the operator tree are traveled simultaneously. Hence the data system is evolved by the operator $U({{{\bf{j}}}})=V({j}_{1},\ldots ,{j}_{l})={V}_{l{j}_{l}}\circ \cdots \circ {V}_{1{j}_{1}}$ for all possible j. An example of the operator tree with n = 3 and k = 2 is depicted in Fig. 2.

Fig. 2: Operator tree.

a The operator tree spanned by a binary example (k = 2) of ${{{\mathcal{V}}}}$ for three time steps with the edges named. Each edge represents a state transformation from a parent node to a child node, and each node represents a quantum state. Three states at the final leaves starting from an initial state $\left|\psi \right\rangle$ at the root node are explicitly shown as an example. b The path j = (2, 1, 2)^⊤ ∈ K³ and the operator U(j) = V₃₂V₂₁V₁₂ are shown as an example.

Path-dependent increments

For a DSP with path-dependent increments, the probability of a particular realization can be expressed as

$$\begin{array}{lll}{\mathbb{P}}\left[{{{\bf{X}}}}={{{\bf{x}}}}({{{\bf{j}}}})\right]\,=\,\mathop{\prod }\limits_{i=2}^{n}{\mathbb{P}}\left[{X}_{i}={x}_{i,{j}_{i}}| {X}_{i-1}={x}_{i-1,{j}_{i-1}}\right]\\ \qquad\qquad\qquad\quad\times {\mathbb{P}}\left[{X}_{1}={x}_{1,{j}_{1}}\right].\end{array}$$

(18)

This is the first-order Markov chain that the probability to take a particular path in a given time step is determined by which path was taken in the previous step. Discussions thus far can easily be extended to such DSPs. The only difference is in the preparation of the index system, i.e., in the construction of the state ${\sum }_{{{{\bf{j}}}}\in {K}^{n}}p({{{\bf{j}}}})\left|{{{\bf{j}}}}\right\rangle$. Unlike in the case of the independent increments, one needs to introduce entangling operations directly within the index system. Without loss of generality, we use the index system consisting of qubits, i.e., two paths at each level, to describe the procedure. First, the index qubit for the first level is prepared in ${A}_{0}\left|0\right\rangle =\cos ({\theta }_{0}/2)\left|0\right\rangle +\sin ({\theta }_{0}/2)\left|1\right\rangle$ as before, while the rest of the qubits are in $\left|0\right\rangle$. Then the second index qubit is prepared by using the controlled operation $\left|0\right\rangle \left\langle 0\right|\otimes {R}_{y}({\theta }_{2}^{(0)})+\left|1\right\rangle \left\langle 1\right|\otimes {R}_{y}({\theta }_{2}^{(1)})$, controlled by the first index qubit, where the superscript indicates the path index of the previous step. Then the second index qubit is used as the control to prepare the third index qubit and so on. Thus, the index system state preparation can be done in n steps and the lth index qubit is prepared by applying a controlled operator $\left|0\right\rangle \left\langle 0\right|\otimes {R}_{y}({\theta }_{l}^{(0)})+\left|1\right\rangle \left\langle 1\right|\otimes {R}_{y}({\theta }_{l}^{(1)})$. An example quantum circuit for preparing the index quantum state for a DSP of n = 3 time steps (levels), each branch to two possibilities, is shown in Fig. 3.

Fig. 3: Quantum circuit to prepare the index system for simulating a path-dependent DSP.

The figure depicts an example of the first-order Markov chain of two steps each consisting of two realizations.

It is also straightforward to generalize the above procedure to implement path-dependence between events that are more than one time steps away. As an example, let us consider the n = 3, k = 2 cases depicted in Fig. 3. When the events at step 0 and step 1 have an impact on the event at step 2 (i.e., second-order Markov chain), then the single-qubit controlled rotations applied on the index qubit for step 2 should be replaced with the two-qubits controlled rotations controlled by both step 0 and step 1 index qubits. The number of three-qubit operations applied to the step 2 index qubit is four. Similarly, more complicated path-dependence, such as higher-order Markov chains, can be realized by designing multiqubit operations among index registers such that the rotation of the future state is controlled by the past states. The quantum circuit depth increases as ${{{\mathcal{O}}}}({k}^{{D}_{q}})$ where D_q is the quantum topological memory^41,42,43, which satisfies D_q ≤ q for a qth-order Markov chain (i.e., the current state is affected by q past states). Equality is given if each past state generates a unique future state. Note that many interesting applications can be described with small q (e.g., the first- or second-order Markov chain), and in some cases, D_q can even stay constant for unbounded q⁴³.

Besides the index-state preparation procedure, the analysis of the DSP follows exactly the same procedure as described in the previous section.

State-dependent increments

The increments in a given DSP can also vary in each step, determined by the state in the preceding step. In this case, the probability of a particular realization can be expressed as

$$\begin{array}{lll}{\mathbb{P}}\left[{{{\bf{X}}}}={{{\bf{x}}}}({{{\bf{j}}}})\right]\,=\,\mathop{\prod }\limits_{i=2}^{n}{\mathbb{P}}\left[{X}_{i}={x}_{i,{j}_{i}}| \mathop{\sum }\limits_{l=1}^{i-1}{X}_{l}\right]\\ \qquad\qquad\qquad\quad\times \,{\mathbb{P}}\left[{X}_{1}={x}_{1,{j}_{1}}\right].\end{array}$$

(19)

Intuitively, in order to control the increment given a particular realization of the current step, one needs to apply controlled operation to the index register, controlled by the data register in between each successive step. We leave the explicit details on how to realize the above process with quantum circuits as future work.

State machine simulation

In the “Introduction”, we mentioned that there is another way of simulating discrete stochastic processes by using a hidden Markov model (HMM). This is a state machine that has states Σ = {s₁, s₂, …}, output alphabets A = {a₁, …, a_k}, and a transition probability from state s_i to s_j while outputting the symbol a_k, i.e., ${p}^{2}(j,k| i)={\mathbb{P}}\left[{S}_{n}={s}_{j},{A}_{n}={a}_{k}| {S}_{n-1}={s}_{i}\right]$. A quantum advantage in simulating such processes has been reported in several places^32,42,43, which requires provably less memory than its classical counterpart¹⁸. This uses the unifilarity property which states that the output symbol uniquely defines the next state. Consequently, the above probability notation can be shortened to ${p}^{2}(k| i)={\mathbb{P}}\left[{S}_{n}=\lambda (k,i),{A}_{n}={a}_{k}| {S}_{n-1}={s}_{i}\right]$ with a function λ that maps uniquely the output symbol to a state. Models with this property are fairly common through a topological equivalence relation^41,44; unifilar models exist for any stochastic process with finite topological memory, which even includes some instances with infinite Markov order^18,19,32,43.

While the references above focus on sampling from a distribution rather than calculating an expectation value, we point out that our methods can be used to expand these ideas in the following way. First, it is necessary to map s_i to a quantum state $\left|{\sigma }_{i}\right\rangle \in {{{{\mathcal{H}}}}}_{S}\subseteq {{\mathbb{C}}}^{s}$ on a subspace that will be added to the total system. The unifilarity property allows the HMM states to be translated to non-orthogonal quantum states (i.e., $\left|{\sigma }_{i}\right\rangle\, \ne \,\left|{s}_{i}\right\rangle$ in general) which can reduce the memory requirement even further and more interestingly, s < ∣Σ∣. Going forward, as described above, the index space ${{{{\mathcal{H}}}}}_{{{{\mathcal{I}}}}}$ is constructed by nk-dimensional qudits. A unitary operator is applied to ${{{{\mathcal{H}}}}}_{S}\otimes {{{{\mathcal{H}}}}}_{{{{{\mathcal{I}}}}}_{l}}$ on the lth step. To be precise, given an initial state $\left|{\sigma }_{i}\right\rangle$, the first step

$$U\left|{\sigma }_{i}\right\rangle \left|0\right\rangle =\mathop{\sum}\limits_{{k}_{1}\in A}p({k}_{1}| i)\left|{\sigma }_{\lambda ({k}_{1},i)}\right\rangle \left|{k}_{1}\right\rangle$$

(20)

creates a superposition of all possible outputs and their current state. The subsequent step creates

$$U\mathop{\sum}\limits_{{k}_{1}\in A}p({k}_{1}| i)\left|{\sigma }_{\lambda ({k}_{1})}\right\rangle \left|{k}_{1}\right\rangle \left|0\right\rangle = \mathop{\sum}\limits_{{k}_{1},{k}_{2}\in A}p({k}_{2}| \lambda ({k}_{1},i))p({k}_{1}| i)\left|{\sigma }_{\lambda ({k}_{2},\lambda ({k}_{1},i))}\right\rangle \left|{k}_{1}\right\rangle \left|{k}_{2}\right\rangle .$$

(21)

By repeating the application of U with a fresh qudit initialized in $\left|0\right\rangle \ l$ times, a quantum state that encodes all possible paths of the l-step HMM can be created.

By introducing a mapping from the output alphabet to a numerical value $g:A\to {\mathbb{R}}$, we can create the process X_n = g(A_n) and then apply propositions 1 or 2 by adding a data system ${{{{\mathcal{H}}}}}_{{{{\mathcal{D}}}}}$. Therefore the quantum memory advantage reported¹⁸ and experimentally verified^19,20 can be carried over to our reported advantages to estimate the characteristic function efficiently. An interesting avenue for future work is also to apply these methods to rare-event sampling strategies³³.

The Delta for European call option

An exciting potential application of quantum computing is financial analysis^15,16,31. In particular, the framework developed in this work can be employed to compute the Delta of an European call option, which is central to various hedging strategies and hence of significant importance in financial engineering²¹. In brief, options are financial contracts that give the holder the right to buy (call) or sell (put) an underlying financial asset (e.g., stock) at a prescribed price (strike) on or before a prescribed date (expiration), whose value derives from the underlying asset. For European options, the holder can exercise the option only at the time of expiration. In this context, Delta measures the rate of change of the theoretical option value with respect to changes in the price of the underlying asset, which is instrumental for risk analysis.

Let S_t be stochastic process of an underlying asset then the Delta of a European call option can be expressed as

$$f({S}_{t})={{\Phi }}\left(\frac{{{\mathrm{ln}}}\,\frac{{S}_{t}}{K}+\left(r+\frac{{\sigma }^{2}}{2}\right)(T-t)}{\sigma \sqrt{T-t}}\right)$$

(22)

where ${{\Phi }}:{\mathbb{R}}\to [0,1]$ is the cumulative distribution function (CDF) of the standard normal distribution, K > 0 is the strike price, r is the risk-free interest rate, T − t is the time to maturity and σ is the volatility of the underlying asset. We are interested in the expectation value of the Delta, ${\mathbb{E}}\left[f({S}_{t})\right]$ when the underlying asset is described by a geometric Brownian motion, i.e., ${S}_{t}={S}_{0}\exp (\left(\mu -{\sigma }^{2}/2\right)t+\sigma {W}_{t})$ where $\mu \in {\mathbb{R}}$ and S₀ denote the drift and the starting value, respectively. Indeed, Eq. (22) considers a value reminiscent of the log-return, which is modeled by the Brownian motion and can be approximated as a random walk by Donsker’s invariance principle^45,46. The following result establishes the way to implement this on a quantum computer.

Proposition 3 Given n independent and identically distributed random variables X_l with ${\mathbb{P}}\left[{X}_{l}={x}_{1}\right]={\mathbb{P}}\left[{X}_{l}={x}_{2}\right]=1/2$ where

$${x}_{1}=\frac{\mu -\frac{{\sigma }^{2}}{2}}{n\sigma \sqrt{T-t}}-\frac{1}{\sqrt{n}\sqrt{T-t}}$$

(23)

$${x}_{2}=\frac{\mu -\frac{{\sigma }^{2}}{2}}{n\sigma \sqrt{T-t}}+\frac{1}{\sqrt{n}\sqrt{T-t}}$$

(24)

and an initial starting point of

$${x}_{0}=\frac{{{\mathrm{ln}}}\,{S}_{0}-{{\mathrm{ln}}}\,K+\left(r+\frac{{\sigma }^{2}}{2}\right)(T-t)}{\sigma \sqrt{T-t}}$$

(25)

with ${\tilde{S}}_{n}={x}_{0}+\mathop{\sum }\nolimits_{l = 1}^{n}{X}_{l}$, we find that

$${\mathbb{E}}\left[f({S}_{t})\right]=\frac{1}{2}-\mathop{\sum}\limits_{l=-\infty }^{{\infty }\,\,\,\,\,_{\prime}}\frac{i}{2\pi l}{e}^{-2{\pi }^{2}{l}^{2}/{P}^{2}}{\varphi }_{{\tilde{S}}_{n}}\left(\frac{2\pi l}{P}\right)$$

(26)

when Φ is limited on the interval [−P/2, P/2]. Note that we define the sum with prime as the sum over all summands except for l = 0 (see Supplementary Information).

When using the Pauli measurement scheme as explained in Proposition 1, one needs to use V(vx) = R_z(2vx) as operators with constants v = 2πl/P for l = −L, …, L to evaluate the characteristic function at those points for the Fourier-series approximation. This makes a total of 2L experiments (L measurements for each Pauli observable) with n Hadamard gates on n index qubits for encoding the probability information, n bit-flip gates on the index qubits for implementing the controlled operations that operate if the control qubit is 0, and 2n controlled-Rz gates, which of each can be further decomposed to two controlled-NOT and two R_z gates, applied on a data qubit controlled by the index qubit for implementing x₁ and x₂. In addition, the initial value x₀ can be implemented by one R_z gate (see Supplementary Fig. 2).

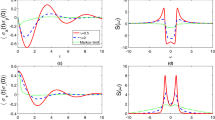
To demonstrate the proof-of-principle, we performed classical simulations and experiments of the quantum algorithm for calculating the Delta of an European call option on a IBM quantum device named ibmqx2. As an example, the underlying asset is given with μ = 0, σ = 0.02, r = 0.02, S₀ = 100, t = 1, and the time of maturity T = 10. The Fourier-series approximation is performed by choosing L = 100 and P = 100. The standard error mitigation protocol available in qiskit⁴⁷ is applied to reduce experimental errors. Despite imperfections, the experiment predicts the expectation value with high accuracy for the most important region, which is where it changes drastically, i.e., where the strike price varies between 100 and 150. We also performed a classical simulation of the quantum algorithm with the standard noise model provided in qiskit. These results are compared with the theoretical values in Fig. 4. The comparison shows that the noise model provided in qiskit explains the experimental error reasonably well (see “Methods” for a brief comment on the remaining difference between the two results).

Fig. 4: Evaluation of the Delta for the European call option.

Left: The Delta of an European call option is calculated for various strike prices. The underlying asset is defined with μ = 0, σ = 0.02, r = 0.02, S₀ = 100, t = 1, and the time of maturity T = 10. The dotted black line is the true evaluation of the Delta. The black (blue) solid line is the real (imaginary) part of the theoretical Delta calculation obtained by a Fourier approximation with P = 100 and L = 100, which serves as the reference for the experimental validation. The black crosses (blue tri-downs) are the real (imaginary) part of the Delta calculated with the experiment on the IBM quantum computer with error mitigation applied. The black dots (blue triangles) are the simulation with noise model provided in qiskit with the same error mitigation applied. Right: This plot shows the characteristic function calculated in theory ( × ), by simulation with noise and error mitigation (dot) and the IBM quantum experiment with error mitigation (tri-down) for the example strike price of K = 110.

Correlated random walks

The quantum advantage against classical methods manifests when the DSP strictly requires the ability to simulate path-dependent increments. We demonstrate the simulation of correlated random walks as one such example in this section.

Correlated random walk (CRW) is a mathematical model that describes discrete random processes with correlations between successive steps⁴⁸. It has been a useful tool to study biological processes^49,50, and can also be used to approximate fractional Brownian motion^51,52, which has broad applications for example in mathematical finance^53,54,55 and data network^56,57,58,59. The correlation, often referred to as persistence, results in a local directional bias as the walker moves. More precisely, the CRW denoted by ${S}_{n}=\mathop{\sum }\nolimits_{l = 0}^{n}{X}_{l}$ with n discrete random variables X_l, l = 1, …, n and persistence parameters p_l ∈ [0, 1] and q_l ∈ [0, 1] has the following properties: (1) X₀ = x₀, (2) ${\mathbb{P}}\left[{X}_{1}={x}_{1}\right]={\mathbb{P}}\left[{X}_{1}={x}_{2}\right]=1/2$, and (3) ${\mathbb{P}}\left[{X}_{l+1}={x}_{1}| {X}_{l}={x}_{1}\right]={p}_{l}$ and ${\mathbb{P}}\left[{X}_{l+1}={x}_{2}| {X}_{l}={x}_{2}\right]={q}_{l}$ ∀ l ≥ 1. The first two properties can be incorporated in quantum simulations easily by following the same procedure used in the previous example. Given p_l and q_l, the third property can be implemented as follows. First, all index qubits except the first one that encodes the probability distribution of X₁ are initialized in $\left|0\right\rangle$. The first index qubit is prepared in $(\left|0\right\rangle +\left|1\right\rangle )/\sqrt{2}$ in accordance with the second property. Then a controlled rotation gate is applied from each index qubit to an index qubit of the successive step. The controlled operation can be expressed as

$$\left|0\right\rangle \left\langle 0\right|\otimes {R}_{y}({\theta }_{{p}_{l}})+\left|1\right\rangle \left\langle 1\right|\otimes {R}_{y}({\theta }_{{q}_{l}}),$$

(27)

where ${\theta }_{{p}_{l}}=2{\cos }^{-1}(\sqrt{{p}_{l}})$ and ${\theta }_{{q}_{l}}=2{\cos }^{-1}(\sqrt{{q}_{l}})$. For example, after one application of the above-controlled operation, the index qubits representing the probability distribution of the first two steps of the CRW is given as

$$\frac{\left|0\right\rangle (\sqrt{{p}_{1}}\left|0\right\rangle +\sqrt{1-{p}_{1}}\left|1\right\rangle )+\left|1\right\rangle (\sqrt{1-{q}_{1}}\left|0\right\rangle +\sqrt{{q}_{1}}\left|1\right\rangle )}{\sqrt{2}}.$$

(28)

The above state shows that ${\mathbb{P}}\left[{X}_{2}={x}_{1}| {X}_{1}={x}_{1}\right]={p}_{1}$ and ${\mathbb{P}}\left[{X}_{2}={x}_{2}| {X}_{1}={x}_{2}\right]={q}_{1}$ as required by the property (3) of the CRW.

We demonstrate the proof-of-principle with an example designed as follows. The correlated random walk is given by increments x_l1 = 1 and x_l2 = −1 with an initial value x₀ = 0. The persistence parameters are p_l = (1/2, 2/3, 5/6, 1) and q_l = (1/2, 1/3, 1/6, 0) with l = 1, 2, 3, 4. Experiments were performed to calculate the characteristic function for v_l = 2πl/P, l = −L, …, L with L = 100 and P = 100 on ibmqx2. The standard error mitigation protocol available in qiskit is applied to reduce experimental errors. We also performed classical simulation of the quantum algorithm with the standard noise model provided by qiskit. These results are compared with the theoretical values in Fig. 5.

Fig. 5: Characteristic functions of a correlated random walk.

Characteristic functions of a random walk is calculated theoretically ( × ), by simulation (dot), and by experiment (tri-down). The simulation includes the standard noise model provided in qiskit. The experiment employs the standard error mitigation technique provided in qiskit. The parameters that define the correlated random walk is described in the main text.

Discussion

We presented a quantum-classical hybrid framework for estimating an expectation value of a random variable based on a discrete stochastic process under the action of function that admits a Fourier-series approximation. As the main ingredient of the framework, we developed a quantum algorithm for efficiently calculating point evaluations of the characteristic function of a random variable. This may also lead to other interesting applications since the probability distribution of a random variable can be completely defined by its characteristic function. More specifically, in the quantum part, the framework proposes a succinct representation of a classical DSP as a quantum state in the form of Eq. (2). The joint probability and the value of each realization are encoded in an entangled state $\left|{{{\Psi }}}_{f}\right\rangle$, and therefore all necessary information about a DSP is present. We also detailed the construction of a quantum circuit for preparing the quantum state $\left|{{{\Psi }}}_{f}\right\rangle$ using the number of circuit elements that only grow linearly with the total number of time steps. For a DSP of n total steps each consisting of k possibilities, there are kⁿ paths. Such a process can be encoded in a quantum state using nk-dimensional index qudits (or $\lceil {{{\mathrm{log}}}\,}_{2}(k)\rceil$ qubits) and nk controlled gates. There is no need for sampling strategies since all realizations exist in quantum superposition.

Two different measurement schemes are proposed for the estimation of expectation values ${\mathbb{E}}\left[\cos ({S}_{n})\right]$ and ${\mathbb{E}}\left[\sin ({S}_{n})\right]$. The first scheme is to measure an expectation value of σ_x and σ_y directly on the data system of $\left|{{{\Psi }}}_{f}\right\rangle$, resulting in a convergence error of ${{{\mathcal{O}}}}(1/\sqrt{N})$ for N repeated experiments for any N > 0. This shows that the quantum brute-force approach acquires the optimal importance distribution. Furthermore, the sampling convergence can be improved by utilizing the quantum amplitude estimation technique, which promises to reduce the approximation error by a factor of ${{{\mathcal{O}}}}(1/{2}^{m})$ using m additional qubits. However, the resource overhead of the latter approach is m ancilla qubits, ${{{\mathcal{O}}}}({{{\rm{poly}}}}(m))$ Grover-like controlled operations, and ${{{\mathcal{O}}}}({m}^{2})$ one- and two-qubit gates for implementing QFT. Therefore, with the noisy intermediate-scale quantum (NISQ) devices, it may be desirable to use the former approach.

The advantage of this algorithm lies in two facts. First, it is a quantum-classical hybrid computation and thus is a viable candidate to be solved with near-term quantum devices. One can envisage multiple near-term quantum devices running in parallel to calculate all 2L terms independently at the same time. Similar parallelization is also suitable for multiple partitions of a large quantum device where the qubit connectivity is high within each partition but low among partitions. Second, given one type of process S_n, we can pre-compute a number of evaluations of the characteristic functions ${\varphi }_{{S}_{n}}(\!{\pm {v}_{i}})$ for ${v}_{1} < \cdots < \,{v}_{L}\in {\mathbb{R}}$ a priori. With those evaluations at hand, it is possible to assemble the Fourier-series on-demand when given the Fourier-coefficients of a function f. This approach makes it possible to invest resources to maximize the precision of the characteristic function evaluation for regularly used DSPs. Furthermore, our framework promotes the idea for a co-design quantum computer^60,61,62,63, which focuses on optimizations and design decisions at the hardware level to particularly support the DSP simulations at hand.

We underscore our findings with two interesting examples. First, we showed an application to finance, the calculation of the Delta of a European call option. The key idea was to model the stochastic behavior of an underlying asset as a Brownian motion, which is then approximated as a random walk by Donsker’s invariance principle. Next, an application to DSPs with path-dependent increments is demonstrated by an example of correlated random walks. We presented the results of proof-of-principle experiments for each example to demonstrate the validity and the feasibility of our method.

The framework can be extended to multivariate functions $f:{{\mathbb{R}}}^{d}\to {\mathbb{R}}$. Given ${P}_{1},\ldots ,{P}_{d}\in {\mathbb{R}}$, the period of the respective argument of f and ${L}_{1},\ldots ,{L}_{d}\in {{\mathbb{N}}}_{+}$, a multi-dimensional Fourier-series approximation

$$f({x}_{1},\ldots ,{x}_{d})=\mathop{\sum }\limits_{{l}_{1}=1}^{{L}_{1}}\cdots \mathop{\sum }\limits_{{l}_{d}=1}^{{L}_{d}}c({\omega }_{1},\ldots ,{\omega }_{d}){e}^{i\mathop{\sum}\limits_{j}\frac{2\pi {l}_{j}}{{P}_{j}}{x}_{j}}$$

can be applied like Eq. (11) and consequently Eq. (12). The primary harmonics to calculate are thus ${\varphi }_{{S}_{n}}({{{\bf{v}}}})={\mathbb{E}}\left[{e}^{i{{{\bf{v}}}}\cdot {{{\bf{{S}}}_{n}}}}\right]$, which can be achieved by increasing the dimension of the index system and applying a new set of a unitary family ${{{{\mathcal{V}}}}}_{r}$ (r = 1, …, d) to the same data system ${{{\mathcal{D}}}}$.

The ability to simulate multivariate stochastic dynamics with the optimal variance and quadratic quantum speed-up without requiring any sampling strategies is highly beneficial for various analyses in the quantitative and computational science. The path-dependent and state-dependent DSP simulations are excellent fits for studying random walks with internal states⁶⁴, and discrete processes that converge to Ornstein–Uhlenbeck⁶⁵ and fractional Brownian motion⁵¹. Due to the broad applicability of these mathematical models, the framework developed in this work opens tremendous and extensive opportunities in physics, biology, epidemiology, hydrology, engineering, and finance.

In future work, we plan to provide explicit quantum circuit design for simulating state-dependent DSPs. Interesting applications to accompany this model include the analysis of stochastic epidemic models^66,67 and of hot streak⁶⁸.

Methods

All experiments are performed using one of the publicly available IBM quantum devices consisting of five superconducting qubits, named as ibmqx2. In order to fully utilize the IBM quantum cloud platform, we used the IBM quantum information science kit (qiskit) framework⁴⁷. The versions—as defined by PyPi version numbers—used for this work were 0.20.0.

Superconducting quantum computing devices that are currently available via the cloud service, such as those used in this work, have limited coupling between qubits. Resolving coupling constraints as well as optimizations are done in qiskit with a preset of so-called pass managers. The optimization level ranges from 0 to 3. As we chose the ibmqx2 for our experiments the mapping of data register and index register follow the connectivity. For the family of devices that contains ibmq_ourense, one swap operation must be used to exchange the physical qubit 3 and 4. For both layouts see Supplementary Fig. 1a, b. During the compilation step of the experiments, we first use a level 0 pass and then a subsequent level 3 pass to optimize and resolve connectivity constraints. To reduce experimental errors, we used the standard error mitigation functionality of qiskit. This requires an extra set of experiments to be executed prior to the main experiment.

In order to understand the source of experimental discrepancy, the experimental results were compared to simulation results that take a realistic noise model into account. During the execution of an experiment, the current device parameters were gathered and stored. Upon completion, a simulation was executed with the standard qiskit noise model, also applying error mitigation on the result. The remaining discrepancy between experimental and simulation results can be attributed to errors that are not included in the basic error model, such as various cross-talk effects, drift, and non-Markovian noise. The standard noise model is described in the supplementary information of ref. ⁶⁹ in detail.

The example for the Delta applied the strike price K from 10 to 220 in increments of 5 for the theoretical calculation, while the experiments were performed for K = 25, 55, 85, 105, 110, 115, 120, 125, 130, 160, 190, 220. The experiment for each K is executed for characteristic function evaluations at v_l = 2πl/P with l = −L, …, L, L = 100 and P = 100, each with 8129 shots. For the correlated random walk experiment, we used 32786 shots for each of the evaluations of v_l = 2πl/P with l = −L, …, L and P = L = 100. Note that this example did not use the Fourier approximation, and P has been chosen to be the same as L so that v_l goes through one period on each side, resulting in a symmetric picture. As the IBM quantum cloud platform allows for 8192 shots per execution, we created multiple identical experiments and manually added the results.