No CrossRef data available.
Article contents
Completion versus removal of redundancy by perturbation
Part of:
Nontrigonometric harmonic analysis
Published online by Cambridge University Press: 05 July 2021
Abstract
A sequence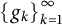 
$\left \{g_k\right \}_{k=1}^{\infty }$
in a Hilbert space 
${\cal H}$
has the expansion property if each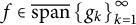 
$f\in \overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty }$
has a representation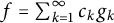 
$f=\sum _{k=1}^{\infty } c_k g_k$
for some scalar coefficients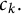 
$c_k.$
In this paper, we analyze the question whether there exist small norm-perturbations of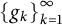 
$\left \{g_k\right \}_{k=1}^{\infty }$
which allow to represent all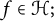 
$f\in {\cal H};$
the answer turns out to be yes for frame sequences and Riesz sequences, but no for general basic sequences. The insight gained from the analysis is used to address a somewhat dual question, namely, whether it is possible to remove redundancy from a sequence with the expansion property via small norm-perturbations; we prove that the answer is yes for frames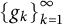 
$\left \{g_k\right \}_{k=1}^{\infty }$
such that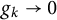 
$g_k\to 0$
as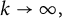 
$k\to \infty ,$
as well as for frames with finite excess. This particular question is motivated by recent progress in dynamical sampling.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
References
Aldroubi, A., Cabrelli, C., Çakmak, A. F., Molter, U., and Petrosyan, A., Iterative actions of normal operators. J. Funct. Anal. 272(2017), no. 3, 1121–1146.Google Scholar
Aldroubi, A., Cabrelli, C., Molter, U., and Tang, S., Dynamical sampling. Appl. Harm. Anal. Appl. 42(2017), no. 3, 378–401.Google Scholar
Aldroubi, A., Davis, J., and Krishtal, I., Dynamical sampling: time-space trade-off. Appl. Comp. Harm. Anal. 34(2013), no. 3, 495–503.Google Scholar
Balan, R., Casazza, P., Heil, C., and Landau, Z., Deficits and excesses of frames. Adv. Comp. Math. 18(2003), 93–116.CrossRefGoogle Scholar
Casazza, P. G. and Christensen, O., Frames containing a Riesz basis and preservation of this property under perturbation. SIAM J. Math. Anal. 29(1998), no. 1, 266–278.CrossRefGoogle Scholar
Chen, D. Y., Li, L., and Zheng, B. T., Perturbations of frames. Acta Math. Sin. (Engl. Ser.) 30(2014), no. 7, 1089–1108.CrossRefGoogle Scholar
Christensen, O., Operators with closed range and perturbation of frames for a subspace. Canad. Math. Bull. 42(1999), no. 1, 37–45.CrossRefGoogle Scholar
Christensen, O., An introduction to frames and Riesz bases. 2nd expanded ed., Birkhäuser, Basel, 2016.Google Scholar
Christensen, O., deFlicht, C., and Lennard, C., Perturbation of frames for a subspace of a Hilbert space. Rocky Mountain J. Math. 30(2000), no. 4, 1237–1249.Google Scholar
Christensen, O. and Hasannasab, M., Frame properties of iterated systems. Appl. Comp. Harm. Anal. 46(2019), 664–673.Google Scholar
Christensen, O., Hasannasab, M., and Philipp, F., Frame properties of operator orbits. Math. Nachr. 293(2020), 52–66.CrossRefGoogle Scholar
Holub, J., Pre-frame operators, Besselian frames and near-Riesz bases. Proc. Amer. Math. Soc. 122(1994), 779–785.CrossRefGoogle Scholar
Marcus, A. W., Spielman, D. A., and Srivastava, N., Interlacing families II: mixed characteristic polynomials and the Kadison–Singer problem. Ann. of Math. (2) 182(2015), no. 1, 327–350.CrossRefGoogle Scholar
Olevskii, V., On orthonormal bases and translates. J. Approx. Theory 202(2016), 1–4.CrossRefGoogle Scholar
Young, R., An introduction to nonharmonic Fourier series. Academic Press, New York, 1980 (revised first edition 2001).Google Scholar