1 Introduction

In the field of business, companies offer products and services, and they seek to maximize the revenue achieved by these sales. Determining the right price is crucial for obtaining the optimal revenue, and this is controlled by the well-known price-demand relation. Setting a high price will drive customers away and therefore reduce demand. On the other hand, choosing a low price will lead to increasing demand, but lower revenue due to the lower price. Companies attempt to set an optimal price that maximizes revenue based on their knowledge of price-demand relation. However, the shape or the parameters are not known beforehand, and have to be inferred from actual selling situations. This may have corporations test a number of different prices, in order to learn the demand curve parameters.

Some firms could perform the price experimentation as a part of the market research phase before the actual business operation. For example, the companies selling their products on the internet can utilize digital price tags to gather price-demand data for online customers (den Boer 2015). However, other firms could have business constraints on the frequency of price changes for their products (Cheung et al. 2017; Chen and Chao 2019; Rhuggenaath et al. 2019)). Moreover, excessive price experimentation may lead to a long initial period of non-optimal pricing, and will therefore compromise the revenue. On the other hand, too little experimentation may be insufficient to discover accurate parameter values.

Generally, price experimentation is used to learn the demand model by testing a number of prices in order to estimate the price demand relation. This is known in literature as the learning problem. On the other hand, companies should also seek to choose the optimal price that maximizes the gained revenue, which is known as the earning problem. Typically, there is an inherent trade-off between these two problems, named as the learning/earning trade-off (Rothschild 1974; Cheung et al. 2017). It is akin to the trade-off of exploration versus exploitation that we encounter in machine learning and evolutionary optimization (Tokic 2010; Črepinšek et al. 2013; Rezaei and Safavi 2020; Jerebic et al. 2021; Mahesh and Sushnigdha 2021).

Fast and accurate estimation of the demand curve becomes particularly important for the novel field of dynamic pricing for revenue management (Bertsimas and Perakis 2006; Besbes et al. 2014; den Boer 2012, 2015). Dynamic pricing means pricing the product in a time varying way, according to the changes in demand, in order to maximize revenue (Ibrahim and Atiya 2016). Dynamic pricing has proved its powerful impact in various applications such as hotel revenue management (Bayoumi et al. 2013), airline industry (McAfee and Te Velde 2006), mobile data services (Elreedy et al. 2017), electricity (Triki and Violi 2009), and e-services (Xia and Dube 2007).

The problem with dynamic pricing is that firms usually do not know the underlying demand price relation that characterizes customers’ response upon any price change. Moreover, the price demand curve shifts frequently with time and with seasonal fluctuations (which is the reason why we would apply dynamic pricing). The learning window is therefore too short, and one has to make the most out of few data.

Another factor that could result in sudden shift in demand is catastrophic events such as wars, economic downturns, or pandemics like COVID-19. Also some lesser effects, such fluctuations of demand by season or due to shift in fashion tastes, lead to smaller and more gradual shifts of the demand curve. This necessitates speedy learning of the new demand relation. A timely algorithm that can quickly track the new demand variations, like the methods we propose here, would be very useful.

In this paper, we make use of the knowledge in the machine learning field of the exploration versus exploitation concept, in order to solve the problem of price demand function determination. Initially, the algorithm is more focused on exploration. It is a discovery phase with the goal being to accurately estimate the parameters of the price demand relation. Gradually, the algorithm shifts to exploitation, where it puts more attention toward revenue maximization (rather than exploration of the parameter space). Moreover, in the proposed approach we make use of machine learning approaches and signal processing algorithms, to explore efficient algorithms for learning the demand function. Specifically, we propose an objective function that is a combination of revenue and accuracy of the parameter estimates. Revenue is the ultimate goal that needs to be optimized. However, parameter estimate accuracy will positively impact future revenue. This is a novel formulation that can combine the effects of exploration and exploitation. By having a decaying weighting coefficient for the accuracy term of the objective function, exploration will gradually make way for exploitation as time goes by.

Essentially, the proposed approach formulates a sequential optimization problem, where the objective function is the revenue minus a term that measures the error or uncertainty in the price demand parameters. We propose three different formulations for handling the problem, where each corresponds to a different way of defining the parameter uncertainty.

We use a simple parametric model, assuming a linear demand curve. We consider a simple parametric model for several reasons: first, at early time steps, not much information is available, which hinders the performance of nonparametric models. In addition, generally, parametric models are less computationally intensive than nonparametric ones. Another argument raised by Keskin and Zeevi (2014) is that the linear demand function could approximate any demand function especially that firms usually do not use a very broad range of prices, they rather experiment with prices around a certain predefined price or within a certain range, where such predefined prices are set according to business considerations and marketing conditions. Operating at a narrow range means that a linear model is approximately valid. Finally, linear demand models are the dominant models used in the operations research and the economics literature (Lobo and Boyd 2003; Bertsimas and Perakis 2006; Cheng 2008; Keskin and Zeevi 2014; Besbes and Zeevi 2015).

In our work, we apply the recursive linear regression model proposed by Atiya et al. (2005) for estimating the demand curve due to its efficiency since it fits the sequential nature of the problem. We provide Sect. 4 for briefly describing the recursive linear regression model and presenting its formulation. The purpose of this work is to propose several simple, closed-form, efficient, and effective pricing strategies that can be conveniently applied by firms for revenue maximization and demand learning. We conduct a set of experiments to our proposed pricing strategies, to some standard baseline pricing strategies, and to some pricing methods in the literature. The experiments show that our proposed formulations outperform the competing methods and benchmarks in terms of the achieved revenue.

The main contributions of this work are summarized as follows:

  • To the best of our knowledge, the explicit incorporation of model uncertainty is essentially novel in the context of managing the exploration versus exploitation trade-off.

  • In this work, we propose several novel formulations incorporating the target objective function (revenue) and model uncertainty.

  • This work presents different pricing methods that are simple and easy to implement taking into account business considerations of pricing constraints and little price experimentation.

  • We apply our proposed pricing methods to real and synthetic datasets, and they achieve superior performance in terms of the gained revenue compared to the other pricing methods in the literature including: myopic pricing, myopic pricing with dithering (Lobo and Boyd 2003), and controlled variance pricing (CVP) (den Boer and Zwart 2013).

The paper is organized as follows: Sect. 2 presents a literature review. Section 3 presents the problem formulation. Section 4 briefly describes the recursive formulation of linear regression model that is applied in our experiments. Then, our proposed pricing formulations are represented in Sect. 5. After that, Sect. 6 presents experimental results. The results are further analyzed in Sect. 7. Finally, Sect. 8 concludes the paper and mentions potential future work.

2 Related work

2.1 Dynamic pricing with demand learning

In this section, we review the work in the literature considering dynamic pricing in case of unknown demand price curve. Our work relates to the literature in both operations research and sequential optimization. Regarding the operations research literature, there are several contributions handling dynamic pricing with demand learning (comprehensive reviews are provided in Araman and Caldentey (2010); Aviv and Vulcano (2012); den Boer (2012, 2015)).

We discuss dynamic pricing in two main settings: with no inventory restrictions (i.e., infinite inventory) and finite inventory where there is a limitation on the supply of products/services to sell.

2.1.1 Infinite inventory

One intuitive dynamic pricing strategy is the greedy or myopic pricing where at each time step, the price is chosen so as to maximize the immediate revenue. Definitely, this policy is myopic and sub-optimal since this pricing strategy does not learn the demand curve parameters.

Lobo and Boyd (2003) propose a basic simple pricing policy for linear demand learning of a single product based on the simple myopic pricing policy. The authors modify the myopic pricing and introduce some exploration to it by adding a random perturbation to the myopic price.

Another work extending the simple myopic pricing is the work by den Boer and Zwart (2013). The proposed pricing policy, named controlled variance pricing (CVP), chooses the optimal price given the current estimate of the model (like myopic greedy pricing). However, the CVP policy imposes a constraint that the chosen price is not very close to the average of the prices previously selected. This constraint ensures diversity of chosen prices and incorporates some exploration to enhance the accuracy of estimating demand model parameters.

Since price experimentation is costly as pointed out in the introduction (see Sect. 1), Cheung et al. (2017) propose a dynamic pricing model with unknown demand function, and under the constraint of having a limited number of price adjustments for demand learning. The authors propose a pricing policy minimizing the worst-case regret, \(O(log^mT)\), where T is the length of the sales horizon and m is the maximum limit of number of price changes. However, their model assumes that the demand function belongs to a finite set of functions.

Besbes and Zeevi (2015) investigate how model misspecification could affect revenue loss. They consider a multi-period single product pricing problem and prove that some pricing strategies based on two parameter linear demand models could converge to near-optimal pricing decisions even in case of model misspecification.

Keskin and Zeevi (2014) handle pricing not only for a single product, but also for multiple products along finite, T-time step horizon. They propose some variants of the greedy iterative least squares strategy which utilizes sequential model learning, and myopic price optimization given the learned model.

Carvalho and Puterman (2005) consider the dynamic pricing problem in the context of online pricing over the internet. They model the individual customer’s response to price change as a binary random variable following binomial distribution. Their proposed pricing method maximizes the one-step look-ahead revenue using Taylor series expansion to approximate the next step revenue. Their proposed method outperforms myopic pricing. Further, Elreedy et al. (2021) develop a multi-step look-ahead pricing policy for uncertain linear demand models. Their approach incorporates future revenues into the objective function by maximizing the expected multi-step look-ahead revenue in addition to the immediate revenue. They implement two methods considering a single and two look-ahead revenues. Their approach outperforms the myopic pricing.

2.1.2 Finite inventory

There are various contributions in literature that handle finite inventory setting in the dynamic pricing with learning problem, where the seller has a fixed finite number of products to sell over a sales horizon. An example of the work considering the finite inventory setting is the work by Aviv and Pazgal (2002). The authors develop a Bayesian dynamic pricing control model where customers arrive according to a Poisson process with unknown arrival rate. However, the customer’s potential buying probability is assumed to be known. Prices are derived by solving a differential equation, and in case of no solution of the equation, one of the these simple heuristics is applied: fixed pricing policy, certainty equivalent pricing (CEP), and a basic pricing policy that ignores demand uncertainty and uses initial expected values for demand parameters.

Araman and Caldentey (2009) consider a similar problem setting of finite inventory. They model the dynamic pricing problem as an intensity control problem, and propose a heuristic pricing policy based on approximating the value function of the underlying problem.

Farias and Van Roy (2010) handle dynamic pricing with finite inventory, in case of unknown demand. They consider maximizing the expected discounted revenue over an infinite time horizon. In their model, they assume that a customer buys the product/service only if his reservation price equals or exceeds the seller’s price. The authors propose a heuristic pricing strategy named as decay balancing. They show that their proposed decay balancing strategy outperforms certainty equivalent pricing (CEP) (Aviv and Pazgal 2002) and the greedy strategy proposed by Araman and Caldentey (2009). In addition, the authors extend their model to handle sellers with multiple branches.

Another piece of work that considers dynamic pricing with finite inventory is proposed by Bertsimas and Perakis (2006). Since the dynamic pricing problem is a sequential optimization problem, the authors develop dynamic programming based models considering both competitive and non-competitive marketing environments, assuming perishable products. However, since dynamic programming considers the whole state space, it is intractable. Consequently, the authors propose several lower-dimensional approximations. The proposed pricing policies outperform the myopic pricing; however, these methods are still computationally intensive.

Another piece of work done by Wang et al. (2014) applies a nonparametric demand model for pricing with finite inventory constraint. The proposed model applies a sequence of shrinking pricing intervals before choosing a price within each iteration. This model achieves low regret bounds \(O(n^{-1/2})\); however, it is computationally intensive.

Cao et al. (2019) develop a Bayesian pricing method for a single product in a finite time horizon with unknown customers’ arrival rate. The authors assume that the customers’ buying behavior is affected by the reference price. They formulate the dynamic pricing problem with the imposed assumptions using Bayesian dynamic programming. Moreover, they study how demand learning is influenced by having sufficient inventory. In addition, they analyze the impact of the reference price on the gained revenue. Price et al. (2019) use a Gaussian Process methodology to track and estimate the dynamic changes in demand, taking into consideration the necessity to unconstrain the demand (estimating the true demand in case inventory is assumed unlimited from finite inventory data). The Gaussian Process is a machine learning/statistical approach that models data as a joint multivariate Gaussian (Atiya et al. 2020).

Some dynamic pricing approaches do not use a fixed price for all customers, they rather tailor a different price per customer based on each customer’s buying behavior, commonly known in the literature as personalized pricing (Aydin and Ziya 2009; Diao et al. 2011). A piece of work that develops an adjusted price per customer in case of unknown demand is presented by Morales-Enciso and Branke (2012). In this paper, the authors assume a different potential buying probability per customer. They develop two different pricing policies. One of them chooses the price maximizing the expected improvement of revenue. On the other hand, the other pricing policy selects the price maximizing the summation of expected immediate revenue and expected revenue of the next time step. However, the myopic greedy pricing policy outperforms both of their proposed pricing methods.

Another work adopting personalized pricing is developed by Ban and Keskin (2020). In this work, the authors develop a personalized pricing policy that learns the customer behavior over time horizon T. In their work, the authors model the customer behavior as a d-dimensional feature vector where only s out of the d features are the personalized ones. The authors analyze their proposed policy and prove that the expected regret of their policy is \(O(s \sqrt{T}(\log d+ \log T))\).

Not only product pricing, but also option pricing exhibits uncertainty in the financial market environment as indicated by (Ji and Zhou 2015; Sun et al. 2018; Chen et al. 2019; Gao et al. 2021). Several works study option pricing under the uncertain stock market. Chen et al. (2019) examine pricing the European call options under a fuzzy environment. Furthermore, Gao et al. (2021) investigate pricing the Asian rainbow option under the uncertain stock model. The authors model assets’ prices as uncertain processes, and they derive pricing formulas for the Asian rainbow option.

Crises such as COVID-19 usually result in a tremendous change of customers’ purchase behavior. Liu et al. (2020) analyze the impact of COVID-19 on the demand price relation. They develop a Bayesian approach for learning the demand function. In their work, the authors handle a single-product periodic-review inventory system. They adopt a multiplicative demand model where the demand is defined as the product of a price function and a random perturbation term representing the fluctuations in the market environment. The authors formulate the dynamic pricing problem as a Bayesian dynamic program to learn the demand distribution.

2.2 Studies of the exploration–exploitation trade-off

Exploration versus exploitation trade-off is studied in many contexts including: reinforcement learning (Ishii et al. 2002; Tokic 2010; Asiain et al. 2019), dynamic pricing (Araman and Caldentey 2009; Harrison et al. 2012; den Boer and Zwart 2013; Besbes and Zeevi 2015), evolutionary optimization (Črepinšek et al. 2013; Singh and Deep 2019), sequential optimization (Martinez-Cantin et al. 2009), sequential design (Crombecq et al. 2011), and online advertising (Li et al. 2010). Furthermore, the exploration–exploitation trade-off is investigated in the context of multi-armed bandit problem setting (Auer et al. 2002; Vermorel and Mohri 2005; Valizadegan et al. 2011; Besbes et al. 2014).

Multi-armed bandit (MAB) is a class of sequential decision-making problems originally developed by Thompson (1933); Robbins (1985). Multi-armed bandit problems aim to maximize rewards, but under uncertainty and incomplete feedback about rewards, so there is a trade-off between performing an action that gathers information regarding reward (exploration), and making a decision that maximizes the immediate reward given the information gathered so far (exploitation) (Audibert et al. 2009). Many problems can be formulated using the multi-armed bandit setting such as our target problem: dynamic pricing with unknown demand (den Boer 2012), online advertising (Pandey et al. 2007), and clinical trials (Villar et al. 2015).

Trovo et al. (2015) utilize the multi-armed bandit formulation for solving the revenue maximization problem in case of unknown demand model. They propose two pricing policies that are, essentially, refined versions of the upper confidence bound (UCB) algorithm proposed by Auer (2002) to adapt the pricing problem. In addition, Rhuggenaath et al. (2020) develop an auction pricing algorithm based on one of the main multi-armed bandit algorithms: Thompson Sampling (Thompson 1933, 1935).

Reinforcement learning is extensively applied in dynamic pricing frameworks (Kutschinski et al. 2003; Cheng 2008; Han et al. 2008; Rana and Oliveira 2015). As an example of using reinforcement learning for dynamic pricing with unknown demand is the work developed by Cheng (2008) where Q-learning is applied for learning the value function, with the objective of revenue maximization. However, the reinforcement learning approach is computationally expensive, and under the constraint of having limited price experimentation. Accordingly, reinforcement learning could be challenging for the underlying problem of dynamic pricing with unknown demand curve.

Deep learning (Shrestha and Mahmood 2019) and deep reinforcement learning (Arulkumaran et al. 2017; Caviglione et al. 2020) have gained much interest in recent years. Kastius and Schlosser (2021) employ deep reinforcement learning for dynamic pricing. The authors mainly apply Deep Q-Networks (DQN) to model market competitors in e-commerce. Moreover, they develop another pricing model using a policy gradient algorithm named soft actor-critic (SAC). Furthermore, the work developed by Zhong et al. (2021) applies deep reinforcement learning to dynamic pricing in regenerative electric heating.

Recently, active learning has proved its powerfulness, especially in applications where the cost of data collection is significant (Settles 2009; Fazakis et al. 2019). Elreedy et al. (2019) propose an active learning framework for handling the exploration–exploitation trade-off in optimization problems. They apply the proposed framework to the dynamic pricing with demand learning problem.

Another approach for optimizing multiple contradictory objectives is the multi-objective evolutionary algorithms which seek to find Pareto-optimal solutions (Schaffer 1985; Curiel et al. 2012). An example of the multi-objective evolutionary algorithms is the multi-objective differential evolution (DE) algorithm developed by Awad et al. (2017). Another work by Srinivasan and Kamalakannan (2018) introduces a multi-objective genetic algorithm (MOGA) for analyzing financial data for risk management. However, generally, the performance of evolutionary algorithms is highly dependent on the applied crossover, mutation, and selection strategies. Recently, Farahani and Hajiagha (2021) employ meta-heuristic algorithms: social spider optimization (SSO) and bat algorithm (BA) along with artificial neural networks for stock price forecasting. However, generally, the performance of evolutionary algorithms is highly dependent on the applied crossover, mutation, and selection strategies.

Recently, fuzzy optimization has been applied to uncertain environments, especially in financial markets as indicated by Bisht and Srivastava (2019). For example, Li et al. (2020) design a multi-objective fuzzy optimization algorithm for portfolio selection of time-inconsistent investors.

Several game theoretical approaches have been developed for dynamic pricing in different contexts such as smart grids by Tang et al. (2019) and resource pricing by Zhu et al. (2020). For example, Zhu et al. (2020) design a dynamic pricing model for cloud computing services using game theory. Specifically, the authors model pricing and resource allocation as a Stackelberg game in order to resolve the conflict of maximizing revenues for both the software as a service (SaaS) providers that deliver software services and the infrastructure as a service (IaaS) providers that offer the infrastructure.

3 Problem formulation

In this work, we use a linear price demand model (or price elasticity model), as typically used in the economics/finance literature. The price is the main controlling variable for demand. We assume a monopolist seller who has a sufficient inventory to satisfy all potential demand, which is known in literature as infinite inventory setting. Our work considers pricing a single product over a finite selling horizon T.

We formulate a dynamic pricing problem for the case of unknown demand as a sequential optimization problem. Our work is algorithmic in general and attempts to derive efficient algorithms for tackling this problem. At each time step n, a price \(p_n\) is chosen so as to maximize a certain utility function incorporating the two objectives of demand estimation and revenue maximization. For any new price \(p_n\), we observe the corresponding demand \(D_n\), and this pair \((p_n,D_n)\) is considered an extra data point that can fine tune more accurate parameter estimates (for the price demand relation). We apply a weighted least squares recursive formulation for updating these parameter estimates given the new acquired data point \((p_n, D_n)\). This process iterates until the number of iterations defining the horizon T is reached.

The linear demand model equation is defined as follows:

$$\begin{aligned} D=a+bp+\epsilon \end{aligned}$$
(1)

such that \(b<0\) and \(\epsilon \sim {\mathcal {N}}(0,\sigma ^{2})\). Let \(x=[1\,\,\,\,p]^T\), so we can express the linear regression problem as:

$$\begin{aligned} y=\beta ^T x+\epsilon \end{aligned}$$
(2)

where \(\beta =[a\,\,\,\, b]^T\).

4 Preliminaries: recursive formulation of weighted linear regression

In this section, we briefly describe the weighted linear regression model developed by Atiya et al. (2005) that we employ in our proposed optimization strategies. We apply such a recursive regression model because it conforms with the sequential nature of the dynamic pricing problem in case of unknown demand where at each time step a new price is tested, and the model is updated accordingly. Moreover, it becomes more computationally efficient, due to the sequential update nature.

4.1 Estimating model’s parameter vector \(\beta \) and its covariance matrix \(\Sigma _\beta \)

In this subsection, we present the recursive formulations of the weighted linear regression for the regression model parameter’s vector \(\beta \), and its covariance matrix \(\Sigma _{\beta }\) using the work presented in (Atiya et al. 2005).

Let \(x_n\) be the d-dimensional vector example, picked at time n, and let \(y_n\) be the predicted response variable, which defines the demand in our problem. In addition, let \({\hat{\beta }}\) be the \(d\times 1\) estimated coefficient vector \([{\hat{a}}\ \ \ {\hat{b}}]^T\) used for the linear prediction, for the linear demand estimation problem (\(d=2\)) according to Eq. (1). A discounted error function is defined as follows:

$$\begin{aligned} E(T)={\sum _{n=1}^T}{\gamma ^{T-n}}\bigl [{{x_n}^T}{\hat{\beta }}-y_n]^2 \end{aligned}$$
(3)

where \(\gamma \) is the discount factor, such that \(0< \gamma \le 1\), and usually \(\gamma \) is set close to 1. Define the matrix X, where the rows of X are the input vectors \({{x_n}^T}\). Similarly, let y represent the vector of target outputs \(y_n\), and let W denote the discount matrix, which is a \(n\times n\) diagonal matrix with \(W_{nn}={\gamma ^{T-n}}\). Then, the estimated model parameter \({\hat{\beta }}\) is given by the least square solution formula according to (Atiya et al. 2005) as follows:

$$\begin{aligned} {\hat{\beta }}=(X^T W X)^{-1}X^T W y \end{aligned}$$
(4)

However, evaluating Eq. (4) in a continuous manner is computationally extensive, so recursive formulas are used.

Similarly, as indicated in (Atiya et al. 2005), the covariance matrix of \(\beta \) can be calculated as follows:

$$\begin{aligned} \Sigma _{\beta }=\sigma ^2(X^T W X)^{-1} \end{aligned}$$
(5)

When a new data point comes at instant n, the parameter vector is updated recursively. According to (Atiya et al. 2005), the recursive update for the model parameter \(\beta (n)\) in terms of previous estimates is:

$$\begin{aligned} {\hat{\beta }}(n)={\hat{\beta }}(n-1)+{{\Sigma _{\beta }(n-1)x_n\bigl [y_n-{x_n}^T{\hat{\beta }}(n-1)\bigr ]}\over {\sigma ^2\gamma + {x_n}^T \Sigma _{\beta }(n-1)x_n }} \end{aligned}$$
(6)

Similarly, the recursive formula for the covariance matrix \(\Sigma _{\beta }(n)\) can be written as follows:

$$\begin{aligned} \Sigma _{\beta }(n) ={1\over {\gamma }}\Sigma _{\beta }(n-1)-{{\Sigma _{\beta }(n-1)x_n {x_n}^T\Sigma _{\beta }(n-1)}\over {\sigma ^2\gamma ^2+\gamma {x_n}^T\Sigma _{\beta }(n-1)}x_n} \end{aligned}$$
(7)

4.2 Estimating variance of random error term (\(\sigma ^2\))

In the last subsection, we showed the recursive formulas for the regression model’s parameter vector \(\beta \), and covariance matrix \(\Sigma _{\beta }\) using the work of Atiya et al. (2005). However, there is still an unknown parameter not explicitly considered in (Atiya et al. 2005), namely the variance \(\sigma ^2\) of the \(\epsilon \) error term. Accordingly, in this subsection, we estimate the variance parameter \(\sigma ^2\) recursively using the maximum likelihood estimator.

The likelihood function can be expressed as:

$$\begin{aligned} {\mathcal {L}}(\sigma ^2,\beta )=\prod _{n=1}^T \frac{1}{\sqrt{2\pi } \sigma }e^{\frac{\sum _{n=1}^T-\gamma ^{T-n}(y_n-\beta ^Tx_n)^2}{2\sigma ^2}} \end{aligned}$$
(8)

where T denotes the number of data points used in the estimate and \(\gamma \) is the discount factor of the weighted linear regression. Accordingly, the log likelihood can be calculated as follows:

$$\begin{aligned} {l}(\sigma ^2,\beta )= & {} -T\log \sigma -T\log \sqrt{2 \pi }\nonumber \\&-\frac{\sum _{n=1}^T\gamma ^{T-n}(y_n-\beta ^Tx_n)^2}{2\sigma ^2} \end{aligned}$$
(9)

Maximizing the log likelihood in Eq. (9) results in the following estimate \({\hat{\sigma }}^2\):

$$\begin{aligned} {\hat{\sigma }}^2=\frac{\sum _{n=1}^T\gamma ^{T-n}(y_n-\beta ^Tx_n)^2}{T} \end{aligned}$$
(10)

which represents an estimate of the variance of data.

A recursive version of the above formula can be written as

$$\begin{aligned} {\hat{\sigma }}^2(n)=\frac{\gamma (n-1)}{n} \sigma ^2(n-1)+\frac{e^2(n)}{n} \end{aligned}$$
(11)

where \(e(n)=y_n-\beta ^Tx_n\).

5 Formulations of pricing policies

In the proposed dynamic pricing formulations, we seek to optimize both objectives of maximizing the immediate revenue (exploitation), and minimizing the uncertainty of demand model parameters (exploration). This is achieved by combining the two objectives into one hybrid utility function in three different ways. At each time step n, the price value maximizing the expected utility is used as the pricing for the next period. This price choice would simultaneously achieve good revenue and provide some exploration to test different portions of the price space in order to obtain better parameter estimates. Every successive step would provide gains in parameter accuracy, until ultimate exploration would almost no longer be necessary, and exploitation (i.e., focusing on just maximization of the revenue) would dominate.

The general form of the considered constrained optimization problem at any time step n can be expressed as follows:

$$\begin{aligned} max_{p^*} \,\,\, E[U(p^*)_n|\beta _{n-1}] \,\,\,\, s.t.\,\,\, p_l \le p^* \le p_u \end{aligned}$$
(12)

where \(\beta _{n-1}\) is the estimated regression model parameters at time step \(n-1\), \(U_n\) is the utility to be maximized, and \(p_l\) and \(p_h\) are imposed price bounds which are set by business owners to keep the prices in a controlled range. The utility function \(U(p^*)_n\) consists of the revenue \(R(p^*)\) for the selected price (exploitation term), minus a term that measures the uncertainty or error in parameter estimates (exploration term). The coefficient multiplier of the exploration term \(\eta \), presented in the three formulations (Eqs. 13, 21 and 26, decays with iteration, as the initial emphasis on exploration will gradually give way to more exploitation as we proceed with the iterations. After solving the constrained optimization problem defined in Eq. (12), then the price at time step n, \(p_n\) is set to \(p^*\). We propose three different formulations, with each suggesting a different parameter uncertainty term.

Exploration means inspecting the parameter space, and in the process narrowing down onto the true parameter values, thereby reducing the uncertainty. At the beginning uncertainty is high, but the more we explore, the more information about the parameters will be uncovered and uncertainty will decrease.

In the three proposed formulations, exploration is performed by minimizing different forms of model parameters’ variances. The reason for adopting the variances of model parameters to express exploration is that the ultimate objective of exploration is minimizing the model estimation error. Furthermore, the model estimation error can be expressed in terms of the variances of the model parameters due to the bias-variance decomposition of the learning model error (Geman et al. 1992; Taieb and Atiya 2015; Elreedy and Atiya 2019). The model bias results from model misspecification. On the other hand, the model variance is caused by the disparity of the model performance when learning using different sets of training samples. Increasing training data points reduces the model variance (Elreedy and Atiya 2019).

5.1 Formulation 1

The first proposed utility function aggregates the immediate revenue \(R(p^*)\), and the model uncertainty expressed in terms of the total summation of variances of the estimated model parameters \({tr[\Sigma _\beta ]}\), i.e., equal to the trace of covariance matrix \(\Sigma _\beta \). However, for keeping units consistent, the square root of the trace of \([\Sigma _\beta ]\) is taken. Consequently, the utility function of a certain price \(p^*\) is defined as:

$$\begin{aligned} U(p^*)=R(p^*)-\eta \sqrt{tr[\Sigma _\beta ]} \end{aligned}$$
(13)

where \(\eta \) represents the trade-off parameter between exploitation (choosing a price maximizing the gained revenue) and exploration (choosing a price minimizing the model uncertainty). We consider \(\eta \) to be exponentially decreasing in time according to Eq. (14). At early iterations, more emphasis is imposed on exploration in order to have better estimate for the demand model parameters. However, at later iterations since the model estimates improve over time, more attention should be devoted to the ultimate goal of revenue maximization. This setting of \(\eta \) is applied for all of the three formulations, and it is given by:

$$\begin{aligned} \eta =\eta _0 e^{-\alpha n} \end{aligned}$$
(14)

where n is the time step and \(\alpha > 0\). Taking the expectation of the utility function defined in Eq. (13):

$$\begin{aligned} E[U(p^*)_n]=E[R(p^*)_n]-\eta \sqrt{tr[{\Sigma _\beta }(n)]} \end{aligned}$$
(15)

The expected revenue \(E[R(p^*)]\) for linear demand model is calculated as follows:

$$\begin{aligned} E[R(p^*)]=p^*(a+bp^*)=b{p^*}^2+ap^* \end{aligned}$$
(16)

Substituting from Eq. (7) and Eq. (16) into Eq. (15) results in:

$$\begin{aligned}&E[U(p^*)_n]=b{p^*}^2+ap^*-\eta \frac{1}{2 \sqrt{tr[\Sigma _{\beta (n)}]}} tr\nonumber \\&\quad \Big [{1\over {\gamma }}\Sigma _{\beta }(n-1)-{{\Sigma _{\beta }(n-1)x_n {x_n}^T\Sigma _{\beta }(n-1)}\over {\sigma ^2\gamma ^2+\gamma {x_n}^T\Sigma _{\beta }(n-1)}x_n}\Big ] \end{aligned}$$
(17)

where \(x_n=[1\,\,\,p^*]^T\).

Since our target is to find the price \(p^*\) that maximizes the expected utility function defined in Eq. (17), we evaluate the derivative of \(E[U(p^*)_n]\) w.r.t. \(p^*\):

$$\begin{aligned} \frac{\partial E[U(p^*)_n]}{\partial p^*}=a+2bp^* + \eta \frac{tr\big [{\frac{1}{{g^2(p^*)}}\Sigma _{\beta }^2(n-1)Z(p*)}\big ]}{2 \sqrt{tr[\Sigma _{\beta (n)}]}}\nonumber \\ \end{aligned}$$
(18)

where \(g(p^*)={(\sigma ^2\gamma ^2+\gamma [{\sigma _a^2}+2\sigma _{ab}p^*+{\sigma _b}^2{p^*}^2])}\), and \(Z(p*)\) is a \(2\times 2\) matrix with elements: \(Z_{11}\), \(Z_{12}\), and \(Z_{22}\) given as

$$\begin{aligned} Z_{11}= & {} -2\gamma (\sigma _{ab}+{\sigma _b}^2 p^*) \nonumber \\ Z_{12}= & {} \gamma (\sigma ^2\gamma +\sigma _a^2-\sigma _b^2{p^*}^2) \nonumber \\ Z_{22}= & {} \gamma (2\sigma ^2\gamma p^* +2\sigma _a^2p^*+2\sigma _{ab}{p^*}^2) \end{aligned}$$
(19)

Then, by equating Eq. (18) to zero and solving the resulting equation, we can get the price \(p^*\) maximizing the expected utility function at time step n using a simple one-dimensional search.

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}=a+2bp^*\nonumber \\&\quad + \eta \frac{tr\big [{\frac{1}{{g^2(p^*)}}\Sigma _{\beta }^2(n-1)Z(p*)}\big ]}{2 \sqrt{tr[\Sigma _{\beta (n)}]}}=0 \end{aligned}$$
(20)

The details of the derivative computation of the expected utility of this formulation, defined in Eq. (17), can be found in Appendix A.

5.2 Formulation 2

Similar to the first formulation, we define a utility function in terms of the immediate revenue \(R(p^*)\) and model uncertainty. However, the model uncertainty in this formulation is expressed as a summation of normalized standard deviations of model parameters \(\sigma _a\) and \(\sigma _b\) We normalize the standard deviations \(\sigma _a\) and \(\sigma _b\) in order to have the uncertainty relative to the value of the parameters. For example, consider a problem where \(a=1000\), and another one where \(a=10\), and if the standard deviation \(\sigma _a=5\), this value for the uncertainty in parameter a would be more significant for the case of \(a=10\) than for \(a=1000\).

The proposed utility function can then be written as:

$$\begin{aligned} U(p^*)=R(p^*)-\eta \Big (\frac{\sigma _a}{a}+\frac{\sigma _b}{|b|}\Big ) \end{aligned}$$
(21)

Calculating the expectation of the utility function defined in Eq. (21):

$$\begin{aligned}&E[U(p^*)_n]=E[R(p^*)_n] -\eta \Big (\frac{{\sigma _a}(n)}{a}+\frac{{\sigma _b}(n)}{|b|} \Big ) \end{aligned}$$
(22)

Using Eq. (7) and the definition of \(g(p^*)\) in formulation 1, Sect. 5.1, accordingly, the expected utility can be calculated as:

$$\begin{aligned}&E[U(p^*)_n]=E[R(p^*)_n]-\eta \Big (\frac{{\Sigma _\beta (n)}_{11}}{a} +\frac{{\Sigma _\beta }(n)_{22}}{|b|} \Big )\nonumber \\ \end{aligned}$$
(23)

The first derivative of the expected utility \(\frac{\partial E[U(p^*)_n]}{\partial p^*}\) with respect to \(p^*\) can be evaluated as follows; the details are presented in Appendix A.

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*} = a+2bp^*\nonumber \\&\quad + \eta \frac{\gamma }{2ag^2(p^*)\sqrt{{\Sigma _\beta }_{11}(n)}} \nonumber \\&\quad \times \Big ({p^*}^2({\sigma _{ab}}^3-\sigma _{ab}\sigma _a^2\sigma _b^2)+p^*(\sigma ^2\gamma \sigma _{ab}^2\nonumber \\&\quad -\sigma _a^4\sigma _b^2)+\sigma ^2\gamma \sigma _a^2\sigma _{ab}\Big ) \nonumber \\&\quad + \eta \frac{\gamma }{2|b|\sqrt{{\Sigma _\beta }_{22}(n)}g^2(p^*)}\times \Big (p^*(\sigma ^2\gamma \sigma _{b}^4-\sigma _{ab}^2\sigma _b^2\nonumber \\&\quad + \sigma _b^4\sigma _a^2)+(\sigma ^2\gamma \sigma _{ab}\sigma _b^2 +\sigma _b^2\sigma _a^2\sigma _{ab}-\sigma _{ab}^3)\Big ) \end{aligned}$$
(24)

Similar to formulation 1, by equating Eq. (24) to zero, and solving the resulting equation, we can get the price \(p^*\) maximizing the expected utility function at time step n using a simple one-dimensional search.

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*} = a+2bp^*\nonumber \\&\quad + \eta \frac{\gamma }{2ag^2(p^*)\sqrt{{\Sigma _\beta }_{11}(n)}} \nonumber \\&\quad \times \Big ({p^*}^2({\sigma _{ab}}^3-\sigma _{ab}\sigma _a^2\sigma _b^2)+p^*(\sigma ^2\gamma \sigma _{ab}^2\nonumber \\&\quad -\sigma _a^4\sigma _b^2)+\sigma ^2\gamma \sigma _a^2\sigma _{ab}\Big )\nonumber \\&\quad + \eta \frac{\gamma }{2|b|\sqrt{{\Sigma _\beta }_{22}(n)}g^2(p^*)} \Big (p^*(\sigma ^2\gamma \sigma _{b}^4-\sigma _{ab}^2\sigma _b^2\nonumber \\&\quad + \sigma _b^4\sigma _a^2)+(\sigma ^2\gamma \sigma _{ab}\sigma _b^2 +\sigma _b^2\sigma _a^2\sigma _{ab}-\sigma _{ab}^3)\Big )=0 \end{aligned}$$
(25)

The details of deriving the derivative of the expected utility defined in Eq. (22) are presented in the appendix.

5.3 Formulation 3

For the third proposed formulation, we define the utility function in terms of the immediate revenue \(R(p^*)\), but the focus here is on the uncertainty of the immediate revenue \(\sigma _{R(p^*)}\), instead of uncertainty of demand model parameters. The intuition for including uncertainty of revenue in the model is to promote the potential of selecting prices that maximize the expected revenue with high confidence. Thus, the utility function is defined as:

$$\begin{aligned} U(p^*)=R(p^*)-\eta \sigma _{R(p^*)} \end{aligned}$$
(26)

where \(\sigma _{R(p^*)}\) is the standard deviation of revenue. Taking the expectation of the utility function:

$$\begin{aligned} E[U(p^*)_n]=E[R(p^*)_n]-\eta \sigma _{R(p^*)_n} \end{aligned}$$
(27)

Given the linear elasticity demand model defined in Eq. (1), the standard deviation of revenue \(\sigma _{R(p^*)}\) can be calculated as follows:

$$\begin{aligned} \sigma _{R(p^*)}={p^*}\sigma _y={p^*} \sqrt{{x^*}^T\Sigma _{\beta (n-1)} x^*+\sigma ^2} \end{aligned}$$
(28)

Accordingly, the utility function can be expressed as:

$$\begin{aligned} E[U(p^*)_n]=E[R(p^*)_n]-\eta {p^*} \sqrt{{x^*}^T\Sigma _{\beta (n-1)} x^*+\sigma ^2}\nonumber \\ \end{aligned}$$
(29)

The derivative of expected utility with respect to \(p^*\), \(\frac{\partial E[U(p^*)_n]}{\partial p^*}\) is evaluated as follows:

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}= a+2bp^*\nonumber \\&\quad -\eta \frac{{2{\sigma _b}^2{p^*}^2+3\sigma _{ab}p^*+\sigma _a}^2+\sigma ^2}{\sqrt{(\sigma ^2+\sigma _a^2+2\sigma _{ab}p^*+\sigma _b^2{p^*}^2)}} \end{aligned}$$
(30)

As the two formulations above, by equating Eq. (30) to zero, and solving the resulting equation, we can get the price \(p^*\) maximizing the expected utility function at time step n using a simple one-dimensional search.

$$\begin{aligned}&\frac{\partial E[U(p^*)_n]}{\partial p^*}= a+2bp^*\nonumber \\&\quad -\eta \frac{{2{\sigma _b}^2{p^*}^2+3\sigma _{ab}p^*+\sigma _a}^2+\sigma ^2}{\sqrt{(\sigma ^2+\sigma _a^2+2\sigma _{ab}p^*+\sigma _b^2{p^*}^2)}}=0 \end{aligned}$$
(31)

We provide the details of calculating the derivative of the expected utility defined in Eq. (27) in Appendix A.

6 Experiments

To test the performance of the proposed approaches, we have applied them to different pricing problems. In order to explore the standing of the proposed methods compared to other existing approaches, we have also applied some benchmark or baseline price demand estimation methods, and some other algorithms proposed in the literature.

6.1 Benchmarks

One benchmark pricing strategy that we apply is the basic myopic pricing policy, which selects the price maximizing the immediate revenue at each time step. Such price is estimated as \(\frac{-{\hat{a}}}{2{\hat{b}}}\) for the standard linear demand model. Clearly, this pricing strategy greedily focuses on exploitation only. In addition, we compare our proposed methods to two other strategies from the literature, the myopic pricing with dithering proposed by Lobo and Boyd (2003), and the controlled variance pricing (CVP) policy proposed by den Boer and Zwart (2013). We have briefly described these methods in Sect. 2.

Furthermore, we investigate a strategy consisting of two phases: exploration then exploitation. In this strategy the first phase of exploration (for example in the first half of the period) is essentially performed in order to obtain an accurate estimate of model parameters. In the next phase (the remaining portion of the considered period), we use the estimated model, and apply pure exploitation by applying the greedy myopic pricing policy. We consider two variants of this two-phase approach: the random-myopic policy where the exploratory phase is performed by selecting random prices, and then exploitation is performed by means of myopic pricing. Similarly, the second approach is the uncertain-myopic pricing whereby the exploratory phase is performed by minimizing the model uncertainty, expressed as the summation of variances of the two model parameters a and b. Following this, the exploitation phase is performed using myopic pricing.

6.2 Performance metrics

We evaluate the performance of the different pricing policies with respect to two main objectives. The primary objective is revenue maximization, while the secondary objective is the accuracy of the estimated demand. The revenue management objective is basically the revenue gain, or a normalized version of the total discounted revenue Rev(T) achieved in the considered time period, as follows:

$$\begin{aligned}&Rev\,\,Gain=\frac{Rev(T)}{Rev_{opt}} =\frac{\sum _{n=1}^{T}\gamma ^{n-1} R(n)}{{\sum _{n=1}^{T}\gamma ^{n-1} R_{opt}}} \end{aligned}$$
(32)

where R(n) is the revenue in step n and \(R_{opt}\) is the optimal revenue given the true model parameters a and b, which is calculated as:

$$\begin{aligned} R_{opt}=p_{opt}(a+b p_{opt})=b {p^2}_{opt} +a {p_{opt}} \end{aligned}$$
(33)

where \(p_{opt}\) is the optimal price, which equals to \(\frac{-a}{2b}\) for our case of linear demand model where a and b are the ground truth values for the linear demand model parameters.

Simplifying \(\sum _{n=1}^{T}\gamma ^{n-1}\) by using the summation of geometric series formula, this becomes:

$$\begin{aligned}&Rev\,\,Gain=\frac{Rev(T)}{Rev_{opt}} =\frac{\sum _{n=1}^{T}\gamma ^{n-1} R(n)}{ (1-\gamma ^T)/(1-\gamma )R_{opt}} \end{aligned}$$
(34)

In addition to evaluating the gained revenue, we test whether the final price converges to the true optimal price by measuring the deviation of the price \(p_T\), at last iteration T, from the true optimal price \(p_{opt}\).

$$\begin{aligned} \delta _p=\frac{|p_T-p_{opt}|}{p_{opt}} \end{aligned}$$
(35)

Concerning the demand model estimation accuracy, we evaluate it in terms of the deviation of the final estimated demand model parameters \({\hat{\beta }}_T\), at iteration T, from the true parameter’s vector \(\beta \) as shown in Eq.(36):

$$\begin{aligned} \delta _{\beta }=\frac{||\beta -{\hat{\beta }}_T||_2}{||\beta ||_2} \end{aligned}$$
(36)

6.3 Experimental setup

The simulation proceeds as follows: after generating a pool of price-demand data, we start with a very limited number of points, \(N_0=3\) points (less than three points cannot give any sensible initial parameter estimate). Then, we train a regression model to obtain an initial estimate for the model parameters \(\beta _{0}\), and the corresponding covariance matrix \({\Sigma _{\beta }}_0\). After that, we apply the proposed sequential optimization methods (which maximize the utility function) in order to obtain the optimal price at iteration n, denoted as \(p_n\). The optimization is under the constraint that \(p_n\) is within the pricing interval defined by the seller where the minimum allowable price is \(p_{l}\), and the maximum possible price \(p_{u}\), i.e., \( p_{l} \le p_n \le p_{u}\). Once the price is determined, the demand \(D_n\) is observed. It follows the linear demand model (Eq. (1)), with of course the error term \(\epsilon \) giving random fluctuations around the true demand line. We use this point \((p_n,D_n)\) to update the model estimates \(\beta \) and \(\Sigma _{\beta }\) using recursive weighted linear regression update equations (Eqs. 6 and 7). The simulation loop continues till reaching a certain predefined number of iterations T. For each dataset, we run the experiment 100 runs and we present the average results over the runs.

One can observe from the equations of three proposed utility functions (Eqs. 17, 23 and 29) that the true values of demand model a and b are present in parts of the formulas that determine the price. However, since the demand model parameters are unknown, we use current estimates of model parameters \({\hat{a}}_{n-1}\) and \({\hat{b}}_{n-1}\), respectively, at each time step n.

In our experiments, we set the number of iterations T to 100, and the discount factor of the weighted linear regression, \(\gamma \) is set to 0.99. Since the optimization problem is over one variable, the price p, any simple grid search over the pricing values could be used. In our implementation, we use the interior point optimization algorithm (Byrd et al. 1999). Regarding the exploration–exploitation hyper-parameter \(\alpha \) presented in Eq. (14), we set \(\alpha \) such that at the last iteration T, where the exploration is nearly diminished, \(\eta \) equals to a small value: \(\eta =0.25\). For \(\eta _0\), we use values that make the weights (impacts) of the two underlying objectives of revenue and model uncertainty comparable at the first iteration.

In our implementation, for the considered two-phase benchmark strategies we use the same number of iterations for the exploration phase as for the exploitation phase, i.e., 50 for each. Regarding the myopic pricing with dithering method (Lobo and Boyd 2003), we set the amount of dithering to 0.1.

We use a unified method for estimating the demand model parameters for all pricing methods, which is the weighted recursive linear regression described in Sect. 4 in order to have a fair comparison among the different pricing policies.

6.4 On price-demand elasticity

In our experiments, we test several values for the demand slope parameter b in order to explore the performance for three main cases of demand elasticity ranges (to be described shortly). Elasticity is defined as the ratio of the percentage change in demand change to the percentage change in price change (see Eq. (37) and refer to (Gillespie 2014; Gwartney et al. 2014)).

$$\begin{aligned} Elasticity= \frac{\Delta _{D}\%}{\Delta _{p}\%} \end{aligned}$$
(37)

where \(\Delta _{p}\) denotes the price change, and \(\Delta _{D}\) is the corresponding demand change. The elasticity parameter is related to the slope of linear demand model b in Eq. (2). Naturally, demand elasticity is negative because of the inverse relation between price and demand.

The demand-price elasticity varies for different types of products or services. Demand can be inelastic (elasticity \(<1\)), e.g., for necessities or indispensable products, neutrally elastic (elasticity \(\approx 1\)), and elastic (elasticity \(>1\)), e.g., for luxury goods. We test the performance of our proposed methods for each of these three cases by setting appropriate values for the elasticity parameter b.

6.5 Experiments using synthetic datasets

First, we apply our proposed methods as well as the other pricing methods and benchmarks to artificial datasets. The advantage of using artificial data is that the true model parameters \(\beta =[a\,\,\,\,b]^T\) are known. Therefore, the revenue gain can be accurately estimated with the knowledge of the true optimal revenue. Moreover, the estimation error of demand model parameter’s vector \(\beta \) can be accurately evaluated. We create synthetic datasets by generating several price points and then assuming linear demand model, we calculate the corresponding demands using Eq. (1). We adopt different values for the standard deviation \(\sigma \) of the error term \(\epsilon \), so that we can analyze the impact of the error term on the different pricing policies, and evaluate their immunity toward errors. Moreover, we use different values for the variance of the error term because it can be conceived as aggregating all other influencing factors that may be hard to model, such as competition, seasonality, or perishability of the products.

We generate twenty different synthetic datasets using diverse values for parameters a, b, and \(\sigma \). Specifically, we investigate different values for the parameter b including the three demand elasticity cases of inelastic, neutral, and elastic demands. The detailed results for revenue gain, parameter accuracy, and price convergence are represented in Tables 1,  2, and  3, respectively.

Tables 1,  2, and  3 represent the gain in revenue, the estimation error of model parameter’s vector \(\beta \), and the percentage error of the estimated price with respect to the optimal price, respectively. These tables show the results averaged over the twenty synthetic datasets in case of low error setting and high error setting.

Table 1 Revenue gain of different methods, averaged over twenty different synthetic datasets over two different settings of the standard deviation of the error term
Full size table
Table 2 Percentage error in estimating model parameter’s vector \(\beta \) of different methods, averaged over twenty different synthetic datasets over two different settings of the standard deviation of the error term
Full size table
Table 3 Percentage error of the final estimated price \(p_T\) for all methods, averaged over twenty different synthetic datasets over two different settings of the standard deviation of the error term
Full size table

In order to investigate the behavior of different pricing methods over time horizon T, we provide, as an example, the figures for one artificial dataset with \(a=1000\), \(b=-1\), and \(\sigma =200\). Figure 1 shows the cumulative discounted revenue for different methods over time steps of the horizon. Figure 2 shows the model percentage error for regression coefficients \(\beta \) using different pricing methods at different time steps. Figure 3 represents the chosen price at different iterations by different methods.

Fig. 1
figure 1

Cumulative discounted revenue using different formulations for the synthetic dataset \(a=1000\), \(b=-1\), and \(\sigma =200\)

Full size image
Fig. 2
figure 2

Estimated regression model percentage error using different formulations for the synthetic dataset \(a=1000\), \(b=-1\), and \(\sigma =200\)

Full size image
Fig. 3
figure 3

Estimated prices using different formulations for the synthetic dataset \(a=1000\), \(b=-1\), and \(\sigma =200\)

Full size image
Table 4 A description for the real-world datasets
Full size table

6.6 Experiments using real parameter sets

To have more realistic parameter values, we have adopted seven real datasets of nineteen different products described in Table 4. First, we have gathered some data online though surveys. The dataset is a transportation ticket pricing data, where we ask users about the minimum and the maximum fares they would pay for an economy class bus ticket between any generic certain two cities. We collected 41 responses from different users. In order to have data in the form of price and demand pairs, we perform the following. For each price, we calculate the corresponding demand as the number of users who can afford this price according to their stated minimum and maximum prices.

Another dataset is the so-called beef dataset. It is obtained from the USDA Red Meats Yearbook Library (2001). Similarly, the sugar dataset is adopted from Schultz (1933). The spirits dataset is obtained from Durbin and Watson (1950), and the coke dataset is acquired from Sun (2011).

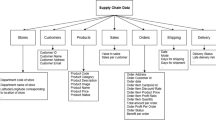
In addition, we have considered a large sales dataset of a café offering four products at a single store Zavarella (2018). The four offered products are a burger and three other meals. Each product has 1351 sales transactions. For the café dataset, we estimate the demand model for each product separately. In the experimental results, the four products are denoted as: Café-1, Café-2, Café-3, and Café-4. Furthermore, we have used the Walmart retail goods dataset offered by the University of Nicosia, named as M5 Forecasting dataset of Nicosia (2020). This dataset is quite large; it has 42,840 sales records for 3049 products of three main categories (Hobbies, Household, and Food) placed in seven departments. The M5 Forecasting dataset includes the sales data of ten stores of Walmart in three states. For space limitations, we present the results of ten different products of the M5 Forecasting dataset. We follow the naming convention described in (Makridakis et al. 2020) for the dataset products shown in Table 4. For example, \(HOUSEHOLD-2-505 \) defines a household product at department 2 with id 505.

In our sequential optimization framework, the selected price \(p_n\) at each time step n could potentially be outside the available prices provided in the dataset. Thus, we use any of the real datasets mainly for estimating linear demand model parameter’s vector \(\beta \) only. Then, we generate data using the estimated parameters, with the same methodology described in Sect. 6.5. The regression model coefficients a and b are estimated using ordinary least squares linear regression. For the error variance parameter \(\sigma ^2\), we estimate it using the maximum likelihood estimator (Eq. (10) with \(\gamma =1\)). The estimated parameter values for the adopted real datasets are presented in Table 4.

The following tables summarize the results of our conducted experiments on the real datasets described in Table 4, for the different pricing policies. Tables 5,  6, 7 represent the gain in revenue, the estimation error of model parameter’s vector \(\beta \), and the percentage error of the estimated price with respect to the optimal price, respectively.

Table 5 Revenue gain of different methods for the nineteen products of the seven real datasets
Full size table
Table 6 Percentage error in estimating model parameter’s vector \(\beta \) of different methods for the nineteen products of the seven real datasets
Full size table
Table 7 Percentage error of the final estimated price \(p_T\) for all methods for the nineteen products of the seven real datasets
Full size table

7 Discussion

From the experiments, we observe the following findings. We categorize our findings with respect to the three performance evaluation aspects: revenue gain, model estimation error, and price convergence.

7.1 Revenue gain

  • From the presented results, we can observe that our proposed models generally outperform the competing methods in terms of the achieved revenue, for most of the synthetic and real datasets as indicated in Tables 1 and  5, respectively. They obtain on average better results compared to the standard benchmarks of random-myopic, uncertain-myopic, and myopic pricing, as well as the two state-of-the art methods in revenue management literature: myopic with dithering (Lobo and Boyd 2003), and controlled variance pricing (den Boer and Zwart 2013). The reason for this outperformance of our proposed methods over other approaches is the way we incorporate both aspects of the target objective which is the gained revenue, and model uncertainty into one hybrid utility function with the aim of maximizing the immediate revenue in addition to having better estimates of model parameters that help maximizing future revenues.

  • Regarding the myopic pricing policy, typically, it yields sub-optimal performance due to its greedy nature. Even for myopic pricing with dithering, the dithering level, which is a major hyper-parameter for balancing exploration and exploitation, is a user input parameter. It turns out that this method’s performance is not significantly better than the myopic pricing policy. One can observe from Figure 1 that the curves of myopic pricing and myopic pricing with dithering are very close. In addition, Tables 1 and  5 show that the two methods obtain very close average revenue gains over the synthetic and real datasets, respectively.

  • It could be inferred from Figure 1 that our proposed methods, especially formulation 1 and formulation 2, convincingly have superior performance in terms of the gained revenue over other methods over the whole time horizon T. In addition, Tables 1 and 5 indicate that formulation 2 is the best performing method on average, over the synthetic and real datasets, respectively.

  • Table 5 demonstrates that our proposed methods, especially the second formulation, outperform other benchmarks for the real datasets. Furthermore, one can observe that the myopic and myopic with dithering strategies perform comparably well and this occurs since the inherent random error in the data is low as shown in Table 4. Similarly, for synthetic datasets with low error settings, our first and second formulations surpass the performance of other methods in terms of the gained revenue over, as indicated in Table 1.

  • For the more challenging synthetic datasets with high error settings, our proposed methods have robust performance and outperform other methods in terms of the gained revenue as shown in Table 1. This is due to the explicit incorporation of model uncertainty in the underlying objective functions we optimize.

7.2 Model estimation error

  • Regarding the model estimation error, Tables 2 and  6 show that the uncertain-myopic benchmark achieves the minimum estimation error. This result is essentially reasonable since the first phase of uncertain-myopic is totally devoted for minimizing model uncertainty, by explicitly minimizing the trace of covariance matrix \(\Sigma _{\beta }\). Accordingly, the uncertain-myopic benchmark obtains accurate model parameters’ estimates. However, the first, relatively long, exploration phase compromises revenue, and accordingly the uncertain-myopic benchmark obtain poor revenues as indicated in Tables 1 and 5 for the synthetic and real datasets, respectively.

  • Similarly, the random-myopic benchmark obtains relatively accurate model estimates as indicated in Tables 2 and  6 since the first phase is pure exploration via random sampling. In addition, the CVP method achieves low estimation error rates for synthetic and real datasets as shown in Tables 2 and  6, respectively. The reason for that is that the CVP method inherently imposes emphasis on exploration by ensuring the diversity of the chosen prices in order to improve the regression model accuracy. Consequently, the CVP method results in near-optimal values for model parameters as well. However, similar to the uncertain-myopic baseline, both of the random-myopic and the CVP method compromise the gained revenue. However, the CVP method achieves more robust performance in terms of the gained revenue, especially in high error settings since it inherently emphasizes exploration through choosing diverse prices, as indicated in Table 1.

  • Tables 2 and 6 demonstrate that our proposed methods achieve comparable performance in terms of model estimation error. Moreover, our proposed methods mainly emphasize the ultimate objective: the utility (revenue) maximization, while treating the convergence to the true model parameters as an important, but a secondary objective. Furthermore, there is a trade-off between parameter estimation accuracy (exploration) and revenue maximization (exploitation). Too much focus on parameter estimation may be at the expense of some foregone revenue, and vice versa. This is valid in the short term ahead. However, in the long run, better parameter accuracy should positively impact revenue. Therefore, it is imperative to attempt to improve the accuracy, if possible without too much sacrifice in revenue.

  • The myopic and myopic with dithering policies obtain poor estimates for model parameters, especially for high noisy datasets as represented in Table 2.

  • Figure 2 shows the model estimation error for one noisy synthetic dataset, as an example. Beside the final estimates represented in Table 2, here we seek to investigate the performance of different methods over time. One can observe from Fig. 2 that over iterations, the model estimation is enhanced, and this is intuitive because more training points are added as iterations go on. It can be noticed that our proposed third formulation achieves comparable performance to the best performing benchmarks uncertain-myopic and random-myopic, and these results agree with the results of the Monte Carlo simulation presented in Table 2.

7.3 Price convergence

  • Figure 3 shows that in the initial period the price changes rapidly, often going up and down. The algorithm is literally exploring the space in order to learn the price demand model. Later in the iterations the price stabilizes. It now enters the exploitation phase, whereby it narrows down on the price that maximizes revenue.

  • Regarding the price convergence to the optimal price \(p_{opt}\), Tables 3 and  7 indicate that the best performing methods are our defined random-myopic baseline for the synthetic datasets and the uncertain-myopic method for the real datasets, respectively. However, our three proposed formulations produce comparable results. The two-phase pricing policies: random-myopic and uncertain-myopic perform well with regard to price convergence because sufficient exploration during the first phase leads to fairly accurate parameter estimates (see Tables 2 and  6 for synthetic and real datasets results, respectively).

  • For the other methods including: myopic and myopic with dithering methods, they have a considerable deviation error from the optimal price, especially for the high error setting according to Table 3. These methods do not converge to optimal prices because they do not obtain accurate model estimates. Accordingly, they do not reveal the true demand model, and cannot converge to the optimal pricing.

  • Figure 3 shows the price convergence to the optimal price which is the obtained price if the true model parameters are known, for one noisy synthetic dataset. For all methods, along iterations, the convergence improves due to the corresponding enhancement in model estimation presented in Fig. 2. It can be inferred that all of our proposed methods produce promising results (near-optimal prices). Figure 3 indicates that the random-myopic benchmark performs the best in terms of price convergence, but at the expenses of sacrificing revenues as indicated in Table 1 and Fig. 1.

8 Conclusions and future work

In this work, we have proposed several dynamic pricing strategies for revenue maximization with demand learning. The proposed methods seek to balance the trade-off between exploitation (revenue maximization) and exploration (demand model estimation). We compare our proposed methods to different benchmarks and popular methods in literature with respect to different aspects including: the total discounted gained revenue, the accuracy of the estimated demand model, and the price convergence to optimal price. We test the pricing methods using different twenty synthetic datasets with different parameter settings and error settings, and seven different real datasets including nineteen different products.. The experiments show a significant performance improvement of our pricing strategies, especially in terms of the gained revenue, while achieving comparable performance in demand learning. Moreover, our pricing policies are easy to analyze and implement since we use simple formulations. Furthermore, our proposed methods are computationally efficient as we apply regression model with incremental updates. For future research directions, we can extend our proposed methods to different demand models such as exponential, and logit demand functions. Furthermore, other factors could be taken into consideration in demand estimation to maximize the obtained revenue such as market environment and customers’, and competitor’s related features. Finally, we may thoroughly investigate the impact of the counterfeit products on demand, and we could develop pricing strategies with the aim of combating the counterfeiting adverse effects.