Skip to main content
SpringerLink
Log in

Nonlinear pyrocoupled deflection of viscoelastic sandwich shell with CNT reinforced magneto-electro-elastic facing subjected to electromagnetic loads in thermal environment

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

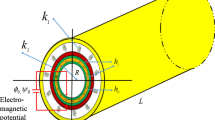
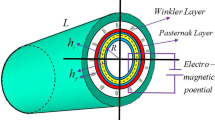
The current work puts forward a finite element (FE)-based numerical formulation to evaluate the nonlinear deflections of multifunctional sandwich composite (MSC) shells. These shells possess a viscoelastic core, and face sheets made of functionally graded carbon nanotube-reinforced magneto-electro-elastic (FG-CNTMEE) materials. The viscoelastic core is considered to be temperature-dependent and is modelled via the complex modulus approach. Two different forms of viscoelastic cores, such as Dyad 606 and EC 2216, are considered in this study. The shell kinematics is realized with the aid of the higher-order shear deformation theory (HSDT). Furthermore, Donnell's nonlinear strain displacement relations are incorporated to account for the nonlinear behaviour. The total potential energy principle is utilized to get the global equations of motion which are solved using direct iterative method. Predominant emphasis is also placed to assess the impact of pyroeffects, coupling fields and electromagnetic (EM) boundary restrictions on the nonlinear deflections of MSC shells working in the thermal environment and subjected to EM loads, which is first of its kind. Also, parametric studies dealing with the shell geometries, CNT distributions and volume fractions, core-to-face sheet thickness ratio, aspect ratio, curvature ratio has been discussed in detail. The results of this work are believed to be unique and serve as a guide for the design engineers towards developing sophisticated smart structures for various engineering applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig.1
Fig.2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Abbreviations

a, b, h :

Length, width, and thickness of the composite sandwich shell

h 1 and h 2 :

z-Coordinate of the bottom and top surface of the bottom FG-CNTMEE face sheet

h 3 and h 4 :

z-Coordinate of the bottom and top surface of the top FG-CNTMEE face sheet

R 1 and R 2 :

Principal radii of curvature at the mid-plane of sandwich shell along x- and y- directions, respectively

\({V}_{CNT}^{*}\) :

Total volume fraction of CNT reinforcement

\({V}_{CNT}\) and\({V}_{m}\) :

The effective volume fractions of CNT and the matrix

[e], \(\left[{e}^{CNT}\right]\),\(\left[{e}^{m}\right]\) :

Piezoelectric coefficients of effective FG-CNTMEE composite, CNT fiber, matrix, respectively

[C],\(\left[{C}^{CNT}\right],\left[{C}^{m}\right]\) :

Elastic stiffness coefficients of effective FG-CNTMEE composite, CNT fiber, matrix, respectively

\(\left[{N}_{t}\right], \left[{N}_{r}\right], \left[{N}_{r*}\right],\) :

Shape function matrices related to translational displacement, rotational displacement, higher-order rotational displacement, respectively

\(\left[{N}_{\phi }\right] and \left[{N}_{\psi }\right]\) :

Shape function matrices related to electric potential and magnetic potential degrees of freedom, respectively

[q],\(\left[{q}^{CNT}\right], \left[{q}^{m}\right]\) :

Magnetostrictive coefficients of effective FG-CNTMEE composite, CNT fiber, matrix, respectively

[η],\(\left[{\eta }^{CNT}\right], \left[{\eta }^{m}\right]\) :

Dielectric coefficients of effective FG-CNTMEE composite, CNT fiber, matrix, respectively

[m], \(\left[{m}^{CNT}\right]\),\(\left[{m}^{m}\right]\) :

Electro-magnetic coefficients of effective FG-CNTMEE composite, CNT fiber, matrix, respectively

[μ],\(\left[{\mu }^{CNT}\right], \left[{\mu }^{m}\right]\) :

Magnetic permeability coefficients of effective FG-CNTMEE composite, CNT fiber, matrix, respectively

\(\left[\alpha \right], \left[{\alpha }^{CNT}\right],\left[{\alpha }^{m}\right]\) :

Thermal expansion coefficients of effective FG-CNTMEE composite, CNT fiber, matrix, respectively

\(\left[p\right],\left[\tau \right]\) :

Pyroelectric and pyromagnetic coefficients

\(\left\{\varepsilon \right\}\) :

Strain tensor

\(\left\{B\right\}\) :

Magnetic flux vector

\(\left\{E\right\}\) :

Electric field vector

\(\left\{\sigma \right\}\) :

Stress tensor

\(\left\{H\right\}\) :

Magnetic field vector

\(\left\{D\right\}\) :

Electric displacement vector

u 0, v 0, and w 0 :

Displacements at the midplane along the x-, y- and z-axes

\({\theta }_{x}, {\theta }_{y}\) :

Normal transverse rotation about x- and y-axes

\(\psi \) :

Magnetic potential

\(\phi \) :

Electric potential

\(\left\{{d}_{t}\right\}\) :

Linear displacement

\(\left\{{d}_{r}\right\}\) :

Rotational displacement

\(\left\{{d}_{r*}\right\}\) :

Higher-order rotational displacement

References

  1. A.R. Setoodeh, M. Shojaee, P. Malekzadeh, Vibrational behavior of doubly curved smart sandwich shells with FG-CNTRC face sheets and FG porous core. Compos. B Eng. 165, 798–822 (2019)

    Article  Google Scholar 

  2. R. Moradi-Dastjerdi, K. Behdinan, Stability analysis of multifunctional smart sandwich plates with graphene nanocomposite and porous layers. Int. J. Mech. Sci. 167, 105283 (2020)

    Article  Google Scholar 

  3. M.H. Hajmohammad, A. Farrokhian, R. Kolahchi, Smart control and vibration of viscoelastic actuator-multiphase nanocomposite conical shells-sensor considering hygrothermal load based on layerwise theory. Aerosp. Sci. Technol. 78, 260–270 (2018)

    Article  Google Scholar 

  4. M. Karimiasl, F. Ebrahimi, V. Mahesh, Nonlinear forced vibration of smart multiscale sandwich composite doubly curved porous shell. Thin-Walled Struct. 143, 106152 (2019)

    Article  Google Scholar 

  5. M. Karimiasl, F. Ebrahimi, Large amplitude vibration of viscoelastically damped multiscale composite doubly curved sandwich shell with flexible core and MR layers. Thin-Walled Struct. 144, 106128 (2019)

    Article  Google Scholar 

  6. K.C. Le, J.H. Yi, An asymptotically exact theory of smart sandwich shells. Int. J. Eng. Sci. 106, 179–198 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  7. M. Khayat, A. Baghlani, M.A. Najafgholipour, The propagation of uncertainty in the geometrically nonlinear responses of smart sandwich porous cylindrical shells reinforced with graphene platelets. Compos Struct. 258, 113209 (2020). https://doi.org/10.1016/j.compstruct.2020.113209

    Article  Google Scholar 

  8. B. Keshtegar, M. Motezaker, R. Kolahchi, N.T. Trung, Wave propagation and vibration responses in porous smart nanocomposite sandwich beam resting on Kerr foundation considering structural damping. Thin-Walled Struct. 154, 106820 (2020)

    Article  Google Scholar 

  9. B. Keshtegar, A. Farrokhian, R. Kolahchi, N.T. Trung, Dynamic stability response of truncated nanocomposite conical shell with magnetostrictive face sheets utilising higher order theory of sandwich panels. Eur. J. Mech. A Solids. 2020:104010.

  10. H. Raissi, Time-depended stress analysis of a sector of the spherical sandwich shell with piezoelectric face sheets and FG-CNT core subjected to blast pressure. Thin-Walled Struct. 157, 106864 (2020)

    Article  Google Scholar 

  11. R. Moradi-Dastjerdi, K. Behdinan, Thermo-electro-mechanical behavior of an advanced smart lightweight sandwich plate. Aerospace Science and Technology. 106, 106142 (2020)

    Article  Google Scholar 

  12. A. Ahmed, S. Kapuria, An efficient facet shell element with layerwise mechanics for coupled electromechanical response of piezolaminated smart shells. Thin-Walled Structures. 150, 106624 (2020)

    Article  Google Scholar 

  13. V. Pradeep, N. Ganesan, Thermal buckling and vibration behavior of multi-layer rectangular viscoelastic sandwich plates. J. Sound Vib. 310(1–2), 169–183 (2008)

    Article  ADS  Google Scholar 

  14. V. Pradeep, N. Ganesan, Buckling and vibration of rectangular composite viscoelastic sandwich plates under thermal loads. Compos. Struct. 77(4), 419–429 (2007)

    Article  Google Scholar 

  15. P. Jeyaraj, C. Padmanabhan, N. Ganesan, Vibro-acoustic behavior of a multilayered viscoelastic sandwich plate under a thermal environment. J. Sandwich Struct. Mater. 13(5), 509–537 (2011)

    Article  Google Scholar 

  16. W. Yan, B. Li, S. Yan, W. Wu, Y. Li, Experiment and simulation analysis on noise reduction of cylindrical shells with viscoelastic material. Results Phys. 14, 102385 (2019)

    Article  Google Scholar 

  17. P. Kavalur, P. Jeyaraj, G.R. Babu, Static behaviour of visco-elastic sandwich plate with nanocomposite facings under mechanical load. Procedia Mater. Sci.. 5, 1376–1384 (2014)

    Article  Google Scholar 

  18. G. Wang, S. Veeramani, N.M. Wereley, Analysis of sandwich plates with isotropic face plates and a viscoelastic core. J. VibAcoust. 122(3), 305–312 (2000)

    Google Scholar 

  19. A.K. Gupta, L. Kumar, Thermal effect on vibration of non-homogenous visco-elastic rectangular plate of linearly varying thickness. Meccanica 43(1), 47–54 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. D.K. Biswal, S.C. Mohanty, Free vibration and damping characteristics study of doubly curved sandwich shell panels with viscoelastic core and isotropic/laminated constraining layer. Eur. J. Mech.-A/Solids. 72, 424–439 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. D.K. Biswal, S.C. Mohanty, Free vibration study of multilayer sandwich spherical shell panels with viscoelastic core and isotropic/laminated face layers. Compos. B Eng. 159, 72–85 (2019)

    Article  Google Scholar 

  22. N.K. Sahu, D.K. Biswal, S.V. Joseph, S.C. Mohanty, Vibration and damping analysis of doubly curved viscoelastic-FGM sandwich shell structures using FOSDT. Structures 26, 24–38 (2020)

    Article  Google Scholar 

  23. X. Song, T. Cao, P. Gao, Q. Han, Vibration and damping analysis of cylindrical shell treated with viscoelastic damping materials under elastic boundary conditions via a unified Rayleigh-Ritz method. Int. J. Mech. Sci.. 165, 105158 (2020)

    Article  Google Scholar 

  24. E. Hernandez, C. Naranjo, J. Vellojin, Modelling of thin viscoelastic shell structures under Reissner-Mindlin kinematic assumption. Appl. Math. Model. 79, 180–199 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  25. S.H. Kordkheili, R. Khorasani, On the geometrically nonlinear analysis of sandwich shells with viscoelastic core: a layerwise dynamic finite element formulation. Composit Struct. 230, 111388 (2019)

    Article  Google Scholar 

  26. M.R. Permoon, M. Shakouri, H. Haddadpour, Free vibration analysis of sandwich conical shells with fractional viscoelastic core. Compos. Struct. 214, 62–72 (2019)

    Article  MATH  Google Scholar 

  27. V. Kallannavar, B. Kumaran, S.C. Kattimani, Effect of temperature and moisture on free vibration characteristics of skew laminated hybrid composite and sandwich plates. Thin walled Structures. 150, 107113 (2020)

    Article  Google Scholar 

  28. M. Malikan, R. Dimitri, F. Tornabene, Transient response of oscillated carbon nanotubes with an internal and external damping. Compos. B Eng. 158, 198–205 (2019)

    Article  Google Scholar 

  29. D.J. Huang, H.J. Ding, W.Q. Chen, Analytical solution for functionally graded magneto-electro-elastic plane beams. Int. J. Eng. Sci. 45(2–8), 467–485 (2007)

    Article  Google Scholar 

  30. A. Milazzo, Refined equivalent single layer formulations and finite elements for smart laminates free vibrations. Compos Part B-Eng. 61, 238–253 (2014)

    Article  Google Scholar 

  31. M. Vinyas, D. Harursampath, N.T. Trung, Influence of active constrained layer damping on the coupled vibration response of functionally graded magneto-electro-elastic plates with skewed edges. Defence Technol. (2019). https://doi.org/10.1016/j.dt.2019.11.016

    Article  Google Scholar 

  32. M. Vinyas, Interphase effect on the controlled frequency response of three-phase smart magneto-electro-elastic plates embedded with active constrained layer damping: FE study. Mater. Res. Exp. 6, 125707 (2020)

    Article  Google Scholar 

  33. M. Vinyas, Vibration control of skew magneto-electro-elastic plates using active constrained layer damping. Compos. Struct. 208, 600–617 (2019)

    Article  Google Scholar 

  34. E. Pan, F. Han, Exact solution for functionally graded and layered magneto-electro-elastic plates. Int. J. Eng. Sci. 43(3–4), 321–339 (2005)

    Article  Google Scholar 

  35. F. Ramirez, P.R. Heyliger, E. Pan, Discrete layer solution to free vibrations of functionally graded magneto-electro-elastic plates. Mech. Adv. Mater. Struct. 13(3), 249–266 (2006)

    Article  Google Scholar 

  36. C.P. Wu, Y.H. Tsai, Dynamic responses of functionally graded magneto-electro-elastic shells with closed-circuit surface conditions using the method of multiple scales. Eur. J. Mech. A-Solid 29(2), 166–181 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  37. C.P. Wu, Y.H. Tsai, Static behavior of functionally graded magneto-electro-elastic shells under electric displacement and magnetic flux. Int. J. Eng. Sci. 45, 744–769 (2007)

    Article  Google Scholar 

  38. M. Vinyas, D. Harursampath, Computational evaluation of electromagnetic circuits’ effect on the coupled response of multifunctional magneto-electro-elastic composites plates exposed to hygrothermal fields. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 1, 0954406220954485 (2020 Sep)

    Google Scholar 

  39. M. Vinyas, S.C. Kattimani, M.A.R. Loja, M. Vishwas, Effect of BaTiO3/CoFe2O4 micro-topological textures on the coupled static behaviour of magneto-electro-thermo-elastic beams in different thermal environment. Mater. Res. Exp.. 5, 125702 (2018)

    Article  Google Scholar 

  40. X.Y. Li, H.J. Ding, W.Q. Chen, Three-dimensional analytical solution for functionally graded magneto-electro-elastic circular plates subjected to uniform load. Compos. Struct. 83, 381–390 (2008)

    Article  Google Scholar 

  41. J. Sladek, V. Sladek, S. Krahulec, C.S. Chen, D.L. Young, Analyses of circular magnetoelectroelastic plates with functionally graded material properties. Mech. Adv. Mater. Struct. 22, 479–489 (2015)

    Article  Google Scholar 

  42. M. Vinyas, S.C. Kattimani, Static studies of stepped functionally graded magneto-electro-elastic beam subjected to different thermal loads. Compos. Struct. 163, 216–237 (2017)

    Article  Google Scholar 

  43. M. Vinyas, S.C. Kattimani, Static analysis of stepped functionally graded magneto-electro-elastic plates in thermal environment: A finite element study. Compos. Struct. 178, 63–85 (2017)

    Article  Google Scholar 

  44. M. Vinyas, Computational analysis of smart magneto-electro-elastic materials and structures: review and classification. Arch. Comput. Methods Eng. (2020). https://doi.org/10.1007/s11831-020-09406-4

    Article  MathSciNet  Google Scholar 

  45. M. Vinyas, K.K. Sunny, D. Harursampath, N.T. Trung, M.A.R. Loja, Influence of interphase on the multiphysics coupled frequency of three phase smart magneto-electro-elastic composite plates. Compos. Struct.. 226, 111254 (2019)

    Article  Google Scholar 

  46. M. Vinyas, G. Nischith, M.A.R. Loja, F. Ebrahimi, N.D. Duc, Numerical analysis of the vibration response of skew magneto-electro-elastic plates based on the higher-order shear deformation theory. Compos. Struct. 214, 132–142 (2019)

    Article  Google Scholar 

  47. J.M.S. Moita, C.M.M. Soares, C.A.M. Soares, Analyses of magneto-electro-elastic plates using a higher order finite element model. Compos. Struct. 91(4), 421–426 (2009)

    Article  Google Scholar 

  48. R.G. Lage, C.M.M. Soares, C.A.M. Soares, J.N. Reddy, Layerwise partial mixed finite element analysis of magneto-electro-elastic plates. Comput. Struct. 82(17), 1293–1301 (2004)

    Article  Google Scholar 

  49. A. Shooshtari, S. Razavi, Vibration analysis of a magnetoelectroelastic rectangular plate based on a higher-order shear deformation theory. Latin Am. J. Solids Struct. 13(3), 554–572 (2016)

    Article  Google Scholar 

  50. M. Vinyas, S.C. Kattimani, Finite element evaluation of free vibration characteristics of magneto-electro-elastic plates in hygrothermal environment using higher order shear deformation theory. Compos. Struct. 202, 1339–1352 (2018)

    Article  Google Scholar 

  51. Vinyas M, Kattimani SC, Harursampath D, Nguyen Thoi-T. Coupled evaluation of the free vibration characteristics of magneto-electro-elastic skew plates in hygrothermal environment. Smart Structures and Systems. 2019; 24(2): 267–292

  52. M. Vinyas, A higher order free vibration analysis of carbon nanotube-reinforced magneto-electro-elastic plates using finite element methods. Compos Part B. Eng. 158, 286–301 (2019)

    Article  Google Scholar 

  53. Vinyas M, Harursampath D, Nguyen-Thoi T. A higher order coupled frequency characteristics study of smart magneto-electro-elastic composite plates with cut-outs using finite element method, Defence Technology, 2020: https://doi.org/10.1016/j.dt.2020.02.009

  54. M. Vinyas, A.S. Sandeep, N.T. Trung, F. Ebrahimi, N.D. Duc, A finite element based assessment of free vibration behaviour of circular and annular magneto-electro-elastic plates using higher order shear deformation theory. J. Intell. Mater. Syst. Struct. 30(6), 2478–2501 (2019)

    Article  Google Scholar 

  55. M. Vinyas, On frequency response of porous functionally graded magneto-electro-elastic circular and annular plates with different electromagnetic conditions using HSDT. Compos Struct 240, 112044 (2020)

    Article  Google Scholar 

  56. M. Vinyas, D. Harursampath, S.C. Kattimani, On vibration analysis of functionally graded carbon nanotube reinforced magneto-electro-elastic plates with different electromagnetic conditions using higher order finite element methods. Defence Technology (2020). https://doi.org/10.1016/j.dt.2020.03.012

    Article  Google Scholar 

  57. M. Mohammadimehr, S.V. Okhravi, S.M. AkhavanAlavi, Free vibration analysis of magneto-electro-elastic cylindrical composite panel reinforced by various distributions of CNTs with considering open and closed circuits boundary conditions based on FSDT. J. Vib. Control 24(8), 1551–1569 (2018)

    Article  MathSciNet  Google Scholar 

  58. M. Vinyas, D. Harursampath, S.C. Kattimani, Thermal response analysis of multi-layered magneto-electro-thermo-elastic plates using Reddy’s third order shear deformation theory. Struct. Eng. Mech. 73(6), 667–684 (2020)

    Google Scholar 

  59. J. Sladek, V. Sladek, S. Krahulec, E. Pan, The MLPG analyses of large deflections of magnetoelectroelastic plates. Eng. Anal. Boundary Elem. 37(4), 673–682 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  60. C.X. Xue, E.N. Pan, S.Y. Zhang, H.J. Chu, Large deflection of a rectangular magnetoelectroelastic thin plate. Mech. Res. Commun. 38(7), 518–523 (2011)

    Article  MATH  Google Scholar 

  61. A. Shooshtari, S. Razavi, Linear and nonlinear free vibration of a multilayered magneto-electro-elastic doubly-curved shell on elastic foundation. Compos. B Eng. 78, 95–108 (2015)

    Article  Google Scholar 

  62. A. Alaimo, I. Benedetti, A. Milazzo, A finite element formulation for large deflection of multilayered magneto-electro-elastic plates. Compos. Struct. 107, 643–653 (2014)

    Article  Google Scholar 

  63. A. Milazzo, Large deflection of magneto-electro-elastic laminated plates. Appl. Math. Model. 38(5–6), 1737–1752 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  64. S.C. Kattimani, M.C. Ray. Active control of large amplitude vibrations of smart magneto–electro–elastic doubly curved shells. Int. J. Mech. Mater. Des. 2014; 351–378.

  65. M. Vinyas, D. Harursampath, Nonlinear vibrations of magneto-electro-elastic doubly curved shells reinforced with carbon nanotubes. Compos Struct. 253, 112749 (2020)

    Article  Google Scholar 

  66. V. Mahesh, D. Harursampath, Nonlinear vibration of functionally graded magneto-electro-elastic higher order plates reinforced by CNTs using FEM. Eng. Comput. (2020). https://doi.org/10.1007/s00366-020-01098-5

    Article  Google Scholar 

  67. V. Mahesh, D. Harursampath, Nonlinear deflection analysis of CNT/magneto-electro-elastic smart shells under multiphysics loading. Mech. Adv. Mater. Struct. 2020: https://doi.org/10.1080/15376494.2020.1805059

  68. M. Vinyas, D. Harursampath, Large deflection analysis of functionally graded magneto-electro-elastic porous flat panels. Eng. Comput. (2020). https://doi.org/10.1007/s00366-020-01270-x

    Article  Google Scholar 

  69. V. Mahesh, Nonlinear deflection of carbon nanotube reinforced multiphase magneto-electro-elastic plates in thermal environment considering pyrocoupling effects. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6858

    Article  Google Scholar 

  70. M. Malikan, V.A. Eremeyev, Effect of surface on the flexomagnetic response of ferroic composite nanostructures; nonlinear bending analysis. Compos. Struct. 271, 114179 (2021)

    Article  Google Scholar 

  71. M. Malikan, V.A. Eremeyev, Flexomagnetic response of buckled piezomagnetic composite nanoplates. Composite Structures 267, 113932 (2021)

    Article  Google Scholar 

  72. M. Malikan, V.A. Eremeyev, Flexomagneticity in buckled shear deformable hard-magnetic soft structures. Continuum Mech. Thermodyn. (2021). https://doi.org/10.1007/s00161-021-01034-y

    Article  Google Scholar 

  73. M. Malikan, N.S. Uglov, V.A. Eremeyev, On instabilities and post-buckling of piezomagnetic and flexomagnetic nanostructures. Int. J. Eng. Sci. 2020(157), 103395 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  74. Garner RS. Method For Determination of Complex Moduli Associated with Viscoelastic Material. Master thesis, University of Tennessee, Knoxville, 2011. https://trace.tennessee.edu/cgi/viewcontent.cgi?article=1933&context=utk_gradthes

  75. J.N. Reddy, An Introduction to Nonlinear Finite Element Analysis (Oxford University Press, Cambridge, 2004)

    Book  MATH  Google Scholar 

  76. K. Mehar, S.K. Panda, Numerical investigation of nonlinear thermomechanical deflection of functionally graded cnt reinforced doubly curved composite shell panel under different mechanical loads. Compos Struct. 161, 287–298 (2017)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Institute of Technology, Silchar, Assam, 788010, India

    Vinyas Mahesh

Authors
  1. Vinyas Mahesh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vinyas Mahesh.

Ethics declarations

Conflict of interest

None.

Appendix

Appendix

The relation between various stiffness matrices contributing towards equivalent linear stiffness matrix \(\left[{K}_{L\_eq}\right]\) appearing in Eq. (20a) is expressed as,

$$ \begin{aligned} \left[ {K_{1}^{e} } \right] & = \left[ {K_{{tb1}}^{e} } \right] + \left[ {K_{{ts1}}^{e} } \right];\quad \left[ {K_{2}^{e} } \right] = \left[ {K_{{rtb24}}^{e} } \right]^{T} + \left[ {K_{{rts13}}^{e} } \right]^{T} \hfill \\ \left[ {K_{3}^{e} } \right] & = \left[ {K_{{rtb4}}^{e} } \right]^{T} + \left[ {K_{{rts3}}^{e} } \right]^{T} ;\quad \left[ {K_{4}^{e} } \right] = \left[ {K_{{tb\phi 1}}^{e} } \right]^{T} + \left[ {K_{{ts\phi 1}}^{e} } \right]^{T} \hfill \\ \left[ {K_{5}^{e} } \right] &= \left[ {K_{{tb\psi 1}}^{e} } \right]^{T} + \left[ {K_{{ts\psi 1}}^{e} } \right]^{T} ;\left[ {K_{6}^{e} } \right] = \left[ {K_{{rtb24}}^{e} } \right] + \left[ {K_{{rts13}}^{e} } \right] \hfill \\ \left[ {K_{7}^{e} } \right] &= \left[ {K_{{rrb3557}}^{e} } \right] + \left[ {K_{{rrs3513}}^{e} } \right];\left[ {K_{8}^{e} } \right] = \left[ {K_{{rrb57}}^{e} } \right] + \left[ {K_{{rrs35}}^{e} } \right] \hfill \\ \left[ {K_{9}^{e} } \right] &= \left[ {K_{{rb\phi 24}}^{e} } \right]^{T} + \left[ {K_{{r\phi s13}}^{e} } \right]^{T} ;\left[ {K_{{10}}^{e} } \right] = \left[ {K_{{rb\psi 24}}^{e} } \right]^{T} + \left[ {K_{{r\psi s13}}^{e} } \right]^{T} \hfill \\ \left[ {K_{{11}}^{e} } \right] &= \left[ {K_{{rtb4}}^{e} } \right] + \left[ {K_{{rts3}}^{e} } \right];\left[ {K_{{12}}^{e} } \right] = \left[ {K_{{rrb57}}^{e} } \right] + \left[ {K_{{rrs35}}^{e} } \right] \hfill \\ \left[ {K_{{13}}^{e} } \right] &= \left[ {K_{{rrb7}}^{e} } \right] + \left[ {K_{{rrs5}}^{e} } \right];\left[ {K_{{14}}^{e} } \right] = \left[ {K_{{rb\phi 4}}^{e} } \right]^{T} + \left[ {K_{{r\phi s3}}^{e} } \right]^{T} \hfill \\ \left[ {K_{{15}}^{e} } \right] &= \left[ {K_{{rb\psi 4}}^{e} } \right]^{T} + \left[ {K_{{r\psi s3}}^{e} } \right]^{T} ;\left[ {K_{{16}}^{e} } \right] = \left[ {K_{{tb\phi 1}}^{e} } \right]^{T} + \left[ {K_{{ts\phi 1}}^{e} } \right]^{T} \hfill \\ \left[ {K_{{17}}^{e} } \right] &= \left[ {K_{{rb\phi 2}}^{e} } \right]^{T} + \left[ {K_{{rb\phi 4}}^{e} } \right]^{T} + \left[ {K_{{r\phi s1}}^{e} } \right]^{T} + \left[ {K_{{r\phi s3}}^{e} } \right]^{T} ;\left[ {K_{{18}}^{e} } \right] = \left[ {K_{{rb\phi 4}}^{e} } \right]^{T} + \left[ {K_{{r\phi s3}}^{e} } \right]^{T} ; \hfill \\ \left[ {K_{{19}}^{e} } \right] &= \left[ {K_{{tb\psi 1}}^{e} } \right]^{T} + \left[ {K_{{ts\psi 1}}^{e} } \right]^{T} \left[ {K_{{20}}^{e} } \right] = \left[ {K_{{rb\psi 2}}^{e} } \right]^{T} + \left[ {K_{{rb\psi 4}}^{e} } \right]^{T} + \left[ {K_{{r\psi s1}}^{e} } \right]^{T} + \left[ {K_{{r\psi s3}}^{e} } \right]^{T} ; \hfill \\ \left[ {K_{{21}}^{e} } \right] &= \left[ {K_{{rb\psi 4}}^{e} } \right]^{T} + \left[ {K_{{r\psi s3}}^{e} } \right]^{T} ;\left[ {K_{{22}}^{e} } \right] = \left[ {K_{{16}}^{e} } \right] - \left[ {K_{{\phi \psi }}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{19}}^{e} } \right]; \hfill \\ \left[ {K_{{23}}^{e} } \right] &= \left[ {K_{{17}}^{e} } \right] - \left[ {K_{{\phi \psi }}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{20}}^{e} } \right];\left[ {K_{{24}}^{e} } \right] = \left[ {K_{{18}}^{e} } \right] - \left[ {K_{{\phi \psi }}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{21}}^{e} } \right]; \hfill \\ \left[ {K_{{25}}^{e} } \right] & = \left[ {K_{{\phi \phi }}^{e} } \right] - \left[ {K_{{\phi \psi }}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{\phi \psi }}^{e} } \right]^{T} ;\left[ {K_{{26}}^{e} } \right] = \left[ {K_{{25}}^{e} } \right]^{{ - 1}} \left[ {K_{{22}}^{e} } \right]^{T} ;\hfill\\ \left[ {K_{{27}}^{e} } \right] & = \left[ {K_{{25}}^{e} } \right]^{{ - 1}} \left[ {K_{{23}}^{e} } \right]^{T} ;\left[ {K_{{28}}^{e} } \right] = \left[ {K_{{25}}^{e} } \right]^{{ - 1}} \left[ {K_{{24}}^{e} } \right]^{T} \hfill \\ \left[ {K_{{29}}^{e} } \right] &= \left[ {K_{{11}}^{e} } \right] - \left[ {K_{{15}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{19}}^{e} } \right];\left[ {K_{{30}}^{e} } \right] = \left[ {K_{{12}}^{e} } \right] - \left[ {K_{{15}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{20}}^{e} } \right]; \\ \left[ {K_{{31}}^{e} } \right] &= \left[ {K_{{13}}^{e} } \right] - \left[ {K_{{15}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{21}}^{e} } \right];\left[ {K_{{32}}^{e} } \right] = \left[ {K_{{14}}^{e} } \right] - \left[ {K_{{15}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{\phi \psi }}^{e} } \right]^{T} \hfill \\ \left[ {K_{{33}}^{e} } \right] & = \left[ {K_{{29}}^{e} } \right] - \left[ {K_{{32}}^{e} } \right]\left[ {K_{{26}}^{e} } \right];\left[ {K_{{34}}^{e} } \right] = \left[ {K_{{30}}^{e} } \right] - \left[ {K_{{32}}^{e} } \right]\left[ {K_{{27}}^{e} } \right]; \hfill \\ \left[ {K_{{35}}^{e} } \right] & = \left[ {K_{{31}}^{e} } \right] - \left[ {K_{{32}}^{e} } \right]\left[ {K_{{28}}^{e} } \right];\left[ {K_{{36}}^{e} } \right] = \left[ {K_{{35}}^{e} } \right]^{{ - 1}} \left[ {K_{{33}}^{e} } \right]^{T} ; \hfill \\ \left[ {K_{{37}}^{e} } \right] &= \left[ {K_{{35}}^{e} } \right]^{{ - 1}} \left[ {K_{{34}}^{e} } \right]^{T} ;\left[ {K_{{38}}^{e} } \right] = \left[ {K_{6}^{e} } \right] - \left[ {K_{{10}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{19}}^{e} } \right]; \hfill \\ \left[ {K_{{39}}^{e} } \right] & = \left[ {K_{7}^{e} } \right] - \left[ {K_{{10}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{20}}^{e} } \right];\left[ {K_{{40}}^{e} } \right] = \left[ {K_{8}^{e} } \right] - \left[ {K_{{10}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{21}}^{e} } \right]; \hfill \\ \left[ {K_{{41}}^{e} } \right] & = \left[ {K_{9}^{e} } \right] - \left[ {K_{{10}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{\phi \psi }}^{e} } \right]^{T} ;\left[ {K_{{42}}^{e} } \right] = \left[ {K_{{38}}^{e} } \right] - \left[ {K_{{41}}^{e} } \right]\left[ {K_{{26}}^{e} } \right] \hfill \\ \left[ {K_{{43}}^{e} } \right] & = \left[ {K_{{39}}^{e} } \right] - \left[ {K_{{41}}^{e} } \right]\left[ {K_{{27}}^{e} } \right];\left[ {K_{{44}}^{e} } \right] = \left[ {K_{{40}}^{e} } \right] - \left[ {K_{{41}}^{e} } \right]\left[ {K_{{28}}^{e} } \right]; \hfill \\ \left[ {K_{{45}}^{e} } \right] & = \left[ {K_{{42}}^{e} } \right] - \left[ {K_{{44}}^{e} } \right]\left[ {K_{{36}}^{e} } \right];\left[ {K_{{46}}^{e} } \right] = \left[ {K_{{43}}^{e} } \right] - \left[ {K_{{44}}^{e} } \right]\left[ {K_{{37}}^{e} } \right]; \hfill \\ \left[ {K_{{47}}^{e} } \right] &= \left[ {K_{{46}}^{e} } \right]^{{ - 1}} \left[ {K_{{45}}^{e} } \right];\left[ {K_{{48}}^{e} } \right] = \left[ {K_{1}^{e} } \right] - \left[ {K_{5}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{19}}^{e} } \right]; \hfill \\ \left[ {K_{{49}}^{e} } \right] & = \left[ {K_{2}^{e} } \right] - \left[ {K_{5}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{20}}^{e} } \right];\left[ {K_{{50}}^{e} } \right] = \left[ {K_{3}^{e} } \right] - \left[ {K_{5}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{21}}^{e} } \right] \hfill \\ \left[ {K_{{51}}^{e} } \right] & = \left[ {K_{4}^{e} } \right] - \left[ {K_{5}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{\phi \psi }}^{e} } \right]^{T} ;\left[ {K_{{52}}^{e} } \right] = \left[ {K_{{48}}^{e} } \right] - \left[ {K_{{51}}^{e} } \right]\left[ {K_{{26}}^{e} } \right] \hfill \\ \left[ {K_{{53}}^{e} } \right] & = \left[ {K_{{49}}^{e} } \right] - \left[ {K_{{51}}^{e} } \right]\left[ {K_{{27}}^{e} } \right];\left[ {K_{{54}}^{e} } \right] = \left[ {K_{{50}}^{e} } \right] - \left[ {K_{{51}}^{e} } \right]\left[ {K_{{28}}^{e} } \right] \hfill \\ \left[ {K_{{55}}^{e} } \right] & = \left[ {K_{{52}}^{e} } \right] - \left[ {K_{{54}}^{e} } \right]\left[ {K_{{36}}^{e} } \right];\left[ {K_{{56}}^{e} } \right] = \left[ {K_{{53}}^{e} } \right] - \left[ {K_{{54}}^{e} } \right]\left[ {K_{{37}}^{e} } \right] \hfill \\ \left[ {K_{{L\_eq}}^{e} } \right] & = \left[ {K_{{55}}^{e} } \right] - \left[ {K_{{56}}^{e} } \right]\left[ {K_{{47}}^{e} } \right] \hfill \\ \end{aligned} $$
(A1)

The equivalent nonlinear stiffness matrix [KNL_eq] can be condensed as follows:

$$ \begin{aligned} \left[ {K_{{NL\_1}}^{e} } \right] & = \left[ {K_{{tbNLbNL1\_tbtbNL1}}^{e} } \right];\left[ {K_{{NL\_2}}^{e} } \right] = \left[ {K_{{rbNL\_rtb24}}^{e} } \right]^{T} \hfill \\ \left[ {K_{{NL\_3}}^{e} } \right]& = \left[ {K_{{rbNL4}}^{e} } \right]^{T} ;\left[ {K_{{NL\_4}}^{e} } \right] = \left[ {K_{{bNL\phi 1}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_5}}^{e} } \right] & = \left[ {K_{{bNL\psi 1}}^{e} } \right];\left[ {K_{{NL\_6}}^{e} } \right] = \left[ {K_{{rbNL24}}^{e} } \right]^{T} \hfill \\ \left[ {K_{{NL\_7}}^{e} } \right] & = \left[ {K_{{rbNL4}}^{e} } \right]^{T} ;\left[ {K_{{NL\_8}}^{e} } \right] = \left[ {K_{{bNL\phi 1}}^{e} } \right]^{T} ;\left[ {K_{{NL\_9}}^{e} } \right] = \left[ {K_{{bNL\psi 1}}^{e} } \right]^{T} \hfill \\ \left[ {K_{{NL\_10}}^{e} } \right]& = \left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{NL\_9}}^{e} } \right];\left[ {K_{{NL\_11}}^{e} } \right] = \left[ {K_{{\phi \psi }}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{NL\_9}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_12}}^{e} } \right] & = \left[ {K_{{25}}^{e} } \right]^{{ - 1}} \left[ {K_{{NL\_11}}^{e} } \right];\left[ {K_{{NL\_13}}^{e} } \right] = \left[ {K_{{15}}^{e} } \right]^{{ - 1}} \left[ {K_{{NL\_10}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_14}}^{e} } \right] & = \left[ {K_{{32}}^{e} } \right]\left[ {K_{{NL\_12}}^{e} } \right];\left[ {K_{{NL\_15}}^{e} } \right] = \left[ {K_{{NL\_14}}^{e} } \right] - \left[ {K_{{NL\_13}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_16}}^{e} } \right] & = \left[ {K_{{35}}^{e} } \right]^{{ - 1}} \left[ {K_{{NL\_15}}^{e} } \right];\left[ {K_{{NL\_17}}^{e} } \right] = \left[ {K_{{10}}^{e} } \right]\left[ {K_{{NL\_10}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_18}}^{e} } \right] & = \left[ {K_{{NL\_6}}^{e} } \right] - \left[ {K_{{NL\_17}}^{e} } \right];\left[ {K_{{NL\_19}}^{e} } \right] = \left[ {K_{{41}}^{e} } \right]\left[ {K_{{NL\_12}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_20}}^{e} } \right] & = \left[ {K_{{NL\_19}}^{e} } \right] + \left[ {K_{{NL\_18}}^{e} } \right];\left[ {K_{{NL\_21}}^{e} } \right] = \left[ {K_{{44}}^{e} } \right]\left[ {K_{{NL\_16}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_22}}^{e} } \right] & = \left[ {K_{{NL\_20}}^{e} } \right] - \left[ {K_{{NL\_21}}^{e} } \right];\left[ {K_{{NL\_23}}^{e} } \right] = \left[ {K_{{46}}^{e} } \right]^{{ - 1}} \left[ {K_{{NL\_22}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_24}}^{e} } \right] & = \left[ {K_{{NL\_1}}^{e} } \right] - \left[ {K_{{NL\_5}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{19}}^{e} } \right] - \left[ {K_{5}^{e} } \right]\left[ {K_{{NL\_10}}^{e} } \right] - \left[ {K_{{NL\_5}}^{e} } \right]\left[ {K_{{NL\_10}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_25}}^{e} } \right] & = \left[ {K_{{NL\_2}}^{e} } \right] - \left[ {K_{{NL\_5}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{20}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_26}}^{e} } \right] & = \left[ {K_{{NL\_3}}^{e} } \right] - \left[ {K_{{NL\_5}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{21}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_27}}^{e} } \right] & = \left[ {K_{{NL\_4}}^{e} } \right] - \left[ {K_{{NL\_5}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \left[ {K_{{\psi \phi }}^{e} } \right] \hfill \\ \left[ {K_{{NL\_28}}^{e} } \right] & = \left[ {K_{{51}}^{e} } \right]\left[ {K_{{NL\_12}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_29}}^{e} } \right] & = \left[ {K_{{NL\_28}}^{e} } \right] + \left[ {K_{{NL\_24}}^{e} } \right] - \left[ {K_{{NL\_27}}^{e} } \right]\left[ {K_{{26}}^{e} } \right] + \left[ {K_{{NL\_27}}^{e} } \right]\left[ {K_{{NL\_12}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_30}}^{e} } \right] & = \left[ {K_{{NL\_25}}^{e} } \right] - \left[ {K_{{NL\_27}}^{e} } \right]\left[ {K_{{27}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_31}}^{e} } \right] & = \left[ {K_{{NL\_26}}^{e} } \right] - \left[ {K_{{NL\_27}}^{e} } \right]\left[ {K_{{28}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_32}}^{e} } \right] & = \left[ {K_{{54}}^{e} } \right]\left[ {K_{{NL\_16}}^{e} } \right]; \hfill \\ \left[ {K_{{NL\_33}}^{e} } \right] & = \left[ {K_{{NL\_29}}^{e} } \right] - \left[ {K_{{NL\_32}}^{e} } \right] - \left[ {K_{{NL\_31}}^{e} } \right]\left[ {K_{{36}}^{e} } \right] - \left[ {K_{{NL\_31}}^{e} } \right]\left[ {K_{{NL\_16}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_34}}^{e} } \right] & = \left[ {K_{{NL\_30}}^{e} } \right] - \left[ {K_{{NL\_31}}^{e} } \right]\left[ {K_{{37}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_35}}^{e} } \right] & = \left[ {K_{{56}}^{e} } \right]\left[ {K_{{NL\_23}}^{e} } \right],\left[ {K_{{NL\_36}}^{e} } \right] = \left[ {K_{{NL\_34}}^{e} } \right]\left[ {K_{{47}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_37}}^{e} } \right] & = \left[ {K_{{NL\_34}}^{e} } \right]\left[ {K_{{NL\_23}}^{e} } \right] \hfill \\ \left[ {K_{{NL\_eq}}^{e} } \right] & = \left[ {K_{{NL\_33}}^{e} } \right] - \left[ {K_{{NL\_35}}^{e} } \right] - \left[ {K_{{NL\_36}}^{e} } \right] - \left[ {K_{{NL\_37}}^{e} } \right] \hfill \\ \end{aligned} $$
(A2)

The equivalent force \(\{{F}_{eq}\}\) can be represented as follows:

$$ \left\{ {{F_{eq}}} \right\} = \left\{ {F_t} \right\} - \left[ {K_{F\phi }^e} \right]\left( {\left\{ {F_\phi } \right\} + \left\{ {{F_{t\phi }}} \right\}} \right) - \left[ {K_{F\psi }^e} \right]\left( {\left\{ {F_\psi } \right\} + \left\{ {{F_{t\psi }}} \right\}} \right)$$

where

$$ \begin{aligned} \left[ {K_{{F\phi }}^{e} } \right] & = \left[ {K_{{F31}}^{e} } \right] - \left[ {K_{{F35}}^{e} } \right] - \left[ {K_{{F33}}^{e} } \right]; \hfill \\ \left[ {K_{{F\psi }}^{e} } \right] & = \left[ {K_{{F32}}^{e} } \right] - \left[ {K_{{F36}}^{e} } \right] - \left[ {K_{{F34}}^{e} } \right] \hfill \\ \left[ {K_{{F1}}^{e} } \right] & = \left[ {K_{{25}}^{e} } \right]^{{ - 1}} \left[ {K_{{\phi \phi }}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} ;\left[ {K_{{F2}}^{e} } \right] = \left[ {K_{{15}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \hfill \\ \left[ {K_{{F3}}^{e} } \right] & = \left[ {K_{{32}}^{e} } \right]\left[ {K_{{25}}^{e} } \right]^{{ - 1}} ;\left[ {K_{{F4}}^{e} } \right] = \left[ {K_{{32}}^{e} } \right]\left[ {K_{{F1}}^{e} } \right] \hfill \\ \left[ {K_{{F5}}^{e} } \right] & = \left[ {K_{{F2}}^{e} } \right] - \left[ {K_{{F4}}^{e} } \right];\left[ {K_{{F6}}^{e} } \right] = \left[ {K_{{35}}^{e} } \right]^{{ - 1}} \left[ {K_{{F5}}^{e} } \right] \hfill \\ \left[ {K_{{F7}}^{e} } \right] & = \left[ {K_{{35}}^{e} } \right]^{{ - 1}} \left[ {K_{{F3}}^{e} } \right];\left[ {K_{{F8}}^{e} } \right] = \left[ {K_{{10}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \hfill \\ \left[ {K_{{F9}}^{e} } \right] & = \left[ {K_{{41}}^{e} } \right]\left[ {K_{{F1}}^{e} } \right];\left[ {K_{{F10}}^{e} } \right] = \left[ {K_{{41}}^{e} } \right]\left[ {K_{{25}}^{e} } \right]^{{ - 1}} ; \hfill \\ \left[ {K_{{F11}}^{e} } \right] & = \left[ {K_{{F8}}^{e} } \right] - \left[ {K_{{F9}}^{e} } \right];\left[ {K_{{F12}}^{e} } \right] = \left[ {K_{{44}}^{e} } \right]\left[ {K_{{F6}}^{e} } \right] \hfill \\ \left[ {K_{{F13}}^{e} } \right] & = \left[ {K_{{44}}^{e} } \right]\left[ {K_{{F7}}^{e} } \right];\left[ {K_{{F14}}^{e} } \right] = \left[ {K_{{F10}}^{e} } \right] - \left[ {K_{{F14}}^{e} } \right] \hfill \\ \left[ {K_{{F15}}^{e} } \right]& = \left[ {K_{{F11}}^{e} } \right] - \left[ {K_{{F12}}^{e} } \right];\left[ {K_{{F16}}^{e} } \right] = \left[ {K_{{46}}^{e} } \right]^{{ - 1}} \left[ {K_{{F14}}^{e} } \right]; \hfill \\ \left[ {K_{{F17}}^{e} } \right] & = \left[ {K_{{46}}^{e} } \right]^{{ - 1}} \left[ {K_{{F15}}^{e} } \right];\left[ {K_{{F18}}^{e} } \right] = \left[ {K_{5}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} \hfill \\ \left[ {K_{{F19}}^{e} } \right] & = \left[ {K_{{NL\_5}}^{e} } \right]\left[ {K_{{\psi \psi }}^{e} } \right]^{{ - 1}} ;\left[ {K_{{F20}}^{e} } \right] = \left[ {K_{{F18}}^{e} } \right] + \left[ {K_{{F19}}^{e} } \right] \hfill \\ \left[ {K_{{F21}}^{e} } \right] & = \left[ {K_{{51}}^{e} } \right]\left[ {K_{{F1}}^{e} } \right];\left[ {K_{{F22}}^{e} } \right] = \left[ {K_{{51}}^{e} } \right]\left[ {K_{{25}}^{e} } \right]^{{ - 1}} \hfill \\ \left[ {K_{{F23}}^{e} } \right] & = \left[ {K_{{NL\_27}}^{e} } \right]\left[ {K_{{F1}}^{e} } \right];\left[ {K_{{F24}}^{e} } \right] = \left[ {K_{{NL\_27}}^{e} } \right]\left[ {K_{{25}}^{e} } \right]^{{ - 1}} \hfill \\ \left[ {K_{{F25}}^{e} } \right] & = \left[ {K_{{F22}}^{e} } \right] + \left[ {K_{{F24}}^{e} } \right];\left[ {K_{{F26}}^{e} } \right] = \left[ {K_{{F20}}^{e} } \right] - \left[ {K_{{F21}}^{e} } \right] - \left[ {K_{{F23}}^{e} } \right] \hfill \\ \left[ {K_{{F27}}^{e} } \right] & = \left[ {K_{{54}}^{e} } \right]\left[ {K_{{F6}}^{e} } \right];\left[ {K_{{F28}}^{e} } \right] = \left[ {K_{{54}}^{e} } \right]\left[ {K_{{F7}}^{e} } \right] \hfill \\ \left[ {K_{{F29}}^{e} } \right] & = \left[ {K_{{NL\_31}}^{e} } \right]\left[ {K_{{F6}}^{e} } \right];\left[ {K_{{F30}}^{e} } \right] = \left[ {K_{{NL\_31}}^{e} } \right]\left[ {K_{{F7}}^{e} } \right] \hfill \\ \left[ {K_{{F31}}^{e} } \right] & = \left[ {K_{{F25}}^{e} } \right] - \left[ {K_{{F30}}^{e} } \right] - \left[ {K_{{F28}}^{e} } \right]; \hfill \\ \left[ {K_{{F32}}^{e} } \right] & = \left[ {K_{{F26}}^{e} } \right] - \left[ {K_{{F29}}^{e} } \right] - \left[ {K_{{F27}}^{e} } \right];\left[ {K_{{F33}}^{e} } \right] = \left[ {K_{{56}}^{e} } \right]\left[ {K_{{F16}}^{e} } \right];\left[ {K_{{F34}}^{e} } \right] = \left[ {K_{{56}}^{e} } \right]\left[ {K_{{F17}}^{e} } \right]; \hfill \\ \left[ {K_{{F35}}^{e} } \right] & = \left[ {K_{{NL\_34}}^{e} } \right]\left[ {K_{{F16}}^{e} } \right];\left[ {K_{{F36}}^{e} } \right] = \left[ {K_{{NL\_34}}^{e} } \right]\left[ {K_{{F17}}^{e} } \right] \hfill \\ \end{aligned} $$
(A3)

The different stiffness matrices appearing in the condensation process are as follows:

$$ \begin{gathered} \left[ {K_{{rrs35}}^{e} } \right] = \left[ {K_{{rrs3}}^{e} } \right] + \left[ {K_{{rrs5}}^{e} } \right],\left[ {K_{{rrs13}}^{e} } \right] = \left[ {K_{{rrs1}}^{e} } \right] + \left[ {K_{{rrs3}}^{e} } \right], \hfill \\ \left[ {K_{{rrs3513}}^{e} } \right] = \left[ {K_{{rrs35}}^{e} } \right] + \left[ {K_{{rrs13}}^{e} } \right],\left[ {K_{{rts13}}^{e} } \right] = \left[ {K_{{rts1}}^{e} } \right] + \left[ {K_{{rts3}}^{e} } \right], \hfill \\ \left[ {K_{{_{{r\psi s13}} }}^{e} } \right] = \left[ {K_{{_{{r\psi s1}} }}^{e} } \right] + \left[ {K_{{_{{r\psi s3}} }}^{e} } \right],\left[ {K_{{_{{r\phi s13}} }}^{e} } \right] = \left[ {K_{{_{{r\phi s1}} }}^{e} } \right] + \left[ {K_{{_{{r\phi s3}} }}^{e} } \right] \hfill \\ \left[ {K_{{tbtbNL1}}^{e} } \right] = \left[ {K_{{tb1}}^{e} } \right] + \left[ {K_{{tbNL1}}^{e} } \right],\left[ {K_{{rtb24}}^{e} } \right] = \left[ {K_{{rtb2}}^{e} } \right] + \left[ {K_{{rtb4}}^{e} } \right] \hfill \\ \left[ {K_{{tbNLbNL1\_tbtbNL1}}^{e} } \right] = \left[ {K_{{tbNLbNL1}}^{e} } \right] + \left[ {K_{{tbtbNL1}}^{e} } \right], \hfill \\ \left[ {K_{{rbNL\_rtb24}}^{e} } \right] = \left[ {K_{{rbNL24}}^{e} } \right] + \left[ {K_{{rtb24}}^{e} } \right],\left[ {K_{{rbNL\_rtb4}}^{e} } \right] = \left[ {K_{{rbNL4}}^{e} } \right] + \left[ {K_{{rtb4}}^{e} } \right], \hfill \\ \left[ {K_{{bNL\_tb\phi 1}}^{e} } \right] = \left[ {K_{{bNL\phi 1}}^{e} } \right] + \left[ {K_{{tb\phi 1}}^{e} } \right],\left[ {K_{{bNL\_tb\psi 1}}^{e} } \right] = \left[ {K_{{bNL\psi 1}}^{e} } \right] + \left[ {K_{{tb\psi 1}}^{e} } \right] \hfill \\ \left[ {K_{{rrb57}}^{e} } \right] = \left[ {K_{{rrb5}}^{e} } \right] + \left[ {K_{{rrb7}}^{e} } \right],\left[ {K_{{rtbrbNL4}}^{e} } \right] = \left[ {K_{{rtb4}}^{e} } \right] + \left[ {K_{{rbNL4}}^{e} } \right] \hfill \\ \left[ {K_{{rtbrbNL2}}^{e} } \right] = \left[ {K_{{rtb2}}^{e} } \right] + \left[ {K_{{rbNL2}}^{e} } \right],\left[ {K_{{rtbrbNL24}}^{e} } \right] = \left[ {K_{{rtbrbNL2}}^{e} } \right] + \left[ {K_{{rtbrbNL4}}^{e} } \right] \hfill \\ \left[ {K_{{rrb35}}^{e} } \right] = \left[ {K_{{rrb3}}^{e} } \right] + \left[ {K_{{rrb5}}^{e} } \right],\left[ {K_{{rrb5735}}^{e} } \right] = \left[ {K_{{rrb57}}^{e} } \right] + \left[ {K_{{rrb35}}^{e} } \right] \hfill \\ \left[ {K_{{rb\phi 24}}^{e} } \right] = \left[ {K_{{rb\phi 2}}^{e} } \right] + \left[ {K_{{rb\phi 4}}^{e} } \right],\left[ {K_{{rb\psi 24}}^{e} } \right] = \left[ {K_{{rb\psi 2}}^{e} } \right] + \left[ {K_{{rb\psi 4}}^{e} } \right] \hfill \\ \left[ {K_{{tbNLbNL1}}^{e} } \right] = \left[ {K_{{tbNL1}}^{e} } \right] + \left[ {K_{{bNL1}}^{e} } \right],\left[ {K_{{rbNL24}}^{e} } \right] = \left[ {K_{{rbNL2}}^{e} } \right] + \left[ {K_{{rbNL4}}^{e} } \right] \hfill \\ \end{gathered} $$
(A4)

The expressions for stiffness matrices and force vectors are as follows:

$$ \begin{aligned} \left[ {K_{{rtb4}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b4}} } \right]} } \left[ {B_{{tb}} } \right]{\text{ }}dxdy;\left[ {K_{{rbNL4}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{bNL4}} } \right]} } \left[ {B_{1} } \right]{\text{ }}\left[ {B_{2} } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{rrb5}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b5}} } \right]} } \left[ {B_{{rb}} } \right]{\text{ }}dxdy;\left[ {K_{{rrb7}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b7}} } \right]} } \left[ {B_{{rb}} } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{rb\phi 4}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b\phi 4}} } \right]} } \left[ {B_{\phi } } \right]{\text{ }}dxdy;\left[ {K_{{rb\psi 4}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b\psi 4}} } \right]} } \left[ {B_{\psi } } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{rtb4}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b4}} } \right]} } \left[ {B_{{tb}} } \right]{\text{ }}dxdy;\left[ {K_{{rtb2}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b2}} } \right]} } \left[ {B_{{tb}} } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{rbNL2}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{bNL2}} } \right]} } \left[ {B_{1} } \right]{\text{ }}\left[ {B_{2} } \right]{\text{ }}dxdy;\left[ {K_{{rrb3}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b3}} } \right]} } \left[ {B_{{rb}} } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{rrb5}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b5}} } \right]} } \left[ {B_{{rb}} } \right]{\text{ }}dxdy;\left[ {K_{{rb\phi 2}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b\phi 2}} } \right]} } \left[ {B_{\phi } } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{rb\psi 2}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{{b\psi 2}} } \right]} } \left[ {B_{\psi } } \right]{\text{ }}dxdy;\left[ {K_{{tbNL1}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{tb}} } \right]^{T} \left[ {D_{{bNL1}} } \right]} } \left[ {B_{1} } \right]{\text{ }}\left[ {B_{2} } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{bNL1}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{2} } \right]{\text{ }}^{T} \left[ {B_{1} } \right]{\text{ }}^{T} \left[ {D_{{bbNL1}} } \right]} } \left[ {B_{1} } \right]{\text{ }}\left[ {B_{2} } \right]{\text{ }}dxdy; \hfill \\ \left[ {K_{{bNL\phi 1}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{\phi } } \right]^{T} \left[ {D_{{bNL\phi 1}} } \right]} } \left[ {B_{1} } \right]{\text{ }}\left[ {B_{2} } \right]{\text{ }}dxdy;\hfill\\ \left[ {K_{{bNL\psi 1}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{\psi } } \right]^{T} \left[ {D_{{bNL\psi 1}} } \right]} } \left[ {B_{1} } \right]{\text{ }}\left[ {B_{2} } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{tb1}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{tb}} } \right]^{T} \left[ {D_{{b1}} } \right]} } \left[ {B_{{tb}} } \right]{\text{ }}dxdy;\left[ {K_{{tb\phi 1}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{tb}} } \right]^{T} \left[ {D_{{b\phi 1}} } \right]} } \left[ {B_{\phi } } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{tb\psi 1}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{tb}} } \right]^{T} \left[ {D_{{b\psi 1}} } \right]} } \left[ {B_{\psi } } \right]{\text{ }}dxdy;\left[ {K_{{_{{rts3}} }}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{s3}} } \right]\left[ {B_{{ts}} } \right]} } {\text{ }}dxdy \hfill \\ \left[ {K_{{rrs3}} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{s3}} } \right]\left[ {B_{{rs}} } \right]} } {\text{ }}dxdy;\left[ {K_{{_{{r\phi s3}} }}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{s\phi 3}} } \right]\left[ {B_{\phi } } \right]} } {\text{ }}dxdy \hfill \\ \left[ {K_{{ts\phi 1}}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{ts}} } \right]^{T} \left[ {D_{{s\phi 1}} } \right]} } \left[ {B_{\phi } } \right]{\text{ }}dxdy;\left[ {K_{{ts\psi 1}}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{ts}} } \right]^{T} \left[ {D_{{s\psi 1}} } \right]} } \left[ {B_{\psi } } \right]{\text{ }}dxdy \hfill \\ \left[ {K_{{_{{r\phi s1}} }}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{s\phi 1}} } \right]\left[ {B_{\phi } } \right]} } {\text{ }}dxdy;\left[ {K_{{r\psi s1}} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{s\psi 1}} } \right]\left[ {B_{\psi } } \right]} } {\text{ }}dxdy \hfill \\ \left[ {K_{{_{{rts1}} }}^{e} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{s1}} } \right]\left[ {B_{{ts}} } \right]} } {\text{ }}dxdy;\left[ {K_{{_{{rrs1}} }}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{s1}} } \right]\left[ {B_{{rs}} } \right]} } {\text{ }}dxdy \hfill \\ \left[ {K_{{ts1}} } \right] & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{ts}} } \right]^{T} \left[ {D_{{s1}} } \right]\left[ {B_{{ts}} } \right]} } {\text{ }}dxdy;\left[ {K_{{_{{rts3}} }}^{e} } \right] = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{s3}} } \right]\left[ {B_{{ts}} } \right]} } {\text{ }}dxdy \hfill \\ \left\{ {F_{\psi } } \right\} & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {N_{\psi } } \right]^{T} Q^{\psi } } } {\text{ }}dxdy;\left\{ {F_{\phi } } \right\} = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ {N_{\phi } } \right]^{T} Q^{\phi } } } {\text{ }}dxdy; \hfill \\ \left\{ {F_{t} } \right\}& = \int\limits_{{\Omega ^{N} }} {\left[ {C_{b} } \right]^{N} \left[ \alpha \right]^{N} \Delta T} d\Omega ^{N} ;\left\{ {F_{{t\phi }} } \right\} = \int\limits_{{\Omega ^{N} }} {\left[ p \right]\Delta T} d\Omega ^{N} ;\left\{ {F_{{t\psi }} } \right\} = \int\limits_{{\Omega ^{N} }} {\left[ \tau \right]\Delta T} d\Omega ^{N} ; \hfill \\ \end{aligned} $$
(A5)

The various rigidity matrices contributing to Eq. (A5) can be denoted as follows:

$$ \begin{aligned} \left[ {D_{{b1}} } \right] & = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left[ {C_{b} } \right]^{N} } {\text{ }}dz;}\,\,\, \left[ {D_{{bbNL1}} } \right] = \frac{1}{4}\left[ {D_{{b1}} } \right];\left[ {D_{{bNL1}} } \right] = \frac{1}{2}\left[ {D_{{b1}} } \right]; \hfill \\ \left[ {D_{{b2}} } \right] & = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {z\left[ {C_{b} } \right]^{{\text{N}}} {\text{ }}} dz} ;\left[ {D_{{bNL2}} } \right] = \frac{1}{2}\left[ {D_{{b2}} } \right];\left[ {D_{{b3}} } \right] = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {z^{2} \left[ {C_{b} } \right]^{N} } dz;} \hfill \\ \left[ {D_{{b4}} } \right] & = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {c_{1} z^{3} \left[ {C_{b} } \right]^{N} } dz;}\,\,\, \left[ {D_{{bNL4}} } \right] = \frac{1}{2}\left[ {D_{{b4}} } \right];\left[ {D_{{b5}} } \right] = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {c_{1} z^{4} \left[ {C_{b} } \right]^{N} } dz;} \hfill \\ \left[ {D_{{b7}} } \right] & = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {c_{1} ^{2} z^{6} \left[ {C_{b} } \right]^{N} } dz;} \left[ {D_{{b\phi 1}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{t} } \right]\left[ {e_{b} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{b} } \right]\left[ {e_{b} } \right]} dz; \hfill \\ \left[ {D_{{bNL\phi 1}} } \right] & = \left[ {D_{{b\phi 1}} } \right];\left[ {D_{{b\phi 2}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {z\left[ {Z_{t} } \right]\left[ {e_{b} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {z\left[ {Z_{b} } \right]\left[ {e_{b} } \right]} dz; \hfill \\ \left[ {D_{{b\phi 4}} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {c_{1} z^{3} \left[ {Z_{t} } \right]\left[ {e_{b} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {c_{1} z^{3} \left[ {Z_{b} } \right]\left[ {e_{b} } \right]} dz;\left[ {D_{{s1}} } \right] = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left[ {C_{s} } \right]^{N} } dz;} \hfill \\ \left[ {D_{{b\psi 1}} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{t} } \right]\left[ {q_{b} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{b} } \right]\left[ {q_{b} } \right]} dz;\left[ {D_{{bNL\psi 1}} } \right] = \left[ {D_{{b\psi 1}} } \right] \hfill \\ \left[ {D_{{b\psi 2}} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {z\left[ {Z_{t} } \right]\left[ {q_{b} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {z\left[ {Z_{b} } \right]\left[ {q_{b} } \right]} dz; \hfill \\ \left[ {D_{{b\psi 4}} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {c_{1} z^{3} \left[ {Z_{t} } \right]\left[ {q_{b} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {c_{1} z^{3} \left[ {Z_{b} } \right]\left[ {q_{b} } \right]} dz;\left[ {D_{{s3}} } \right] = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {c_{2} z^{2} \left[ {C_{s} } \right]^{N} } {\text{ }}dz{\text{ }}} \hfill \\ \left[ {D_{{s5}} } \right] & = \sum\limits_{{N = 1}}^{3} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {c_{2} ^{2} z^{4} \left[ {C_{s} } \right]^{N} } dz;} \left[ {D_{{s\phi 1}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{t} } \right]\left[ {e_{s} } \right]^{T} } dz + \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{b} } \right]\left[ {e_{s} } \right]^{T} } dz; \hfill \\ \left[ {D_{{s\phi 3}} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {c_{2} z^{2} \left[ {Z_{t} } \right]\left[ {e_{s} } \right]^{T} } dz + \int\limits_{{h_{1} }}^{{h_{2} }} {c_{2} z^{2} \left[ {Z_{b} } \right]\left[ {e_{s} } \right]^{T} } dz; \hfill \\ \left[ {D_{{s\psi 1}} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{t} } \right]\left[ {q_{s} } \right]^{T} } dz + \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{b} } \right]\left[ {q_{s} } \right]^{T} } dz; \hfill \\ \left[ {D_{{s\psi 3}} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {c_{2} z^{2} \left[ {Z_{t} } \right]\left[ {q_{s} } \right]^{T} } dz + \int\limits_{{h_{1} }}^{{h_{2} }} {c_{2} z^{2} \left[ {Z_{b} } \right]\left[ {q_{s} } \right]^{T} } dz; \hfill \\ \left[ {D_{{\phi \phi }} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{t} } \right]^{T} \left[ \eta \right]\left[ {Z_{t} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{b} } \right]^{T} \left[ \eta \right]} \left[ {Z_{b} } \right]dz; \hfill \\ \left[ {D_{{\psi \psi }} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{t} } \right]^{T} \left[ \mu \right]\left[ {Z_{t} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{b} } \right]^{T} \left[ \mu \right]} \left[ {Z_{b} } \right]dz; \hfill \\ \left[ {D_{{\phi \psi }} } \right] & = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{t} } \right]^{T} \left[ m \right]\left[ {Z_{t} } \right]} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{b} } \right]^{T} \left[ m \right]} \left[ {Z_{b} } \right]dz; \hfill \\ \end{aligned} $$
(A6)

The derivative of shape function matrices appearing in the FE formulation can be represented by

$$ \begin{aligned} \left[ {B_{{tb}} } \right] & = \left[ {\begin{array}{*{20}l} {N_{{i,x}} } \hfill & 0 \hfill & {\frac{1}{{R_{1} }}} \hfill \\ 0 \hfill & {N_{{i,y}} } \hfill & {\frac{1}{{R_{2} }}} \hfill \\ {N_{{i,y}} } \hfill & {N_{{i,x}} } \hfill & 0 \hfill \\ \end{array} } \right],\left[ {B_{{rb}} } \right] = \left[ {\begin{array}{*{20}l} {N_{{i,x}} } \hfill & 0 \hfill \\ 0 \hfill & {N_{{i,y}} } \hfill \\ {N_{{i,y}} } \hfill & {N_{{i,x}} } \hfill \\ \end{array} } \right],\left[ {B_{{ts}} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {N_{{i,x}} } \hfill \\ 0 \hfill & 0 \hfill & {N_{{i,y}} } \hfill \\ \end{array} } \right],\left[ {B_{{rs}} } \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill \\ \end{array} } \right] \hfill \\ \left[ {B_{1} } \right] &= \left[ {\begin{array}{*{20}l} {W_{{0,x}} } \hfill & 0 \hfill & {W_{{0,y}} } \hfill \\ 0 \hfill & {W_{{0,y}} } \hfill & {W_{{0,x}} } \hfill \\ \end{array} } \right],\left[ {B_{2} } \right] = \left[ {\begin{array}{*{20}l} {B_{{21}} } \hfill & {B_{{22}} } \hfill & \ldots \hfill & {B_{{28}} } \hfill \\ \end{array} } \right]; \hfill \\ \left[ {B_{\phi } } \right] & = \left[ {B_{\psi } } \right] = \left[ {\begin{array}{*{20}l} {N_{{i,x}} } \hfill \\ {N_{{i,y}} } \hfill \\ {N_{{i,z}} } \hfill \\ \end{array} } \right] \hfill \\ \end{aligned} $$
(A7)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mahesh, V. Nonlinear pyrocoupled deflection of viscoelastic sandwich shell with CNT reinforced magneto-electro-elastic facing subjected to electromagnetic loads in thermal environment. Eur. Phys. J. Plus 136, 796 (2021). https://doi.org/10.1140/epjp/s13360-021-01751-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-021-01751-y

Search

Navigation