Hospital service levels during drug shortages: Stocking and transshipment policies for pharmaceutical inventory

Abstract

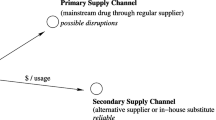
In this study, we consider a health network that faces uncertain supply disruptions in the form of regional, nationwide, or worldwide drug shortages. Each hospital observes stochastic demand and if the drug is unavailable, patients leave and receive care in another network. As these instances of unavailability diminish the brand value, health networks look for inventory sharing mechanisms among hospitals to mitigate the effect of uncertain supply disruptions. In line with this expectation, we propose a proactive inventory sharing approach for critical drugs to investigate the effect of the inventory-related parameters on service levels.

Appendices

Appendix

Proofs of the Theorems and Lemmas

1.1 A Proof of Theorem 1

N hospitals consume ${\mathcal {B}}-\Omega$ items together first. They satisfy the observed demand from their own inventory. Any demand when a hospital reaches an inventory level of zero becomes lost.

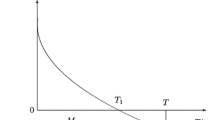
The random variable that denotes the time until the next patient arrival at hospital i is denoted by $T_i$, where $T_i\sim \text{ Exponential }(\lambda _i)$. The random variable $T_d$ denotes the time until the next demand occurrence in the system and $T_d \sim \text{ Exponential }(\sum _{j}\lambda _j)$. W denotes the time until the supplier becomes available and $W\sim \text{ Exponential }(\mu )$.

We define $\Omega$ as the total transshipment thresholds, and the threshold for hospital i is defined as $\gamma _i\Omega$, where $\sum _{i}\gamma _i = 1$.

The total expected lost sales during a shortage can be written using conditioning as follows:

$$\begin{aligned} E[L]&= P(T_d =\min (T_d, W))^{{\mathcal {B}}-\Omega }\sum _{i}P(T_i =\min (T_i, W))^{\gamma _i\Omega }E\nonumber \\&\qquad [\text{ arrivals } \text{ with } \text{ rate } \lambda _i \text{ before } \text{ shortage } \text{ ends}] \nonumber \\&= \left( \frac{\sum _j\lambda _j}{\mu +\sum _{j}\lambda _j}\right) ^{{\mathcal {B}}-\Omega }\sum _{i}\left( \frac{\lambda _i}{\lambda _i+\mu }\right) ^{\gamma _i\Omega }\frac{\lambda _i}{\mu }. \end{aligned}$$

(5)

Service level, denoted by $\alpha _S$, can be calculated as follows:

$$\begin{aligned} \alpha _S&= 1-\frac{E[L]}{E[total\ demand\ during\ shortage]}=1 - \frac{\left( \frac{\sum _{j}\lambda _j}{\mu +\sum _{j}\lambda _j}\right) ^{{\mathcal {B}}-\Omega }\sum _{i}\left( \frac{\lambda _i}{\lambda _i+\mu }\right) ^{\gamma _i\Omega }\frac{\lambda _i}{\mu }}{\frac{\sum _j\lambda _j}{\mu }} \end{aligned}$$

(6)

$$\begin{aligned}&= 1 - \left( \frac{\sum _{j}\lambda _j}{\mu +\sum _{j}\lambda _j}\right) ^{{\mathcal {B}}-\Omega }\sum _{i}\left( \frac{\lambda _i}{\lambda _i+\mu }\right) ^{\gamma _i\Omega }\frac{\lambda _i}{\sum _j\lambda _j}. \end{aligned}$$

(7)

1.2 B Proof of Theorem 2

We can remove the $\sum _i \gamma _i=1$ constraint by substituting the N-th hospital’s threshold with $\gamma _N = 1 - \sum _{j=1}^{N-1}\gamma _i$. Keeping in mind $0\le \gamma _i\le 1$ for all i, the Type I service level can be written as

$$\begin{aligned} \alpha _S&= 1 - \left( \frac{\sum _{j}\lambda _j}{\mu +\sum _{j}\lambda _j}\right) ^{{\mathcal {B}}-\Omega }\left( \sum _{i=0}^{N-1}\left( \frac{\lambda _i}{\lambda _i+\mu }\right) ^{\gamma _i\Omega }\frac{\lambda _i}{\sum _j\lambda _j}\right) \nonumber \\&\quad + \left( \frac{\lambda _N}{\lambda _N+\mu }\right) ^{(1 - \sum _{j=1}^{N-1}\gamma _i)\Omega }\frac{\lambda _N}{\sum _j\lambda _j}. \end{aligned}$$

(8)

To find the globally optimal $\gamma _i$ values, we find the Jacobian, where the i-th entry is

$$\begin{aligned} \frac{\partial \alpha _S}{\partial \gamma _i} =&- \left( \frac{\sum _{j}\lambda _j}{\mu +\sum _{j}\lambda _j}\right) ^{{\mathcal {B}}-\Omega }\bigg [\Omega \ln \left( \frac{\lambda _i}{\lambda _i+\mu }\right) \frac{\lambda _i}{\sum _j\lambda _j}\left( \frac{\lambda _i}{\lambda _i+\mu }\right) ^{\gamma _i\Omega } \nonumber \\&-\Omega \ln \left( \frac{\lambda _N}{\lambda _N+\mu }\right) \frac{\lambda _N}{\sum _j\lambda _j}\left( \frac{\lambda _N}{\lambda _N+\mu }\right) ^{(1 - \sum _{j=1}^{N-1}\gamma _j)\Omega }\bigg ]. \end{aligned}$$

(9)

Equating the Jacobian to zero yields the following condition for critical points:

$$\begin{aligned} \lambda _i\ln \left( \frac{\lambda _i}{\lambda _i+\mu }\right) \left( \frac{\lambda _i}{\lambda _i+\mu }\right) ^{\gamma _i\Omega }&= \lambda _N \ln \left( \frac{\lambda _N}{\lambda _N+\mu }\right) \left( \frac{\lambda _N}{\lambda _N+\mu }\right) ^{(1 - \sum _{j=1}^{N-1}\gamma _j)\Omega } \forall i. \end{aligned}$$

(10)

Therefore, for hospitals k and m, at the critical point, we have

$$\begin{aligned} \lambda _k \ln \left( \frac{\lambda _k}{\lambda _k+\mu }\right) \left( \frac{\lambda _k}{\lambda _k+\mu }\right) ^{\gamma _k\Omega }&= \lambda _m \ln \left( \frac{\lambda _m}{\lambda _m+\mu }\right) \left( \frac{\lambda _m}{\lambda _m+\mu }\right) ^{\gamma _m\Omega }, \end{aligned}$$

(11)

which leads to

$$\begin{aligned} \gamma _m \ln \left( \frac{\lambda _m}{\mu +\lambda _m}\right) -\gamma _k\ln \left( \frac{\lambda _k}{\mu +\lambda _k}\right) = \frac{1}{\Omega } \ln \left( \frac{\lambda _k\ln \left( \frac{\lambda _k}{\mu +\lambda _k}\right) }{\lambda _m\ln \left( \frac{\lambda _m}{\mu +\lambda _m}\right) }\right) . \end{aligned}$$

(12)

Next, we use the Hessian to prove the concavity of the Type I service level function, where

$$\begin{aligned}&\frac{\partial ^2\alpha _S}{\partial \gamma _i^{2}} = - \left( \frac{\sum _{j}\lambda _j}{\mu +\sum _{j}\lambda _j}\right) ^ {{\mathcal {B}}-\Omega }\nonumber \\&\quad \frac{\Omega ^2\left( \lambda _i\ln ^2\left( \frac{\lambda _i}{\lambda _i+\mu }\right) \left( \frac{\lambda _i}{\lambda _i+\mu }\right) ^{\gamma _i\Omega } + \lambda _N\ln ^2\left( \frac{\lambda _N}{\lambda _N+\mu }\right) \left( \frac{\lambda _N}{\lambda _N+\mu }\right) ^{(1 - \sum _{j=1}^{N-1}\gamma _j)\Omega } \right) }{\sum _j\lambda _j} \end{aligned}$$

(13)

and

$$\begin{aligned} \frac{\partial ^2\alpha _S}{\partial \gamma _i\partial \gamma _l}&= - \left( \frac{\sum _{j}\lambda _j}{\mu +\sum _{j}\lambda _j}\right) ^{{\mathcal {B}}-\Omega }\frac{\Omega ^2\left( \lambda _N\ln ^2\left( \frac{\lambda _N}{\lambda _N+\mu }\right) \left( \frac{\lambda _N}{\lambda _N+\mu }\right) ^{(1 - \sum _{j=1}^{N-1}\gamma _j)\Omega } \right) }{\sum _j\lambda _j}. \end{aligned}$$

(14)

At the critical point, all off-diagonal entries of the Hessian are negative constants, whereas each diagonal entry depends on the individual demand rates; however, they are definitely less than the off-diagonal constants. It can easily be shown that all the eigenvalues of this matrix are negative, guaranteeing that the Hessian is negative definite and $\alpha _S$ is concave. Thus, the critical point is the global maximizer for $\alpha _S$.

1.3 C Proof of Lemma 1

For a system with a demand rate of $\lambda$, a recovery rate of $\mu$, and a total inventory of $\phi$, the expected demand satisfied can be written as

$$\begin{aligned} E[\text{ demand } \text{ satisfied}]&= \sum _{j=0}^{\phi -1} j\times P(\text{ Demand }= j) + \phi \times P(\text{ Demand }\ge \phi ) \nonumber \\&= \sum _{j=0}^{\phi -1}j\left( \frac{\lambda }{\mu +\lambda }\right) ^j\frac{\mu }{\mu +\lambda }+\phi \left( 1-\sum _{j=0}^{\phi -1}\left( \frac{\lambda }{\mu +\lambda }\right) ^j\frac{\mu }{\mu +\lambda }\right) \nonumber \\&=\frac{\mu \lambda }{(\mu +\lambda )^2}\sum _{j=0}^{\phi -1}j\left( \frac{\lambda }{\mu +\lambda }\right) ^{j-1}+\phi -\phi \left( 1-\left( \frac{\lambda }{\mu +\lambda }\right) ^\phi \right) . \end{aligned}$$

(15)

Knowing that

$$\begin{aligned} \sum _{j=0}^{\phi -1}jp^{j-1} =\sum _{j=0}^{\phi -1}\frac{\partial p^j}{\partial p} = \frac{\partial }{\partial p}\sum _{j=0}^{\phi -1} p^j = \frac{\partial }{\partial p}\frac{1-p^\phi }{1-p}=\frac{-\phi p^{\phi -1}(1-p)+1-p^\phi }{(1-p)^2}, \end{aligned}$$

(16)

the expected demand satisfied can be written as follows:

$$\begin{aligned} E[\text{ demand } \text{ satisfied}]&= \frac{\mu \lambda }{(\mu +\lambda )^2}\frac{-\phi \left( \frac{\lambda }{\mu +\lambda }\right) ^{\phi -1}\left( \frac{\mu }{\mu +\lambda }\right) +1-\left( \frac{\lambda }{\mu +\lambda }\right) ^\phi }{\left( \frac{\mu }{\mu +\lambda }\right) ^2}\nonumber \\&\quad +\phi -\phi \left( 1-\left( \frac{\lambda }{\mu +\lambda }\right) ^\phi \right) \nonumber \\&=\frac{\lambda }{\mu }\left( 1-\left( \frac{\lambda }{\mu +\lambda }\right) ^\phi \right) . \end{aligned}$$

(17)

1.4 D Proof of Theorem 3

Let us introduce the following notation for this part. First, the random variables:

D: demand during shortages,

H: demand during sharing,

P: demand satisfied from hospitals’ pooled inventories, $\phi _i$, directly,

T: demand satisfied by transshipment,

S: demand satisfied from each hospital’s safety stock, $\gamma _i\Omega$,

L: unsatisfied demand.

For a system of hospitals, demand during shortages can be calculated as

$$\begin{aligned} D&=P+T+S+L \\ E[D]&= E[P] + E[T] + E[S] + E[L]. \end{aligned}$$

Alternatively, we can use demand during sharing

$$\begin{aligned} E[H] = E[P] + E[T]. \end{aligned}$$

From Lemma 1, since we know that

$$\begin{aligned} E[H] = \frac{\sum _i\lambda _i}{\mu }\left( 1-\left( \frac{\sum _i\lambda _i}{\mu +\sum _i\lambda _i}\right) ^{\sum _i \phi _i}\right) \end{aligned}$$

and

$$\begin{aligned} E[P] = \sum _i \frac{\lambda _i}{\mu }\left( 1-\left( \frac{\lambda _i}{\mu +\lambda _i}\right) ^{\phi _i}\right) , \end{aligned}$$

the expected demand satisfied by transshipment can be calculated as follows:

$$\begin{aligned} E[T] = \sum _i \frac{\lambda _i}{\mu }\left( \left( \frac{\lambda _i}{\mu +\lambda _i}\right) ^{\phi _i}-\left( \frac{\sum _j\lambda _j}{\mu +\sum _j\lambda _j}\right) ^{\sum _j \phi _j}\right) . \end{aligned}$$

(18)

1.5 E Proof of Theorem 5

The Type II service level can be maximized when the expected number of transshipments (E[T]) is minimized because demand during shortages is not affected by the allocation of the pooled inventory. Thus, we can find the optimal allocation of the inventory pool to minimize the number of transshipments within the system by taking the derivative of Equation (18) with respect to $\phi _i$:

$$\begin{aligned} \frac{\partial E[T]}{\partial \phi _i} = \frac{\lambda _i}{\mu } \ln \left( \frac{\lambda _i}{\mu +\lambda _i}\right) \left( \frac{\lambda _i}{\mu +\lambda _i}\right) ^{\phi _i}-\frac{\sum _j\lambda _j}{\mu }\ln \left( \frac{\sum _j\lambda _j}{\mu +\sum _j\lambda _j}\right) \left( \frac{\sum _j\lambda _j}{\mu +\sum _j\lambda _j}\right) ^{\sum _j\phi _j}. \end{aligned}$$

(19)

Using (19), the obtained Jacobian can be set to zero, which yields

$$\begin{aligned} \lambda _i \ln \left( \frac{\lambda _i}{\mu +\lambda _i}\right) \left( \frac{\lambda _i}{\mu +\lambda _i}\right) ^{\phi _i}= \sum _j\lambda _j \ln \left( \frac{\sum _j\lambda _j}{\mu +\sum _j\lambda _j}\right) \left( \frac{\sum _j\lambda _j}{\mu +\sum _j\lambda _j}\right) ^{\sum _j\phi _j}, \end{aligned}$$

(20)

where $\sum _j \phi _j = \Phi$. Therefore, for hospitals k and m, the critical points for the allocated inventory pool to minimize the expected number of transshipments must hold the equality below:

$$\begin{aligned} \lambda _k \ln \left( \frac{\lambda _k}{\mu +\lambda _k}\right) \left( \frac{\lambda _k}{\mu +\lambda _k}\right) ^{\phi _k}&= \lambda _m \ln \left( \frac{\lambda _m}{\mu +\lambda _m}\right) \left( \frac{\lambda _m}{\mu +\lambda _m}\right) ^{\phi _m} \nonumber \\ \phi _m\ln \left( \frac{\lambda _m}{\mu +\lambda _m}\right) -\phi _k\ln \left( \frac{\lambda _k}{\mu +\lambda _k}\right)&=\ln \left( \frac{\lambda _k\ln \left( \frac{\lambda _k}{\mu +\lambda _k}\right) }{\lambda _m\ln \left( \frac{\lambda _m}{\mu +\lambda _m}\right) }\right) . \end{aligned}$$

(21)