Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-18T22:59:13.739Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow rate–pressure drop relation for shear-thinning fluids in narrow channels: approximate solutions and comparison with experiments

Published online by Cambridge University Press:  30 July 2021

Evgeniy Boyko Open the ORCID record for Evgeniy Boyko [Opens in a new window]  and
Howard A. Stone Open the ORCID record for Howard A. Stone [Opens in a new window]
Evgeniy Boyko*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Howard A. Stone*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email addresses for correspondence: eboyko@princeton.edu, hastone@princeton.edu
†Email addresses for correspondence: eboyko@princeton.edu, hastone@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

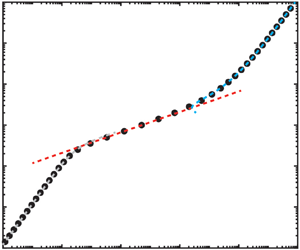
Non-Newtonian fluids are characterized by complex rheological behaviour that affects the hydrodynamic features, such as the flow rate–pressure drop relation. While flow rate–pressure drop measurements of such fluids are common in the literature, a comparison of experimental data with theory is rare, even for shear-thinning fluids at low Reynolds number, presumably due to the lack of analytical expressions for the flow rate–pressure drop relation covering the entire range of pressures and flow rates. Such a comparison, however, is of fundamental importance as it may provide insight into the adequacy of the constitutive model that was used and the values of the rheological parameters. In this work, we present a theoretical approach to calculating the flow rate–pressure drop relation of shear-thinning fluids in long, narrow channels that can be used for comparison with experimental measurements. We utilize the Carreau constitutive model and provide a semi-analytical expression for the flow rate–pressure drop relation. In particular, we derive three asymptotic solutions for small, intermediate and large values of the dimensionless pressures or flow rates, which agree with distinct limits previously known and allow us to approximate analytically the entire flow rate–pressure drop curve. We compare our semi-analytical and asymptotic results with the experimental measurements of Pipe et al. (Rheol. Acta, vol. 47, 2008, pp. 621–642) and find excellent agreement. Our results rationalize the change in the slope of the flow rate–pressure drop data, when reported in log–log coordinates, at high flow rates, which cannot be explained using a simple power-law model.

JFM classification

Non-Newtonian Flows: Non-Newtonian Flows Non-Newtonian Flows: Rheology Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , R5
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anand, V., David, J. Jr. & Christov, I.C. 2019 Non-Newtonian fluid–structure interactions: static response of a microchannel due to internal flow of a power-law fluid. J. Non-Newtonian Fluid Mech. 264, 62–72.CrossRefGoogle Scholar
Bird, R.B., Armstrong, R.C. & Hassager, O. 1987 Dynamics of Polymeric Liquids, Volume 1: Fluid Mechanics, 2nd edn. John Wiley and Sons.Google Scholar
Carreau, P.J. 1972 Rheological equations from molecular network theories. Trans. Soc. Rheol. 16 (1), 99–127.CrossRefGoogle Scholar
Christov, I.C., Cognet, V., Shidhore, T.C. & Stone, H.A. 2018 Flow rate–pressure drop relation for deformable shallow microfluidic channels. J. Fluid Mech. 841, 267–286.CrossRefGoogle Scholar
Datt, C., Zhu, L., Elfring, G.J. & Pak, O.S. 2015 Squirming through shear-thinning fluids. J. Fluid Mech. 784, R1.CrossRefGoogle Scholar
Ewoldt, R.H., Johnston, M.T. & Caretta, L.M. 2015 Experimental challenges of shear rheology: how to avoid bad data. In Complex Fluids in Biological Systems (ed. S.E. Spagnolie), pp. 207–241. Springer.CrossRefGoogle Scholar
Gupta, S., Wang, W.S. & Vanapalli, S.A. 2016 Microfluidic viscometers for shear rheology of complex fluids and biofluids. Biomicrofluidics 10 (4), 043402.CrossRefGoogle ScholarPubMed
Happel, J.R. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics, 2nd edn. Martinus Nijhoff Publishers.Google Scholar
Kang, K., Lee, L.J. & Koelling, K.W. 2005 High shear microfluidics and its application in rheological measurement. Exp. Fluids 38 (2), 222–232.CrossRefGoogle Scholar
Lodge, A.S. & de Vargas, L. 1983 Positive hole pressures and negative exit pressures generated by molten polyethylene flowing through a slit die. Rheol. Acta 22 (2), 151–170.CrossRefGoogle Scholar
Macosko, C.W. 1994 Rheology: Principles, Measurements and Applications. Wiley-VCH.Google Scholar
Metzner, A.B. 1957 Non-Newtonian fluid flow: relationships between recent pressure-drop correlations. Ind. Engng Chem. 49 (9), 1429–1432.CrossRefGoogle Scholar
Metzner, A.B. & Reed, J.C. 1955 Flow of non-Newtonian fluids—correlation of the laminar, transition, and turbulent-flow regions. AIChE J. 1 (4), 434–440.CrossRefGoogle Scholar
Middleman, S. 1965 Flow of power law fluids in rectangular ducts. Trans. Soc. Rheol. 9 (1), 83–93.CrossRefGoogle Scholar
Mooney, M. 1931 Explicit formulas for slip and fluidity. J. Rheol. 2 (2), 210–222.CrossRefGoogle Scholar
Morozov, A. & Spagnolie, S.E. 2015 Introduction to complex fluids. In Complex Fluids in Biological Systems (ed. S.E. Spagnolie), pp. 3–52. Springer.CrossRefGoogle Scholar
Moukhtari, F.E. & Lecampion, B. 2018 A semi-infinite hydraulic fracture driven by a shear-thinning fluid. J. Fluid Mech. 838, 573–605.CrossRefGoogle Scholar
Picchi, D., Ullmann, A., Brauner, N. & Poesio, P. 2021 Motion of a confined bubble in a shear-thinning liquid. J. Fluid Mech. 918, A7.CrossRefGoogle Scholar
Pinho, F.T., Oliveira, P.J. & Miranda, J.P. 2003 Pressure losses in the laminar flow of shear-thinning power-law fluids across a sudden axisymmetric expansion. Intl J. Heat Fluid Flow 24 (5), 747–761.CrossRefGoogle Scholar
Pipe, C.J., Majmudar, T.S. & McKinley, G.H. 2008 High shear rate viscometry. Rheol. Acta 47 (5-6), 621–642.CrossRefGoogle Scholar
Pipe, C.J. & McKinley, G.H. 2009 Microfluidic rheometry. Mech. Res. Commun. 36 (1), 110–120.CrossRefGoogle Scholar
Rabinowitsch, B. 1929 Über die viskosität und elastizität von solen. Z. Phys. Chem. 145 (1), 1–26.CrossRefGoogle Scholar
Shahsavari, S. & McKinley, G.H. 2015 Mobility of power-law and Carreau fluids through fibrous media. Phys. Rev. E 92 (6), 063012.CrossRefGoogle ScholarPubMed
Sochi, T. 2015 Analytical solutions for the flow of Carreau and Cross fluids in circular pipes and thin slits. Rheol. Acta 54 (8), 745–756.CrossRefGoogle Scholar
Stone, H.A. 2007 Introduction to fluid dynamics for microfluidic flows. In CMOS Biotechnology (ed. H. Lee, R.M. Westervelt & D. Ham), pp. 5–30. Springer.CrossRefGoogle Scholar
Sutera, S.P. & Skalak, R. 1993 The history of Poiseuille's law. Annu. Rev. Fluid Mech. 25 (1), 1–19.CrossRefGoogle Scholar
Wrobel, M. 2020 An efficient algorithm of solution for the flow of generalized Newtonian fluid in channels of simple geometries. Rheol. Acta 59 (9), 651–663.CrossRefGoogle Scholar